PRACTICAL GEOMETRY for Class 7 MATHS
INTRODUCTION
Hello Bachcho, aap apni real life mai bht sari shapes ko dekhte ho jaise square, rectangle, circle, etc. Aur aapko bahot sari shapes draw bhi karni aati hogi jaisa ki aap ihne apni pichli classes mai bhi padh chuke ho to aap inse familiar honge. Jaisa ki aapko line segment of given length, a line perpendicular to a given line segment, an angle, an angle bisector ye sab already draw karna aata hai. Abh aap log sikhoge ki how to draw parallel lines and some types of triangles. Iss chapter mai aapko bada maza aayega kyuki iss chapter mai construction ka work bahot hain.
Practical Geometry
Practical geometry is to constructing geometrical figuers. ex-square ,triangle etc.
Explanation
To jaisa aap logo ko introduction se pta chal gaya hoga ki hum isme construction karne wale hai to kuch essential tools aapki geometry mai hone chhahiye jaise ki ruler, compass, a sharp pencil, protractor, etc. Toh chaliye kuch interesting examples ke sath iss chapter ko padhte hai.
CONSTRUCTION OF A LINE PARALLEL TO A GIVEN LINE, THROUGH A POINT NOT ON THE LINE
Toh isko samjhne ke liye hum ek activity karte hai.
(i) Sabse pehle ek sheet lijiye aur use fold kar lijiye. This
fold represents a line l.
(ii) Unfold the paper. Mark a point A on the
paper outside l.
(iii) Fold the paper perpendicular to the line such
that this perpendicular passes through A.
Name the perpendicular AN.
(iv) Make a fold perpendicular to this
perpendicular through the point A. Name
the new perpendicular line as m. Now, l||m.
(v) Abh sheet ko pura unfold kijiye aap dekh sakte hai ki line l parallel hai line m ke. 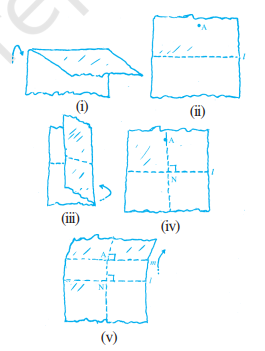
EXAMPLE 1
EXAMPLE 2
What will be the other angles of a right-angled isosceles triangle?
Solution:
In right angled isosceles triangle ABC,∠B=90°
∠A+∠C=180°–90°=90°
But ∠A=∠B
∠A=∠C=902=45°
Hence the required angles are ∠A=∠C=45° 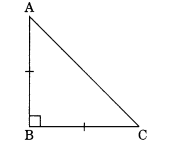
CONSTRUCTION OF TRIANGLES
The construction of a triangle is possible if,
* All the three sides of a triangle are mentioned
* Two sides of a triangle one included angle is given.
* Two angles of a triangle and one included side is given.
* The measurement of the hypotenuse side and one other side is given.
EXAMPLE 3
State whether the triangle is possible to construct if
(a)InΔABC,m∠A=80°,m∠B=60°,AB=5.5cm
(b)InΔPQR,PQ=5cm,QR=3cm,PR=8.8cm
Solution:
(a)m∠A=80°,m∠B=60°m∠A+m∠B=80°+60°=140°<180°
So, ΔABC can be possible to construct.
(b)PQ=5cm,QR=3cm,PR=8.8cm
PQ+QR=5cm+3cm=8cm<8.8cmorPQ+QR<PR
So, the ΔPQR can not be constructed.
EXAMPLE 4
Draw an equilateral triangle whose each side is 4.5cm.
Solution:
Steps of construction:
(i) Draw AB=4.5cm
.
(ii) Draw two arcs with centres A and B and same radius of 4.5cm to meet each other at C.
(iii) Join CA and CB.
(iv) ΔCAB is the required triangle. 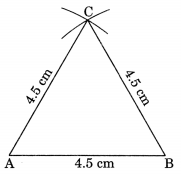
CONSTRUCTING A TRIANGLE WHEN THE LENGTHS OF ITS THREE SIDES ARE KNOWN (SSS CRITERION)
Hum SSS mai triangles construct karenge jisme hume uski all (teeno) sides pta hongi.
eg :- Construct a triangle ABC, given that AB=5cm,BC=6cm and AC=7cm.
Step 1 : First, we draw a rough sketch with given measure. 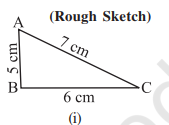
Step 2 : Draw a line segment BC of length 6cm 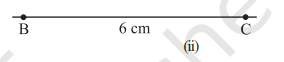
Step 3 : From B, point A is at a distance of 5 cm. So, with B as centre, draw an arc of
radius 5cm 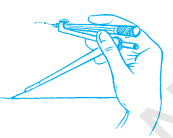
Step 4 : From C, point A is at a distance of 7 cm. So, with C as centre, draw an arc of
radius 7 cm. 
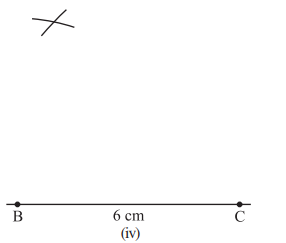
Step 5 : A has to be on both the arcs drawn. So, it is the point of intersection of arcs.
Mark the point of intersection of arcs as A. Join AB and AC. ΔABC is now ready. 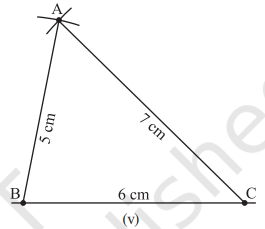
EXAMPLE 5
Draw a ΔPQR, in which QR=3.5cm,m∠Q=40°,m∠R=60°
Solution:
Steps of construction:
(i) Draw QR=3.5cm.
(ii) Draw ∠Q=40°,∠R=60° which meet each other at P.
(iii) ΔPQR is the required triangle. 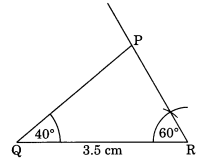
CONSTRUCTING A TRIANGLE WHEN THE LENGTHS OF TWO SIDES AND THE MEASURE OF THE ANGLE BETWEEN THEM ARE KNOWN. (SAS CRITERION)
Isme hume 2 sides aur ek angle given hota hai . Pehle hum ek rough sketch draw karenge and then draw one of the given line segments. Abh hum ek example ke through isko samjhenge.
Construct a triangle PQR, given
that PQ=3cm,QR=5.5cm
and ∠PQR=60°.
Step 1 : First, we draw a rough sketch with
given measures. 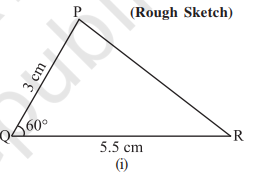
Step 2 : Draw a line segment QR of length
5.5 cm. 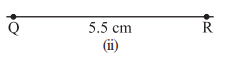
Step 3 : At Q, draw QX making 60° with QR. 
Step 4 : (To fix P, the distance QP has been
given).
With Q as centre, draw an arc of radius
3 cm. It cuts QX at the point P.
Step 5 : Join PR. ΔPQR is now
obtained. 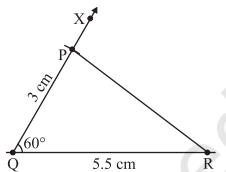
EXAMPLE 6
State whether the given pair of triangles are congruent.
Solution:
Here, AB=PQ=3.5cm
AC=PR=5.2cm
∠BAC=∠QPR=70°
ΔABC=ΔPQR [By SAS rule] 
CONSTRUCTING A TRIANGLE WHEN THE MEASURES OF TWO OF ITS ANGLES AND THE LENGTH OF THE SIDE INCLUDED BETWEEN THEM IS GIVEN. (ASA CRITERION)
In the two triangles AOC and BOD, 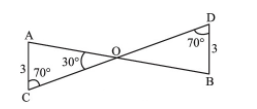
∠C=∠D (each 70°)
Also, ∠AOC=∠BOD=30° (vertically opposite angles)
So, ∠A of ΔAOC=180°–(70°+30°)=80° (using angle sum property of a triangle)
Similarly, ∠B of ΔBOD=180°–(70°+30°)=80°
Thus, we have ∠A=∠B,AC=BD and ∠C=∠D
Now, side AC is between ∠A and ∠C and side BD is between ∠B and ∠D.
So, by ASA congruence rule, ΔAOC≅ΔBOD.
EXAMPLE 7
Draw a ΔABC in which BC=5cm,AB=4cm and m∠B=50°
Solution:
Steps of construction:
(i) Draw BC=5cm.
(ii) Draw ∠B=50° and cut AB=4cm.
(iii) Join AC.
(iv) ΔABC is the required triangle. 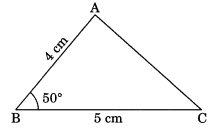
EXAMPLE 8
What is the measure of an exterior angle of an equilateral triangle?
Solution:
We know that the measure of each interior angle =60°
Exterior angle =180°–60°=120° 
CONSTRUCTING A RIGHT-ANGLED TRIANGLE WHEN THE LENGTH OF ONE LEG AND ITS HYPOTENUSE ARE GIVEN (RHS CRITERION)
The triangles are said to be congruent, then the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle.
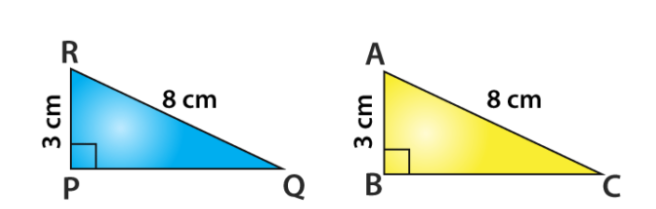
Solution :
Given : ∠B=∠P=90∘),
Hypotenuse side AC=RQ=8cm and
side AB=RP=3cm
So, by RHS Congruence rule, the symbolic form of the congruent triangle is written as
ΔABC≅ΔRPQ
EXAMPLE 9
In ΔABC,∠A=∠B=50° . Name the pair of sides which are equal. 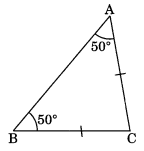
Solution:
∠A=∠B=50°
AC=BC [∵ Sides opposite to equal angles are equal]
Hence, the required sides are AC and BC.
SUMMARY
In this Chapter, we looked into the methods of some ruler and compasses constructions.
1. Given a line l and a point not on it, we used the idea of ‘equal alternate angles’ in a transversal diagram to draw a line parallel to l.
We could also have used the idea of ‘equal corresponding angles’ to do the
construction.
2. We studied the method of drawing a triangle, using indirectly the concept of congruence
of triangles.
The following cases were discussed:
(i)SSS: Given the three side lengths of a triangle.
(ii)SAS: Given the lengths of any two sides and the measure of the angle between these sides.
(iii)ASA : Given the measures of two angles and the length of side.
(iv)RHS : Given the length of hypotenuse of a right-angled triangle and
the length of one of its legs.
included between them.
