LINES AND ANGLES for Class 7 MATHS
INTRODUCTION
Baccho aapne apni surroundings m bohot si shapes and lines notice ki hongi. Humare environment m bohot si shapes hoti hai and most shapes are formed using line segments. Aap sabne ye bhi pdha hai ki jab do line segments intersect krti hai ya koi corner form krti hai, then we get an angle. Iss chapter m hum lines and angles k baare m aur jaanenge but before starting with it, let's revise our previous concepts.
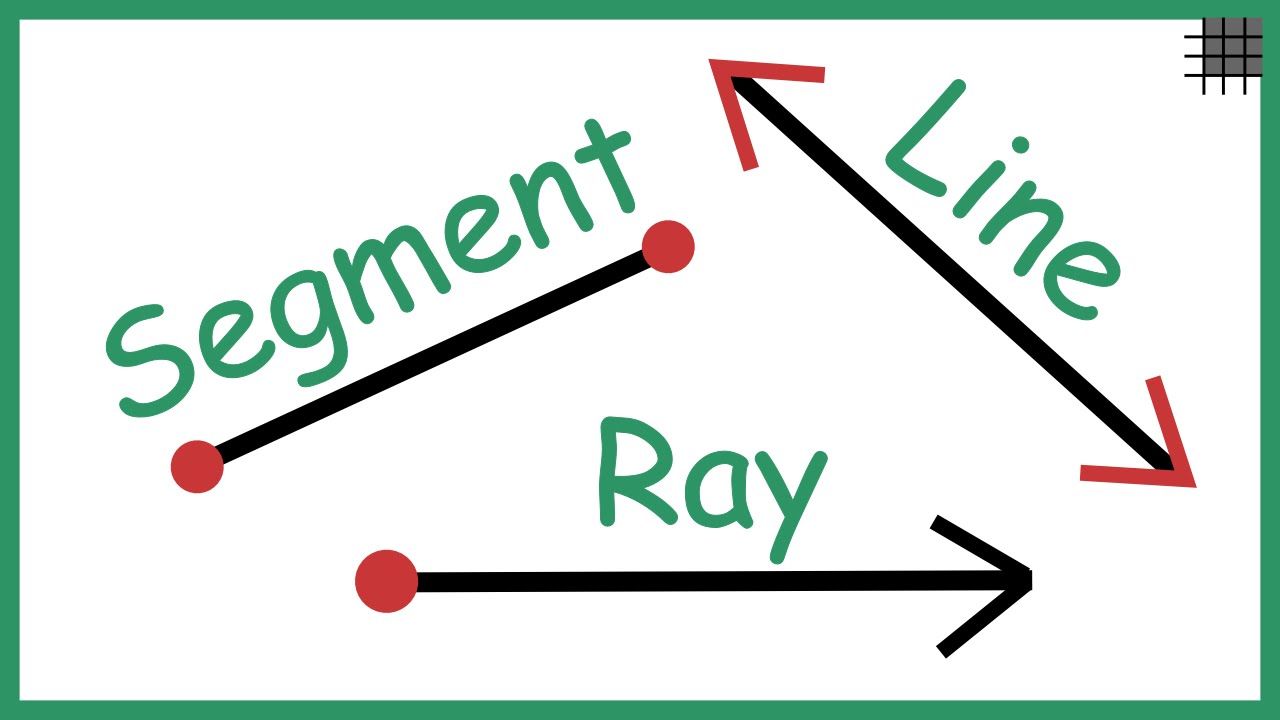
Baccho line segment ek line ka part hoti hai jiski ek definite measurement hoti hai. It has two end points. If we extend those two end points indefinitely in either direction, we would get a line. Isse hume ye pta chlta hai ki a line has no end points.
Agar hum ek line segment k sirf ek end point ko indefinitely extend krenge taaki uska sirf ek end point ho, then we'll get a ray
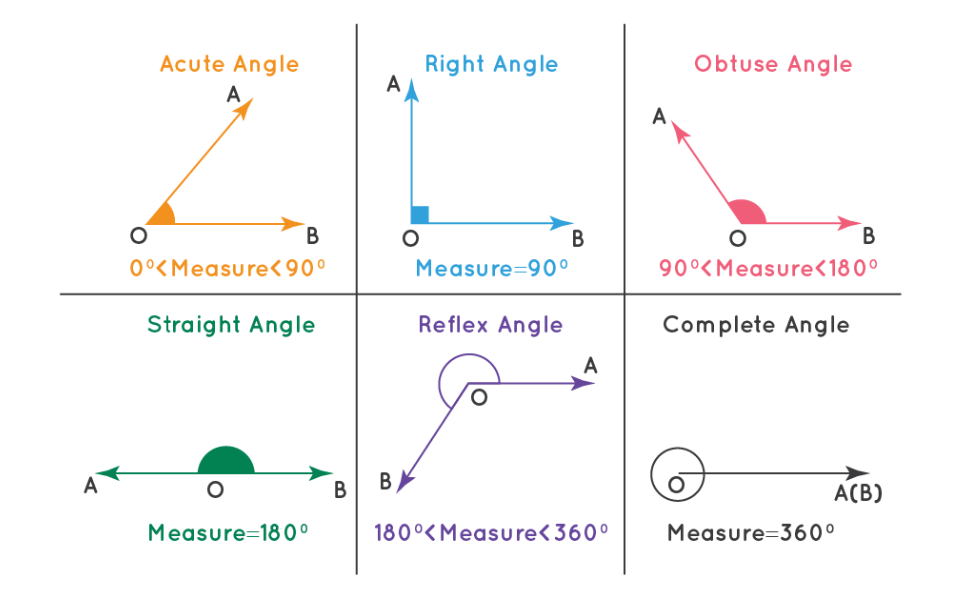
Baccho jab lines, line segments ya rays meet/intersect krti hai to ek corner form hota hai. Whenever a corner is formed we get an angle. An angle always measures between 0∘−360∘. These are the different classifications of angles:
Look at the following image and point out the line segments and angles.

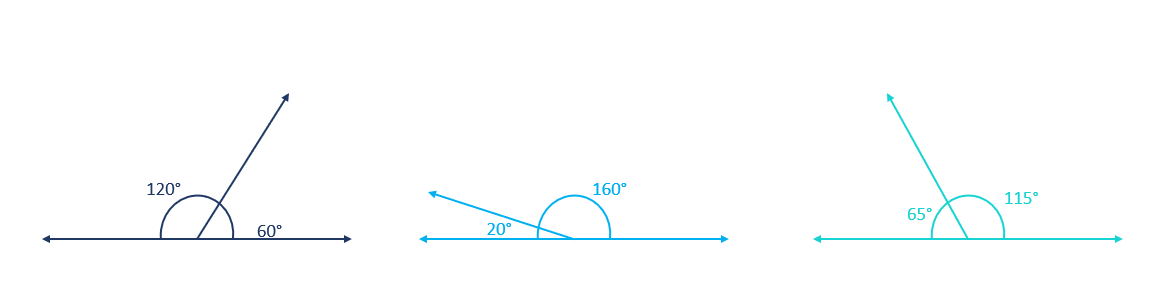
COMPLEMENTARY ANGLES AND SUPPLEMENTARY ANGLES
Complementary Angles: When the sum of the measures of two angles is 90∘, the angles are called complementary
angles. The following pair of angles are examples of complementary angles:
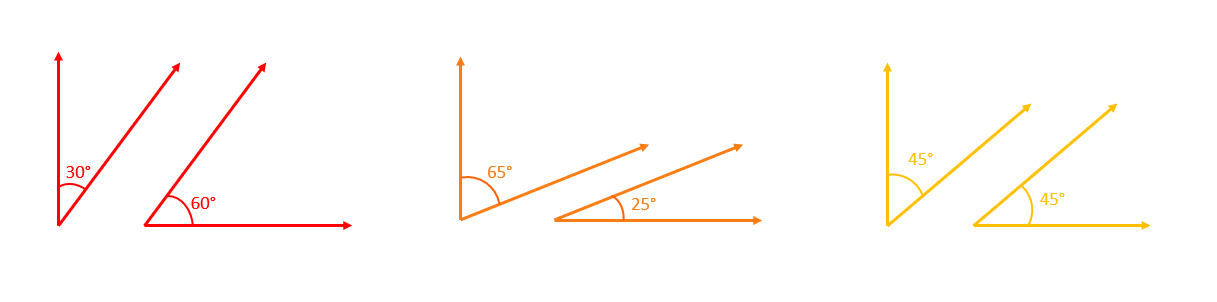
Whenever two angles are complementary, each angle is said to be the complement
of the other angle.
Supplementary Angles: If the sum of two angles is 180∘ then they are said to be supplementary angles. The following pair of angles are examples of complementary angles:
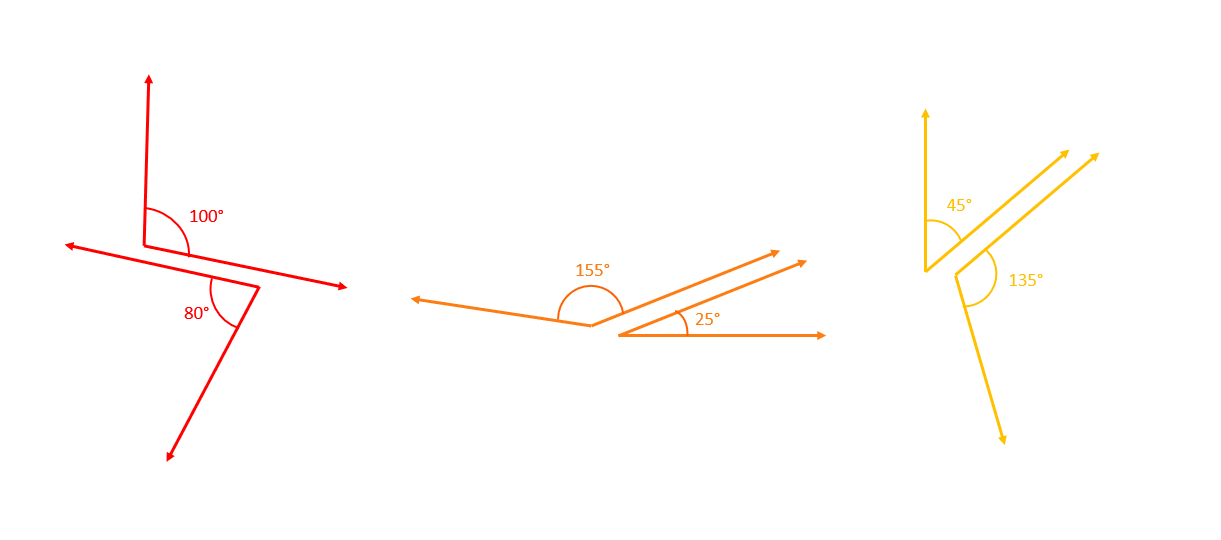
If two angles are supplementary then they are the supplement to each other.
Example 1
Find the angle which is equal to its supplement.
Let the angle is x. Then, the supplement of this angle will be 180−x
We are given,
x=180−x⇒2x=180⇒x=90∘
So, 90∘ is the angle that is equal to its supplement.
ADJACENT ANGLES
Baccho adjacent ka mtlb hota hai "next to each other". Adjacent angles ka mtlb hota hai jab do angles ek common vertex aur ek common arm share kre. This implies that adjacent angles have :
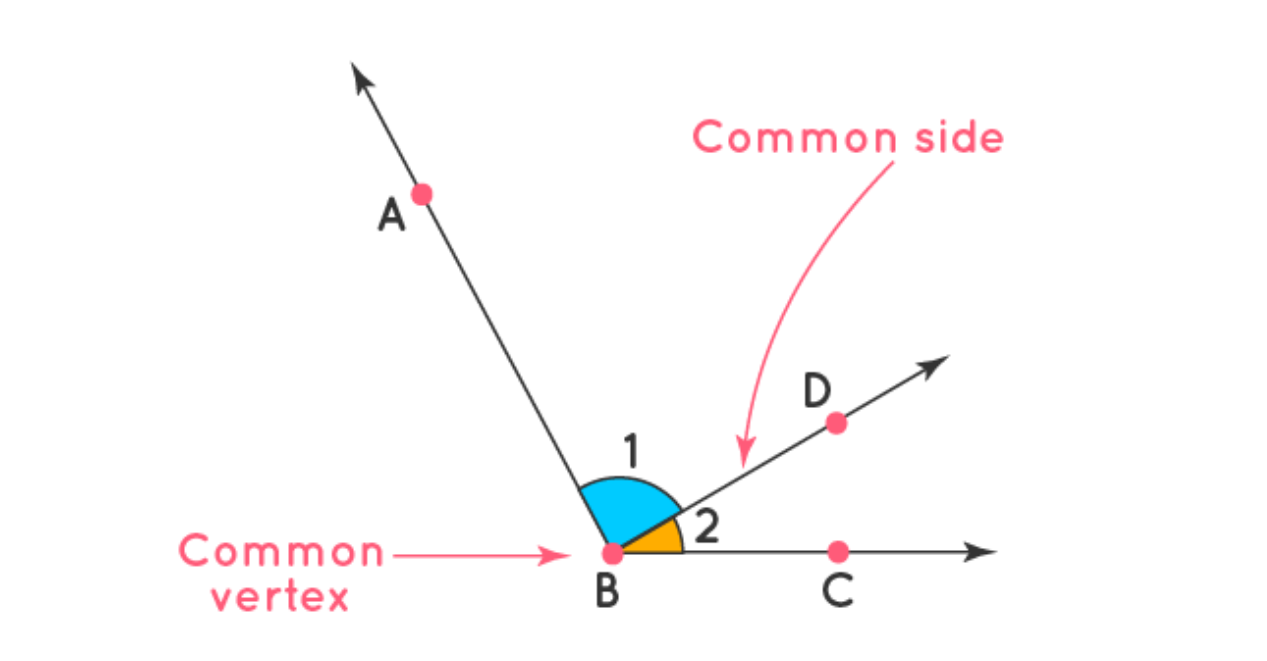
LINEAR PAIR
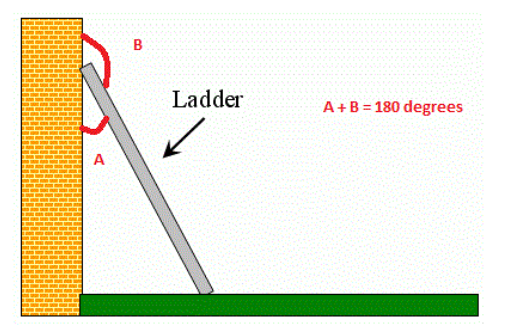
We just learnt about the concept of supplementary angles and adjacent angles. When we combine these two topics we get linear pairs. A linear pair is a pair of adjacent angles which add to 180∘ and the non-common arms form a straight line. Hence, the non-common arms are opposite rays in a linear pair.
Examples of linear pair are:
We can find linear pairs forming in our surroundings. Look at the following examples and observe the linear pairs being formed:
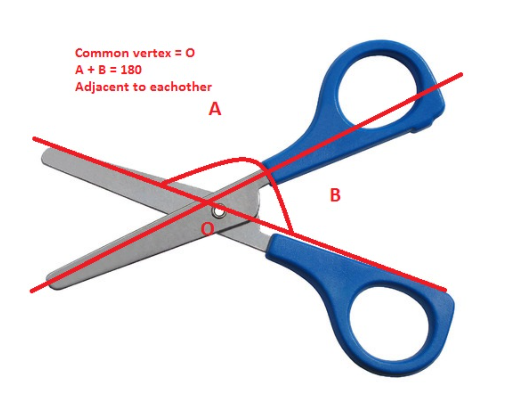
Example 2
If the angles of a linear pair are equal, then each angle is _____
Let the required angle be x
x+x=180∘
⇒2x=180∘
⇒x=180∘2
⇒x=90∘
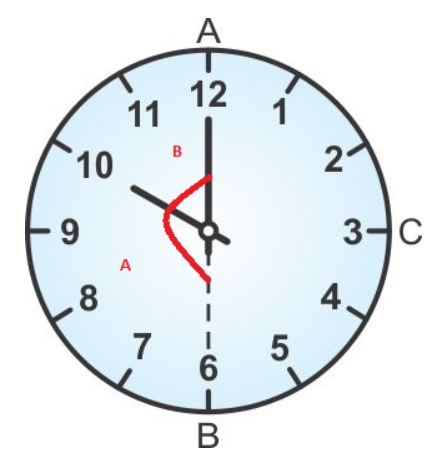
VERTICALLY OPPOSITE ANGLES
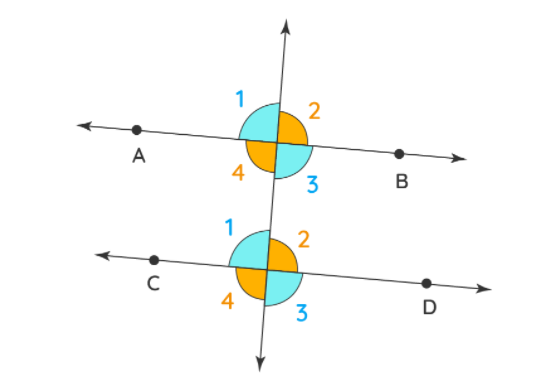
Baccho let's do a quick exercise to understand the concept of vertically opposite angles. Make a cross with your fingers like the image given below and observe the four angles that are formed at the point of intersection.

The opposite angles which are formed in such intersections are equal in measurement and are known as vertically opposite angles. There are two pairs of nonadjacent angles.
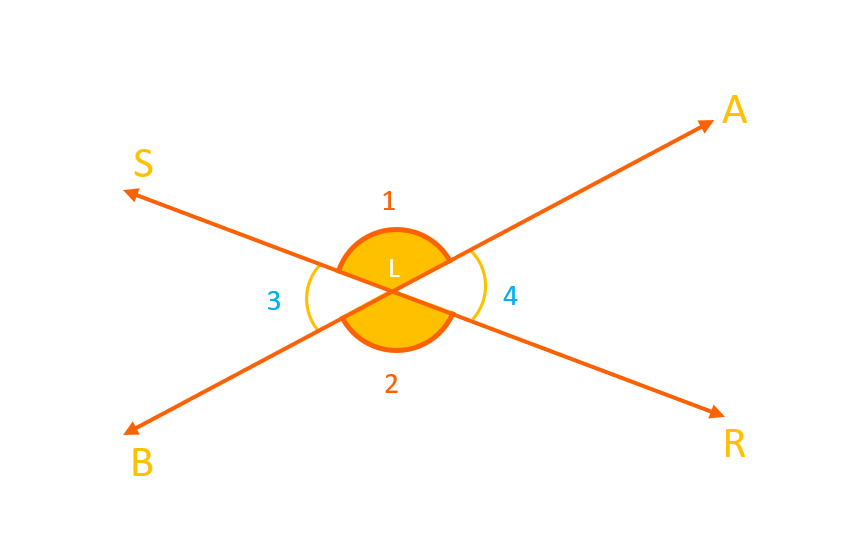
In the above figure, ∠SLA=∠BLR and ∠SLB=∠ALR since they're vertically opposite angles.
Vertically Opposite Angles theorem
When two lines intersect, the pair of vertically angles formed are always equal in measure
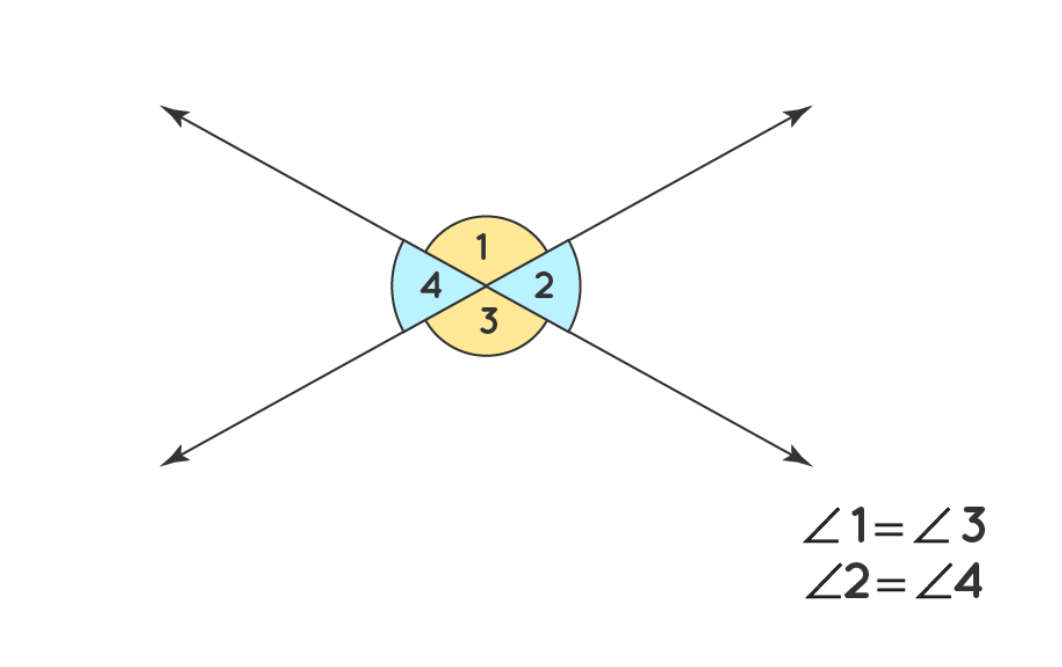
In the above figure,
∠1+∠2=180∘ (Since they are a linear pair of angles) --------- (1)
∠1+∠4=180∘ (Since they are a linear pair of angles) --------- (2)
From equations (1) and (2), ∠1+∠2=180∘=∠1+∠4.
⇒ a=b and b=c then a=c.
Therefore, we can rewrite the statement as ∠1+∠2=∠1+∠4. --------(3)
By eliminating ∠1 on both sides of the equation (3), we get ∠2=∠4.
Similarly. we can use the same set of statements to prove that ∠1=∠3. Therefore, we conclude that vertically opposite angles are always equal.
Example 3
In the given figure identify:
(i) Five pairs of adjacent angles.
(ii) Three linear pairs.
(iii) Two pairs of vertically opposite angles
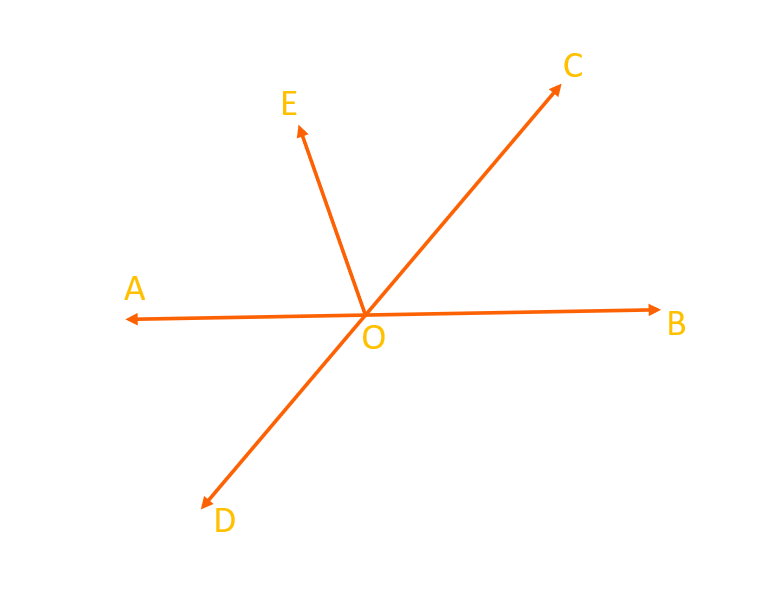
(i) Five pairs of adjacent angles are (∠AOE,∠EOC),(∠EOC,∠COB),(∠AOC,∠COB),(∠COB,∠BOD),(∠EOB,∠BOD)
(ii) Linear pairs are (∠AOE,∠EOB),(∠AOC,∠COB),(∠COB,∠BOD)
(iii) Vertically opposite angles are: (∠COB,∠AOD),and(∠AOC,∠BOD)
INTERSECTING LINES
If two lines touch each other in such a way that there is a point in common then these lines are called intersecting lines.
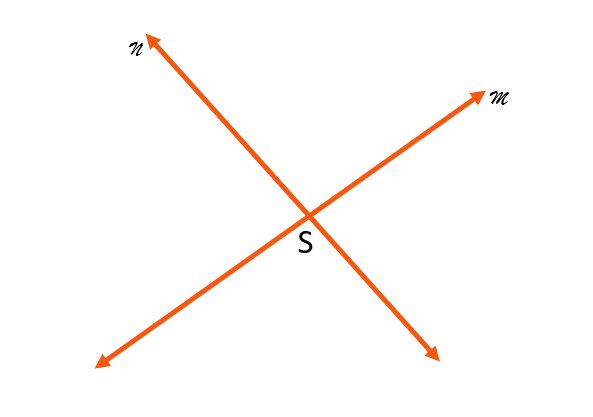
Here, lines m and n are intersecting at point S
That common point is called a Point of Intersection. We can spot several intersecting lines from our surroundings like:



Example 4
In the given figure, the lines AB, CD and EF intersect at a point O. If ∠BOD=x∘,∠AOE=2x∘and∠COF=90∘, find ∠AOEand∠AOC
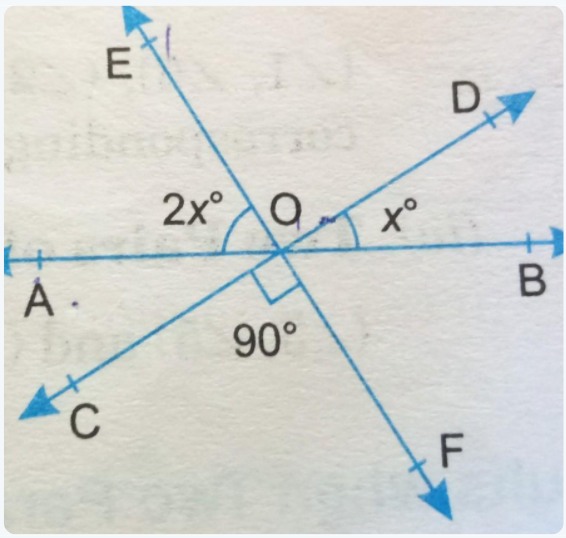
∠EOD=∠FOC (Vertically Opposite Angles)
So,∠EOD=90∘
∠EOA+∠EOD+∠DOB=180∘ (supplementary angles)
So, 2x+x+90∘=180∘
3x=90∘
x=30∘
Therefore, angle x is equal to 30∘.
∠AOE=2×30∘=60∘
∠AOC=180∘−(90∘+60∘) [Supplementary Angles]
=180∘−150∘
=30∘
TRANSVERSAL
Baccho aapne maps m ya railings and fences m dekha hoga ki ek single line multiple lines ko cross krte hue jaati hai. That single line gives us the concept of a transversal


Transversal is a straight line that crosses two or more other lines. The lines which the transversal crosses may or may not be parallel. When a transversal cuts two parallel lines, it makes 8 angles. When a transversal cuts n parallel lines, it makes 4×n angles. Based on the positions of the angles above or below the transversal or to the left or right of transversal, the angle pairs are determined and classified into different categories like alternate interior angles, corresponding angles, alternate exterior angles, vertically opposite angles, etc.
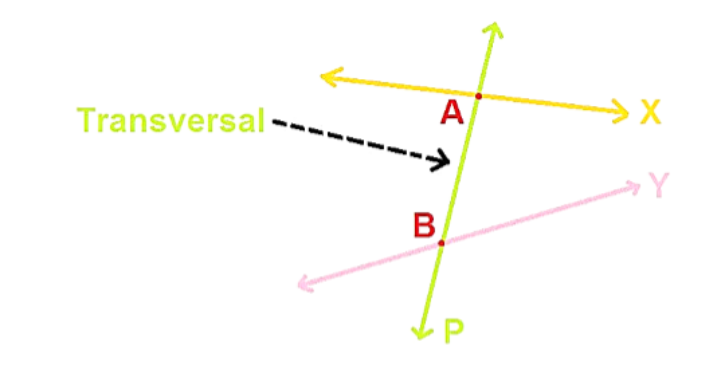
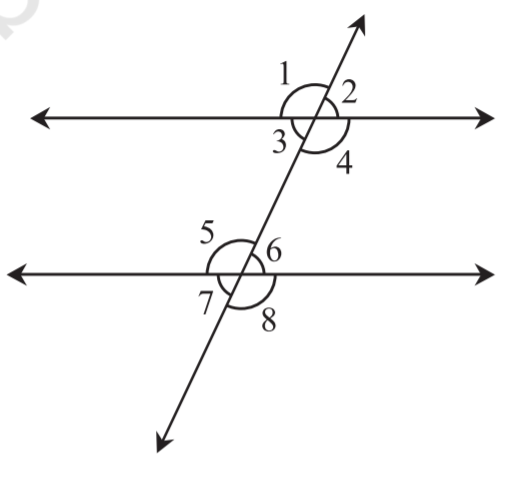
ANGLES MADE BY A TRANSVERSAL
When two lines are intersected by a transversal, 8 angles are formed. Among these,
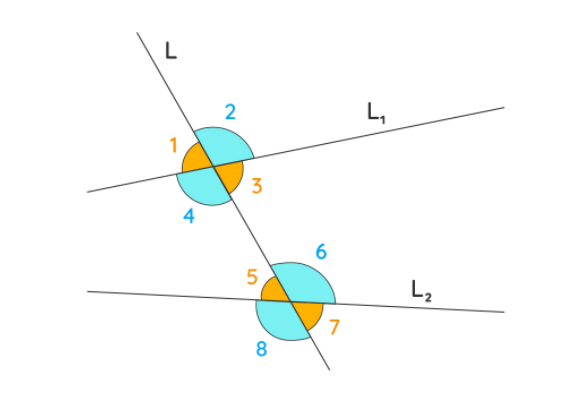
These angles are classified into the following types based on their positions.
TRANSVERSAL OF PARALLEL LINES
Baccho abhi humne pdha ki jab ek transversal 2 random lines ko cut krti hai to hume various related angles milte hai. Now we'll see ki agar ek transversal do parallel lines ko cut kregi to related angles m kya changes aate hai.
∠1=∠5
∠2=∠6
∠4=∠8
∠3=∠7
∠3=∠5
∠4=∠6
∠1=∠8
∠2=∠7
∠3+∠6=180∘
∠4+∠5=180∘
You can very easily remember these results if you can look for relevant ‘shapes’.
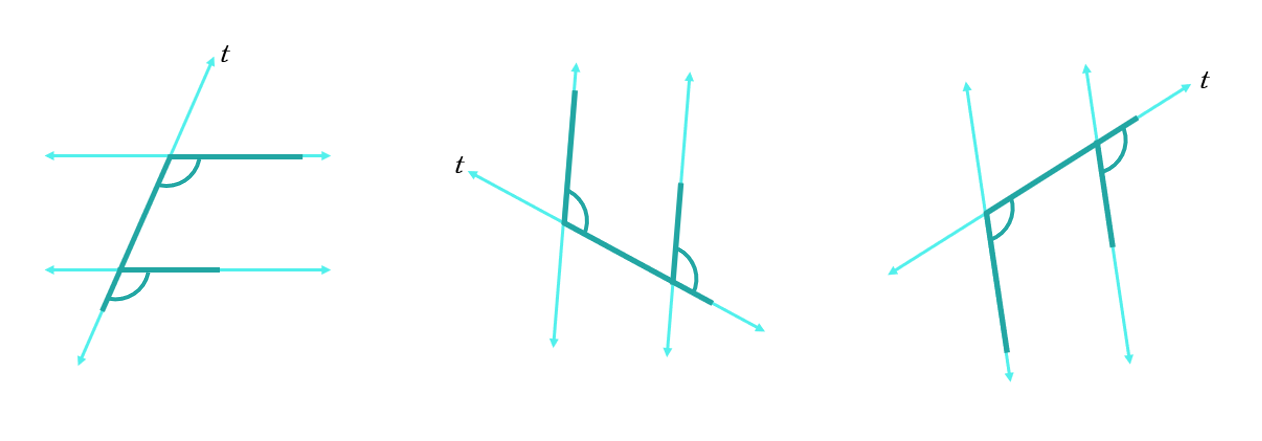
The F-shape stands for corresponding angles:
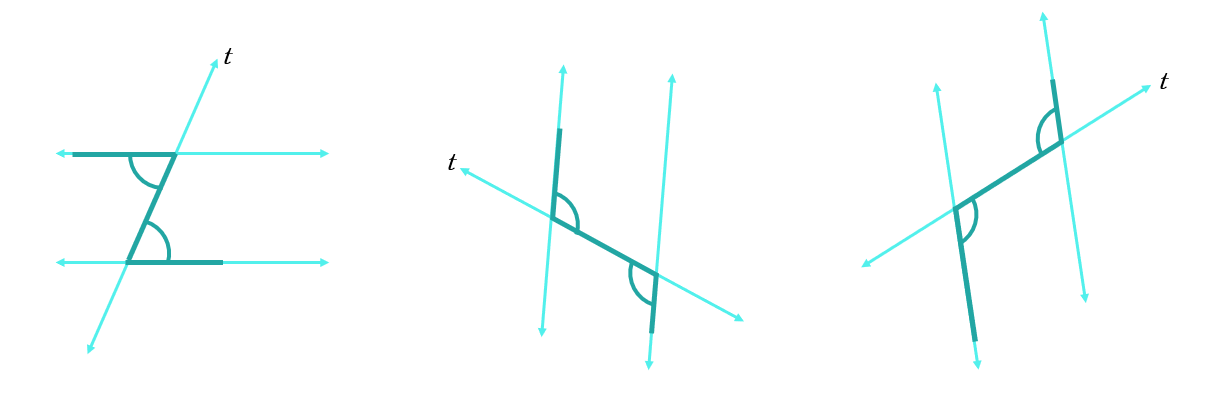
The Z - shape stands for alternate angles
Example 5
In the given figure, AB∣CD and EF is a transversal. If ∠AGE=110∘, find ∠x,∠yand∠z, marked in the figure:

Since, ∠AGE=110∘
⇒∠x=110∘......(Vertically opposite angles)
Given that, AB∣∣CD, ⇒∠x=∠y=∠110∘.......(Alternate Interior Angles)
⇒∠y+∠z=180∘........(Linear Pair)
⇒110∘+∠z=180∘
⇒∠z=180∘−110∘
⇒∠z=70∘
∴∠x=110∘
∠y=110∘
∠z=70∘
Example 6
In the given figure, AB∣∣CD and EF is a transversal. If ∠EGB=x∘and∠GHC=(4x)∘, find the value of x.
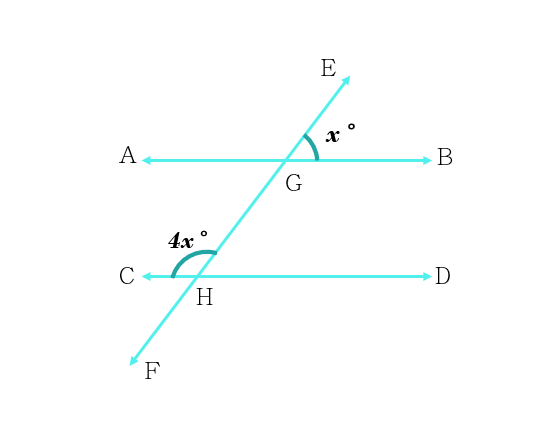
Since AB∣∣CD
⇒∠EGB=∠AGH......(Vertically Opposite Angles)
⇒∠AGH=x
Also, ∠CHG+∠AGH=180∘....(Angles on the same side of a transversal are supplementary)
⇒4x∘+x∘+180∘
⇒5x∘=180∘
⇒x∘=180∘5
⇒x=36∘
∴x=36∘
Example 7
In the following figure, AB∣∣CD and EF is a transversal. Find each one of the unknown angles x,y,z.
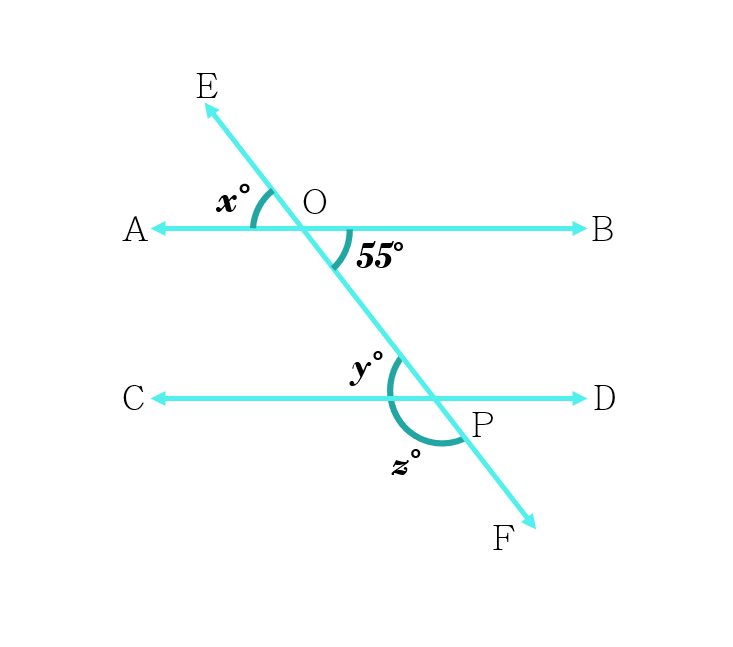
ATQ, ∠x=∠BOF.....(Vertically Opposite Angles)
∴x=55∘ Also, ∠y=∠BOF......(Alternate Interior Angles)
⇒∠y=55∘
∠y+∠z=180∘...(Linear Pair)
⇒55∘+∠z=180∘
⇒∠z=180∘−∠55∘
⇒∠z=125∘
∴∠x=55∘
∠y=55∘
∠z=125∘
CHECKING FOR PARALLEL LINES
Baccho ab hum seekhenge ki parallel lines ko kaise recognise krte hai. Humne abhi pdha ki jab ek transversal parallel lines ko intersect krti hai to hume equal corresponding angles, equal alternate interior angles, equal alternate exterior angles milte hai.
Isi concept ko reverse krke hum ye jaan skte hai ki do lines parallel hai ya nahi.
Ye skill bohot si life-oriented situations m use hota hai. For example, A draftsman uses a carpenter’s square and a straight edge (ruler)
to draw these segments by keeping the corresponding angles equal which guarantees that the line segments are parallel too.
There are three conditions to check whether the two lines are parallel.
They are:
(i) If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.
(ii) If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
(iii) If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Summary
1. We recall that :
(i) A line-segment has two end points.
(ii) A ray has only one end point (its vertex); and
(iii) A line has no end points on either side.
2. An angle is formed when two lines (or rays or line-segments) meet.
| Pairs of Angles | Condition |
|---|---|
| Two complementary angles | Measures add up to 90∘ |
| Two supplementary angles | Measures add up to 180∘ |
| Two adjacent angles | Have a common vertex and a common arm but no common interior. |
| Linear pair | Adjacent and supplementary |
3.When two lines l and m meet, we say they intersect; the meeting point is called the point of intersection.
When lines drawn on a sheet of paper do not meet, however far produced, we call them to be parallel lines.
4. (i) When two lines intersect (looking like the letter X) we have two pairs of opposite angles. They are called vertically opposite angles. They are equal in measure.
(ii) A transversal is a line that intersects two or more lines at distinct points.
(iii) A transversal gives rise to several types of angles.
(iv) In the figure, we have
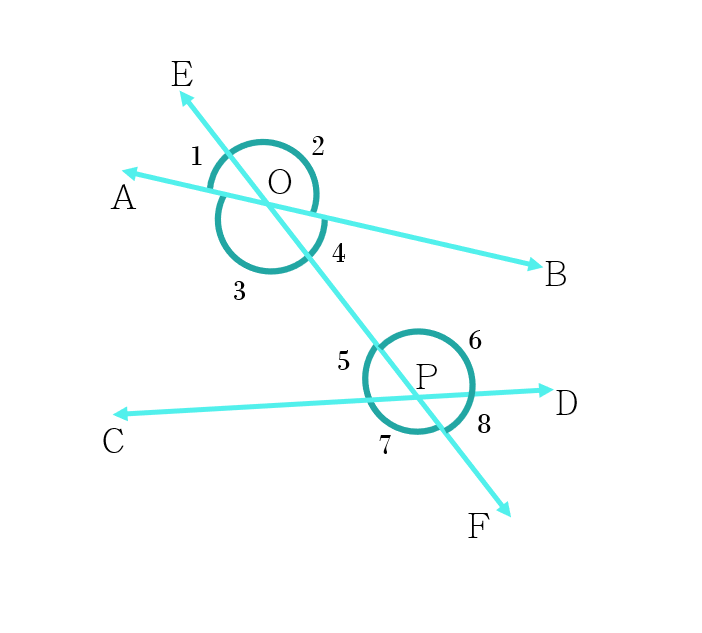
(v) When a transversal cuts two parallel lines, we have the following interesting relationships:
Each pair of corresponding angles are equal.
∠1=∠5,∠3=∠7,∠2=∠6,∠4=∠8
Each pair of alternate interior angles are equal.
∠3=∠6,∠4=∠5
Each pair of interior angles on the same side of transversal are supplementary.
∠3+∠5=180∘,∠4+∠6=180∘
Let's Revise
1.Baccho iss chapter m humne pdha ki humare surroundings m hum kitni different types ki line segments, rays and angles ko observe krte hai.
2.Complementary angles vo angles hote hai jinka sum 90∘ hota hai aur supplementary angles vo angles hote hai jinka sum 180∘ hota hai.
3. Jab do angles ek common vertex aur ek common arm share krte hai to unhe adjacent angles kaha jaata hai.
4. Agar do adjacent angles ka sum 180∘ ho aur unke dono opposite arms ek straight line form kre to vo linear pair kehlaate hai.
5. Jab do lines intersect krti hai to hume 4 angles milte hai. Inn angles m se jo opposite angles hote hai unka measurement equal hota hai and they are known as vertically opposite angles.
6. Jab multiple lines ko ek single line cross krti hai to uss line ko transversal kaha jaata hai. Jab ek transversal do alag lines ko intersect krti hai to hume 8 angles milte hai. Inn angles ko related angles kaha jata hai kyunki inn sabme relation hota hai. These angles are called:
7. Jab ek transversal do parallel lines ko intersect krti hai to hum related angles m special properties dekh paate hai. These are:
8. Using the same concept stated above, we can identify parallel lines by checking:
Agar ye conditions satisfy hoti hai to hum ye conclude kr skte hai ki vo do lines parallel hai.