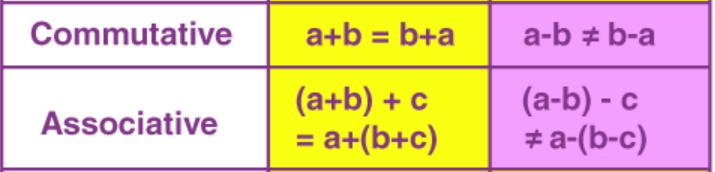INTEGERS for Class 7 MATHS
INTRODUCTION
To bacchon, pichli classes se hi aap sab different types of numbers and unke collection dekhte aaye hain. For example you already know about positive numbers, negative numbers, whole numbers, natural numbers as well as integers. We already know that integers are nothing but the collection of numbers which can be positive, negative or zero, but cannot be a fraction. These numbers are used to perform various arithmetic operations, like addition, subtraction, multiplication and division. In this chapter, we will study more about integers, their properties and operations. Sabse pehle to we will review and revise what we have learnt about integers in our previous class.
Let’s recapitulate
To bacchon aap sabne number line ke bare me pdha hai sath hi sath aapne numbers ko number line par represent karna bhi sikha hai. Aap ye already jante hai ki number line par zero (0) ke right side represent hone wale sare numbers positive hote hai and zero (0) ke left side wale sare numbers negative hote hai.
So, integers ko detail me padhne se pehle hum special collection of numbers ke bare mai bhi revision kar lete hai
Natural Numbers
Natural numbers are all positive numbers like 1, 2, 3, 4, and so on. They are the numbers you usually count and they continue till infinity. They do not include any decimal or fractional numbers.
Whole Numbers
The whole numbers are the collection of numbers without fractions, decimals, or even negative integers. It is a collection of positive integers and zero i.e. 0,1,2,3,4,5…...and so on.
Example 1
Use the sign of <,> or = in the box to make the statement true
(a) (−8)+(−4) ____ (−8)−(−4)
(b) (−3)+7−(19) ____ 15−8+(−9)
(c) 23−41+11 ____ 23−41−11
(d ) 39+(−24)−(15)____ 36+(−52)−(−36)
(e) −231+79+51 ____ −399+159+81
(a) In question (a) we can see that on the left part (−8)+(−4)=−12
Now, taking the right part
(−8)−(−4)=−4
So, (−8)+(−4)<(−8)−(−4)
(b) Similarly for question (b)
Takin the left part (−3)+7−(19)=−15
Now takin the right part of the question i.e.
15−8+(−9)=−2
So, (−3)+7−(19)<15−8+(−9)
So students, dekha aapne ki kitni aasani se hum is type ke questions ko solve kar sakte hai. Thik ise treh you have to check for questions (c), (d), and (e).
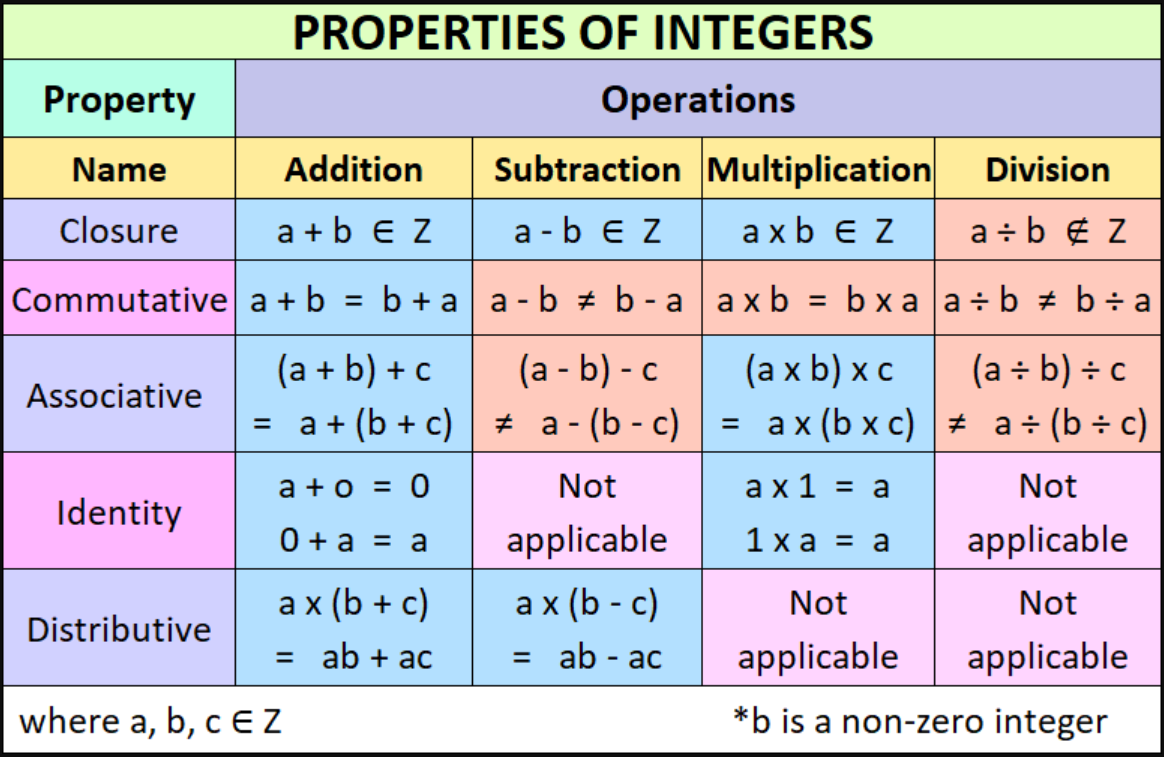
PROPERTIES OF ADDITION AND SUBTRACTION OF INTEGERS
Closure under Addition
Bacchon ye property kehti hai ki if we add two integers the result will be also an integer. In that condition we say integers are closed under addition. In general, for any two integers aandb,a+b is an integer. Aao ise example se smjhte hai.
Maan lo we have two integers aandb. Let a=5andb=−4. Now a+b=5+(−4)=1.<br>Where1isalsoan∫e≥r.<br><b>ClosureunderSubtraction<b><br>Tobahonkyajoadditionme∈hum≠dekhathikwaisaSubtractionkecasemehihoga?<be>Jawabhaihan,∫e≥rsareclosedunder⊂traction.Aasanlangua≥me,ifa and baretwo∫e≥rsthena – bisalsoan∫e≥r.Forexamp≤≤tusconsrtwo∫e≥rssuchtˆa=5 and b=3.Nowa-b = 2.Herewecanseetˆ2 is also an integer.
Commutative Property
While adding the two integers the order of addition does not alter the sum. In general, for any two integers aandb, we can say that a+b=b+a.
Explanation
Ise samajhne ke liye chalo ek example use krte hai
We have 5+(–6)=–1and(–6)+5=–1.
So, 5+(–6)=(–6)+5.
To bacchon humne dekha ki integers ka addition commutative property ko follow karta hai.
Note: Lakin kya yahi result Subtraction of integers ke liye bhi follow hoga?
Jawab hai nahi. Subtraction is not commutative for integers. Consider the integers 5and(–3). Is 5–(–3) the same as (–3)–5? No, because 5–(–3)=5+3=8, and (–3)–5=–3–5=–8.
Associative Property
Addition is associative for integers. In general for any integers a, b and c, we can say
a+(b+c)=(a+b)+c
For example consider the integers –3, –2 and –5.
Now, Look at (–5)+[(–3)+(–2)]and[(–5)+(–3)]+(–2). Aap yha dekh sakte hai, in the first sum (–3)and(–2) are grouped together and in the second (–5)and(–3) are grouped together. In both cases, we get –10.
So hum ye keh sakte hai (–5)+[(–3)+(–2)]=[(–5)+(–3)]+(–2).
Now, kya hum ye keh sakte hai, subtraction is also associative with integers?
Iska jawab hai nahi, look at (–5)−[(–3)−(–2)]=(−5)−(−1)=−4. Now agar hum numbers ki grouping ko change kar de i.e.[(–5)−(–2)]−(–3)=(−3)−(−3)=0. To bacchon hum yha dekh sakte hai ki subtraction is not associative for integers.
So, abhi humne jo bhi pdha use ek table me tabulate kar lete hai taki hume samjhne me aasani ho.
Additive Identity
When we add zero to any integer, we get the same integer. Zero is an additive identity for integers. In general, for any integer a we can say a+0=a=0+a.
Example 2
Verify a−(−b)=(a+b) for the following values of a and b. (i) a=21,b=18 (ii) a=118,b=125 (iii) a=75,b=84 (iv) a=75,b=11.
(i) a=21,b=18
So, a−(−b)=21−(−18)=21+18=39
a+b=21+18=39
∴a−(−b)=(a+b)
(ii)a=118,b=125
So, a−(−b)=118−(−125)=118+125=243
a+b=118+125=243
∴a−(−b)=(a+b)
(iii)a=75,b=84
So, a−(−b)=75−(−84)=75+84=159
a+b=75+84=159
∴a−(−b)=(a+b)
(iv)a=75,b=11
So, a−(−b)=75−(−11)=75+11=86
a+b=75+11=86
∴a−(−b)=(a+b)
MULTIPLICATION OF INTEGERS
To bacchon, chalo ab integers ke multiplication ki baat karte hai. Dhyan se ek ek topic hum dicuss karte huye jayenge taki humare concepts aurr bhi aache se clear ho jaye.
Multiplication of a Positive and a Negative Integer
Multiplying a positive integer and a negative integer, we multiply them as whole numbers and put a minus sign (–) before the product. We thus get a negative integer.
In general, for any two positive integers a and b we can say a×(–b)=(–a)×b=–(a×b).
Explanation
Let us find 3 × (–5). First find 3×5 and then put minus sign (–) before the product obtained. We find –(3×5) to get –15. Similarly if we change the order of numbers i.e. (−5)×3=−15 we get the same result.
Multiplication of two Negative Integers
The product of two negative integers is a positive integer. We multiply the two negative integers as whole numbers and put the positive sign before the product.
In general, for any two positive integers aandb, (–a)×(–b)=a×b.
Explanation
Let us find the product (–3)×(–2). First find 3×2 and put (+) before the product. We find (–3)×(–2)=6. Based on this observation, we can say that –3×–3=9, similarly –3×–4=12.
Product of three or more Negative Integers
if the number of negative integers in a product is even, then the product is a positive integer similarly if the number of negative integers in a product is odd, then the product is a negative integer. Ise samajhne ke liye aao kuch examples dekhte hai.
(a) (–4)×(–3)=12
(b) (–4)×(–3)×(–2)=[(–4)×(–3)]×(–2)=12×(–2)=–24
(c) (–4)×(–3)×(–2)×(–1)=[(–4)×(–3)×(–2)]×(–1)=(–24)×(–1)
(d) (–5)×[(–4)×(–3)×(–2)×(–1)]=(–5)×24=–120
Upar ke four examples me humne kya dekha :
(a) the product of two negative integers is a positive integer. Yha two negative integers ki baat ho rahi hai and two is an even number so the product is positive
b) the product of three negative integers is a negative integer. Yha three negative integers ki baat ho rahi hai and three is an odd number so the product is odd also.
(c) product of four negative integers is a positive integer. Yha bhi four negative integers ki baat ho rahi hai and four is an even number so the product is positive.
So, we can conclude that if the negative integers are multiplied, even number of times, the product is positive and if the negative integers are multiplied, odd number of times, the product is negative.
Example 3
Find each of the following products:
(i) (−2)×36×(−5)
(ii) (−2)×(−4)×(−6)×(−8)
(i) We have given (−2)×36×(−5)
We can write this as
−2×36×−5
⇒−(2×36)×−5
⇒−72×−5
⇒360
(ii) We have given (−2)×(−4)×(−6)×(−8)
Taking first two and last two terms together
(−2×−4)×(−6×−8)
=8×48
=384
Example 4
Find the value of:
(i) 1487×327+(−487)×327
(ii) 28945×99−(−28945)
(i) We have given 1487×327+(−487)×327
We can write this as
1487×327−487×327
Taking 327 common.
⇒327×(1487−487)
⇒327×1000
⇒327000
Q. Similarly students you have to solve second part of this question.
PROPERTIES OF MULTIPLICATION OF INTEGERS
Students addition and subtraction ki properties to humne dekh li now we are going to see the properties of multiplication one by one.
Closure under Multiplication
This gives us an idea that the product of two integers is again an integer. So we can say that integers are closed under multiplication. In general, a×b is an integer, for all integers a and b.
3×(–4)=–12
(– 4) × 3 = –12
3 × (– 4) = (– 4) × 3
In general, for any two integers a and b, a×b=b×a.
Multiplication by Zero
Any integer when multiplied by zero gives zero. In general , for any integer a,a×0=0×a=0.
Multiplicative Identity
1 is the multiplicative identity for whole numbers. In general, for any integer a we have, a×1=1×a=a.
Observe the following products of integers with 1
<br>(–3) × 1 = –3
1 × 5 = 5
Note : 0 is the additive identity whereas 1 is the multiplicative identity for integers. We get additive inverse of an integer a when we multiply (–1) to a, i.e. a×(–1)=(–1)×a=–a.
Associativity for Multiplication
The product of three integers does not depend upon the grouping of integers and this is called the associative property for multiplication of integers. In general, for any three integers a,bandc<br>(a×b)×c=a×(b×c)
Explanation
Look at [(–3)×(–2)]×5and(–3)×[(–2)×5]. In the first case (–3)and(–2) are grouped together and in the second (–2)and5 are grouped together. We see that [(–3)×(–2)]×5=6×5=30 and (–3)×[(–2)×5]=(–3)×(–10)=30 So, we get the same answer in both the cases. Thus, [(–3)×(–2)]×5=(–3)×[(–2)×5].
Distributive Property
Distributivity of multiplication over addition or subtraction for any integers a, b and c, is given by a×(b+c)=a×b+a×c and for any three integers a, b and c
a×(b–c)=a×b–a. × c
Exaplanation
Aao ise ek example se samajhte hai .
(–2)×(3+5)=–2×8=–16
and [(–2)×3]+[(–2)×5]=(–6)+(–10)=–16
So, (–2)×(3+5)=[(–2)×3]+[(–2)×5]
Similarly let us check : 4×(3–8)=4×(–5)=–20
4×3–4×8=12–32=–20So,4×(3–8)=4×3–4×8.
Making Multiplication Easier
Consider the following:
(i) We can find (–25) × 37 × 4 as [(–25) × 37] × 4 = (– 925)× 4 = –3700.
To, kya hum kise or bhi meathod se solve kar sakte hai ?
We can do it this way also, (–25)×37×4=(–25)×4×37=[(–25)×4]×37=(–100)×37=–3700
Ab ye aapko decide karna hai ki which is the easier way ?
Obviously the second methos is easier because multiplication of (–25)and4 gives –100 which is easier to multiply with 37.
Note : The second way involves commutativity and associativity of integers.
So, we find that the commutativity, associativity and distributivity of integers help to make our calculations simpler.
Example 4
Divide:
(i) -161 by -23
(ii) 76 by -19
(i) We have been given −161−23
We have minus sign in both numerator and denominator. So they can cancel each other
Now we have
16123
⇒7
(ii) We have been given 76−19
We can write it as−7619.
⇒−4.
DIVISION OF INTEGERS
So students ab tak jo bhu humne pdha unke basis par division of integers and uske properties ko samjhna or bhi aasan ho gya hai.
The division of integers also involves the same cases.
(i) Dividing 2 positive numbers
(ii) Dividing 2 negative numbers
(iii) Dividing 1 positive and 1 negative number
Case (i) : When you divide integers with two positive signs, Positive ÷ Positive = Positive. For example : 16÷8=2.
Case (ii) : When you divide integers with two negative signs, Negative ÷ Negative = Positive. For example : –16÷–8=2.
Case (iii) :When you divide integers with one negative sign and one positive sign, Negative ÷ Positive = Negative. For example : –16÷8=–2.
Properties of Division
Closure Property :Integers are closed under addition, subtraction, and multiplication. However, they are not closed under division. For example : a÷b is not always an integer i.e. –34 is a form of fraction.
Commutative Property :The addition and multiplication of integers follow the commutative property, while division of integers does not hold this property. For example : a÷b≠b÷a i.e. 15÷3=5 but 3÷15=15.
Associative Property : The associative property applies to the addition and multiplication of two integers but not in case of division of integers. For example : (a÷b)÷c≠a÷(b÷c) i.e. (20÷5)÷2=2 but 20÷(5÷2)=8.
Note :Like whole numbers, any integer divided by zero is meaningless and zero divided by
an integer other than zero is equal to zero i.e., for any integer a, a÷0 is not defined
but 0÷a=0 for a≠0.
To bacchon ab tak humne jo bhi discuss kiya hai we can tabulate them in a single table.
Example 5
The temperature at 12 noon was 10∘C above zero. If it decreases at the rate of 2∘C per hour until midnight, at what time would the temperature be 8∘C below zero? What would be the temperature at mid-night?
So, we have been given
12 noon par humra temperature 10∘C tha.
Now rate of decreasing temperature =2∘C per hour.
(i) To find the time at which the temperature is −8∘C
Total decrease in temperature = final temperature − initial temperature.
⇒−8−10.
∴ Total decrease in temperature =−18.
Let the time taken in temperature decrease =t.
Total decrease in temperature =t× rate of decrease in temperature,
⇒−18=t×2
∴t=−182
⇒t=(−9)
Lakin hum ye bhi jante hai ki time can not be negative so t=9 hours.
So the time at which temperature is −8∘C = 12PM + 9 hours.
⇒9PM.
(ii) We have to find what will be the temperature at midnight.
Temperature decrease in one hour =2∘C.
So the decrease in temperature in 12hour=2×12=24∘C
We we consider it negative because temperature is decreasing ⇒(−24)
Now, temperature at midnight = temperature at 12PM + change in temperature in 12 hours.
=10∘C+(−24)=−14∘C
Summary
1. Integers are a bigger collection of numbers which is formed by whole numbers and their negatives. These were introduced in Class VI.
2. You have studied in the earlier class, about the representation of integers on the number line and their addition and subtraction.
3. We now study the properties satisfied by addition and subtraction.
(a) Integers are closed for addition and subtraction both. That is, a + b and
a – b are again integers, where a and b are any integers.
(b) Addition is commutative for integers, i.e., a + b = b + a for all integers
a and b.
(c) Addition is associative for integers, i.e., (a + b) + c = a + (b + c) for all integers
a, b and c.
(d) Integer 0 is the identity under addition. That is, a + 0 = 0 + a = a for every
integer a.
4. We studied, how integers could be multiplied, and found that product of a positive
and a negative integer is a negative integer, whereas the product of two negative
integers is a positive integer. For example, – 2 × 7 = – 14 and – 3 × – 8 = 24.
5. Product of even number of negative integers is positive, whereas the product of odd number of negative integers is negative.
6. Integers show some properties under multiplication.
(a) Integers are closed under multiplication. That is, a × b is an integer for any two
integers a and b.
(b) Multiplication is commutative for integers. That is, a × b = b × a for any integers
a and b.
(c) The integer 1 is the identity under multiplication, i.e., 1 × a = a × 1 = a for any
integer a.
(d) Multiplication is associative for integers, i.e., (a × b) × c = a × (b × c) for any
three integers a, b and c.
7. Under addition and multiplication, integers show a property called distributive property. That is, a × (b + c) = a × b + a × c for any three integers a, b and c.
8. The properties of commutativity, associativity under addition and multiplication, and the distributive property help us to make our calculations easier.
9. We also learnt how to divide integers. We found that,
(a) When a positive integer is divided by a negative integer, the quotient obtained is
a negative integer and vice-versa.
(b) Division of a negative integer by another negative integer gives a positive integer
as quotient.
10. For any integer a, we have
(a) a ÷ 0 is not defined
(b) a ÷ 1 = a.
Let's Revise
Closure Property
Associative Property
Commutative Property
Distributive Property
Additive Inverse Property
Multiplicative Inverse Property
Identity Property.

All the the properties of integers can be explained wil the help of single table i.e.