EXPONENTS AND POWERS for Class 7 MATHS
INTRODUCTION
Baccho kya aap jaante hai ki Earth ka mass 5,970,000,000,000,000,000,000,000kg hai!. Similarly, mass of Uranus is 86,800,000,000,000,000,000,000,000kg. Isn't it difficult to read and compare such large numbers?To make these numbers easy to read, understand and compare, we use exponents. Baccho Iss chapter m hum exponents and powers k baare m pdhenge aur seekhenge ki hum aise large numbers ko easily kaise express kr skte hai. Hum laws of exponents k baare m bhi briefly pdhenge. So let's begin!
EXPONENTS
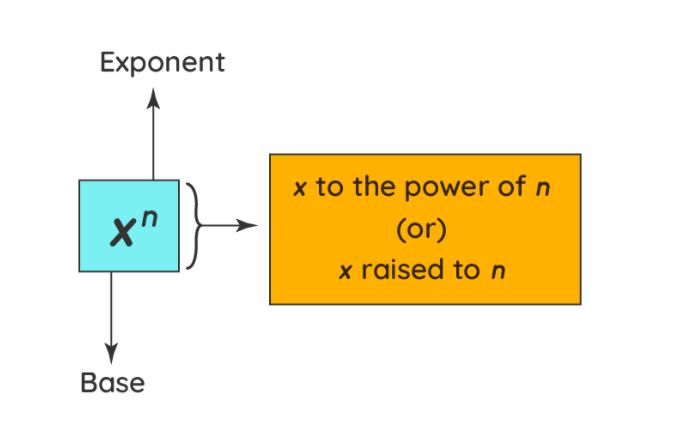
Baccho, exponents ko use krke hum large numbers ko shorter method m express kr skte hai. Exponent of a number shows how many times we are multiplying a number by itself. For example, 34 means we are multiplying 3 four times. Its expanded form is 3×3×3×3. Here, 3 is called the "base" and 4 is called the "exponent" or "power." In general, xn means that x is multiplied by itself for n times.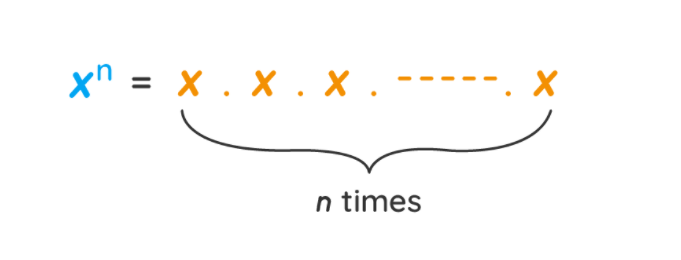
Here, in the term xn,
Examples of Exponents Some examples of exponents are as follows:
3×3×3×3×3=35
−2×−2×−2=(−2)3
a×a×a×a×a×a=a6
How to Write in Exponential Form?
To write numbers in exponential form, we have to express them raised to certain powers of their prime factors based on the given way:
8=2×2×2=23
72=2×2×2×3×3=23×32
121=112
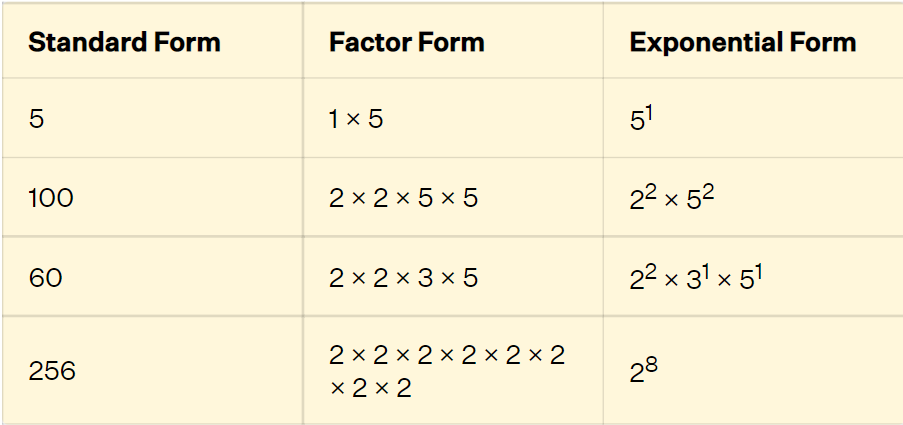
These are the exponential forms of the corresponding numbers. When it comes to representing numbers, there are three forms in which we can do that. Those are exponential form, factor form, and standard form. Any number can be represented in all three forms. Let us understand it in detail through the table given below:
Example 1
LAWS OF EXPONENTS
The different 'rules and laws of exponents' are also known as the 'properties of exponents'. A few of them are listed as follows: the product rule of exponents, the quotient rule of exponents, the zero rule of exponents, and the negative rule of exponents. Let us learn each of these in detail now.
1.Multiplying Powers with the Same Base
The product rule of exponents is used to multiply expressions with the same bases. This rule says, "To multiply two expressions with the same base, add the exponents while keeping the base the same."

Observe the following example.
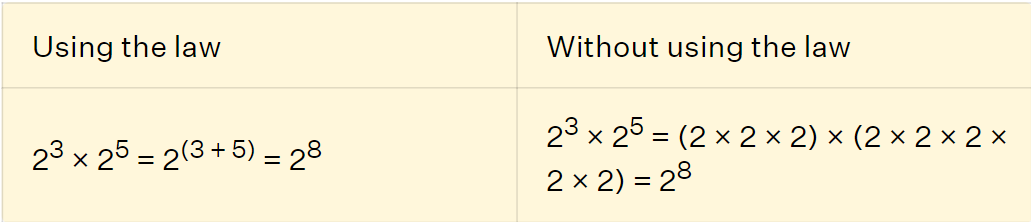
This shows that without using the law, the expression involves more calculation.
2.Dividing Powers with the Same Base
The quotient property of exponents is used to divide expressions with the same bases. This property says, "To divide two expressions with the same base, subtract the exponents while keeping the base same."
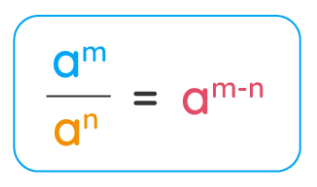
Let us simplify 37÷34?
37÷34=3734=3×3×3×3×3×3×33×3×3×3
=3×3×3=33=37–4
Thus ,37÷34=37–4=33
3.Taking Power of a Power
The 'power of a power property of exponents' is used to simplify expressions of the form (am)n. This property says, "When we have a single base with two exponents, just multiply the exponents." The two exponents are available one over the other. These can be conveniently multiplied to make a single exponent.
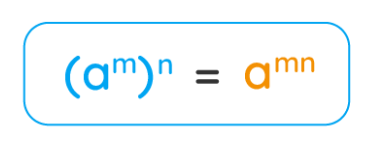
4.Multiplying Powers with the Same Exponents
The 'power of a product property of exponents' is used to find the result of a product that is raised to an exponent. This property says, "Distribute the exponent to each multiplicand of the product."
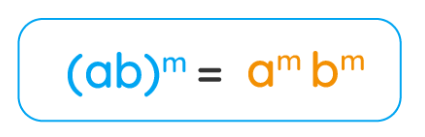
5.Dividing Powers with the Same Exponents
The power of a quotient property of exponents is used to find the result of a quotient that is raised to an exponent. This property says, "Distribute the exponent to both the numerator and the denominator." Here, the bases are different and the exponents are the same for both the bases.
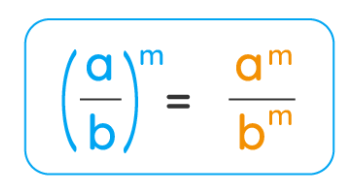
6.Numbers with exponent zero
The zero property of exponents is applied when the exponent of an expression is 0. This property says, "Any number (other than 0) raised to 0 is 1." Note that 00 is not defined. The will help us understand that irrespective of the base the value for a zero exponent is always equal to 1.
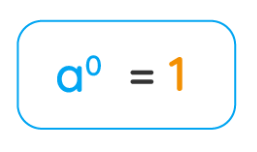
Example 2
Example (a): Can you tell which one is greater(52)×3 or (52)5 ?
Example (b): Express the following terms in the exponential form :
(i) (2×3)5
(ii) (2a)4
(iii) (−4m)3
Solution (a):
(52)⋅3=25⋅3=75
(52)3=52⋅52⋅52
=25⋅25⋅25
=56=15625
15625>75
so, (52)3>(52)⋅3
Solution (b):
(i) (2⋅3)5
=(2⋅3)(2⋅3)(2⋅3)(2⋅3)(2⋅3)
=2⋅2⋅2⋅2⋅2⋅3⋅3⋅3⋅3⋅3
=25⋅35
(ii) (2a)4
=(2⋅a)4=24⋅a4
(iii)(−4m)3
=[(−4)⋅m]3
=(−4)3⋅m3
=(−1)3⋅43⋅m3
Example 3
Write exponential form for 8×8×8×8 taking base as 2.
=8⋅8⋅8⋅8
=23⋅23⋅23⋅23
=23+3+3+3
using ax⋅ay⋅az=ax+y+z
212
Example 4
Simplify and write the answer in the exponential form.
(i) (3732)×35
(ii) 23×22×55
(iii) (62×64)÷63
(iv) [(2)3×36]×56
(i) 3732⋅35=37⋅3532
=37+522
=31232
=312−2=310
(ii) 23⋅22⋅55
=25⋅55
=(2⋅5)5=105
(iii) (62⋅64)÷63
=62+4−3=63
(iv) [(2)3⋅36]⋅56
=22⋅3⋅36⋅56
=(2⋅3⋅6)6
=306
Example 5
Simplify : (i) 124+93×463×82×27 (ii) 23×a3×5a4
(i) 124⋅93⋅463⋅82⋅27
=(22⋅3)4⋅(32)3⋅22(2⋅3)3⋅(23)2⋅33
=28⋅34⋅36⋅2223⋅33⋅26⋅33
=28+2−3−6⋅34+6−3−3
=2⋅34=162
(ii)23⋅a3⋅5a4
=23⋅a3⋅a4⋅5
=23⋅5⋅a3+4
=8⋅5⋅a7=40a7
DECIMAL NUMBER SYSTEM
Baccho ab hum seekhenge ki hum exponents ko use krke large numbers ko expanded form m kaise represent kr skte hai using powers of 10 in the exponent form.
Let us look at the expansion of 47561, which we already know:
47561=4×10000+7×1000+5×100+6×10+1
We can express it using powers of 10 in the exponent form:
Therefore, 47561=4×104+7×103+5×102+6×101+1×100
(Note 10,000=104,1000=103,100=102,10=101and1=100)
Baccho, isko better smjhne k lie hum ek aur example lenge:
104278=1×100,000+0×10,000+4×1000+2×100+7×10+8×1
=1×105+0×104+4×103+2×102+7×101+8×100
=1×105+4×103+2×102+7×101+8×100
Notice how the exponents of 10 start from a maximum value of 5 and go on decreasing by 1 at a step from the left to the right upto 0.
Baccho notice kijiye ki kaise exponents of 10, maximum value 5 se start hoti hai aur 1 step se decrease hote hue 0 p pohonch jaati hai.
Example 6
Write the following numbers in the expanded forms:279404,3006194,2806196,120719,20068
(i) 279404=2×105+7×104+9×103+4×102+0×101+4×100
(ii) 3006194=3×106+6×103+1×102+9×101+4
(iii) 2806196=2×106+8×105+6×103+1×102+9×101+6
(iv) 120719=1×105+2×104+7×102+1×101+9
(v) 20068=2×104+6×101+8
EXPRESSING LARGE NUMBERS IN THE STANDARD FORM
Baccho, following statements ko observe kriye:
1. Sun is located
300,000,000,000,000,000,000m from the centre of our Milky Way
Galaxy.
2. Number of stars in our Galaxy is 100,000,000,000.
3. Mass of the Earth is 5,976,000,000,000,000,000,000,000kg.
Ye numbers pdhne aur likhne m convenient nahi hai islie hum inko exponents ko use krke standard form m express krenge.
If very large numbers or very small numbers are given, then it is better to use the standard exponential form to represent them. For example, it is difficult to make sense of the number 2030000000000000, but it will be easier if we write it in standard form as 2.03×1015. It is also known as a scientific notation to write numbers. To write a number in standard exponential form, follow the steps given below:
Step 1: Count the number of trailing zeros in the number.
Step 2: Use the beginning of the number and write the digits from the right till the last non-zero digit followed by a 10 raise to power which is equal to the number of trailing zeros.
Step 3:
Place a decimal point after the first digit from the right side and add the number of decimal places created to the power of 10. For example, in the example written above, if we place a decimal point after 2, then two decimal places will be created in the number 2.03. So, we will add 2 to the power of 10. The power of 10 was 13 as there were 13 trailing zeros, but now it will become 15.
Step 4: It will be the standard exponential form.
Example 6
Express the following numbers in the standard form:(i)5985.3 (ii)65,950 (iii)3,430,000 (iv)70,040,000,000
1.)5985.3=5.9835×103
2.)65950=6.595×104
3.)3430000=3.43×106
4.)70040000000=7.04×104
Example 7
Express the following numbers in standard form:(i)5,00,00,000(ii)70,00,000(iii)3,18,65,00,000(iv)3,90,878(v)39087.8(vi)3908.78
(i) 5,00,00,000=5×107
(ii) 70,00,000=7×106
(iii) 3,18,65,00,000=3.1865×109
(iv) 390878=3.90878×105
(v) 39087.8=3.90878×104
(vi) 3908.78=3.90878×103
SUMMARY
1.Very large numbers are difficult to read, understand, compare and operate upon. To make all these easier, we use exponents, converting many of the large numbers in a
shorter form.
2. The following are exponential forms of some numbers?
10,000=104
(read as 10 raised to 4)
243=35, 128=27
Here, 10,3 and 2 are the bases, whereas 4,5 and 7 are their respective exponents.
We also say, 10,000 is the 4th power of 10,243 is the 5th power of 3, etc.
3. Numbers in exponential form obey certain laws, which are:
For any non-zero integers a and b and whole numbers m and n: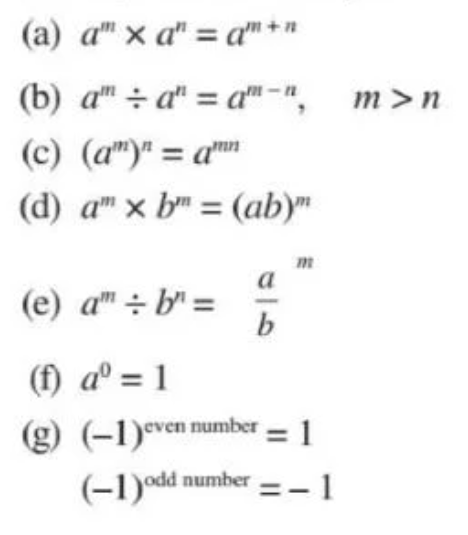
Let's Revise
1.Baccho iss chapter m humne pdha ki kaise hum exponents and powers ko use krke large numbers ko pdhna aur compare krna convenient bnata hai.
2. We learnt about the basics of exponents and powers and saw some examples.
3. Fir humne laws of exponents k baare m pdha aur seekha ki kaise hum inn laws ko use krke easily calculate kr skte hai jab large numbers given ho.
4. Humne ye bhi seekha ki exponents of 10 to the power ko use krke hum large numbers ko expand krke express kr skte hai.
5. Lastly, we learnt about the standard form of expressing large numbers in exponential form.