CONGRUENCE OF TRIANGLES for Class 7 MATHS
INTRODUCTION
Baccho, hum apni day to day life m aise bohot si shapes and figures ko dekhte hai jo ki exactly same hoti hai. For example, two 1 rupee coins will have the same shape and size but a 1 rupee and a 2 rupee coin might have different sizes and would not overlap each other completely. Jo shapes ek dusre ko completely overlap krti hai unhe congruent shapes kaha jaata hai. Let's play a quick game to understand this better. Look at the following pair of shapes and identify which all are congruent figures.
In geometry, congruent means identical in shape and size. Congruence can be applied to line segments, angles, and figures. Any two line segments are said to be congruent if they are equal in length. Two angles are said to be congruent if they are of equal measure. Two triangles are said to be congruent if their corresponding sides and angles are equal. Baccho, aapne apne previous chapter m triangles aur unki properties k baare m pdha tha. Jab do triangles ki saari properties jaise ki sides, angles, vertices, etc. same hoti hai to unhe congruent triangles kaha jaata hai. Iss chapter m hum congruent triangles k baare m detail m pdhenge. Hum alag alag criterias k baare m seekhenge jinse triangles m congruency define ho skti hai. So let's begin.
CONGRUENCE OF PLANE FIGURES
Baccho, before learning about congruency in triangles we'll learn about how congruency exists in different plane figures as well. Baccho agar hume ye pta lgana hota hai ki do figures congruent hai ya nahi, we use the the method of superposition.
Iss method m hum basically ye ta lgate h ki agar dono figures ek dusre p completely overlap horhi hai ya nahi. We can use tracing paper to trace the figure and put on top of the other figure to check.
NOTE: For congruency to exist, the figures need to completely overlap each other without bending, twisting, stretching or distorting the figure in any way. Although, if the figure is rotated, it still remains congruent. Let's look at some congruent plane figures.

CONGRUENCE AMONG LINE SEGMENTS
Two line segments are said to be congruent if they are equal in length. Similarly, if two line segments are congruent then they are equal in lengths too.
We use the sign ≅ to represent congruency between two lines or figures. We can use the "trace-copy" superposition method to figure out if two line segments are congruent or not. But the quickest way to figure out congruency between two line segments is by measuring them with a tool like a scale.
Look at the following pair of congruent line segments for better understanding.
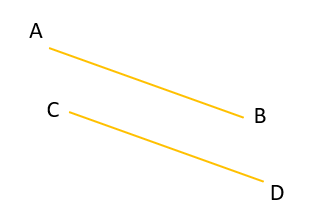
AB≅CD
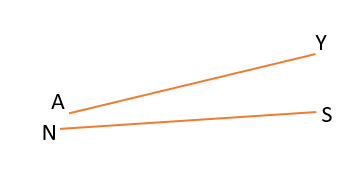
AY≅NS
CONGRUENCE OF ANGLES
Baccho, jab do angles k measurements equal hote hai, then they are known as congruent angles. Aapne congruent angles phle bhi dekhe hue hai. For example, in equilateral triangles, isosceles triangles or when a transversal cuts through a parallel line and equal angles are formed. Jo angles congruent hote hai vo equal bhi hote hai aur jo angles equal hote hai vo congruent bhi hote hai bacho. In further topics we'll learn how we can prove congruency in two triangles by proving their angles congruent. The following are examples of congruent angles:

∠ABC≅∠DEF
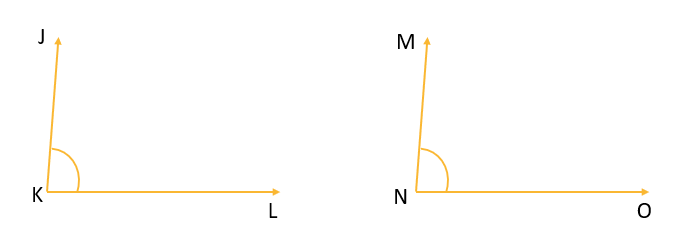
∠JKL≅∠MNO
CONGRUENCE OF TRIANGLES
Congruence in two or more triangles depends on the measurements of their sides and angles. The three sides of a triangle determine its size and the three angles of a triangle determine its shape. Two triangles are said to be congruent if pairs of their corresponding sides and their corresponding angles are equal. They are of the same shape and size. There are many conditions of congruence in triangles.
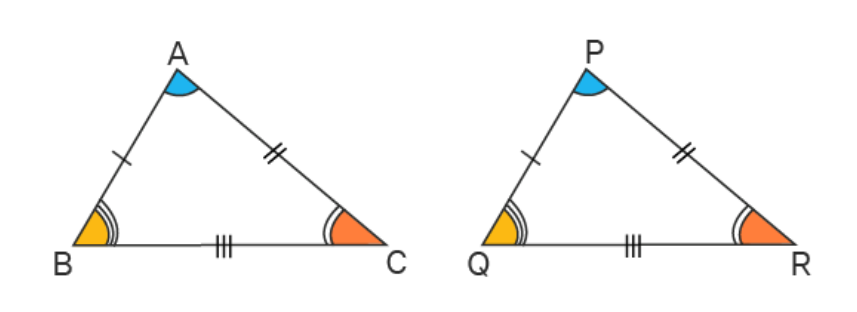
In the figure given above, △ABC and △PQR are congruent triangles. This means that the corresponding angles, corresponding vertices and corresponding sides in both the triangles are equal.
Vertices :A and P,B and Q,C and R
Sides:AB=PQ,BC=QRandAC=PR;
Angles:∠A=∠P,∠B=∠Q,and∠C=∠R.
Therefore, △ABC≅△PQR
The position of vertices are very important in congruency of triangles. Two triangles might have the same shape but if the vertices do not correspond then the triangles aren't congruent. Let's understand with the following example.
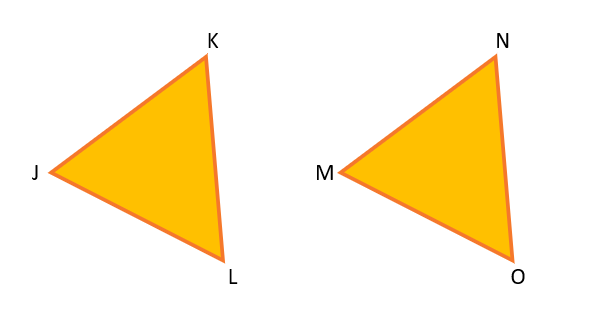
In the above figure, △JKL≅△MNO but we CANNOT say that △JKL≅△NOM. Let's see why - Try to super impose the above vertices on each other and check if they cover each other completely or not.
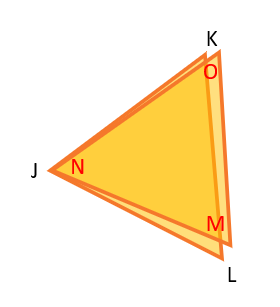
We can clearly see that the two triangles do not over lap. Hence, if the vertices are not corresponding, the triangle is won't be congruent.
Note: Two congruent triangles can be renamed in a cyclic order as long as there corresponding vertices match. For example, △ABC≅△DEF can be written as:
The following are the congruence theorems or the triangle congruence criteria that help to prove the congruence of triangles.
CRITERIA FOR CONGRUENCE OF TRIANGLES
Baccho do triangles congrent tab hote hai jab unke size aur shape same hoti hai. Lekin ye zaroori nahi ki dono triangles k saare 6 elements (3 angles and 3 sides) same ho in order to determine that they are congruent. Based on studies and experiments, there are 5 conditions for two triangles to be congruent. They are SSS, SAS, ASA, AAS, and RHS congruence properties.
1. SSS Criterion for Congruence
SSS Criterion stands for Side-Side-Side Criterion. Baccho, iss creterion k according agar do triangles ki corresponding sides k measurements same hai, to vo congruent prove hoti hai.
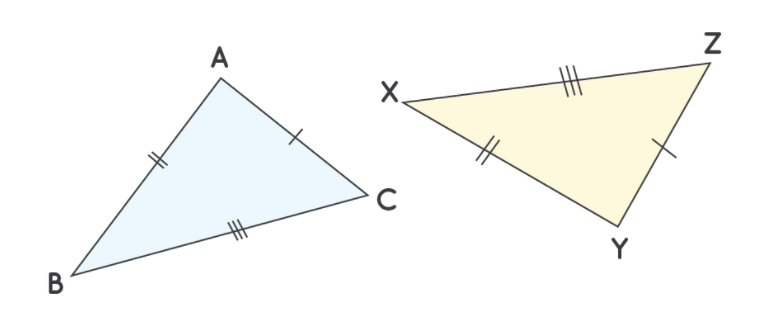
If △BAC≅△XYZ under SSS criterion, then the three angles of △BAC are bound to be equal to the corresponding angles of △XYZ.
Baccho, jab ek triangle congruent prove hota hai to uske baaki elements bhi equal prove hojaate hai. Which means, if a triangle is proved congruent because of its 3 equal sides, then its 3 angles will also be proven equal. This is known as Corresponding parts of congruent triangles (CPCT) theorem which states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other.
∴ We can conclude that if under a given correspondence, the three sides of one triangle are equal to the three
corresponding sides of another triangle, then the triangles are congruent.
2. SAS Criterion for Congruence
SAS Criterion stands for Side-Angle-Side Criterion. Baccho, iss criterion k according agar do triangles k do corresponding sides aur unke beech k angle ka measurement same hota hai, to vo congruent prove hote hai.
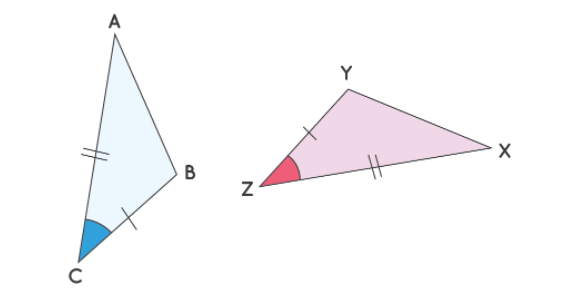
If △ABC≅△XYZ under SAS criterion, then the third side (AB) and the other two angles of △ABC are bound to be equal to the corresponding side (XY) and the angles of △XYZ.
∴ We can conclude that if under a correspondence, two sides and the angle included between them of a triangle
are equal to two corresponding sides and the angle included between them of another
triangle, then the triangles are congruent.
Example 1
In the given figure, AD=CDandAB=CB. (i) state the three pairs of equal in ΔABDandΔCBD. (iii) Is ΔABD[≡~?]ΔCBD ? Why or why not ? (iii) Does BD bisect ? ABC ? Given reasons
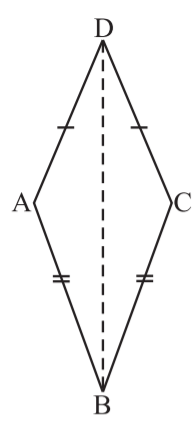
(i) In △ABD and △CBD, the three pairs of equal parts are as given below:
AB=CB (Given)
AD=CD (Given)
and BD=BD (Common in both)
(ii) From (i) above, △ABD≅△CBD (By SSS congruence rule)
(iii)∠ABD=∠CBD (Corresponding parts of congruent triangles)
So, BD bisects ∠ABC.
Example 2
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using SAS congruence rule. If the triangles are congruent, write them in symbolic form.
△ABC △DEF
(a)AB=7cm,BC=5cm,∠B=50∘ DE=5cm,EF=7cm,∠E=50∘ (b)AB=4.5cm,AC=4cm,∠A=60∘ DE=4cm,FD=4.5cm,∠D=55∘ (c)BC=6cm,AC=4cm,∠B=35∘
DF=4cm,EF=6cm,∠E=35∘
(a) Here, AB=EF(=7cm),BC=DE(=5cm) and
included ∠B= included ∠E(=50∘). Also, A↔FB↔E and C↔D.
Therefore, △ABC≅△FED (By SAS congruence rule)
(b) Here, AB=FD and AC=DE
But included ∠A≠ included ∠D. So, we cannot say that the triangles are
congruent.
(c) Here, BC=EF,AC=DF and ∠B=∠E.
But ∠B is not the included angle between the sides AC and BC.
Similarly, ∠E is not the included angle between the sides EF and DF.
So, SAS congruence rule cannot be applied and we cannot conclude
that the two triangles are congruent.
Example 3
In the given figure, AB=ACandAD is the bisector of ? BAC. (i) State three pairs of equal parts in triangles ADBandADC. (ii) Is ΔADB≅ΔADC ? Given reasons. (iii) Is ∠B=∠C ? Given reasons
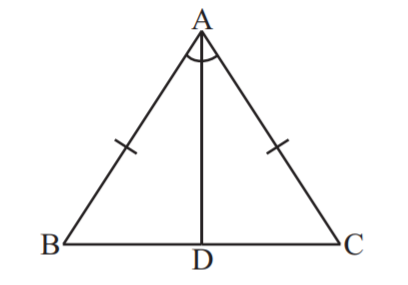
1)AB=AC(given)
∠BAD=∠CAD(angle bisector)
AD=AD(Common)
2)∠ABD≅∠ADC(SAS)
3)∠B=∠C
(because ∠ABD≅∠ADC(SAS)).
Example 4
By applying ASA congruence rule, it is to be established that △ABC≅△QRP and it is given that BC=RP. What additional information is needed to establish the congruence?
For ASA congruence rule, we need the two angles between which the two sides BC and RP are included. So, the additional information is
as follows:
∠B=∠R
and ∠C=∠P
Example 5
In the given figure, can you use ASA congruence rule and conclude that △AOC≅△BOD?
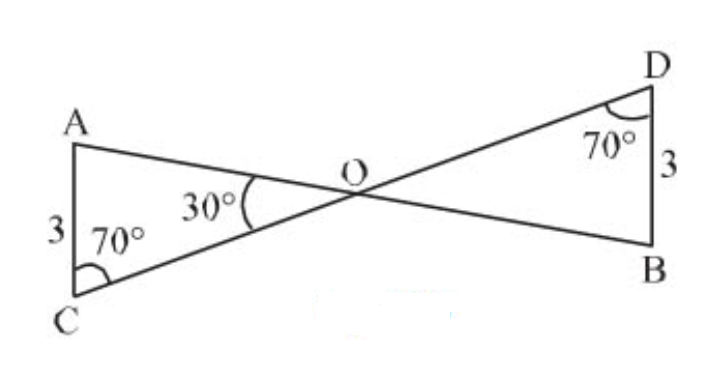
In the two triangles AOC and BOD, ∠C=∠D (each 70∘ )
Also, ∠AOC=∠BOD=30∘ (vertically opposite angles)
So, ∠A of △AOC=180∘–(70∘+30∘)=80∘
(using angle sum property of a triangle)
Similarly, ∠Bof△BOD=180∘–(70∘+30∘)=80∘
Thus, we have ∠A=∠B,AC=BD and ∠C=∠D
Now, side AC is between ∠A and ∠C and side BD is between ∠B and ∠D.
So, by ASA congruence rule, △AOC≅△BOD.
CONGRUENCE AMONG RIGHT-ANGLED TRIANGLES
The above four criterions that we studied can be applied to any classification of triangles like isosceles triangles or scalene triangles but when we deal with Right angled triangles, we get a special criterion to judge their congruency. Right angled triangles are the triangles which have one of their angle equal to 90∘. The side opposite to the right angle is known as the hypotenuse and is the longest side of this type of triangle. The other two sides are called legs of the triangle which are- the base and the perpendicular.
5. RHS Criterion for Congruence
RHS criterion stands for right angle-hypotenuse-side congruence criterion. Under this criterion, two triangles are congruent, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle.
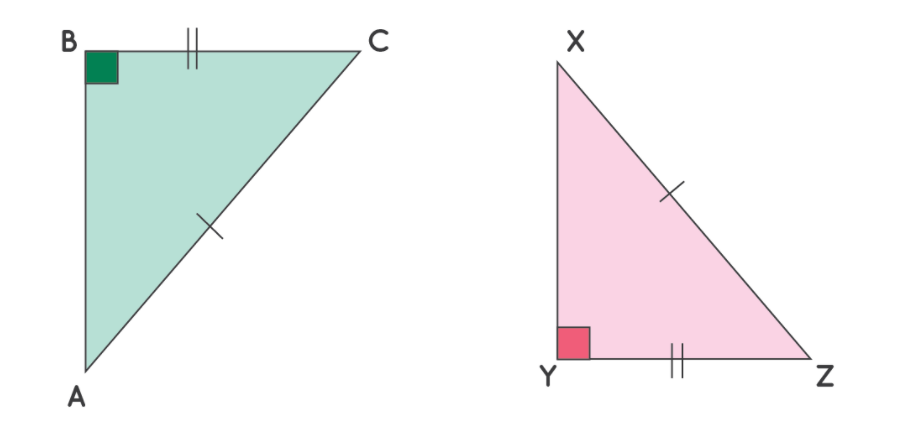
If △ABC≅△XYZ under RHS criterion, then the third side (AB) and the other two angles of △ABC are bound to be equal to the corresponding side (XY) and angles of △XYZ.
∴ We can conclude that if under a correspondence, the hypotenuse and one side of a right-angled triangle are
respectively equal to the hypotenuse and one side of another right-angled triangle, then the triangles are congruent.
Important notes
Example 6
Given below are measurements of some parts of two triangles. Examinewhether the two triangles are congruent or not, using RHS congruencerule. In case of congruent triangles, write the result in symbolic form
△ABC △PQR
(i)∠B=90∘,AC=8cm,AB=3cm ∠P=90∘,PR=3cm,QR=8cm (ii)∠A=90∘,AC=5cm,BC=9cm ∠Q=90∘,PR=8cm,PQ=5cm
The three pairs of equal parts are:
∠ABC=∠BAD(=90∘)
AC=BD (Given)
AB=BA (Common side)
From the above, △ABC≅△BAD (By RHS congruence rule).
So, statement (i) is true
Statement (ii) is not meaningful, in the sense that the correspondence among the vertices
is not satisfied.
Example 7
In Fig 7.31, DA⊥AB,CB⊥ABandAC=BD. State the three pairs of equal parts in ΔABCandΔDAB. Which of the following statements is meaningful?
(i) ΔABC≅ΔBAD
(ii) ΔABC≅ABD
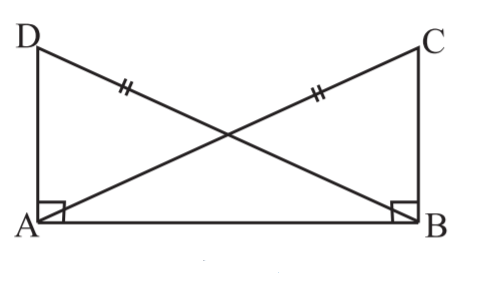
The three pairs of equal parts are:
∠ABC=∠BAD(=90∘)
AC=BD (Given)
AB=BA (Common side)
From the above, △ABC≅△BAD (By RHS congruence rule).
So, statement (i) is true
Statement (ii) is not meaningful, in the sense that the correspondence among the vertices is not satisfied.
Let's Summarize
1. Congruent objects are exact copies of one another.
2. The method of superposition examines the congruence of plane figures.
3. Two plane figures, say, F1 and F2 are congruent if the trace-copy of F1 fits exactly on
that of F2. We write this as F1≅F2.
4. Two line segments, say, AB and CD , are congruent if they have equal lengths. We
write this as AB≅CD . However, it is common to write it as AB=CD .
5. Two angles, say, ∠ABC and ∠PQR, are congruent if their measures are equal. We write this as ∠ABC≅∠PQR or as m∠ABC=m∠PQR. However, in practice, it is
common to write it as ∠ABC=∠PQR.
6. SSS Congruence of two triangles:
Under a given correspondence, two triangles are congruent if the three sides of the
one are equal to the three corresponding sides of the other.
7. SAS Congruence of two triangles:
Under a given correspondence, two triangles are congruent if two sides and the angle
included between them in one of the triangles are equal to the corresponding sides and
the angle included between them of the other triangle.
8. ASA Congruence of two triangles:
Under a given correspondence, two triangles are congruent if two angles and the side
included between them in one of the triangles are equal to the corresponding angles
and the side included between them of the other triangle.
9. RHS Congruence of two right-angled triangles:
Under a given correspondence, two right-angled triangles are congruent if the hypotenuse
and a leg of one of the triangles are equal to the hypotenuse and the corresponding leg
of the other triangle.
10. There is no such thing as AAA Congruence of two triangles:
Two triangles with equal corresponding angles need not be congruent. In such a
correspondence, one of them can be an enlarged copy of the other. (They would be
congruent only if they are exact copies of one another).
Let's Revise
1. Baccho, iss chapter m humne congruency k baare m pdha aur seekha ki kaise congruency ka concept line segments aur different fugures m apply hota hai especially with respect to a triangle.
2. Do objects congruent tab khelaata hai jab vo ek dusre k exact copies hote hai. Agar do figures ya line segments ek dusre ko completely overlap krte hai to vo congruent hote hai.
3. Jab do angles ka measurements equal hota hai to vo congruent angles kehlaate hai.
4. Congruency is depicted with the symbol ≅.
5. We write congruent line segments as AB≅CD and congruent angles as ∠ABC≅∠DEF
6. Jab do triangles k saare elements (like vertices, sides and angles) equal hote hai, to unhe congruent triangles kaha jaata hai. We represent them as △ABC≅△DEF.
7. There are 5 criterions to judge the congruency of two triangles. Ther are -SSS, SAS, ASA, AAS, RHS
8. Agar do triangles ki corresponding sides k measurements equal ho to vo congruent traingles hote hai. This is known as SSS congruency criterion.
9. Agar do triangles k do corresponding angles aur unke beech ki included side equal ho to vo triangles congruent hote hai. This is known as ASA congruency criterion.
10.Agar do triangles k do corresponding side k measurements aur unke beech ke included angle equal ho to vo triangles congruent hote hai. This is known as SAS congruency criterion.
11. Jab ek triangle k do angles aur ek non-included side dusre triangle k corresponding angles aur corresponding non-included side k equal ho to vo dono triangles congruent hote hai. This is known as ∀S congruency criterion.
12. Jab do right angled triangles k corresponding hypotenuses aur koi bhi ek aur corresponding side (perpendicular or base) equal ho measurement m to vo congruent triangles kehlaate hai. This is because of RHS congruency criterion.