सममिति कक्षा 7 गणित
भूमिका
बच्चों! अध्याय के शीर्षक के अनुसार इस अध्याय में सममिति का अध्ययन करेंगे। ऐसी आकृति जो बराबर संतुलित अनुपात में हो अर्थात एक आकृति के दो भाग एक - दूसरे के पूर्णतः बराबर हो, सममित आकृति (Symmetric Figure) कहलाती है। एक आकृति में सममित रेखा होती है, यदि एक खींची गई रेखा आकृति को दो बराबर या समान भागों में बांटती हो, तो यह रेखा सममित रेखा (Symmetric Line) कहलाती है।
आइये जानते है, सममिति को और करीब से...
हमारे दैनिक जीवन मे हमे बहुत से सममित आकृतियाँ देखने को मिलती रहती हैं।

ऊपर आकृति मे हम देख सकते हैं, कि तितली और पुष्प के दोनों भाग पूर्णतः एक - दूसरे के बराबर हैं। अतः ये सममित आकृति हैं।
इसी प्रकार,
प्रकृति मे पुष्प, मछली, गाय, कछुआ और बहुत से प्राणियों की आकृतियाँ सममित होती हैं।

बहुत से वस्तुओं, इमारतों को बनाने में भी सममिति का ध्यान रखा जाता हैं।
जैसे: नीचे आकृति में देख सकते हैं:


यदि, एक खींची गई रेखा आकृति को दो बराबर या समान भागों में विभाजित करती हैं, तो रेखा सममित रेखा कहलाती है।
आइए समझते हैं:-
जब किसी कागज को इस प्रकार मोड़ते हैं कि चित्र दो बराबर भागों में विभाजित हो जाता है, तो विभाजित करने वाली रेखा ही सममित रेखा है।

यहाँ, रेखा तारे को दो पूर्णतः बराबर भागों में विभाजित करती है इसलिए यह सममित रेखा है। इसे दर्पण रेखा भी कहा जाता है क्योंकि अगर हम उस रेखा पर दर्पण रखेंगे तो आकृति का एक भाग बिल्कुल दूसरी भाग के जैसा दिखेगा।
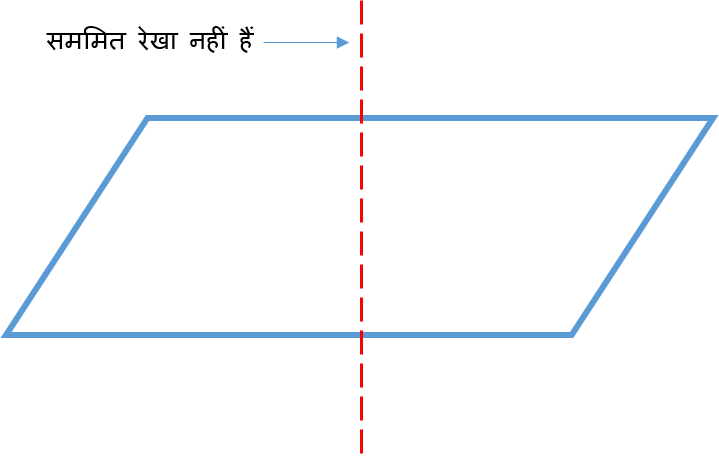
यह, आकृति सममित नहीं है क्योंकि यदि हम इस आकृति को दो भागों मे विभाजित करते हैं, तो इसके दोनों भाग एक - दूसरे के बराबर नहीं है।
सममित आकृतियां बनाना
आइए सममित आकृति बनाने के लिए कुछ क्रियाकलाप करते हैं:

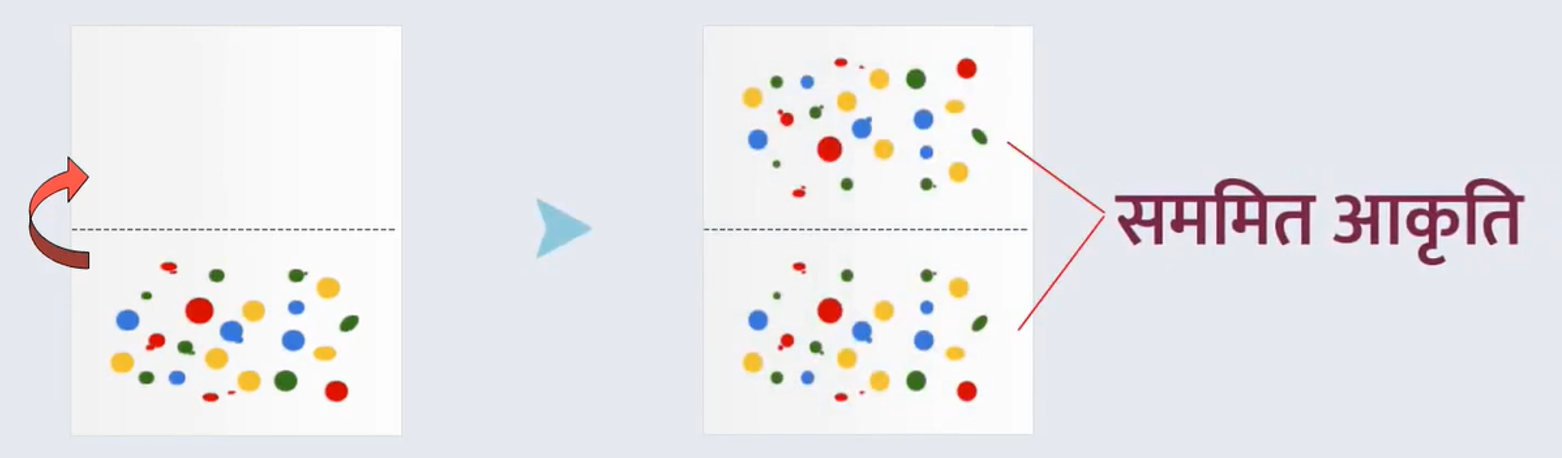
इस क्रियाकलाप में हमने देखा कि कागज में स्याही (इंक) की मदद से सममित आकृति कैसे प्राप्त कर सकते हैं।
आइए एक और क्रियाकलाप करते हैं:
यह क्रियाकलाप भी, ऊपर हमने जो क्रियाकलाप किया हैं उसी के जैसा ही हैं, यहाँ हम कागज मे स्याही से भीगी हुई धागे को रखेंगे।


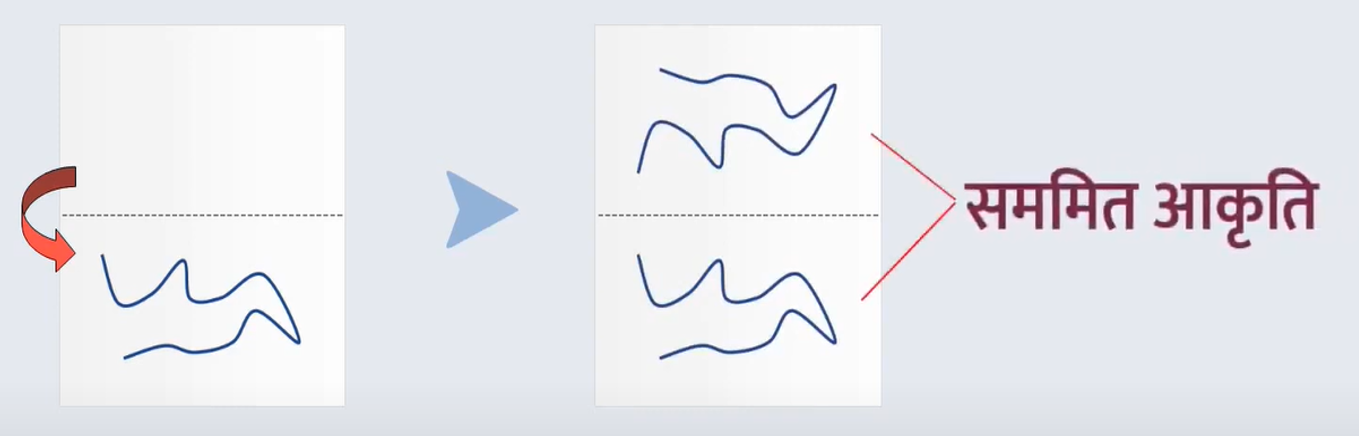
अतः, दोनों भागों मे बनी स्याही के निशान से स्पष्ट हैं कि पहले भाग में बनी आकृति दूसरे भाग में बनी आकृति से सममित हैं।
अंग्रेजी वर्णमाला के अक्षरों की सममिति
हम जानते हैं कि, एक आकृति में सममित रेखा होती है, यदि एक खींची गई रेखा आकृति को दो बराबर या समान भागों में बांटती हो, यह रेखा सममित रेखा या दर्पण रेखा कहलाती है।जैसे:-

कुछ आकृतियों में दो सममित रेखाएँ होती हैं।
दो सममित रेखाओं वाले अक्षर :- यदि हम कागज का एक आयताकार टुकड़ा लें और उसे दो बार मोड़कर दो सममित रेखाएँ बना लें और उसे किसी नए आकार में काट लें, तो उसे खोलने के बाद हमें दो सममित रेखाओं के साथ आकृति प्राप्त होती हैं।
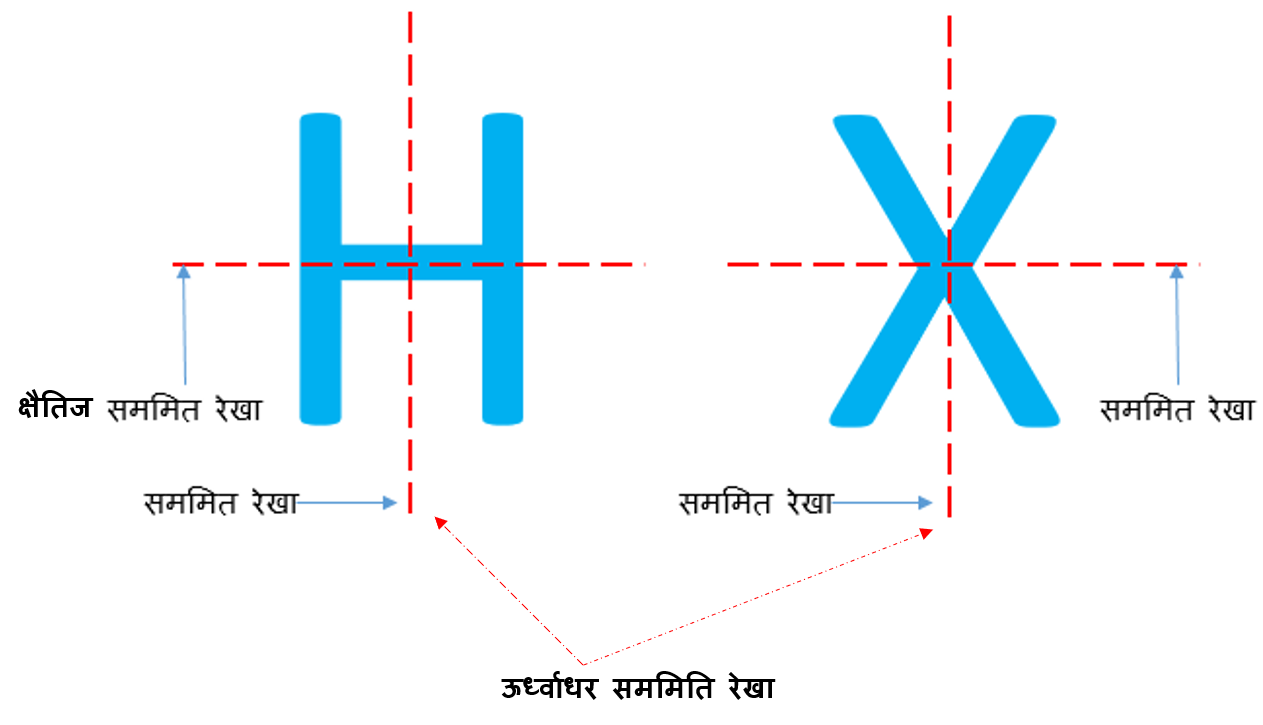
इस प्रकार अंग्रेजी वर्णमाला के अक्षरों के लिए भी हम सममित रेखा खींच सकते है।
सम बहुभुजों के लिए सममित रेखाएं
बच्चों! अब तक हमने आकृतियों में एक और दो सममित रेखाओं वाले आकृति का अध्ययन किया है।
आइए अब हम सम बहुभुजों के लिए सममित रेखाओं का निर्माण करते है :-
एक वर्गाकार कागज़ का टुकड़ा लेते हैं।
इसे ऊर्ध्वाधर (vertically) में आधे से मोड़ते हैं और पुन: क्षैतिज (horizontally) से आधे भाग से मोड़ते हैं (अर्थात् इसे दो बार मोड़ते हैं)।
इसे खोलकर पुनः वर्ग को आधे भाग से मोड़ते हैं (अर्थात् तीसरी बार), लेकिन इस बार विकर्ण के साथ-साथ जैसा कि आकृति में दिखाया गया है।
इसे पुनः खोलिए और आधे भाग से मोड़िए (चौथी बार) दूसरे विकर्ण के साथ।
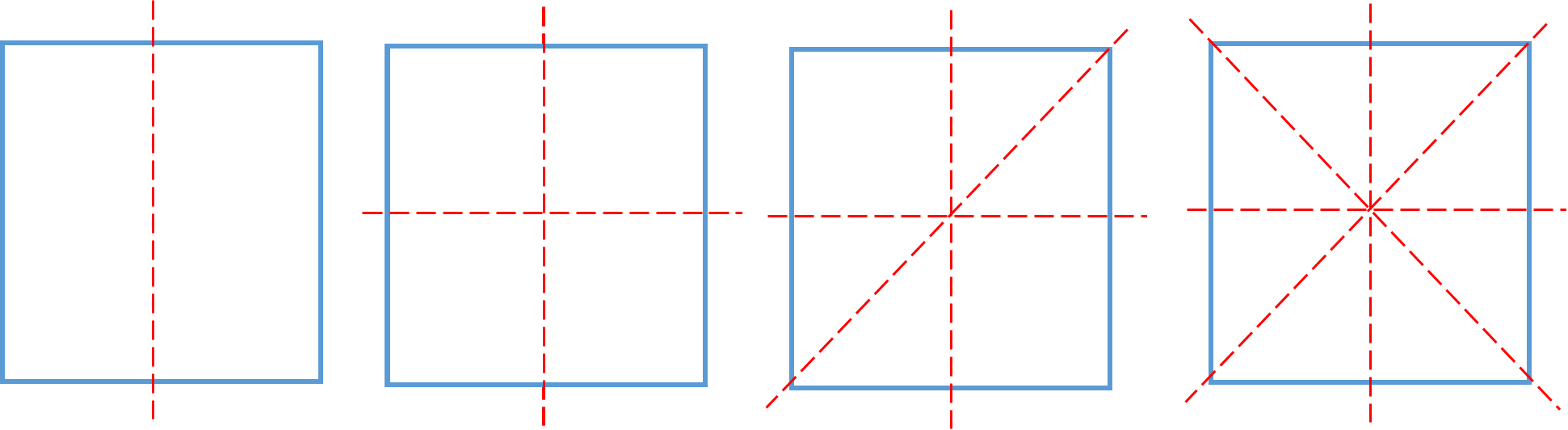
अब जैसे कि हम देख सकते हैं कि वर्ग में हमे 4 सममित रेखाएँ प्राप्त होती हैं।
दो से अधिक सममित रेखाओं वाली कुछ और आकृति:
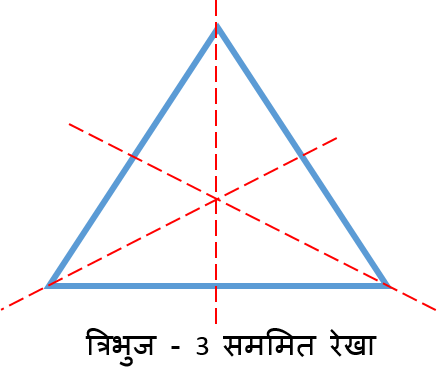
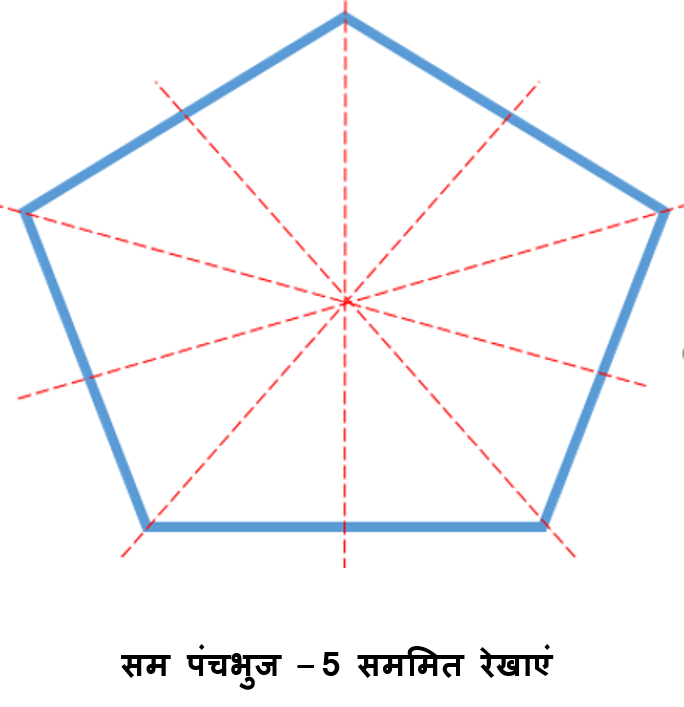
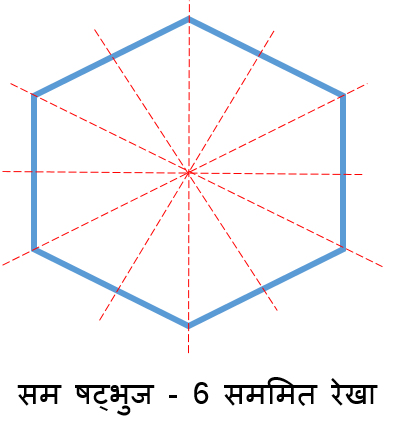
OMR (One Minute Revision)
उदाहरण 1
दी गई आकृति में जाँच कीजिए कि क्या ये आकृतियाँ सममित हैं या नहीं तथा उनकी सममित रेखा खींचिये।
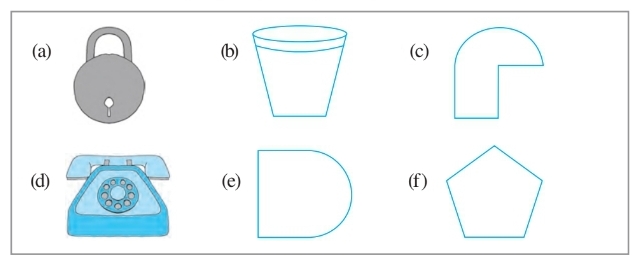
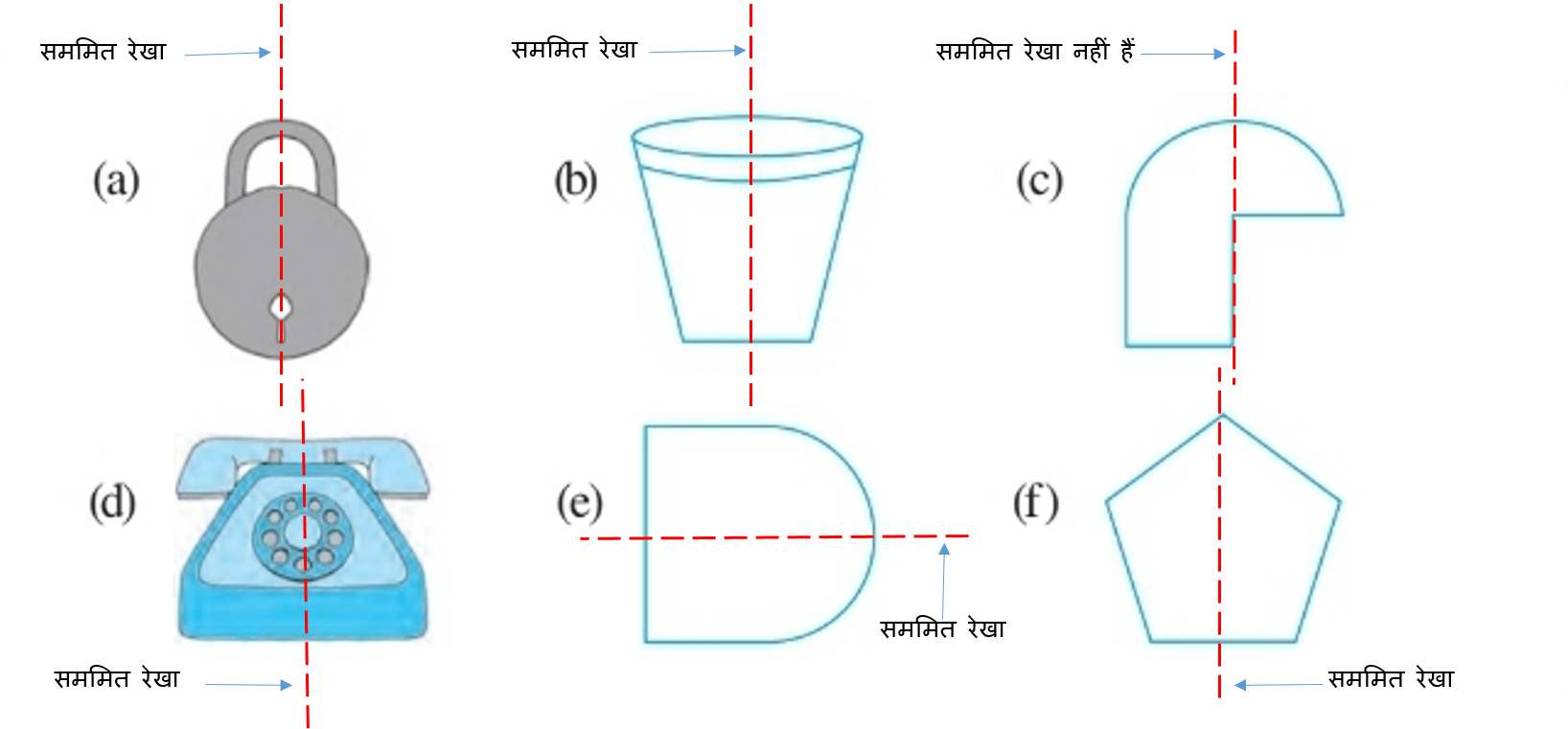
हम जानते है कि, किसी आकृति को दो भागों मे बांटने पर, आकृति के दोनों भाग एक - दूसरे के पूर्णतः बराबर हो, तो आकृति सममित आकृति कहलाती है तथा आकृति को दो बराबर भागों में बांटने वाली रेखा, सममित रेखा होती है।
अतः दिए गये आकृति मे आकृति (a), आकृति (b), आकृति (d), आकृति (e) और आकृति (f) सममित आकृति हैं क्योंकि आकृति को दो भागों में बांटने पर इनके दोनों भाग एक - दूसरे के पूर्णतः बराबर हैं।
आकृति (c) सममित आकृति नहीं हैं क्योंकि आकृति को दो भागों में बांटने पर इनके दोनों भाग एक - दूसरे के बराबर नहीं हैं।
उदाहरण 2
नीचे दी गई अंग्रेजी वर्णमाला के अक्षरों में सममित अक्षरों को चुनिए।
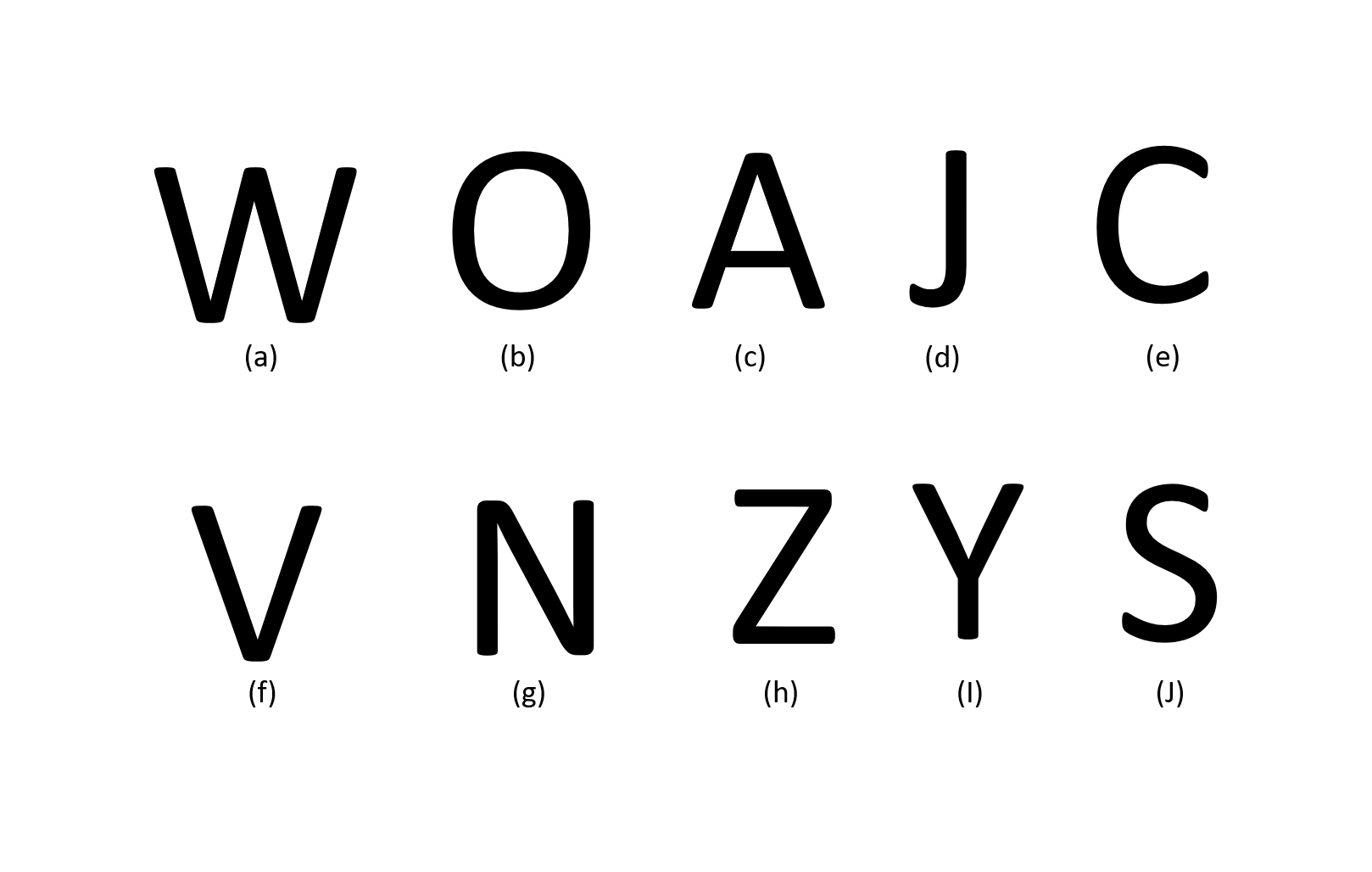
(a) यदि हम W को ऊर्ध्वाधर दो भागों में विभाजित करे तो, इसके दोनों भाग (दायाँ एवं बायाँ) एक - दूसरे के पूर्णतः बराबर होंगे।
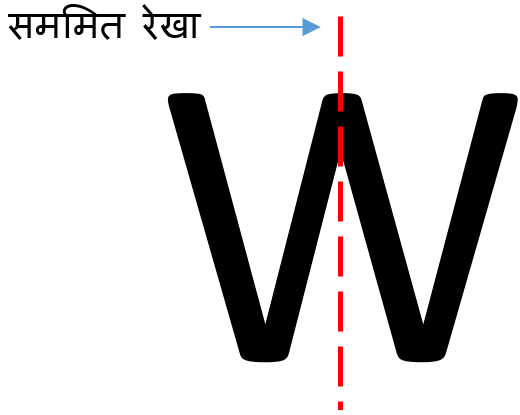
∴ W एक सममित अक्षर हैं।
(b) यदि हम O को दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
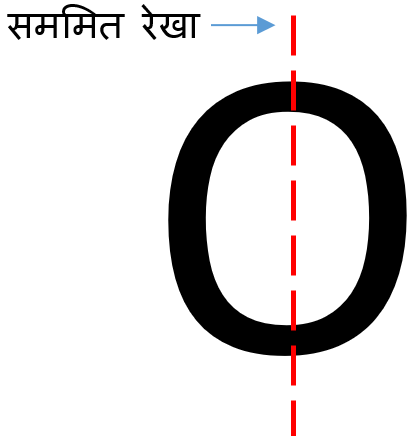
∴ O एक सममित अक्षर हैं।
(C) यदि A को ऊर्ध्वाधर दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
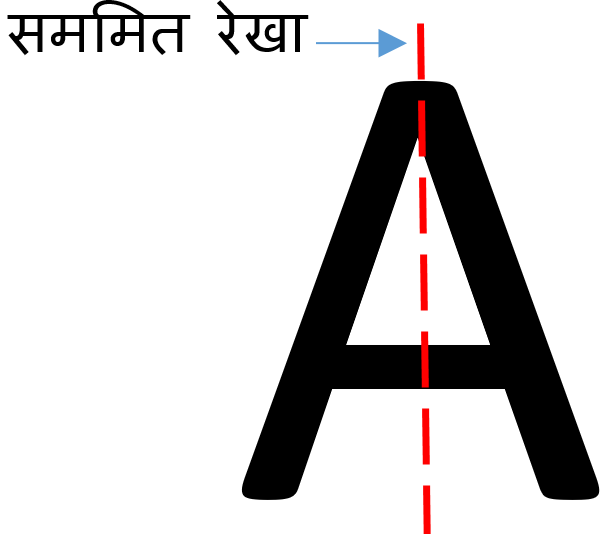
∴ A एक सममित अक्षर हैं।
(d) यदि J को दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के बराबर नहीं होंगे।
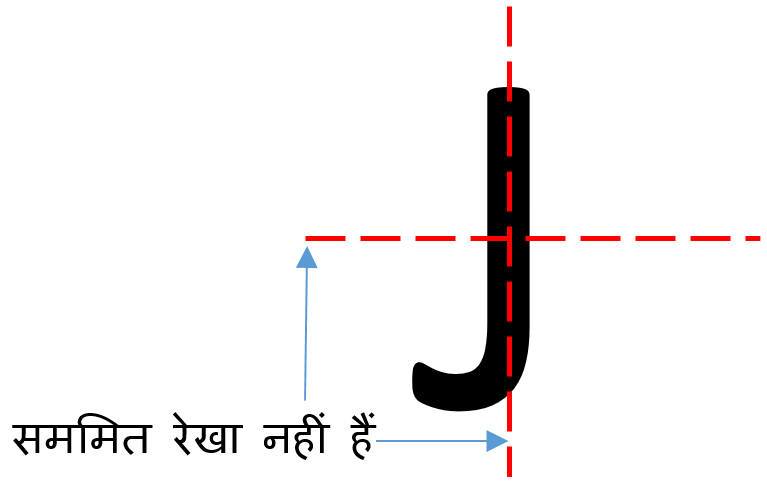
∴J एक सममित अक्षर नहीं हैं।
(e) यदि C को क्षैतिज दो भागों में विभाजित करे, इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
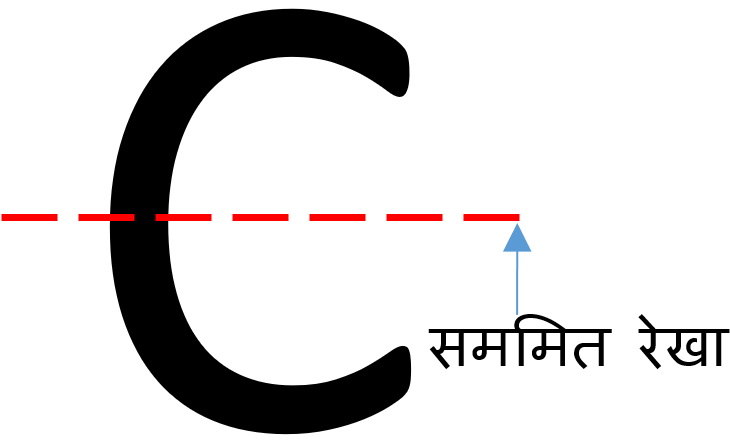
∴ C एक सममित अक्षर हैं।
(f) यदि V को ऊर्ध्वाधर दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
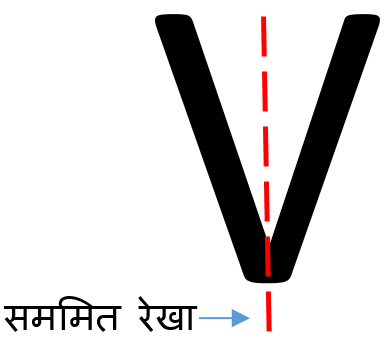
∴ V एक सममित अक्षर हैं।
(g) यदि N को दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के बराबर नहीं होंगे।
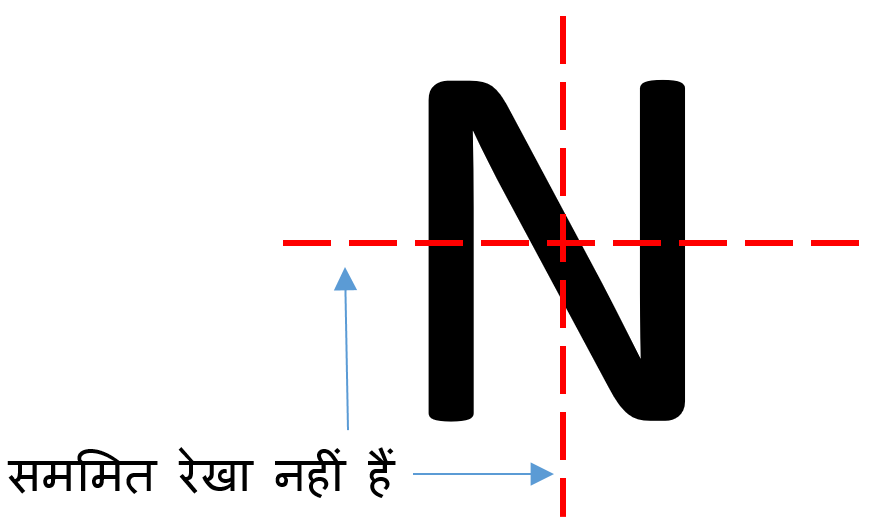
∴ N एक सममित अक्षर नहीं हैं।
(h) यदि Z को दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के बराबर नहीं होंगे।
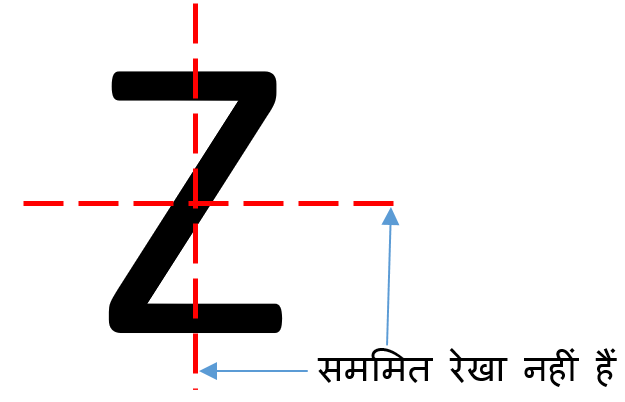
(i) यदि Y को ऊर्ध्वाधर दो भागों में विभाजित करे तो इसके दोनों भाग एक - दूसरे के पूर्णतः बराबर होंगे।
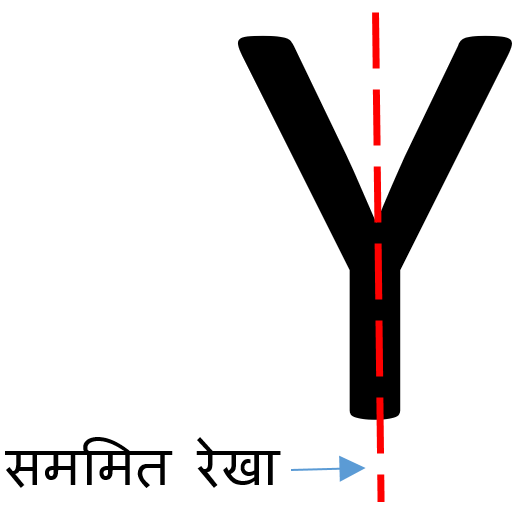
∴ Y एक सममित अक्षर हैं।
(J) यदि S को दो भागों में विभाजित करे, इसके दोनों भाग एक - दूसरे के बराबर नहीं होंगे।
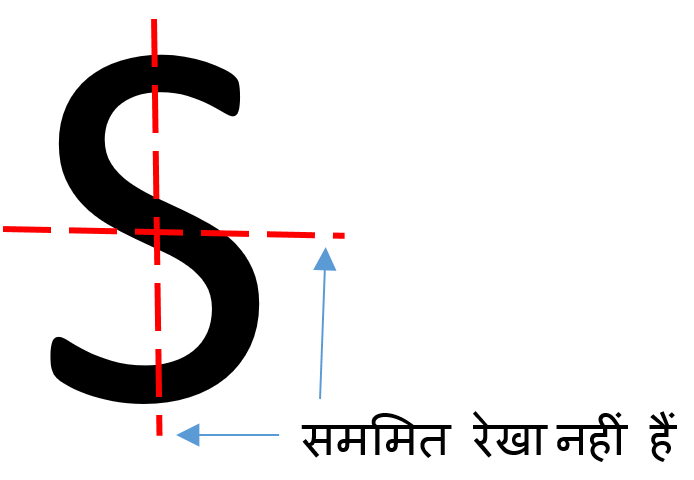
∴ S एक सममित अक्षर नहीं हैं।
अतः स्पष्ट है कि, W, O, A, C, V, और Y सममित अक्षर हैं।
उदाहरण 3
M, H, E, V में से किस अक्षर में ऊर्ध्वाधर सममित रेखा नहीं है ?
यदि M, H तथा V को एक ऊर्ध्वाधर सममित रेखा खींचकर दो भागों में विभाजित करे, तो इनके दोनों भाग एक - दूसरे के पूर्णतः बराबर होते हैं, तथा एक भाग को दूसरे के ऊपर रखेंगे तो उसे पूरी तरह से ढ़क लेगा।
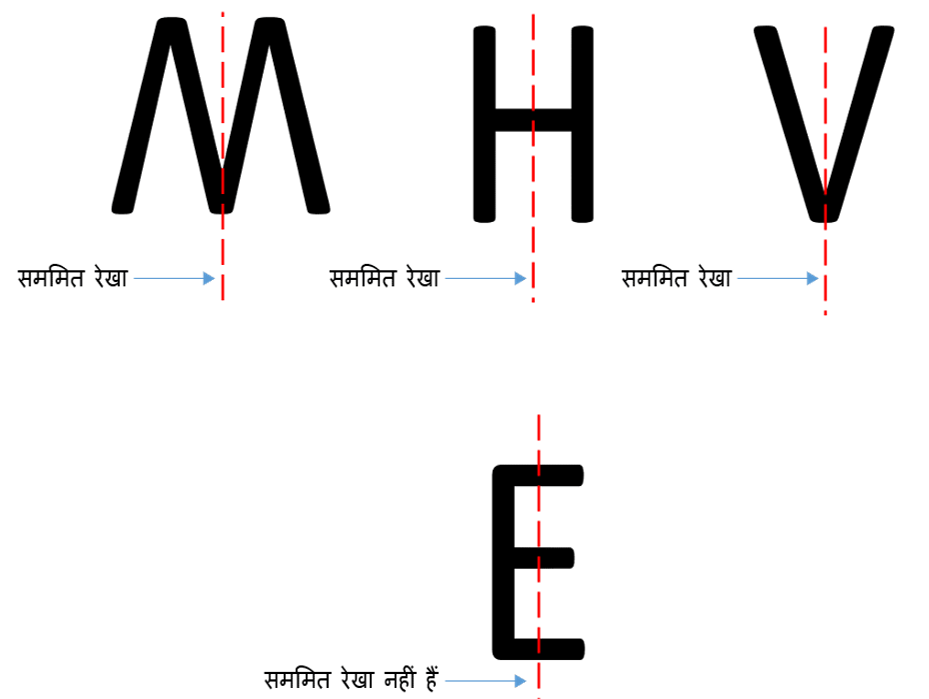
लेकिन E को एक ऊर्ध्वाधर सममित रेखा खींचकर दो भागों में विभाजित करे तो इसके दोनों भाग बराबर नहीं होंगे। अतः E में, ऊर्ध्वाधर सममित रेखा नहीं खींची जा सकती हैं।
उदाहरण 4
किस प्रकार के त्रिभुज में
(a) कोई सममिति रेखा नहीं होती है।
(b) एक सममिति रेखा होती है।
(c) तीन सममिति रेखाएँ होती हैं। उनके चित्र भी खींचें।
(a) माना कि ΔABC एक विषमबाहु त्रिभुज हैं।
∵ विषमबाहु त्रिभुज की तीनों भुजाओं की माप अलग-अलग होती हैं, इसलिए इन्हे बराबर भागों मे विभाजित करने पर, दोनों भाग बराबर नहीं होते हैं।
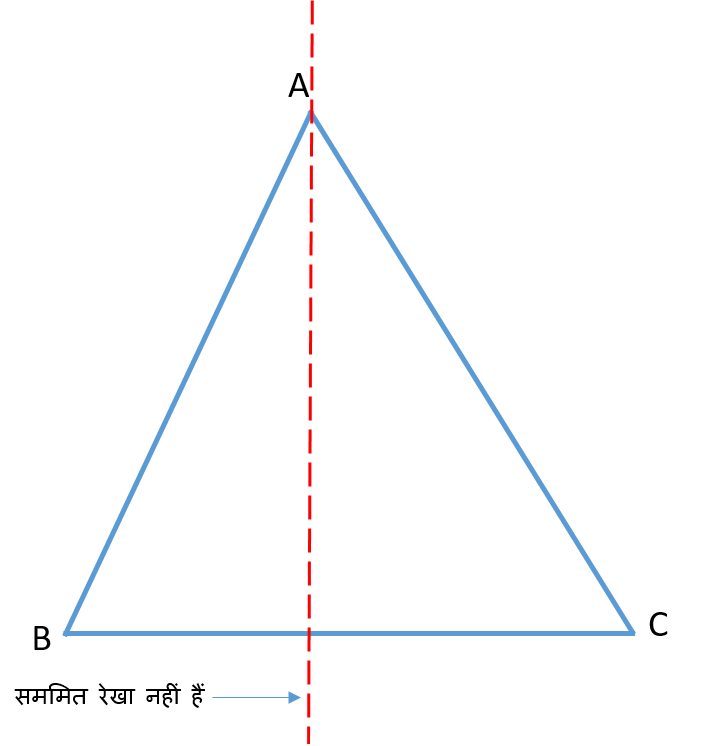
अतः, विषमबाहु त्रिभुज में कोई सममिति रेखा नहीं होती है।
(b) माना कि ΔPQR एक समद्विबाहु त्रिभुज हैं।
∵ समद्विबाहु त्रिभुज की दो भुजाओं की माप बराबर होती हैं, यहाँ भुजा PQ=PR हैं।
∴ यदि समद्विबाहु त्रिभुज को दो बराबर भागों मे विभाजित करे तो, दोनों भाग एक - दूसरे के पूर्णतः बराबर होते हैं।
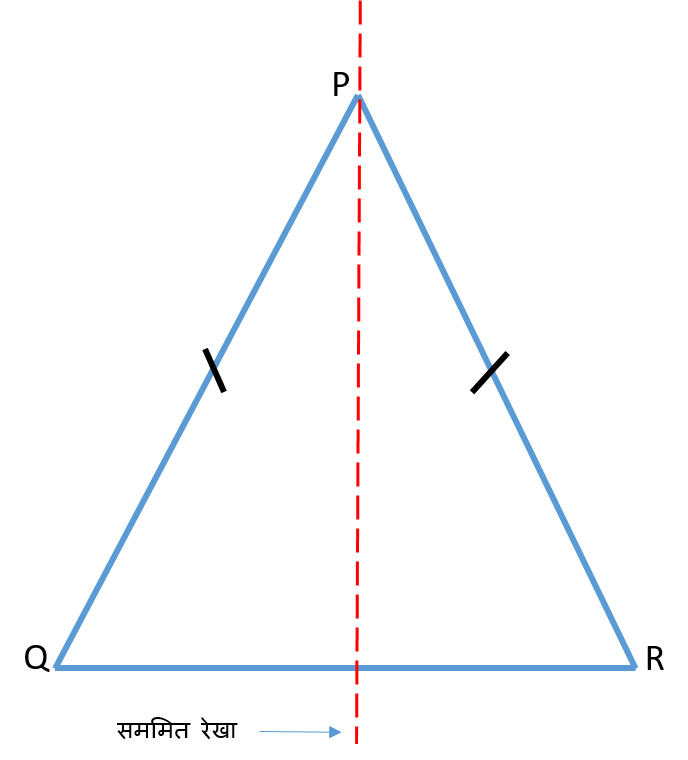
अतः, समद्विबाहु त्रिभुज में 1 सममिति रेखा होती है।
(c) माना कि ΔDEF एक समबाहु त्रिभुज हैं।
∵ समबाहु त्रिभुज की तीनों भुजाओं की माप बराबर होती हैं, यहाँ DE=EF=FD
∴ समबाहु त्रिभुज में तीन सममिति रेखाएँ खींची जा सकती हैं, जैसा कि आकृति में दिखाया गया हैं।
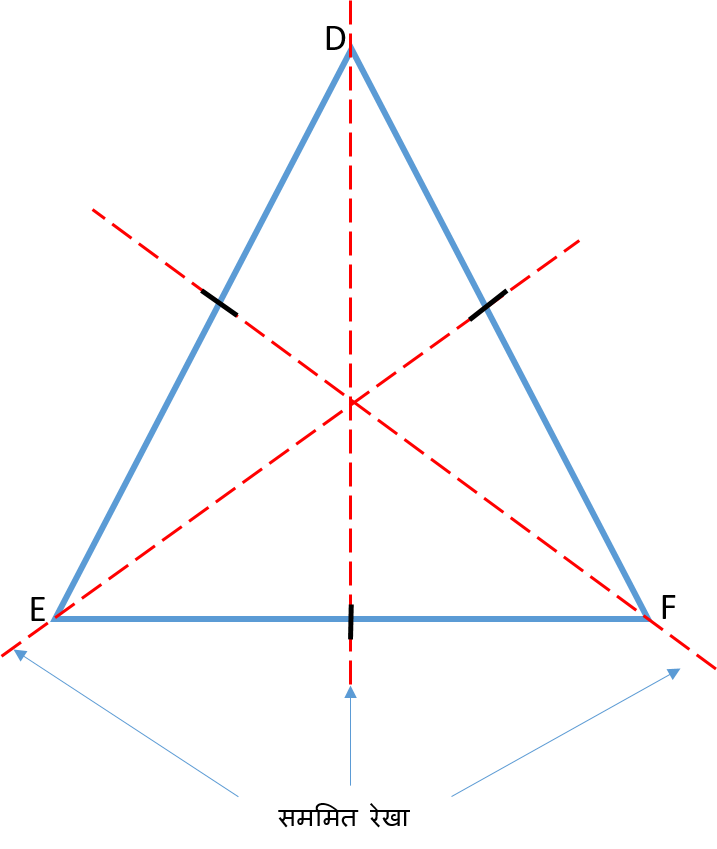
अतः समबाहु त्रिभुज में 3 सममिति रेखा होती है।
उदाहरण 5
निम्नलिखित आकृति के लिए सममित रेखाओं की संख्या बताइए :
एक समचतुर्भुज
वह रेखाखंड जो आकृति को दो बराबर भागों में बांटती है, सममित रेखा कहलाती हैं।

एक समचतुर्भुज में सममित रेखाओं की संख्या =2
घूर्णन सममिति
किसी आकृति को उसके केंद्र बिंदु के सापेक्ष 360∘ या आंशिक रूप से घूमाने पर, वह आकृति जितनी बार समान दिखती है, वह उसकी घूर्णी समरूपता को दर्शाती है। अर्थात किसी आकृति को तब तक घुमाया जाता हैं जब तक वह अपनी प्रारम्भिक आकार मे ना आ जाए।
घूर्णी समरूपता पर महत्वपूर्ण बिन्दु :-
=
उदाहरण 6
क्या हमें क्रम 1 से अधिक की घूर्णन सममिति प्राप्त हो सकती है, जिसके घूर्णन का कोण 45∘ हो ?
घूर्णन सममिति के हम निम्नलिखित सूत्र का प्रयोग करते है :-
यदि हमे घूर्णन का कोण दिया गया हो तो उसे उपर्युक्त सूत्र मे रखने पर :-
स्थिति 1: यदि हमे पूर्ण (सम) संख्या प्राप्त हो तो उसमे हमे क्रम 1 से अधिक की घूर्णन सममिति प्राप्त होती है।
स्थिति 2: यदि हमे अपूर्ण (विषम) संख्या प्राप्त हो तो उसमे हमे क्रम 1 से अधिक की घूर्णन सममिति प्राप्त नहीं होती है।
चूंकि घूर्णन कोण =45∘
सुत्रानुसार :-
=
= 8 (सम संख्या)
अतः हमे इस आकृति मे क्रम 1 से अधिक की घूर्णन सममिति प्राप्त होगी।
उदाहरण 7
यदि किसी आकृति की दो या अधिक सममित रेखाएँ हों, तो क्या यह आवश्यक है कि उसमें क्रम 1 से अधिक की घूर्णन सममिति होगी ?
जब किसी आकृति मे दो या दो से अधिक सममित रेखाएं हो तो यह आवश्यक है कि उसमे क्रम 1 से अधिक की घूर्णन सममिति होती है। जैसे :-
हम एक वर्ग की आकृति बनाते है तथा उसमे सममित रेखाएं खींचते है।
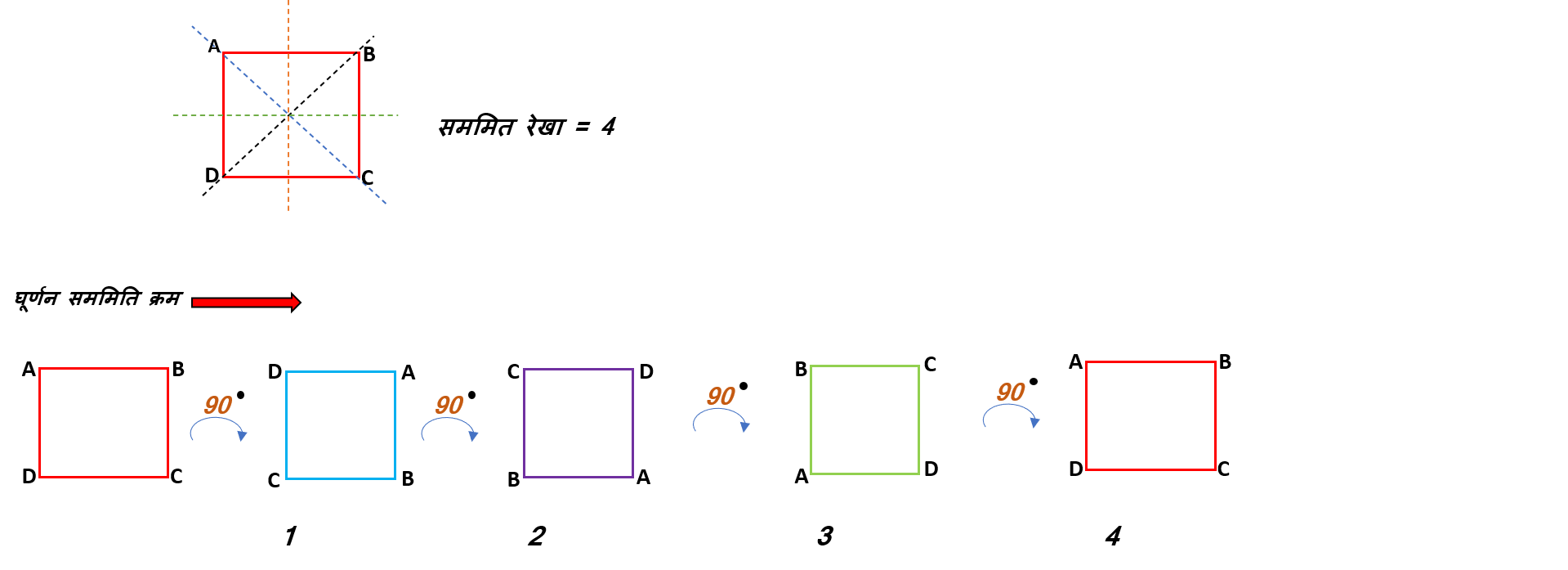
उदाहरण 8
आकृति में दिए गए हवाई चकरी के घूर्णन सममिति की व्याख्या कीजिए।

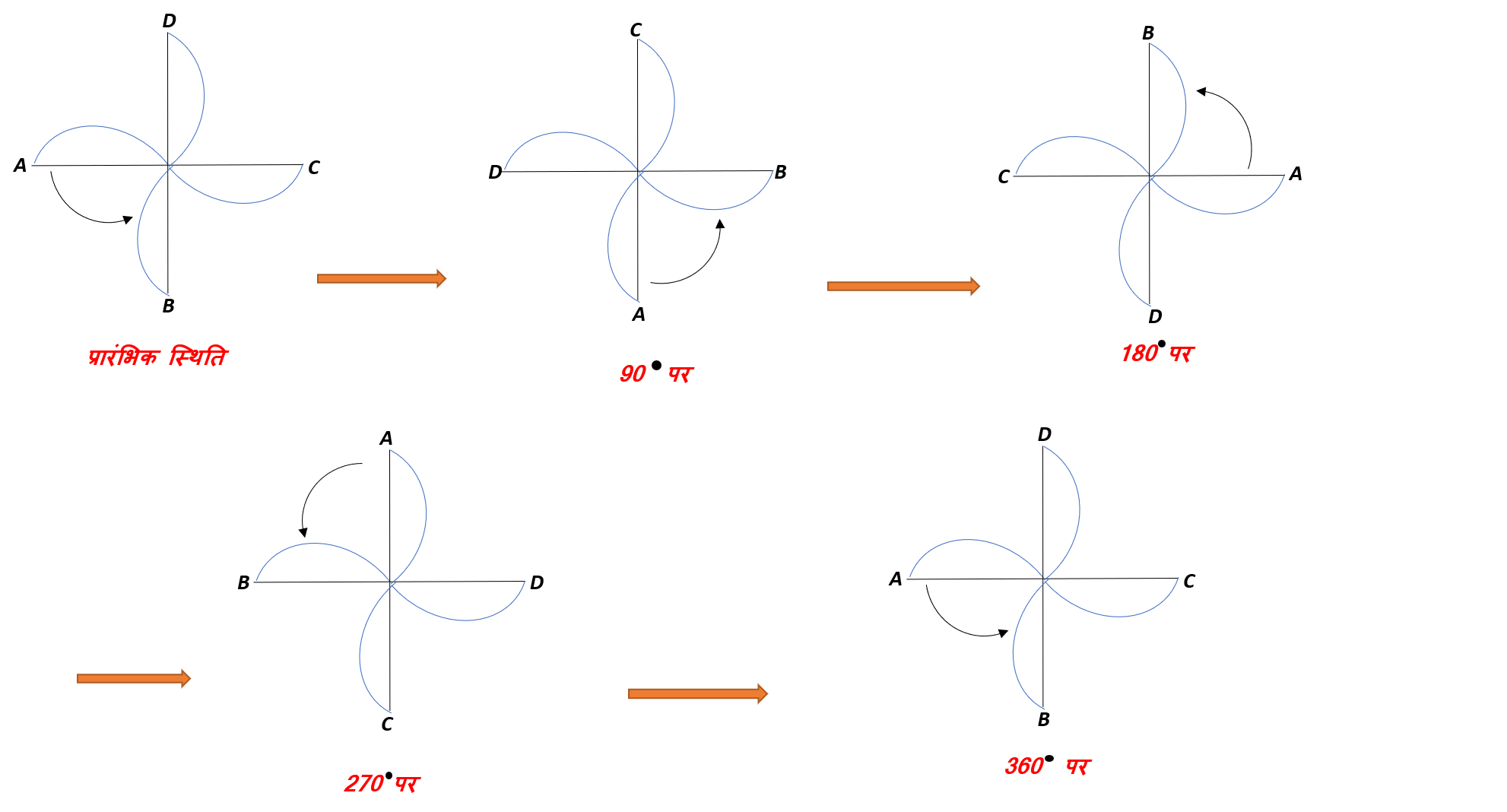
घूर्णन कोण =90∘
सममिति का क्रम =360∘90∘=4
अतः इस आकृति मे 4 क्रम की घूर्णन सममिति है।
रैखिक सममिति और घूर्णन सममिति
जब कोई ऐसी रेखा प्राप्त की जा सके जिसके अनुदिश उस आकृति को मोड़ने पर, उसके दोनों भाग परस्पर संपाती (Coincide) हो जाएँ, तब आकृति में रैखिक सममिति होती है।
घूर्णन सममिति में, आकृति की घूर्णन के पहले की स्थिति और घूर्णन के बाद की स्थिति एक-जैसी होती है।
बच्चों! अभी तक हमने अनेक आकारों और उनकी सममितियों का अध्ययन किया हैं, कुछ आकारों में केवल रैखिक सममिति होती है, कुछ में केवल घूर्णन सममिति होती है तथा कुछ आकारों में रैखिक तथा घूर्णन दोनों प्रकार की सममितियाँ होती हैं।
उदाहरणार्थ, नीचे आकृति में देख सकते है:
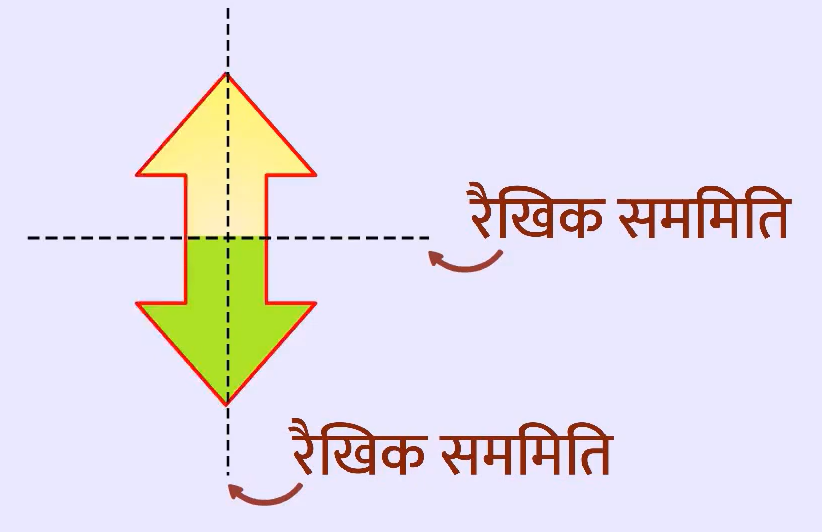
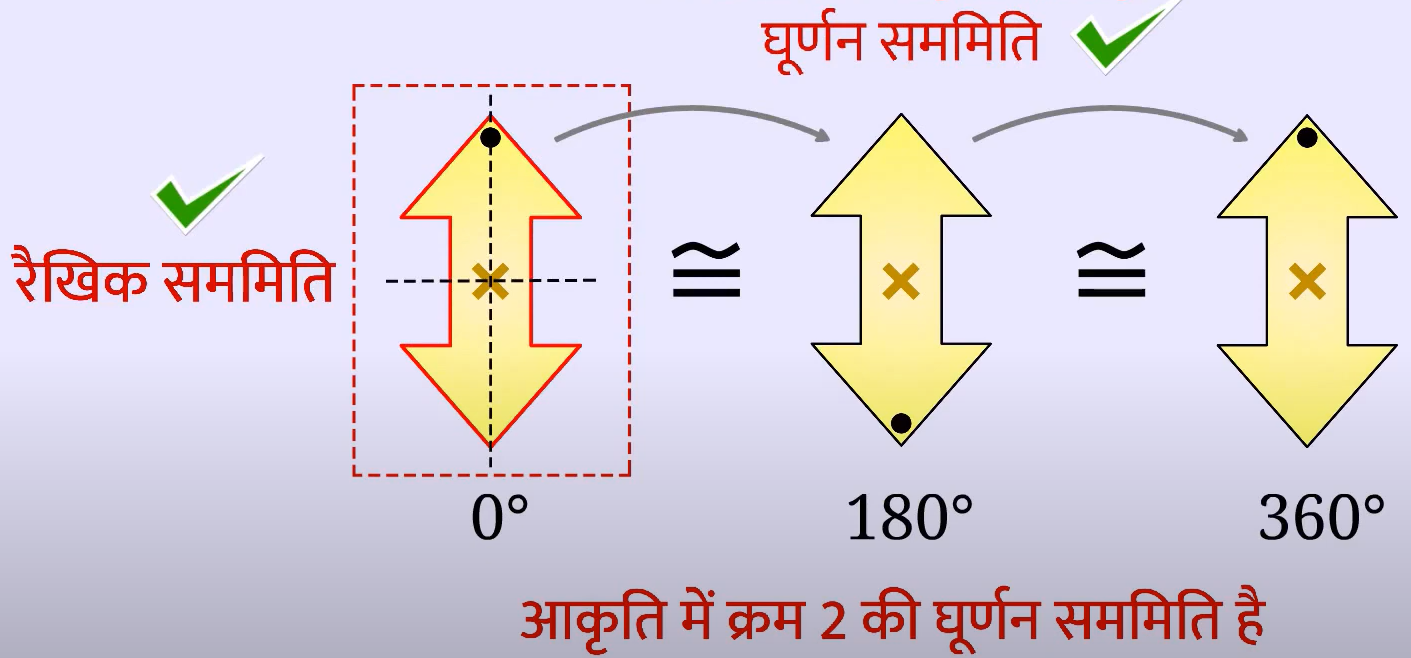
आकृति मे रैखिक एवं घूर्णन दोनों प्रकार की सममितियाँ हैं।
इसी तरह,
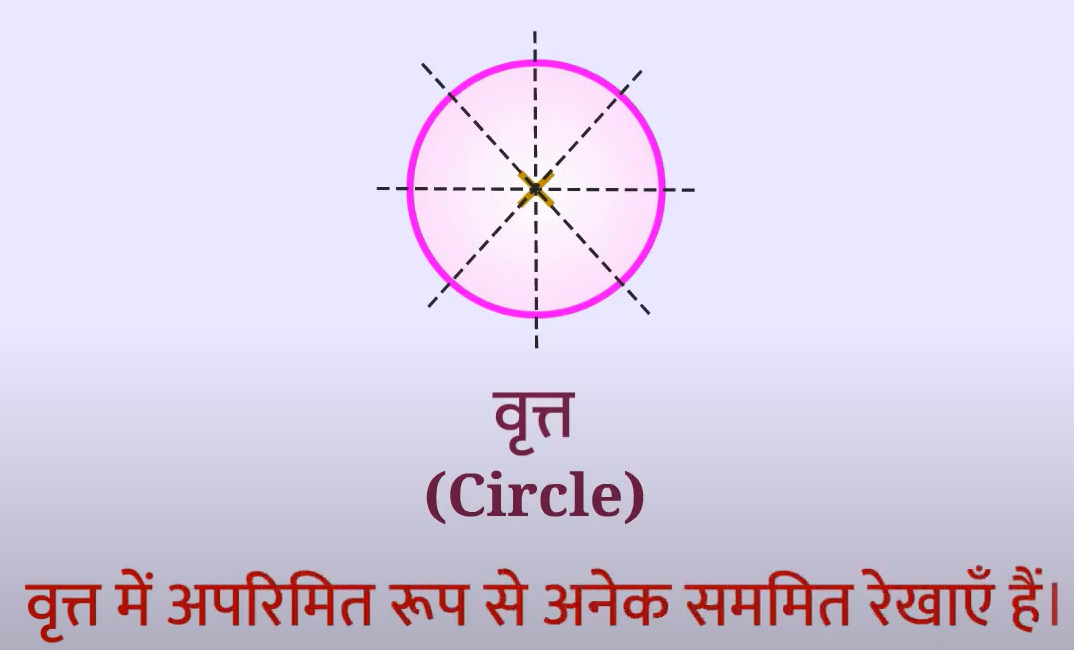
एक वृत्त सबसे अधिक पूर्ण सममित आकृति है, क्योंकि इसको इसके केंद्र के परित किसी भी कोण पर घुमा कर वही आकृति प्राप्त की जा सकती है, अर्थात् इसमें अपरिमित रूप से अनेक क्रम की घूर्णन सममिति है तथा साथ ही इसकी अपरिमित सममित रेखाएँ हैं। केंद्र से होकर जाने वाली प्रत्येक रेखा (अर्थात् प्रत्येक व्यास) परावर्तन सममिति की एक सममिति रेखा है तथा केंद्र के परित: प्रत्येक कोण के लिए इसकी एक घूर्णन सममिति है।
OMR (One Minute Revision)
जब कोई ऐसी रेखा प्राप्त की जा सके जिसके अनुदिश उस आकृति को मोड़ने पर, उसके दोनों भाग परस्पर संपाती (Coincide) हो जाएँ, तब आकृति में रैखिक सममिति होती है।
घूर्णन सममिति में, आकृति की घूर्णन के पहले की स्थिति और घूर्णन के बाद की स्थिति एक-जैसी होती है।
उदाहरण 9
निम्नलिखित के लिए आकृति खींचिए।
एक चतुर्भुज जिसमें क्रम 1 से अधिक की घूर्णन सममिति हो, परंतु रैखिक सममिति न हो।

यह चतुर्भुज समांतर चतुर्भुज है जिसमे कोई सममित रेखा नहीं खींची जा सकती है। अतः इसमे कोई रैखिक सममिति नहीं है।
अब इसको 180∘ के कोण पर घूमाते है :-

अतः घूर्णन की सममिति =360∘180∘=2
अतः आकृति मे 2 क्रम की घूर्णन सममिति है।
उदाहरण 10
निम्नलिखित की एक रफ आकृति खींचिए :
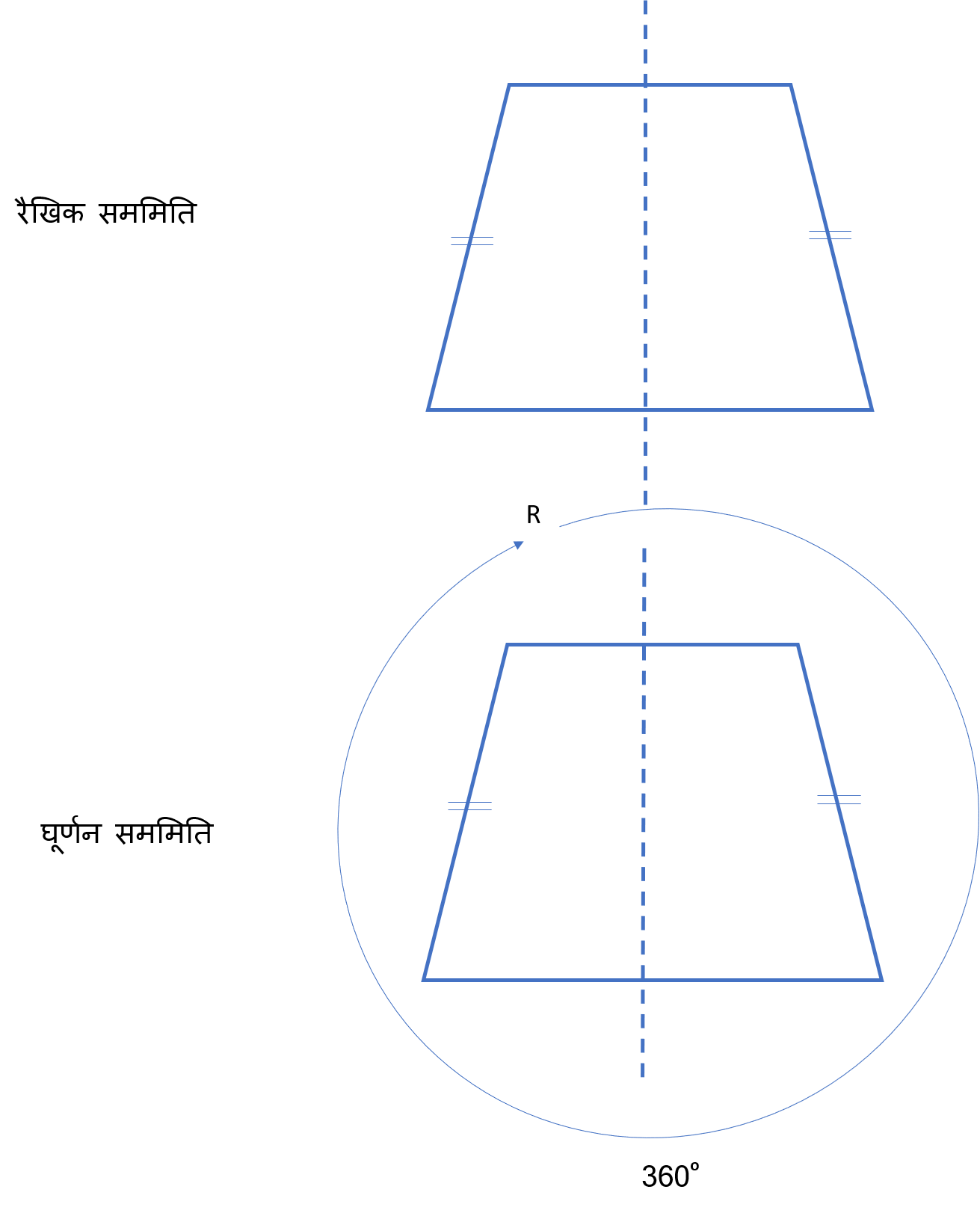
एक चतुर्भुज जिसमे केवल रैखिक सममिति हो और क्रम 1 से अधिक की घूर्णन सममिति न हो।
एक चतुर्भुज जिसमें केवल रैखिक सममिति हो और क्रम 1 से अधिक की घूर्णन सममिति न हो समद्विबाहु समलंब कहलाता है।
सारांश
| आकार | सममित रेखाओं की संख्या |
|---|---|
| समबाहु त्रिभुज | 3 | वर्ग | 4 | आयत | 2 |
| समद्विबाहु त्रिभुज | 1 |
| समचतुर्भुज | 2 |