WHOLE NUMBERS for Class 6 MATHS
INTRODUCTION
Hello baccho, I hope you all are fit and well. To baccho humne pichle chapter m numbers k baare m pdhna start kia tha and iss chapter m we'll study about natural numbers and whole numbers. Aap sabko jab kuch count krna hota hai to aap 1,2,3,4.. se counting start krte h. Inhe bolte hai counting numbers and ye hote h humare natural numbers. But agar 1,2,3,4,... se phle hum 0 lgade, to ye bnjate h whole numbers. Let's read in detail about these two sets of numbers.
NATURAL NUMBERS
To baccho jaise humne briefly abhi discuss kia, Natural numbers are the counting numbers jinhe hum day to day lives m bhi use krte hai while counting objetcs or other things.
Example 1
Write the next three natural numbers after 10999.
The next 3 natural numbers after 10999 are
10999+1=11000
10999+2=11000+1=11001
10999+3=11000+2=11002
PREDECESSOR AND SUCCESSOR
Baccho aapne apni previous classes m "what comes before" and "what comes after" ka concept seekha tha. Predecessor and successor bhi usi se related hai. Predecessor ka mtlb hota hai vo number jo given number se phle aata hai. Aur successor ka mtlb hai vo number jo given number k baad mai aata hai. For example : Predecessor of 8 is 7 and successor of 8 is 9.
Example 2
Write the successor of : (a) 2440701 (b) 100199 (c) 1099999 (d) 2345670.
Successor of :
(a) 2440701 = 2440701 + 1 = 2440702
(b) 100199=100199+1=100200
(c) 1099999=1099999+1=1100000
(d) 2345670=2345670+1=2345671
Example 3
Write the predecessor of : (a) 94 (b) 10000 (c) 208090 (d) 7654321
(a) Predecessor of
94
⇒ 94−1=93
(b) Predecessor of
10000
⇒ 10000−1=9999
(c) Predecessor of
208090
⇒ 208090−1=208089
(d) Predecessor of
7654321
⇒ 7654321−1=7654320
WHOLE NUMBERS
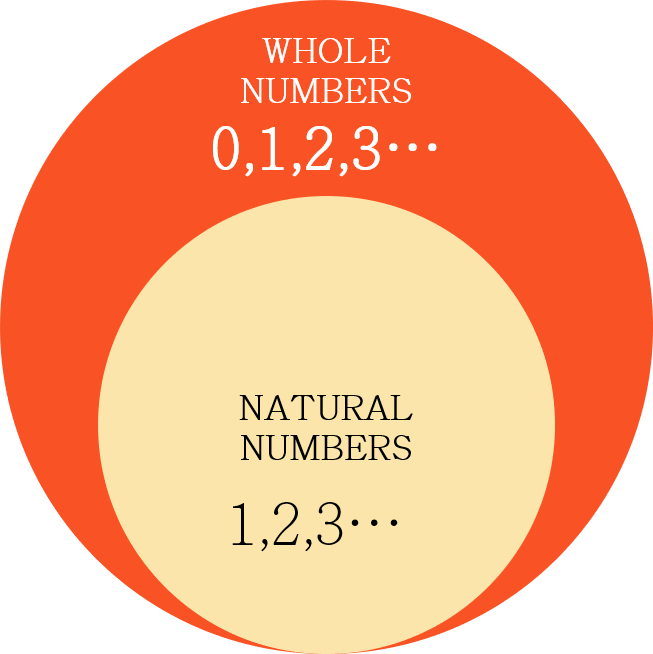
To baccho ab hum pdhenge whole numbers k baare m. Whole numbers hote hai humare 0,1,2,3,.. and so on. Agar aap notice krenge to you will see ki whole numbers are basically natural numbers including 0.
Example 4
Write the three whole numbers occurring just before 10001.
The 3 whole numbers occurring before 10001 are
10001−1=10000
10001−2=10000−1=9999
10001−3=10000−2=9998
Example 5
Which is the smallest whole number?
Whole numbers are
0, 1, 2, 3...
∴ Smallest whole no is 0
THE NUMBER LINE
I hope aap sabko natural numbers and whole numbers ka concept clear hogya ho. Ab hum discuss krenge ki hum numbers ko ek line p kaise represent kr skte hai. To baccho ab hum seekhenge ki hum numbers ko ek line p represent kaise kr skte hai.(+1).
Aur saath hi saath hum ye bhi seekhenge ki hum uss number line ko addition, subtraction aur multiplication k lie kaise use kr skte hai.
Example 6
In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line. Also write them with the appropriate sign (<>) between Them.
(a) 530,503
(b) 370,307
(c) 98765,56789
(d) 9830415,10023001
(a) 503 is on the left of 530 on the number line. 503<530
(b) 307 is on the left of 370 on the number line. 307<370
(c) 56789 is on the left of 98765 on the number line. 56789<98765
(d) 9830415 is on the left of 10023001 on the number line. 9830415<10023001
Operations on a Number Line
To baccho humne number line ki definition m pdha ki it is used to carry out mathematical operations like addition and subtraction. So let's learn how to add and subtract on the number line.
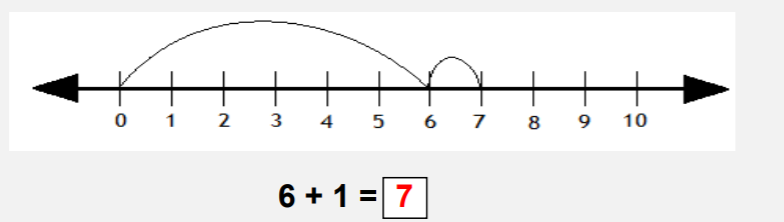
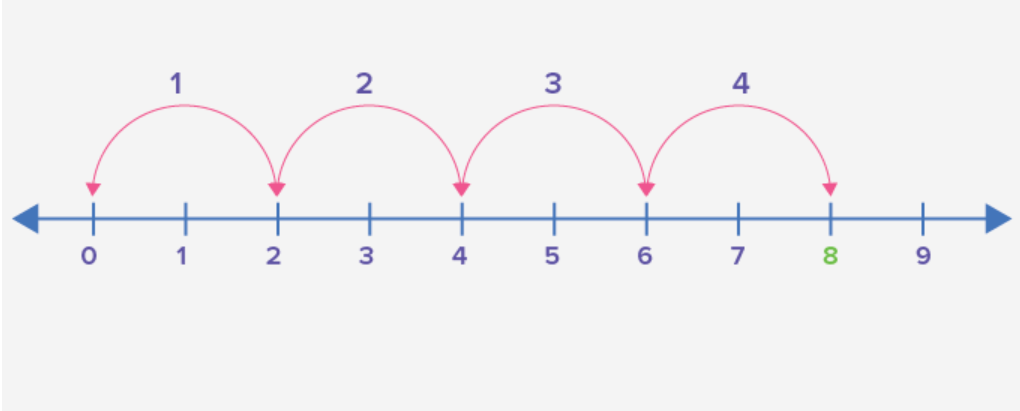
ADDITION on a number line
To add two numbers using number line, like 6+1, we first locate 6 on the number line and then jump 1 place towards its right and note down the number where we land upon.
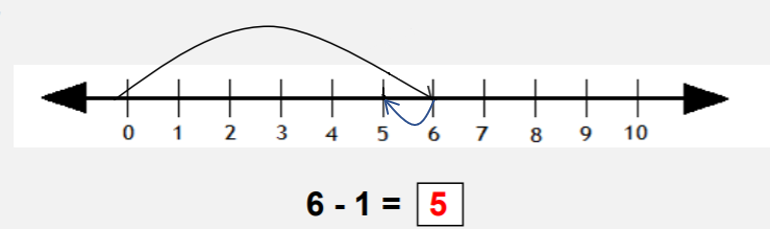
SUBTRACTION on a number line
To subtract two numbers on a number line, for example 6−1, first locate 6 on the number line then move 1 place to the left of it. The number you land upon will be the answer.
MULTIPLICATION on a number line
To multiply two numbers on a number line, like 2×4, Start from 0, move 2 units at a time to the right, make
such 4 moves. You'll land on 8, which is the answer.
PROPERTIES OF WHOLE NUMBERS
To baccho ab hum seekhenge ki whole numbers ki aisi konsi properties hoti hai jo ki humare lie mathematical operations ko carry out krna asaan kr skti hai
Closure under Addition
When we add two whole numbers like (5+6), the sum we get (11) is also a whole number. This is true for all whole numbers. Hence, we say that whole numbers are closed under addition.

Closure under multiplication
When we multiply two whole numbers like (5×6), the product we get (30) is also a whole number. This is true for all whole numbers. Hence, we say that whole numbers are closed under multiplication.

Closure under subtraction and division
Whole numbers are NOT CLOSED under subtraction and division.
For example, 4 and 8 are two whole numbers but when we subtract them (4−8), we get (−4), which is not a whole number.

Similarly, 5 and 7 are two whole numbers, but when we divide them (57), the resultant is not a whole number.

∴ We can conclude that whole numbers are not closed under subtraction and division.
Division by Zero
Divison of any whole number (0,1,2,3,4...) is NOT DEFINED.
Baccho, division ka mtlb hota hai ki ek number mai se dusre number ko baar baar subtract krna.
Let's understand with an example
Division of 8 by 2 (82)
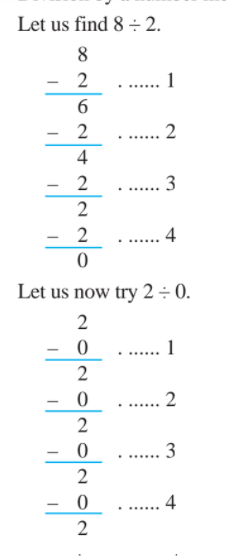
Jaisa ki aap dekh skte hai baccho, ki 8 baar baar carry down horha hai, aur hota rahega till infinity.
Hence, Division of whole numbers by 0 is not defined.
Commutativity of addition and multiplication
Commutative property states that the numbers in a mathematical operation can be re-arranged without affecting the answer.
For example, 5+7=12 and 7+5=12. This means a+b=b+a, where, a and b are whole numbers. This is known as commutative property of addition.
The same is applicable for multiplication of whole numbers.
For example, 5×3=15, and 3×5=15. This means that, a×b=b×a, where a and b are whole numbers.
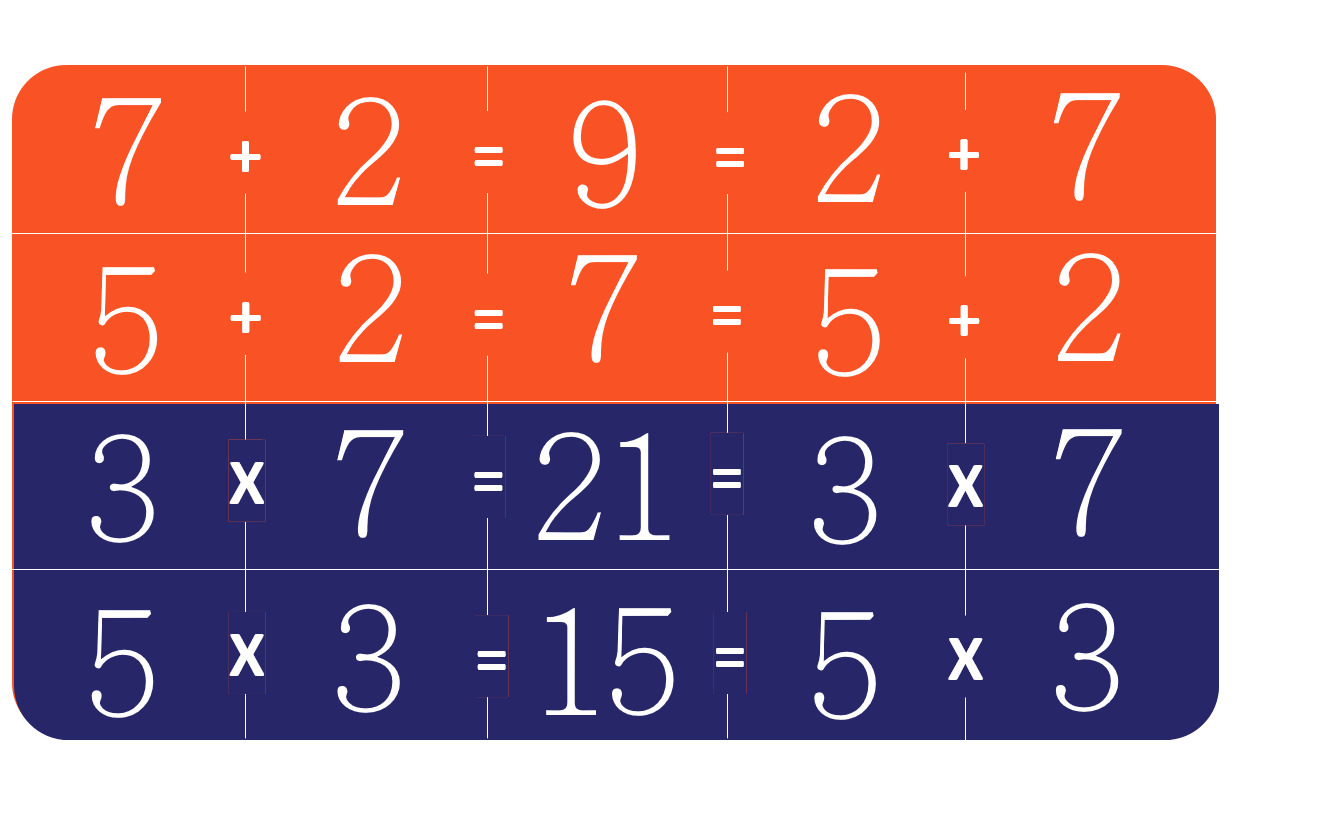
Commutativity of subtraction and division
Commutative property subtraction aur division m apply nahi hoti hai baccho..
For example, 4−7=(−3), but 7−4=3.
∴ a−b≠b−a
Similarly, 63=2, but 36=12.
∴ ab≠ba
Hence, we can conclude that commutativity is not true for subtraction and division of whle numbers.
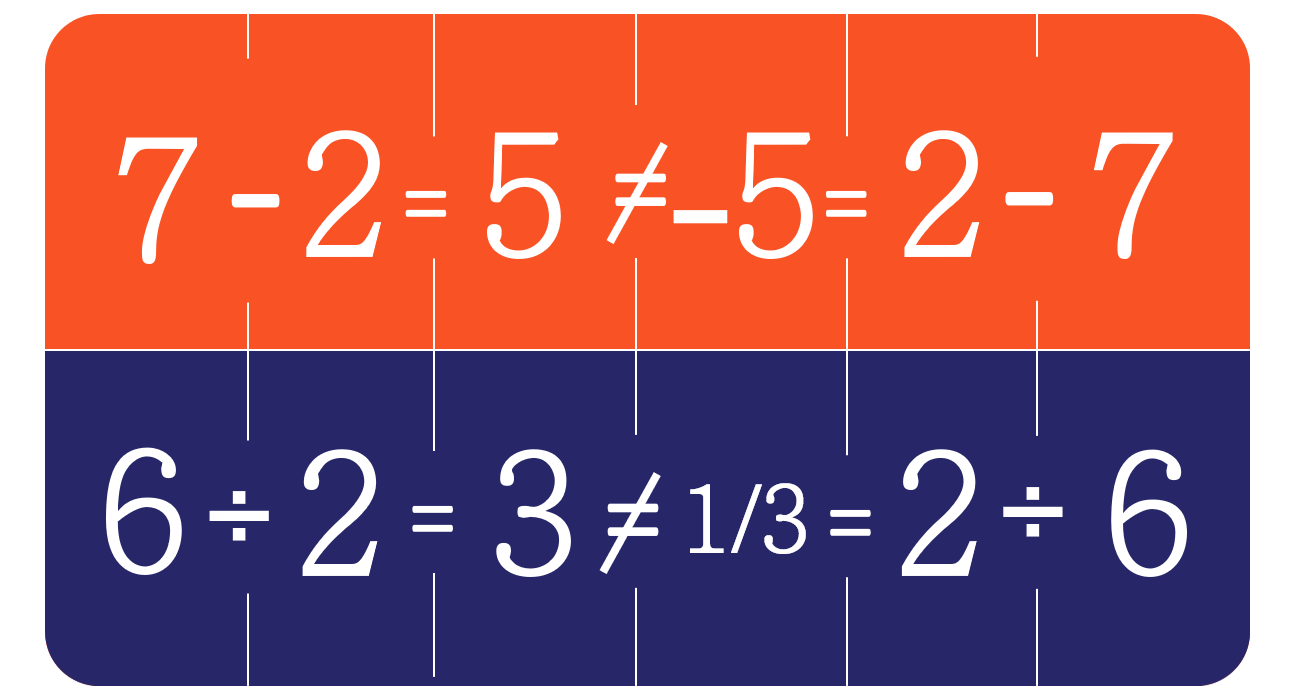
Associativity of Addition and Multiplication
Associative property states that when two or more numbers are multiplied or added, the resultant remains the same regardless of the way the numbers have been grouped.
For example, (2+5)+3=(7)+3=10
Also,
2+(5+3)=2+(8)=10
To baccho, jaisa ki aap dekh skte hai ki grouping change krne k bawajood bhi humara sum same aaya. This means that whole numbers are associative under addition.

The same is true for multiplication of whole numbers
For example, (3×4)×2=(12)×2=24
Also, 3×(4×2)=3×8=24
As you all can see, despite of re-grouping the numbers, our product remained the same. This means that, whole numbers are associative under multiplication.
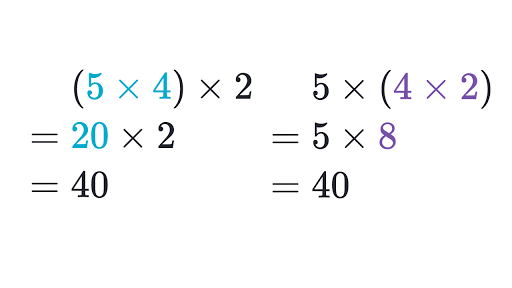
Associativity under subtraction and division
Associative property does not hold true for subtraction and division. Let us see why -
(2−3)−4=(−1)−4=(−5)
But,
2−(3−4)=2−(−1)=2+1=3
As you can observe that after regrouping the numbers, our resultant changed.
The same is true for division, Try it out yourself!
Distributivity of multiplication over addition
According to the distributive property, when two numbers are added as a group and are being multiplied by a third number, we can show the two numbers being multiplied separately.
For example, (2+3)×4
⇒ (2×4)+(3×4)
Both of these arrangements will give the same answer 20.
This is known as distributivity of multiplication over addition
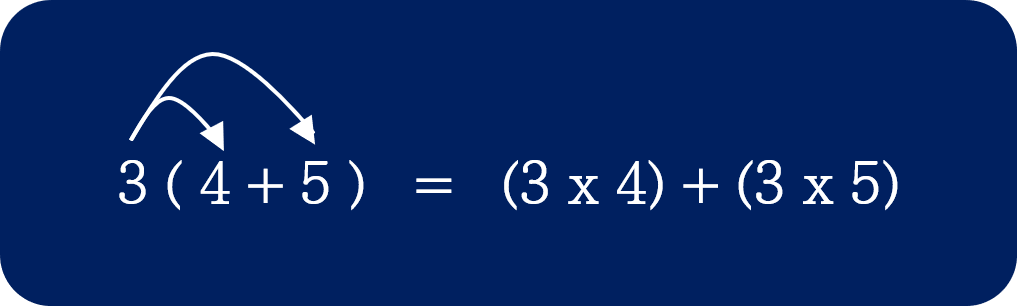
Example 7
Find using distributive property:
(a) 728×101
(b) 5437×1001
(c) 824×25
(d) 4275×125
(e) 504×35
(a) 73528
(b) 5442437
(c) 20600
(d) 534375
(e) 17640
Additive Identity
The Additive Identity is a number which when added to other whole numbers, give the same result as the number. Look at the following examples and observe
1+0=1
2+0=2
3+0=3
Did you notice that when we add 0 to any whole number, the sum remains the same.
This states that the additive identity for whole numbers is 0
Multiplicative Identity
Multiplicative identity is a number which when multiplied with any whole number gives the same product as the number. Look at the following examples and observe−
3×1=3
6×1=6
77×1=77
Can you guess the multiplicative identity by looking at the above examples?
You're right! 1 is the multiplicative identity for whole numbers.
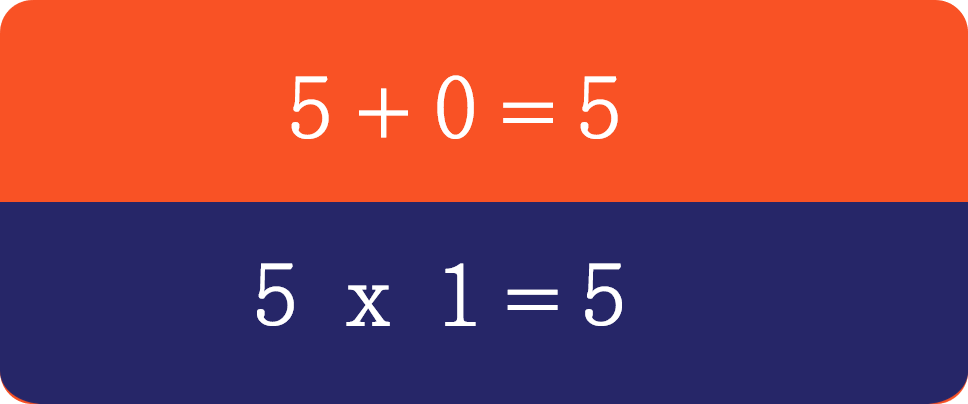
PATTERNS IN WHOLE NUMBER


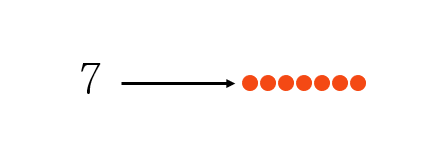
Every number greater than 0 can be represented as a line.
Some numbers can be represented as rectangles too.
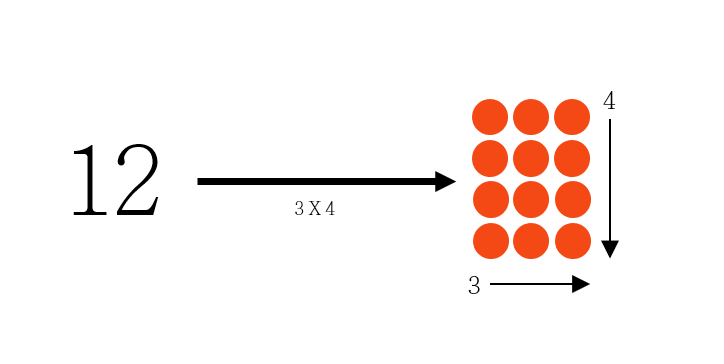
Some numbers can also be arranged as a square.

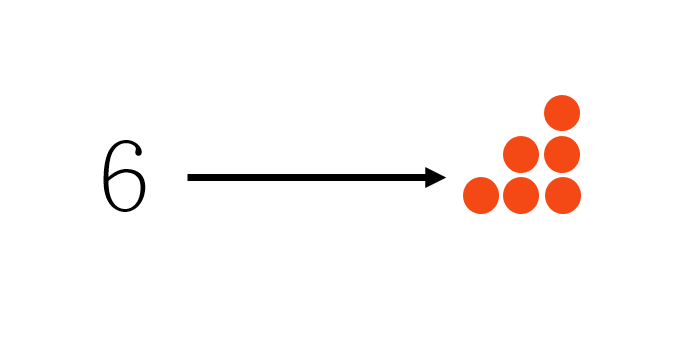
Some numbers can be represented as triangles too
Patterns Observation
To baccho, ab hum seekhenge ki patterns ko observe krke hum apni calculations kaise quick and easy kr skte hai.
Observe the following simplification :
(a) 117+9=117+10–1=127–1=126
(b) 117–9=117–10+1=107+1=108
(c) 117+99=117+100–1=217–1=216
(d) 117–99=117–100+1=17+1=18
Baccho, dhyaan se dekhiye ki kaise humne complex terms ko breakdown kia hai jisse ki humari calculation aasaan aur accurate rahe. It's easier to add 117 and 10 and then subtract 1 instead of adding 117 and 9 (example (a)).
Agar aap iss concept ko achhe se practice krle to aap aisi calculations orally bhi kr skte hai.
The same method can be applied while multiplying.
For example, 99×9=(90+9)×9=(90×9)+(9×9)=810+81=891
Example 8
Study the patten :
1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
12345×8+5=98765
Write the next two steps. Can you say how the pattern works?
(a)123456×8+6=987654
(b)1234567×8+7=9876543
Baccho, agar aap dhyaan se observe krenge to aap dekhenge ki har ek part m jo phla number hai usme ek pattern ban rha hai (1,12,123,1234,12345...). Aur jab ye numbers 8 se multiply hokr 1 m add horhe hai, to answers ka bhi ek alag patterns bnrha hai (9,98,987,9876,98765...). Isi pattern ko use krke humne apna answer nikaala.
Numbers between Numbers
In order to find the number of whole numbers that exist between two different whole numbers is (m−n)−1, where m and n are two different whole numbers.
For example, How many whole numbers exist between 5 and 50?
SOLUTION
(50−5)−1
=45−1
=44
∴ 45 whole numbers exist between 5 and 50.
Exercise 9
How many whole numbers are there between 32 and 53?
The formula to find the whole nos. between m and n is (m−n)−1
So, applying the formula
=(53−32)−1
=21−1
=20
Example 9
How many whole numbers are there between 32 and 53?
The formula to find the whole nos. between m and n is (m−n)−1
So, applying the formula
=(53−32)−1
=21−1
=20
Example 10
Which of the following statements are true (T) and which are false (F)?
(a) Zero is the smallest natural number.
(b) 400 is the predecessor of 399.
(c) Zero is the smallest whole number.
(d) 600 is the successor of 599.
(e) All natural numbers are whole numbers.
(f) All whole numbers are natural numbers.
(g) The predecessor of a two digit number is never a single digit number.
(h) 1 is the smallest whole number.
(i) The natural number 1 has no predecessor.
(j) The whole number 1 has no predecessor.
(k) The whole number 13 lies between 11 and 12.
(l) The whole number 0 has no predecessor.
(m) The successor of a two digit number is always a two digit number
(a) false
(b) 399−1=398, false
(c) true
(d)599+1=600, true
(e) 0 is a whole no but not a natural number, true
(f) since 0 is not a natural no, false
(g) 10−1=9, false
(h) smallest whole no is 0, false
(i) 0 is not a natural no, true
(j) 0 since 0 is a whole no, false
(k) false
(l) since −1 is not a whole no, true
(m) successor of 99 is 99+1=100, false
LET'S SUMMARIZE!
1. The numbers 1,2,3,... which we use for counting are known as natural numbers.
2. If you add 1 to a natural number, we get its successor. If you subtract 1 from a natural
number, you get its predecessor.
3. Every natural number has a successor. Every natural number except 1 has a predecessor.
4. If we add the number zero to the collection of natural numbers, we get the collection of
whole numbers. Thus, the numbers 0, 1, 2, 3,... form the collection of whole numbers.
5. Every whole number has a successor. Every whole number except zero has a
predecessor.
6. All natural numbers are whole numbers, but all whole numbers are not natural
numbers.
7. We take a line, mark a point on it and label it 0. We then mark out points to the right
of 0, at equal intervals. Label them as 1, 2, 3,.... Thus, we have a number line with the
whole numbers represented on it. We can easily perform the number operations of
addition, subtraction and multiplication on the number line.
8. Addition corresponds to moving to the right on the number line, whereas subtraction
corresponds to moving to the left. Multiplication corresponds to making jumps of
equal distance starting from zero.
9. Adding two whole numbers always gives a whole number. Similarly, multiplying two
whole numbers always gives a whole number. We say that whole numbers are closed
under addition and also under multiplication. However, whole numbers are not closed
under subtraction and under division.
10. Division by zero is not defined.
11. Zero is the identity for addition of whole numbers. The whole number 1 is the identity
for multiplication of whole numbers.
12. You can add two whole numbers in any order. You can multiply two whole numbers in
any order. We say that addition and multiplication are commutative for whole numbers.
13. Addition and multiplication, both, are associative for whole numbers.
14. Multiplication is distributive over addition for whole numbers.
15. Commutativity, associativity and distributivity properties of whole numbers are useful
in simplifying calculations and we use them without being aware of them.
16. Patterns with numbers are not only interesting, but are useful especially for verbal
calculations and help us to understand properties of numbers better.
Let's Revise
a)To baccho, humne iss chapter m seekha ki jo numbers hum day to day life m use krte hai for counting, they are called counting numbers or NATURAL NUMBERS (1,2,3,4,5...)
b) When we add 0 to the set of natural numbers, we get WHOLE NUMBERS. (0,1,2,3,4,5..)
c) Jab hum kisi number m 1 add krte hai, to hume uss number ka successor milta hai. Jab hum kisi number m se 1 subtract krte hai, to we get the predecessor of that number.
d) Saare natural numbers, whole numbers hote hai but saare whole numbers natural numbers nahi hote ( 0 is a whole number but not a natural number).
e) Number line is a horizontal straight line where whole numbers are marked at equal intervals. Number line is used for addition, subtraction, multiplication and division of whole numbers.
f) 2 whole numbers ka sum aur product humesha ek whole number hota hai. Ise closure property kaha jaata hai. This property does not hold true for subtraction and division.
g) Kisi se bhi whole number ko 0 se divide krne par answer not defined hota hai.
h) 2 whole numbers ko kisi bhi order m add ya multiply krne se answer same aata hai. Ise commutative property of whole numbers kaha jaata hai.
i) Teen ya teen se zyada whole numbers ko kisi bhi tarah group krne p, unka sum ya product same hi rehta hai. This is known as associative property of whole numbers. This property does not hold true for division and subtraction.
j) Distributive property k according, agar do numbers add horhe h aur ek teesre number se multiply horhe hai, to hum unn dono numbers ko alag alag multiply krke add kr skte hai. For example, (a+b)×c=(a×c)+(b×c)
k) 0 is the additive identity of whole numbers, mtlb ki 0 ek aisa number hai jise kisi bhi whole number m add krne se, number nahi badalta. 1 is the multiplicative identity of whole numbers, mtlb ki 1 ek aisa whole number hai jise kisi bhi whole number se multiply krne m product remains the same as the number.
l) In order to know the number of whole numbers existing between two different numbers m and n hum ye formula use krte hai (m−n)−1
m) Sum of first n natural odd numbers is n2.
n) Apni calculations ko easy krne k lie hum whole numbers k patterns ko observe krte hai.