PLAYING WITH NUMBERS for Class 6 MATHS
INTRODUCTION
Baccho, humne apne previous chapters m numbers k baare m pdha, ki numbers kitne type k hote hai, natural numbers, whole numbers, and their properties. Baccho, ab hum iss chapter m factors and multiples, prime and composite numbers, divisibility tests of numbers, common factors and common multiples, divisibility rules, prime factorisation and HCF and LCM jaise topics m pdhenge. Factors and multiples ka relation multiplication and division se hota hai. They are simple concepts and we'll learn them in detail taaki humare concepts ekdam clear rahe.
Types of Numbers
Let's recall the different types of numbers that we have learnt about!
Prime Numbers
Baccho, prime numbers vo numbers hote hai jo ki sirf khud se ya 1 se divide ho skte hai. For example, 5,7,11,13, etc, these numbers can only be divide by themselves or 1.
Even numbers
Even numbers vo numbers hote hai jo ki two equal parts m divide ho skte hai. For example, 2,4,6,8,10,etc. These numbers always end in 0,2,4,6and8.
Odd numbers
Odd numbers vo numbers hote hai jo ki 2 se completely divide nahi ho skte. They always leave a remainder 1. These numbers end in 1,3,5,7and9.
Natural numbers
Natural numbers is a set of numbers which start from 1 and go till infinity. For example, 1,2,3,4,5...and so on.
Whole numbers
Jab hum natural numbers k set m 0 add krdete hai, we get whole numbers. So we can say that, whole numbers start from 0 and go till infinity. For example, 0,1,2,3,4,5...and so on.
Composite numbers
Composite numbers are those numbers which can be divided at least by one other number except for 1 and the number itself. For example, 4 can be divide by 2, 1 and 4.
FACTORS AND MULTIPLES
Factors
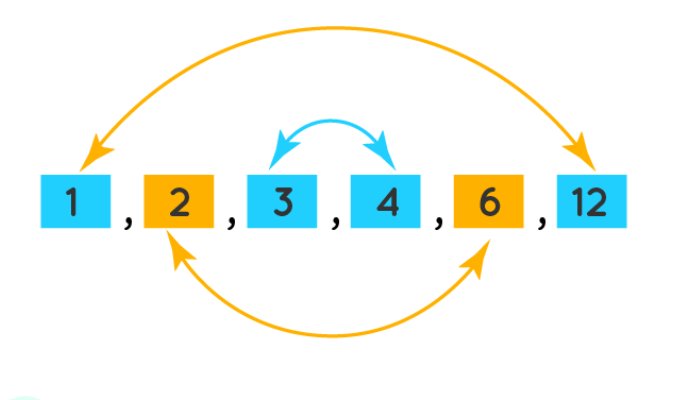
A factor of a number is an exact divisor of that number
For example, 1,2,3 and 6 are factors of 6 since they completely divide the number 6.
Properties of factors
Baccho, ab hum pdhenge ki factors k properties kya kya hote hai. Mainly factors have 6 major properties. They are as follows :
1) 1 is a factor of every number.
Baccho, kyunki 1 har number ko divide kr skta hai, that's why 1 is a factor of every number.
2) Every number is a factor of itself.
Har number khud se divide hokr 1 quotient deta hai. This is why every number is a factor of itself.
3) Every factor of a number is an exact divisor of that number.
Jaisa ki humne factor ki definition m pdha, a factor is an exact divisor of the number itself, this tells us that a factor is an exact divisor of itself.
4)Every factor is less than or equal to the given number.
In order to divide a number exactly, the divisor always needs to be either less than or equal to the dividend.
6) Number of factors of a given number are finite.
A number does not have infinite factors. for example, 6 has only 4 factors, which are 1,2,3 and 6.
Example 1
Write all the factors of 68.
We note that
68=1×68
68=2×34
68=4×17
68=17×4
Stop here, because 4 and 17 have occurred earlier.
Thus, all the factors of 68 are 1,2,4,17,34 and 68.
Example 2
Find the factors of 36 .
We note that,
36=1×36
36=2×18
36=3×12
36=4×9
36=6×6
Stop here, because both the factors (6) are same. Thus, the factors are 1,2,3,4,6,9,12,18 and 36.
MULTIPLES
Multiples of a number are those numbers which we get on multiplying the number by any number.
Example: Multiples of 3 are 6,9,12,15,18 etc.

Properties of multiples
There are 3 major properties of multiples.
1)Every multiple of a number is greater than or equal to that number.
Baccho, jab hum ek number ko ek dusre integer se multiply krte hai, to answer yaa to wahi number aata hai (when multiplied with 1) ya fir the product is greater than the number itself. For example, 6×5=30, 30>6
2)Number of multiples of a given number is infinite.
Hum ek number ko infinite numbers se multiply kr skte hai, jisse hume infinite multiples milte hai.
3)Every number is a multiple of itself.
Jab hum ek number ko 1 se multiple krte hai, to the answer is the number itself. This is why every number is a multiple of itself.
Example 3
Write first five multiples of 6
The required multiples are:
6×1=6
6×2=12
6×3=18
6×4=24
6×5=30 i.e. 6,12,18,24 and 30.
PERFECT NUMBERS
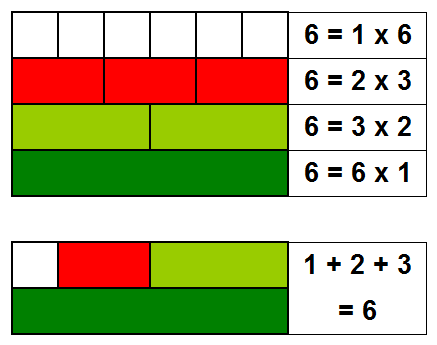
Baccho, perfect number is a very interesting concept. Basically, a number for which sum of all its factors is equal to twice the number is called a perfect number.
This means that agar ek number k saare factors ko add krne p the sum is equal to or twice of the number itself, then its a perfect number.
Example: Factors of 28 are 1,2,4,7,14 and 28.
Here, 1+2+4+7+14+28=56=2×28
Therefore, sum of factors of 28 is equal to twice the number 28.
Try and find more numbers like this!
PRIME NUMBERS
Baccho, after learning about factors and multiples, now we'll learn about other types of numbers which are based on factors and multiples.
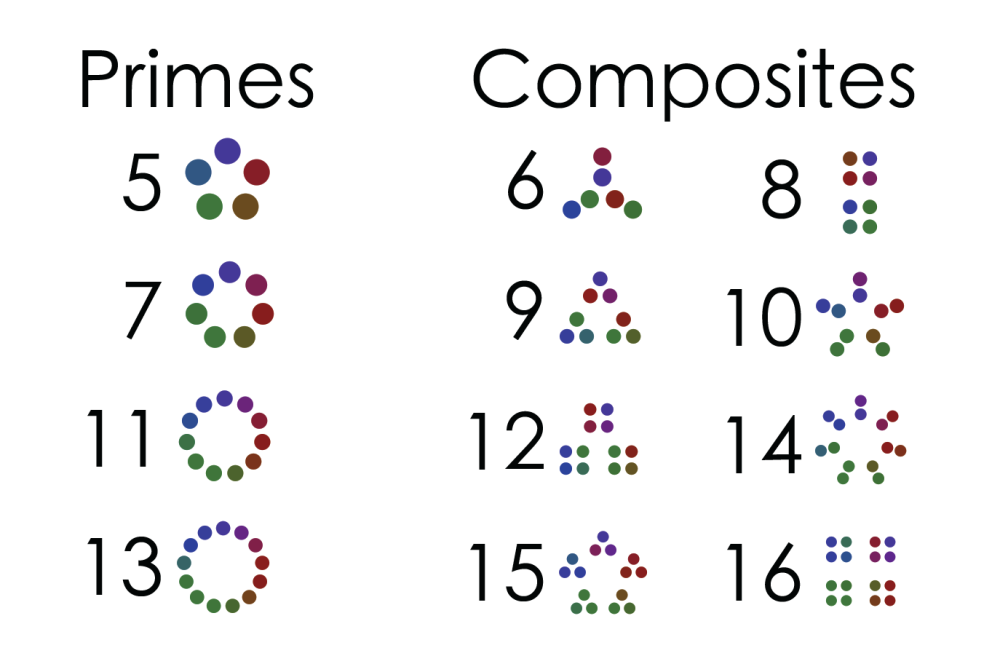
Prime numbers vo numbers hote hai which have only two factors : 1 and the number itself.
For example, 7 is a prime number because only two numbers can divide 7 completely. One is 1 and the other is 7.

Example 4
COMPOSITE NUMBERS
Numbers having more than two factors are called Composite numbers. For example, 10 is a composite number because it has more than two factors, which are : 1,2,5,10
0 and 1 are neither prime nor composite numbers.
Even and Odd numbers

A number which is a multiple of 2 is called an even number.
For example: 2,4,6,8,10,….
A number with 0,2,4,6,8 at the unit’s place is an even number.
So, 280,2730,2544,3468 are even numbers.
A number which is not a multiple of 2 is called an odd number.
For example: 1,3,5,7,9,…
Odd numbers are the numbers which have 1,3,5,7,9 at unit's place. So, 197,329,73 are odd numbers.
DIVISIBILITY TESTS FOR NUMBERS
Baccho, hum apni day to day life m aisi situations face krte hai when we look at a large number and we think ki vo number kis number se divide ho skta hai. To solve such problems, we use divisibility tests.
Hum iss chapter m 2,3,4,5,6,7,8,9,10,11 k divisibility rules k baare m pdhenge.
COMMON FACTOR
Baccho, let us understand the concept of common factor by looking at the following example,
Factors of 8 are 1,2,4 and 8.
Factors of 120 are 1,2,3,4,5,6,8,10,12,15,20,24,30,40,60 and 120.
1,2,4 and 8 appears as factors for both of these numbers. Hence, the numbers 1,2,4 and 8 are common factors of both 8 and 120.
When two numbers have only 1 as a common factor, they are called co-prime numbers. For example, 3 and 5 are co-prime numbers.
Example 5
Find the common factors of :
(a) 4,8 and 12
(b) 5,15 and 25
(a) factors are :
4=1,2,4
8=1,2,4,8
12=1,2,3,4,6,12
common factors =1,2,4
(b) factors are :
5=1,5
15=1,3,5,15
25=1,5,25
common factors : 1,5
COMMON MULTIPLES
Let us look at the following example to understand common multiples :
Multiples of 3 are 3,6,9,12,15,18,….
Multiples of 5 are 5,10,15,20,25,30,…
Multiples of 6 are 6,12,18,24,30,36,…
Therefore, common multiples of 3,5 and 6 are 30,60,….
Example 6
Find first three common multiples of :
(a) 6 and 8
(b) 12 and 18
(a) Multiples of
6=6,12,18,24,30,36,42,48,54,60,66,72,78,84...
Multiples of
8=8,16,24,32,40,48,56,64,72,80,88...
So, first 3 common multiples of
6 and 8=24,48,72
(b) Multiples of 12=12,24,36,48,60,72,84,96,108,120...
Multiples of
18=18,36,54,72,90,108,126,144...
So, first 3 common multiples of
12and18=36,72,108
PRIME FACTORIZATION
Baccho, jab hum ek number ko prime numbers k product ki form m represent krte hai, then its called prime factorization.
A number when expressed as a product of its factors is said to be factorized.
For example: 12=3×4. We say that 12 has been factorized. This is one of the several factorizations of 12. But since, 4 can be written as 2×2, therefore, prime factorization of 12=3×2×2
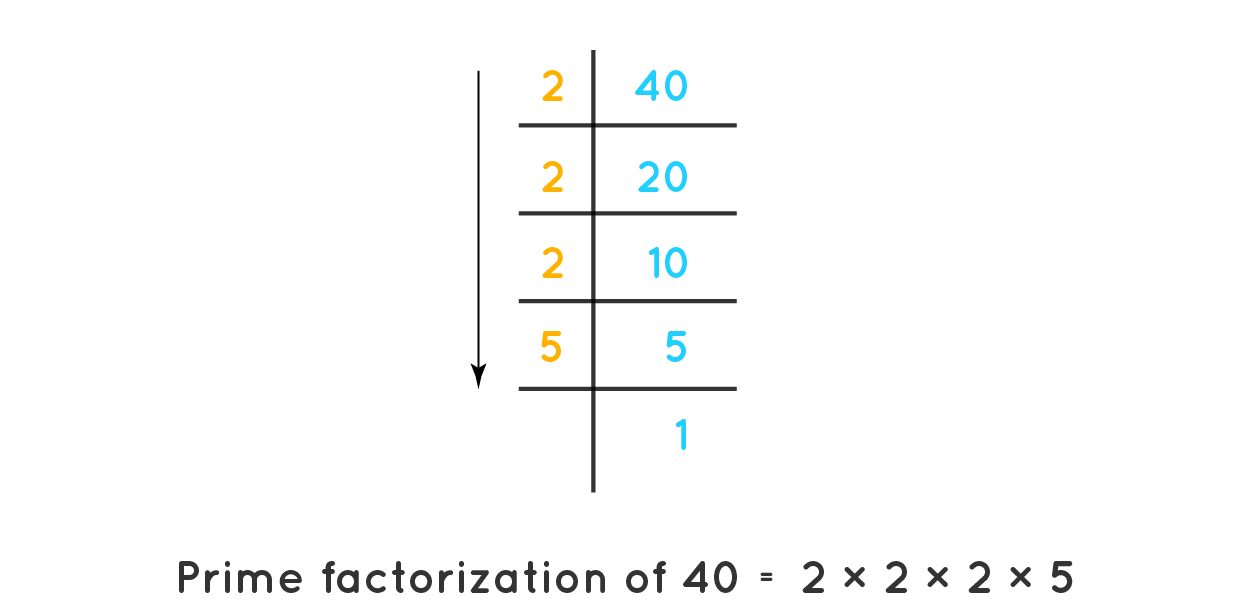
Example 7
In which of the following expressions, prime factorisation has been done?
(a) 24=2×3×4
(b) 56=7×2×2×2
(c) 70=2×5×7
(d) 54=2×3×9
1 and 4 are not prime factors
2 and 3 are prime factors.
Factor Tree
Jab hum ek number ko end tak factorize krte hai and we write the process as follows, we get the shape of a tree called Factor tree.
For example: Let us factorize 850.
Let us see below:
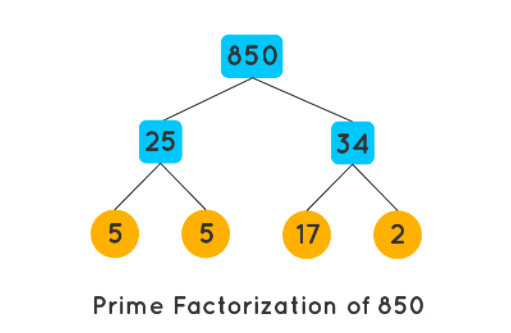
Thus. 850=2×5×5×17.
Highest Common Factor (HCF)
The Highest Common Factor (HCF) of two or more given numbers is the highest (or greatest) of their common factors. It is also known as the Greatest Common Divisor (GCD).
For example: Consider two numbers 12 and 20. Factors of 12 are 1,2,3,4,6 and 12. Factors of 20 are 1,2,4,5,10 and 20. The common factors of 12 and 20 are 1,2 and 4. The highest of these is 4. So, 4 is the HCF of 12 and 20.
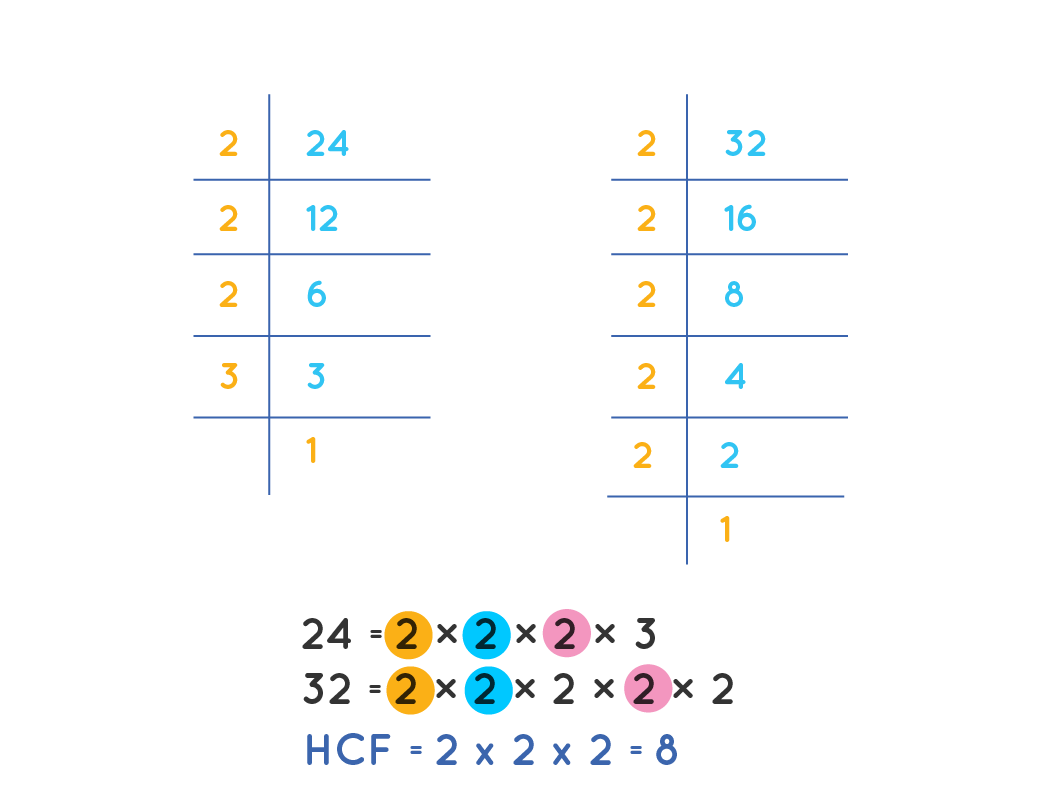
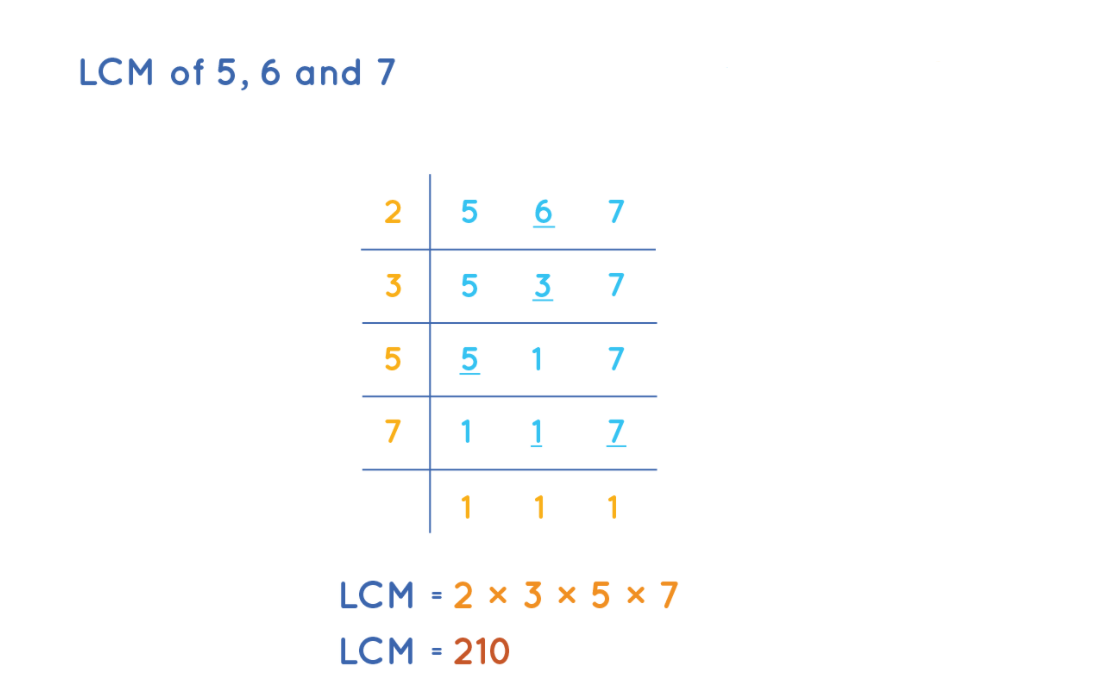
Lowest Common Multiple (LCM)
The Lowest Common Multiple (LCM) of two or more given numbers is the lowest (or smallest or least) of their common multiples.
For example: Consider two numbers 12 and 20.
Multiples of 12 are 12,24,36,48,60,72,84,96,108,120,…
Multiples of 20 are 20,40,60,80,100,120,……..
The common multiples of 12 and 20 are 60,120,…
The lowest of these is 60.
So, 60 is the LCM of 12 and 20.
Example 8
Find the LCM of 20,25 and 30
40=2×2×2×5
48=2×2×2×2×5
45=3×3×5
LCM=(2×2×2×2)×(3×3)×5
=16×9×5
=720
LET'S SUMMARIZE !
1. We have discussed multiples, divisors, factors and have seen how to identify factors
and multiples.
2. We have discussed and discovered the following :
(a) A factor of a number is an exact divisor of that number.
(b) Every number is a factor of itself. 1 is a factor of every number.
(c) Every factor of a number is less than or equal to the given number.
(d) Every number is a multiple of each of its factors.
(e) Every multiple of a given number is greater than or equal to that number.
(f) Every number is a multiple of itself.
3. We have learnt that –
(a) The number other than 1, with only factors namely 1 and the number itself, is a
prime number. Numbers that have more than two factors are called composite
numbers. Number 1 is neither prime nor composite.
(b) The number 2 is the smallest prime number and is even. Every prime number other
than 2 is odd.
(c) Two numbers with only 1 as a common factor are called co-prime numbers.
(d) If a number is divisible by another number then it is divisible by each of the factors
of that number.
(e) A number divisible by two co-prime numbers is divisible by their product also.
4. We have discussed how we can find just by looking at a number, whether it is divisible
by small numbers 2,3,4,5,8,9 and 11. We have explored the relationship between
digits of the numbers and their divisibility by different numbers.
(a) Divisibility by 2,5 and 10 can be seen by just the last digit.
(b) Divisibility by 3 and 9 is checked by finding the sum of all digits.
(c) Divisibility by 4 and 8 is checked by the last 2 and 3 digits respectively.
(d) Divisibility of 11 is checked by comparing the sum of digits at odd and even
places.
5. We have discovered that if two numbers are divisible by a number then their
sum and difference are also divisible by that number.
6. We have learnt that –
(a) The Highest Common Factor (HCF) of two or more given numbers is the highest
of their common factors.
(b) The Lowest Common Multiple (LCM) of two or more given numbers is the lowest
of their common multiples
Let's Revise
Baccho, humne is chapter m kaafi saare topics kre, let's revise them:
1) Factor of a number is an exact divisor of that number. For example, 3 is a factor of 6, since 63=2
2)Multiply of a number ek aisa number hota hai jo hume ek number ko ek integer se multiply krne p milta hai. For example 6×3=18,∴18 is a multiple of 6.
3) Agar ek number k saare factors ko add krne se sum wahi number ya uska double aata hai, then it's a perfect number.
For example, 28 is a perfect number because all the factors of 28 are 1,2,4,7,14 and 28 whose sum =1+2+4+7+14+28=56=2×28
4) Jin numbers k sirf 2 factors hote hai ( 1 and the number itself), they are called prime numbers.
5) Jin numbers k do se zyada factors hote hai, they are called composite numbers.
6) Even numbers are numbers which are divisible by 2. Odd numbers are numbers which are not perfectly divisible by 2
7) Numbers ki divisibility check krne k lie hum divisibility tests use krte hai. We have divisibility rules for 2,4,5,6,7,8,9,10 and 11.
8) Jab hum ek number ko uske factors k product ki tarah present krte hai, its called prime factorization.
9) Highest common factor is the number which is the greatest amongst the common factors of two numbers. For example, factors of 6=1,2,3 and 6 and factors of 8=1,2,4,8. The common factors are 1 and 2, and 2>1. ∴2 is HCF of 6 and 8.
10) LCM is the lowest common multiple of two numbers. LCM vo number hota hai jo do numbers k common multiples m se sabse chota hota hai.