INTEGERS for Class 6 MATHS
Introduction
Baccho, aapne apne previous chapters m numbers and unki collection k baare m pdhna start kia tha. Aap sab natural numbers, positive numbers and whole numbers se familiar hai. Iss chapter m hum Integers k baare m pdhenge. Integers basically vo set of numbers hote hai jinme saare positive natural numbers (1,2,3,4...) include hote hai, 0 include hota hai, aur negative numbers (−1,−2,−3,4,....) include hote hai. We will learn more about negative numbers. These numbers are used to perform various arithmetic operations, like addition, subtraction, multiplication and division. In this chapter, we will study more about integers, their properties and operations.
RECAPITULATION
Baccho before learning about integers, we'll revise about the natural numbers, whole numbers and the concept of zero.
NEGATIVE NUMBERS
Negative numbers are the numbers which have a minus (−) sign on their left like −1,−2,−3,−4,.. and so on.
When there is movement on the right of a number i.e when any number is added to another number, it is considered a positive move. When there is a movement on the left of a number i.e when a number is subtracted from another number, it is known as a negative move.
If a movement of only 1 is made on the right of a number, we get the successor of that number. For example, sucessor of 3 is 3+1=4. Successor of 1826 is 1827.
If a movement of only 1 is made on the left of a number, we get the predecessor of that number. For example, predecessor of 3 is 3−1=2. Predecessor of 1826 is 1825.

USE OF SIGNS
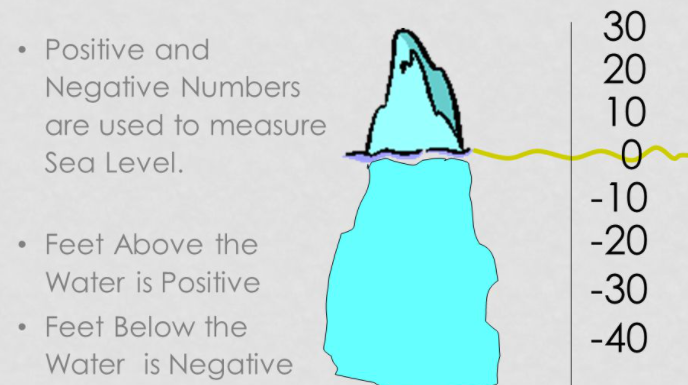
In our daily life we come across several situations where we need to present-various positive and negative values. for example:

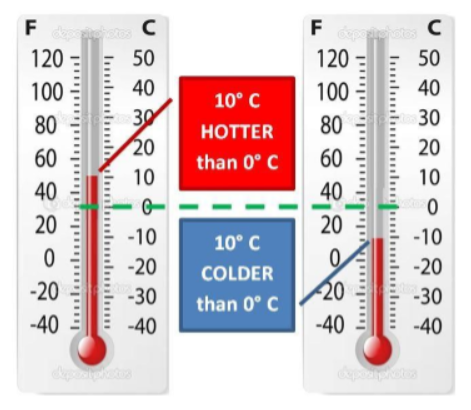
INTEGERS
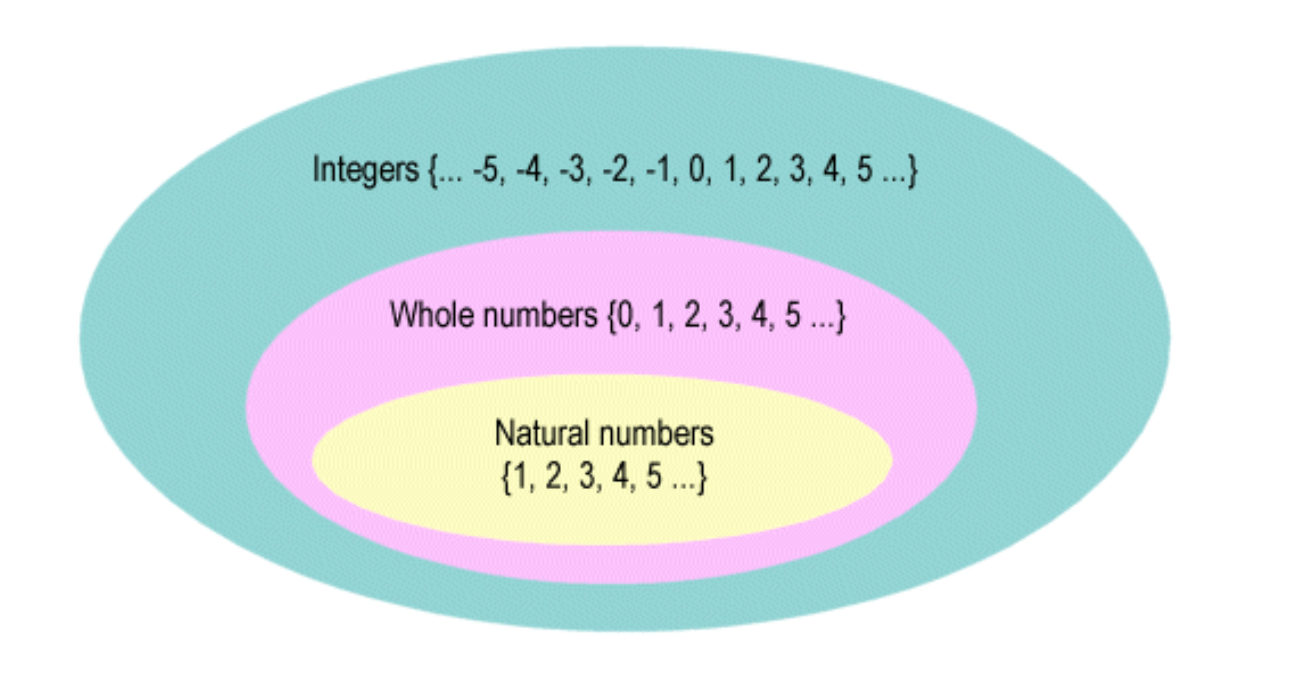
Baccho whole numbers aur negative numbers k collection ko integers kaha jaata hai jisme saare negative numbers, negative integers kehlaate hai aur positive numbers positive integers kehlaate hai.
Look at the following representation to understand the relationship between Integers, Whole numbers and Natural numbers.
INTEGERS ON NUMBER LINE
We understood that in a number line, the negative numbers lie on the left of 0 and the positive numbers lie on the right of 0. Let's learn how to create a number line.
Step 1: Draw a straight horizontal line.
Note: Since it's a number "line", it will have arrows on its both ends.
Step 2: On the cetre of th line, mark the number 0.
Step 3: Mark all the positive integers (1,2,3,4,5,....) on the right of 0 with the same distance. These are our positive integers.
Step 4: Mark all the negative integers (−1,−2,−3,−4,−5,....) on the left of 0 with the same distance. These are our negative integers.
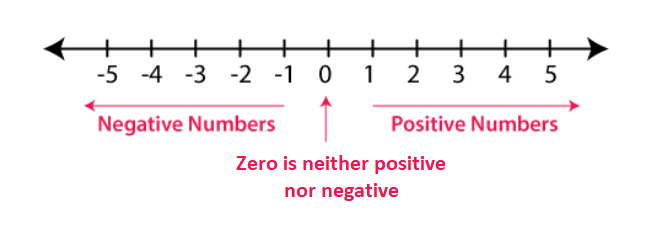
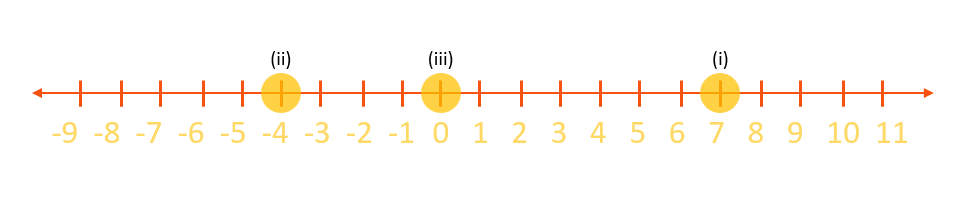
Now we'll see how to represent integers on a number line. Look at the folllowing examples:
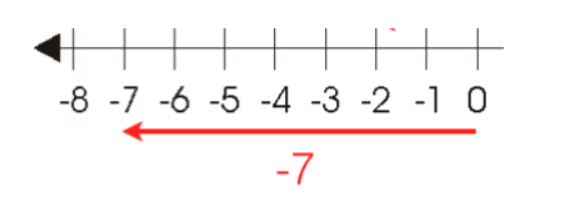
Example: Represent −7 on a number line.
Solution: To mark (−7) we have to move 7 points to the left of zero.
Example: Represent 5 on a number line.
Solution: To mark (5) we have to move 5 points to the right of zero.
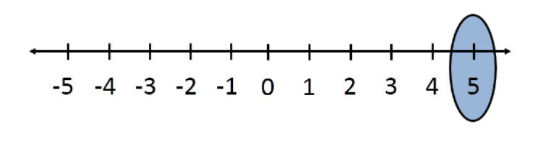
Example 1
ORDERING OF INTEGERS
Baccho aapne pdha ki jaise jaise hum number line m right side move krte hai, to numbers increase hote hai aur left side m move krne se numbers decrease hote hai.
Isi concept se hum ye conclude kr skte hai ki 2<3, 5<6 and −4<−3
Order of integers ka basically mtlb hota hai ki integers ko asending/descending order m arrange krna jisse hume ek comparison mil ske ki konsa integer kisse bdha hai.
By looking at the number line we can say that the order of integers is as follows:
...−8,−7,−6,−5,−4,−3,−2,−1,0,1,2,3,4,5,6,7,8,...
Example 2
Write all the integers between the given pairs (write them in the increasing order.)
(a) 0and−7
(b) −4and4
(c) −8and−15
(d) −30and−23 2)
WRITE 4 integers greater than −20 and 4 integers less than −10.
(a) −6,−5,−4,−3,−2,−1
(b) −3,−2,−1,0,1,2,3
(c) −14,−13,−12,−11,−10,−9
(d) −29,−28,−27,−26,−25,−24
Example 3
Write the following integers in the decreasing order :
(i)0,7,−3,−9,−132,36
(ii)51,−53,−8,0,−2
(iii)−71,−81,36,0,−5
(iv)−365,−515,102,413,−7
(i)36,7,0,−3,−9,−132
(ii)51,0,−2,−8,−53
(iii)36,0,−5,−71,−81
(iv)413,102,−7,−365,−515
ADDITION OF INTEGERS
Baccho humne seekha ki negative numbers ko represent krn ek lie hum unke saath minus ka sign lgate hai. Every integer has an absolute value. Absolute value ka mtlb hota hai numerical value of the integer without considering its sign.
Example: Absolute value of −7 is 7 and of +5 is 5.
The four basic arithmetic operations associated with integers are:
There are some rules for doing these operations. In this chapter we'll learn addition of integers, addition of integers on number line and subtraction of integers on number line.
Jab hum do integers ko add krte hai to we come across three different cases. Let's see these three cases and learn how to add integers in each of the cases.
1st Case: Positive integer + Negative integer
Jab hum ek positive integer aur negative integer ko add krte hai, to hum unki absolute values ko subtract krke larger number ka sign lgate hai.
For example: Calculate 5+(−7)
Solution:
Step 1: Subtract the absolute values. Absolute value of 5 is 5 and absolute value of (−7) is 7. Therefore, difference of absolute values = 7−5=2
Step 2: Put the sign of the larger number with the resultant. Since 7>5, therefore we'll put the minus sign (−7) with the resultant 2.
Answer : 5+(−7)=−2
2nd Case: Positive integer + Positive integer
Baccho jab hum do positive integers ko add krte hai, to hum unki absolute values ko add krte hai aur positive sign lgate hai.
NOTE: It is not necessary to put the positive (+) sign always. When there is no sign with a number, it automatically means a positive sign. For example, +5=5.
Let's look at an example to understand this case better:
Example: Add 5+8
Solution:
Step 1: Add the absolute values of 5 and 8.
⇒5+8=13
Step 2 : Put the positive sign against the resultant.
∴ Answer=5+8=(+)13
3rd Case: Negative integer + Negative integer
Baccho jab hum do negative numbers ko add krte hai to hum unki absolute values ko add krke, resultant k saath minus ka sign lgaate hai. Let's understand this with an example:
Example: Add (−9) and (−4)
Solution:
Step 1: Add the absolute values of −9 and −4. Therefore, absolute value of −9 is 9 and absolute value of −4 is 4.
⇒ Sum of absolute values =9+4=13
Step 2: Put the minus sign (−) with the resultant.
∴Answer =(−9)+(−4)=−13
Example 4
Add the following integers :
(i)+27 and+19
(ii)−42 and−35
(i) 27+19
=46
(ii) (−42)+(−35)
=−(42+35)
=−77
Example 5
Example 6
ADDITION OF INTEGERS ON NUMBER LINE
We can also add integers using a number line. The rules for the addition of integers on the number line are:
Always start from "0".
Example:Let's find the value of 5+(−10) using a number line.
In the given problem, the first number is 5 which is positive. So, we start from 0 and move 5 units to the right side.
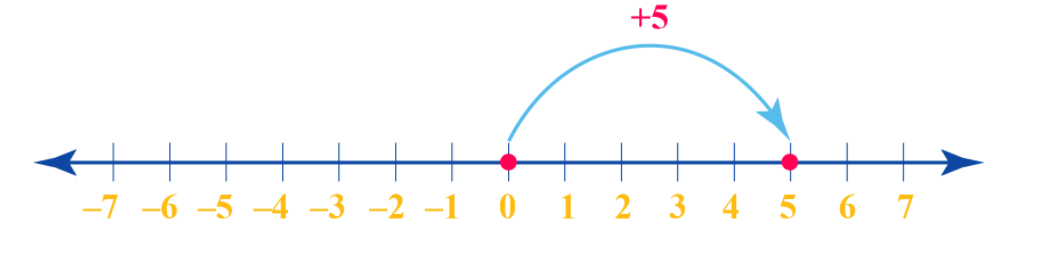
The next number in the given problem is −10, which is negative.
We move (from the fifth unit) 10 units to the left side.
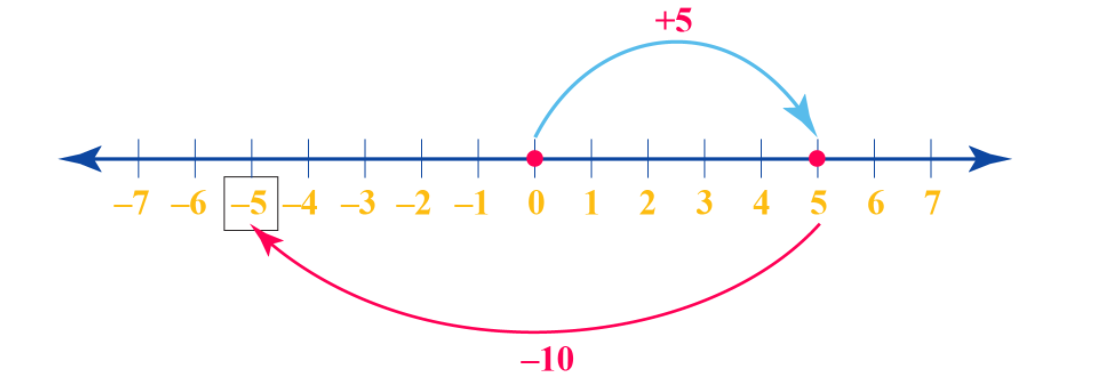
The number we have moved to finally is −5
∴ ANSWER =−5
ADDITIVE INVERSE
When a number is added to another number and the resultant is zero, then that number is known as the additive inverse of that number.
For example, if we take the number 3 and add −3 to it, the result is zero. Hence, the additive inverse of 3 is −3. We come across such situations in our daily-life where we nullify the value of a quantity by taking its additive inverse. The right amount of fire and ice will cancel out each other and the result will be no effect.
More examples:

Example 7
Example 8
SUBTRACTION OF INTEGERS ON NUMBER LINE
Baccho, humne seekha ki hum ek number line use krke integers ko kaise add kr skte hai. Ab hum seekhenge ki ek number line ko use krke hum integers ko subtract kaise krenge. Subtraction generally means to decrease the value. But, in the case of integers, a subtraction operation might lead to an increase or decrease in the value of the given number. If we subtract a negative integer from a number, the value of the given number will increase (6−(−2)=6+2=8)and if we subtract a positive integer the value will decrease (6−2=4). Consider a few examples given below and observe the operation we are using on integers.
Example 1 :A worker steps down the ladder by 2 steps from the 5th step he is working on: (5−2=3)
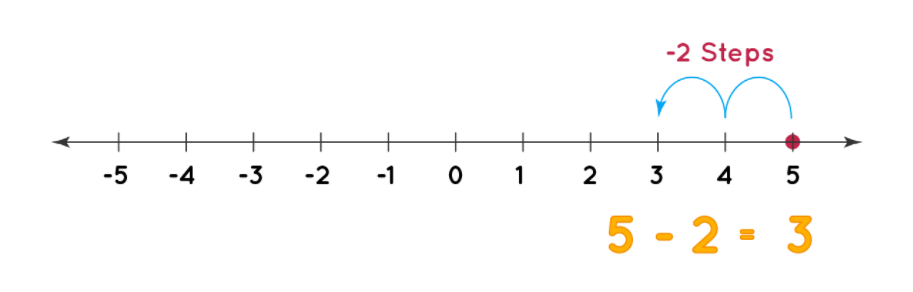
Example 2 :The temperature drips down by 4∘ from −1∘ Fahrenheit: (−1−4=−5)
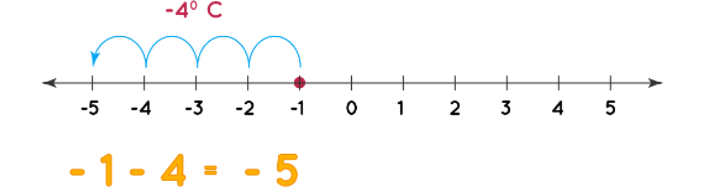
Baccho, in the above two cases, phle humne ek larger positive integer m se ek smaller positive integer subtract kia aur dusre case m humne ek integer ko ek dusre negative integer m se minus kia. Ab hum dekhenge ki agar hum ek negative integer m se ek negtaive integer minus krenge to kya hoga.
To subtract an integer from another negative integer it is enough to add the additive inverse of the integer that is being subtracted, to the other integer.
In other words, Jab hum ek negative integer (−a) m se ek dusra negative integer (−b) ko subtract krte hai ((−a)−(−b)), to hum isko aise represent kr skte hai jisme first integer m second integer ka additive inverse add horha ho i.e ((−a)+b).
To represent ((−a)+b) on number line, we'll first move a units to the left of 0 on number line and then b units on the right to reach our final answer. Isko smjhne k lie hum ek example lenge.
Example: Subtract (−4) from (−10)
Solution: (−10)−(−4)=(−10)+(additive inverse of−4)
⇒=−10+4=−6

Example 9
Draw a number line and represent each of the
following on it:
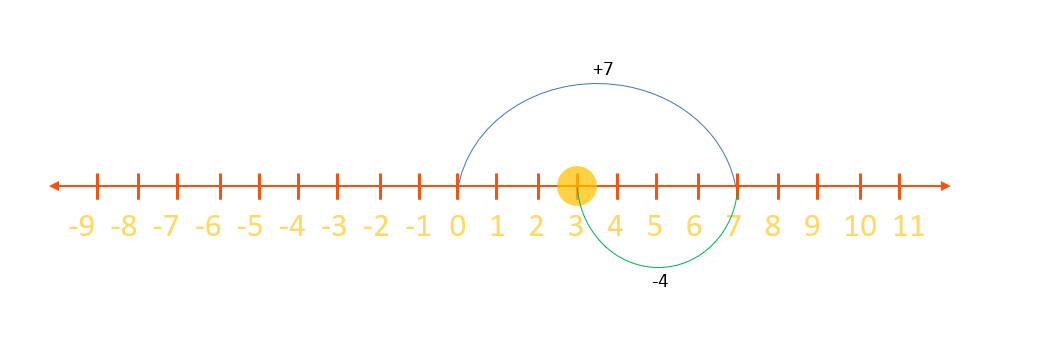
(i)(−1)+(−2)+2
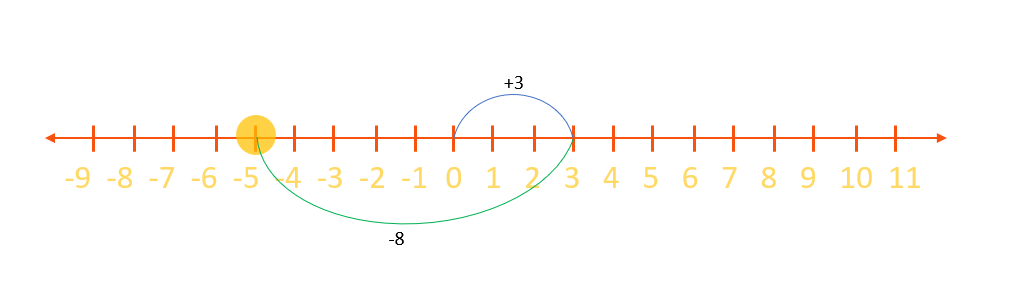
(ii)(−2)+7+(−9)
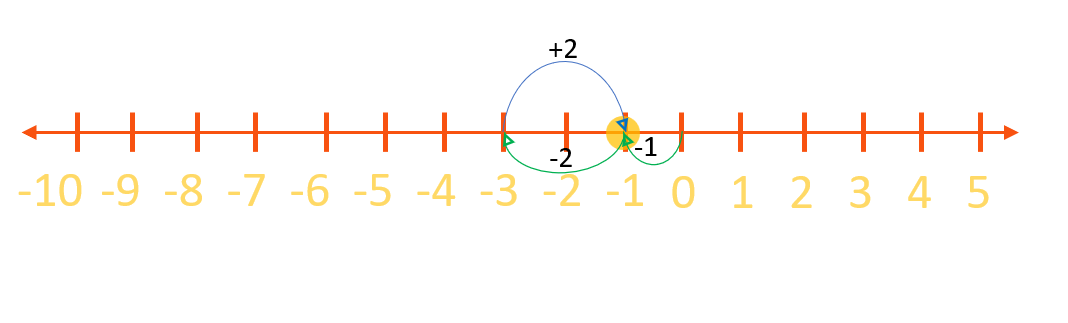
Answer : −1
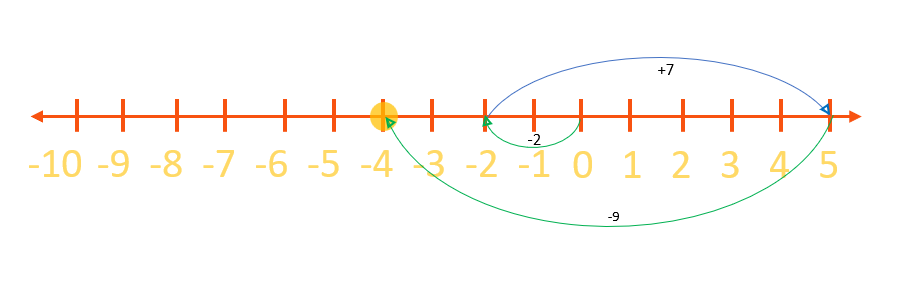
Answer : −4
Let's Summarize
1. We have seen that there are times when we need to use numbers with a negative
sign. This is when we want to go below zero on the number line. These are
called negative numbers. Some examples of their use can be in temperature scale,
water level in lake or river, level of oil in tank etc. They are also used to denote
debit account or outstanding dues.
2. The collection of numbers...,–4,–3,–2,–1,0,1,2,3,4,... is called integers.
So, –1,–2,–3,–4,... called negative numbers are negative integers and 1,2,3,4,... called positive numbers are the positive integers.
3. We have also seen how one more than given number gives a successor and one less than given number gives predecessor.
4. We observe that:
(a) When we have the same sign, add and put the same sign.
(i) When two positive integers are added, we get a positive integer [e.g.(+3)+(+2)=+5].
(ii) When two negative integers are added, we get a negative integer [e.g.(–2)+(–1)=–3].
(b) When one positive and one negative integers are added we subtract them as
whole numbers by considering the numbers without their sign and then put the
sign of the bigger number with the subtraction obtained. The bigger integer is
decided by ignoring the signs of the integers [e.g.(+4)+(–3)=+1and(–4)+(+3)=–1].
(c) The subtraction of an integer is the same as the addition of its additive inverse.
5. We have shown how addition and subtraction of integers can also be shown on a number line.
Let's Revise
1. Baccho iss chapter m humne phle humare previous concepts revise kiye. Humne whole numbers, negative numbers, naturals numbers k baare m pdha.
2. Negative numbers vo numbers hote hai jo ki 0 se kam hote hai aur number line p 0 se left m hote hai. Negative numbers ko represent krne k lie minus (−) ka sign use kia jaata hai like −1,−2,−3,...
3. Whole numbers aur negative numbers k collection ko Integers kaha jaata hai i.e. ...−4,−3,−2,−1,0,1,2,3,4,... are integers.
4. Integers are used in our day to day lives to conduct several operations and to measure several values like sea level, temperature, etc.
5. Jab ek integer m 1 add kia jaata hai, to hume uss number ka successor milta hai.
6.ab ek integer m se 1 substract kia jaata hai, to hume uss number ka predecessor milta hai.
7. Jab hum ek number line m right side move krte hai to integers increase hote hai aur jab hum left side move krte hai to integers decrease hote hai. Isi concept ko use krke hum Order of Integers smjh skte hai. Order ka basically mtlb hota hai descending ya ascending order. We can say that integers are in the following order : ...−7,−,−5,−4,−3,−2,−1,0,1,2,3,4,5,6,7,....
8. Baccho humne seekha ki integers ko number line p represent krke hum unko add aur subtract kaise kr skte hai.
9. Ek integer ki numerical value ko absolute value kaha jaata hai. For example, absolute value of −9 is 9 and absolute value 7 is 7.
10. Cases for adding integers:
(i) Do positive integers ko add krne k lie hum unki absolute values ko add krke positive sign lgate hai. (ii) Jab ek negative aur ek positive integer add hota hai, to hum unke absolute values ka difference lekr, larger number ka sign lgate hai. For example, −10+3=−7
(iii) Jab do negative integers add krna hota hai to hum unki absolute values ko add krke minus ka sign lgate hai. For example, −6+(−3)=−9
11. Jab ek integer m dusre integer ko add krne se resultant 0 aata hai, to vo dusra integer phle integer ka additive inverse kehlaya jata hai. For example, since, 6+(−6)=0, therefore, −6 is the additive inverse of 6.
12. Cases for subtracting integers:
(i) Jab ek smaller positive integer m se ek larger positive integer subtract hota hai, to hum unke absolute values ka difference lekr minus ka sign lgate hai. For example, 2−10=−8
(ii) Jab ek larger positive integer m se ek smaller positive integer subtract hota hai to hum unke absolute values ka difference lekr, positive sign lgate hai. For example, 6−2=4
(iii) Jab do negative integers subtract hote hai, to hum second integer ko subtract krne ki jagah uske additive inverse ko add kr skte hai. For example, −4−(2)=−4+2=−2.
13. Jab hum ek number line p add ya subtract krte hai, to har positive integer k lie hum right side move krte hai aur har negative integer k lie hum left side move krte hai.