FRACTIONS for Class 6 MATHS
Introduction
Baccho, hum fractions ka concept humari daily life m use krte hai jab bhi hum kisi tarah ki division ki baat krte hai. Suppose ki aapke paas ek paper hai aur aapko use apne chaar dosto m divide krna hai. Aap uss papaer ko phle half m cut krte hai aur fir unn dono halves ko firse half m divide krte hai taaki aapke paas 4 equal parts hojaye. Jab aap unn 4 pieces m se 1 piece, i.e, 1 by 4 piece (14) apne dost ko dete hai to aapke paas 3 out of 4 pieces bachh jaate hai. Fir jab aap ek aur piece apne dusre dost ko dete hai to aapke paas 2 out of 4, i.e, 2 by 4 pieces (24) bacch jate hai. Jab aap apne teesre dost ko third piece dete hai to aapke paas 1 out of 4, i.e, 1 by 4 pieces (14) bacch jaate hai. Jab aap last piece apne fourth friend ko dedete hai to aapke paas kitne pieces bachenge? Correct! 0 pieces.
Baccho iss situation m numbers like 14,24,34 are examples of fractions. Iss chapter m hum Fractions k baare m pdhenge aur unke different types k baare m bhi jaanenge. We'll also learn about representation of fractions on number line and some other topics. So let's begin!
FRACTIONS
Baccho, fractions ka simple meaning hota hai ki they are a part of a whole. Whole ka mtlb hota hai "complete" and fractions ka mtlb bnjata hai "part of that complete term" yaani ki part of a whole.
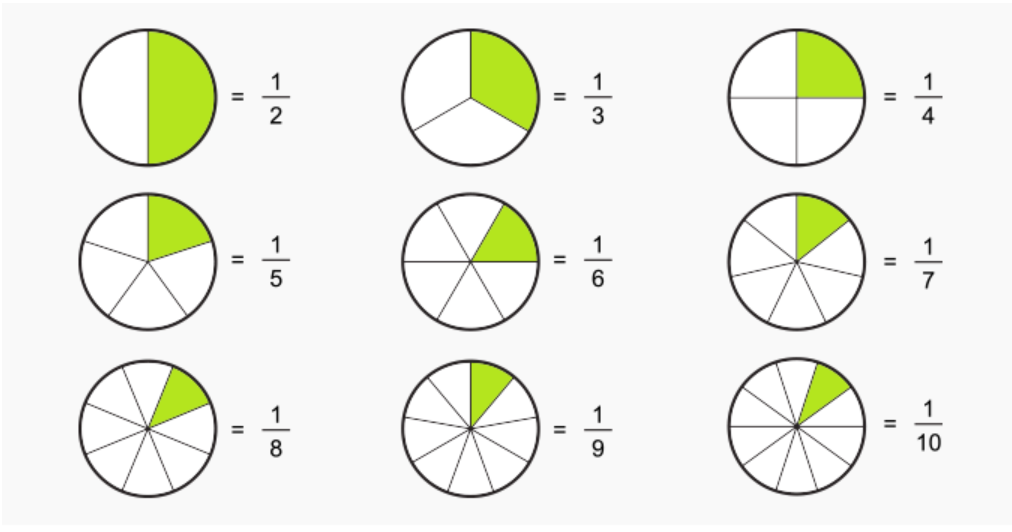
. Baccho, jab aap apne dosto k saath pizza khaa rhe hote hai aur uss pizza k 4 parts m se aapko one piece milta hai, to vo 14 of the pizza kehlaata hai. Similarly, aapne kabhi apni mummy se bola hoga ki vo aapko aadhi roti dede, to vo 12 of chapati kehlata hai. Ab hum fractions and decimals k concepts ko detail m pdhenge. The word fraction is derived from the Latin word "fractio" which means 'to break'. The Egyptians, being the earliest civilization to study fractions, learned fractions to resolve their mathematical problems, which included the division of food, supplies, etc. ractions are represented as a numerical value, can be defined as the parts of a whole.
<> A fraction can be a portion or section of any quantity out of a whole, where, the whole can be any number, a specific value, or a thing. Let us understand this concept using an example. Here's a chocolate that is divided into 8 equal parts.

Do you know what 18 means?
It means one in eight equal parts. It can also be read as:
bb" Parts of a Fraction"
All fractions consist of a numerator and a denominator.
CLASSIFICATIONS OF FRACTIONS
Baccho, in this section we'll learn about the classifications of fractions based on the numerator and denominator. The classifications are as follows:
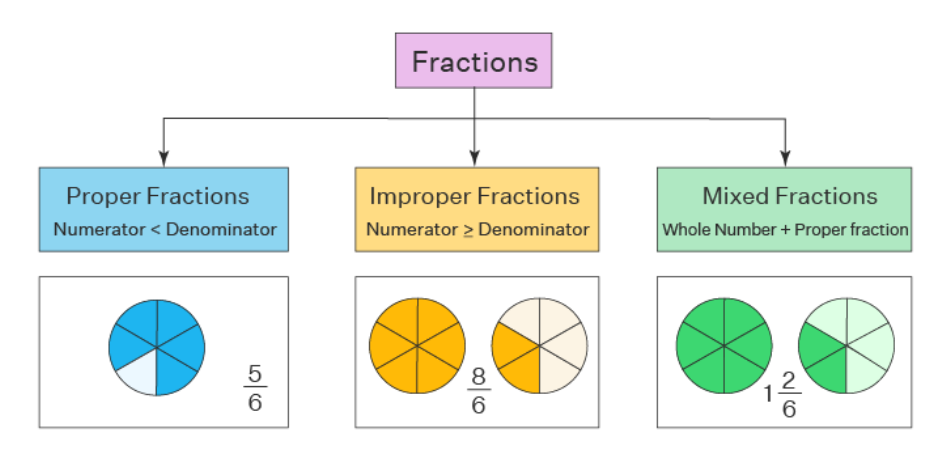
1.Proper fraction
Proper fractions is the type of fraction where, the numerator is smaller than the denominator. For example, 310, 17, 419. In these examples, 3<10, 1<7 and 4<19. Hence, these are proper fractions.
Baccho, suppose you have a pizza and aapne usko 5 parts m divide kia. Aapne unn 5 parts m se 3 parts apne dost ko dedie aur 2 parts khud rakhlie. To iss case m, aapka portion 25 hua and aapke dost ka portion 35. Both of these terms are proper fractions.
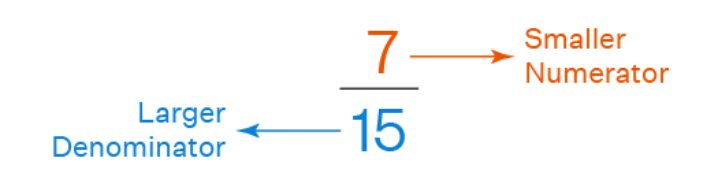
2.Improper and Mixed Fraction
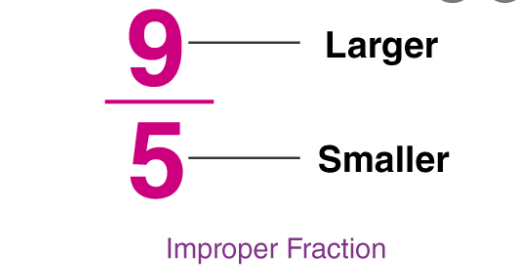
Improper Fractions is a type of fraction in which numerator is greater than the denominator. For example, 52, 83, 95. In these examples, 5>2, 8>3, 9>5.
Baccho, suppose ki aapne apne lie ek pizza order kia jisme 6 slices thi, but vo saari 6 slices aapke dost n khaali. Fir aapne ek aur pizza order kia jisme se aapne ek slice khaai bas. To total number of pizza slices eaten by you and your friend will be 7. To iss situation ko hum 76 k form m present krenge which is an improper fraction because 7>6.
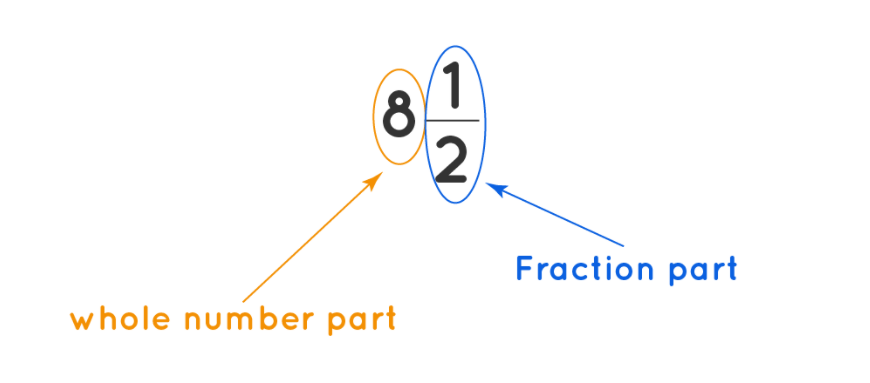
Mixed fraction is a type of fraction which is represented as a whole number and a proper fraction.
For example, in the above case, jaha p number of pizza slices eaten was represented as 76, to baccho 76 ka mtlb hua 66 (whole) + 16(proper fraction), which can be written as 116.
3.
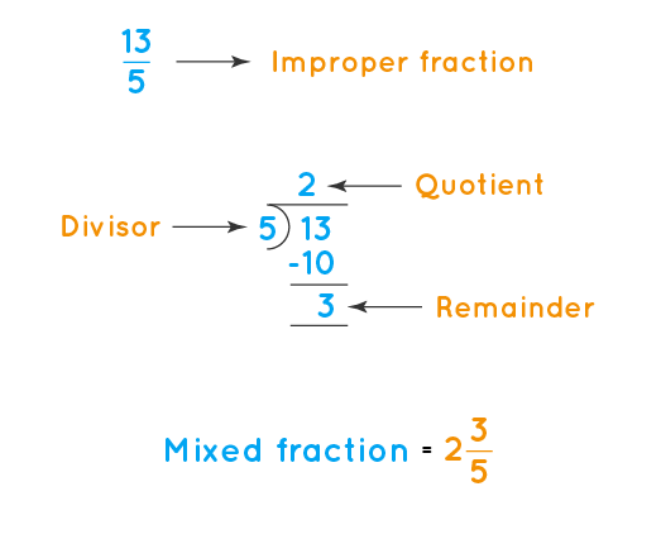
Let's see how we can convert improper fractions into mixed fraction:
Let's also learn how to convert mixed fractions back to improper fractions:

Now, let us study the types of fractions that are classified in groups. When a group of fractions is classified they determine the comparison between two or more fractions. They are categorized as follows:
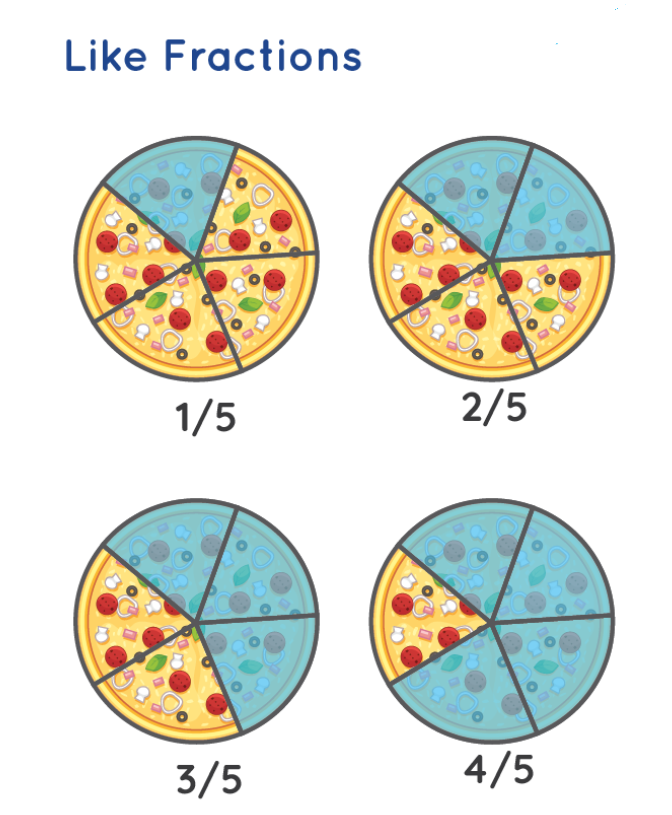
Like Fractions
Like fractions are those fractions which have the same denominator. For example, 16,26,36,46 are like fractions.
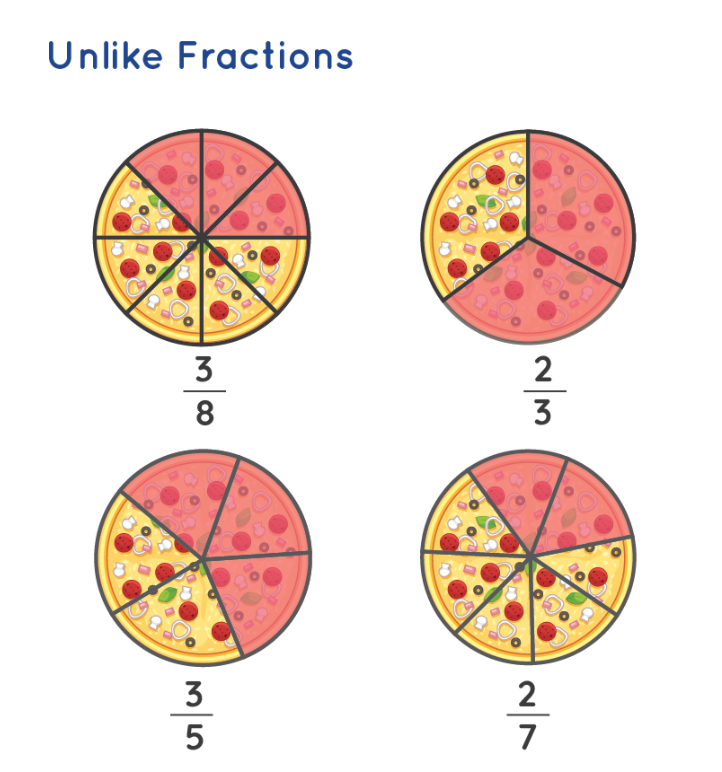
Unlike Fractions
Unlike fractions are those fractions which do not have the same denominator. For example, 17,38,49 are unlike fractions.
Equivalent Fractions are those fractions which have different numerator and different denominators, but they have the same simplest form. For example, 39 and 618 have different numerators and denominators but 39=13 and 618=13, hence, they are equivalent fractions.
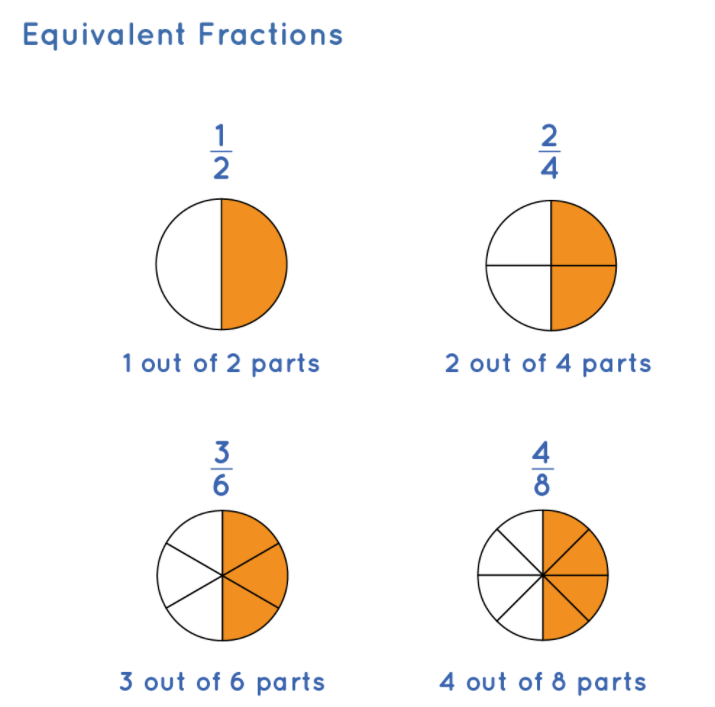
How To Find Equivalent Fractions?
Equivalent fractions can be written by multiplying or dividing both the numerator and the denominator by the same number. This is the reason why these fractions get reduced to the same number when they are simplified. Let us understand the two ways in which we can make equivalent fractions:
1. Multiply the Numerator and Denominator by the Same Number
To find the equivalent fractions for any given fraction, multiply the numerator and the denominator by the same number. For example, to find an equivalent fraction of 34, multiply the numerator 3 and the denominator 4 by the same number, say, 2. Thus, 68 is an equivalent fraction of 34.
Thus, the equivalent fractions of 34 are 68, 912, 1216, and 1520.
2. Divide the Numerator and Denominator by the Same Number
To find the equivalent fractions for any given fraction, divide the numerator and the denominator by the same number. For example, to find an equivalent fraction of 72108, we will first find their common factors. We know that 2 is a common factor of both 72 and 108. Hence, an equivalent fraction of 72108 can be found by dividing its numerator and denominator by 2. Thus, 3654 is an equivalent fraction of 72108. Let us see how the fraction is further simplified:
Example 1
Express the following as mixed fractions : (a) 174 (b) 113(c) 275 (d) 73
(a) 4 whole and
14 more, or 414
(b) 3 whole and 23 more, or 323
(c) 5 whole and 25 more, or 525
(d) 2 whole and 13 more, or 2 1/3
Example 2
Express the following mixed fractions as improper fractions (a) 234 (b) 719 (c) 537
(a) 234=2+34+2×44+34=114
(b) 719=7×9+19=649
(c) 537=5×7+37=387
Example 3
Example 4
Find the equivalent fraction of 3648 with:
(a) numerator 9
(b) denominator 4
(a) 3648=36÷448÷4=912
(b) 3648=36÷1248÷12=34
FRACTIONS ON NUMBER LINE
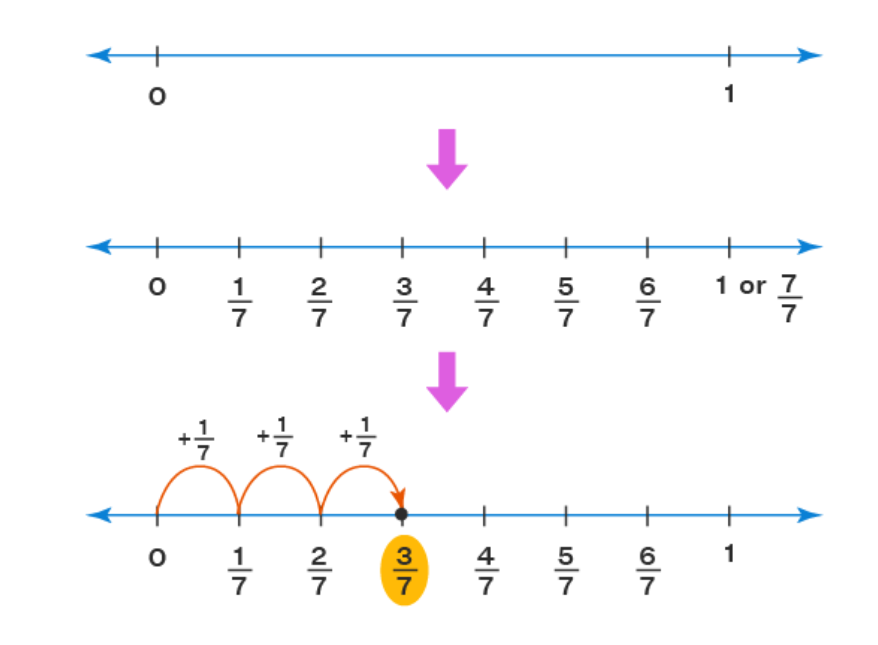
Baccho, aapne apne previous chapters m whole numbers ( like 0,1,2,3, etc) ko number line p represent krna seekha tha. Iss chapter m hum seekhenge ki hum fractions ko number line p kaise represent kr skte hai. Baccho number line p fractions ko represent krne k lie we need to understand a few concepts before. We know that half of something (12) is greater than nothing (0) and less than a whole (1). From this we know that the fraction 12 will be marked exactly between 0 and 1 on number line.
Representing fractions on a number line means that we can plot fractions on a number line, which is similar to plotting whole numbers and integers. Fractions represent parts of a whole. So, fractions on the number line are represented by making equal parts of a whole i.e. 0 to 1, and the number of those equal parts would be the same as the number written in the denominator of the fraction. For example, to represent 18 on the number line, we have to divide 0 to 1 into 8 equal parts and mark the first part as 18.

How to Plot Fractions on Number Line?
To plot fractions on the number line, follow the steps given below:
Step 1: Draw a number line of a suitable length.
Step 2: If the given fraction is a proper fraction, then mark points 0 and 1 on the number line. Or, if it is an improper fraction, then first convert it into a mixed fraction, and then mark two integers between those the given fraction lies. For example, to represent 32 or 1(12)
, mark points 1 and 2 on the number line.
Step 3: Draw an equal number of parts of the numbers marked in step 2 which will be equal to the denominator of the fraction.
Step 4: Starting from the left point, count forward the number of parts shown by the numerator.
Step 5: Mark the point on the line.
An example of 37 is shown in the image below to help you understand how to plot fractions on a number line step-wise.
SIMPLEST FORM OF FRACTION
Baccho simplest form of a fraction vo hoti hai jisme numerator aur denominator ka 1 k alawa koi common factor nahi hota hai. The simplest form of a fraction is equivalent to the given fraction. For example, the fraction 34 is in the simplest form because 3 and 4 have no common factor except 1.
Let's try simplifying the fraction 824 step by step.
The factors of 8 and 24 are:
Factors of 8:1,2,4, and 8
Factors of 24:1,2,3,4,6,8,12, and 24
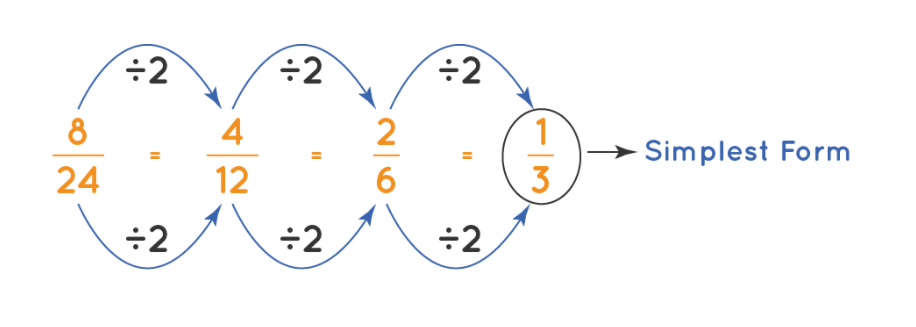
Thus, 13 is the simplest form of the fraction 824.
Baccho, even though ye method correct hai but to simplify bigger fractions, it might seem lengthy to repeatedly divide the numerators and denominators. To calculate the simplest form, let's learn a shortcut.
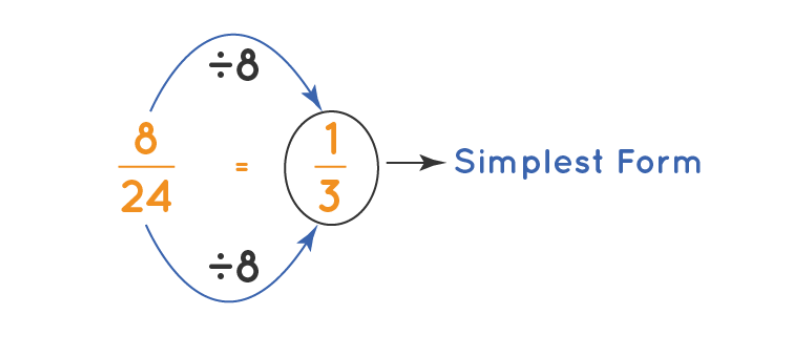
The Shortest Way
Follow the steps given below to learn the shortest way.
Let's get back to the same problem of simplifying the fraction 824. The highest common factor of 8 and 24 is 8. Dividing the numerator 8 and the denominator 24 by 8 will directly give us the simplest form of the fraction, that is, 13.
Example 5
Reduce the following fractions to simplest form : (a) 4860 (b) 15060 (c) 8498 (d) 1252 (e) 728
(a) 4860=4⋅125⋅12=45
(b) 15060=5⋅302⋅30=52
(c) 8498=12⋅714⋅7=6⋅147⋅14=67
(d) 1252=3⋅413⋅4=313
(e) 728=1⋅74⋅7=14
COMPARISON OF FRACTIONS
Baccho, suppose ki aapke paas 312 rotis hai aur aapke dost k paas 234 rotis hai. Kya aap inn fractions ko dekh k bta skte hai ki kiske paas zyada rotis hai? Clearly, aapke paas 3 whole rotis and 12 roti hai aur aapke dost k paas sirf 2 whole rotis and 34 roti hai. Yaani ki aapke paas zyada rotis hai. Similarly, look at the following representation of fractions 48 and 46.
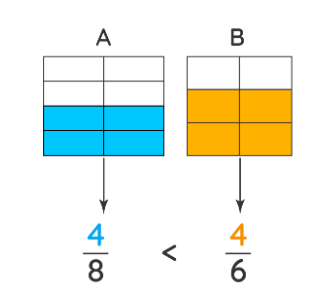
Baccho aap dekh skte hai ki 46>48.
Isko kehte hai Comparison of Fractions. But often it is not easy to say which one out of a pair of fractions is larger. For
example, which is greater,14 or 310? Let's learn how to compare different types of fractions.
Example 6
Compare 45and56
The fractions are unlike fractions. Their numerators are different
too. Let us write their equivalent fractions.
LCM of 5 and 6 is 30.
⇒45×66 and 56×55
⇒2430 and 2530
Since, 2430<2530 so, 45>56
Example 7
Compare 56and1315
The fractions are unlike. We should first get their equivalent fractions
with a denominator which is a common multiple of 6 and 15.
LCM of 6 and 15 is 30.
⇒56×55 and 1315×22
⇒2530 and 2630
Since, 2530<2630 so, 56<1315
Example 8
Compare the fractions and put an appropriate sign.
(a) 36 , 56 (b) 17, 14 (c) 45 , 55 (d) 35 , 37
(a) 36<56
(b) 17<14
(c) 45<55
(d)35>37
ADDITION AND SUBTRACTION OF FRACTIONS
Baccho, humne apne previous chapters m seekha tha ki hum whole numbers, natural numbers ko add aur subtract kaise kr skte hai. Iss chapter m hum seekhenge ki hum fractions ko add aur subtract kaise krte hai. Hum apni daily life m boht si situations face krte hai jaha hume alag alag fractions ko add ya subtract krna hota hai. For example, suppose aapne morning m 112 litres milk consume kia aur shyaam ko 214 litres milk consume kia. Kya aap bta skte hai ki aapne total kitna milk consume kia? For this we'll have to add these two fractions. Similarly, suppose ki aapke paas 534 chapatis hai aur usme se aapne 214 chapatis apne dost ko dedi. To aapke paas kitni chapatis bachi? For this you'll have to subtract these two fractions. Let's learn how to add and subtract different types of fractions.
Adding or subtracting like fractions
It is very easy to add or subtract two or more like fractions. Follow the step given below for the addition and subtraction of like fractions:
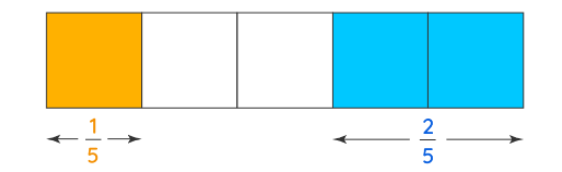
For example, let us add 213 and 513.
The first step is to add their numerators, i.e, 2+5=7. So, the sum of fractions 213 and 513 is 713.
Similarly, to subtract 34 from 74, subtract 3 from 7, i.e., 7−3=4. So, the difference is 44, which can be reduced to 1.
The following figure represents addition of two like fractions in the same model.
Adding or subtracting Unlike fractions
Baccho, unlike fractions ko add ya subtract krna ka method bhi same hota hai, but before adding or subtracting their numerators, we simply need to convert them into fractions with same denominators. Humne above topics m unlike fractions k equivalent fractions nikaalna seekha tha. Using the same method, we'll convert unlike fractions and will then subtract and add the numerators. Let us see the steps to be followed if we want to add the fractions 13 and 35.
So, 515+915=5+915=1415.
The following figure represents subtraction of two unlike fractions in the same model.
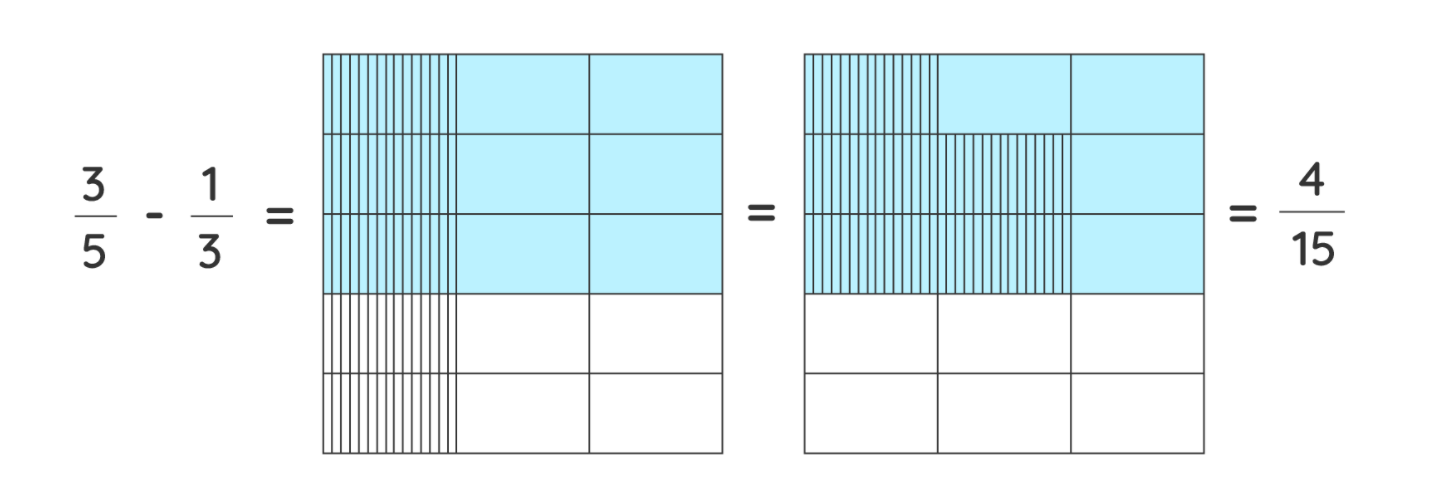
We see that our model is divided into 15 parts. This is our denominator, or, in other words, the LCM of the denominators of the given fraction. As we need to remove 13 from 35, we will move the selected two parts which are not part of the 35, to remove it from 35. We see that there are only 4 parts of the remaining which are not shaded out.
Therefore, 35−13=415
Adding or subtracting Mixed fractions
Baccho aap already seekh chuke hai ki mixed fractions ko do tarah se represent kia jaata hai:
Mixed fractions ko add ya subtract krne k bhi do methods hote hai. Let's see what they are:
1. Add or subtract the whole parts of the mixed fractions and then add or subtract the fractions separately. Let's look at an example for better understanding.
Example: Add 245and356
Solution : 245+356=2+45+3+56=5+45+56
Now 45+56=4×65×6+5×56×5 (Since LCM of 5 and 6=30)
=2430+2530=4930=30+1930=1+1930
Thus, 5+45+56=5+1+1930=6+1930=61930
And, therefore, 245+356=61930
2. Mixed fractions ko add ya subtract ka second method hota hai jisme hum unhe improper fractions m convert krte hai. Agar obtained improper fractionsk denominators same hote hai to hum directly unke numerators ko add ya subtract krdete hai. Agar unke denominators alag hote hai, to hum unka LCM lekr, unhe like equivalent fractions m convert krke unhe add ya subtract kre. Ise smjhne k lie hum ek example lenge.
Converting the fractions to improper fractions we get, 32 and 52 . On adding 32 and 52 , we get 82 . Further simplifying 82 , we get 4.
Converting the fractions to improper fractions we get, 113 and 73 . On subtracting 113 and 73 , we get 43 . Converting 43 to mixed fraction, we get 113 .
Example 9
Subtract 34 from 56.
We need to find equivalent fractions of 34 and 56, which have the same denominator. This denominator is given by the LCM of 4 and 6. The
required LCM is 12.
56−34=5×26×2−3×34×3=1012−912=112
Example 10
Example 11
Let's Summarize
1.(a) A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects.
(b) When expressing a situation of counting parts to write a fraction, it must be ensured that all parts are equal.
2. In 57, 5 is called the numerator and 7 is called the denominator.
3. Fractions can be shown on a number line. Every fraction has a point associated with it
on the number line.
4. In a proper fraction, the numerator is less than the denominator. The fractions, where the numerator is greater than the denominator are called improper fractions. An improper fraction can be written as a combination of a whole and a part, and such fraction then
called mixed fractions.
5. Each proper or improper fraction has many equivalent fractions. To find an equivalent fraction of a given fraction, we may multiply or divide both the numerator and the
denominator of the given fraction by the same number.
6. A fraction is said to be in the simplest (or lowest) form if its numerator and the denominator have no common factor except 1.
Let's Revise
1. Baccho iss chapter m humne seekha ki fractions kya hote hai aur hum apni daily life m fractions ko kaha use krte hai.
2. Fractions vo numbers hote hai jo ki part of a whole ko represent krte hai. They have two components : a numerator and a denominator.
3. 45 ek fraction hai jo ki 0 aur 1 k beech m lie krta hai. In this fraction, 4 is the numerator and 5 is the denominator.
4. Jaise hum natural numbers aur whole numbers ko number line p represent krte hai, usi tarah hum fractions ko bhi number line p represent kr skte hai.
5. There are 3 types of fractions: Proper fractions, improper fractions and mixed fractions.
6. Jin fractions k numerator unke denominator se chote hote hai, vo proper fractions kehlaate hai and they always lie between 0 and 1 on the number line. Examples: 23,1678,3356,etc.
7. Jin fractions k numerators unke denominators se badhe hote hai h unhe improper fractions kaha jaata hai. Example: 86,154,5623, etc.
8. Jab hum improper fractions ko divide krte hai jisse hume ek quotient aur remainder milta hai, uss form ko mixed fractions kehte hai. They represent the combination of a whole and a part. For example, the improper fraction 83 can be written as the mixed fraction 223
9. There is a group of fractions which is used for comparison between fractions. These are: like fractions, unlike fractions and equivalent fractions.
10. Like fractions vo fractions hote hai jinke denominators same hote hai. Unlike fractions vo hote hai jinke different denominators hote hai. Equivalent fractions tab milte hai jab hum ek fraction k numerator aur denominator ko same number se multiply ya divide kre. For example, equivalent fractions of 23 are 46,69,812, etc.
11. Simplest form of a fraction tab hoti hai jab kisi fraction k numerator aur denominator k 1 k alawa koi common factor nahi hote. For example, 13,1317,2315, etc.
12. There are different ways to compare like and unlike fractions that we learnt in this chapter. 13. Baccho, jis tarah se aapne whole numbers ko add aur subtract krna seekha tha, fractions ko bhi add aur subtract kia jaata hai. We face various situations in our lives where we need to add or subtract various fractions. In this chapter, we learnt how to add and subtract like fractions, unlike fractions and mixed fraction.