DECIMAL for Class 6 MATHS

Baccho aapne apni previous classes m parts and wholes ka aur unse related basic concepts pdhe hai. Aapne previous chapter m fractions k baare m bhi pdha aur ye jaana ki jab hume ek part aur ek whole ko represent krna hota hai to hum unhe fractions k form m krte hai. Decimal bhi ek aisa standard system hota hai jisse integers and non-integer numbers ko denote kia jaata hai. It is based on or counted in tens or tenths. Aapne apni day to day lives m decimals ko use hote hue dekha hoga. For example, Suresh scored $9.8$ marks out of $10$ in his maths exam. Or, a packet of chips contains 10.05 grams of fat.
In this chapter we will learn more about decimals and will build a better understanding on our previous topics. So let's get started!

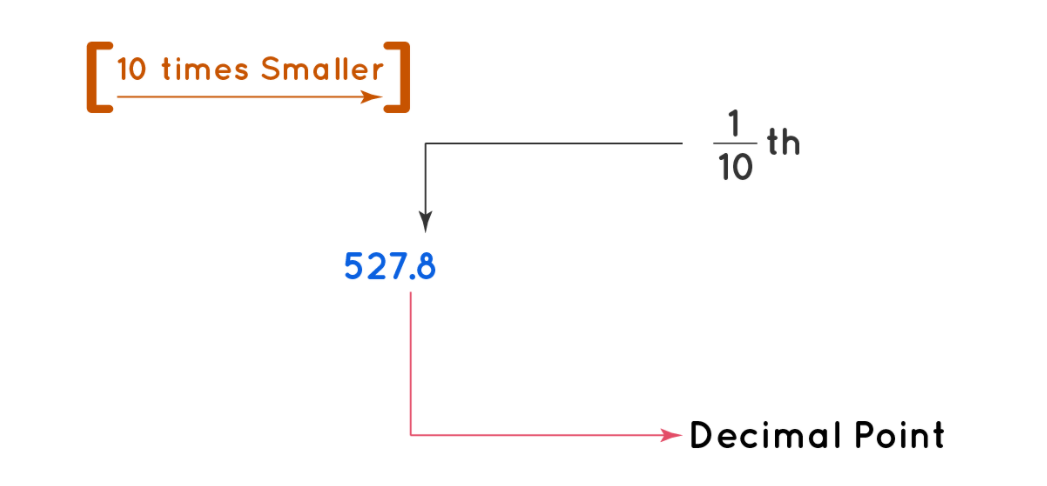
A decimal number system is used to express the whole number and fraction together. Here, we will separate the whole number from the fraction by inserting a ".", which is called a decimal point. The numbers to the left of the decimal point are the integers or whole numbers and the numbers to the right of the decimal point are called decimal numbers. If we go right from the ones' place, the next place will be $\left(\frac{1}{10}\right)$ times smaller, which will be ${\left(\frac{1}{10}\right)}^{th}$ or one-tenth position. There are many real-life situations in which you might be using decimals without even realizing it. For example, let's say you are going to take a cone of ice cream. The vendor tells you that the price of ice cream is $\text{Rs. 20}$ and $\text{50 paise}$. Now, if you want to express this whole amount in one figure, you will say that the price of the ice cream cone is $\text{Rs. 20.50}$.

Baccho humne place value system k baare m previous chapters m pdha tha. Decimals k case m bhi same place value system hota hai for the whole number part of it (left of decimal point). But after the decimal point, there is a different world of numbers going on in which we use decimal fractions to represent the value. Jab hum left side move krte hai, each place is ten times greater than the previous place digit. So, to the right of one's place, we have tenths $\left(\frac{1}{10}\right)$ and to the right of tenths, we have hundredths $\left(\frac{1}{100}\right)$, and so on.

Let's look at an example to see how we can express using decimals.
EXAMPLE: Ravi and Raju measured the lengths of their pencils. Ravi’s pencil was $\text{7 cm 5mm}$ long and Raju’s pencil was $\text{8 cm 3 mm}$ long. Can you express these lengths in centimeter using decimals?"
SOLUTION:
We know that $10mm=1cm$
Therefore, $1mm=\frac{1}{10}cm$ or one-tenth cm $=0.1cm$
Now, length of Ravi’s pencil$=7cm5mm$
$=7\frac{5}{10}cm$ i.e. $7cm$ and $5$ tenths of a $cm$
$=7.5cm$
The length of Raju’s pencil $=8cm3mm$
$=8\frac{3}{10}cm$ i.e. $8cm$ and $3$ tenths of a $cm$
$=8.3cm$
$\text{Representing Decimals on number line}$
Decimals are another form of a fraction in which the whole number is separated from the fractional part using a dot. Baccho aapne previously fractions ko number line p represent krna seekha tha. Decimals on a number line are very similar to the representation of fractions on a number line except for its way of representation.
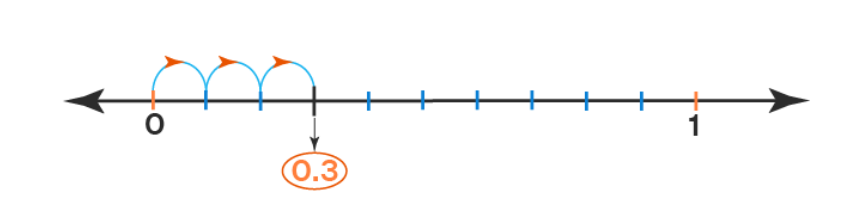
The right-hand side of $0$ represents the positive region. Let us represent $0.3$ on a number line using the following steps shown below.
Step I: Draw a number line by marking $0$ as the reference.
Step II: Identify the integers between which the decimal lies and mark them. $0.3$ lies between $0$ and $1$.
Step III: We will now be making $10$ divisions between the integers $0$ and $1$.
Step IV: Now, we will be moving towards the right starting from $0$ by the number of steps equivalent to the right-most digit value after the decimal point. For $0.3$ we will be moving $3$ places towards the right.

$\text{Inter-conversion of fractions and decimals}$
$1.$ Fractions as decimals
Baccho humne seekha ki hum kisi fraction ko jiska denominator $10$ ho usko decimals m kaise represent kr skte hai.
Let us now try to find decimal representation of
$\left(a\right)$ $\frac{11}{5}$
$\left(b\right)$ $\frac{1}{2}$
$\left(a\right)$ We know that $\frac{11}{5}=\frac{22}{10}=\frac{20+2}{10}+=\frac{20}{10}+\frac{2}{10}=2+\frac{2}{10}=2.2$
Therefore, $\frac{22}{10}=2.2$ (in decimal notation.)
$\left(b\right)$ In $\frac{1}{2}$ , the denominator is $2$. For writing in decimal notation, the denominator should be $10$. We already know how to make an equivalent fraction. So,
$\frac{1}{2}=\frac{1\times 5}{2\times 5}=\frac{5}{10}=0.5$
Therefore, $\frac{1}{2}$ is $0.5$ in decimal notation.

$2.$ Decimals as fractions
Baccho abhi tk humne seekha ki hum fractions ko jinke denominators $10,2$ ya $5$ ho, unko decimals m kaise represent krte hai. Let us now see how to write $1.2$ as a fraction.
$1.2=1+\frac{2}{10}=\frac{10}{10}+\frac{2}{10}=\frac{12}{10}$

Write each of the following as decimals :
(a) Seven-tenths
(b) Two tens and nine-tenths
(c) Fourteen point six
(d) One hundred and two ones
(e) Six hundred point eight

$\left(a\right)$ Seven-tenths $=\frac{7}{10}=0.7$
$\left(b\right)$ Two tens and nine-tenths $=2\times 10+9\times \frac{1}{10}=20.9$
$\left(c\right)$ Fourteen point six $=14.60$
$\left(d\right)$ One hundred and two one $=1\times 100+2\times 1=102.0$
$\left(e\right)$Six hundred point eight $=600.8$

Write each of the following as decimal :
(a) $30+6+\frac{2}{10}$
(b) $600+2+\frac{8}{10}$

$\left(a\right)30+6+\frac{2}{10}$
We have $3$ tens, $6$ ones and $2$ tenths. Therefore, the decimal representation is $36.2$.
$\left(b\right)600+2+\frac{8}{10}$
Note that it has $6$ hundreds, no tens, $2$ ones and $8$ tenths. Therefore, the decimal representation is $602.8$

The value of the digit at the second place after the decimal point is hundredths place value. The number in that place tells you how many hundredths are there. Hundredths can be calculated as $1$ unit divided in $100$ equal parts i.e 0.01.One block divided into $100$ equal parts means each part is $\frac{1}{100}$ (one-hundredth) of a unit. It can be written as $0.01$ in decimal notation.
Every fraction with denominator $100$ can be written in decimal notation and vice-versa.

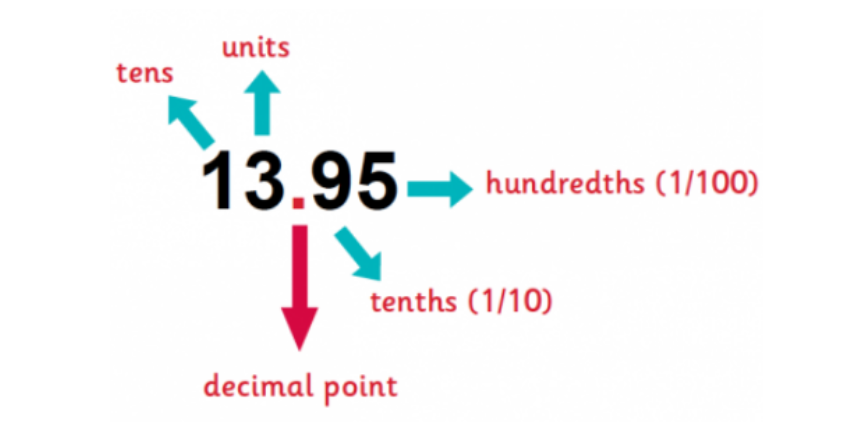
Let us consider a decimal number $0.5694$ to see the different place values of each digit:

Write as fractions in lowest terms.
$\left(a\right)0.60$    
$\left(b\right)0.05$     
$\left(c\right)0.75$    
$\left(d\right)0.18$    
$\left(e\right)0.25$    
$\left(f\right)0.125$ 
$\left(g\right)0.066$

(a) $0.60=\frac{60}{100}=\frac{3\times 2}{5\times 2}=\frac{6}{10}=\frac{3}{5}$
(b) $0.05=\frac{5}{100}=\frac{5\times 1}{20\times 5}=\frac{1}{20}$
(c) $0.75=\frac{75}{100}=\frac{3\times 25}{4\times 25}=\frac{3}{4}$
(d) $0.18=\frac{18}{100}=\frac{9\times 2}{50\times 2}=\frac{9}{50}$
(e) $0.25=\frac{25}{100}=\frac{25}{25\times 4}=\frac{1}{4}$
(f) $0.125=\frac{125}{1000}=\frac{125}{8\times 125}=\frac{1}{8}$
(g) $0.066=\frac{66}{1000}=\frac{33}{500}$

Write each of the following as a decimal.
(a) Three hundred six and seven-hundredths.
(b) Eleven point two three five.
(c) Nine and twenty five thousandths

(a) Three hundred six and seven-hundredths $=306+\frac{7}{100}=306.07$

(b) Eleven point two three five $=11+.235=11.235$

(c) Nine and twenty five thousandths $=9+\frac{25}{1000}=9.025$

Baccho ab hum dekhenge ki hum decimals ko compare kaise krte hai. Hume do cheezon ka dhyaan rakhna hota hai while comparing decimals.

Which is greater?
$\left(a\right)0.3\text{or}0.4$
$\left(b\right)0.07\text{or}0.02$
$\left(c\right)3\text{or}0.8$
$\left(d\right)0.5\text{or}0.05$
$\left(e\right)1.23\text{or}1.2$
$\left(f\right)0.099\text{or}0.19$
$\left(g\right)1.5\text{or}1.50$
$\left(h\right)1.431\text{or}1.490$
$\left(i\right)3.3\text{or}3.300$
$\left(j\right)5.64\text{or}5.603$

(a) $0.4>0.3$
(b) $0.07>0.02$
(c) $3>0.8$
(d) $0.5>0.05$
(e) $1.23>1.2$
(f) $0.19>0.099$
(g) $1.5=1.50$
(h) $1.490>1.431$
(i)$3.3=3.300$
(j)$5.64>5.603$

We often use decimals in our daily life in multiple fields. Let us look at some of them:
$1.$ MONEY
$1$ paisa $=\text{Rs.}\frac{1}{100}=Rs.0.01$
$85$ paise $=\text{Rs.}\frac{85}{100}=\text{Rs.}0.85$
$125$ paise $=\text{Rs.}1$ and $25$ paise $=\text{Rs.}1.25$
$65$ paise $=\text{Rs.}\frac{65}{100}=\text{Rs.}0.65$
$2.$ LENGTH
$1cm=\frac{1}{100}m=0.01m$
$46cm=\frac{46}{100}m=0.46m$
$126cm=100cm+26cm=1m+\frac{26}{100}m=1.26m$
$3.$ WEIGHT
$1g=\frac{1}{1000}kg=0.001kg$
$2650g=2000g+650g=\frac{2000}{1000}kg+\frac{650}{1000}kg=2kg+0.650kg=2.650kg$

Express as meters using decimals.
$\left(a\right)15cm$
$\left(b\right)6cm$
$\left(c\right)2m45cm$
$\left(d\right)9m7cm$
$\left(e\right)419cm$

We know, $100$ cm = $1$ m
So,
(i) $15$ cm $=\frac{15}{100}=0.15$ m
(ii) $6$ cm $=\frac{6}{100}=0.06$ m
(iii) $2$ m $45$ cm $=(2+\frac{45}{100})=2.45$ m
(iv) $9$ m $7$ cm $=(9+\frac{7}{100})=9.07$ m
(v) $419$ cm $=\frac{419}{100}=4.19$ m

Express as cm using decimals.
$\left(a\right)5mm$
$\left(b\right)60mm$
$\left(c\right)164mm$
$\left(d\right)9cm8mm$
$\left(e\right)93mm$

We know, $10$ mm = $1$ cm
So,
(i) $5$ mm$=\frac{5}{10}=0.5$ cm
(ii) $60$ mm$=\frac{60}{10}=6$ cm
(iii) $164$ mm$=\frac{164}{10}=16.4$ cm
(iv)$9$ cm $8$ mm$=(9+\frac{8}{10})=9.8$ cm
(v) $93$ mm$=\frac{93}{10}=9.3$ cm

Express as kg using decimals:
$\left(a\right)2g$
$\left(b\right)100g$
$\left(c\right)3750g$
$\left(d\right)5kg8g$
$\left(e\right)26kg50g$

We know, $1000$ g = $1$ kg
So,
(i) $2$ g $=\frac{2}{1000}=0.002$ kg
(ii) $100$ g $=\frac{100}{1000}=0.1$ kg
(iii) $3750$ g $=\frac{3750}{1000}=3.75$ kg
(iv) $5$ kg $8$ g $=(5+\frac{8}{1000})=5.008$ kg
(v) $26$ kg $50$ g $=(26+\frac{50}{1000})=26.05$ kg

Express as rupees using decimals.
$\left(a\right)5$ paise        
$\left(b\right)75$ paise
$\left(c\right)20$ paise
$\left(d\right)50$ rupees $90$ paise
$\left(e\right)725$ paise

We know, $100$ paise = $1$ rupee
So,
(i) $5$ paise = $\frac{5}{100}$ = $0.05$ rupees
(ii) $75$ paise = $\frac{75}{100}$ = $0.75$ rupees
(iii) $20$ paise = $\frac{20}{100}$ = $0.20$ rupees
(iv) $50$ rupees $90$ paise = $(50+\frac{90}{100})$ = $50.90$ rupees
(v) $725$ paise = $\frac{725}{100}$ = $7.25$ rupees

Baccho before learning how to add two decimal numbers we need to learn some basic rules or steps to do that.
For the operation of addition in decimals, follow the steps given below:
Step 1: Write the numbers, such that the decimals are lined perfectly.
Step 2: Write zeroes in the places wherever the length of decimal numbers is not the same.
Step 3: Now add the decimal numbers and find the output to addition.
Example: Add: $2.53+1.14$.
Solution:
If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.

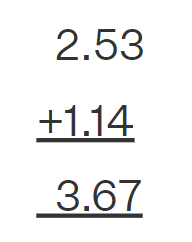
Therefore, after adding the decimals, we get the sum as $3.67$

Samson travelled $5$ km $52$ m by bus, $2$ km $265$ m by car and the rest $1$km $30$ m he walked. How much distance did he travel in all?

Distance travelled by Samson by bus $=$ $5$ km $52$ m $=5.052$ km
Distance travelled by Samson by car $=$ $2$ km $265$ m $=2.265$ km
Distance travelled by Samson by walking $=$ $1$ km $30$ m $=1.030$ km
So, total distance travelled by Samson $=5.052+2.265+1.030=8.347$ km

Rahul bought $4$ kg $90$ g of apples, $2$ kg $60$ g of grapes and $5$ kg $300$ g of mangoes. Find the total weight of all the fruits he bought

Weight of apples bought by Rahul $=$ $4kg90g$ $=4.090$ kg
Weight of grapes bought by Rahul $=$ $2kg60g$ $=2.060$ kg
Weight of mangoes bought by Rahul $=$ $5kg300g$ $=5.3$ kg
So, total weight of fruits $=4.090+2.060+5.300=11.450$ kg

For the operation of subtraction in decimals, the rule of carryover is followed as in the normal whole numbers.

Urmila’s school is at a distance of $5km350m$ from her house. She travels $1km70m$ on foot and the rest by bus. How much distance does she travel by bus?

Total distance$=5.350km$
distance traveled by on foot$=1.070km$
distance travelled by bus=total distance traveled - distance travelled by on foot
$=5.35-1.07$
$=4.28km.$

Nasreen bought $3m20cm$ cloth for her shirt and $2m5cm$ cloth for her trouser. Find the total length of cloth bought by her.

Length of cloth bought for Nasreen shirt $=3m20cm=3m+\frac{20}{100}m=3.2m$
Length of cloth bought for Nasreen trouser $=2m5cm=2m+\frac{5}{100}m=2.05m$
So, total length of cloth bought by Nasreen $=3.2+2.05=5.25m=5m25cm$

$1.$ To understand the parts of one whole (i.e. a unit) we represent a unit by a block. One block divided into $10$ equal parts means each part is $\frac{1}{10}$ (one-tenth) of a unit. It can be written as $0.1$ in decimal notation. The dot represents the decimal point and it comes between the units place and the tenths place.
$2.$ Every fraction with denominator $10$ can be written in decimal notation and vice-versa.
$3.$ One block divided into $100$ equal parts means each part is $\frac{1}{100}$ (one-hundredth) of a unit. It can be written as $0.01$ in decimal notation.
$4.$ Every fraction with denominator $100$ can be written in decimal notation and vice-versa.
$5.$ In the place value table, as we go from left to the right, the multiplying factor becomes $\frac{1}{10}$ of the previous factor. The place value table can be further extended from hundredths to $\frac{1}{10}$ of hundredths i.e. thousandths $\left(\frac{1}{1000}\right)$, which is written as $0.001$ in decimal notation.
$6.$ All decimals can also be represented on a number line.
$7.$ Every decimal can be written as a fraction.
$8.$ Any two decimal numbers can be compared among themselves. The comparison can start with the whole part. If the whole parts are equal then the tenth parts can be compared and so on.
$9.$ Decimals are used in many ways in our lives. For example, in representing units of money, length and weight.

$1.$ Baccho iss chapter m humne decimals k baare m seekha aur dekha ki hum apni day to day life m decimals ko kaha use krte hai.
$2.$ Decimals ek aisa standard system hota hai jisse whole aur part ko saath m represent kia jaata hai. For example, One and a half can be written as $1.5$.
$3.$ Deceimals ko represent krne k lie hum whole aur part ko saath m likhte h by dividing them with a $\text{.}$ between them. For example, $2.3,4.56,4.87,4245.343,$ etc.
$4.$ Jab hum decimal point se right side move krte hai, to the first place is called tenths place and as we move forward the multiplying factor becomes $\frac{1}{10}$ times the previous factor yaani ki tenths k baad we get hundredths, thousandths and so on.
$5.$ Humne decimals ko number line p present krna bhi seekha. Number line p represent krne k lie hum do whole numbers k beech m ten divisions krte hai. For example, in order to represent $2.4$ on number line, we'll show ten divisions between $2$ and $3$ and will mark the fourth division as $2.4$.
$6.$ Har decimal number fraction ki form m likha jaa skta hai. For example, $0.75$ can be written as $\frac{3}{4}$.
$7.$ Humne decimals ko compare krna bhi seekha. In order to compare two decimals, we start with the whole part. If they are equal then we move to compare the tenths place, hundredths place and so on, until we find an inequality.
$8.$ Hum decimals ko humari day to day life m bohot vastly use krte hai. For example, in money, we use terms like $\text{Rs. 70}$ and $50$ paise which can be denoted as $\text{Rs. 70.50}$. We also use decimals in places like while measuring lengths ($68.7cm,39.21m,$ etc) or while measuring weights like $73.4g,9.7kg,$ etc.