ALGEBRA for Class 6 MATHS
INTRODUCTION
Baccho, aapne apni previous classes m mathematics ki alag alag fields k baare m pdha hai jaise ki geometry, arithmentics. Iss chapter m hum ek aur field k baare m pdhenge jo ki alphabets se deal krti hai. It is called Algebra. Chaliye ek game khelte hai to understand how algebra works. Follow the following steps:
Baccho, aapka answer aaya hai 2!
Surprised? This is an algebra trick. Basically agar aap observe krenge to hum isme chosen number ko x maan lete hai and usi around we multiply, divide and subtract iss tarah se taaki humara original number subtract hojaye and answer humesha 2 aaye.
Iss chapter m hum seekhenge ki variables, constants, expressions aur equations kya hoti hai, unko solve kaise kia jaata hai using different operations like addition and subtraction. Then we'll learn ki hum ek equation ka solution kaise nikaalte hai and lastly, we'll see the application of algebra in our day-to-day lives. So let's begin!
ALGEBRA
Algebra helps in the representation of problems or situations as mathematical expressions. It involves variables like x,y,z, and mathematical operations like addition, subtraction, multiplication, and division to form a meaningful mathematical expression.
Algebra is a branch of mathematics that deals with symbols and the arithmetic operations across these symbols. These symbols do not have any fixed values and are called variables. In our real-life problems, we often see certain values that keep on changing. But there is a constant need to represent these changing values. Here in algebra, these values are often represented with symbols such as x,y,z,p, or q, and these symbols are called variables. Further, these symbols are manipulated through various arithmetic operations of addition, subtraction, multiplication, and division, with an objective to find the values.
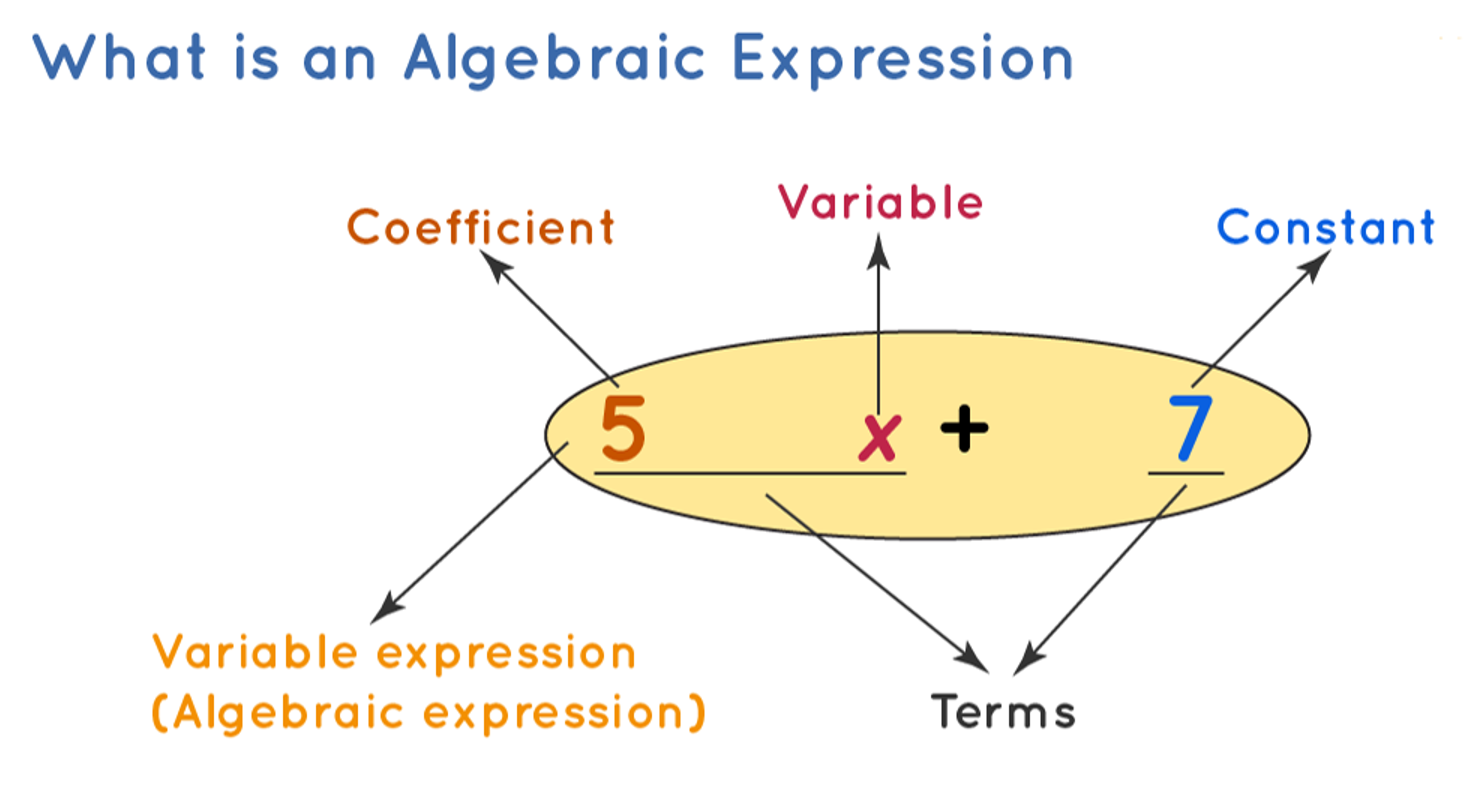
The above algebraic expressions are made up of variables, operators, and constants. Here the number 7 is a constant, x is the variable, and the arithmetic operation of addition is performed.
Variable
Baccho, variables algebra ka ek bohot important component hota hai. To understand what variables are, let's look at the following matchstick patters.
James and Natalie were playing with match sticks and they thought of forming patterns of numbers using the matchsticks.
James took 4 match sticks and formed the number
4
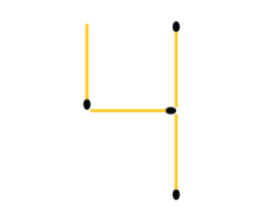
Natalie added 3 more match sticks to form a pattern with two 4's.
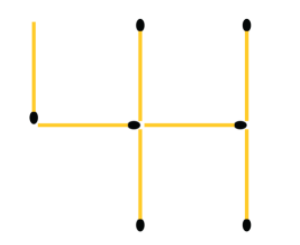
Then James again added 3 more match sticks to form a pattern with three 4's.
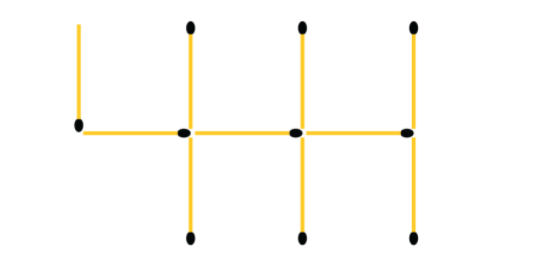
Suddenly, Natalie got a doubt that how many match sticks are required to make a pattern of ten 4's?
They understood from the existing pattern that they need 4+9(3) sticks to get it done as they want a pattern with ten
4's
From this, they concluded that they need 4+(n−1)3 sticks, in general, to make a pattern with n number of 4's.
Here, 4+(n−1)3 is called an algebraic expression.
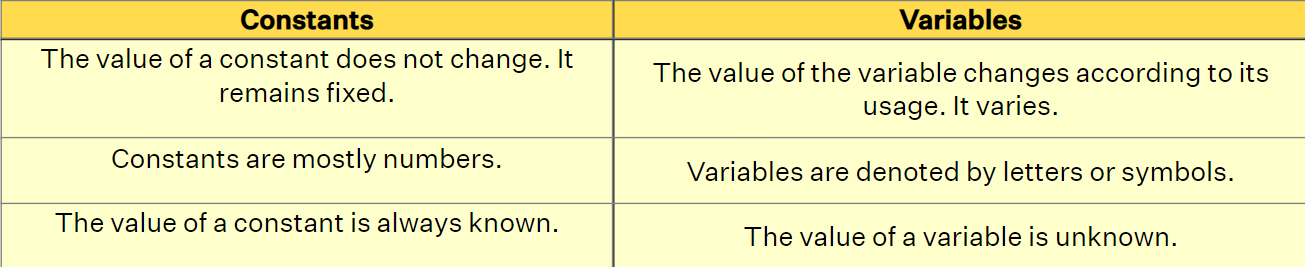
Bachho, we can conclude that, A symbol that doesn't have a fixed value is called a variable in Math. It can take any value.
In the above example, n is a variable and here it can take the values 1,2,3,...Some examples of variables in Math are a,b,x,y,z,m, etc.
The list below show some real-life examples, where the value of a variable changes with the change in place and time.

Constant
Constant is said to be the entity whose value is always fixed irrespective of the change in its usage.
These values do not change even after the change in expression.
Constants are numerical values like a natural number, whole number, real number, integer, or decimal number.
Let us see some real-life constants examples.
Difference Between Constants and Variables
Use of Variables in Common Rules
Baccho, iss section m hum dekhenge ki algebra baaki mathematical fields se kaise interact krti hai.
Rules from geometry
We have already learnt about the perimeter of a square and of a rectangle in the chapter on Mensuration. Here, we go back to them to write them in the form of a rule.
1. Perimeter of Square
The perimeter of a square = Sum of all sides
=4×side
=4l
Thus, p=4l
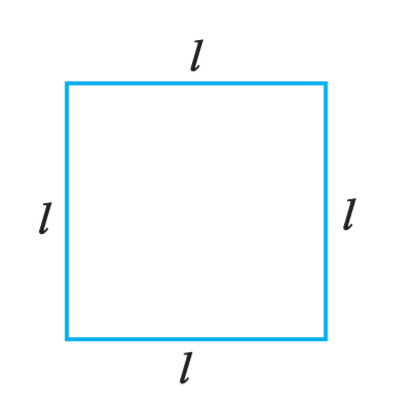
Here l is variable, so the perimeter changes as the value of side change.
2. Perimeter of Rectangle
Perimeter of rectangle =2(length + breadth)
=2(l+b)or2l+2b
Thus, p+2×(l+b)or2l+2b
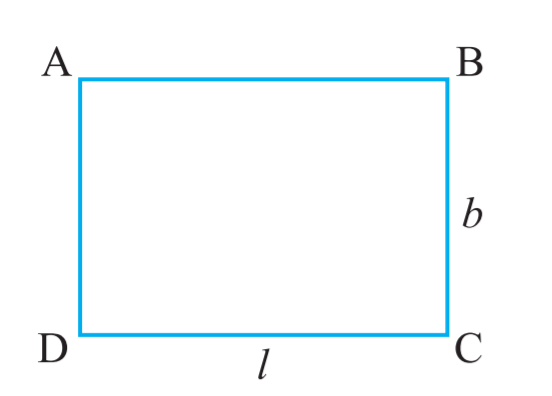
Where, l and b are variable and the value of perimeter changes with the change in l and b.
Rules from arithmetic
1.Commutativity of Addition
5+4=9
4+5=9
Thus, 5+4=4+5
This is the commutative property of addition of the numbers, in which the result remains the same even if we interchanged the numbers.
a+b=b+a
Here, a and b are different variables.
Example
a=16 and b=20
According to commutative property
16+20=20+16
36=36
2. Commutativity of Multiplication
8×2=16
2×8=16
Thus, 8×2=2×8
This is the commutative property of multiplication, in which the result remains the same even if we interchange the numbers.
a×b=b×a
Here, a and b are different variables.
Example
18×12=216,12×18=216
Thus, 18×12=12×18
3.Distributivity of Numbers
6×32
It is a complex sum but there is an easy way to solve it. It is known as the distributivity of multiplication over the addition of numbers.
6×(30+2)
=180+12
=192
Thus, 6×32=192
A×(b+c)=a×b+a×c
Here, a,b and c are different variables.
4. Associativity of Addition
This property states that the result of the numbers added will remain same regardless of their grouping.
(a+b)+c=a+(b+c)
Example
(4+2)+7=4+(2+7)
6+7=4+9
13=13
Expressions with Variables
Algebraic expressions basically vo expressions hote hai jo ki constants and variables ko use krke bnte hai. In an expression, constants and variables are used along with mathematical operations like addition, subtraction, multiplication, etc. Baccho, An algebraic expression (or) a variable expression is a combination of terms by the operations such as addition, subtraction, multiplication, division, etc. Ek algebraic expression k different components hote hai. These are known as Variables, Constants, Terms, and Coefficients of any algebraic expression. Inhe smjhne k lie hum ek expression ka example lenge.
Let us have a look at the expression 5x+7.
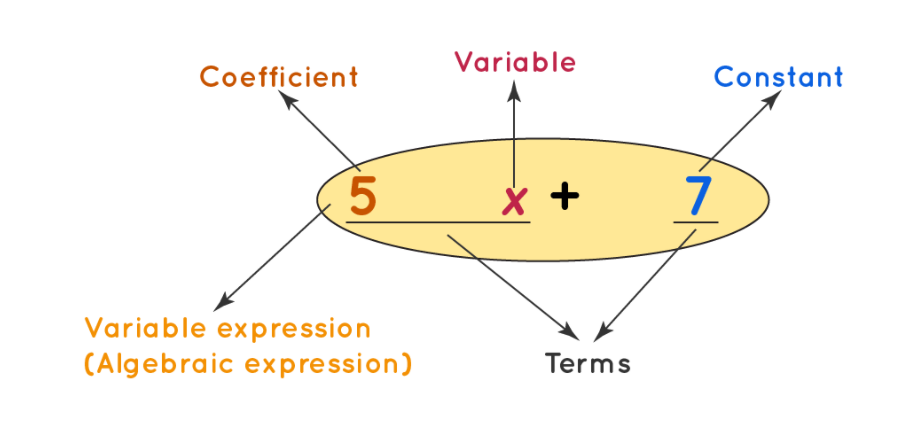
Let's see how we form these expressions.

Example 1
Give expressions in the following cases.
(a) 11 added to 2 m
(b) 11 subtracted from 2 m
(c) 5 times y to which 3 is added
(d) 5 times y from which 3 is subtracted
(e) y is multiplied by −8
(f) y is multiplied by −8 and then 5 is added to the result
(g) y is multiplied by 5 and the result is subtracted from 16
(h) y is multiplied by −5 and the result is added to 16.
(a) 11 added to 2 m =2m+11
(b) 11 subtracted from 2 m =2m−11
(c) 5 times y to which 3 is added =5y+3
(d) 5 times y from which 3 is subtracted =5y−3
(e) y is multiplied by - 8 =−8y
(f) y is multiplied by - 8 and then 5 is added to the result =−8y+5
(g) y is multiplied by 5 and the result is subtracted from 16 =16−5y
(h) y is multiplied by - 5 and the result is added to 16 =−5y+16
Practical use of Expressions
Now we will see how to frame an algebraic expression. The rules are that variables are to be represented with alphabetic letters, say lower case a−z and constants in numeric form.
Examples
1. Amanda has 10 storybooks more than Alex. Express the number of storybooks Amanda has in terms of the number of storybooks Alex has.
Let the number of storybooks Alex has =y
Therefore the number of storybooks Amanda has =y+10
2. Sweets from a big box are equally distributed in 10 small boxes. Express the number of sweets in one small box in terms of the total number of sweets.
Let x be the total number of sweets.
Number of sweet boxes =10
Therefore, the number of sweets in one box is =x10
Let us look at some other such situations.
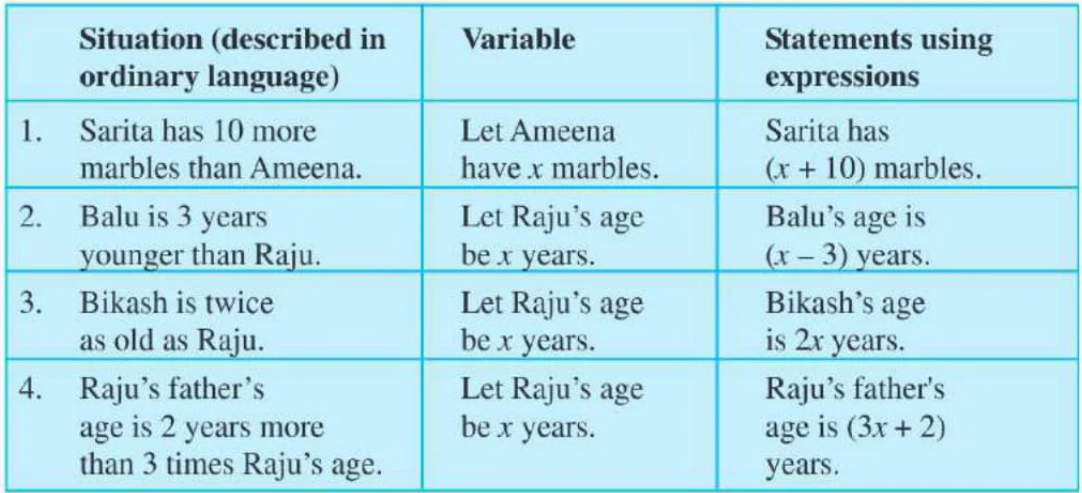


Example 2
To find sum of three numbers 14,27and13, we can have two ways: (a) We may first add 14 and 27 to get 41 and then add 13 to it to get the total sum 54 or (b) We may add 27 and 13 to get 40 and then add 14 to get the sum 54. Thus, (14+27)+13=14+(27+13) This can be done for any three numbers. This property is known as the associativity of addition of numbers. Express this property which we have already studied in the chapter on Whole Numbers, in a general way, by using variables a, b and c.
a+b+c
a+(b+c),(a+b)+c
association of addition.
Example 3
Identify the operations (addition, subtraction, division, multiplication) in forming the following expressions and tell how the expressions have been formed. (a) z+1,z−1,y+17,y−17 (b) 17y,y17,5z (c) 7m,−7m+3,−7m−3
1)addition,subtraction,addition,subtraction
2)multiplication,division,multiplication
3)multiplication and additon, multiplication and sabtraction.
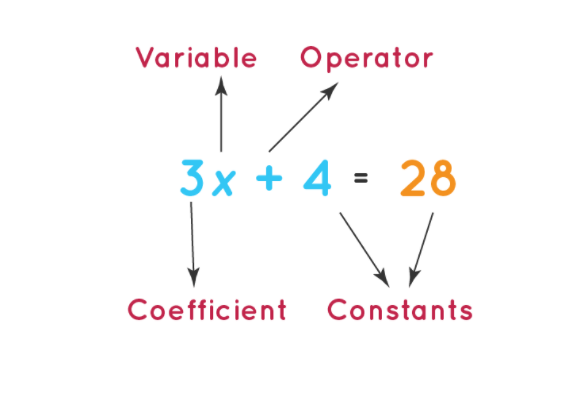
Equations
Baccho, abhi tk humne algebraic expressions aur unke components k baare m pdha. Jab ek algebraic expression m equal to ka sign aajata hai to vo ek equation bn jaati hai.
An equation satisfies only for a particular value of the variable.
The equal sign says that the LHS is equal to the RHS and the value of a variable which makes them equal is the only solution of that equation
Example
3+2x=13
5m–7=3
p6=18
If there is the greater then or less than sign instead of the equal sign then that statement is not an equation.
Some examples which are not an equation
23+6x>8
6f–3<24
The Solution of an Equation
Let us see how practical applications of algebra can be used to solve equations. You will often see equations like 3x+4=5, where you want to find x.
Consider a situation from our daily life.
The cost of a book is Rs.5 more than the cost of a pen. Let us take the cost of the pen as Rs.x. Then the cost of the book is Rs.(x+5) . If the cost of the book is Rs.20, what is the cost of the pen?
We know that the book’s cost is x+5 and it is given that x+5=20. This is an equation in the variable x.
A table is prepared as shown below for various values of x:

It is clear from the table that x+5=20 only for x=15. So, the cost of the pen is Rs.15.
In general we say that x=15 is the solution of the equation x+5=20. This is the trial and error method where we substitute different values for the variable that satisfies the given equation.
An equation has two parts which are connected by an equal to sign. The two parts or sides of an equation are denoted as LHS (Left Hand Side) and RHS (Right Hand Side). If LHS=RHS we get an equation. 2x=6 is an algebraic equation, whereas 3x>10 or 4x<12 are not equations.
Example 4
Leela is Radha's younger sister. Leela is 4 years younger than Radha. Can you write Leela's age in terms of Radha's age? Take Radha's age to be x years.
Let radhika age be x years
Acording the question
age of leela=age of radhika -4
age of leela=x-4 years.
SUMMARY
1. We looked at patterns of making letters and other shapes using matchsticks. We
learnt how to write the general relation between the number of matchsticks
required for repeating a given shape. The number of times a given shape is
repeated varies; it takes on values 1,2,3,.... It is a variable, denoted by some
letter like n.
2. A variable takes on different values, its value is not fixed. The length of a square can have any value. It is a variable. But the number of angles of a triangle has a fixed value 3. It is not a variable.
3. We may use any letter n,l,m,p,x,y,z, etc. to show a variable.
4. A variable allows us to express relations in any
practical situation.
5. Variables are numbers, although their value is not fixed. We can do the operations of addition,
subtraction, multiplication and division on them just as in the case of fixed numbers. Using
different operations we can form expressions with variables like x–3,x+3,2n,5m,3p,2y+3,3l–5, etc.
6. Variables allow us to express many common rules in both geometry and arithmetic in a general way. For example, the rule that the sum of two numbers remains the same if the order in which the numbers are taken is reversed can be expressed as a+b=b+a. Here, the variables a and b stand for any number, 1,32,1000–7,–20, etc.
7. An equation is a condition on a variable. It is expressed by saying that an expression with a variable is equal to a fixed number, e.g. x–3=10.
8. An equation has two sides, LHS and RHS, between them is the equal (=) sign.
9. The LHS of an equation is equal to its RHS only for a definite value of the variable in the equation. We say that this definite value of the variable satisfies the equation. This value itself is called the solution of the equation.
10. For getting the solution of an equation, one method is the trial and error method. In this method, we give some value to the variable and check whether it satisfies the equation. We go on giving this way different values to the variable until we
find the right value which satisfies the equation.
Let's Revise
1. baccho iss chapter m humne mathematics ki ek nayi field k baare m pdha jo ki alphabets se deal krti hai. It is known as algebra.
2. Inn alphabets ko variables kaha jaata hai kyunki inki koi fixed value nahi hoti. Examples of variables are x,y,z,a,b,c,....
3. Constants are those symbols which have a fixed value that can't be changed. For example, all numbers like 1,2,3,4,... are constants because they represent a particular value.
4. jab hum constants, variables ko arithmetic operations k saath use krte hai to we get expressions. For example, 3x+2,2x+2,65y−3, etc.
5. Humne ye bhi seekha ki algebra, geometry aur arithmetics k saath kaise interact krti hai aur hum kaise algebra ko use krke unke formulas form kr skte hai.
6. Humne pdha ki jab hum algebraic expression m equal to ka sign add krte hai to vo ek equation bn jaati hai. Har equation k do sides hote hai- Right Hand Side (RHS) and Left Hand Side (LHS).
7.We also learnt how to turn our daily life situations into equations using algebra.
8. Lastly, humne seekha ki hum unn equations ko kaise solve krte hai.