ELECTROSTATIC POTENTIAL AND CAPACITANCE for Class 12 PHYSICS
INTRODUCTION
Electrostatic ke bare me humne previous chapter me baat kiya jisme electric charges ruka hua hota hai. Jisme hume bht sare examples bhi dekhe, comb ya pen ko balo me rub krna or glass rods and plastic rods etc. Is chapter me hume electric potential ki calculation krni hai. Iske pehle humne ruke hue charge ke karan electric field padha hai, ab is electric field ke karan electric potential padhenge. Kisi point pr kisi point charge ke karan potential, electric dipole ke karan potential, system of charges ke karan potential aur potential energy ki baat karenge.
Potential kya hai?
Class 11th me humne potential energy padha hai – Jisme humne dekha ki kisi object ko jab hum kuchh height me leker jate hai tab jitna energy aapne us object ko uper lekar jane me laga hai utna hi energy wo object gain karta hai jo energy gain hui use potential energy kahte hai). In other words work is needed to give the system potential energy. Eg. It takes energy to lift the ball, stretch the rubber band etc.
Potential energy also can be transformed into other energy such as Kinetic Energy (K.E). For eg. Jab hum koi ball ko kisi bhi height se release karte hai tab woh ball me movement shuru hoti hai, us movement ki wajah se jo energy ball gain karta hai use hum kinetic energy kahte hai. Object jitna kinetic energy gain krta hai same amount ka potential energy loose karta hai. Aisa isliye hota hai kyunki potential energy only defined for conservative forces. Isliye kinetic energy aur potential energy ka sum conserved hota hai.
Conservative forces ka mtlb hota hai - Aisa forces jo energy ko conserve rakhne me helpful hoti hai. Jaha friction hoga waha conservative forces nahi laga sakte. Conservative force: woh force hai jisme kisi bhi object ko ek point(A) se hatakar dusre (different) point(B) me laate hai. It depends only on the initial and final position of the object. [A conservative force is a force with the property total work done in moving a particle from one point to another and is independent to the path taken]. Eg. Gravitational force and elastic spring forces.
Non conservative force (NCF) - Ek round trip me work done zero nahi hota use non conservative force kahte hai. NCF woh force hai jisme work depend karta hai object kai path ke uper. Eg.Friction.
Iske pehle jo humne gravitational forces and coulomb’s forces ke bare me padha hai, ye bhi conservative forces hai.
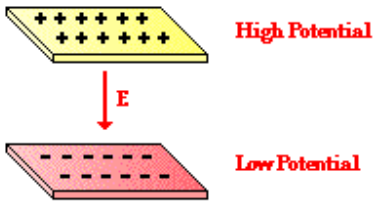
The potential is characteristic of the field only, jo ki kisi test charge particle se bhi independent hota hai jo kisi electric field me rakha ho.
Potential energy characteristic hai charge - field system ka kyunki kisi electric field me rakhe charged particle ka interaction us electric field ke sath hota hai.
Maana ki kisi charge Q ke karan koi electric field E hai. Is charge Q ko origin maan lete hai. Jaisa ki niche diye gaye figure me dikhaya gaya hai, koi test charge hai q jise hum charge Q ke electric field me R point se P point tk leker aate hai.
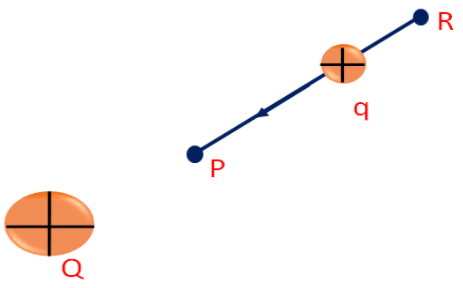
Test charge ka mtlb hota hai ki wo charge jiske bare me hume sari information ho jiski properties aur behaviour ke baare me hume sb kuchh pta ho.
Yaha pr humne jo test charge liya hai wo q>0 liye hai. Humne assume kiya hai ki ye test charge bht hi small hai jo ki origin pr rakhe charge Q ki configuration ko disturb nahi krna chaiye.
Humne charge Q positive liya hai. Ager test charge q bhi positive ho to is test charge ko point R se point P tak lane ke liye jo work done karna hoga wo against me hoga mtlb workdone negative hoga (same charges repel each other) isliye force bhi repulsive hoga.
Jab hum test charge q ko point R se point P tak leker aate hai to uske liye hum jo external force laga rae hai wo equal aur opposite hota hai us test charge pr charge Q ke karan lagane wale repulsive force ke jiske karan net force zero ho jata hai kyunki ye dono force ek dusre ko cancel out kr dete hai.
Ab ye test charge ko R point se P point tak lane ke liye kiya gaya work done potential energy ke form me store hota hai aur ye stored potential energy hi test charge q se external force ko remove karne ke baad ise charge Q se dur jaane ke liye kinetic energy provide karta hai. Ye K.E. aur P.E. ka sum conserved hota hai jo humne iske pehle smjha tha.
Is prakar ager hum test charge q ko point R se P tak lane ke liye kiye gaye work ko equation ke form me likhna chahe to work done hoga -
WRP=∫PRFext.dr<br≥−∫PRFE.dr………(1)
Difference of potential energy – Change in potential energy is work done by conservative force.
Conservative force jo work karta hai particle ke uper uska negative lele use change in potential energy kehte hai.
Uf−Ui=mgh
Test charge q hr point pr kuchh amount me potential energy gain karte jaega, is tarah se jab q, R point tk pahuchega to uski potential energy point P ki potential energy or point R ki potential energy ke difference ke barabar hogi.
i.e., ΔU=UP−UR=WRP……….(2)
Electrostatic potential energy difference between two points P and R as the minimum work required to be done by an external force in moving without acceleration a test charge q from R to P.
Change in potential energy conservative force ke work done ke barabar hota hai.
ELECTROSTATIC POTENTIAL
Uper diye gaye figure me humne koi charge configuration liya jo ki electrostatic field create kr raha hai. Is electrostatic field me jab kisi external force dwara kisi test charge ko R point se P point tak lane me jo work kiya jata hai use ager usi test charge ke magnitude se divide kr de to hume charge configuration ke karan electrostatic potential mil jaega.
V_P ‒ V_R = (U_P-U_R)/q =W_(RP)/q ………..(3)
ΔV=WRPq…………(4)
Ager hum electrostatic potential ki definition smjhe to kisi field me ek unit positive charge ko ek point se kisi dusre point tk move karne ke liye jitna work karna padta hai, use electrostatic potential kahte hai.
In do points ke bich ka electrostatic potential difference 1V hoga jab 1C ke positive charge ko ek point se dusre point tak move karne ke liye 1 joule ka work karna padta hai.
OMR (One Minute Revision)
- * The amount of work done by an external force in moving a unit positive charge slowly (or without acceleration) from one point to another in an electrostatic field.
- When both the points are within the electrostatic field work done per unit positive charge is called potential difference.
- When the first point lies at infinity, work done per unit positive charge is called potential at the second point
POINT 1
1. Definition of Electrostatic Potential - Inside a field, the amount of work needed to move a unit positive charge from one initial point to any specified point without producing any acceleration is known as Electrostatic Potential (or also known as Electric Potential and Electric Field Potential).
Electrostatic Potential (V) = Work done (W) / Charge(Q)
Its SI unit is volt (V) and 1 V=1 J/C and its dimensional formula is [ML2T−3A−1].
2. Definition of 1 V Electrostatic Potential - Electrostatic Potential difference between any two points in an electrostatic field is said to be one volt, when one joule of work is done in moving a positive charge of one coulomb from one point to the other against the electrostatic force of the field without any acceleration.
1V=1J1C=1JC−1=1NmC−1
EXAMPLE 1
What is Electric Potential Difference?
In an electrical circuit, the potential between two points (E) is defined as the amount of work done (W) by an external agent in moving a unit charge (Q) from one point to another.
Mathematically we can say that,
E=WQ
Where,
E = electrical potential difference between two points
W = Work done in moving a change from one point to another
Q = Quantity of charge in coulombs.
POTENTIAL DUE TO A POINT CHARGE
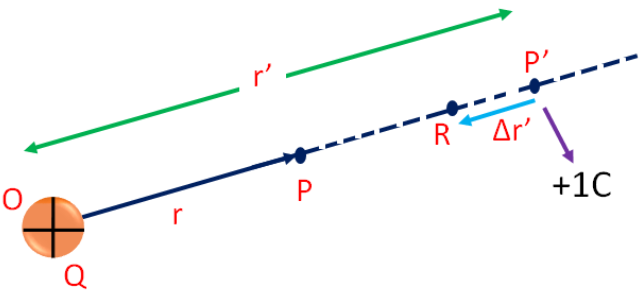
Kisi point charge ke karan potential nikalne ke liye hum consider krte hai ki kahi pr ek point charge rakha hai Q. Is point charge se r duri pr potential nikalna hai. Iske liye ek test charge lenge q0 jise hum infinity se us point tak leker aaenge jis point pr potential nikalna hai.
Physics me actually potential define nahi hota balki potential difference define hota hai isliye jo test charge humne liya hai use infinite se point P tak lane me jo external workdone krna hota hai. Is work done ko ager hum test charge ke magnitude se divide krde to point P ka potential nikal jaega jo ki jis point se hum test charge ko jis point tak la rahe hai un dono point ke potential difference ke barabar hoga.
VP−V∞=Wextq0..........(6)
Ager maan le kisi bhi random time pe ager charge r’ duri pe hai use Δr’ duri pr khiskaya to isme force dur ke direction me lagega kyuki charges positive hai.
Humne Δr chhota sa displacement diya. Is displacement ke liye jitna work karna padhta hai. Ise hum integrate karenge mtlb hr chhote chhote displacement ka work done jod diya hai.
Q se r duri mtlb point P pr potential difference nikalna hai.
Ext. force ka work done Wext=KQq0r..........(7)
Ye ek scalar quantity hai. Ager hume kisi bhi do charge ki potential energy likhni hai to infinite se P point tak lane me jo kaam krna padha hai use potential energy ke form me store kiya jata hai.

OMR (One Minute Revision)
- * Electric potential of a point charge is :
* Electric potential is a scalar, and electric field is a vector. Addition of voltages as numbers gives the voltage due to a combination of point charges, whereas addition of individual fields as vectors gives the total electric field.
* The work done in moving a unit positive test charge over a closed path in an electric field is zero. Thus, electrostatic forces are conservative in nature.
* Work done on a test charge by the electrostatic field due to any given charge configuration is independent of the path, hence potential difference is also the same for any path.
EXAMPLE 2
Charges in static electricity are typically in the nanocoulomb (nC) to microcoulomb (µC) range. What is the voltage 5.00 cm away from the center of a 1-cm diameter metal sphere that has a −3.00 nC static charge?
As we have discussed in Electric Charge and Electric Field, charge on a metal sphere spreads out uniformly and produces a field like that of a point charge located at its center. Thus we can find the voltage using the equation
V=kQr
Solution
Entering known values into the expression for the potential of a point charge, we obtain
V=kQr
=(8.99×109N⋅m2C2)(−3.00×10−9C5.00×10−2m
=−539V
Discussion
The negative value for voltage means a positive charge would be attracted from a larger distance, since the potential is lower (more negative) than at larger distances. Conversely, a negative charge would be repelled, as expected.
EXAMPLE 3
(a) Calculate the potential at a point P due to a charge of 4×10–7 C located 9 cm away. (b) Hence obtain the work done in bringing a charge of 2×10–9 C from infinity to the point P. Does the answer depend on the path along which the charge is brought?
(a) V=14πε0Qr=9×109Nm2C−2×(4×10−7C0.09m)=4×104V
(b) W=qV=2×10–9C×4×104V=8×10−5J
No, work done will be path independent. Any arbitrary infinitesimal path can be resolved into two perpendicular displacements: One along r and another perpendicular to r. The work done corresponding to the later will be zero.
EXAMPLE 4
The electric field outside a charged long straight wire is given by E=1000rVm−1, and is directed outwards. What is the sign of the charge on the wire ? If two points A and B are situated such that rA=0.2m and rB=0.4m, find the value of (VB−VA).
As the field is directed outwards, charge on the wire must be positive
VB−VA=−∫BA→E.Vec(dl)=−∫r=0.4mr=0.2m1000rdr
VB−VA=−1000[loger]r=0.4mr=0.2m
=−1000[loge0.4−loge0.2]
=−1000[loge(0.4)0.2]
=−1000loge2
VB−VA=−1000×0.6931
=−693.1 volt
POTENTIAL DUE TO AN ELECTRIC DIPOLE
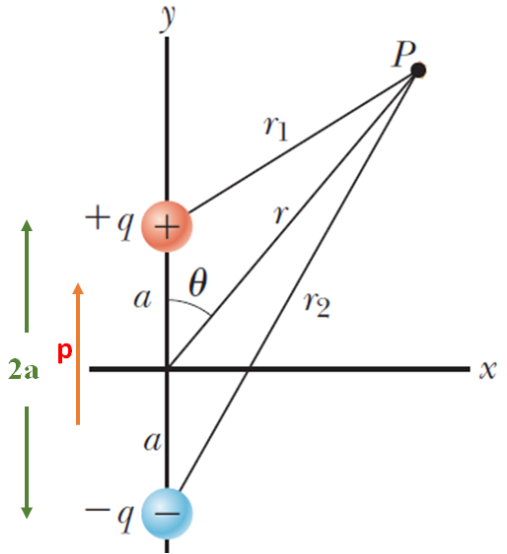
Maan le ki ek negative (−q) aur ek positive (+q) charge hai. Humne electric field padha hai dipole ke karan aur yaha hum log electric potential padhenge dipole ke karan. Electric dipole ke karan hum ye potential general point pr nikalenge.
Electric dipole ager 2a duri se separated ho to hum jante hai ki dipole moment hoga -
|→p|=q×2a ……..(9)
Electrostatic Potential at P due to −q charge at A
V1=−q4πε0r1
and Electrostatic potential at P due to +q charge
V2=q4πε0r2
V=V2+V1
V=q4πε0[1r2−1r1]……….(10)
Now by geometry,
r21=r2+a2+2arcosθ,
and
r22=r2+a2+2arcos(180∘−θ)
=r2+a2−2arcosθ
We may write r21=r2(1+a2r2+2arcosθ)
If a<<r,ar is small, a2r2 can be neglected,
∴r21=r2(1+2arcosθ)
r1=r√1+2arcosθ
1r1=1r(1+2arcosθ)−12
Similarly, 1r2=1r(1−2arcosθ)−12
putting these values in eq. (10), we get V=q4πε0⎡⎣1r(1−2arcosθ)−12−1r(1+2arcosθ)−12⎤⎦
using binomial theorem and retaining terms upto the first order in a/r, we get
V=q4πε0r[1+arcosθ−(1−arcosθ)]
V=q4πε0r[1+arcosθ−1+arcosθ)]
V=q×2acosθ4πε0r2
As pcosθ=→p.ˆr, where ˆr is unit vector along the position vector −−→OP=→r,∴ Electric potential P due to a short dipole (a<<r) is
V=→pˆr4πε0r2 ………..(12)
On the dipole axis, θ=0orπ
∴V=±p4πε0r2
Positive sign for θ=0∘ and negative sign for θ=π
At any point on the equatorial plane, θ=π2;<br>cosθ=cos(π)2=0,
∴V=0
- Perpendicular bisector pe potential zero hota hai aur axial point pr potential maximum hota hai.
EXAMPLE 5
What is the electric potential due to an electric dipole at an equatorial point?
Zero, as potential on equatorial point, due to charges of electric dipole, are equal in magnitude but opposite in nature and hence their resultant is zero.
EXAMPLE 6
Let us say we have two charges of magnitude 1C and 2C placed at a distance 2 metre from each other. Calculate the electric potential between these two charges. (Take: k = 1)
Given that, the magnitude of charges are q1=1C and q2=2C. The distance between these two charges is r=2m.
The electric potential between these two charges is given by,
Ur=−kqqor
Substituting the given values in the above equation we get,
Ur=−1J.
EXAMPLE 7
Derive the expression for the electric potential at any point along the axial line of an electric dipole.
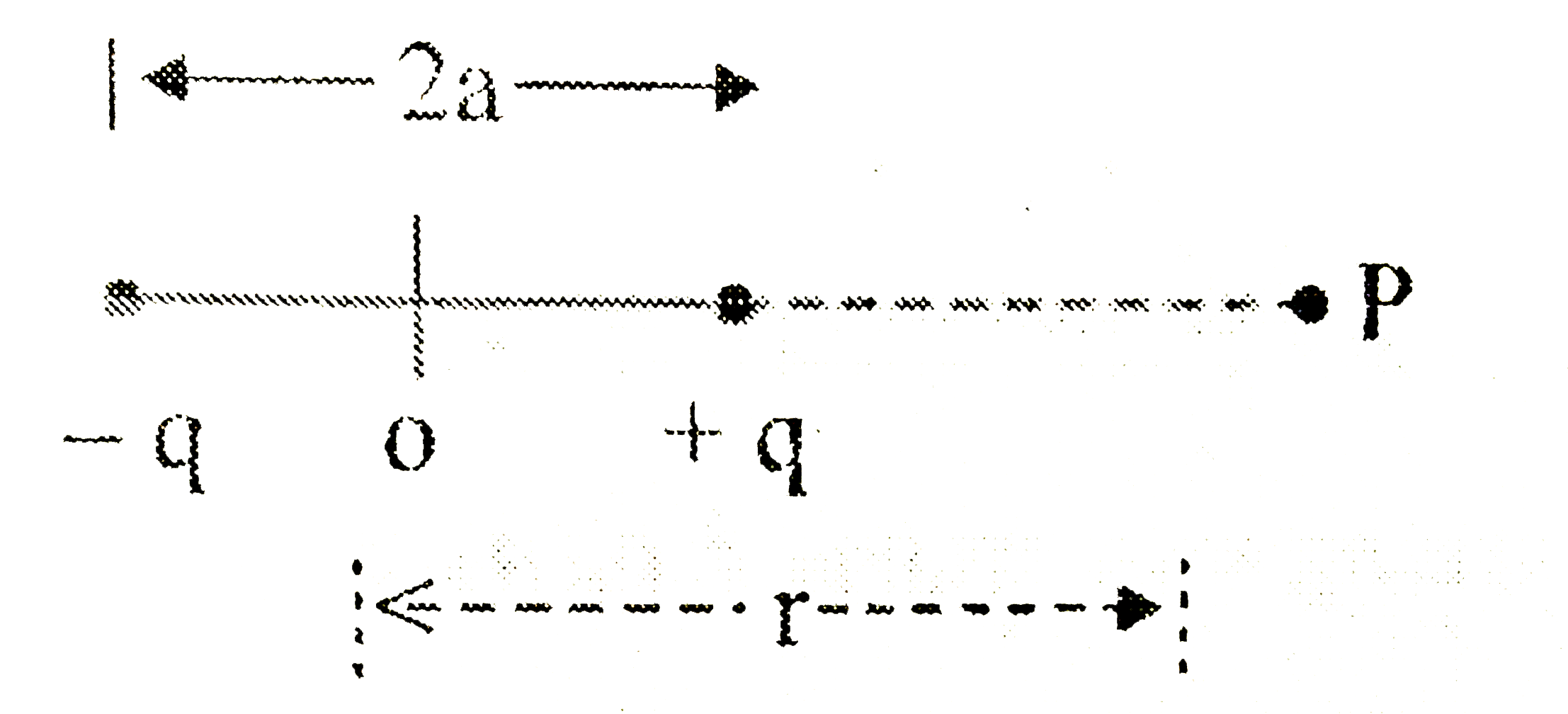
Let P be an axial point at distance r from the centre of the dipole. Electric potential at Point P will be
V=V1+V2=−14π∈0qr+a+14π∈0.qr−a=q4π∈0[1r−a−1r+a]=q4π∈0.2ar2−a2
=14π∈0.pr2−a2 [∵p=q(2a)]
For a far away point, r>>a ∴V=14π∈0.pr2.
EXAMPLE 8
A short electric dipole has dipole moment of 4×10−9 Cm. Find the following
(a) Electric Potential at a point distance .3m from center of the dipole on the axial line
(b) Electric Potential at a point distance 1 m from center of the dipole on the equatorial line
(c) Electric Potential at a point distance .3m from center of the dipole on an line making at angle 30° with the dipole axis
Given
p=4×10−9 Cm
Potential of dipole is given as
V=14πϵ0pcosθr2
(a) θ=0∘, r=.3m
V=14πϵ0pr2
=400V
(b) θ=90∘, r=1m
V=0
(c) θ=30∘, r=.3m
V=14πϵ0pcosθr2
Substituting the values
V=200√3 V
POTENTIAL DUE TO A SYSTEM OF CHARGES

Maan le 5 charge hai q1,q2,q3,q4,q5. Hume P point potential calculate krna hai to in charges ki P point se duri lete hai r1P,r2P,r3P,r4P,r5P.
q1 ke karan point P pr potential -
V1=Kq1r1P
isi prakar hr charge k karan potentials honge-
V2=Kq2r2P
V3=Kq3r3P
V4=Kq4r4P
V5=Kq5r5P
Potential ek scalar quantity hai islie ye aise judh jaenge jaise numbers judte hai to hr points k potential ko jod dete hai.
Charge ka potential nikalte time uske sign k sath hi rakhna hai.
∴V=V1+V2+V3+..........Vn
=Kq1r1P+Kq2r2P+Kq3r3P+Kq4r4P+Kq5r5P
OMR (One Minute Revision)
- * An electric dipole consists of two equal and opposite charges a fixed distance apart, with a dipole moment →p=q→d where d=2a
* Kinetic energy of a charged particle moving through a potential difference:-
K. E = ½ mv^2 = eV
* The electrostatic potential on the perpendicular bisector due to an electric dipole is zero.
* Electric field is in the direction in which the potential decreases steepest.
EXAMPLE 9
Two charges 3×10–8C and (–2)×10–8C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Let us take the origin O at the location of the positive charge. The line joining the two charges is taken to be the x-axis; the negative charge is taken to be on the right side of the origin (Fig). 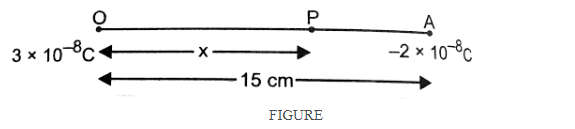
Let P be the required point on the x-axis where the potential is zero. If x is the x-coordinate of P, obviously x must be positive. (There is no possibility of potentials due to the two charges adding up to zero for (x<0) If x lies between O and A, we have
14πε0[3×10−8x×10−2−2×10−8(15−x)×10−2]=0
where x is in cm. That is, 3x−215−x=0 which gives x = 9 cm.
If x lies on the extended line OA, the required condition is 3x−2x−15=0
which gives x = 45 cm
Thus, electric potential is zero at 9 cm and 45 cm away from the positive charge on the side of the negative charge. Note that the formula for potential used in the calculation required choosing potential to be zero at infinity.
EXAMPLE 10
Figures (a) and (b) show the field lines of a positive and negative point charge respectively
(a) Give the signs of the potential difference VP−VQ;VB–VA.
(b) Give the sign of the potential energy difference of a small negative charge between the points Q and P; A and B.
(c) Give the sign of the work done by the field in moving a small positive charge from Q to P.
(d) Give the sign of the work done by the external agency in moving a small negative charge from B to A.
(e) Does the kinetic energy of a small negative charge increase or decrease in going from B to A?
(a) As V∝1r,VP>VQ. Thus, (VP–VQ) is positive. Also VB is less negative than VA. Thus, VB>VA or (VB–VA) is positive.
(b) A small negative charge will be attracted towards positive charge. The negative charge moves from higher potential energy to lower potential energy. Therefore the sign of potential energy difference of a small negative charge between Q and P is positive. Similarly, (P.E.)A>(P.E.)B and hence the sign of potential energy differences is positive.
(c) In moving a small positive charge from Q to P, work has to be done by an external agency against the electric field. Therefore, work done by the field is negative. (d) In moving a small negative charge from B to A work has to be done by the external agency. It is positive. (e) Due to force of repulsion on the negative charge, velocity decreases and hence the kinetic energy decreases in going from B to A.
EXAMPLE 11
ABCD is a square of side 0.2m. Charges of 2×10−9C,4×10−9Cand8×10−9C are placed at the corners A, B and C respectively. Calculate work required to transfer a charge of 2×10−9C from corner D to centre of the square.
Here, qA=2×10−9C,qB=4×10−9C,
qC=8×10−9C
AB=BC=CD=DA=0.2m, Fig

∴AC=BD=√0.22+0.22=0.2√2m
AO=BO=CO=DO=02√22=0.1√2m
Potential at point D is
VD=k[qAAD+qBBD+qCCD]=577.26V
Potential at point O is
VO=k[qAAO+qBBO+qCCO]=890.82V
work done =q(V0−VD)
=2×10−9(890.82−577.26)
=6.27×10−7 joule
EQUIPOTENTIAL SURFACES
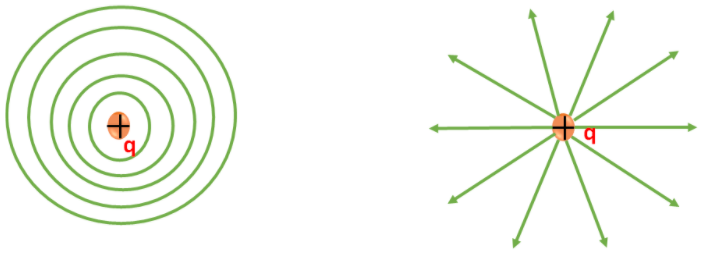
Equipotential surface ek aisa surface hai jiske hr point pe potential saman hoga use equipotential surface kahte hai.
Koi point charge ke karan equipotential surface hogi sphere kyunki us charge se r duri pr bht saare points le lenge jo sphere form karega.
V constant hai mtlb E zero ho jaega isiliye electric field ke ander E zero hota hai jo humne last chapter me bhi samjha tha.
Equipotential surface ke kisi do points ke bich potential difference zero hota hai. Isliye equipotential surface ke kisi ek point se dushre point kisi charge ko le jane me kiya gaya workdone zero hota hai. (ye tabhi possible hai jb charge ko electric field ke perpendicular le jaya jaye.)
Iska mtlb hai ki equipotential surface ke hr point pr electric field lines surface ke perpendicular hoti hai. Ise hum aisa bhi kah sakte hai ki equipotential surface me hr point pr electric field ki direction perpendicular hoti hai.
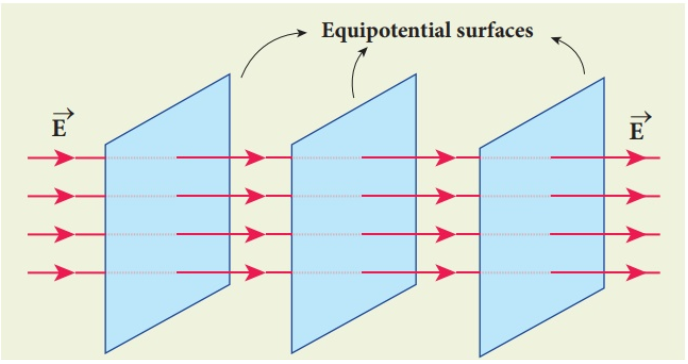
Properties of Equipotential Surface
1. Electric field lines equipotential surface ko hamesha perpendicular katati hai.2. Ager kisi charge ko equipotential surface se kisi dusre equipotential surface pr le jane ke liye kuchh work done karna padhta hai jo un dono surface ke potential difference pr depend karta hai. (kyunki same surface me potential to same hota hai pr humne yaha pr kisi charge ko ek se dusre surface me le gya, dusre surface ka potential kuchh aur ho sakta hai isliye humne yaha pr jo work done ki baat ki wah surface ke potential difference pr depend kr raha hai.)
3. Kisi equipotential surface pr kisi charge ko ek point se dusre point tk le jane me koi bhi work done nahi karna padhta kyunki potential sare points pr same surface me same hai.
4. Do equipotential surface kabhi bhi ek dusre ko nahi katate, kyuki ager aisa hua to dono surface ke cross point pr potential ke do values honge jo possible nahi hai.
5. Kisi bhi conductor ka surface hamesha ek equipotential surface hota hai.
6. Point charges ke liye equipotential surface, equicenter spheres hote hai.
Niche diye gaye figures me hum dekh sakte hai ki figure (a) me jab do opposite charges ko paas paas rakha jata hai to unke dwara bna equipotential surface ek dusre ko nahi katata.
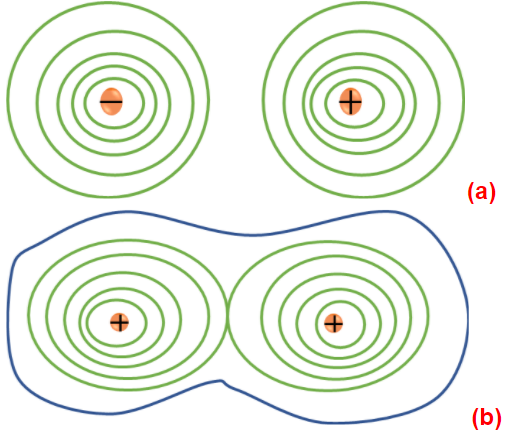
Jab do same charges ko pass pass rakha jata hai to aap figure (b) me dekh sakte hai ki dono charges ke dwara bana equipotential surface ek dusre ko nahi kat raha hai.
Relation between field and potential

Humne point charge liya use ek point se displace karne wala work likh de use usi charge ke magnitude se divide karke electric potential calculate kr skte hai.
Without changing its kinetic energy electric field me kisi charge ko ek point se doosre point tk le jana hai.
Opposite direction me equal amount ka kinetic energy lagana hoga taki E change na ho.
Work done external force ka
−→E.→δl=δV
E=−δVδl
- Electric field ki direction me potential hamesha decrease hoga.
OMR (One Minute Revision)
- * An equipotential surface is the collection of points in space that are all at the same potential. Equipotential lines are the two-dimensional representation of equipotential surfaces.
* Equipotential surfaces do not intersect each other as it gives two directions of electric field E at intersecting points which is not possible.
* Equipotential surfaces are closely spaced in the region of strong electric field and vice-versa.
* Electric field is always normal to an equipotential surface at every point of it and directed from one equipotential surface at higher potential to the equipotential surface at lower potential.
* For a point charge concentric spheres centered at a location of charge are equipotential surfaces.
* The electric field E at a point is perpendicular to the equipotential surface through the point.
* Work done in moving a test charge from one point of equipotential surface to other is zero.
POINT 2
1. Definition of Equipotential Surface - An equipotential surface is that surface at every point of which electric potential is the same.
EXAMPLE 12
A charged particle (q=1.4mC) moves a distance of 0.4m along an equipotential surface of 10 V, Calculate the work done by the field during this motion.
The work done by the field is given by the expression
W=−qΔV
Since ΔV = 0, for equipotential surfaces, the work done is zero, W=0.
EXAMPLE 13
Two charges 2 µC and −2µC are placed at points A and B, 6 cm apart.
(1) Identify the equipotential surface of the system.
(2) What is the direction of the electric field at every point on this surface?
(1) An equipotential surface is defined as the surface over which the total potential is zero. In the given question the plane is normal to line AB. The plane is located at the mid – point of the line AB as the magnitude of the charges are same.
(2) At every point on this surface the direction of the electric field is normal to the plane in the direction of AB.
EXAMPLE 14
A positive particle of charge 1.0 C accelerates in a uniform electric field of 100 V/m. The particle started from rest on an equipotential plane of 50 V. After t = 0.0002 seconds, the particle is on an equipotential plane of V = 10 volts. Determine the distance travelled by the particle.
The work done in moving a charge in an equipotential surface is given by W=−qΔV
Substituting the values, we get
W=(−1.0,C)(10V–50V)=40J
We know that, the work done in moving a charge in an electric field:
W=qEd
40=(1.0)(100)d
d=0.4m
POTENTIAL ENERGY OF A SYSTEM OF CHARGES
Hum jante hai ki do opposite charges ke bich attraction force aur same charges ke bich repulsion force lgta hai. Isliye charges ko ek dusre se dur le jane ya ek dusre ke paas lane me koi work krna padta hai ye work un dono charges ke electric potential energy se milti hai ya potential energy ke form me save ho jati hai
Different point charges se mil kr bane surface ki electric potential energy us kiye gaye work ke barabar hoti hai jo un charges ko infinite se lakar us surface ko banane me kiya jata hai.
EXAMPLE 15
(a) Determine the electrostatic potential energy of a system consisting of two charges 7μC and –2μC (and with no external field) placed at (–9 cm, 0, 0) and (9 cm, 0, 0) respectively.
(b) How much work is required to separate the two charges infinitely away from each other?
(c) Suppose that the same system of charges is now placed in an external electric field E=A(1r2); A=9×105Cm–2. What would the electrostatic energy of the configuration be?
(a)U=14πε0q1q22=9×109×7×(−2)×10−120.18=–0.7J
(b) W=U2–U1=0–U=0–(–0.7)=0.7J
(c) The mutual interaction energy of the two charges remains unchanged. In addition, there is the energy of interaction of the two charges with the external electric field. We find,
q1V(r1)+q2V(r2)=A(7μC0.09m)+A(−2μC0.09m)
and the net electrostatic energy is
q1V(r1)+q2V(r2)+q1q24πε0r12=A(7μC0.09m)+A(−2μC0.09m)−0.7J
=70−20−.7=49.3J
POTENTIAL ENERGY IN AN EXTERNAL FIELD
Potential energy of a single charge
Yadi kisi single charge q ko infinite se kisi point tak laya jaye to lane me kiya gaya work W us charge ki potential energy ke barabar hogi.W = Charge ki potential energy U
W = Charge q × us Point pr Potential
U=qV
Potential energy of a system of two charges in an external field
Jaisa ki aap figure (a) me dekh sakte hai ki do point charges +q1 or +q2 ek dusre se r duri pr dielectric K medium me present hai. Iske liye electric potential energy nikalne ke liye hum mante hai ki starting me charge +q2 infinite pr hai aur charge +q1 figure ke according apne starting point pr hai tab electric potential energy, charge +q2 ko infinite se +q1 se r duri pr lane me kiye gaye work ke barabar hogi.U = Charge q2× Point charge ko infinite se charge q1 se infinite duri tak lane me kiya gya work hai.
U = q2× charge q1 ke karan r duri pr potential V
Lekin charge q1 ke karan r duri pr potential
V=14πε0Kq1r volt
Isliye electric potential Energy
U=q2×14πε0Kq1r
U=14πε0Kq1q2r joule
Electric potential energy ek scalar quantity hai do ya do se jyada charges se bane group ki electric potential energy nikalne ke liye charges ke pair ki alag alag electric potential energy nikal kr inhe jod diya jata hai. Jaisa ki figure me three charges ke liye total potential energy charges ki alag alag potential energy nikal ke jod diya jata hai.
U=14πε0K[q1q2r12+q2q3r23+q3q1r31] joule
Isi prakar n q1,q2,q3,……….,qn charges ke liye total potential energy
U=n∑i=1n∑j=i+114πε0Kqiqjrij
U=½n∑i=1n∑(j=1)j≠i14πε0K(qiqj) joule
Potential energy of a dipole in an external field
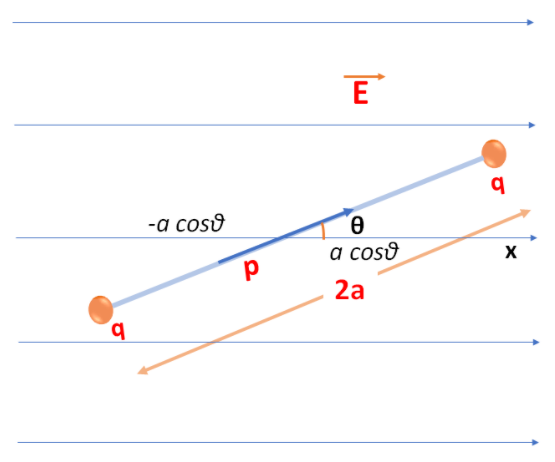
Hum ek electric dipole lete hai jo ki same magnitude q ke opposite charges se milkar bana hai is dipole ko hum kisi uniform electric filed E me rakh dete hai jaisa ki upper diye gye figure me dikhaya gya hai humne chapter 1 me uniform electric filed me rkhe dipole ke bare me study kia hai jo ki net force experience nhi krta pr torque τ experience krta hai τ=p×E jb hum is dipole me present torque ko neutralize karne ke liye (cancel out karne ke liye ) external torque τext apply karte hai to ye electric dipole θ angle se rotate hoti hai.
External torque ke dwara kiya gaya ye work done
W=∫θ1θ0τext(θ)dθ
=∫θ1θ0pEsinθdθ
=pE(cosθ0−cosθ1)
Ye work potential energy (U(θ)) ke form me store hota hai.
Potential energy U, angle θ pe depend karta hai.
U(θ)=pE(cos(π2)−cosθ)
=pEcosθ
=p.E
Ager hum is electric dipole ke system me do charges +q aur -q le to hume system ki potential energy ko is form me likh sakte hai.
U’(θ)=q[V(r1)−V(r2)]−q24πε0×2a
Yaha par r1 or r2 charge +q or −q ke position vectors hai isliye uper ke equation me potential difference r1 or r2 ke bich unit positive charge ko lane me kiya gaya work done hai -
U’(θ)=−pEcosθ−q24πε0×2a
=−p.E−q24πε0×2a
Uper diye gaye equations me hum dekh skte hai ki U’(θ) different hai U(θ) se yeh difference ek constant value hai isliye hum yaha se smjh skte hai ki agar θ=π2 ho to is case me +q or −q ke liye electric field equal aur opposite hai jo ek dusre ko cancel out kr deti hai isliye net electric filed zero ho jata hai aur dipole ki potential energy bhi zero ho jati hai (q[V(r1)−V(r2)]=0).
EXAMPLE 16
A molecule of a substance has a permanent electric dipole moment of magnitude 10–29 C m. A mole of this substance is polarised (at low temperature) by applying a strong electrostatic field of magnitude 106Vm–1. The direction of the field is suddenly changed by an angle of 60∘. Estimate the heat released by the substance in aligning its dipoles along the new direction of the field. For simplicity, assume 100% polarisation of the sample.
Here, dipole moment of each molecules = 10–29 C m
As 1 mole of the substance contains 6×1023 molecules, total dipole moment of all the molecules, p=6×1023×10–29Cm=6×10–6Cm
Initial potential energy, Ui=–pEcosθ=–6×10–6×106cos0∘=–6J
Final potential energy (when θ=60∘), Uf=–6×10–6×106cos60∘=–3J
Change in potential energy =–3J–(–6J)=3J
So, there is loss in potential energy. This must be the energy released by the substance in the form of heat in aligning its dipoles.
EXAMPLE 17
A point charge q moves form a point P to a point S along the path PQRS in a uniform electric field →E along positive direction of x-axis. Calculate work done in this process, when co-ordinates of P,Q,R,S are (a,b,0),(2a,0,0),(a,−b,0) and (0,0,0) respectively.
Here, P(a,b,0),Q(2a,0,0),R(a,−b,0)andS(0,0,0), fig
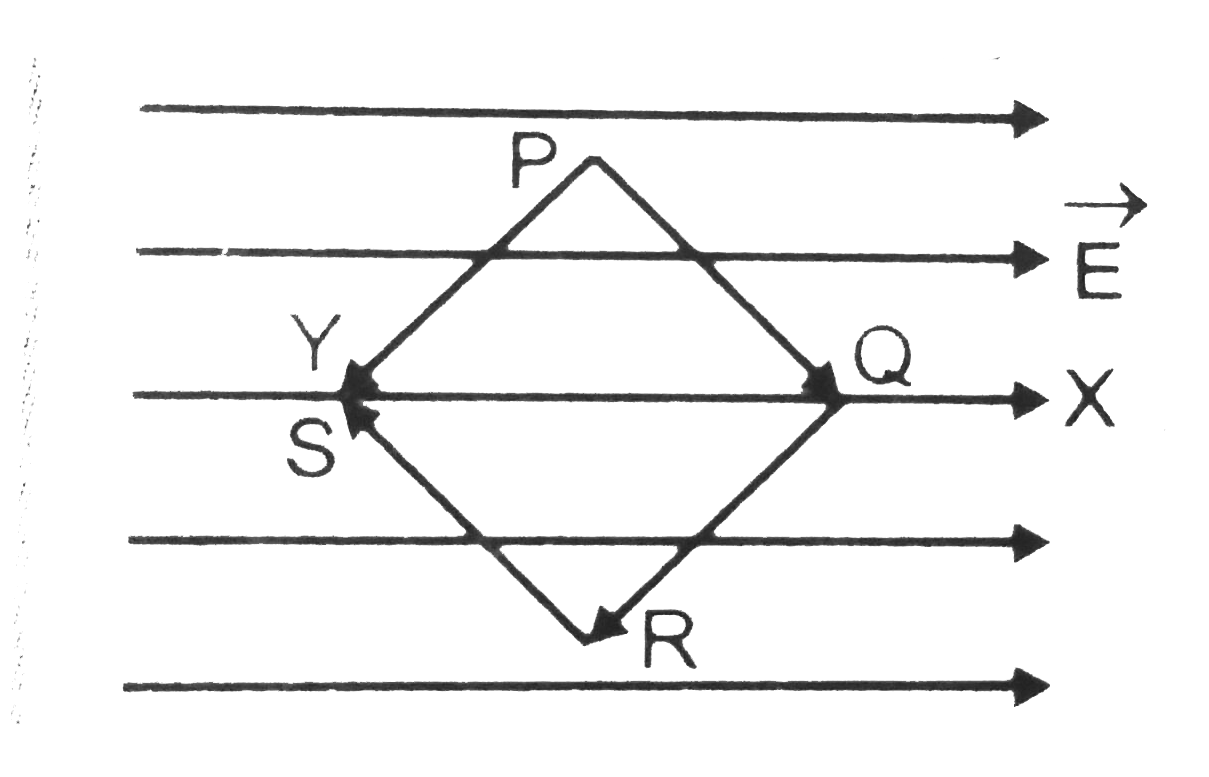
Effective desplacement is going from P to S via any path is
=−→PS=(0−a)ˆi+(0−b)ˆj+(0−0)ˆk
=−aˆi−bˆj
force on the charge . →F=qEˆi
work done, W=→F.−→PS
=qEˆi.(−aˆi−bˆj)
=−qEa
Negative sign shows that work is done against the electric field by some external agency moving the charge.
ELECTROSTATICS OF CONDUCTORS
Hume pata hai electrostatic ka mtlb charge at rest. Yaha hum conductor ki electrostatics ke bare me baat karenge. Iske liye charge ko rest pe maan lete hai.
1. Inside a conductor, electrostatic field is zero
Humne ek conductor liya is conductor ke ander hum electric field zero le rahe hai kyu le rahe hume ye proof karna hai. Iske liye hum assume kr lete hai ki electric field inside conductor zero nahi hai. Ager humne is baat ko wrong proof kr diya to hum jo proof krna chahte hai wo proof ho jaega. Yaha se hume pta chal jaega ki sare charges conductor ke surface pr kyu chale jate hai ye pata chal jaega.Ager kisi conductor ke ander charge present ho to charges me electric field lagega or ye charges move karne lag jayenge mtlb force fill karne ki wajah se current flow ho jaega. Iska mtlb charge at rest maintain nahi honge or electrostatic ki condition fulfil nahi hogi. Isliye electrostatic ki property ko fulfil krne ke liye conductor ke ander charge nahi hota sare ke sare bahar surface pe chale jate hai jaha ye charges rest me hote hai or conductor ke ander net electric field zero ho jata hai. Jaise ki hum jante hai ki conductor me electric flow hota hai, jab koi conductor mai hum external charge hum apply nahi karte tab conductor constant (samanaya) stage mai rehta hai, iske wajah sai total charge jo conductor kai ander hota hai wo zero hota hai kyu ki sare charge particle jo conductor me hote hai wo sare surface me aa jate hai karan ki un charge ke bich replusion nahi hota, tab conductor equilibrium yane ki constant stithi me hota hai.
2. At the surface of a charged conductor, electrostatic field must be normal to the surface at every point
Conductor ke surface pr electric field ki direction find karne ke liye ek electrostatic conductor lete hai, to ab is conductor ke ander to net electric field zero hoga. Electric field zero hone ka mtlb hai conductor me change in potential zero hoga means conductor ke surface ke hr point pr potential same hai. Ye show krta hai ki conductor ka surface equipotential surface hai. Humne iske phle equipotential surface me dekha ki aise surfaces me electric field ki direction surface ke hr point pe perpendicular hoti hai.3. The interior of a conductor can have no excess charge in the static situation
Conductor ke ander net electric field zero hai ye humne proof kiya hai. Ab ager Enet=0 hai iska mtlb hai conductor ke hr part me equal positive or negative charge hai jo aapas me neutralize ho jate hai. Jab conductor me extra charge chala jaye to ye conductor ke surface pr hi jaker ruke hue charge ke form rhta hai. Ager hum is conductor ke kisi chhote se volume ke liye gauss law ka use karke flux calculate karna chahe to us closed surface ke liye total flux zero hoga kyuki conductor ke ander hr point pr net charge zero hai.4. Electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface
Jaisa ki humne already proof kr diya hai ki conductor ke ander net electric field zero hai. Isliye conductor ke ander ka surface equipotential surface hai mtlb conductor ke ander hr point pr potential same hoga. Ager conductor ke ander kisi test charge ko ek point se dusre point tk le jane me kiya gaya work zero hoga kyuki un dono point ka potential difference hi zero hai iska mtlb potential conductor ke ander or surface ke hr point pr constant hua. Ab kisi ek conductor ke liye to potential constant hai pr kisi dusre conductor ke liye potential us conductor me to constant jarur hoga pr phle conductor ke compare dusre conductor ka potential kuchh or bhi ho sakta hai.5. Electric field at the surface of a charged conductor
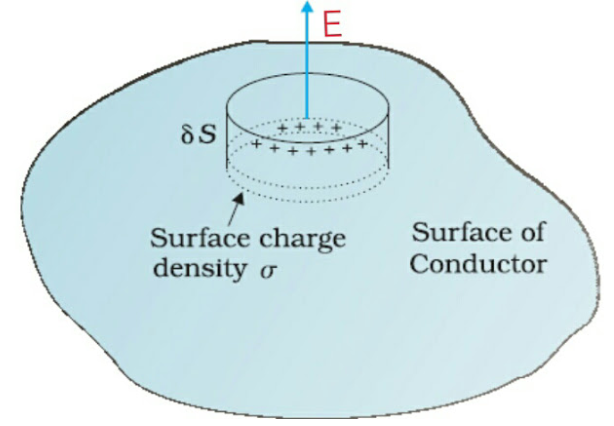
Conductor ke ander electric field to zero hota hai pr conductor ke surface pr kuchh na kuchh electric field present hota hai. Ye electric field conductor ke surface ke hr ek point ke perpendicular hota hai. Hum yaha conductor ke surface pr electric field calculate karne wale hai.E=σε0ˆn
σ surface charge density hai or ˆn unit vector hain joki normal to the surface hota hai or conducting surface ke outward direction me hota hai.
Ise derive krne ke liye hum koi bhi ek conductor lenge kisi bi shape ka ho jisme hum ek gaussian surface assume karte hai jaisa ki figure me dikhaya gaya hai. Electric field ki direction normal to the surface bahar ki taraf hogi ya hum kah skte hai surface ke perpedicular outward direction me hogi. Ab ager is gaussian surface me small surface δS ke liye gauss law ka use krke charge enclosed by the surface δS calculate karenge to hoga-
EδS=|σ|δSε0
yaha pr charge enclosed by the surface |σ|δS hai.
E=|σ|ε0
6. Electrostatic shielding
Maan lete hai ki koi conductor jiske ander cavity hai means ek layer hai. Cavity ko smjhne ke liye hum ek example lete hai ki jaise kisi metal ke box me bht lambe smy tk water bhara rakha rah jaye to aapne dekha hoga ki uske ander white colour ki layer jam jati hai jise hum cavity kahte hai. Isi prakar yaha pe humne conductor ke ander ek layer consider kiya hai jaisa kisi figure me dikhaya gaya hai. Jis tarah se kisi electric field ke ander E=0 hota hai usi tarah is cavity me bhi E=0 hi hota hai. Yah cavity outside ke electric influence se inside of conductor ko protect krne ka kam krti hai jise hum shield kahte hai. Shielding ke karan conductor ke ander or cavity me bhi humesha electric field zero bana rehta hai yahi electrostatic shielding kehlati hai. Electrostatic ki kuchh important properties niche diye gaye figure me dikhaya gaya hai.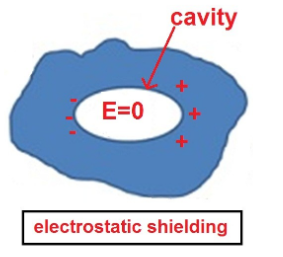
OMR (One Minute Revision)
- * The process which involves the making of a region free from any electric field is known as electrostatic shielding.
DIELECTRICS AND POLARISATION
Aisa substance jo apne me se current ko flow nahi hone deta pr jab in substance ko electric field mein rakha jata hai to isme electric effects show karte hai unhe dielectric kahte hai. Dielectric me free electrons lagbhag na ke barabar hote hai. Kuchh dielectric substances ke example hai- ebonite, glass, paper, oil, mica etc. ye substances insulating hote hai, jo external electric field me rakhe jane pr polarised ho jate hai.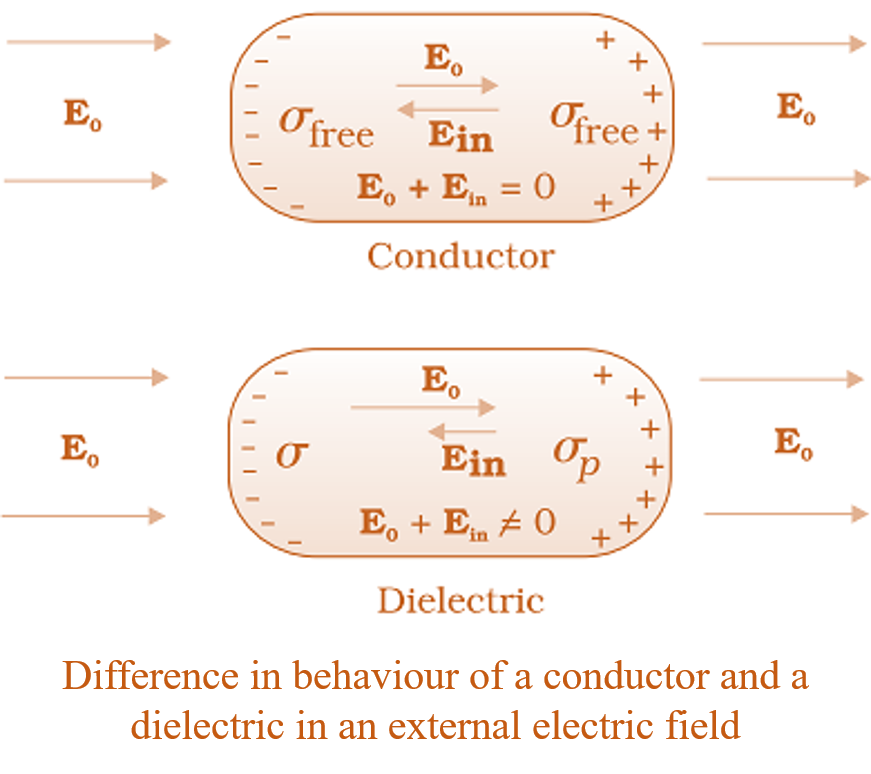
Dielectric substance me electron atom se bonded rahte hain. Inme koi bhi electrons free nahi hote hain. Isliye ise electric field me rakhne se koi bhi current flow nahi hota hai. Electric field me rakhne se inke atoms rearrange ho jate hai, jisse inke behaviour me kuchh changes means electric effect dikhne lagte hain.
Dielectric substance 2 types ke hote hain.
1. Polar dielectric
2. Non polar dielectric
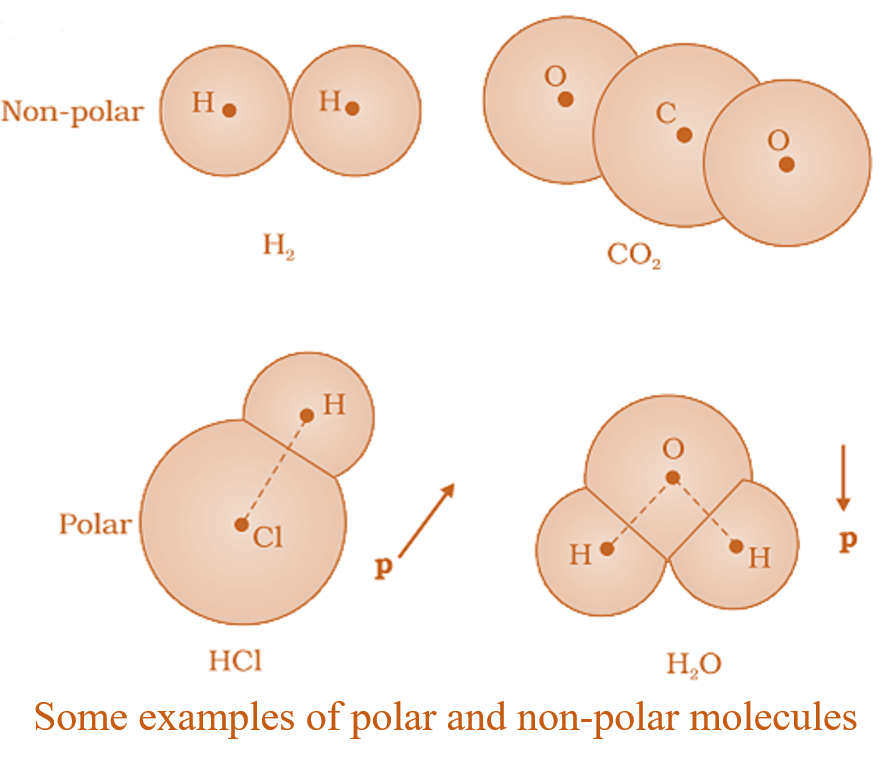
Polar dielectric
Wo substance jinme atoms ke ander positive and negative charge ka centre alag alag hota hai. In substance ko polar dielectric kahte hain.
Kyonki isme ek positive aur negative charge hota hai jo ki dipole ki tarah behave karta hai. Eg. HCL,H2O etc. External electric field ke absence me dipole dielectric substance ka atom thermal energy ke karan irregular form me rahte hain. Isliye resultant dipole moment ka value zero rahta hai. Jab dipole dielectric substance ko electric field me rakha jata hai to ek force kaam let's hai jo isake field ka direction mein dipole ko align karne ki kosis karta hai. Jab external electric field ko badhaya jata hai to jyada se jyada dipole field ke direction mein align hojata hai. Jisse resultant dipole moment ka value milta hai.
Non polar dielectric
Woh substance jinme positive and negative charge ka centre ek hi hota hai. In substance ko non polar dielectric substance kahte hain. Eg. H2.CO2,N2. In substance mein each atom ka dipole zero hota hai. Isliye in substance mein net resultant dipole moment ka value zero hota hai. Jab in substance ko external field mein rakha jata hai to positive charge field ke direction mein air negative charge field ke opposite direction mein allign ho jata hai. Jisse har atoms mein dipole moment ka kuch value form hota hai.
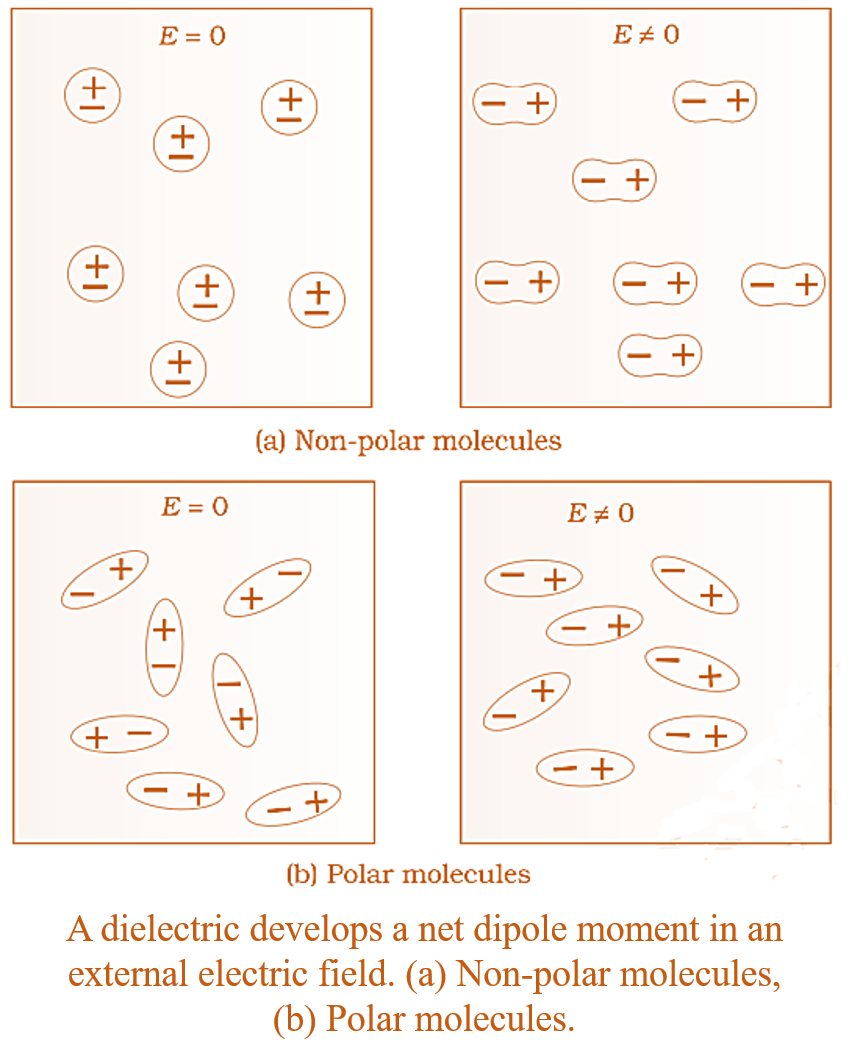
Jab dielectric substance ko external electric field mein rakha jata hai to electric dipole moment induced hota hai. Is substance ko polarization kahte hain.
Agar induced dipole moment, external electric field ke equivalent hota hai to is type ke substance ko LINEAR ISOTROPIC DIELECTRIC substance kahte hain.
External electric field ke presence mein substance ke unit volume mein induced dipole moment ko substance ka vector polarisation kahte hain.
Vector polarisation ko P se denote krte hain.

EXAMPLE 18
A conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2. Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge -3Q, the new potential difference between the same two shells is ?
S1 shell having energy Q is surrounded by an uncharged concentric conducting shell S2 So the potential difference between S1 & S2
V=14πϵ0[Qr1−Qr2]
Now −3Q charge is given to S2 the S1 will be the Then, potential difference , the total charge will be −2Q
V'=14πϵ0[Qr1−Qr2]
V'=1V
EXAMPLE 19
A hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10V. The potential at a distance of 2 cm from the centre of the sphere is?
The metal sphere is a conductor. The potential within or on the surface will be constant because the field inside the conductor is zero. Thus, potential at any point inside the sphere = potential at the surface of the sphere =10V.
POINT 3
1. Definition of Electrostatic shielding - Electrostatic shielding/screening is the phenomenon of protecting a certain region of space from an external electric field.
CAPACITORS AND CAPACITANCE
CAPACITORS - Capacitor ek energy storing device hoti hai. Aisi koi bhi device jo energy ko store karke rakhti hai use capacitor kahate hai.
CAPACITANCE - Charge ko hold karke rakhne ki ability ko capacitance kahte hai. Jaha bhi charge ruk raha hai wo capacitor hai aur jo rok ke rakh raha hai wo capacitance hai.

Capacitor me energy do conductors ke bich me store hoti hai. Is tarah se ek capacitor do coductors ka combination hai jo ek dusre se kuchh duri pr rakhe ho. In conductors ke combination me se ek positive charge hota hai aur dusra conductor equal amount me hi negative charges hota hai. Is capacitor me charge kaha se aata hai? Iske liye initially hum capacitor ko kisi battery se connect karke rakhte hai jisse battery ke positive terminal ka charge ek conductor me aur negative terminal ka charge equal amount me dusre conductor me chala jata hai jisse dono conductor ke potential alag alag hone ke karan potential difference create hota hai yahi capacitor ka potential kahlata hai.
Capacitor me present charge capacitor ke potential ke directly proportional hota hai.
Q∝V
Q=CV
yaha C proportionality constant hi capacitor ka capacitance hai.

THE PARALLEL PLATE CAPACITOR
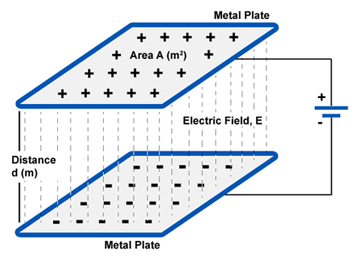
Capacitor form karne ke liye ager do badhe plane plates le jise ek dusre ke parallel rakhe, ye capacitors parallel plate capacitor kehlate hai. Maan lete hai ki jo plane plate humne liya usme hr ek ka area A hai or in do plate ko d duri pr separate karke rakha gaya hai. Hume assume karna hai ki dono plate ke bich ke space me vacuum hai.Ek plate me charge +Q or dusre plate me charge −Q lete hai jo ki plate ke surfaces me faila hua hota hai. Plates ka surface area dono plates ke bich ke distance ke compare me bht large hota hai. In plates ke bich ka electric field hum gauss’s law ka use karke find kr skte hai.
OMR (One Minute Revision)
- * The capacity of a conductor is defined as the ratio between the charge of the conductor to its potential C=QV
POINT 4
1. Definition of Capacitor -Capacitor, device for storing electrical energy, consisting of two conductors in close proximity and insulated from each other.
2. Definition of Capacitance -Capacitance is the ability to store electrical energy.
or
The capacitance C is the ratio of the amount of charge q on either conductor to the potential difference V between the conductors, or simply
C=qV.
3. Definition of Parallel Plate Capacitor -A parallel plate capacitor is an arrangement of two metal plates connected in parallel separated from each other by some distance. A dielectric medium occupies the gap between the plates. The dielectric medium can be air, vacuum or some other non conducting material like mica, glass, paper wool, electrolytic gel and many others.
EXAMPLE 20
A parallel plate capacitor has the capacitance of 20 μ F where the distance between the plates is 16 cm. If the distance between the plates is reduced to 4 cm, its capacitance will be
(a) 20 μ F
(b) 5 μ F
(c) 60 μ F
(d) 80 μ F
C∝1d
Therefore C1C2=164=4
Or C1=4,C2=80μF
EXAMPLE 21
A parallel plate capacitor with air between the plates has a capacitance of 8pF (1pF=10−12F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?
Capacitance between the parallel plates of the capacitor, C=8pF
Initially, distance between the parallel plates was d and it was filled with air. Dielectric constant of air, k=1
Capacitance, C, is given by the formula,
C=kε0Ad
=ε0Ad......(i)
Where,
A = Area of each plate
ε0= Permittivity of free space
If distance between the plates is reduced to half, then new distance,
d’=d2
Dielectric constant of the substance filled in between the plates, k’=6
Hence, capacitance of the capacitor becomes C’=kε0Ad'
=6ε0Ad2.....(ii)
=kε0Ad
Taking ratios of equations (i) and (ii), we obtain
C’=2×6C
=12C
=12×8=96pF
Therefore, the capacitance between the plates is 96pF.
EFFECT OF DIELECTRIC ON CAPACITANCE
Kisi medium ki permittivity (ε) or vacuum ya air ki permittivity ka ratio us medium ka dielectric constant 'K' kahlata hai.
K=εε0
Dielectric constant dimensionless quantity hai jo ki relative permittivity bhi kahlata hai. Relative permittivity ko εr se bhi show karte hai.
Kisi external field me dielectric ka behaviour samajhne ke baad, hum yaha pr dekhte hai ki kaise parallel plate capacitor ka capacitance dielectric ke presence se modified hota hai.
Phle ki tarah hi humare paas do bade plates hai. Jisme hr ek ka area A hai or dono ek dusre se d distance se separated hai. Plates me ±Q charge present hai isliye corresponding plates ki charge density ±σ (with σ = Q/A) ho jayegi.
Jab plates ke bich vacuum present hai,
E0=σε0
and the potential difference V0 is
V0=E0d
The capacitance C0 in this case is
C0=QV0=ε0Ad ………..(i)
Ab ager plates ke bich dielectric insert kiya jaye jo plates ke bich pure space ko occupy karta hai.
Plate ke bich inserted dielectric capacitor ke electric field ke karan polarised ho jata hai, ye effect two charged sheet ke bich hone wale effect ke equivalent hai (at the surfaces of the dielectric normal to the field) jisme surface charge densities σp and –σp hoti hai. The electric field in the dielectric then corresponds to the case when the net surface charge density on the plates is ±(σ–σp).
That is,
E=σ−σpε0 …….(ii)
so that the potential difference across the plates is
V=Ed=σ−σpε0d ……..(iii)
For linear dielectrics, we expect σp to be proportional to E0, i.e., to σ. Thus, (σ–σp) is proportional to σ and we can write
σ−σp=σK ………..(iv)
where K is a constant characteristic of the dielectric. Clearly, K>1. We then have
V=σdε0K=QdAε0K ………….(v)
The capacitance C, with dielectric between the plates, is then C=QV=ε0KAd ………..(vi)
The product ε0K is called the permittivity of the medium and is denoted by ε
ε=ε0K ……….(vii)
For vacuum K = 1 and ε=ε0; ε0 is called the permittivity of the vacuum. The dimensionless ratio
K=εε0 ………..(viii)
is called the dielectric constant of the substance. As remarked before, from Eq. (iv), it is clear that K is greater than 1. From Eqs. (i) and (vi)
K=CC0 ………(ix)
Isliye, kisi substance ka dielectric constant wo factor hai jo (>1) hota hai or iske liye capacitance ki value vacuum se jyada hoti hai, jab dielectric ko capacitor ke bich me fully insert kiya jata hai. Though we arrived at Eq. (ix) for the case of a parallel plate capacitor, it holds good for any type of capacitor and can, in fact, be viewed in general as a definition of the dielectric constant of a substance.
EXAMPLE 22
Electric field inside a dielectric decreases when it is placed in an external field. Give reason to support this statement.
An electric field EP is induced inside the dielectric in a direction opposite to the direction of the external electric field E0. Thus net field becomes
E=E0−EP
EXAMPLE 23
A slab of material of dielectric constant K has the same area as the plates of a parallel-plate capacitor but has a thickness (3/4)d, where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates?
Let E0=V0d be the electric field between the plates when there is no dielectric and the potential difference is V0. If the dielectric is now inserted, the electric field in the dielectric will be E=E0K. The potential difference will then be
V=E0d(14d)+E0K(34d)
=E0d(14+34K)=V0K+34K
The potential difference decreases by the factor (K + 3)/K while the free charge Q0 on the plates remains unchanged. The capacitance thus increases
C=Q0=4KK+3Q0V0=4KK+3C0
EXAMPLE 24
The area of parallel plates of an air capacitor is 0.2m2 and the distance between them is 0.01m The potential difference between the plates, the potential difference between the plates is 3000V. When a 0.01m thick sheet of an insulating material is placed between the plates, the potential difference decreases to 1000 volt. Determine (i) capacitance of capacitance before placing the sheet (ii) charge on each plate (iii) dielectric constant of material (iv) capacitance after placing the insulator (v) absolute permittivity of the dielectric.
(i) C=∈0Ad
(ii) Q0=CV0,V0=3000 volt
(iii) K=E0E=V0V=30001000=3
(iv) C=∈0Ad−t(1−1K)
(v) ∈=K∈0=3×8.85×10−12C2N−1m−2
=2.66×10−11F.m
COMBINATION OF CAPACITORS
Jab hume two or more then two capacitors ko connect karna ho to hum in capacitors ko series me, parallel me ya series or parallel ke combination me connect kr skte hai. In capacitors me combination ke do terminals battery connect karne ke liye honge jisse hum supply provide karenge jo ki battery ke positive aur negative terminal se connect hoga.
Capacitors in series
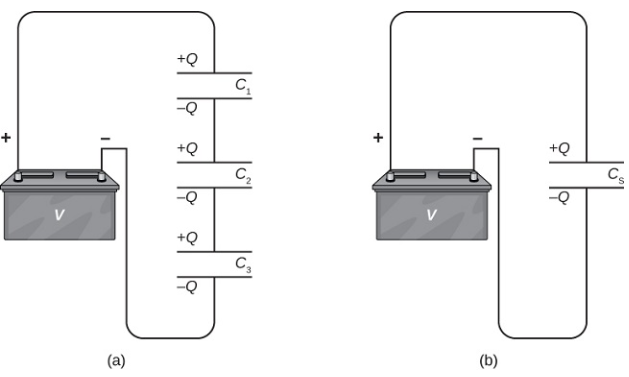
Uper diye gaye figure me three capacitors ko series me combine karke dikhaya gaya hai. Jisme phle capacitor ka right hand plate next capacitor ke left hand plate se connected hai or aage ke capacitors bhi isi tarah se series me connect hote hai.
ek capacitor ke phle plate me charge Q or dusre plate me –Q hai. Iska mtlb C1 ke right plate me charge –Q or C2 ke left plate me charge Q hai to net charge on each capacitor zero ho jayega. Isliye charge tb tk flow hota rahega jab tak each capacitor me net charge zero hoga kyuki net charge zero hone ke karan net electric field bhi zero ho jayega. Yahi karan hai ki capacitor ke series combination me sare capacitors se flow hone wala charge q same hota hai.
The total potential drop V across the combination is the sum of the potential drops V1, V2 and V3 across C1, C2 and C3, respectively.
V=V1+V2+V3=QC1+QC2+QC3 ………..(i)
i.e.,
VQ=1C1+1C2+1C3 ………..(ii)
Now we can regard the combination as an effective capacitor with charge Q and potential difference V. The effective capacitance of the combination is
C=QV ………..(iii)
We compare Eq. (iii) with Eq. (ii), and obtain
1C=1C1+1C2+1C3 ………..(iv)
The proof clearly goes through for any number of capacitors arranged in a similar way. Equation (i), for n capacitors arranged in series, generalises to
V=V1+V2+....+Vn=QC1=QC2+...+QCn ………..(v)
Following the same steps as for the case of two capacitors, we get the general formula for effective capacitance of a series combination of n capacitors:
1C=1C1+1C2+1C3+.....+1Cn ………..(vi)
- All capacitors of a series combination have the same charge.
Capacitors in parallel
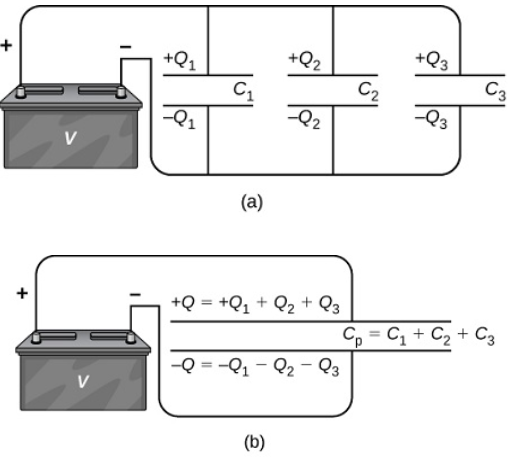
Uper diye gaye figure me three capacitors ko parallel me connect karke dikhaya gaya hai. Is case me each capacitor ke 1st part ko ek sath connect karte hai or 2nd part ko connect karte hai to parallel combination form hota hai. Is parallel combination ke across battery se voltage supply kiya jaya hai. Is combination me capacitor C1 me charge Q1, C2 me charge Q2 or C3 me charge Q3 hoga jabki teeno capacitors ke liye voltage V same hoga.
Q1=C1V,Q2=C2V,Q3=C3V ………..(i)
The equivalent capacitor is one with charge
Q=Q1+Q2+Q3 ………..(ii)
and potential difference V.
Q=CV=C1V+C2V+C3V ………..(iii)
The effective capacitance C is, from Eq. ,
C=C1+C2+C3 ………..(iv)
The general formula for effective capacitance C for parallel combination of n capacitors follows similarly,
Q=Q1+Q2+....+Qn ………..(v)
i.e., CV=C1V+C2V+......CnV ………..(vi)
which gives
C=C1+C2+...Cn ………..(vii)
- All capacitors of a parallel combination have the same voltage V across their plates.
EXAMPLE 25
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel.
(1) What is the total capacitance of the combination?
(2) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
(1) Given, C1=2pF,C2=3pF and C3=4pF
Equivalent capacitance for the parallel combination is given by Ceq .
Therefore, Ceq=C1+C2+C3=2+3+4=9pF
Hence, the total capacitance of the combination is 9pF.
(2) Supply voltage, V=100V
The three capacitors are having the same voltage, V=100V
q=VC
where,
q= charge
C= capacitance of the capacitor
V= potential difference
for capacitance, C=2pF
q=100×2=200pC=2×10−10C
for capacitance, C=3pF
q=100×3=300pC=3×10−10C
for capacitance, C=4pF
q=100×4=400pC=4×10−10C
EXAMPLE 26
Three capacitors each of capacitance 9 pF are connected in series.
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
(a) Capacitance of each of the three capacitors, C = 9 pF
Equivalent capacitance (C’) of the combination of the capacitors is given by the relation,
1C'=1C+1C+1C
⇒1C'=19+19+19=13
⇒C'=3pF
Therefore, total capacitance of the combination is 3 pF.
(b) Supply voltage, V=120V
Potential difference (V') across each capacitor is equal to one-third of the supply voltage.
∴V’=V3=1203=40
Therefore, the potential difference across each capacitor is 40 V.
EXAMPLE 27
A network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)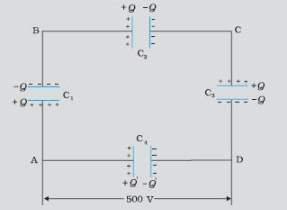
(a) In the given network, C1, C2 and C3 are connected in series. The effective capacitance C′ of these three capacitors is given by
1C’=1C1+1C2+1C3
For C1=C2=C3=10μF, C'=(103)μF. The network has C′ and C4 connected in parallel. Thus, the equivalent capacitance C of the network is
C=C’+C4=(103+10)μF=13.3μF
(b) Clearly, from the figure, the charge on each of the capacitors, C1, C2 and C3 is the same, say Q. Let the charge on C4 be Q′. Now, since the potential difference across AB is QC1, across BC is QC2, across CD is QC3 , we have
QC1+QC2+QC3=500V
Also, Q'C4=500V.
This gives for the given value of the capacitances,
Q=500V×103μF=1.7×10−3C
and
Q’=500V×10μF=5.0×10−3C
EXAMPLE 28
There are infinite number of a capacitance each of capacitance 1μF. They are connected in rows, such that number of capacitors in first, second, third rows are respectively 1,2,4,8………, The rows of these capacitors are connected between A and B as shown in Fig. Determine teh equivalent capacitance of the network between points A and B
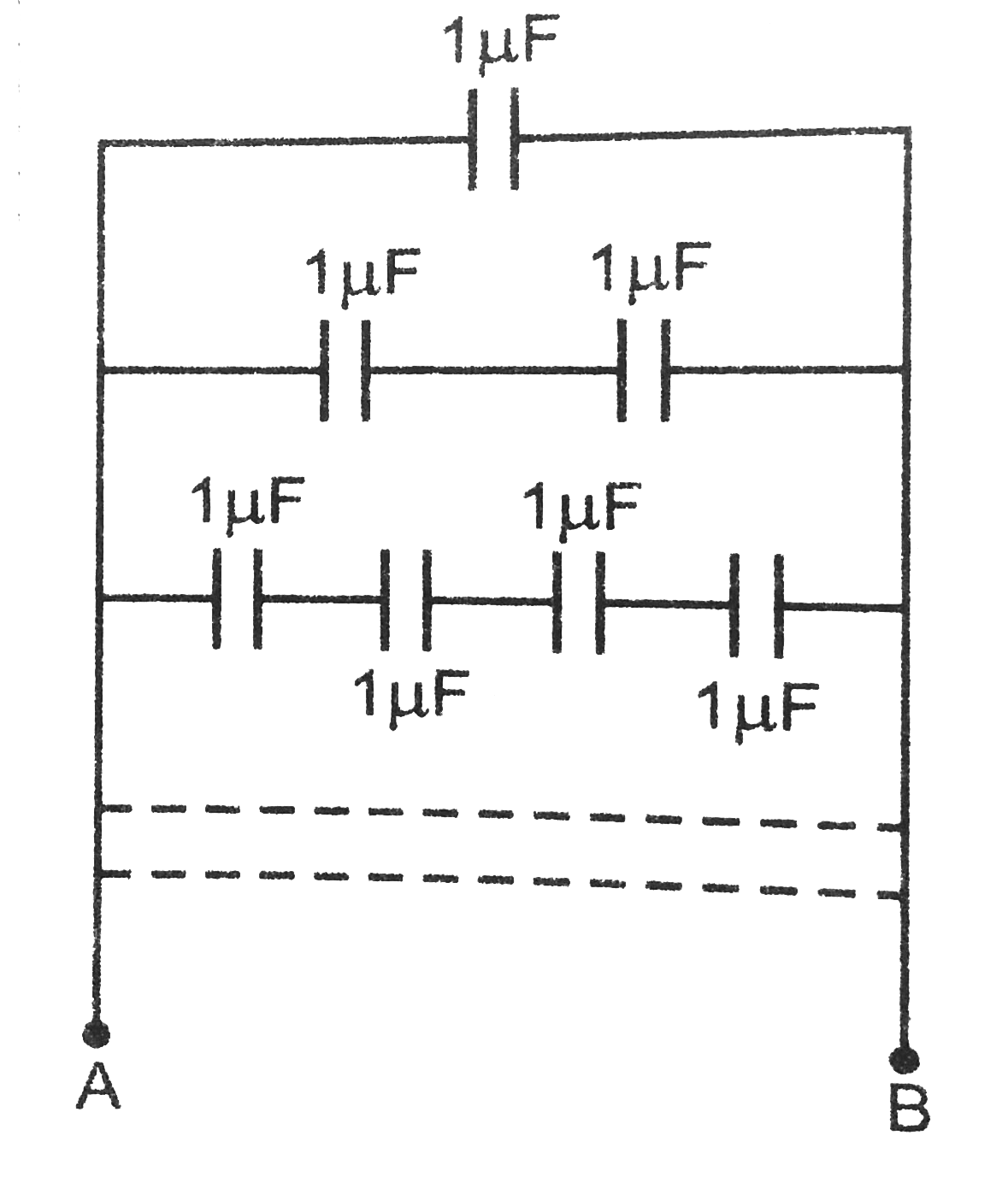
Let C1,C2,C3, …….. be the capacitance of first, second, third row ….. Respectively. Then
C1=1μF
C2=1×11+1=12μF
1C3=11+11+11+11=4
C3=14μF
Similarly C4=18μF and so on,
So, equivalent capacitance capacitance 'C' as they are connected in parallel is
C=C1+C2+C3 + .......
=1+12+14 + ......
= sum of geometrical progression
C=a1−r=11−1/2=2μF
EXAMPLE 29
A spherical capacitor has an outer sphere of radius 0.15m and the inner sphere of diameter 0.2m The outer sphere is earthed and the inner shere is given charge of 6μC. The space between the concentric spheres is filled with a material of dielectric constant 6. Calculate capacitance and potential of inner sphere.
Here, ra=0.22=0.1m,rb=0.15m
q=6μC=6×10−6C,K=6.
C=4π∈0K=rarbrb−ra
C=69×1090.1×0.15(0.15−0.1)=0.2×109F
V=q4π∈0rb−rarbra
V=9×109×6×10−6×0.15−0.10.15×0.1=18×104V
ENERGY STORED IN A CAPACITOR
Ek capacitor jo ki do conductor ke combination se bnta hai is capacitor me store energy find krne ke liye initially do uncharged conductor lete hai is uncharged conductor me se ek conductor me jab charge diya jata hai to dusre conductor me charge transfer hota hai pehla conductor agar q charge se charged hua to conservation of charge ke karan dusra conductor −q charge se charge ho jata hai jab ek conducter se dusre conductor me charge tranfer hota hai to iske liye kuch work done hota hai ye work hi capaciter me store energy hai jo ki electric potential ke form me store hoti hai.
Energy Density - Kisi capacitor ki energy density us capacitor me store energy ke per unit volume ke barabar hoti hai kisi electric field ki energy density
u=½ε0E2
hoti hai.
Iske dwara hum kisi parallel plate capacitor ki energy density bhi calculate kr skte hai (us parallel plate capacitor ki electric field nikal ke).
The energy stored in a capacitor can be expressed in three ways:
Ecap=QV2=CV22=Q22C
where Q is the charge, V is the voltage, and C is the capacitance of the capacitor. The energy is in joules for a charge in coulombs, voltage in volts, and capacitance in farads.
POINT 5
1. Definition of Series Combination -For capacitors connected in a series combination, the reciprocal of the equivalent capacitance is the sum of reciprocals of individual capacitances :
1CS=1C1+1C2+1C3+…
2. Definition of Parallel Combination -For capacitors connected in a parallel combination, the equivalent (net) capacitance is the sum of all individual capacitances in the network,Cp=C1+C2+C3+...
3. Definition of Energy Density -Energy density is the amount of energy stored in a given system or region of space per unit volume.
EXAMPLE 30
How much work is required to be done, in order to bring two charges of magnitude 3C and 5C from a separation of infinite distance to a separation of 0.5 m?
ΔE=E0–Eg
=0–[−9×109×5×30.5]=27×1010.
Therefore, ΔE=27×1010.
EXAMPLE 31
A capacitor is connected to a battery. If we move its plates further apart, work will be done against the electrostatic attraction between the plates. What will be the effect on the energy of the capacitor?
Since the battery remains connected, the potential difference V between the plates of the capacitor will remain constant.
Now Since Capacitance depends on the distance between the plates, it will decrease with the movement.
Now we know that
Q=CV
Now C is decreasing and V remains constant, the charge will decrease on the capacitor.
Some charges from plates passing through the connecting wire will charge the battery.
Thus some energy of the capacitor will be transferred to the battery. So energy of the capacitor will decrease.
The work done in moving apart the plates will be used up in this transference and dissipated in the form of heat in the connecting wires.
EXAMPLE 32
(a) A 900pF capacitor is charged by 100 V battery [Fig.]. How much electrostatic energy is stored by the capacitor? (b) The capacitor is disconnected from the battery and connected to another 900 pF capacitor [Fig.]. What is the electrostatic energy stored by the system?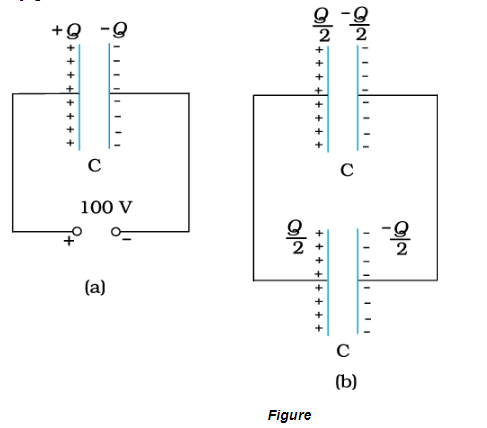
(a) The charge on the capacitor is
Q=CV=900×10–12F×100V=9×10–8C
The energy stored by the capacitor is
=(12)CV2=(12)QV
=(12)×9×10–8C×100V=4.5×10–6J
(b) In the steady situation, the two capacitors have their positive plates at the same potential, and their negative plates at the same potential. Let the common potential difference be V'. The charge on each capacitor is then Q'=CV'. By charge conservation, Q'=Q2. This implies V'=V2. The total energy of the system is
=2×12Q’V’=14QV=2.25×10−6J
Thus in going from (a) to (b), though no charge is lost; the final energy is only half the initial energy. Where has the remaining energy gone?
There is a transient period before the system settles to the situation (b). During this period, a transient current flows from the first capacitor to the second. Energy is lost during this time in the form of heat and electromagnetic radiation.
EXAMPLE 33
Find the ratio of the p.d. that must be applied across the parallel and the series combination of two capacitors C1 and C2 with their capacitances in the ratio 1:3, so that energy stored in two cases, becomes the same.
Given, C1:C2=1:3
UP=Us
12CPV2P=12CSV2S
V2PV2S=CSCP=C1C2/(C1+C2)C1+C2
=C1C2(C1+C2)2=C1C2(C1C2+1)2=13(13+1)2=316
VPVS=√34
KEY FORMULA
* Potential energy of a two-charge system U(r)=kqQr
* Work done to assemble a system of charges W12⋯N=k2∑Ni∑Njqiqjrij for i≠j
* Potential difference ΔV=ΔUq or ΔU=qΔV
* Electric potential V=Uq=−∫RP→E⋅→dl
* Potential difference between two points ΔVAB=VB−VA=−∫BA→E⋅→dl
* Electric potential of a point charge V=kqr
* Electric potential of a system of point charges VP=k∑N1qiri
* Electric dipole moment →p=q→d
* Electric potential due to a dipole VP=k→p.ˆrr2
* Electric potential of a continuous charge distribution VP=k∫dqr
SUMMARY
1. Electrostatic force is a conservative force. Work done by an external force (equal and opposite to the electrostatic force) in bringing a charge q from a point R to a point P is VP–VR, which is the difference in potential energy of charge q between the final and initial points.
2. Potential at a point is the work done per unit charge (by an external agency) in bringing a charge from infinity to that point. Potential at a point is arbitrary to within an additive constant, since it is the potential difference between two points which is physically significant. If potential at infinity is chosen to be zero; potential at a point with position vector r due to a point charge Q placed at the origin is given is given by
V(r)=14πε0Qr
3. The electrostatic potential at a point with position vector r due to a point dipole of dipole moment placed at the origin is
V(r)=14πε0p.ˆrr2
The result is true also for a dipole (with charges –q and q separated by 2a) for r>>a.
4. For a charge configuration q1,q2,...,qn with position vectors r1,r2,...rn, the potential at a point P is given by the superposition principle
V=14πε0(q1r1P+q2r2P+............+qnrnP)
where r1P is the distance between q1 and P, as and so on.
5. An equipotential surface is a surface over which potential has a constant value. For a point charge, concentric spheres centered at a location of the charge are equipotential surfaces. The electric field E at a point is perpendicular to the equipotential surface through the point E is in the direction of the steepest decrease of potential.
6. Potential energy stored in a system of charges is the work done (by an external agency) in assembling the charges at their locations. Potential energy of two charges q1,q2 at r1,r2 is given by
U=14πε0q1q2r12
where r12 is distance between q1 and q2.
7. The potential energy of a charge q in an external potential V(r) is qV(r).
The potential energy of a dipole moment p in a uniform electric field E is –p.E.
8. Electrostatics field E is zero in the interior of a conductor; just outside the surface of a charged conductor, E is normal to the surface given by E=σε0ˆn where ˆn is the unit vector along the outward normal to the surface and σ is the surface charge density. Charges in a conductor can reside only at its surface. Potential is constant within and on the surface of a conductor. In a cavity within a conductor (with no charges), the electric field is zero.
9. A capacitor is a system of two conductors separated by an insulator. Its capacitance is defined by C = Q/V, where Q and –Q are the charges on the two conductors and V is the potential difference between them. C is determined purely geometrically, by the shapes, sizes and relative positions of the two conductors. The unit of capacitance is farad:,
1F=1CV–1. For a parallel plate capacitor (with vacuum between the plates),
C=ε0(Ad)
where A is the area of each plate and d the separation between them.
10. If the medium between the plates of a capacitor is filled with an insulating substance (dielectric), the electric field due to the charged plates induces a net dipole moment in the dielectric. This effect, called polarisation, gives rise to a field in the opposite direction. The net electric field inside the dielectric and hence the potential difference between the plates is thus reduced. Consequently, the capacitance C increases from its value C0 when there is no medium (vacuum),
C=KC0
where K is the dielectric constant of the insulating substance.
11. For capacitors in the series combination, the total capacitance C is given by
1C=1C1+1C2+1C3+.......
In the parallel combination, the total capacitance C is:
C=C1+C2+C3+…
where C1,C2,C3... are individual capacitances.
12. The energy U stored in a capacitor of capacitance C, with charge Q and voltage V is
U=12QV=12CV2=12(Q2C)
The electric energy density (energy per unit volume) in a region with electric field is (12)ε0E2.
13. Electrostatics deals with forces between charges at rest. But if there is a force on a charge, how can it be at rest? Thus, when we are talking of electrostatic force between charges, it should be understood that each charge is being kept at rest by some unspecified force that opposes the net Coulomb force on the charge.
14. A capacitor is so configured that it confines the electric field lines within a small region of space. Thus, even though the field may have considerable strength, the potential difference between the two conductors of a capacitor is small.
15. Electric field is discontinuous across the surface of a spherical charged shell. It is zero inside and outside. Electric potential is, however continuous across the surface, equal to q4πε0R at the surface.
16. The torque p×E on a dipole causes it to oscillate about E. Only if there is a dissipative mechanism, the oscillations are damped and the dipole eventually aligns with E.
17. Potential due to a charge q at its own location is not defined – it is infinite.
18. In the expression qV(r) for potential energy of a charge q, V(r) is the potential due to external charges and not the potential due to q. As seen in point 17, this expression will be ill-defined if V(r) includes potential due to a charge q itself.
19. A cavity inside a conductor is shielded from outside electrical influences. It is worth noting that electrostatic shielding does not work the other way round; that is, if you put charges inside the cavity, the exterior of the conductor is not shielded from the fields by the inside charges.