ATOMS for Class 12 PHYSICS

INTRODUCTION

Bachhon is universe mein jitney bhi matter hai wo sabhi bhut sare atoms se milkar bane hai, lekin sawal ye hai ki atoms hai kya aur uska shape kaisa hai? To in sare savalon ka jawab khojane ke liye histry me 18th aur 19th century me bhut sare experiments kiye gaye ki atoms ka shape kaisa hai iska structure kaisa hai. Is discovery me mainly 4 scientists ke naam samne aatein hai, jisme sabse pehle Dalton aaye, uske baad J. J. Thomson, uske baad Rutherford aur last me Neil Bhor aaye. Inhone ek dusre ke limitations ko overcome karke ek naya model dete gaye.
Inke dwara diye gaye models ko hi hum is chapter me ek ek karke hum samjhenge ki atoms kya hai aur iska structure kaisa hota hai.

ocr_image

ATOMIC MODEL

Model : A model is simply a set of hypothesis based on logical and scientific facts.
Scientific fact aur logical facts ko dhyan me rakh ke koi scientist jab koi kahani likhte hai use model kahte hai.

Theory : Kisi model ko jab baki ke majority of scientist ke dwara varify kr diya jata hai use theory kahte hai.
Hr theory ek model hai but hr model theory ho ye jaruri nahi hai.

Dalton Model
Dalton sabse phle scientist the jinhone hume atomic model diya.
(i) Hr ek element bht hi chhote particles se milkr bana hota jo devide nahi kiya ja sakta aur ise atoms kahte hai. But ye model baad me galat proof ho gaya kyuki atoms; electrons, protons aur neutrons me devide hota hai.
(ii) Same element ke atoms ki physical aur chemical properties same hote hai. Jaise ke copper ke sare atoms ki physical aur chemical property same hogi. Jabki different elements ke atoms ki properties different hogi.
(iii) Sare atoms hydrogen atoms se bane hai means sare atoms hydrogen atoms ke multiples hai. Sabse heaviest atom ke mass ko hydrogen atom se compare karne pr heaviest atom ka mass hydrogen atom ka 250 guna hota hai aur radius ko compare karne pr heaviest atom ka radius hydrogen atom ka 10 guna hota hai.
(iv) Atom stable aur electrically neutral hai means atom me jitna positive charge hai utna hi negative charge hai.

Thomson Atomic Model
Thomson ne Dalton ke model me kami nikal di fr unka model chalne lg gaya. Thomson ne jo atoms ke liye discription diya wo is prakar hai.
(i) Watermelon ko katne pr uske ander jaise chhote chhote bij hote hai thk aise hi atom ko bhi ek solid sphere bataya jisme watermelon ki tarah atom ka sara part solid shpere me proton ki tarah hai jo uniformely distributed hai jabki electrons ko watermelon ki bij ki tarah kahi kahi faila hua bataya.
(ii) Atoms me charge zero hai, electrically neutral hai means atom me jitna positive charge hai utna hi negative charge hai.

ALPHA-PARTICLE SCATTERING AND RUTHERFORD’S NUCLEAR MODEL OF ATOM

Rutherford ne ek experiment kiya jisme unhone $α$ -particle liya aur is particles ko bht hi ptli gold leaf pe bouchhar karwa di ( $α$ - particles ka mtlb hai $._{2}^{4} H e$ ).

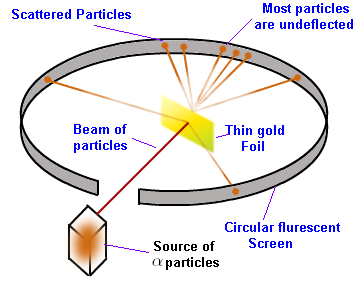
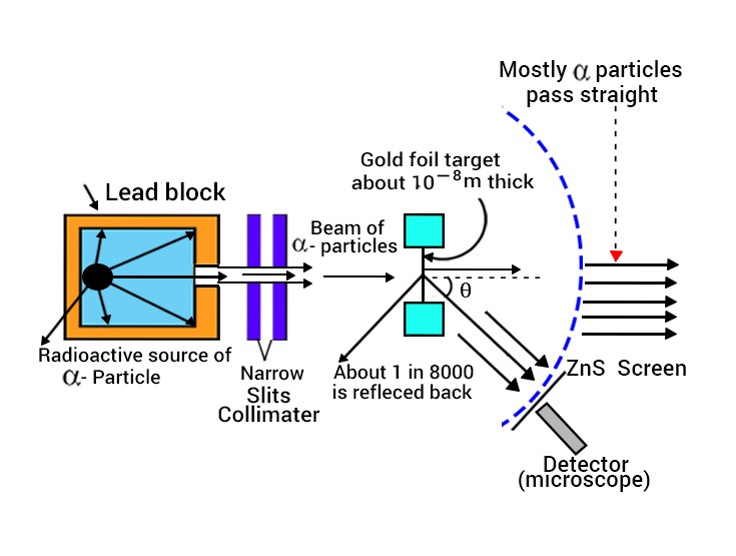
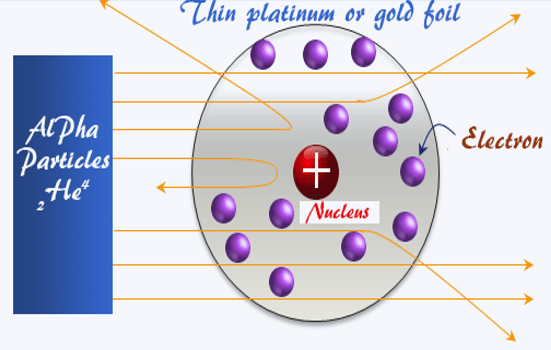
ocr_image

$α$ particle positive particles hai aur jab gold foil pe iski bouchhar karai to dekha gaya ki bht sare particles sidhe nikal ja rae hai, kuchh particles deflect ho ja rahi hai aur bht hi km particles pichhe reflect ho ja rahi hai (shown in below figure). Isse thomson ke dwara diya gaya model fail ho gaya kyuki kuchh particles jo sidhe aage nikl rahi hai, isse ye proof hota hai ki atom ek solid sphere nahi hai aur atom me negative charged particles hai jo $α$ joki positive particle hai use attract kr rahi hai aur atom pura solid na hone ke karan means isme kuchh gap hone ke karan $α$ particles sidhe aaghe nikl ja rahi hai. Kuchh particles center ke pass se wapas reflect ho rahi hai ye bht hi km hai means atom me nucleus me positive particles proton present hai jo $α$ positive particles ko itna repel kr rahi hai ki wo pichhe ki taraf mud ja rahi hai. Yaha se ye pata chala ki atom ke center me bht sara positive charge particle rakha hua hai jo $α$ particles ko strongly reflect kr raha hai.

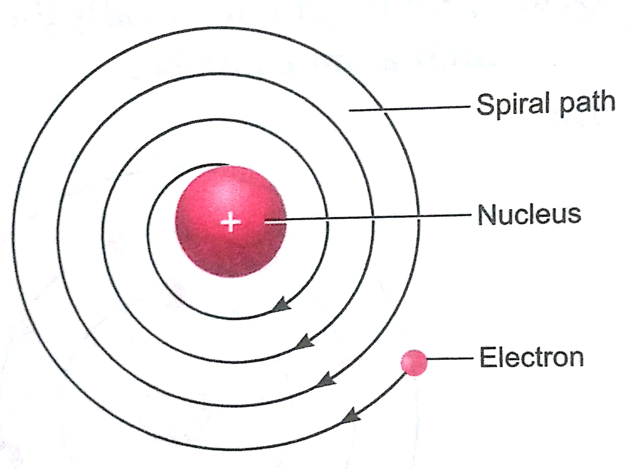
ocr_image

REASON OF FAILURES OF RUTHERFORD MODEL
Rutherford ne finally conclusion diya ki atom ke center me nucleus hai jisme charo electrons chakker kat raha hai. Electrons aise hi nucleus ke chakker kat raha hai, jaise planets sun ke charo taraf ghumte hai. Electrons ghum rahe hai means uski velocity variable hogi aur electron accelerated hoga. Kyuki hume pata hai, accelerated charge electromagnetic wave radiate karta hai. Isliye yaha electron accelerated charge hone ke karan continue radiation produce karna chaiye but aisa nahi hota means yaha pe rutherford ka model fail ho gaya. Atom se contineously light radiate nahi hoti tabhi jab electron apni orbit change karta hai. Rutherford ke according atom se continuously light nikl rahi hai means continuously electron ki energy km ho rahi hai to electrons ghumte hue nucleus pr aake girna chaiye jaise niche figure me dikhaya gaya hai.

ocr_image

DISTANCE OF CLOSEST APPROACH
Ek positive charge hai jiska atomic number $Z_{1}$ hai isme ek proton ka charge electron ke charge ke baraber hota hai isliye proton ka charge $+ e$ ho jayega. Dusra ek positive charge hai jiska atomic no. $Z_{2}$ hai means isme do proton hai isliye iske proton ka charge hoga $+ 2 e$ .
Pehle positive charge ko jab hum dusre positive charge ke pass bhejenge to wo kitni duri tk jayega ye distance hume define karna hai.
Jab pehle positive charge ko dusre positive charge ki taraf bhejte hai to pehle charge apne KE energy ke karan hi kisi $v$ velocity se aage badhega aur badhte badhte us charge ki velocity km hogi aur kisi ek point pr aake velocity zero ho jayegi means KE bhi zero ho jayegi.

ocr_image

Jis point pe pehle positive charge ki KE zero ho jayegi usi point pr ye charge pichhe mud jata hai. Aur isi point ko hi hum distance of closest approach kahte hai.

BOHR MODEL OF THE HYDROGEN ATOM

Bohr’s model rutherford ke model ka correction hai. Rutherford ne kaha ki electron nucleous ke charo taraf ghumega aur ghumte ghumte uski energy dheere dheere km hoti jayegi aur wo nucleous pe gir jayega. Bohr ne bataya ki hr ghumta hua electron energy radiate nahi karega iska mtlb hai ki electron ghumte hue nucleus pe nahi girega. Electron energy radiate tb karega jab wo ek enegy level se dusre energy level me jump karega tb electron energy radiate karega aur electromagnetic waves generate karega. Is waves ki energy do energy ke state ke energy gap ke baraber hogi aur is tarah se electron standing wave create karta hai. Ek state me ghumte hue electron ki energy constant hogi.

BOHR'S MODEL AND ITS POSTULATES
Bohr model ke 3 postulates hai.

First postulate
Electron revolve in stationary circular orbits and massive nucleus.
Kisi bhi positive charge ke around electron move karte hai. Electron ko is positive charge se attract hoke is pr sahi me gir jana chaiye but aisa hota nahi hai kyuki perticular particle ager circular motion me kisi orbit me move kr raha hai. Center me positive charge hai jo electron ke baraber hai ager use hum $Z e$ lete hai to in dono positive charge aur electron ke bich coulomb’s force lg raha hai.
Coulomb's force $F = \frac{K (Z e) e}{r^{2}}$
Kisi bhi perticular particle ke liye circular motion me move karne ke liye centripetal force ki need hoti hai jo instantaneous velocity ke perpendicular hota hai. Yaha pr coulomb force hi wo centripetal force hai joki along the radius toward the center hai.
Centripetal force $F = \frac{m v^{2}}{r}$
$\Rightarrow \frac{m v^{2}}{r} = \frac{K (Z e) e}{r^{2}}$
Bohr’s ki theory kevel single electron items ke liye valid hogi jaise ki H, He, Li in tino ke outer surface me ek ek electrons hote hai.
Massive nucleus ki baat rutherford ne sabse pehle ki thi jiske according kisi bhi atom ka 99% mass kisi ek perticular point means nucleus pr rhta hai uske aas pass itna mass nahi hota aur uske charo taraf electrons ghumte hai. Bohr ne isme add kiya ki atoms ke electrons nucleus ke charo taraf stationary circular orbits me ghumte hai.

Second postulate
Jo bhi electron kisi bhi orbit me gum raha hai uska angular momentum hota hai.
Angular momentum $L = \to r \times \to p$
Particle ke Linear momentum ka jis point ke about angular momentum dekh rahe hai us point se particle ki duri ka cross product angular momentum hota hai.
$L = r \times p sin θ = r m v sin θ$
$Sin θ$ $r$ aur $v$ ke bich ka angle hai.
Electron ki velocity orbit ke tangential hogi aur hr instantaneous point pe electron se nucleus ki duri $r$ ke bich ka angle $90^{\circ}$ hoga isliye $sin θ = {sin 90}^{\circ} = 1$ hoga.
So, $L = m v r$
Angular momentum ki direction out side of the plane hogi. Angular momentum ka magnitude aur direction change nahi ho rahi hai isliye ye conserved hai.
$\Rightarrow m v r = \frac{n h}{2 π}$
Angular momentum ki value kyuki constant hai isliye ye $\frac{h}{2 π}$ ki integer value hi lega. Iska mtlb hai ki angular momentum quantized hai.

Third postulate
Koi bhi electron jo ghum raha hai uski total energy (potential energy + kinetic energy) conserved hogi. $E = K E + P E = K + U$
Kisi orbit me revolving electron ki velocity change ho rahi hai kyuki her point pr iski direction badal rahi hai jabki magnitude constant hai.
$K E = \frac{1}{2} m v^{2}$
Hum jante hai $U = \frac{K q_{1} q_{2}}{r}$ do point charges ke bich ki potential energy hai.
Yaha pr PE hogi
$U = \frac{K (Z e) (- e)}{r}$
$U = - \frac{K Z e^{2}}{r}$
$E = \frac{1}{2} m v^{2} - \frac{K Z e^{2}}{r}$
Yaha pe electron ka mass constant hai, electron ki speed bhi constant hai, jis stable orbit me electron revolve ho raha hai uski radius bhi constant hai and electron aur proton ka charge bhi constant hai.

Property of electron in bohr’s atomic model
Particle jis orbit me ghumti hai uski
$\Rightarrow$ Radius constant hoti hai.
$\Rightarrow$ Speed constant hoti hai.
$\Rightarrow$ Energy constant hoti hai.

RADIUS OF Nth ORBIT IN BOHR MODEL
$\Rightarrow m v_{n} r_{n} = \frac{n h}{2 π}$
$\Rightarrow v_{n} = \frac{n h}{2 π m r_{n}}$
$\Rightarrow \frac{m v_{n}^{2}}{r_{n}} = \frac{K Z e^{2}}{r_{n}}$
$\Rightarrow \frac{m {(\frac{n h}{2 π m r_{n}})}^{2}}{r_{n}} = \frac{K Z e^{2}}{r_{n}}$
$\Rightarrow \frac{n^{2} h^{2}}{4 π^{2} m K Z e^{2}} = r_{n}$
$\Rightarrow \frac{h^{2}}{4 π^{2} m K e^{2}} \frac{n^{2}}{Z} = r_{n}$
$\Rightarrow$ $r_{n} = 0.529 \times \frac{n^{2}}{Z} Å$

VELOCITY OF Nth ORBIT IN BOHR MODEL
$\Rightarrow m v_{n} r_{n} = \frac{n h}{2 π}$
$\Rightarrow v_{n} = \frac{n h}{2 π m r_{n}}$
$\Rightarrow v_{n} = \frac{n h}{2 π m (\frac{h^{2}}{4 π^{2} m K e^{2}}) n^{/} Z}$
$\Rightarrow v_{n} = \frac{n h}{2 π m h^{2} n K} . (4 π^{2} m K e^{2} Z)$
$\Rightarrow v_{n} = 2.18 \times 10^{6} \times \frac{Z}{n}$

ENERGY OF Nth ORBIT IN BOHR MODEL
$K E = \frac{1}{2} m v^{2}$
$U = - \frac{K Z e^{2}}{r}$
$E = K + U$
$E = \frac{1}{2} m v^{2} - \frac{K Z e^{2}}{r}$
Because (1/2mv^2)/r_n= ½ K(Ze^2)/r_n^2
$E = ½ K \frac{Z e^{2}}{r_{n}} - \frac{K Z e^{2}}{r_{n}}$
$E = - \frac{1}{2} K \frac{Z e^{2}}{r_{n}}$
$E = - \frac{1}{2} K \frac{Z e^{2}}{0.529 \frac{n^{2}}{Z}}$
$E = - ½ \frac{K e^{2}}{0.529} \frac{Z^{2}}{n^{2}}$
$E = - 13.6 \frac{Z^{2}}{n^{2}} e V$

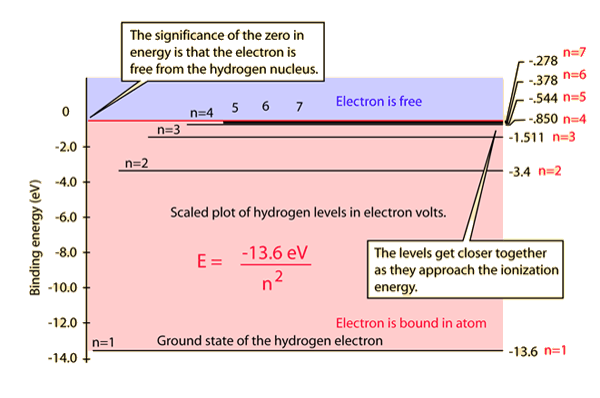
ENERGY OF DIFFERENT ENERGY LEVEL IN HYDROGENIC ATOM

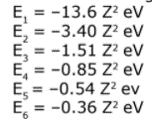
ocr_image

For Hydrogen
$E_{1} = - 13.6 e V$
$E_{2} = - 3.40 e V$
$E_{3} = - 1.51 e V$
$E_{4} = - 0.85 e V$
$E_{5} = - 0.54 e V$
Jaise jaise hum uper ke orbits me ja rahe vaise vaise energy badhati ja rahi hai aur do orbits ke bich energy ka gap km hote ja rahi hai.

EXCITATION AND IONIZATION OF AN ATOM
Kisi bhi perticular electron ko upper energy level me bhejna hai to hume us electron ko energy deni hogi kyuki upper energy levels jyada hota hai isiliye maan lo ki kisi electron ko $n = 1$ orbit se $n = 2$ orbit me bhejna hai to use $- 3.4 + 13.6 = 10.2 e V$ ki energy deni padegi taki wo electron $- 3.4 e V$ ki energy ke sath $n = 2$ orbit pe stay kr paye. Maan lo ki ager electron ko 3rd level me bheje means $n = 3$ me to hum electron ko $E = - 1.51 + 13.6 = 12.09 e V$ energy aur deni hogi taki wo electron 1st orbit se 3rd orbit me ja paye kyuki hum jaise jaise uper jate hai vaise vaise energy badhti jati hai isiliye hume electrons ko upper level me bhejne ke liye aur jyada energy dene ki jarurat hoti hai kyuki hr ek perticular level ke liye energy fix hoti hai aur us energy ki value se jyada ya km energy ki value nahi ho sakti. particle ko upper state me bhejne ke liye extra energy jo hum dete hai use excitation kahte hai. Jab hum kisi perticular particle ko extra energy deke excite kr rahe hai aur upper energy level me bhej rahe hai to wo electron kevel $10^{- 1}$ sec ke liye upper state me rahta hai kyuki wo uska stable state nahi hai isliye fr wapas apne stable state me ajata hai aur energy radiate karta hai.

ocr_image

Kisi electron ko jab hum energy dete hai to wo upper state me jati hai, aur energy de to aur upper state me chali jayegi. Ager hum us electron ko itni energy dede ki wo apne parent atom ko hi chhod kr bahar chali jaye to ise ionization kahte hai. Jab electron apne atom ko chhod kr nikal jati hai to wo infinite me pahuch jati hai aur infinite me energy 0 hoti hai. Iska mtlb hai ki ager kisi ground state ke electron jiski energy $- 13.6 e V$ hoti hai ager use $+ 13.6 e V$ ki energy dede to wo electron apne atom ko chhod kr chali jayegi aur wo atom ionize ho jayega.

THE LINE SPECTRA OF THE HYDROGEN ATOM

Jaise hi koi electron upper energy level se lower energy level me aayega to energy radiate karega means energy emit karega. Kyuki lower energy state me km energy ki jarurat hogi to jo bhi us electron ke pass extra energy hogi wo use emit kr deta hai.
Jab electron energy radiate karta hai to different different tarike se jump mar sakta hai means kisi bhi upper energy level se kisi bhi lower energy level me aa sakta hai. Electron ke hr ek transistion me jo bhi energy emit hogi wo un dono level ke energy ke difference ke baraber hogi. transition ke baad electrons jis bhi state me jump karta hai uske according hydrogen ki line spectra ko different series me devide kiya gaya hai jo niche diye gaye figure me shown hai.

ocr_image

Lyman series - jab kisi bhi higher energy state se electron $n = 1$ state pe aa jaye to use Lyman series kahte hai.
Balmer series - Jab kisi bhi higher energy state se electron $n = 2$ state pe aa jaye to use Balmer series kahte hai.
Paschen series - Jab kisi bhi higher energy state se electron $n = 3$ state pe aa jaye to use Paschen series kahte hai.
Brackett series - Jab kisi bhi higher energy state se electron $n = 4$ state pe aa jaye to use Brackett series kahte hai.
Pfund series - Jab kisi bhi higher energy state se electron $n = 5$ state pe aa jaye to use Pfund series kahte hai.

Radiated Energy $E = E_{n 2} - E_{n 1}$
Because $E = - 13.6 \frac{Z^{2}}{n^{2}}$ and $E = \frac{h c}{λ}$
Hence $\Rightarrow \frac{h c}{λ} = - 13.6 \frac{Z^{2}}{n_{2}^{2}} - (- 13.6 \frac{Z^{2}}{n_{1}^{2}})$
$\Rightarrow \frac{h c}{λ} = - 13.6 Z^{2} (\frac{1}{n_{2}^{2}} - \frac{1}{n_{1}^{2}})$
$\Rightarrow \frac{1}{λ} = \frac{- 13.6}{h c} Z^{2} (\frac{1}{n_{2}^{2}} - \frac{1}{n_{1}^{2}})$
$\frac{- 13.6}{h c} Z^{2} = R$ Rydberg constant
$R = 10^{7} m^{- 1}$

POINT 1

1. Atom- Atom, smallest unit into which matter can be divided without the release of electrically charged particles. Atoms are made up of particles called protons, neutrons, and electrons, which are responsible for the mass and charge of atoms.

2. Stationary Orbits-While revolving in the permissible orbits, an electron does not radiate energy. These non-radiating orbits are called stationary orbits.

3. Bohr's Radius- We define Bohr's radius as the radius of the first orbit of the hydrogen atom.

4. De Broglie’s Hypothesis- This states that the wavelength of electrons is $λ = h / m v$ and the whole number of wavelengths is equal to the orbits circumferencing the main orbit corresponding to the circular standing waves.

5. Hydrogen spectrum- Atoms of each element are stable and emit characteristic spectrum. The spectrum consists of a set of isolated parallel lines termed as line spectrum. It provides useful information about the atomic structure.

EXAMPLE 1

Assume that their is no repulsive force be -tween the electrons in an atom but the force between positive and negative charges is given by Coulomb's law as usual . Under such circumtences, calculate the ground state energy of a He-atom.

For a He-nucleus with charge $2 e$ and electrons of charge $- e$ , the energy level in ground state is
$- E_{n} = Z^{2} \frac{- 13.6 e V}{n^{2}} = 2^{2} \frac{- 13.6 e V}{1^{2}} = - 54.4 e V$
Thus, the ground state will have two electrons each of energy E and the total ground state energy would be $- (4 \times 13.6) e V = - 54.4 e V$

Learn more

EXAMPLE 2

What is the minimum energy that must be given to a H atom in ground state so that it can emit an $H γ$ line in Balmer series. If the angular momentum of the system is conserved, what would be the angular momentum of such $H γ$ photon ?

$H_{γ}$ is Balmer series corresponds to transition $n = 5$ to $n = 2$ . So, the electron in ground state
i.e., from $n = 1$ must first be placed in state $n = 5$ .
Energy required for the transition from $n = 2$ to $n = 5$ is given by
$= E_{1} - E_{5} = 13.6 - 0.54 = 13.06 e V$
Since, angular momentum is conserved,
angular momentum corresponding to Hg proton = change in angular momentum of electron
$= L_{5} - L_{2} = 5 h - 2 h = 3 h = 3 \times 1.06 \times 10^{- 34}$
$= 3.18 \times 10^{- 34} k g - m^{2} / s$

Learn more

EXAMPLE 3

The mass of a H-atom is less than the sum of the masses of a proton and electron. Why is this?

Since, the difference in mass of a nucleus and its constituents, $Δ M$ , is called the mass defect and is given by
$Δ M = [Z m_{p} + (A - Z) m_{n}] - M$
Also, the binding energy is given by $B =$ mass defect $(Δ M) \times c^{2}$
Thus, the mass of a H-atom is
$m_{p} + m_{e} - \frac{B}{c^{2}}$ , where $B \approx 13.6 e V$ is the binding energy.

Learn more

EXAMPLE 4

Show that the first few frequencies of light that are emitted when electrons falls to the nth level form levels higher than n, are approximate harmonics (i.e., in the ratio 1 : 2: 3...) when $n > > 1$ .

The frequency of any line in a series in the spectrum of hydrogen like atoms corresponding to the transition of electrons from $(n + p)$ level to nth level can be expressed as a difference of two terms,
$v_{min} = c R Z^{2} [\frac{1}{{(n + p)}^{2}} - \frac{1}{n^{2}}]$
where, $m = n + p, (p = 1, 2, 3 ....)$ , and R is Ryberg constant.
For $p < < n$
$v_{m n} = c R Z^{2} [\frac{1}{n^{2}} {(1 + \frac{p}{n})}^{- 2} - \frac{1}{n^{2}}]$
$v_{m n} = c R Z^{2} [\frac{1}{n^{2}} - \frac{2 p}{n^{3}} - \frac{1}{n^{2}}]$
[By binomial theorem ${(1 + x)}^{2} = 1 + n x if | x | < 1$ ]
$v_{m n} = c R Z^{2} \frac{2 p}{n^{3}} = (\frac{2 c R Z^{2}}{n^{3}}) p$
Thus, the first few frequencies of light that is emitted when electrons fall to the nth level from levels higher than n, are approximate harmonic (i.e., $1 : 2 : 3 .....$ ) when $n > > 1$

Learn more

SUMMARY

1. Atom, as a whole, is electrically neutral and therefore contains an equal amount of positive and negative charges.

2. In Thomson’s model, an atom is a spherical cloud of positive charges with electrons embedded in it.

3. In Rutherford’s model, most of the mass of the atom and all its positive charge are concentrated in a tiny nucleus (typically one by ten thousand the size of an atom), and the electrons revolve around it.

4. Rutherford nuclear model has two main difficulties in explaining the structure of atom: (a) It predicts that atoms are unstable because the accelerated electrons revolving around the nucleus must spiral into the nucleus. This contradicts the stability of matter. (b) It cannot explain the characteristic line spectra of atoms of different elements.

5. Atoms of most of the elements are stable and emit characteristic spectrum. The spectrum consists of a set of isolated parallel lines termed as line spectrum. It provides useful information about the atomic structure.

6. The atomic hydrogen emits a line spectrum consisting of various series. The frequency of any line in a series can be expressed as a difference of two terms;
Lyman series : $ν = - R_{c} (\frac{1}{1^{2}} - \frac{1}{n^{2}}); n = 2, 3, 4, ...$
Balmer series : $ν = - R_{c} (\frac{1}{2^{2}} - \frac{1}{n^{2}}); n = 3, 4, 5, ...$
Paschen series : $ν = - R_{c} (\frac{1}{3^{2}} - \frac{1}{n^{2}}); n = 4, 5, 6, ...$
Brackett series : $ν = - R_{c} (\frac{1}{4^{2}} - \frac{1}{n^{2}}); n = 5, 6, 7, ...$
Pfund series : $ν = - R_{c} (\frac{1}{1^{2}} - \frac{1}{n^{2}}); n = 6, 7, 8, ...$

7. To explain the line spectra emitted by atoms, as well as the stability of atoms, Niel’s Bohr proposed a model for hydrogenic (single electron) atoms. He introduced three postulates and laid the foundations of quantum mechanics:
(a) In a hydrogen atom, an electron revolves in certain stable orbits (called stationary orbits) without the emission of radiant energy.
(b) The stationary orbits are those for which the angular momentum is some integral multiple of $h / (2 π)$ . (Bohr’s quantisation condition.) That is $L = (n h) / (2 π)$ , where $n$ is an integer called the principal quantum number.
(c) The third postulate states that an electron might make a transition from one of its specified non-radiating orbits to another of lower energy. When it does so, a photon is emitted having energy equal to the energy difference between the initial and final states. The frequency ( $ν$ ) of the emitted photon is then given by
$h ν = E_{i} - E_{f}$
An atom absorbs radiation of the same frequency the atom emits, in which case the electron is transferred to an orbit with a higher value of $n$ .
$E_{i} + h ν = E_{f}$

8. As a result of the quantisation condition of angular momentum, the electron orbits the nucleus at only specific radii. For a hydrogen atom it is given by
$r_{n} = (\frac{n^{2}}{m}) (\frac{h}{2 π}) \frac{4 π ε_{0}}{e^{2}}$
The total energy is also quantised :
$E_{n} = \frac{m e^{4}}{8 n^{2} ε_{0}^{2} h^{2}}$
$= - 13.6 e V / n^{2}$
The $n = 1$ state is called ground state. In hydrogen atom the ground state energy is $- 13.6 e V$ . Higher values of $n$ correspond to excited states ( $n > 1$ ). Atoms are excited to these higher states by collisions with other atoms or electrons or by absorption of a photon of right frequency.

9. de Broglie’s hypothesis that electrons have a wavelength $λ = h / m v$ gave an explanation for Bohr’s quantised orbits by bringing in the wave particle duality. The orbits correspond to circular standing waves in which the circumference of the orbit equals a whole number of wavelengths.

10. Bohr’s model is applicable only to hydrogenic (single electron) atoms. It cannot be extended to even two electron atoms such as helium. This model is also unable to explain for the relative intensities of the frequencies emitted even by hydrogenic atoms.

11. Both the Thomson’s as well as the Rutherford’s models constitute an unstable system. Thomson’s model is unstable electrostatically, while Rutherford’s model is unstable because of electromagnetic radiation of orbiting electrons.

12. What made Bohr quantized angular momentum (second postulate) and not some other quantity? Note, $h$ has dimensions of angular momentum, and for circular orbits, angular momentum is a very relevant quantity. The second postulate is then so natural!

13. The orbital picture in Bohr’s model of the hydrogen atom was inconsistent with the uncertainty principle. It was replaced by modern quantum mechanics in which Bohr’s orbits are regions where the electron may be found with large probability.

14. Unlike the situation in the solar system, where planet-planet gravitational forces are very small as compared to the gravitational force of the sun on each planet (because the mass of the sun is so much greater than the mass of any of the planets), the electron-electron electric force interaction is comparable in magnitude to the electron nucleus electrical force, because the charges and distances are of the same order of magnitude. This is the reason why the Bohr’s model with its planet-like electron is not applicable to many electron atoms.

15. Bohr laid the foundation of the quantum theory by postulating specific orbits in which electrons do not radiate. Bohr’s model includes only one quantum number $n$ . The new theory called quantum mechanics supporters Bohr’s postulate. However in quantum mechanics (more generally accepted), a given energy level may not correspond to just one quantum state. For example, a state is characterised by four quantum numbers ( $n, l, m,$ and $s$ ), but for a pure Coulomb potential (as in hydrogen atom) the energy depends only on n.

16. In Bohr model, contrary to ordinary classical expectation, the frequency of revolution of an electron in its orbit is not connected to the frequency of the spectral line. The later is the difference between two orbital energies divided by $h$ . For transitions between large quantum numbers ( $n$ to $n - 1$ , $n$ very large), however, the two coincide as expected.

17. Bohr’s semiclassical model based on some aspects of classical physics and some aspects of modern physics also does not provide a true picture of the simplest hydrogenic atoms. The true picture is quantum mechanical affairs which differs from Bohr models in a number of fundamental ways. But then if the Bohr model is not strictly correct, why do we bother about it? The reasons which make Bohr’s model still useful are:
(i) The model is based on just three postulates but accounts for almost all the general features of the hydrogen spectrum.
(ii) The model incorporates many of the concepts we have learnt in classical physics.
(iii) The model demonstrates how a theoretical physicist occasionally must quite literally ignore certain problems of approach in hopes of being able to make some predictions. If the predictions of the theory or model agree with experiment, a theoretician then must somehow hope to explain away or rationalise the problems that were ignored along the way.

Home
Ask Doubt
Profile