प्रकाश विद्युत प्रभाव तथा द्रव्य तरंगें कक्षा 12 भौतिकी
भूमिका
इस अध्याय में हम यह जानेंगे की इलेक्ट्रॉन का उत्सर्जन किसी धातु के सतह से कैसे होता है तथा हम प्रकाश विद्युत प्रभाव तथा प्रकाश विद्युत प्रभाव की घटना लेनार्ड के प्रयोग को समझेंगे। इसके बाद हम फ़ोटॉन के बारे में अध्ययन करेंगे की फ़ोटॉन की ऊर्जा क्या होती है इसका व्यवहार कैसा होता है तथा हम आइन्स्टीन का प्रकाश विद्युत समीकरण का भी अध्ययन करेंगे। अध्याय के अंत में हम प्रकाश विद्युत सेल, डी-ब्रॉग्ली परिकल्पना तथा डेविसन-जर्मर के प्रयोग के बारे में भी विस्तार से अध्ययन करेंगे।
भूमिका
इस अध्याय में हम यह जानेंगे की इलेक्ट्रॉन का उत्सर्जन किसी धातु के सतह से कैसे होता है तथा हम प्रकाश विद्युत प्रभाव तथा प्रकाश विद्युत प्रभाव की घटना लेनार्ड के प्रयोग को समझेंगे। इसके बाद हम फ़ोटॉन के बारे में अध्ययन करेंगे की फ़ोटॉन की ऊर्जा क्या होती है इसका व्यवहार कैसा होता है तथा हम आइन्स्टीन का प्रकाश विद्युत समीकरण का भी अध्ययन करेंगे। अध्याय के अंत में हम प्रकाश विद्युत सेल, डी-ब्रॉग्ली परिकल्पना तथा डेविसन-जर्मर के प्रयोग के बारे में भी विस्तार से अध्ययन करेंगे।
इलेक्ट्रॉन उत्सर्जन
हर-एक धातु में अत्यधिक मात्रा में मुक्त इलेक्ट्रॉन उपस्थित होते हैं। ये इलेक्ट्रॉन अपने परमाणुओं से अलग होकर धातु के अन्दर अनियमित रूप से स्वतन्त्रतापूर्वक घूमते रहते हैं, परन्तु धातु को छोड़कर बाहर नहीं निकल सकते हैं, क्योंकि यदि इलेक्ट्रॉन धातु से बाहर आते है तो धातु का पृष्ठ धन आवेश प्राप्त कर लेता है और इलेक्ट्रॉनों को वापस धातु पर आकर्षित कर लेता है। इस प्रकार मुक्त इलेक्ट्रॉन धातु के भीतर आयनों के आकर्षण बलों द्वारा रोककर रखे गए होते है। यदि बाह्य स्रोत से इन इलेक्ट्रॉनों को पर्याप्त ऊर्जा दे दी जाए तो इनकी गतिज ऊर्जा बढ़ जाती है तथा वे धातु सतह को छोड़कर बाहर निकलने लगते हैं। धातु पृष्ठ से इस प्रकार इलेक्ट्रॉनों के बाहर निकलने की घटना को इलेक्ट्रॉन उत्सर्जन कहते हैं।
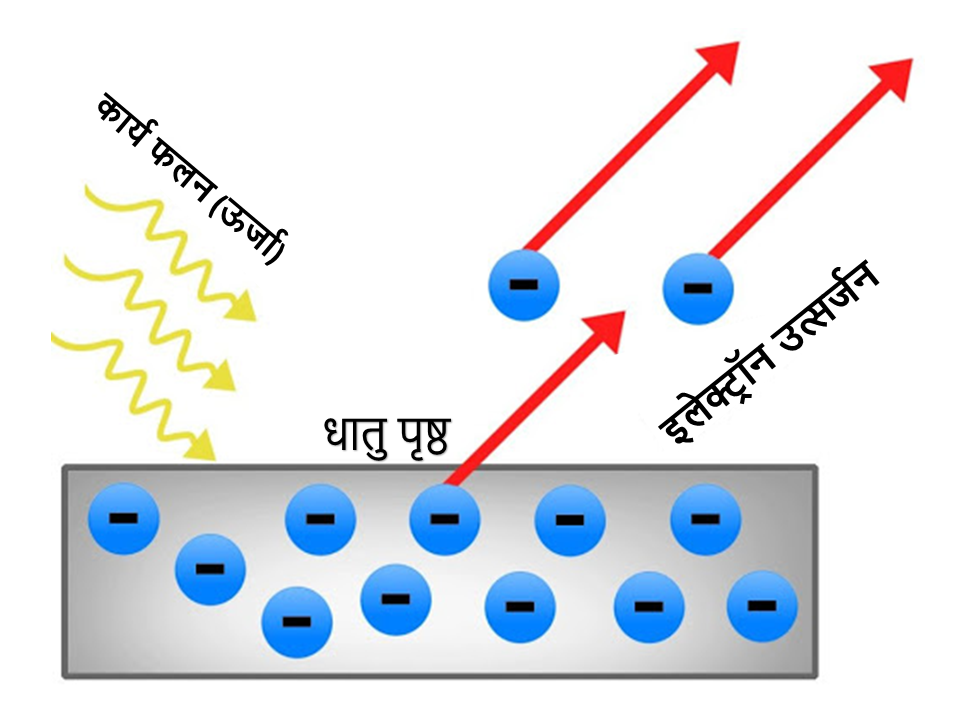
वह न्यूनतम ऊर्जा जो किसी धातु तल से मुक्त इलेक्ट्रॉन के उत्सर्जन के लिए आवश्यक होती है, धातु का कार्य फलन कहलाती है। इसे सामान्यतः ϕo के द्वारा व्यक्त करते है। इसका मान धातु की प्रकृति तथा उसके पृष्ठ की अवस्था पर निर्भर करता है। इसे इलेक्ट्रॉन वोल्ट (eV) में मापते है।
एक इलेक्ट्रॉन वोल्ट किसी इलेक्ट्रॉन को 1 वोल्ट विभवांतर के द्वारा त्वरित कराने पर प्राप्त ऊर्जा का मान है। अतः
1eV=1.602×10−19J
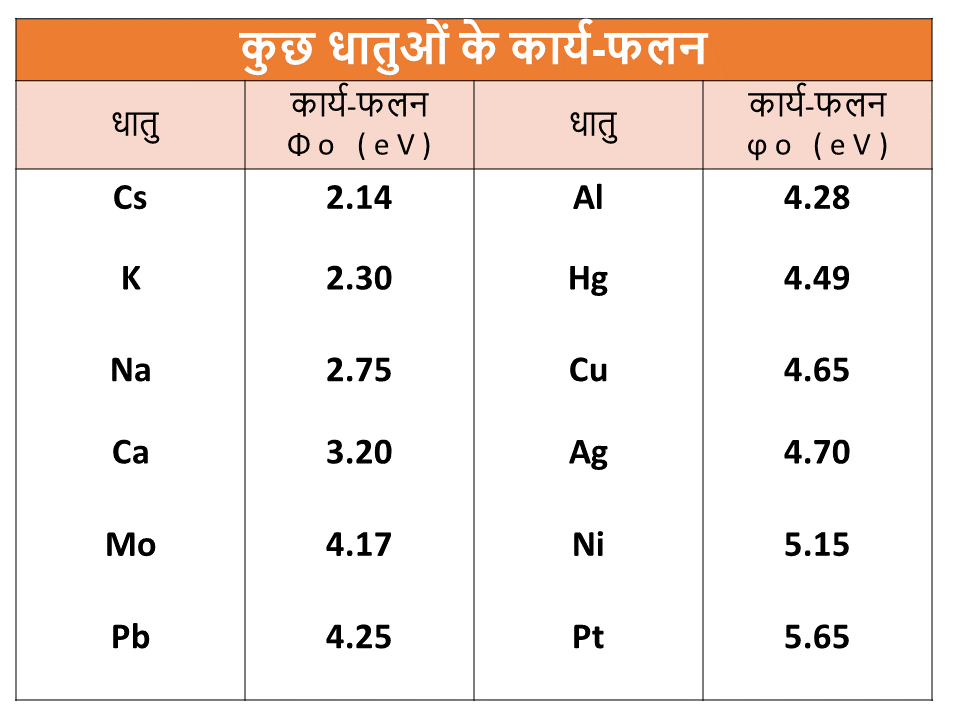
नीचे सारणी में कुछ प्रमुख धातुओं के लिए कार्य फलन का मान दिया गया है-
इलेक्ट्रॉन उत्सर्जन
हर-एक धातु में अत्यधिक मात्रा में मुक्त इलेक्ट्रॉन उपस्थित होते हैं। ये इलेक्ट्रॉन अपने परमाणुओं से अलग होकर धातु के अन्दर अनियमित रूप से स्वतन्त्रतापूर्वक घूमते रहते हैं, परन्तु धातु को छोड़कर बाहर नहीं निकल सकते हैं, क्योंकि यदि इलेक्ट्रॉन धातु से बाहर आते है तो धातु का पृष्ठ धन आवेश प्राप्त कर लेता है और इलेक्ट्रॉनों को वापस धातु पर आकर्षित कर लेता है। इस प्रकार मुक्त इलेक्ट्रॉन धातु के भीतर आयनों के आकर्षण बलों द्वारा रोककर रखे गए होते है। यदि बाह्य स्रोत से इन इलेक्ट्रॉनों को पर्याप्त ऊर्जा दे दी जाए तो इनकी गतिज ऊर्जा बढ़ जाती है तथा वे धातु सतह को छोड़कर बाहर निकलने लगते हैं। धातु पृष्ठ से इस प्रकार इलेक्ट्रॉनों के बाहर निकलने की घटना को इलेक्ट्रॉन उत्सर्जन कहते हैं।

वह न्यूनतम ऊर्जा जो किसी धातु तल से मुक्त इलेक्ट्रॉन के उत्सर्जन के लिए आवश्यक होती है, धातु का कार्य फलन कहलाती है। इसे सामान्यतः ϕo के द्वारा व्यक्त करते है। इसका मान धातु की प्रकृति तथा उसके पृष्ठ की अवस्था पर निर्भर करता है। इसे इलेक्ट्रॉन वोल्ट (eV) में मापते है।
एक इलेक्ट्रॉन वोल्ट किसी इलेक्ट्रॉन को 1 वोल्ट विभवांतर के द्वारा त्वरित कराने पर प्राप्त ऊर्जा का मान है। अतः
1eV=1.602×10−19J
नीचे सारणी में कुछ प्रमुख धातुओं के लिए कार्य फलन का मान दिया गया है-

इलेक्ट्रॉन उत्सर्जन के प्रकार
किसी धातु तल से मुक्त इलेक्ट्रॉन उत्सर्जित कराने के लिए उस धातु को चार प्रकार से ऊर्जा प्रदान की जा सकती है, अतः धातु से इलेक्ट्रॉन उत्सर्जन मुख्यत: चार प्रकार का होता है :
- तापायनिक उत्सर्जन
- क्षेत्र उत्सर्जन
- द्वितीयक उत्सर्जन
- प्रकाश-विद्युत् उत्सर्जन
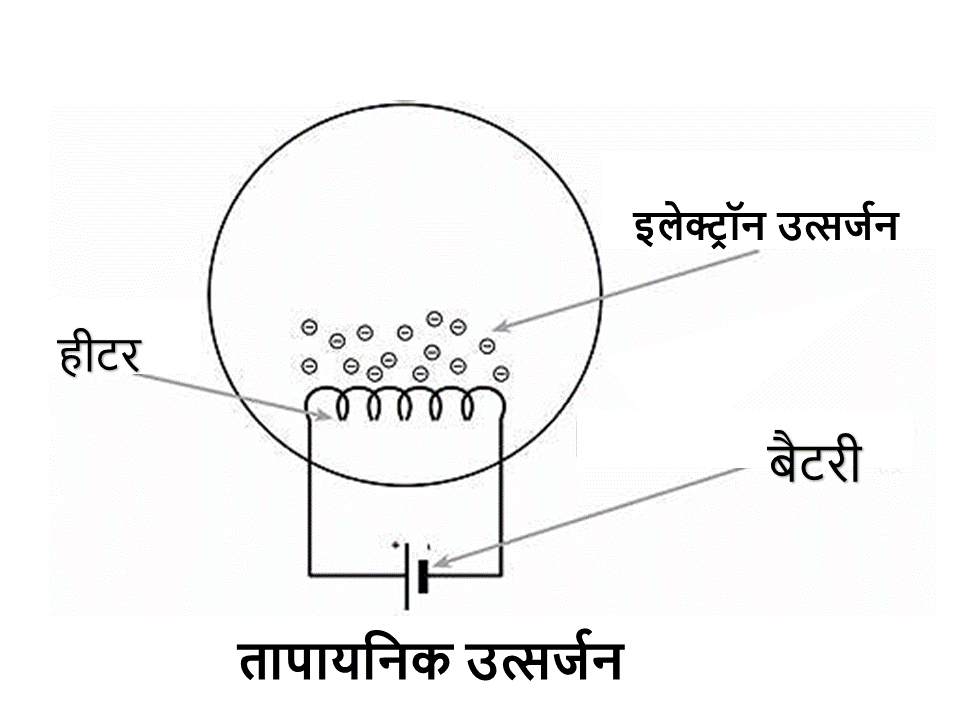
तापायनिक उत्सर्जन :
जब हम किसी धातु को गर्म करते है तो उसकी सतह से इलेक्ट्रॉन निकलने लगते है। चूँकि ये इलेक्ट्रॉन धातु को गर्म करने पर निकलते हैं, इसलिए इन्हें तापायन कहते हैं तथा इस घटना को तापायनिक उत्सर्जन कहते हैं। इस घटना की खोज वैज्ञानिक एडीसन ने सन् 1883 में की थी।
अतः किसी धातु को गर्म करने पर या ऊष्मीय ऊर्जा देने पर उसकी सतह से मुक्त इलेक्ट्रॉनों का निकलना, तापायनिक उत्सर्जन कहलाता है। इस घटना में ऊष्मीय ऊर्जा का विद्युत् ऊर्जा में रूपान्तरण होता है।
तापायनिक उत्सर्जन के लिए उपयुक्त धातु में निम्नलिखित दो गुण होने चाहिए :-
- धातु का गलनांक अधिक होना चाहिए जिससे गर्म करने पर वह पिघल न जाए।
- धातु का कार्यफलन कम होना चाहिए जिससे कि उसे कम ताप तक गर्म करने पर ही उससे अत्यधिक संख्या में इलेक्ट्रॉन निकलने लगें।
क्षेत्र उत्सर्जन :
जब किसी धातु को प्रबल विद्युत क्षेत्र में रखा जाता है तो उस धातु तल से इलेक्ट्रॉन उत्सर्जित होने लगते है| इसके लिए बाह्य विद्युत क्षेत्र अत्यंत प्रबल (≈108वोल्ट/मीटर) आवश्यक होता है। इस प्रकार, एक प्रबल विद्युत् क्षेत्र के प्रभाव में किसी धातु से मुक्त इलेक्ट्रॉन उत्सर्जित होने की घटना को क्षेत्र उत्सर्जन कहते हैं। इसे ठण्डे कैथोड से उत्सर्जन भी कहते हैं।
द्वितीयक उत्सर्जन :
जब अत्यधिक तीव्र वेग से गतिमान इलेक्ट्रॉन बहुत-सी संख्या में किसी धातु तल से टकराते हैं तो उस धातु से अन्य इलेक्ट्रॉन उत्सर्जित होने लगते हैं। इसका कारण यह है कि तीव्र वेग से गतिमान (या ऊर्जायुक्त) प्राथमिक इलेक्ट्रॉन, धातु से टकराने पर अपनी कुछ ऊर्जा धातु के अन्य मुक्त इलेक्ट्रॉनों को प्रदान कर देते हैं। जैसे ही यह प्रदान की गयी ऊर्जा, धातु के कार्य फलन से अधिक होती है, मुक्त इलेक्ट्रॉन धातु तल से बाहर आ जाते हैं। इन इलेक्ट्रॉनों को द्वितीयक इलेक्ट्रॉन कहते हैं। तथा यह क्रिया द्वितीयक उत्सर्जन कहलाती है।
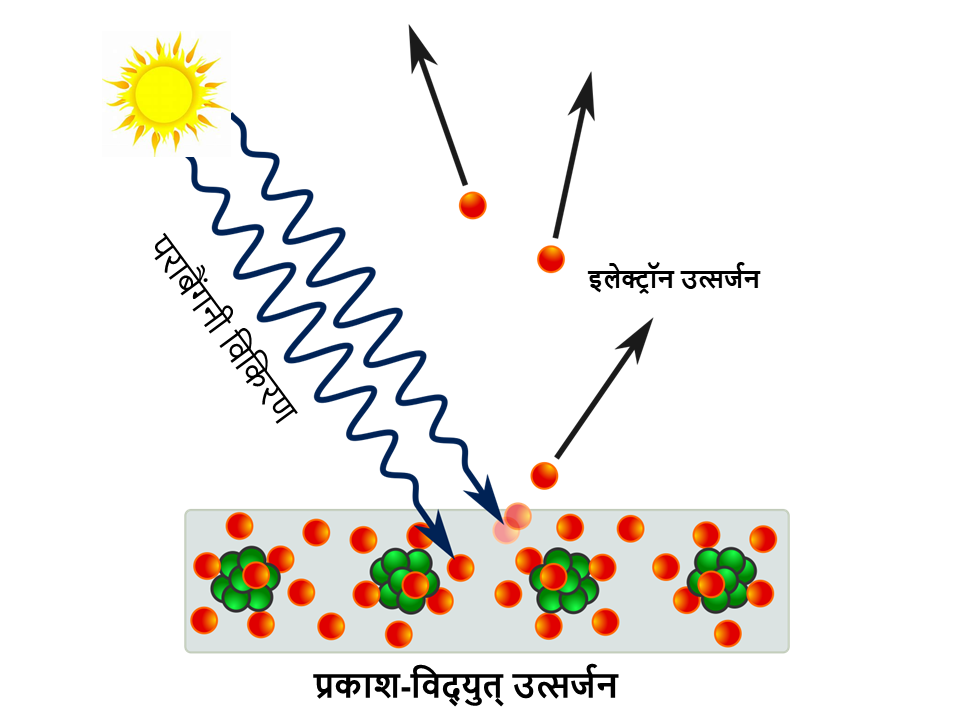
प्रकाश-विद्युत् उत्सर्जन :
वैज्ञानिक हर्ट्ज़ तथा हालवाक्स ने अपने प्रयोगों द्वारा पाया कि जब पराबैंगनी विकिरण किसी धातु तल पर आपतित किए जाते हैं तो उस धातु तल से इलेक्ट्रॉन उत्सर्जित होने लगते हैं। धातु तल से इस प्रकार उत्सर्जित इलेक्ट्रॉनों को फोटो-इलेक्ट्रॉन कहते हैं तथा इस घटना को प्रकाश-विद्युत् उत्सर्जन कहते हैं।
इस प्रकार, किसी धातु तल पर प्रकाश के आपतन से मुक्त इलेक्ट्रॉन उत्सर्जित होने की घटना को प्रकाश-विद्युत् उत्सर्जन कहते हैं यहाँ प्रकाश ऊर्जा का रूपान्तरण विद्युत् ऊर्जा में होता है।
इलेक्ट्रॉन उत्सर्जन के प्रकार
किसी धातु तल से मुक्त इलेक्ट्रॉन उत्सर्जित कराने के लिए उस धातु को चार प्रकार से ऊर्जा प्रदान की जा सकती है, अतः धातु से इलेक्ट्रॉन उत्सर्जन मुख्यत: चार प्रकार का होता है :
- तापायनिक उत्सर्जन
- क्षेत्र उत्सर्जन
- द्वितीयक उत्सर्जन
- प्रकाश-विद्युत् उत्सर्जन
तापायनिक उत्सर्जन :
जब हम किसी धातु को गर्म करते है तो उसकी सतह से इलेक्ट्रॉन निकलने लगते है। चूँकि ये इलेक्ट्रॉन धातु को गर्म करने पर निकलते हैं, इसलिए इन्हें तापायन कहते हैं तथा इस घटना को तापायनिक उत्सर्जन कहते हैं। इस घटना की खोज वैज्ञानिक एडीसन ने सन् 1883 में की थी।
अतः किसी धातु को गर्म करने पर या ऊष्मीय ऊर्जा देने पर उसकी सतह से मुक्त इलेक्ट्रॉनों का निकलना, तापायनिक उत्सर्जन कहलाता है। इस घटना में ऊष्मीय ऊर्जा का विद्युत् ऊर्जा में रूपान्तरण होता है।

तापायनिक उत्सर्जन के लिए उपयुक्त धातु में निम्नलिखित दो गुण होने चाहिए :-
- धातु का गलनांक अधिक होना चाहिए जिससे गर्म करने पर वह पिघल न जाए।
- धातु का कार्यफलन कम होना चाहिए जिससे कि उसे कम ताप तक गर्म करने पर ही उससे अत्यधिक संख्या में इलेक्ट्रॉन निकलने लगें।
क्षेत्र उत्सर्जन :
जब किसी धातु को प्रबल विद्युत क्षेत्र में रखा जाता है तो उस धातु तल से इलेक्ट्रॉन उत्सर्जित होने लगते है| इसके लिए बाह्य विद्युत क्षेत्र अत्यंत प्रबल (≈108वोल्ट/मीटर) आवश्यक होता है। इस प्रकार, एक प्रबल विद्युत् क्षेत्र के प्रभाव में किसी धातु से मुक्त इलेक्ट्रॉन उत्सर्जित होने की घटना को क्षेत्र उत्सर्जन कहते हैं। इसे ठण्डे कैथोड से उत्सर्जन भी कहते हैं।
द्वितीयक उत्सर्जन :
जब अत्यधिक तीव्र वेग से गतिमान इलेक्ट्रॉन बहुत-सी संख्या में किसी धातु तल से टकराते हैं तो उस धातु से अन्य इलेक्ट्रॉन उत्सर्जित होने लगते हैं। इसका कारण यह है कि तीव्र वेग से गतिमान (या ऊर्जायुक्त) प्राथमिक इलेक्ट्रॉन, धातु से टकराने पर अपनी कुछ ऊर्जा धातु के अन्य मुक्त इलेक्ट्रॉनों को प्रदान कर देते हैं। जैसे ही यह प्रदान की गयी ऊर्जा, धातु के कार्य फलन से अधिक होती है, मुक्त इलेक्ट्रॉन धातु तल से बाहर आ जाते हैं। इन इलेक्ट्रॉनों को द्वितीयक इलेक्ट्रॉन कहते हैं। तथा यह क्रिया द्वितीयक उत्सर्जन कहलाती है।
प्रकाश-विद्युत् उत्सर्जन :
वैज्ञानिक हर्ट्ज़ तथा हालवाक्स ने अपने प्रयोगों द्वारा पाया कि जब पराबैंगनी विकिरण किसी धातु तल पर आपतित किए जाते हैं तो उस धातु तल से इलेक्ट्रॉन उत्सर्जित होने लगते हैं। धातु तल से इस प्रकार उत्सर्जित इलेक्ट्रॉनों को फोटो-इलेक्ट्रॉन कहते हैं तथा इस घटना को प्रकाश-विद्युत् उत्सर्जन कहते हैं।
इस प्रकार, किसी धातु तल पर प्रकाश के आपतन से मुक्त इलेक्ट्रॉन उत्सर्जित होने की घटना को प्रकाश-विद्युत् उत्सर्जन कहते हैं यहाँ प्रकाश ऊर्जा का रूपान्तरण विद्युत् ऊर्जा में होता है।

प्रकाश-विद्युत् प्रभाव
इस प्रभाव का अध्ययन सर्वप्रथम वैज्ञानिक हर्ट्ज ने सन् 1887 में किया था। उन्होंने देखा कि जब विद्युत-विसर्जन नलिका की ऋण प्लेट पर पराबैंगनी किरणें डाली जाती है, तो विद्युत विसर्जन अधिक सुगमता से होता है। इसके एक वर्ष पश्यात् हालवैश ने प्रयोग द्वारा इसकी पुष्टि की।
प्रयोग :- हालवैश ने एक निर्वात् बल्ब में जस्ते की दो प्लेटें रखीं। इन प्लेटों से सम्बन्धित दो तारों को बल्ब से बाहर निकाल कर, एक बैटरी तथा सुग्राही धारामापी के द्वारा सम्बन्धित कर दिया।
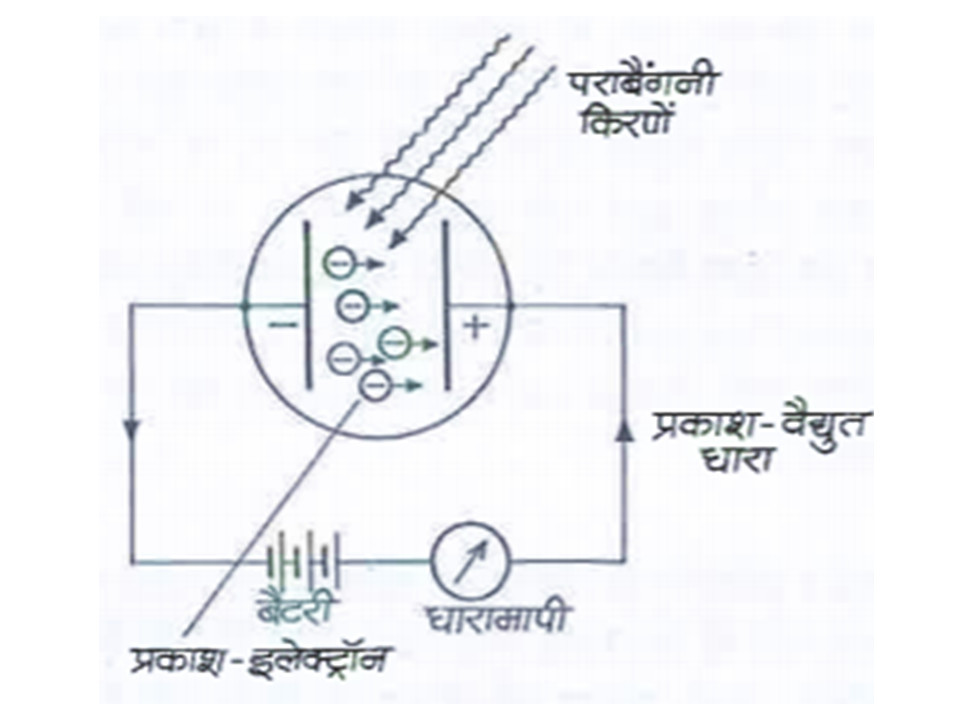
व्याख्या :-
- हालवैश ने देखा कि जब ऋण-प्लेट पर पराबैंगनी प्रकाश की किरणें डाली जाती हैं, तो तुरन्त ही परिपथ में वैद्युत धारा प्रवाहित होने लगती है, और जैसे ही पराबैंगनी किरणे डालनी बन्द कर दी जाती हैं, धारा का प्रवाहित होना भी रुक जाता है।
- परन्तु यदि पराबैगनी किरणें धन-प्लेट पर डाली जाती है तब कोई धारा प्रवाहित नहीं होती (अथवा बहुत क्षीण धारा प्रवाहित होती है)। हालवैश स्वयं इस घटना का कारण न बता सके।
- सन् 1898 में जे० जे० टॉमसन ने यह सिद्ध किया कि प्रकाश के गिरने पर धातु की प्लेट से इलेक्ट्रॉन निकलते है।
- सन् 1900 में लेनार्ड (Lenard) ने बताया कि जब ऋण-प्लेट पर पराबैंगनी किरणें डाली जाती है, तो उससे निकले इलेक्ट्रॉन धन-प्लेट के द्वारा आकर्षित कर लिये जाते हैं जिससे वैद्युत परिपथ पूरा हो जाता है तथा धारा बहने लगती है।
- परन्तु धन-प्लेट पर किरणें डालने से धन-प्लेट से निकले इलेक्ट्रॉन ऋण-प्लेट पर नहीं आ पाते क्योंकि इलेक्ट्रॉनों पर ऋण-आवेश होता है। अतः परिपथ पूरा न होने के कारण धारा नहीं बहती है।
अतः प्रकाश-किरणों के प्रभाव से धातु से इलेक्ट्रॉनों के उत्सर्जन की घटना को प्रकाशवैद्युत प्रभाव अथवा प्रकाशवैद्युत उत्सर्जन कहते है।
प्रकाश द्वारा उत्सर्जित इलेक्ट्रॉनों को 'प्रकाश इलेक्ट्रॉन' अथवा 'फोटो-इलेक्ट्रॉन' तथा उत्पन्न धारा को प्रकाशवैद्युत धारा कहते है इस घटना के लिये लघु तरंगदैर्घ्य (अर्थात उच्च आवृत्ति) का प्रकाश दीर्घ तरंगदैर्ध्य (अर्थात निम्न आवृत्ति) के प्रकाश की अपेक्षा अधिक प्रभावी होता है।
प्रकाश-विद्युत् प्रभाव
इस प्रभाव का अध्ययन सर्वप्रथम वैज्ञानिक हर्ट्ज ने सन् 1887 में किया था। उन्होंने देखा कि जब विद्युत-विसर्जन नलिका की ऋण प्लेट पर पराबैंगनी किरणें डाली जाती है, तो विद्युत विसर्जन अधिक सुगमता से होता है। इसके एक वर्ष पश्यात् हालवैश ने प्रयोग द्वारा इसकी पुष्टि की।
प्रयोग :- हालवैश ने एक निर्वात् बल्ब में जस्ते की दो प्लेटें रखीं। इन प्लेटों से सम्बन्धित दो तारों को बल्ब से बाहर निकाल कर, एक बैटरी तथा सुग्राही धारामापी के द्वारा सम्बन्धित कर दिया।

व्याख्या :-
- हालवैश ने देखा कि जब ऋण-प्लेट पर पराबैंगनी प्रकाश की किरणें डाली जाती हैं, तो तुरन्त ही परिपथ में वैद्युत धारा प्रवाहित होने लगती है, और जैसे ही पराबैंगनी किरणे डालनी बन्द कर दी जाती हैं, धारा का प्रवाहित होना भी रुक जाता है।
- परन्तु यदि पराबैगनी किरणें धन-प्लेट पर डाली जाती है तब कोई धारा प्रवाहित नहीं होती (अथवा बहुत क्षीण धारा प्रवाहित होती है)। हालवैश स्वयं इस घटना का कारण न बता सके।
- सन् 1898 में जे० जे० टॉमसन ने यह सिद्ध किया कि प्रकाश के गिरने पर धातु की प्लेट से इलेक्ट्रॉन निकलते है।
- सन् 1900 में लेनार्ड (Lenard) ने बताया कि जब ऋण-प्लेट पर पराबैंगनी किरणें डाली जाती है, तो उससे निकले इलेक्ट्रॉन धन-प्लेट के द्वारा आकर्षित कर लिये जाते हैं जिससे वैद्युत परिपथ पूरा हो जाता है तथा धारा बहने लगती है।
- परन्तु धन-प्लेट पर किरणें डालने से धन-प्लेट से निकले इलेक्ट्रॉन ऋण-प्लेट पर नहीं आ पाते क्योंकि इलेक्ट्रॉनों पर ऋण-आवेश होता है। अतः परिपथ पूरा न होने के कारण धारा नहीं बहती है।
अतः प्रकाश-किरणों के प्रभाव से धातु से इलेक्ट्रॉनों के उत्सर्जन की घटना को प्रकाशवैद्युत प्रभाव अथवा प्रकाशवैद्युत उत्सर्जन कहते है।
प्रकाश द्वारा उत्सर्जित इलेक्ट्रॉनों को 'प्रकाश इलेक्ट्रॉन' अथवा 'फोटो-इलेक्ट्रॉन' तथा उत्पन्न धारा को प्रकाशवैद्युत धारा कहते है इस घटना के लिये लघु तरंगदैर्घ्य (अर्थात उच्च आवृत्ति) का प्रकाश दीर्घ तरंगदैर्ध्य (अर्थात निम्न आवृत्ति) के प्रकाश की अपेक्षा अधिक प्रभावी होता है।
उदाहरण 1
60 मिलीवॉट शक्ति का एक बल्ब 6000 Å तरंगदैर्ध्य का प्रकाश उत्सर्जित कर रहा है। बल्ब से प्रति सेकण्ड उत्सर्जित फोटॉन की संख्या की गणना कीजिए।
प्रश्नानुसार दिया गया है -
- P=60mW=60×10−3W,
λ=6000Å=6000×10−10m
- nhv = शक्ति
- nhcλ=P
- n=Pλhc
- n=60×10−3×6000×10−106.62×10−34×3×108 फोटॉन / सेकण्ड
n=1.8×1017 फोटॉन / सेकण्ड
उदाहरण 1
60 मिलीवॉट शक्ति का एक बल्ब 6000 Å तरंगदैर्ध्य का प्रकाश उत्सर्जित कर रहा है। बल्ब से प्रति सेकण्ड उत्सर्जित फोटॉन की संख्या की गणना कीजिए।
प्रश्नानुसार दिया गया है -
- P=60mW=60×10−3W,
λ=6000Å=6000×10−10m
- nhv = शक्ति
- nhcλ=P
- n=Pλhc
- n=60×10−3×6000×10−106.62×10−34×3×108 फोटॉन / सेकण्ड
n=1.8×1017 फोटॉन / सेकण्ड
उदाहरण 2
पृथ्वी के पृष्ठ पर पहुँचने वाला सूर्य - प्रकाश का ऊर्जा अभिवाह (फ्लक्स) 1.388×103W/m2 है। प्रति वर्ग मीटर प्रति सेकण्ड पृथ्वी पर कितने फोटान आपतित होते है ? यह मान लें कि सूर्य - प्रकाश में फोटॉन का औसत तरंगदैर्ध्य 550 nm है
प्रश्नानुसार दिया गया है -
- λ=550nm=550×10−9m,
I=1.388×103W/m2
- I = (उत्सर्जित शक्ति)/(क्षेत्रफल)
I=PA=1.388×103W/m2
- E=hcλ
E=6.63×10−34×3×108550×10−9
E=3.616×10−19J
- n=P/AE=IE
n=1.388×1033.616×10−19
n=3.83×1021 फ़ोटॉन/ मी2 से.
उदाहरण 2
पृथ्वी के पृष्ठ पर पहुँचने वाला सूर्य - प्रकाश का ऊर्जा अभिवाह (फ्लक्स) 1.388×103W/m2 है। प्रति वर्ग मीटर प्रति सेकण्ड पृथ्वी पर कितने फोटान आपतित होते है ? यह मान लें कि सूर्य - प्रकाश में फोटॉन का औसत तरंगदैर्ध्य 550 nm है
प्रश्नानुसार दिया गया है -
- λ=550nm=550×10−9m,
I=1.388×103W/m2
- I = (उत्सर्जित शक्ति)/(क्षेत्रफल)
I=PA=1.388×103W/m2
- E=hcλ
E=6.63×10−34×3×108550×10−9
E=3.616×10−19J
- n=P/AE=IE
n=1.388×1033.616×10−19
n=3.83×1021 फ़ोटॉन/ मी2 से.
उदाहरण 3
किसी पूर्ण प्रवर्तक परदे पर 1 N का बल लगाने के लिए उस पर λ=6600nm तरंगदैर्ध्य के कितने फोटॉनों का प्रति सेकण्ड लम्बवत आपतन होना आवश्यक होगा ?
प्रश्नानुसार दिया गया है -
- F=1N,λ=6000×10−9m
- p1=hλ
- p2=−hλ
- Δp=p1−p2=2hλ
- F=ΔpΔt=2nhλ
- n=Fλ2h
n=1×6600×10−92×6.6×10−34
n=5×1027 फ़ोटॉन / सेकण्ड
उदाहरण 3
किसी पूर्ण प्रवर्तक परदे पर 1 N का बल लगाने के लिए उस पर λ=6600nm तरंगदैर्ध्य के कितने फोटॉनों का प्रति सेकण्ड लम्बवत आपतन होना आवश्यक होगा ?
प्रश्नानुसार दिया गया है -
- F=1N,λ=6000×10−9m
- p1=hλ
- p2=−hλ
- Δp=p1−p2=2hλ
- F=ΔpΔt=2nhλ
- n=Fλ2h
n=1×6600×10−92×6.6×10−34
n=5×1027 फ़ोटॉन / सेकण्ड
हर्ट्स तथा लेनार्ड का प्रेक्षण
हर्ट्स, लेनार्ड तथा मिलिकन ने प्रकाशवैद्युत उत्सर्जन पर अनेक प्रयोग किये। उन्होंने भिन्न-भिन्न धातुओं की प्लेटें लेकर उन पर विभिन्न आवृत्तियों तथा विभिन्न तीव्रताओं का प्रकाश डाला तथा प्रत्येक दशा में उत्सर्जित प्रकाश इलेक्ट्रॉनों की ऊर्जा एवं प्रकाश धारा की प्रबलता को मापा। इन प्रयोगों के आधार पर उन्होंने प्रकाशवैद्युत उत्सर्जन के सम्बन्ध में अनेक फल प्राप्त किये।
प्रयोग :-
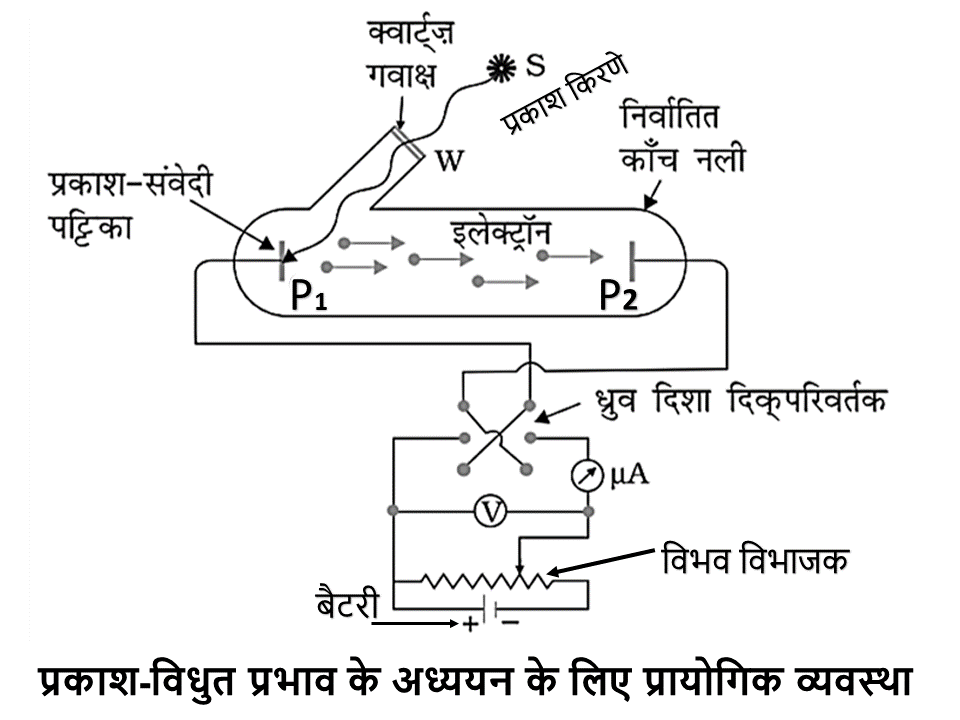
- इस प्रयोग में एक निर्वातित नलिका के भीतर धातु को दो प्लेटें P1 व P2 एक-दूसरे से कुछ दूरी पर लगायी गयी हैं।
- प्लेट P1 एक क्वार्ट्ज की खिड़की W के सामने पड़ती है तथा इस पर प्रकाश की किरणे डाली जाती है।
- इसे "कैथोड-प्लेट" भी कहते हैं। इन प्लेटो का सम्बन्ध एक सुग्राही अमीटर A से तथा एक दिक्परिवर्तक C के द्वारा एक विभव-विभाजक से किया गया है।
- इससे प्लेटों के बीच विभवान्तर को परिवर्तित किया जा सकता है तथा विभवान्तर की दिशा भी बदली जा सकती है।
- इस विभवान्तर को वोल्टमीटर V के द्वारा नापा जा सकता है।
प्रकाश की तीव्रता पर प्रभाव :
जब एक निश्चित आवृत्ति तथा तीव्रता की प्रकाश किरणे प्लेट P1 पर डाली जाती है, तो प्लेट से प्रकाश-इलेक्ट्रॉन निकलने लगते है। यदि दिक्परिवर्तक में केवल प्लग 1,1 लगाकर प्लेट P2 को प्लेट P1 के सापेक्ष धन विभव पर रखा गया है, तो ये सभी प्रकाश इलेक्ट्रॉन प्लेट P2 पर पहुँच जाते हैं तथा परिपथ में अधिकतम प्रकाशवैद्युत धारा बहने लगती है। प्रकाशवैद्युत धारा के इस अधिकतम मान को ही संतृप्त प्रकाशवैद्युत धारा कहते है।
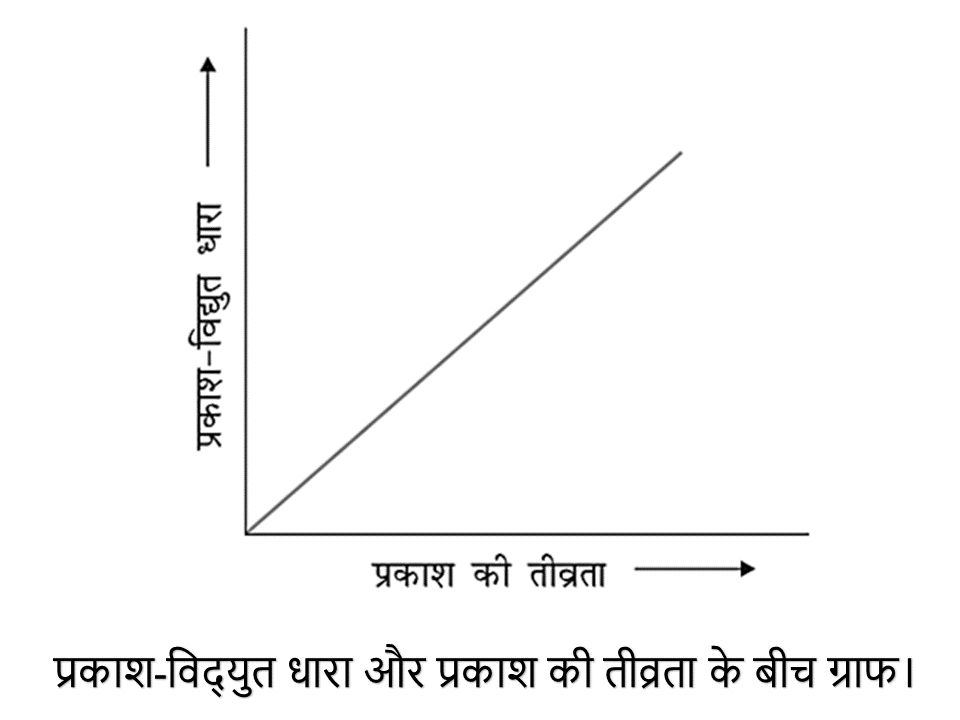
प्लेट P2 के धन विभव को बढ़ाने पर प्रकाशवैद्युत धारा में कोई वृद्धि नहीं होती है क्योकि P1 से निकलने वाले सभी इलेक्ट्रॉन पहले ही P2 पर पहुँच रहे है। यदि हम P1 गिरने वाले प्रकाश की तीव्रता I को दोगुना कर दें तो अधिकतम धारा का मान भी दोगुना हो जाता है। इससे पता चलता है की प्रकाशवैद्युत धारा अर्थात प्रकाश-इलेक्ट्रॉनों के उत्सर्जन की दर आपतित प्रकाश की तीव्रता के अनुक्रमानुपाती होती है।
विभव का प्रभाव :
अब यदि हम दिक्परिवर्तक C में केवल प्लग 2,2 लगाकर प्लेट P2 को P1 के सापेक्ष विभव पर कर दे तो धारा तुरंत घट जाती है, परन्तु शून्य नहीं होती। इससे यह पता चलता है कि P1 से निकलने वाले इलेक्ट्रॉनों में गतिज ऊर्जा होती है। P2 के ऋण विभव को बढ़ाने पर धारा तेजी से घटती जाती है तथा अन्त में शून्य हो जाती है।
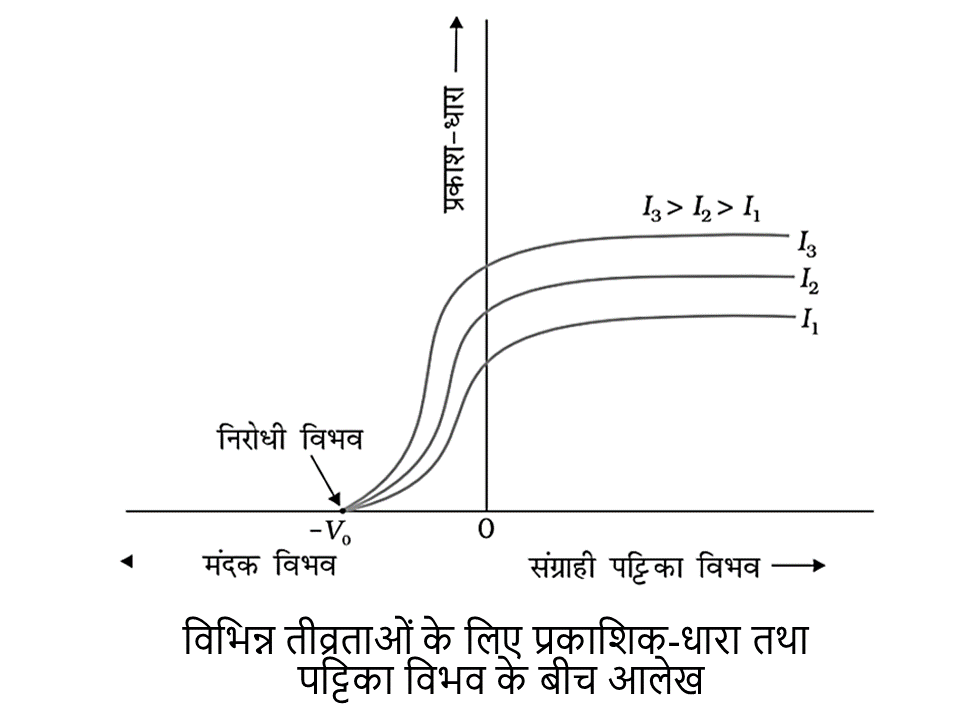
P1 के सापेक्ष P2 के इस ऋण विभव को, जिस पर प्रकाशवैद्युत धारा शून्य हो जाती है, "निरोधी विभव" अथवा 'संस्तब्ध-विभव' कहते हैं। चूँकि निरोधी विभव द्वारा अधिकतम ऊर्जा वाले इलेक्ट्रॉन रुकते है, अत: इससे प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा [Kmax] ज्ञात की जा सकती है। यदि निरोधी विभव का मान Vo हो, तो प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा
Kmax=eVo
जहाँ e इलेक्ट्रॉन पर आवेश है।आवृत्ति का प्रभाव :
यदि निरोधी विभव पर पहुँच जाने पर हम प्लेट P1 पर उतनी ही तीव्रता का परन्तु पहले से ऊंची आवृति का प्रकाश डालें तो परिपथ में उतनी ही प्रकाशवैद्युत धारा फिर से बहने लगती है। प्लेट P2 के ऋण विभव को बढ़ा देने पर यह धारा पुनः रुक जाती है। इससे यह पता चलता है कि प्रकाश की आवृत्ति जितनी ऊँची होगी, उत्सर्जित प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा भी उतनी ही अधिक होगी, अथवा निरोधी विभव उतना ही ऊँचा होगा।
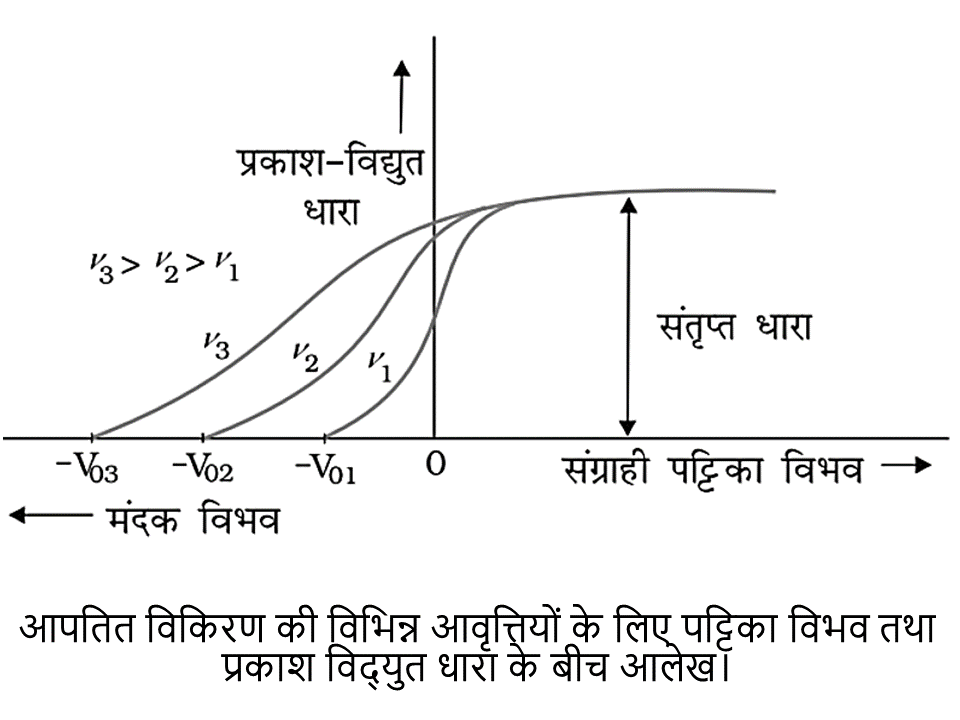
यदि हम विभिन्न आवृत्तियों के प्रकाशों को प्रयुक्त करके, प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा Kmax तथा प्रकाश-आवृत्ति (v) में एक ग्राफ खींचे तो सरल रेखा प्राप्त होती है। इससे यह पता चलता है कि प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा, प्रकाश की आवृत्ति के बढ़ने पर बढ़ती है।
हर्ट्स तथा लेनार्ड का प्रेक्षण
हर्ट्स, लेनार्ड तथा मिलिकन ने प्रकाशवैद्युत उत्सर्जन पर अनेक प्रयोग किये। उन्होंने भिन्न-भिन्न धातुओं की प्लेटें लेकर उन पर विभिन्न आवृत्तियों तथा विभिन्न तीव्रताओं का प्रकाश डाला तथा प्रत्येक दशा में उत्सर्जित प्रकाश इलेक्ट्रॉनों की ऊर्जा एवं प्रकाश धारा की प्रबलता को मापा। इन प्रयोगों के आधार पर उन्होंने प्रकाशवैद्युत उत्सर्जन के सम्बन्ध में अनेक फल प्राप्त किये।
प्रयोग :-

- इस प्रयोग में एक निर्वातित नलिका के भीतर धातु को दो प्लेटें P1 व P2 एक-दूसरे से कुछ दूरी पर लगायी गयी हैं।
- प्लेट P1 एक क्वार्ट्ज की खिड़की W के सामने पड़ती है तथा इस पर प्रकाश की किरणे डाली जाती है।
- इसे "कैथोड-प्लेट" भी कहते हैं। इन प्लेटो का सम्बन्ध एक सुग्राही अमीटर A से तथा एक दिक्परिवर्तक C के द्वारा एक विभव-विभाजक से किया गया है।
- इससे प्लेटों के बीच विभवान्तर को परिवर्तित किया जा सकता है तथा विभवान्तर की दिशा भी बदली जा सकती है।
- इस विभवान्तर को वोल्टमीटर V के द्वारा नापा जा सकता है।
प्रकाश की तीव्रता पर प्रभाव :
जब एक निश्चित आवृत्ति तथा तीव्रता की प्रकाश किरणे प्लेट P1 पर डाली जाती है, तो प्लेट से प्रकाश-इलेक्ट्रॉन निकलने लगते है। यदि दिक्परिवर्तक में केवल प्लग 1,1 लगाकर प्लेट P2 को प्लेट P1 के सापेक्ष धन विभव पर रखा गया है, तो ये सभी प्रकाश इलेक्ट्रॉन प्लेट P2 पर पहुँच जाते हैं तथा परिपथ में अधिकतम प्रकाशवैद्युत धारा बहने लगती है। प्रकाशवैद्युत धारा के इस अधिकतम मान को ही संतृप्त प्रकाशवैद्युत धारा कहते है।

प्लेट P2 के धन विभव को बढ़ाने पर प्रकाशवैद्युत धारा में कोई वृद्धि नहीं होती है क्योकि P1 से निकलने वाले सभी इलेक्ट्रॉन पहले ही P2 पर पहुँच रहे है। यदि हम P1 गिरने वाले प्रकाश की तीव्रता I को दोगुना कर दें तो अधिकतम धारा का मान भी दोगुना हो जाता है। इससे पता चलता है की प्रकाशवैद्युत धारा अर्थात प्रकाश-इलेक्ट्रॉनों के उत्सर्जन की दर आपतित प्रकाश की तीव्रता के अनुक्रमानुपाती होती है।
विभव का प्रभाव :
अब यदि हम दिक्परिवर्तक C में केवल प्लग 2,2 लगाकर प्लेट P2 को P1 के सापेक्ष विभव पर कर दे तो धारा तुरंत घट जाती है, परन्तु शून्य नहीं होती। इससे यह पता चलता है कि P1 से निकलने वाले इलेक्ट्रॉनों में गतिज ऊर्जा होती है। P2 के ऋण विभव को बढ़ाने पर धारा तेजी से घटती जाती है तथा अन्त में शून्य हो जाती है।

P1 के सापेक्ष P2 के इस ऋण विभव को, जिस पर प्रकाशवैद्युत धारा शून्य हो जाती है, "निरोधी विभव" अथवा 'संस्तब्ध-विभव' कहते हैं। चूँकि निरोधी विभव द्वारा अधिकतम ऊर्जा वाले इलेक्ट्रॉन रुकते है, अत: इससे प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा [Kmax] ज्ञात की जा सकती है। यदि निरोधी विभव का मान Vo हो, तो प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा
Kmax=eVo
जहाँ e इलेक्ट्रॉन पर आवेश है।आवृत्ति का प्रभाव :
यदि निरोधी विभव पर पहुँच जाने पर हम प्लेट P1 पर उतनी ही तीव्रता का परन्तु पहले से ऊंची आवृति का प्रकाश डालें तो परिपथ में उतनी ही प्रकाशवैद्युत धारा फिर से बहने लगती है। प्लेट P2 के ऋण विभव को बढ़ा देने पर यह धारा पुनः रुक जाती है। इससे यह पता चलता है कि प्रकाश की आवृत्ति जितनी ऊँची होगी, उत्सर्जित प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा भी उतनी ही अधिक होगी, अथवा निरोधी विभव उतना ही ऊँचा होगा।

यदि हम विभिन्न आवृत्तियों के प्रकाशों को प्रयुक्त करके, प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा Kmax तथा प्रकाश-आवृत्ति (v) में एक ग्राफ खींचे तो सरल रेखा प्राप्त होती है। इससे यह पता चलता है कि प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा, प्रकाश की आवृत्ति के बढ़ने पर बढ़ती है।
प्रकाश विद्युत उत्सर्जन के नियम
लेनार्ड तथा मिलिकन ने प्रकाशवैद्युत उत्सर्जन पर किये गये प्रयोगों के आधार पर निम्नलिखित नियम दिए :-
- किसी धातु के पृष्ठ से प्रकाश इलेक्ट्रॉनों के उत्सर्जन की दर, धातु के पृष्ठ पर आपतित प्रकाश की तीव्रता के अनुक्रमानुपाती होती है।
- उत्सर्जित प्रकाश इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा आपतित प्रकाश की तीव्रता पर निर्भर नहीं करती है।
- प्रकाश इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा आपतित प्रकाश की आवृत्ति के बढ़ने पर बढ़ती है।
- यदि आपतित प्रकाश की आवृत्ति एक न्यूनतम मान से कम है, तो धातु से कोई भी प्रकाश इलेक्ट्रॉन नहीं निकलता। यह न्यूनतम आवृत्ति (देहली आवृत्ति) भिन्न-भिन्न धातुओं के लिए भिन्न-भिन्न होती है।
- प्रकाश के धातु के पृष्ठ पर गिरते ही इलेक्ट्रॉन उत्सर्जित होने लगते है अर्थात् प्रकाश के पृष्ठ पर गिरने तथा इलेक्ट्रॉन के पृष्ठ से बाहर निकलने के बीच कोई समय-पश्चता नहीं होती, चाहे प्रकाश की तीव्रता कितनी भी क्यों न हो।
प्रकाश विद्युत उत्सर्जन के नियम
लेनार्ड तथा मिलिकन ने प्रकाशवैद्युत उत्सर्जन पर किये गये प्रयोगों के आधार पर निम्नलिखित नियम दिए :-
- किसी धातु के पृष्ठ से प्रकाश इलेक्ट्रॉनों के उत्सर्जन की दर, धातु के पृष्ठ पर आपतित प्रकाश की तीव्रता के अनुक्रमानुपाती होती है।
- उत्सर्जित प्रकाश इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा आपतित प्रकाश की तीव्रता पर निर्भर नहीं करती है।
- प्रकाश इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा आपतित प्रकाश की आवृत्ति के बढ़ने पर बढ़ती है।
- यदि आपतित प्रकाश की आवृत्ति एक न्यूनतम मान से कम है, तो धातु से कोई भी प्रकाश इलेक्ट्रॉन नहीं निकलता। यह न्यूनतम आवृत्ति (देहली आवृत्ति) भिन्न-भिन्न धातुओं के लिए भिन्न-भिन्न होती है।
- प्रकाश के धातु के पृष्ठ पर गिरते ही इलेक्ट्रॉन उत्सर्जित होने लगते है अर्थात् प्रकाश के पृष्ठ पर गिरने तथा इलेक्ट्रॉन के पृष्ठ से बाहर निकलने के बीच कोई समय-पश्चता नहीं होती, चाहे प्रकाश की तीव्रता कितनी भी क्यों न हो।
तरंग सिद्धांत की विफलता
प्रकाशवैद्युत प्रभाव के इन अभिलक्षणो की व्याख्या के तरंग-सिद्धांत के द्वारा नहीं की जा सकती। इसके तीन मुख्य कारण है :-
- यदि प्रकाश तरंगो के रूप में है, तो प्रकाश की तीव्रता बढ़ने पर तरंगो का आयाम और इस कारण तरंगो द्वारा संचित ऊर्जा बढ़ेगी। ये तरंगे धातु के पृष्ठ पर गिरने पर, धातु के इलेक्ट्रॉनों को अधिक ऊर्जा प्रदान करेंगी जिससे उत्सर्जित प्रकाश इलेक्ट्रॉनों की ऊर्जा बढ़ेगी। परन्तु यह प्रायोगिक तथ्य के विरुद्ध है, क्योकि प्रकाश-इलेक्ट्रॉनों की ऊर्जा प्रकाश की तीव्रता पर निर्भर नहीं करती है।
- प्रकाश तरंगो की आवृत्ति कुछ भी हो, प्रकाश-इलेक्ट्रॉन अवश्य उत्सर्जित होने चाहिए बशर्ते कि प्रकाश में उतनी तीव्रता है जिससे की वह धातु के इलेक्ट्रॉनों को आवश्यक ऊर्जा प्रदान कर सके। परन्तु प्रयोग यह बताता है की यदि प्रकाश की आवृत्ति एक न्यूनतम मान से कम है, तो प्रकाश-इलेक्ट्रॉन उत्सर्जित नहीं हो सकते चाहे तीव्रता कितनी ही अधिक क्यों न हो।
- प्रकाश-तरंगो द्वारा संचरित ऊर्जा धातु के किसी एक इलेक्ट्रॉन को न मिलकर, प्रकाशित क्षेत्रफल में उपस्थित सभी इलेक्ट्रॉनों में वितरित होगी। अतः इलेक्ट्रॉनों को उत्सर्जित के लिये आवश्यक ऊर्जा संचित करने में कुछ समय लगभग कुछ घंटे लग जायेगा। परन्तु प्रयोग के अनुसार, धातु पर प्रकाश के गिरते ही इलेक्ट्रॉन उत्सर्जित होने लगते है।
तरंग सिद्धांत की विफलता
प्रकाशवैद्युत प्रभाव के इन अभिलक्षणो की व्याख्या के तरंग-सिद्धांत के द्वारा नहीं की जा सकती। इसके तीन मुख्य कारण है :-
- यदि प्रकाश तरंगो के रूप में है, तो प्रकाश की तीव्रता बढ़ने पर तरंगो का आयाम और इस कारण तरंगो द्वारा संचित ऊर्जा बढ़ेगी। ये तरंगे धातु के पृष्ठ पर गिरने पर, धातु के इलेक्ट्रॉनों को अधिक ऊर्जा प्रदान करेंगी जिससे उत्सर्जित प्रकाश इलेक्ट्रॉनों की ऊर्जा बढ़ेगी। परन्तु यह प्रायोगिक तथ्य के विरुद्ध है, क्योकि प्रकाश-इलेक्ट्रॉनों की ऊर्जा प्रकाश की तीव्रता पर निर्भर नहीं करती है।
- प्रकाश तरंगो की आवृत्ति कुछ भी हो, प्रकाश-इलेक्ट्रॉन अवश्य उत्सर्जित होने चाहिए बशर्ते कि प्रकाश में उतनी तीव्रता है जिससे की वह धातु के इलेक्ट्रॉनों को आवश्यक ऊर्जा प्रदान कर सके। परन्तु प्रयोग यह बताता है की यदि प्रकाश की आवृत्ति एक न्यूनतम मान से कम है, तो प्रकाश-इलेक्ट्रॉन उत्सर्जित नहीं हो सकते चाहे तीव्रता कितनी ही अधिक क्यों न हो।
- प्रकाश-तरंगो द्वारा संचरित ऊर्जा धातु के किसी एक इलेक्ट्रॉन को न मिलकर, प्रकाशित क्षेत्रफल में उपस्थित सभी इलेक्ट्रॉनों में वितरित होगी। अतः इलेक्ट्रॉनों को उत्सर्जित के लिये आवश्यक ऊर्जा संचित करने में कुछ समय लगभग कुछ घंटे लग जायेगा। परन्तु प्रयोग के अनुसार, धातु पर प्रकाश के गिरते ही इलेक्ट्रॉन उत्सर्जित होने लगते है।
आइन्स्टाइन का प्रकाश-विद्युत समीकरण
सन् 1905 में आइन्सटाइन ने प्रकाशवैद्युत प्रभाव की व्याख्या प्लांक के क्वाण्टम सिद्धान्त के आधार पर किया। इस सिद्धांत के अनुसार,
प्रकाश ऊर्जा के छोटे-छोटे बण्डलों अथवा पैकेटों के रूप में उत्सर्जित होकर तरंगों के रूप में संचरित होता है जिन्हे फोटॉन कहते हैं। प्रत्येक फोटॉन की ऊर्जा hν होती है, जहाँ ν प्रकाश की आवृत्ति है तथा h प्लांक का सार्वत्रिक नियतांक है। प्रकाश की तीव्रता इन्हीं फोटॉनों की संख्या पर निर्भर करती है।
- जब कोई फोटॉन धातु की प्लेट पर गिरता है, तो वह अपनी 'सम्पूर्ण' ऊर्जा hν को धातु के भीतर उपस्थित इलेक्ट्रॉनों में से किसी एक ही इलेक्ट्रॉन को स्थानान्तरित कर देता है और उसका स्वयं का अस्तित्व समाप्त हो जाता है।
- इस ऊर्जा का कुछ भाग इलेक्ट्रॉन को धातु से बाहर निकालने में व्यय हो जाता है तथा शेष ऊर्जा उत्सर्जित इलेक्ट्रॉन को गतिज ऊर्जा के रूप में मिल जाती है।
- अतः धातु से विभिन्न ऊर्जाओं के इलेक्ट्रॉन निकलते हैं। जो इलेक्ट्रॉन धातु ऊपरी पृष्ठ से उत्सर्जित होते है उनकी गतिज ऊर्जा अधिकतम होती है क्योंकि उनकी ऊर्जा का टक्करों द्वारा ह्रास नहीं होता।
माना कि धातु के पृष्ठ से उत्सर्जित प्रकाश इलेक्ट्रॉन की अधिकतम गतिज ऊर्जा Kmax है तथा धातु से एक प्रकाश इलेक्ट्रॉन को बाहर निकालने के लिए आवश्यक ऊर्जा ϕo है। ϕo को धातु का 'कार्य फलन' कहते है तथा इसका मान भिन्न-भिन्न धातुओं के लिए भिन्न-भिन्न होता है। तब उपरोक्त व्याख्या के अनुसार,
अथवा
जहाँ hν,धातु में इलेक्ट्रॉन द्वारा अवशोषित फोटॉन की ऊर्जा है।
इस समीकरण की प्रायोगिक फलों से प्राप्त समीकरण Kmax=Aν−B से तुलना करने पर यह स्पष्ट हो जाता है की नियतांक A वास्तव में प्लांक-नियतांक h है तथा नियतांक B धातु का कार्य फलन ϕo है।
यदि इलेक्ट्रॉन द्वारा अवशोषित फोटॉन की ऊर्जा धातु के कार्य फलन ϕo से कम हो तब इलेक्ट्रॉन उत्सर्जित नहीं होगा। अतः यदि दी हुई धातु के लिए प्रकाश की देहली आवृत्ति νo हो, तो ऐसे प्रकाश के फोटॉन की ऊर्जा hνo इलेक्ट्रॉन को धातु के पृष्ठ से निकालने में ही व्यय हो जायेगी अर्थात यह कार्य फलन के बराबर होगी। इस प्रकार,
ϕo के इस मान को उपरोक्त समीकरण (1) में रखने पर,
अथवा
यदि उत्सर्जित प्रकाश इलेक्ट्रॉनों का अधिकतम वेग Vmax हो, तब
अतः उपरोक्त समीकरण को इस प्रकार भी लिख सकते है-
12mV2max=h(ν−νo)
इस समीकरण को आइन्स्टाइन का प्रकाशवैद्युत समीकरण कहते है।
आइन्स्टाइन का प्रकाश-विद्युत समीकरण
सन् 1905 में आइन्सटाइन ने प्रकाशवैद्युत प्रभाव की व्याख्या प्लांक के क्वाण्टम सिद्धान्त के आधार पर किया। इस सिद्धांत के अनुसार,
प्रकाश ऊर्जा के छोटे-छोटे बण्डलों अथवा पैकेटों के रूप में उत्सर्जित होकर तरंगों के रूप में संचरित होता है जिन्हे फोटॉन कहते हैं। प्रत्येक फोटॉन की ऊर्जा hν होती है, जहाँ ν प्रकाश की आवृत्ति है तथा h प्लांक का सार्वत्रिक नियतांक है। प्रकाश की तीव्रता इन्हीं फोटॉनों की संख्या पर निर्भर करती है।
- जब कोई फोटॉन धातु की प्लेट पर गिरता है, तो वह अपनी 'सम्पूर्ण' ऊर्जा hν को धातु के भीतर उपस्थित इलेक्ट्रॉनों में से किसी एक ही इलेक्ट्रॉन को स्थानान्तरित कर देता है और उसका स्वयं का अस्तित्व समाप्त हो जाता है।
- इस ऊर्जा का कुछ भाग इलेक्ट्रॉन को धातु से बाहर निकालने में व्यय हो जाता है तथा शेष ऊर्जा उत्सर्जित इलेक्ट्रॉन को गतिज ऊर्जा के रूप में मिल जाती है।
- अतः धातु से विभिन्न ऊर्जाओं के इलेक्ट्रॉन निकलते हैं। जो इलेक्ट्रॉन धातु ऊपरी पृष्ठ से उत्सर्जित होते है उनकी गतिज ऊर्जा अधिकतम होती है क्योंकि उनकी ऊर्जा का टक्करों द्वारा ह्रास नहीं होता।
माना कि धातु के पृष्ठ से उत्सर्जित प्रकाश इलेक्ट्रॉन की अधिकतम गतिज ऊर्जा Kmax है तथा धातु से एक प्रकाश इलेक्ट्रॉन को बाहर निकालने के लिए आवश्यक ऊर्जा ϕo है। ϕo को धातु का 'कार्य फलन' कहते है तथा इसका मान भिन्न-भिन्न धातुओं के लिए भिन्न-भिन्न होता है। तब उपरोक्त व्याख्या के अनुसार,
अथवा
जहाँ hν,धातु में इलेक्ट्रॉन द्वारा अवशोषित फोटॉन की ऊर्जा है।
इस समीकरण की प्रायोगिक फलों से प्राप्त समीकरण Kmax=Aν−B से तुलना करने पर यह स्पष्ट हो जाता है की नियतांक A वास्तव में प्लांक-नियतांक h है तथा नियतांक B धातु का कार्य फलन ϕo है।
यदि इलेक्ट्रॉन द्वारा अवशोषित फोटॉन की ऊर्जा धातु के कार्य फलन ϕo से कम हो तब इलेक्ट्रॉन उत्सर्जित नहीं होगा। अतः यदि दी हुई धातु के लिए प्रकाश की देहली आवृत्ति νo हो, तो ऐसे प्रकाश के फोटॉन की ऊर्जा hνo इलेक्ट्रॉन को धातु के पृष्ठ से निकालने में ही व्यय हो जायेगी अर्थात यह कार्य फलन के बराबर होगी। इस प्रकार,
ϕo के इस मान को उपरोक्त समीकरण (1) में रखने पर,
अथवा
यदि उत्सर्जित प्रकाश इलेक्ट्रॉनों का अधिकतम वेग Vmax हो, तब
अतः उपरोक्त समीकरण को इस प्रकार भी लिख सकते है-
12mV2max=h(ν−νo)
इस समीकरण को आइन्स्टाइन का प्रकाशवैद्युत समीकरण कहते है।
आपतित प्रकाश की आवृत्ति के साथ निरोधी विभव का विचरण
मिलिकन ने विभिन्न आवृत्तिओ के प्रकाश सुग्राही तलों पर डालकर, निरोधी विभव Vo तथा प्रकाश की आवृत्ति ν में ग्राफ खींचा। यह ग्राफ एक सरल रेखा में है।
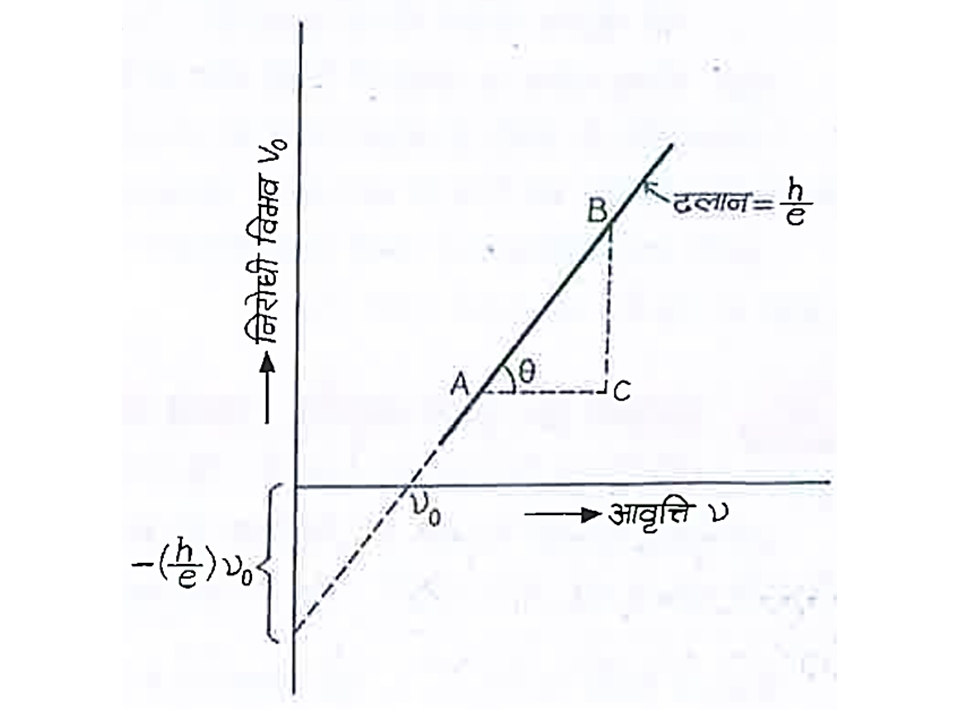
अब आइन्स्टाइन की प्रकाश वैद्युत समीकरण के अनुसार,
चूँकि निरोधी विभव द्वारा अधिकतम ऊर्जा के प्रकाश वैद्युत इलेक्ट्रॉन रुकते है। अतः
समीकरण (1) व (2) से,
Vo=(he)ν−(he)νo .......(3)
इसमें h तथा e नियतांक है तथा νo दी हुई सतह के लिए देहली आवृत्ति है। समीकरण (3) यह प्रदर्शित करती है की यदि निरोधी विभव Vo तथा प्रकाश की आवृत्ति ν में ग्राफ खींचा जाये, तो यह एक सरल रेखा होगी।
समीकरण (3) के अनुसार, सरल रेखा का ढलान he है। इस प्रकार
∴h=BCAC×e
अतः इलेक्ट्रॉनिक आवेश e का मान प्रयुक्त करने पर प्लांक नियतांक h का मान ज्ञात कर सकते है।
महत्वपूर्ण बिंदु :-
देहली ऊर्जा या कार्य फलन :
किसी इलेक्ट्रॉन को किसी धातु की सतह से मुक्त करने के लिए जितनी न्यूनतम ऊर्जा की आवश्यकता होती है, उस न्यूनतम ऊर्जा के मान को देहली ऊर्जा अथवा कार्यफलन कहते है।
माना किसी इलेक्ट्रॉन का कार्यफलन का मान ϕ है तो इसे निम्न सूत्र द्वारा प्रदर्शित किया जाता है
यहाँ h = प्लांक नियतांक है तथा ν0 = देहली आवृत्ति है।
यदि देहली तरंग दैर्ध्य का मान λ0 है तो देहली ऊर्जा अथवा कार्य फलन का मान निम्न सूत्र द्वारा दिया जाता है
ϕ=hcλ0
यहाँ c = प्रकाश का वेग है जिसका मान 3×108ms होता है।देहली आवृत्ति :
किसी धातु पर आपतित प्रकाश या विकिरण की न्यूनतम वह आवृत्ति जो जब धातु के किसी इलेक्ट्रॉन पर गिरता है तो वह इलेक्ट्रॉन धातु की सतह से मुक्त हो जाता है। अर्थात धातु की सतह से किसी इलेक्ट्रॉन को मुक्त कराने के लिए न्यूनतम वह आवृत्ति का विकिरण जो इलेक्ट्रॉन को मुक्त करवाने में आवश्यक हो विकिरण की उस आवश्यक आवृति को देहली आवृति कहते है।
कार्यफलन
ϕ=hν0
यहाँ ν0 = देहली आवृत्ति है।देहली तरंग दैर्ध्य :
किसी धातु की सतह से आपतित विकिरण की वह अधिकतम तरंग दैर्ध्य, जो जब धातु पर गिरती है तो धातु से इलेक्ट्रॉन मुक्त या उत्सर्जित हो जाता है, विकिरण या प्रकाश की उस अधिकतम तरंग दैर्ध्य के मान को देहली तरंग दैर्ध्य कहा जाता है।
इसे λ0 से प्रदर्शित किया जाता है। कार्यफलन
ϕ=hcλ0
यहाँ λ0 = देहली तरंगदैर्ध्य है।आपतित प्रकाश की आवृत्ति के साथ निरोधी विभव का विचरण
मिलिकन ने विभिन्न आवृत्तिओ के प्रकाश सुग्राही तलों पर डालकर, निरोधी विभव Vo तथा प्रकाश की आवृत्ति ν में ग्राफ खींचा। यह ग्राफ एक सरल रेखा में है।

अब आइन्स्टाइन की प्रकाश वैद्युत समीकरण के अनुसार,
चूँकि निरोधी विभव द्वारा अधिकतम ऊर्जा के प्रकाश वैद्युत इलेक्ट्रॉन रुकते है। अतः
समीकरण (1) व (2) से,
Vo=(he)ν−(he)νo .......(3)
इसमें h तथा e नियतांक है तथा νo दी हुई सतह के लिए देहली आवृत्ति है। समीकरण (3) यह प्रदर्शित करती है की यदि निरोधी विभव Vo तथा प्रकाश की आवृत्ति ν में ग्राफ खींचा जाये, तो यह एक सरल रेखा होगी।
समीकरण (3) के अनुसार, सरल रेखा का ढलान he है। इस प्रकार
∴h=BCAC×e
अतः इलेक्ट्रॉनिक आवेश e का मान प्रयुक्त करने पर प्लांक नियतांक h का मान ज्ञात कर सकते है।
महत्वपूर्ण बिंदु :-
देहली ऊर्जा या कार्य फलन :
किसी इलेक्ट्रॉन को किसी धातु की सतह से मुक्त करने के लिए जितनी न्यूनतम ऊर्जा की आवश्यकता होती है, उस न्यूनतम ऊर्जा के मान को देहली ऊर्जा अथवा कार्यफलन कहते है।
माना किसी इलेक्ट्रॉन का कार्यफलन का मान ϕ है तो इसे निम्न सूत्र द्वारा प्रदर्शित किया जाता है
यहाँ h = प्लांक नियतांक है तथा ν0 = देहली आवृत्ति है।
यदि देहली तरंग दैर्ध्य का मान λ0 है तो देहली ऊर्जा अथवा कार्य फलन का मान निम्न सूत्र द्वारा दिया जाता है
ϕ=hcλ0
यहाँ c = प्रकाश का वेग है जिसका मान 3×108ms होता है।देहली आवृत्ति :
किसी धातु पर आपतित प्रकाश या विकिरण की न्यूनतम वह आवृत्ति जो जब धातु के किसी इलेक्ट्रॉन पर गिरता है तो वह इलेक्ट्रॉन धातु की सतह से मुक्त हो जाता है। अर्थात धातु की सतह से किसी इलेक्ट्रॉन को मुक्त कराने के लिए न्यूनतम वह आवृत्ति का विकिरण जो इलेक्ट्रॉन को मुक्त करवाने में आवश्यक हो विकिरण की उस आवश्यक आवृति को देहली आवृति कहते है।
कार्यफलन
ϕ=hν0
यहाँ ν0 = देहली आवृत्ति है।देहली तरंग दैर्ध्य :
किसी धातु की सतह से आपतित विकिरण की वह अधिकतम तरंग दैर्ध्य, जो जब धातु पर गिरती है तो धातु से इलेक्ट्रॉन मुक्त या उत्सर्जित हो जाता है, विकिरण या प्रकाश की उस अधिकतम तरंग दैर्ध्य के मान को देहली तरंग दैर्ध्य कहा जाता है।
इसे λ0 से प्रदर्शित किया जाता है। कार्यफलन
ϕ=hcλ0
यहाँ λ0 = देहली तरंगदैर्ध्य है।फोटॉन के महत्त्वपूर्ण अभिलक्षण
- विकिरण के द्रव्य के साथ अन्योन्य क्रिया में, विकिरण इस प्रकार व्यवहार करता है मानो यह ऐसे कणो से बना हो, जिन्हे फोटॉन कहते है।
- प्रत्येक फोटॉन की ऊर्जा E=hν होती है और संवेग P=hνc तथा चाल c होती है। जहां c प्रकाश की चाल है।
- समान तरंगदैर्घ्य λ अथवा आवृत्ति ν के संगत उत्सर्जित सभी फोटॉनों की ऊर्जा समान {E=hcλ अथवा E=hν} होती है।
- एक ही स्त्रोत से उत्सर्जित सभी फोटॉनों का निर्वात में वेग समान (3×108 मी/से) होता है।
- फोटॉन का विराम द्रव्यमान mo शून्य होता है।
- फोटॉन का द्रव्यमान उसकी गति के कारण होता है। माना ν आवृत्ति अथवा λ तरंगदैर्घ्य का कोई फोटॉन प्रकाश के वेग c से गतिशील है तब उसका गतिज द्रव्यमान,
m=hνc2 अतः फोटॉन का संवेग
[∴E=hν व E=mc2]
m=hcλ
[∴ν=cλ]p=mc=hcλ×c=hλ - फोटॉन विद्युत उदासीन होते है और विद्युत तथा चुंबकीय क्षेत्रों के द्वारा विक्षेपित नहीं होते है।
- फोटॉन-कण संघट्ट में कुल ऊर्जा तथा कुल संवेग संरक्षित रहते है। तथापि, किसी संघट्ट में फोटॉनों की संख्या भी संरक्षित नहीं रह सकती है। फोटॉन अवशोषित हो सकता है अथवा एक नया फोटॉन सृजित हो सकता है।
फोटॉन के महत्त्वपूर्ण अभिलक्षण
- विकिरण के द्रव्य के साथ अन्योन्य क्रिया में, विकिरण इस प्रकार व्यवहार करता है मानो यह ऐसे कणो से बना हो, जिन्हे फोटॉन कहते है।
- प्रत्येक फोटॉन की ऊर्जा E=hν होती है और संवेग P=hνc तथा चाल c होती है। जहां c प्रकाश की चाल है।
- समान तरंगदैर्घ्य λ अथवा आवृत्ति ν के संगत उत्सर्जित सभी फोटॉनों की ऊर्जा समान {E=hcλ अथवा E=hν} होती है।
- एक ही स्त्रोत से उत्सर्जित सभी फोटॉनों का निर्वात में वेग समान (3×108 मी/से) होता है।
- फोटॉन का विराम द्रव्यमान mo शून्य होता है।
- फोटॉन का द्रव्यमान उसकी गति के कारण होता है। माना ν आवृत्ति अथवा λ तरंगदैर्घ्य का कोई फोटॉन प्रकाश के वेग c से गतिशील है तब उसका गतिज द्रव्यमान,
m=hνc2 अतः फोटॉन का संवेग
[∴E=hν व E=mc2]
m=hcλ
[∴ν=cλ]p=mc=hcλ×c=hλ - फोटॉन विद्युत उदासीन होते है और विद्युत तथा चुंबकीय क्षेत्रों के द्वारा विक्षेपित नहीं होते है।
- फोटॉन-कण संघट्ट में कुल ऊर्जा तथा कुल संवेग संरक्षित रहते है। तथापि, किसी संघट्ट में फोटॉनों की संख्या भी संरक्षित नहीं रह सकती है। फोटॉन अवशोषित हो सकता है अथवा एक नया फोटॉन सृजित हो सकता है।
उदाहरण 4
4.9 eV ऊर्जा का प्रकाश क्वान्टा जब एक 4.5 eV कार्यफलन वाली धातु की सतह पर आपतित होता है तो प्रकाश इलेक्ट्रॉनों का उत्सर्जन होता है। धातु की सतह को स्थानान्तरित वह अधिकतम आवेग ज्ञात कीजिए जब प्रत्येक इलेक्ट्रॉन बाहर निकल जाता है।
प्रश्नानुसार दिया गया है -
- hν=4.9eV,ϕ0=4.5eV
- Kmax=12mv2max=hv−ϕ0
Kmax=4.9−4.5=0.4eV
∴ आवेग
- (p2−p1)=mv−(−Ec)=mv+E/c
- अधिकतम आवेग =√2meKmax+Eec
⇒√2×0.4×1.6×10−19×9.1×10−31
+4.9×1.6×10−193×108
⇒3.43×10−25 kg m/s.
उदाहरण 4
4.9 eV ऊर्जा का प्रकाश क्वान्टा जब एक 4.5 eV कार्यफलन वाली धातु की सतह पर आपतित होता है तो प्रकाश इलेक्ट्रॉनों का उत्सर्जन होता है। धातु की सतह को स्थानान्तरित वह अधिकतम आवेग ज्ञात कीजिए जब प्रत्येक इलेक्ट्रॉन बाहर निकल जाता है।
प्रश्नानुसार दिया गया है -
- hν=4.9eV,ϕ0=4.5eV
- Kmax=12mv2max=hv−ϕ0
Kmax=4.9−4.5=0.4eV
∴ आवेग
- (p2−p1)=mv−(−Ec)=mv+E/c
- अधिकतम आवेग =√2meKmax+Eec
⇒√2×0.4×1.6×10−19×9.1×10−31
+4.9×1.6×10−193×108
⇒3.43×10−25 kg m/s.
उदाहरण 5
1.7 eV कार्यफलन वाली धातु से उत्सर्जन फोटो इलेक्ट्रॉनों के लिए निरोधी विभव 10.4 eV है साथ ही हाइड्रोजन परमाणु में उन ऊर्जा स्तरों को बताइये जो यह तरंगदैर्ध्य उत्सर्जित कर सकते है।
प्रश्नानुसार दिया गया है -
- eV0=10.4eV,ϕ0=1.7eV
- hv=KEmax+ϕ0=eV0+ϕ0
hν=10.4eV+1.7eV=12.1eV
- λ=hcE=1240012.1eVeV−Å
λ=1024Å
- ΔE=13.6(1n22−1n21)
ΔE=13.6(112−132)
ΔE=12.1eV
उदाहरण 5
1.7 eV कार्यफलन वाली धातु से उत्सर्जन फोटो इलेक्ट्रॉनों के लिए निरोधी विभव 10.4 eV है साथ ही हाइड्रोजन परमाणु में उन ऊर्जा स्तरों को बताइये जो यह तरंगदैर्ध्य उत्सर्जित कर सकते है।
प्रश्नानुसार दिया गया है -
- eV0=10.4eV,ϕ0=1.7eV
- hv=KEmax+ϕ0=eV0+ϕ0
hν=10.4eV+1.7eV=12.1eV
- λ=hcE=1240012.1eVeV−Å
λ=1024Å
- ΔE=13.6(1n22−1n21)
ΔE=13.6(112−132)
ΔE=12.1eV
उदाहरण 6
जब एक बेरियम उत्सर्जक पर 3300 Å तरंगदैर्ध्य का प्रकाश आपतित होता है तो अधिकतम ऊर्जा के फोटो - इलेक्ट्रॉनों को 50 cm त्रिज्या के वृत्त में डालने के लिए आवश्यक चुम्बकीय क्षेत्र की सामर्थ्य 6.7×10−6T होती है। इन आंकड़ों से फोटो - इलेक्ट्रॉनों के आवेश का क्या मान प्राप्त होता है ? (दिया गया है : बेरियम का कार्य फलन = 2.5 eV , इलेक्ट्रॉन के द्रव्यमान =9×10−31kg)
प्रकाश इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा
- 12mv2max=hcλ−ϕ
- vmax=√2m(hcλ−ϕ)
= ⎷29×10−31(6.6×10−34×3×1083300×10−10−2.5×1.6×10−19)
vmax=√49×1012=23×106ms−1
- Bevmax=Mv2maxRmax⇒e=MvmaxBRmax
- e=9×10−31×23×1066.7×10−6×0.5
e≈1.6×10−19C
उदाहरण 6
जब एक बेरियम उत्सर्जक पर 3300 Å तरंगदैर्ध्य का प्रकाश आपतित होता है तो अधिकतम ऊर्जा के फोटो - इलेक्ट्रॉनों को 50 cm त्रिज्या के वृत्त में डालने के लिए आवश्यक चुम्बकीय क्षेत्र की सामर्थ्य 6.7×10−6T होती है। इन आंकड़ों से फोटो - इलेक्ट्रॉनों के आवेश का क्या मान प्राप्त होता है ? (दिया गया है : बेरियम का कार्य फलन = 2.5 eV , इलेक्ट्रॉन के द्रव्यमान =9×10−31kg)
प्रकाश इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा
- 12mv2max=hcλ−ϕ
- vmax=√2m(hcλ−ϕ)
= ⎷29×10−31(6.6×10−34×3×1083300×10−10−2.5×1.6×10−19)
vmax=√49×1012=23×106ms−1
- Bevmax=Mv2maxRmax⇒e=MvmaxBRmax
- e=9×10−31×23×1066.7×10−6×0.5
e≈1.6×10−19C
उदाहरण 7
निरोधी विभव तथा आपतित विकिरण की आवृत्ति के बीच में ग्रॉफ चित्र में प्रदर्शित है। गणना कीजिए।
(i) प्लान्क नियतांक
(ii) कार्य फलन
प्रश्नानुसार दिया गया है -
- ν=5×1014,ν0=1×1014,V=1.656eV
- eV0=hv−hv0
h=eV0(v−v0)
h=1.6×10−19×1.656(5−1)×1014
h=1.6×1.6564×10−33
h=6.624×10−34J−s
- ϕ0=hv0
ϕ0=6.624×10−34×1×1014
ϕ0=6.624×1020J
ϕ0=6.624×10−201.6×10−19eV
ϕ0=0.414eV
उदाहरण 7
निरोधी विभव तथा आपतित विकिरण की आवृत्ति के बीच में ग्रॉफ चित्र में प्रदर्शित है। गणना कीजिए।
(i) प्लान्क नियतांक
(ii) कार्य फलन
प्रश्नानुसार दिया गया है -
- ν=5×1014,ν0=1×1014,V=1.656eV
- eV0=hv−hv0
h=eV0(v−v0)
h=1.6×10−19×1.656(5−1)×1014
h=1.6×1.6564×10−33
h=6.624×10−34J−s
- ϕ0=hv0
ϕ0=6.624×10−34×1×1014
ϕ0=6.624×1020J
ϕ0=6.624×10−201.6×10−19eV
ϕ0=0.414eV
प्रकाश-वैद्युत सेल
प्रकाश सेल, प्रकाश वैद्युत प्रभाव की घटना का एक व्यवहारिक अनुप्रयोग है। इसकी सहायता से प्रकाश ऊर्जा को विद्युत ऊर्जा में बदला जाता है।
संरचना : प्रकाश विद्युत सेल में काँच की एक बन्द निर्वातित नली में ऐनोड एवं उपयुक्त धातु (सीजियम) का एक अवतल आकार का कैथोड होता है।
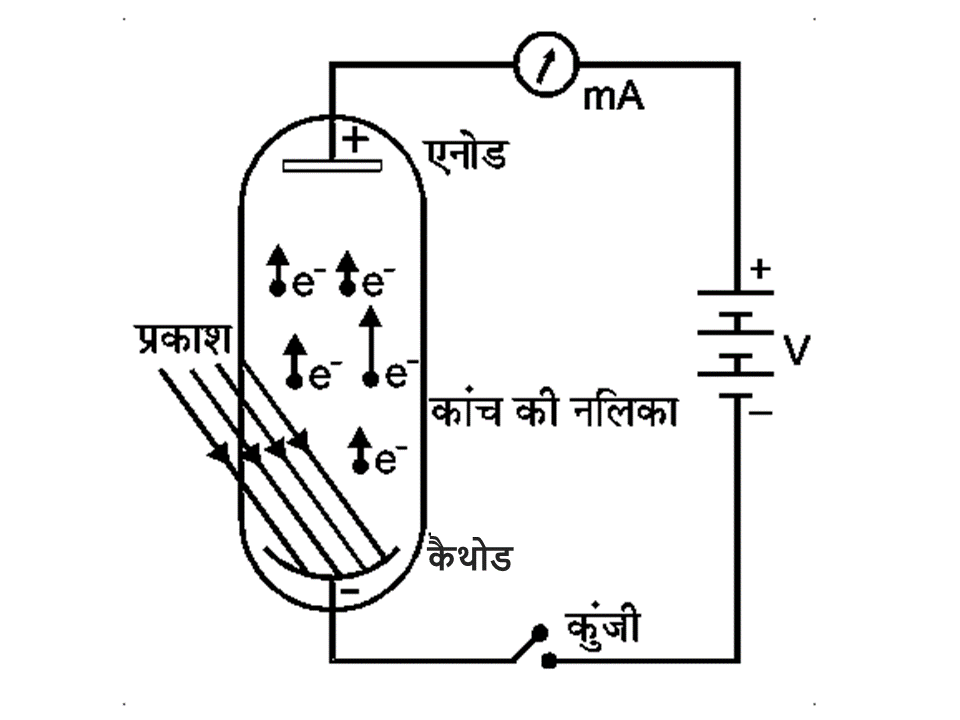
कार्य : जब आपतित प्रकाश की आवृत्ति कैथोड के पदार्थ की देहली आवृत्ति से अधिक होती है, तो प्रकाश को कैथोड पर आपतित करने से फोटो इलेक्ट्रॉन का उत्सर्जन होता है एवं ये फोटो इलेक्ट्रॉन ऐनोड पर एकत्रित होते हैं एवं बाहरी परिपथ में धारा का प्रवाह शुरू हो जाता है। प्रकाश की तीव्रता बढ़ाने पर धारा बढ़ती है। जब कैथोड पर प्रकाश डालना बन्द कर देते हैं तो धारा का प्रवाह रूक जाता है।
प्रकाश वैद्युत सेल का उपयोग :
- सड़कों पर बत्तियों के स्वचालित स्विचों में।
- टेलीविजन में
- स्वत: चलित दरवाजों में।
- चोर सूचक घण्टी में
- सिनेमा में ध्वनि पुनरुत्पादन में
प्रकाश-वैद्युत सेल
प्रकाश सेल, प्रकाश वैद्युत प्रभाव की घटना का एक व्यवहारिक अनुप्रयोग है। इसकी सहायता से प्रकाश ऊर्जा को विद्युत ऊर्जा में बदला जाता है।
संरचना : प्रकाश विद्युत सेल में काँच की एक बन्द निर्वातित नली में ऐनोड एवं उपयुक्त धातु (सीजियम) का एक अवतल आकार का कैथोड होता है।

कार्य : जब आपतित प्रकाश की आवृत्ति कैथोड के पदार्थ की देहली आवृत्ति से अधिक होती है, तो प्रकाश को कैथोड पर आपतित करने से फोटो इलेक्ट्रॉन का उत्सर्जन होता है एवं ये फोटो इलेक्ट्रॉन ऐनोड पर एकत्रित होते हैं एवं बाहरी परिपथ में धारा का प्रवाह शुरू हो जाता है। प्रकाश की तीव्रता बढ़ाने पर धारा बढ़ती है। जब कैथोड पर प्रकाश डालना बन्द कर देते हैं तो धारा का प्रवाह रूक जाता है।
प्रकाश वैद्युत सेल का उपयोग :
- सड़कों पर बत्तियों के स्वचालित स्विचों में।
- टेलीविजन में
- स्वत: चलित दरवाजों में।
- चोर सूचक घण्टी में
- सिनेमा में ध्वनि पुनरुत्पादन में
द्रव्य तरंगे अथवा डी-ब्रॉग्ली तरंग
सन 1924 में फ्रांसीसी वैज्ञानिक लुइस डी-ब्रॉग्ली (Louis de−Broglie) ने यह तर्क दिया की-
"गतिशील कण सदैव एक तरंग सम्बद्ध होते है अर्थात कणो की गति के साथ सदैव तरंग विद्यमान होती है अर्थात फोटॉन में तरंग के गुण भी विद्यमान होते है।" डी-ब्रॉग्ली की इस अवधारणा को द्रव्य की द्वैत-प्रकृति कहते है।
द्वैत-प्रकृति न केवल प्रकाश में होती है बल्कि द्रव्य कणों में भी होती है। डी-ब्रॉग्ली ने बताया की जब भी कोई द्रव्य कण जैसे- इलेक्ट्रॉन, फोटॉन गतिशील होता है, तो वह सदैव तरंग की भाँति व्यवहार करता है। द्रव्य कणों से सम्बद्ध इन तरंगो को द्रव्य तरंगे अथवा डी-ब्रॉग्ली तरंगे कहते है। इनकी तरंगदैर्घ्य को डी-ब्रॉग्ली तरंगदैर्घ्य कहते है।
डी-ब्रॉग्ली तरंग के लिए व्यंजक :
प्रकाश के क्वाण्टम सिद्धांत के अनुसार, आवृत्ति ν की प्रकाश तरंग के साथ सम्बद्ध फोटॉन की ऊर्जा
जहां h प्लांक नियतांक है। यदि फोटॉन को द्रव्यमान m का एक कण मान लिया जाये, तो आइन्स्टाइन के सापेक्षता के विशिष्ट सिद्धांत के अनुसार, फोटॉन की ऊर्जा
जहां c निर्वात में प्रकाश की चाल है। इन दोनों समीकरणों से
अतः
चूँकि फोटॉन प्रकाश की चाल c से चलता है। अतः फोटॉन का संवेग
परन्तु ν=cλ, जहाँ λ प्रकाश की तरंगदैर्घ्य है। अतः
अथवा
फोटॉन से सम्बद्ध तरंगदैर्घ्य, λ=hp
इस प्रकार, फोटॉन से सम्बद्ध तरंगदैर्घ्य का मान hp होता है।
विभिन्न परिस्थितियाँ :
- यदि द्रव्यमान m का कण वेग v से गतिमान है, तो कण का संवेग p=mv तब कण से सम्बद्ध तरंग की डी-ब्रॉग्ली तरंगदैर्घ्य
λ=hmv ....(a) - यदि द्रव्यमान m के कण की गतिज ऊर्जा K है, तो
K=12mv2⇒v=√2Km
तब कण का संवेग- p=mv=m√2Km=√2mK
अतः कण से सम्बद्ध तरंग की तरंगदैर्घ्यλ=h√2mK .....(b) - यदि आवेश से आवेशित कण को विभवान्तर V वोल्ट पर त्वरित किया जाए, तब इलेक्ट्रॉन द्वारा अर्जित की गतिज ऊर्जा
- K=eV
जहाँ e इलेक्ट्रॉन का आवेश है। तब आवेशित कण से सम्बद्ध तरंग की तरंगदैर्घ्य
h,m तथा e के ज्ञात मान रखने पर,λ=h√2meV .......(c) λ=6.63×10−34Js√2×(9.1×10−31kg)×(1.6×10−19K)×(V)
λ=√150V×10−10 मीटर
λ=12.27×10−10m√V
λ=12.27√VÅλ=1.227√Vnm .....(d)
डी-ब्रॉग्ली परिकल्पना से प्राप्त निष्कर्ष :
डी-ब्रॉग्ली परिकल्पना के अनुसार वेग v से गतिमान द्रव्यमान m के कण के साथ सम्बद्ध तरंग की तरंगदैर्घ्य λ=hmv
- यदि v=0 तो λ=∞ तथा यदि v=∞ तो λ=0
इससे निष्कर्ष निकलता है कि किसी भी पदार्थिक कण से तरंग केवल तभी सम्बद्ध होती है जबकि वह गतिमान होता है। कण आवेशित हो या अनावेशित, यदि वह गतिमान है तो उससे तरंग अवश्य ही सम्बद्ध होगी। अतः डी-ब्रॉग्ली तरंगें, विद्युत्-चुम्बकीय तरंगें नहीं होती हैं क्योंकि विद्युत्-चुम्बकीय तरंगें केवल त्वरित आवेशित कणों से ही उत्पन्न होती है। - चूँकि एक तरंग की स्थिति यर्थाथता से नहीं बतायी जा सकती है, अत: गतिमान द्रव्य कण से सम्बद्ध तरंग की तरंगदैर्घ्य, उस कण के पाये जाने की अधिकतम अनिश्चितता बताती है। चित्र में इसे दर्शाया गया है।
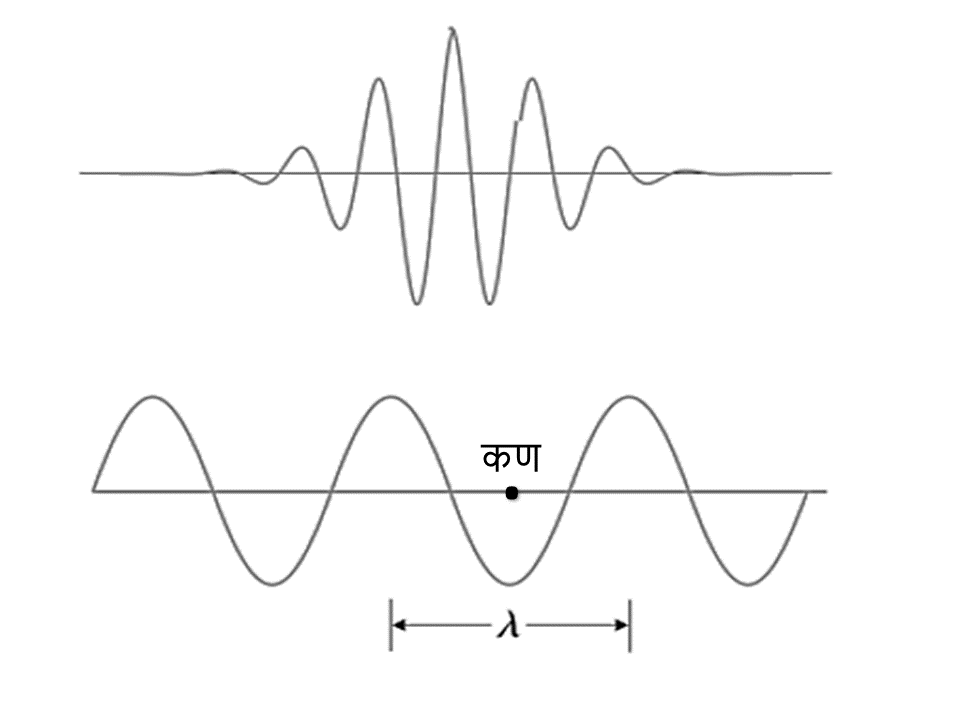
- द्रव्य की तरंग प्रकृति हमारे दैनिक जीवन के प्रेक्षणों में नहीं दिखाई देती है। इसका कारण यह है कि दैनिक जीवन में हम ऐसे पिण्डों से सम्बन्धित घटनाओं का प्रेक्षण करते हैं जिनसे सम्बद्ध डी-ब्रॉग्ली तरंग की तरंगदैर्घ्य बहुत छोटी होती है।
द्रव्य तरंगे अथवा डी-ब्रॉग्ली तरंग
सन 1924 में फ्रांसीसी वैज्ञानिक लुइस डी-ब्रॉग्ली (Louis de−Broglie) ने यह तर्क दिया की-
"गतिशील कण सदैव एक तरंग सम्बद्ध होते है अर्थात कणो की गति के साथ सदैव तरंग विद्यमान होती है अर्थात फोटॉन में तरंग के गुण भी विद्यमान होते है।" डी-ब्रॉग्ली की इस अवधारणा को द्रव्य की द्वैत-प्रकृति कहते है।
द्वैत-प्रकृति न केवल प्रकाश में होती है बल्कि द्रव्य कणों में भी होती है। डी-ब्रॉग्ली ने बताया की जब भी कोई द्रव्य कण जैसे- इलेक्ट्रॉन, फोटॉन गतिशील होता है, तो वह सदैव तरंग की भाँति व्यवहार करता है। द्रव्य कणों से सम्बद्ध इन तरंगो को द्रव्य तरंगे अथवा डी-ब्रॉग्ली तरंगे कहते है। इनकी तरंगदैर्घ्य को डी-ब्रॉग्ली तरंगदैर्घ्य कहते है।
डी-ब्रॉग्ली तरंग के लिए व्यंजक :
प्रकाश के क्वाण्टम सिद्धांत के अनुसार, आवृत्ति ν की प्रकाश तरंग के साथ सम्बद्ध फोटॉन की ऊर्जा
जहां h प्लांक नियतांक है। यदि फोटॉन को द्रव्यमान m का एक कण मान लिया जाये, तो आइन्स्टाइन के सापेक्षता के विशिष्ट सिद्धांत के अनुसार, फोटॉन की ऊर्जा
जहां c निर्वात में प्रकाश की चाल है। इन दोनों समीकरणों से
अतः
चूँकि फोटॉन प्रकाश की चाल c से चलता है। अतः फोटॉन का संवेग
परन्तु ν=cλ, जहाँ λ प्रकाश की तरंगदैर्घ्य है। अतः
अथवा
फोटॉन से सम्बद्ध तरंगदैर्घ्य, λ=hp
इस प्रकार, फोटॉन से सम्बद्ध तरंगदैर्घ्य का मान hp होता है।
विभिन्न परिस्थितियाँ :
- यदि द्रव्यमान m का कण वेग v से गतिमान है, तो कण का संवेग p=mv तब कण से सम्बद्ध तरंग की डी-ब्रॉग्ली तरंगदैर्घ्य
λ=hmv ....(a) - यदि द्रव्यमान m के कण की गतिज ऊर्जा K है, तो
K=12mv2⇒v=√2Km
तब कण का संवेग- p=mv=m√2Km=√2mK
अतः कण से सम्बद्ध तरंग की तरंगदैर्घ्यλ=h√2mK .....(b) - यदि आवेश से आवेशित कण को विभवान्तर V वोल्ट पर त्वरित किया जाए, तब इलेक्ट्रॉन द्वारा अर्जित की गतिज ऊर्जा
- K=eV
जहाँ e इलेक्ट्रॉन का आवेश है। तब आवेशित कण से सम्बद्ध तरंग की तरंगदैर्घ्य
h,m तथा e के ज्ञात मान रखने पर,λ=h√2meV .......(c) λ=6.63×10−34Js√2×(9.1×10−31kg)×(1.6×10−19K)×(V)
λ=√150V×10−10 मीटर
λ=12.27×10−10m√V
λ=12.27√VÅλ=1.227√Vnm .....(d)
डी-ब्रॉग्ली परिकल्पना से प्राप्त निष्कर्ष :
डी-ब्रॉग्ली परिकल्पना के अनुसार वेग v से गतिमान द्रव्यमान m के कण के साथ सम्बद्ध तरंग की तरंगदैर्घ्य λ=hmv
- यदि v=0 तो λ=∞ तथा यदि v=∞ तो λ=0
इससे निष्कर्ष निकलता है कि किसी भी पदार्थिक कण से तरंग केवल तभी सम्बद्ध होती है जबकि वह गतिमान होता है। कण आवेशित हो या अनावेशित, यदि वह गतिमान है तो उससे तरंग अवश्य ही सम्बद्ध होगी। अतः डी-ब्रॉग्ली तरंगें, विद्युत्-चुम्बकीय तरंगें नहीं होती हैं क्योंकि विद्युत्-चुम्बकीय तरंगें केवल त्वरित आवेशित कणों से ही उत्पन्न होती है। - चूँकि एक तरंग की स्थिति यर्थाथता से नहीं बतायी जा सकती है, अत: गतिमान द्रव्य कण से सम्बद्ध तरंग की तरंगदैर्घ्य, उस कण के पाये जाने की अधिकतम अनिश्चितता बताती है। चित्र में इसे दर्शाया गया है।

- द्रव्य की तरंग प्रकृति हमारे दैनिक जीवन के प्रेक्षणों में नहीं दिखाई देती है। इसका कारण यह है कि दैनिक जीवन में हम ऐसे पिण्डों से सम्बन्धित घटनाओं का प्रेक्षण करते हैं जिनसे सम्बद्ध डी-ब्रॉग्ली तरंग की तरंगदैर्घ्य बहुत छोटी होती है।
डेविसन तथा ज़र्मर का प्रयोग
डेविसन और जर्मर ने द्रव्य के तरंग व्यवहार की पुष्टि की। 1924 डी ब्रॉग्ली ने द्रव्य के द्वैत प्रकृति के बारे में बताया इसके अनुसार द्रव्य गतिशील अवस्था में तरंग की तरह और स्थिर अवस्था में कण की तरह व्यवहार करता है, इलेक्ट्रॉन या द्रव्य के तरंग व्यवहार की डेविसन और जर्मर ने अपने इस प्रयोग से पुष्टि की।
प्रयोगिक व्यवस्था :
डेविसन और जर्मर के पूरे प्रयोग को एक निर्वात चेंबर में बंद रखा जाता है ताकि इस प्रयोग में इलेक्ट्रॉनों का विक्षेपण या बिखराव हो तो वे प्रयोग से बाहर न जाए और बंद चैंबर में रहे।
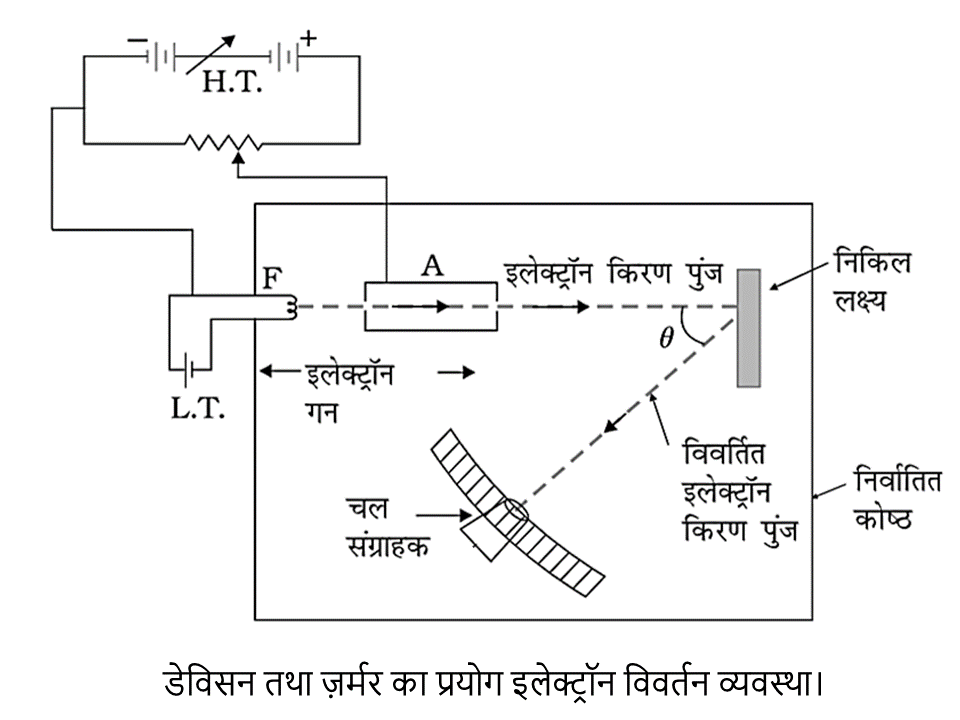
इस प्रयोग के मुख्य भाग निम्न है :-
- इलेक्ट्रॉन गन : इस भाग में एक टंगस्टन का फिलामेंट (तंतु) लगा रहता है जिसे गर्म करने पर यह इलेक्ट्रॉन का पुंज उत्सर्जित करता है, अर्थात इस भाग द्वारा इलेक्ट्रॉनों का उत्सर्जन होता है।
- स्थिर विदयुत कण त्वरक : इस भाग में दो विपरीत आवेशित प्लेट्स लगी रहती है अर्थात इस में धनात्मक तथा ऋणात्मक प्लेट लगी रहती है जो इससे जाने वाले इलेक्ट्रॉन पुंज को त्वरित कर देती है।
- समान्तरकारी छिद्र : इस भाग में सीधा एक छोटा छिद्र बना होता है, इसका कार्य होता है इलेक्ट्रॉन पुंज को सीधी रेखा में और त्वरण के साथ गति करवाना।
- लक्ष्य : लक्ष्य के लिए एक निकल क्रिस्टल की प्लेट रखी होती है जिस पर यह त्वरित इलेक्ट्रॉन पुंज आपतित होती है।
- डिटेक्टर : इलेक्ट्रॉन पुंज लक्ष्य निकल क्रिस्टल से टकराकर सीधा डिटेक्टर पर पहुंचता है, इसे आप दिखाए गए चित्र में स्पष्ट रूप से देख सकते है।
प्रायोगिक विचार या उद्देश्य :
त्वरित इलेक्ट्रॉन पुंज जब निकल क्रिस्टल पर गिरती है तो ये निकल के दो परतों द्वारा परावर्तित होती है यदि परिणाम में सुपोषी या विनाशी व्यतिकरण प्रदर्शित हो जाता है तो इसका तात्पर्य है कि कण या द्रव्य तरंगों की तरह व्यवहार करते है।
कार्यविधि :
तंतु को जब गर्म किया जाता है तो यह तंतु इलेक्ट्रॉन पुंज उत्सर्जित करता है जो त्वरक द्वारा त्वरित हो जाता है तथा समान्तरकारी छिद्र द्वारा एक सीधी रेखा के रूप में छिद्र से निकलता है और निकिल क्रिस्टल प्लेट पर टकराता है।
टकराने के बाद यह इलेक्ट्रॉन पुंज सभी दिशाओं में विवर्तित हो जाता है, विवर्तित पुंजों में एक पुंज डिटेक्टर (संसूचक) पर पहुँचती है जो एक धारामापी से जुड़ा हुआ है।
डिटेक्टर की अलग-अलग स्थिति पर इलेक्ट्रॉन पुंज की तीव्रता का मान नोट करते है और इलेक्ट्रॉन पुंज की तीव्रता व संसूचक (डिटेक्टर) के कोण θ के मध्य ग्राफ खींचते है जो निम्न प्रकार प्राप्त होता है-
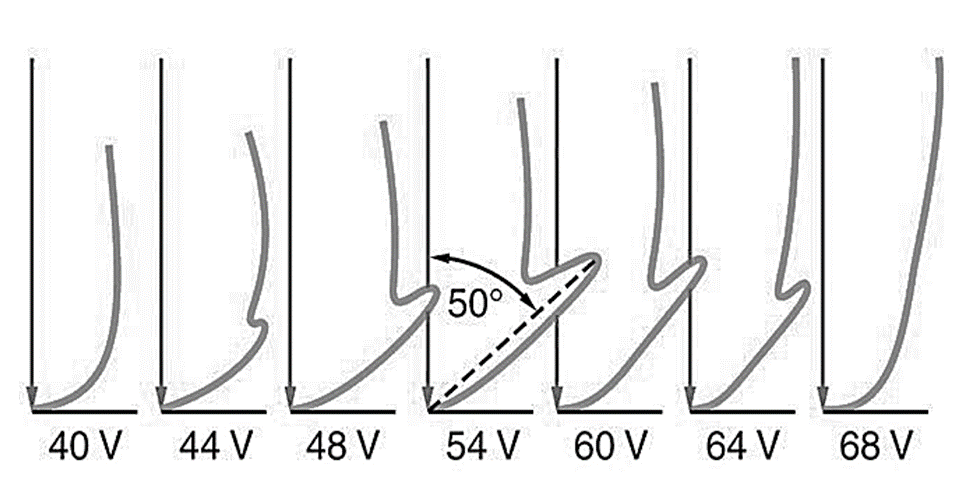
यह मान सतत प्राप्त नहीं होता है, बल्कि इस पर इसका मान अधिकतम और न्यूनतम के रूप में प्राप्त होता है।
प्रेक्षण :
विवर्तन कोण θ=50 पर शिखर प्राप्त होता है जो त्वरक विभव बढ़ाने पर पहले बढ़ता है और V=54 वोल्ट पर या शिखर सर्वाधिक हो जाता है जैसा चित्र में दिखाया गया है।
डेविसन जर्मर प्रयोग द्वारा विवर्तित कोण θ तथा उससे सम्बद्ध विभवान्तर V का मान प्राप्त होता है।
डी ब्रॉग्ली के अनुसार इलेक्ट्रॉन से सम्बद्ध तरंगदैर्घ्य-
अतः V=54V के लिए
λ=1.227√54=0.167nm
जबकि डेविसन-जर्मर विश्लेषण द्वारा ज्ञात इलेक्ट्रॉन से सम्बद्ध तरंगदैर्घ्य
अतः n = 1 ऊपर समीकरण में रखने पर
λ=0.166nm
दोनों तरंगदैर्घ्य के मान लगभग समान है अत: डी-ब्रॉग्ली की परिकल्पना सही है। और हमने ऊपर देख लिया कि कण तरंग की तरह व्यवहार करता है।
डेविसन तथा ज़र्मर का प्रयोग
डेविसन और जर्मर ने द्रव्य के तरंग व्यवहार की पुष्टि की। 1924 डी ब्रॉग्ली ने द्रव्य के द्वैत प्रकृति के बारे में बताया इसके अनुसार द्रव्य गतिशील अवस्था में तरंग की तरह और स्थिर अवस्था में कण की तरह व्यवहार करता है, इलेक्ट्रॉन या द्रव्य के तरंग व्यवहार की डेविसन और जर्मर ने अपने इस प्रयोग से पुष्टि की।
प्रयोगिक व्यवस्था :
डेविसन और जर्मर के पूरे प्रयोग को एक निर्वात चेंबर में बंद रखा जाता है ताकि इस प्रयोग में इलेक्ट्रॉनों का विक्षेपण या बिखराव हो तो वे प्रयोग से बाहर न जाए और बंद चैंबर में रहे।

इस प्रयोग के मुख्य भाग निम्न है :-
- इलेक्ट्रॉन गन : इस भाग में एक टंगस्टन का फिलामेंट (तंतु) लगा रहता है जिसे गर्म करने पर यह इलेक्ट्रॉन का पुंज उत्सर्जित करता है, अर्थात इस भाग द्वारा इलेक्ट्रॉनों का उत्सर्जन होता है।
- स्थिर विदयुत कण त्वरक : इस भाग में दो विपरीत आवेशित प्लेट्स लगी रहती है अर्थात इस में धनात्मक तथा ऋणात्मक प्लेट लगी रहती है जो इससे जाने वाले इलेक्ट्रॉन पुंज को त्वरित कर देती है।
- समान्तरकारी छिद्र : इस भाग में सीधा एक छोटा छिद्र बना होता है, इसका कार्य होता है इलेक्ट्रॉन पुंज को सीधी रेखा में और त्वरण के साथ गति करवाना।
- लक्ष्य : लक्ष्य के लिए एक निकल क्रिस्टल की प्लेट रखी होती है जिस पर यह त्वरित इलेक्ट्रॉन पुंज आपतित होती है।
- डिटेक्टर : इलेक्ट्रॉन पुंज लक्ष्य निकल क्रिस्टल से टकराकर सीधा डिटेक्टर पर पहुंचता है, इसे आप दिखाए गए चित्र में स्पष्ट रूप से देख सकते है।
प्रायोगिक विचार या उद्देश्य :
त्वरित इलेक्ट्रॉन पुंज जब निकल क्रिस्टल पर गिरती है तो ये निकल के दो परतों द्वारा परावर्तित होती है यदि परिणाम में सुपोषी या विनाशी व्यतिकरण प्रदर्शित हो जाता है तो इसका तात्पर्य है कि कण या द्रव्य तरंगों की तरह व्यवहार करते है।
कार्यविधि :
तंतु को जब गर्म किया जाता है तो यह तंतु इलेक्ट्रॉन पुंज उत्सर्जित करता है जो त्वरक द्वारा त्वरित हो जाता है तथा समान्तरकारी छिद्र द्वारा एक सीधी रेखा के रूप में छिद्र से निकलता है और निकिल क्रिस्टल प्लेट पर टकराता है।
टकराने के बाद यह इलेक्ट्रॉन पुंज सभी दिशाओं में विवर्तित हो जाता है, विवर्तित पुंजों में एक पुंज डिटेक्टर (संसूचक) पर पहुँचती है जो एक धारामापी से जुड़ा हुआ है।
डिटेक्टर की अलग-अलग स्थिति पर इलेक्ट्रॉन पुंज की तीव्रता का मान नोट करते है और इलेक्ट्रॉन पुंज की तीव्रता व संसूचक (डिटेक्टर) के कोण θ के मध्य ग्राफ खींचते है जो निम्न प्रकार प्राप्त होता है-

यह मान सतत प्राप्त नहीं होता है, बल्कि इस पर इसका मान अधिकतम और न्यूनतम के रूप में प्राप्त होता है।
प्रेक्षण :
विवर्तन कोण θ=50 पर शिखर प्राप्त होता है जो त्वरक विभव बढ़ाने पर पहले बढ़ता है और V=54 वोल्ट पर या शिखर सर्वाधिक हो जाता है जैसा चित्र में दिखाया गया है।
डेविसन जर्मर प्रयोग द्वारा विवर्तित कोण θ तथा उससे सम्बद्ध विभवान्तर V का मान प्राप्त होता है।
डी ब्रॉग्ली के अनुसार इलेक्ट्रॉन से सम्बद्ध तरंगदैर्घ्य-
अतः V=54V के लिए
λ=1.227√54=0.167nm
जबकि डेविसन-जर्मर विश्लेषण द्वारा ज्ञात इलेक्ट्रॉन से सम्बद्ध तरंगदैर्घ्य
अतः n = 1 ऊपर समीकरण में रखने पर
λ=0.166nm
दोनों तरंगदैर्घ्य के मान लगभग समान है अत: डी-ब्रॉग्ली की परिकल्पना सही है। और हमने ऊपर देख लिया कि कण तरंग की तरह व्यवहार करता है।
उदाहरण 8
यदि इलेक्ट्रॉन का संवेग Pm से परिवर्तित कर दिया जाय तो उससे सम्बद्ध दे - ब्रॉग्ली तरंगदैर्ध्य 0.50 % से परिवर्तित हो जाती है। इलेक्ट्रॉन का प्रारंभिक संवेग क्या होगा ?
प्रश्नानुसार दिया गया है -
- दे - ब्रॉग्ली तरंगदैर्ध्य = dλλ×100=0.5
dλλ=0.5100=1200
- ΔP=Pm
- p=hλ
- dpdλ=−hλ2=−hλ×1λ=−pλ
|dp|p=dλλ
- Pmp=1200
p=200Pm
उदाहरण 8
यदि इलेक्ट्रॉन का संवेग Pm से परिवर्तित कर दिया जाय तो उससे सम्बद्ध दे - ब्रॉग्ली तरंगदैर्ध्य 0.50 % से परिवर्तित हो जाती है। इलेक्ट्रॉन का प्रारंभिक संवेग क्या होगा ?
प्रश्नानुसार दिया गया है -
- दे - ब्रॉग्ली तरंगदैर्ध्य = dλλ×100=0.5
dλλ=0.5100=1200
- ΔP=Pm
- p=hλ
- dpdλ=−hλ2=−hλ×1λ=−pλ
|dp|p=dλλ
- Pmp=1200
p=200Pm
उदाहरण 9
एक ड्यूट्रोन को 500 वोल्ट विभव से त्वरित किया गया है। एकल आयनित हीलियम आयन को उतनी ही डी - ब्रॉग्ली तरंगदैर्ध्य के लिए कितने विभवान्तर से त्वरित करना होगा ?
प्रश्नानुसार दिया गया है -
- Vd=500V
- λ=h√2mqV
- V=P.d.
अतः -
- mHe×VHe=mdVd
- 4VHe=2×500
VHe=250V
उदाहरण 9
एक ड्यूट्रोन को 500 वोल्ट विभव से त्वरित किया गया है। एकल आयनित हीलियम आयन को उतनी ही डी - ब्रॉग्ली तरंगदैर्ध्य के लिए कितने विभवान्तर से त्वरित करना होगा ?
प्रश्नानुसार दिया गया है -
- Vd=500V
- λ=h√2mqV
- V=P.d.
अतः -
- mHe×VHe=mdVd
- 4VHe=2×500
VHe=250V
उदाहरण 10
एक α- कण 0.83 सेमी. त्रिज्या वाले वृत्तीय मार्ग में चुम्बकीय क्षेत्र 0.25 वेबर/ मी2 की उपस्थिति में गति करता है। तो इस कण से सम्बद्ध ब्रॉग्ली तरंगदैर्ध्य कितनी होगी ?
प्रश्नानुसार दिया गया है -
- B=0.25Wb/m2,r=0.83×10−4M
- λ=hp=hqBr
λ=6.62×10−342×11.6×10−19×0.25×83×10−4 मी.
λ=0.01Å
उदाहरण 10
एक α- कण 0.83 सेमी. त्रिज्या वाले वृत्तीय मार्ग में चुम्बकीय क्षेत्र 0.25 वेबर/ मी2 की उपस्थिति में गति करता है। तो इस कण से सम्बद्ध ब्रॉग्ली तरंगदैर्ध्य कितनी होगी ?
प्रश्नानुसार दिया गया है -
- B=0.25Wb/m2,r=0.83×10−4M
- λ=hp=hqBr
λ=6.62×10−342×11.6×10−19×0.25×83×10−4 मी.
λ=0.01Å
उदाहरण 11
कितनी गतिज ऊर्जा वाले न्यूट्रॉन के साथ 1.40×10−10 मीटर डी-ब्रॉग्ली तरंगदैर्ध्य सम्बद्ध होगी ? न्यूट्रॉन का द्रव्यमान 1.675×10−27 किग्रा (h=6.6×10−34 जूल-से)
प्रश्नानुसार दिया गया है -
- m=1.675×10−27kg,λ=1.40×10−10m
- λ=hmv
- v=hmλ
v=6.6×10−341.675×10−27×1.40×10−10ms−1
12mv2
=12×(1.675×10−27)[6.6×10−341.675×10−27×1.40×10−10]2
⇒(6.6×10−34)22×1.675×10−27×1.4×1.4×10−20
⇒6.69×10−21 जूल
उदाहरण 11
कितनी गतिज ऊर्जा वाले न्यूट्रॉन के साथ 1.40×10−10 मीटर डी-ब्रॉग्ली तरंगदैर्ध्य सम्बद्ध होगी ? न्यूट्रॉन का द्रव्यमान 1.675×10−27 किग्रा (h=6.6×10−34 जूल-से)
प्रश्नानुसार दिया गया है -
- m=1.675×10−27kg,λ=1.40×10−10m
- λ=hmv
- v=hmλ
v=6.6×10−341.675×10−27×1.40×10−10ms−1
12mv2
=12×(1.675×10−27)[6.6×10−341.675×10−27×1.40×10−10]2
⇒(6.6×10−34)22×1.675×10−27×1.4×1.4×10−20
⇒6.69×10−21 जूल
उदाहरण 12
एक इलेक्ट्रॉन तथा फ़ोटॉन को डी ब्रॉगली तरंग दैर्ध्य समान दी गई है तो सिद्ध कीजिए कि इलेक्ट्रॉन की कुल ऊर्जा फ़ोटॉन की ऊर्जा से ज्यादा है।
हम जानते है, इलेक्ट्रॉन की कुल ऊर्जा
- Ee=mc2
- λ=hmv
m=hλv
अतः फ़ोटॉन की ऊर्जा -
- EP=hcλ
- EeEP=hc2λv×λhc=cv
- Ee>EP
उदाहरण 12
एक इलेक्ट्रॉन तथा फ़ोटॉन को डी ब्रॉगली तरंग दैर्ध्य समान दी गई है तो सिद्ध कीजिए कि इलेक्ट्रॉन की कुल ऊर्जा फ़ोटॉन की ऊर्जा से ज्यादा है।
हम जानते है, इलेक्ट्रॉन की कुल ऊर्जा
- Ee=mc2
- λ=hmv
m=hλv
अतः फ़ोटॉन की ऊर्जा -
- EP=hcλ
- EeEP=hc2λv×λhc=cv
- Ee>EP
उदाहरण 13
यदि विरामावस्था में स्थित इलेक्ट्रॉन एवं प्रोटॉन को V0 विभवान्तर से त्वरित करने पर इनसे सम्बन्धित डी - ब्रॉग्ली तरंगदैर्ध्य λe एवं λp है, तो λe व λp में सम्बन्ध ज्ञात कीजिये।
हम जानते है कि, डी - ब्रॉग्ली तरंगदैर्ध्य
- λ=h√2mE=h√2mqV0
- λ∝1√m∵mp>me
- λe>λp
- ∵λ=h√2mE=h√2mqV0
- λeλp=√mpme
उदाहरण 13
यदि विरामावस्था में स्थित इलेक्ट्रॉन एवं प्रोटॉन को V0 विभवान्तर से त्वरित करने पर इनसे सम्बन्धित डी - ब्रॉग्ली तरंगदैर्ध्य λe एवं λp है, तो λe व λp में सम्बन्ध ज्ञात कीजिये।
हम जानते है कि, डी - ब्रॉग्ली तरंगदैर्ध्य
- λ=h√2mE=h√2mqV0
- λ∝1√m∵mp>me
- λe>λp
- ∵λ=h√2mE=h√2mqV0
- λeλp=√mpme
उदाहरण 14
प्रोटॉन, ड्यूट्रॉन तथा α- कण के लिए तरंगदैर्ध्य का अनुपात ज्ञात करो यदि उन्हें समान विभवान्तर से त्वरित किया जाए।
हम जानते है -
- λ=h√2mE=h√2mqV
λ∝1√mq
- λp:λd:λα=1√mpqp:1√mdqd:1√mαqα
λp:λd:λα=1√mpqp:1√2mpqp:1√4mp2qp
=1:1√2:12√2
उदाहरण 14
प्रोटॉन, ड्यूट्रॉन तथा α- कण के लिए तरंगदैर्ध्य का अनुपात ज्ञात करो यदि उन्हें समान विभवान्तर से त्वरित किया जाए।
हम जानते है -
- λ=h√2mE=h√2mqV
λ∝1√mq
- λp:λd:λα=1√mpqp:1√mdqd:1√mαqα
λp:λd:λα=1√mpqp:1√2mpqp:1√4mp2qp
=1:1√2:12√2