PROPERTIES OF TRIANGLES for Class 12 MATHS
Introduction
Hello Students, In today's class we will learn a very interesting topic which is Properties of triangles which has a good weightage in the exam of JEE.
These notes are designed keeping in mind the basics and the recent changes in the syllabus and pattern of JEE.
You can follow Doubtnut for all the videos related to JEE 2022
The triangle is a closed polygon that has three angles, three sides, and three vertices. Based upon the length of sides and measure of angles, the triangles are classified into different types of triangles. Properties of a triangle help us to identify a triangle from a given set of figures easily and quickly.
Index
Basic concepts and properties of triangles|Sin rule|Cosine and Projection formula|Trignometric ratios of half angles|Area of a triangle and Napiers analogy|m-n theorem and Appolnius theorem|Solution of triangles|Circles connected with triangle
Basic concepts and properties of triangles
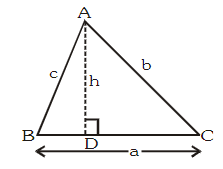
The process of calculating the sides and angles of triangle using given information is called solution of triangle. In a △ABC. the angles are denoted by capital letters A,B and C and the length of the sides opposite these angle are denoted by small letter a,b and c respectively.
In the beginning, we start from understanding the shape of triangles, their types, and properties, theorems based on them such as Pythagoras theorem, etc. Let us learn here some basic properties of triangles.
Sin rule
In any triangle ABC (asinA)=(bsinB)=(csinC)=λ=abc2△=2R
where R is circumradius and △. is area of triangle.
Example 1
If sin2(A2),sin2(B2),andsin2(C2) are in H.P., then prove that the sides of triangle are in H.P.
sin2.A2,sin2.B2,sin2.C2 are in H.P.
⇒(s−b)(s−c)bc,(s−a)(s−c)ac,(s−a)(s−b)ab are in H.P. ⇒as−a,bs−b,cs−c are in H.P
⇒s−aa,s−bb,s−cc are in A.P
⇒sa−1,sb−1,sc−1 are in A.P
So, a, b and c must be in H.P
Example 2
If A, B, C are the angles of a triangle such that sin2A+sin2B=sin2C, then
sin2A+sin2B=sin2C
⇒a2+b2=c2
⇒C=π2 and A,B<π2
Since A+B=π2∴tanAtanB=1
Also sinA>sin2A,sinB>sin2B
⇒sinA+sinB>sin2A+sin2B=sin2C=1
Example 3
In a triangle ABC, if a, b, c are in A.P. and bcsin2C+cbsin2B+basin2A+absin2B=2, then find the value of sin B
bcsin2C+cbsin2B+basin2A+absin2B=2
⇒2sinBcosC+2sinCcosB+2sinBcosA+2sinBcosB=2
⇒sin(B+C)+sin(A+B)=1
⇒sinA+sinC=1
⇒sinB=12 (As 2sinB=sinA+sinC)
Example 4
In a triangle ABC, if cosAa=cosBb=cosCc and the side a=2, then area of triangle is
cosAa=cosBb=cosCc
or cosA2RsinA=cosB2RsinB=cosC2RsinC
or tanA=tanB=tanC
Hence, triangle is equilateral.
Therefore, Area of triangle =√34a2=√3 (as a = 2)
Cosine and Projection formula
Here are the following 3 formulas of cosine
cosA=b2+c2−a22bc
cosB=a2+c2−b22ac
cosC=b2+a2−c22ab
Here are the projection formulas
bcosC+c⋅cosB=b
c⋅cosA+acosC=b
acosB+bcosA=c
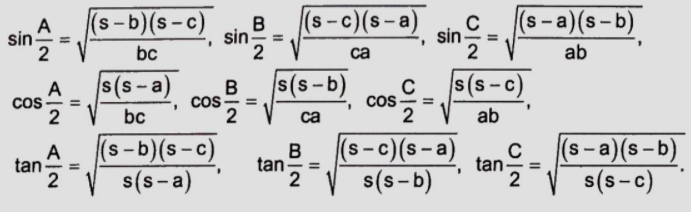
Trignometric ratios of half angles
Area of a triangle and Napiers analogy
△=12(bcsinA)=(12)casinB=(12)absinC=√s(s−a)(s—b)(s—c)=abc4R
Napier’s analogy
tan(B−C)2=b−cb+ccot(A2)
tan(C−A)2=c−ac+acot(B2)
tan(A−B)2=a−ba+bcot(C2)
m-n theorem and Appolnius theorem
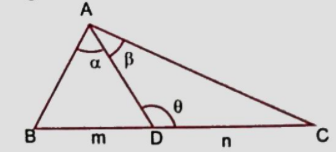
m-n theorem
If D be the point on the side BC of a triangle ABC which then with respect to mentioned figure, we have:
(m+n)cotθ=mcotα—ncotβ
(m+n)cotθ=ncotB−mcotC.
divide the side BC in the ratio m:n.
Apollonius theorem
In a triangle ABC,AD is median through A, then (AB)2+(AC)2=2(AD)2+(BD)2
Example 5
In a triangle ABC, if cosAa=cosBb=cosCc and the side a=2, then area of triangle is
cosAa=cosBb=cosCc
or cosA2RsinA=cosB2RsinB=cosC2RsinC
or tanA=tanB=tanC
Hence, triangle is equilateral.
Therefore, Area of triangle =√34a2=√3 (as a = 2)
Example 6
Prove that b2cos2A−a2cos2B=b2−a2
b2cos2A−a2cos2B
=b2(1−2sin2A)−a2(1−2sin2B)
=b2−a2−2(b2sin2B)
=b2−a2−2(b2sin2A−a2sin2B)=b2−a2 (∵asinB=bsinA)
Example 7
In any triangle ABC , prove that following : ca+b=1−tan(A2)tan(B2)1+tan(A2)tan(B2)
ca+b=2RsinC2R(sinA+sinB)=sin(A+B)sinA+sinB
=2sin.A+B2cos.A+B22sin.12(A+B)cos.12(A−B)
=cos.12(A+B)cos.12(A−B)
=cos.12Acos.12B−sin.12Asin.12Bcos.12Acos.12B+sin.12Asin.12B
=1−tan.12Atan.12B1+tan.12Atan.12B [dividing numerator and denominator by cos.12Acos.12B]
Example 8
If in ΔABC,tan.A2=56andtan.C2=25, then prove that a, b, and c are in A.P.
tan.A2=56,tan.C2=25
⇒tan.A2tan.C2=s−bs=56×25=13
or 3s−3b=s
or 2s=3b
or a+b+c=3b
or a+c=2b
Hence, a,b, c are in A.P
Solution of triangles
The three sides a,b,c and the three angles A,B,C are called the elements of the triangle ABC. When any three of these six elements (except all the three angles) of a triangle are given, the triangle is known completely that is the other three elements can be expressed in terms of the given elements and can be evaluated. This process is called the solution of triangles.
( i ) If the three sides a,b,c are given, angle A is obtained from tan(A2)=√(s−b)(s−c)s(s−a) or cosA=b2+c2—a22bc, B and C can be obtained In the similar way.
( ii ) If two sides b and c and the included angle A are given, then tan(B−C2)=b−cb+ccot(A2) gives B−C2. Also (B+C2)=90−A2 so that B and C can be evaluated. The third side is given by a=bsinAsinB
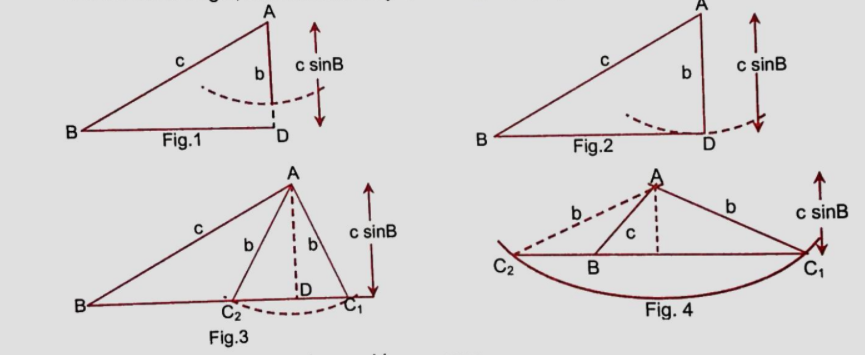
( iii ) If two sides b and c and the angle B (opposite to side b) are given, then sinC=cbsinB,A=180°—(B+C) and b = give the remaining elements. If b<csinB, there is no triangle sinB possible (Fig 1). If b=csinB and B is an acute angle. then only one triangle is possible (Fig 2). If csinB<b<c and B is an acute angle, then there are two values of angle C (Fig 3). If c<b and B is an acute angle , then there is only one triangle (Fig 4)
Example 9
If c2=a2+b2, then prove that 4s(s−a)(s−b)(s−c)=a2b2
c2=a2+b2
Triangle is right angled at vertex C. Hence,
Area of Δ=12ab
Also, Δ2=s(s−a)(s−b)(s−c)=14a2b2
or 4s(s−a)(s−b)(s−c)=a2b2
Example 10
If the sides of a triangle are in the ratio 3:7:8, then find R:r
Let a=3k,b=7k,c=8k. Then,
s=12(a+b+c)=9k
⇒Rr=abc4ΔsΔ=abcs4s(s−a)(s−b)(s−c)
=3k×7k×8k4×6k×2k×k=72
Example 11
In triangle ABC, if a = 2 and bc = 9, then prove that R=9/2Δ
Δ=12bcsinA=92sinA=92a2R=92R
⇒R=92Δ
Example 12
The sides of a triangle are in A.P. and its area is 35 th of an equilateral triangle of the same perimeter. Find the greatest angle of the triangle
Let the sides be x−d,x,x+d. Then
s=3x2,(s−a)=x2+d,
(s−b)=x2,(s−c)=x2−d.
Area of triangle =√3x2.(x2+d).x2.(x2−d)
=x2√3(x24−d2)=x4√3(x2−4d2)
The area of equilateral triangle whose perimeter is 3x is √3x24
Given, 35×√3x24=x4√3(x2−4d2)
or 925×3x416=x216×3(x2−4d2)
or x2−9x225=4d2
or 16x2=100d2
or x=52d
Therefore, the sides of triangle measure (5d2−d),5d2,(5d2+d)
or 3d2,5d2,7d2
Hence, the ratio of sides is 3:5:7
For the greatest angle,
cosθ=32+52−722×3×5=9+25−4930=−12
∴θ=1202
Circles connected with triangle
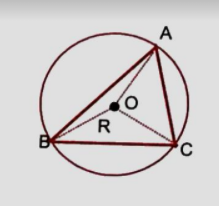
Circum-circle
The circle passing through the vertices of the triangle ABC is called the circum-circle. its radius R is called the circum-radius. In the triangle ABC,
R=a2sinA=b2sinB=c2sinC=abc4△
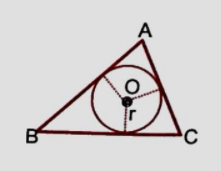
In-circle
The circle touching the three sides of the triangle Internally S called the inscribed or the in-circle of the triangle. Its radius r is called the in-radius of the circle. In the triangle ABC,
r=(△s)=(s−a)tan(A2)=(s−b)tan(B2)=(s−c)tan(C2)=4Rsin(A2)sin(B2)sin(C2)
Remark: From r=4Rsin(A2)sin(B2)sin(C2)
we find that r≤4R.18
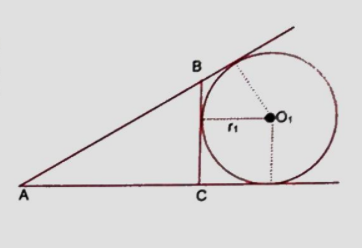
Escribed circles
The circle touching BC and the two sides AB and AC produced of △ABC externally is called the escribed circle opposite A. Its radius is denoted by r1, Similarly r2 and r3 denote the radii of the escribed circles opposite angles B and C respectively.
r1,r2,r3 are called the ex-radij of △ABC. Here △s−a=4Rsin(A2)cos(B2)cos(C2)
△s−b=4Rsin(B2)cos(C2)cos(A2)
△s−c=4Rsin(C2)cos(B2)cos(A2)
r1+r2+r3=4R+r
Example 13
Let f,gandh be the lengths of the perpendiculars from the circumcenter of ΔABC on the sides a, b, and c, respectively. Prove that af+bg+ch=14abcfgh
Distance of circumcenter from of side BC is R cosA=f
Similarly, g=RcosB,h=RcosC
⇒af+bg+ch=2RsinARcosA+2RsinBRcosB+2RsinCRcosC
=2(tanA+tanB+tanC)
Also, afbgch=8tanAtanBtanC
But in triangle, tanA+tanB+tanC=tanAtanBtanC. Thus,
af+bg+ch=14abcfgh
.
Example 14
If the sides of triangle are in the ratio 3:5:7, then prove that the minimum distance of the circumcentre from the side of triangle is half the circmradius
We have a:b:c=3:5:7
Distance of circumcentre from sides are R|cosA|,R|cosB|andR|cosC|.
So, R|cosC| is minimum
cosC=32+52−722×3×5=9+25−4930=−12
so, required minimum distance is R/2
Example 15
If the incircle of the triangle ABC passes through its circumcenter, then find the value of 4sin.A2sin.B2sin.C2
Distance between circumcenter (O) and incenter (I) is √R2−2rR
If incircle of triangle ABC passes through it's circumcenter,
√R2−2rR=r
⇒(rR)2+2(rR)−1=0
⇒rR=−2±√4+42
⇒rR=√2−1 (as rR>0)
⇒1+rR=√2
⇒4sin.A2sin.B2sin.C2=√2−1