LINEAR PROGRAMMING for Class 12 MATHS

Hello bachcho to ab hum padhne vale hai linear programming ke baare mein. Akhir hum isse kyon padhte hai aur iski kya jarurt hai hume ? Ise aapne class XI mein linear inequalities and systems of linear inequalities in two variables and their solutions by graphical method mein padha hai. To dekho agar hum ek real life situation ko case consider karte hai. Maan lo ek furniture dealer hai jo sirf do cheezo mein deal karta hai tables and chairs and he has Rs $50,000$ to invest and has storage space of at most $60$ pieces. Agar ek table ka cost Rs $2500$. aur ek chair ka cost Rs $500$ and he estimated that from the sale of one table, he can make a profit of Rs $250$ and that from the sale of one chair a profit of Rs $75$. Then he wants to know how many tables and chairs he should buy from the available money so as to maximize his total profit, assuming that he can sell all the items which he buys. Such type of problems which seek to maximize (or, minimize) profit (or loss) form a general class of problems called optimization problems. Thus, an optimization problem may involve finding maximum profit, minimum cost, or minimum use of resources etc. A special but a very important class of optimization problems is linear programming problem. The above stated optimization problem is an example of linear programming problem. Linear programming problems are of much interest because of their wide applicability in industry, commerce, management science etc. In this chapter, we shall study some linear programming problems and their solutions by graphical method only, though there are many other methods also to solve such problems.

To dekho bachcho abhi humne upar ek example liya tha furniture dealer ka jisme humne observe kiya
$\left(i\right)$ The dealer can invest his money in buying tables or chairs or combination thereof. Further he would earn different profits by following different investment strategies.
$\left(ii\right)$ There are certain overriding conditions or constraints viz., his investment is limited to a maximum of Rs $50,000$ and so is his storage space which is for a maximum of $60$ pieces.
Ab maan lo he decided to buy only tables no chairs, so he can buy $20$ tables ($50,000÷2,500$). To uska profit kitna hua i.e. Rs $(250\times 20)$ = Rs $5,000$.
Ab maan lo vo sirf agar chairs lena chahe, then he can buy 100 chairs ($50,000÷500$). Lekin vo store sirf $60$ chairs kar sakta hai to vo sirf $60$ chairs hi le sakta hai. To total profit kitna hua Rs ($60\times 75$), i.e., Rs $4500.$
Esi tarh se vo aur bhi possibilities soch sakta hai like to buy $10$ tables and $50$ chairs as he can store $60$ pieces only so the profit would be Rs ($10\times 250+50\times 75$) i.e. Rs $6250$ and so on.
We, thus, find that the dealer can invest his money in different ways and he would earn different profits by following different investment strategies.
Now the problem is : How should he invest his money in order to get maximum profit ? To answer this question, let us try to formulate the problem mathematically.

1. Linear inequations the inequalities of the form $ax+by\le c$, $ax+by<c$, $ax+by\ge c$ and $ax+by>c$ are called linear inequations.
2. Linear programming is the method used in decision making in business for obtaining the least cost and maximum profits through linear expressions subject to certain given conditions called linear constraints.

To bachcho ab tak jo humne sikha usko hume mathematically present karna hai. So let $x$ be the number of tables and $y$ be the number of chairs that the dealer buys. Obviously, $x$ and $y$ must be non-negative, i.e.,
$x\ge 0$, $y\ge 0$ (Non-negative constraints)
The dealer is constrained by the maximum amount he can invest (here it is Rs $50,000$) and by the maximum number of items he can store (here it is $60$). Stated mathematically,
$2500x+500y\le 50000$ (investment constraint)
$5x+y\le 100$
$x+y\le 60$ (storage constraint)
The dealer wants to invest in such a way so as to maximize his profit, say, $Z$ which stated as a function of $x$ and $y$ is given by
$Z=250x+75y$ (called objective function)
So, basically ab hume apna objective function mil gya so what we now need to do is, maximize the linear function $Z$ by using linear inequalities or in some problems minimize to certain conditions. Such problems are called Linear Programming Problems.

A linear function of the involved variables which we want to minimize or maximize subject to the given linear constraints is known as objective function.
1. Optimal Value : The maximum or minimum value of an objective function is known as its optimal value.
2. Feasible Solution : A set of values of the variables satisfying all constraints is known as a feasible solution.
3. Optimal Solution : A feasible solution which leads to the optimal value (maximum or minimum) of an objective function is called its optimal solution.
4. Optimization Techniques : The process of obtaining the optimal values are called optimization techniques.
5. Feasible Region : The common region determined by all the constraints and non-negativity restriction of the problem is called feasible region.

To dekho bachcho Class XI mein humne linear inequalities ko graphically represent karna sikha tha to usi tarh se ab hum linear programming ki problems ko bhi graphically solve krna sikhenge. Let us refer to the example of investment in tables and chairs. We will now solve this problem graphically. Let us graph the constraints stated as linear inequalities :
$5x+y\le 100$$...\left(1\right)$
$x+y\le 60$$...\left(2\right)$
$x\ge 0$$...\left(3\right)$
$y\ge 0$$...\left(4\right)$

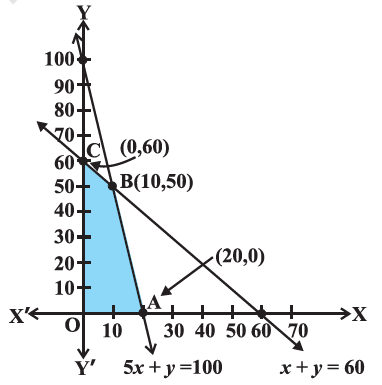
To dekho es graph ka jo shaded region hai that consists of the points common to all half planes determined by the inequalities. Each point in this region represents a feasible choice open to the dealer for investing in tables and chairs. The region, therefore, is called the feasible region for the problem. Every point of this region is called a feasible solution to the problem. Thus, we the region OABC (shaded) is the feasible region for the problem. The region other than feasible region is called an infeasible region.
Optimal (feasible) solution : Any point in the feasible region that gives the optimal value (maximum or minimum) of the objective function is called an optimal solution.
To dekho ab humne dekha har ek point feasible region OABC ka satisfy karta hai sabhi constraints ko given in $\left(1\right)$ to $\left(4\right)$, to jaisa ki yha infinitely bahut se points hai, it is not evident how we should go about finding a point that gives a maximum value of the objective function $Z=250x+75y$. So, to handle this situation, we use the following theorems which are fundamental in solving linear programming problems. The proofs of these theorems are beyond the scope of the syllabus.
Theorem 1 : Let $R$ be the feasible region (convex polygon) for a linear programming problem and let $Z=ax+by$ be the objective function. When $Z$ has an optimal value (maximum or minimum), where the variables $x$ and $y$ are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region.
Theorem 2 : Let $R$ be the feasible region for a linear programming problem, and let $Z=ax+by$ be the objective function. If $R$ is bounded, then the objective function $Z$ has both a maximum and a minimum value on $R$ and each of these occurs at a corner point (vertex) of $R$.

A corner point of a feasible region is a point in the region which is the intersection of two boundary lines.
We observe that the maximum profit to the dealer results from the investment strategy $(10,50)$, i.e. buying $10$ tables and $50$ chairs.
This method of solving linear programming problem is referred as Corner Point Method. The method comprises of the following steps :
1. Find the feasible region of the linear programming problem and determine its corner points (vertices) either by inspection or by solving the two equations of the lines intersecting at that point.
2. Evaluate the objective function $Z=ax+by$ at each corner point. Let $M$ and $m$, respectively denote the largest and smallest values of these points.
3. (i) When the feasible region is bounded, $M$ and $m$ are the maximum and minimum values of $Z$.
(ii) In case, the feasible region is unbounded, we have :
4. (a)$M$ is the maximum value of $Z$, if the open half plane determined by $ax+by>M$ has no point in common with the feasible region. Otherwise, $Z$ has no maximum value.
(b) Similarly, $m$ is the minimum value of $Z$, if the open half plane determined by $ax+by<m$ has no point in common with the feasible region. Otherwise, $Z$ has no minimum value.
We will now illustrate these steps of Corner Point Method by considering some examples :

Draw the graph of the solution set of the system of inequations $2x+3y\le 4,x\ge 0\text{and}y\ge 0.$

Consider the equations
$2x+3y=6,x+4y\le 4,x=0\text{and}y=0.$
Now, $2x+3y=63\Rightarrow \frac{x}{3}+\frac{y}{2}=1.$

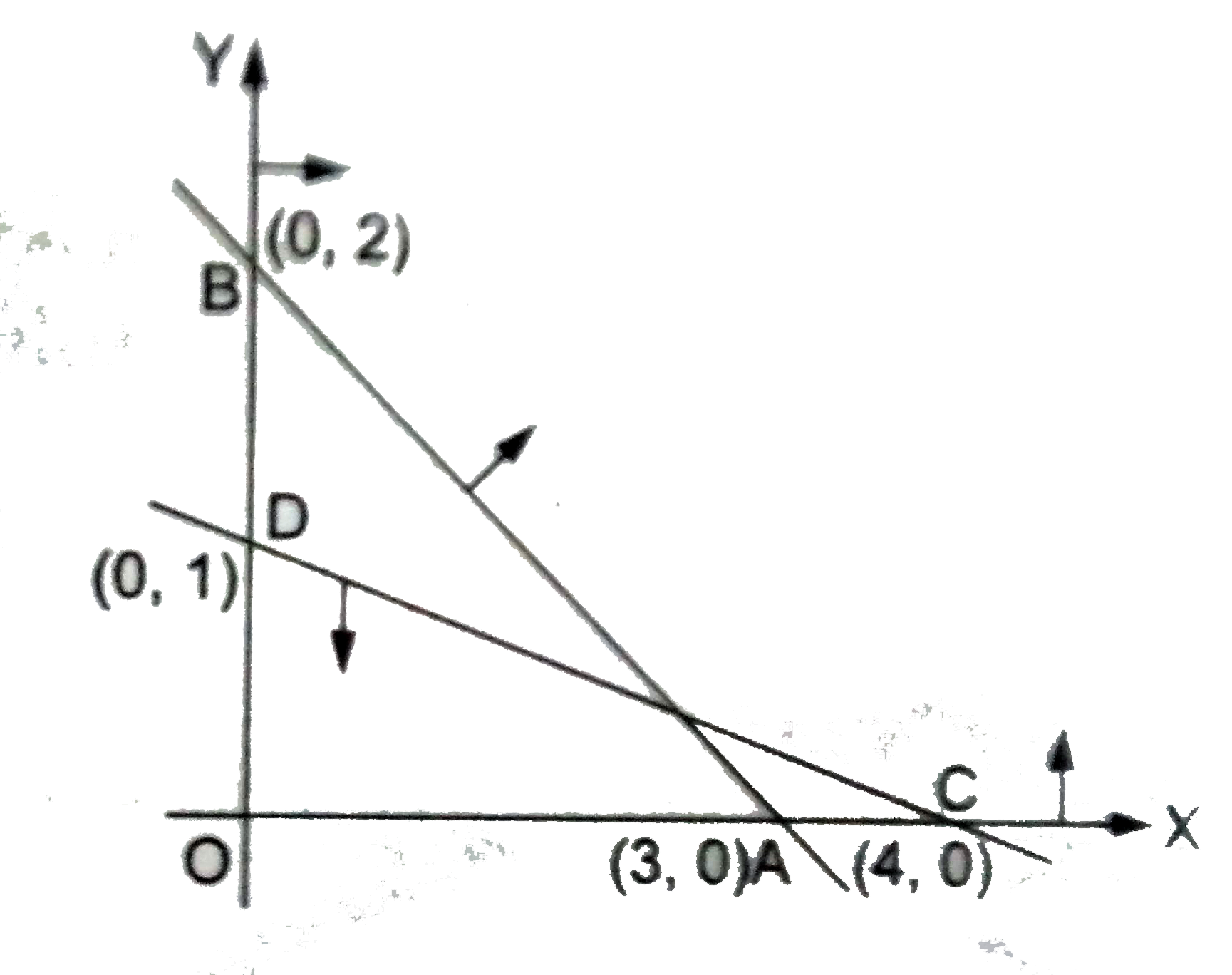
This line meets the axes at $A(3,0)\text{and}B(0,2).$ Join these points and draw a thick line. Clearly, the portion not containing $(0,0)$ represents the solution set of the inequation $2x+3y\ge 6.$ Again, $x+4y=4\Rightarrow \frac{x}{4}+\frac{y}{1}=1.$
This line meets the axes at $C(4,0)\text{and}D(0,1).$ Join these points and draw a tick line. Clearly the portion containing (0,0) represents the solution set of the inequation $x+4y\le 4.$
Clearly, $x\ge 0$ is represented by the $\text{y-axis}$ and the portion on its right-hand side.
Also, $y\ge 0$ is represented by the $\text{x-axis}$ and the portion above the $\text{x-axis}$.
Hence, the shaded region represents the solution set of the given inequations.

Graph the solution set of the inequation $2x-y\ge 1.$

Consider the equation $2x-y=1.$
We may write it as $\frac{x}{(1/2)}+\frac{y}{-1}=1.$
This shows that the line $2x-y=1$ make intercepts of $\frac{1}{2}$ and $-1$ on the axes.
Thus, the line meets the $\text{x-axis}$ at $A(\frac{1}{2},0)$ and the $\text{y-axis}$ at $B(0,-1).$
We plot these points and join them by a thick line Consider $O(0,0)$. Clearly, $(0,0)$ does not satisfy the given inequation. So, out of the portions divided by this line, the one not containing $O(0,0)$ together with the points on the line, forms the solution set.

Solve the following problem graphically :
Minimize and Maximize $Z=3x+9y$$...\left(1\right)$
subject to the constraints: $x+3y\le 60$$...\left(2\right)$
$x+y\ge 10$$...\left(3\right)$
$x\le y$$...\left(4\right)$
$x\ge 0,y\ge 0$ . . . (5)

Region represented by $x+3y\le 60$
Consider the equation $x+3y=60.$
$x=0\Rightarrow 3y=60\Rightarrow y=20,y=0\Rightarrow x=60$
Plot the points $A(2,20)$ and $B(60,0).$ Join $AB$ and produce it both ways.
Putting $x=0$ and $y=0.$ we get $0+3\times 0=0\le 60.$
$\therefore O(0,0)$ line in the region $x+3y\le 60.$
So, the region containing the origin is the solution set of $x+3y\ge 60.$
Region represented by $x+y\ge 10$
Consider the equation $x+y=10.$
Plot the points $C(0,10)$ and $D(10,0)$. Join CD and product it both ways.
Now, $x=0,y=0\Rightarrow 0+0\ge 10$ is not true.
$\therefore O(0,0)$ lies in the region $x-y\le 0.$
We know that:
$x\ge 0$ is the y-axis and the region on its RHS.
$y\ge 0$ is the x-axis and the region above the x-axis.
On solving $x=y\text{and}x+y=10,$ we get the point $G(5,5)$.
On solving $x=y\text{and}x+3y=60,$ we get $H(15,15).$
Thus, the feasible region is ACGH, as shown in the figure.

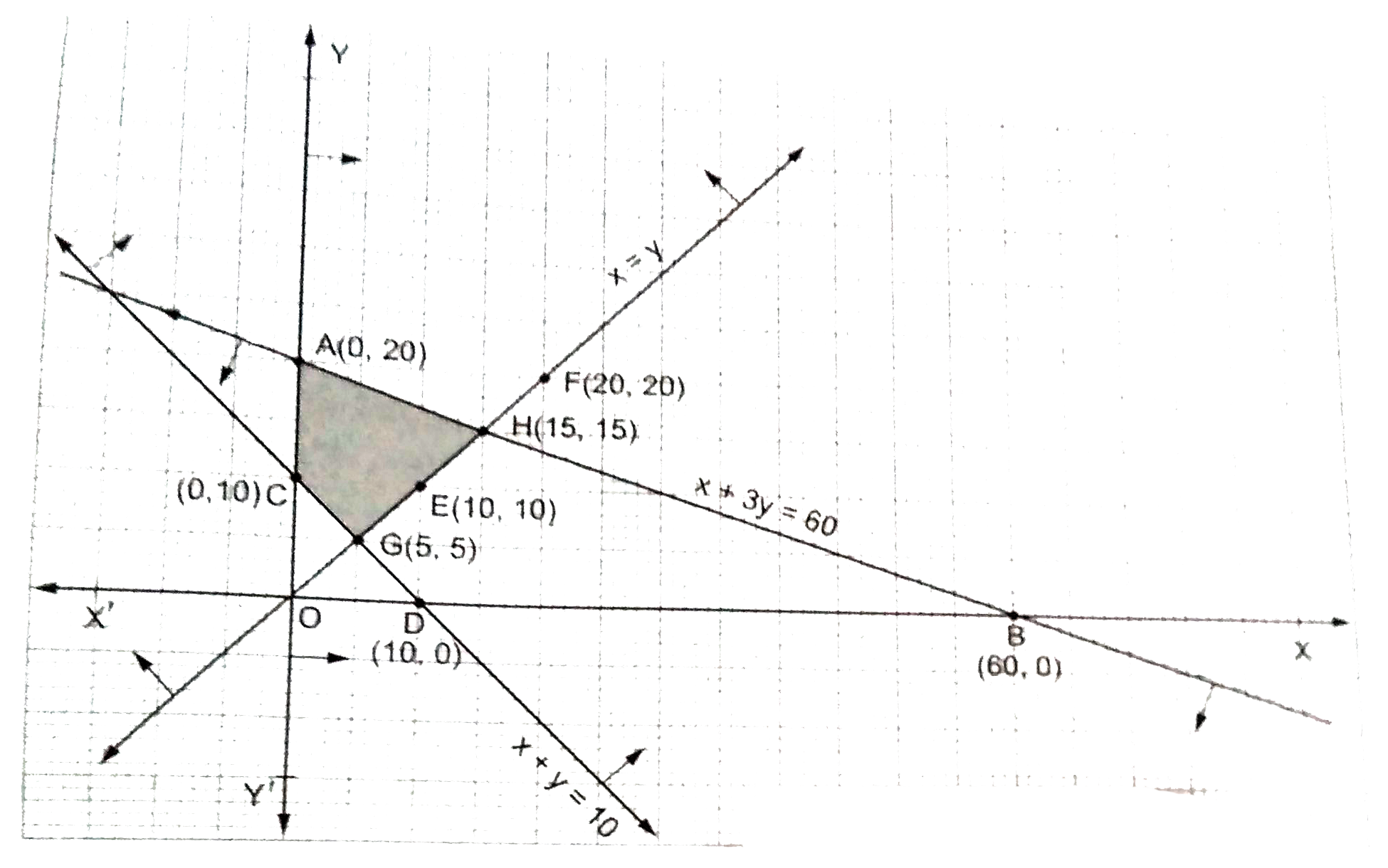
Value of $z=3x+9y:$
$\left(i\right)\text{At}A(0,20)\text{it is}(3\times 0+9\times 20)=180.$
$\left(ii\right)\text{At}C(0,10)\text{it is}(3\times 0+9\times 10)=90.$
$\left(iii\right)\text{At}C(5,5)\text{it is}(3\times 5+9\times 10)=60.$
$\left(iii\right)\text{At}H(15,15)\text{it is}(3\times 15+9\times 15)=180.$
So the minimum value of $z$ is $60$ and its maximum value is $180$.

Maximize $Z=x+y$ subject to $x+4y\le 8,2x+3y\le 12,3x+y\le 9,x\ge 0,\text{and}y\ge 0$

Here the given LPP is

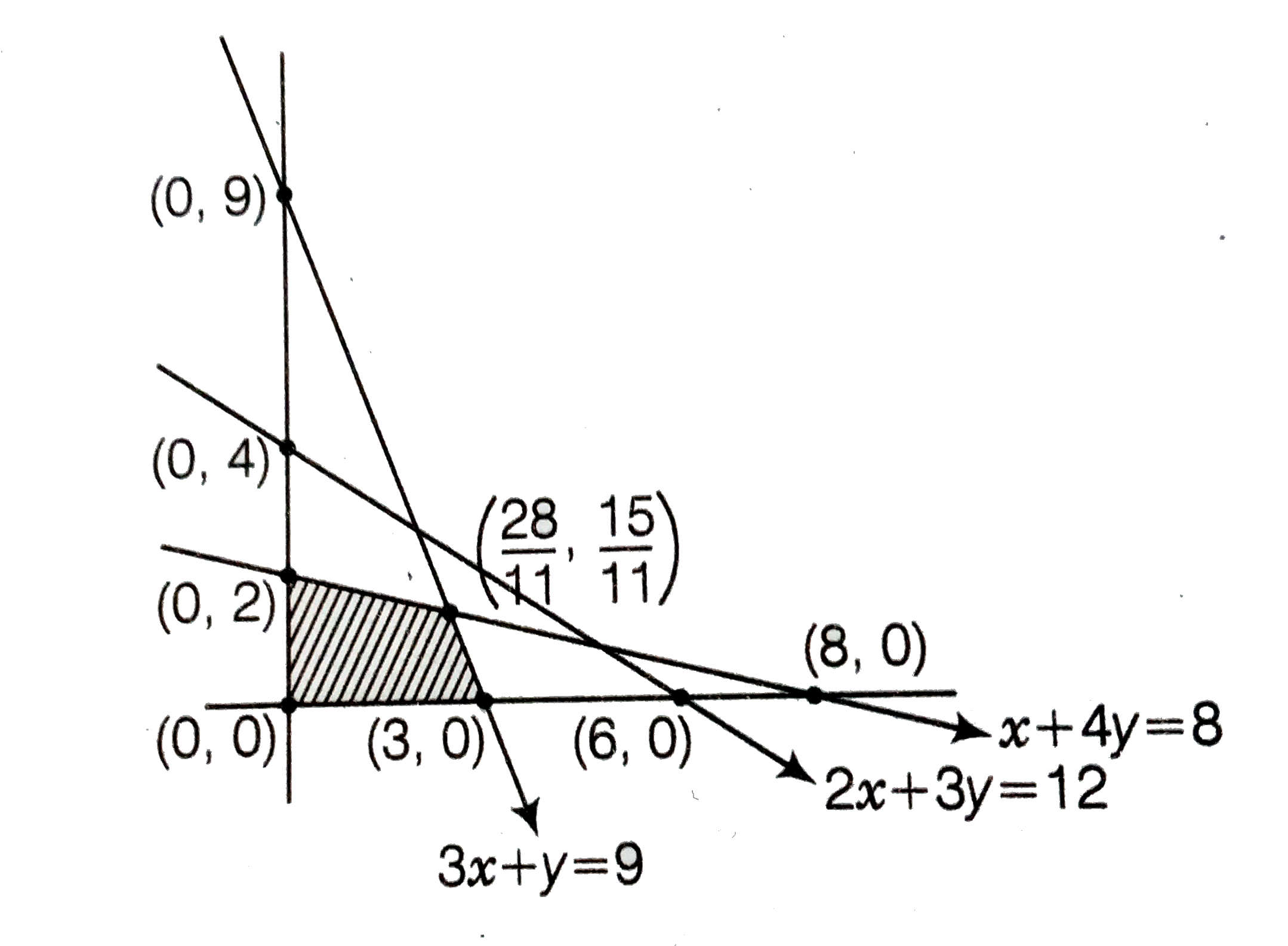
Maximize $Z=X+Y$ subject to
$x+4y\ge 8,2x+3y\le 12,3x+y\le 9,x\ge 0,y\ge 0$
On solving $x+4y=8$ and $3x+y=9$ we get
$x=\frac{28}{11},y=\frac{15}{11}$
From the feasible region, it is clear that coordinates of corner points are $(0,0),(3,0),(\frac{28}{11},\frac{15}{11})$ and $(0,2)$

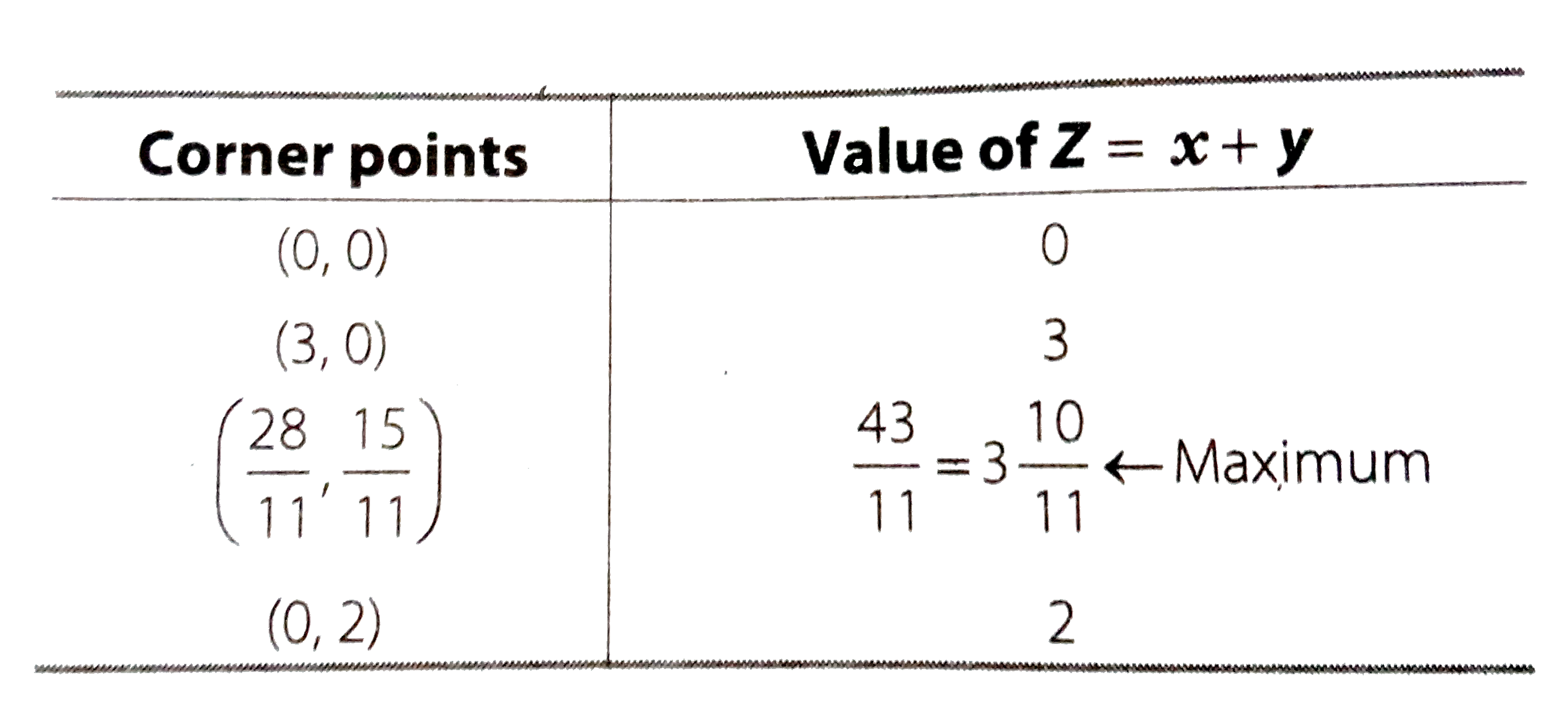
Hence, the maximum value is $3\frac{10}{11}$

A few important linear programming problems are listed below :
1. Manufacturing problems : Es tarh ki problems mein hum number of units nikalte hai different products ki jo ki ek firm ke through produce ki jati hai aur bechi jati hai. Basically product mein hone vala sara kharch karne ke baad maximum profit nikalne ke liye. Like each product requires a fixed manpower, machine hours, labour hour per unit of product, warehouse space per unit of the output etc.
2. Diet problems : En problems mein hum determine karte hai amount of different kinds of constituents/nutrients which should be included in a diet so as to minimize the cost of the desired diet such that it contains a certain minimum amount of each constituent/nutrients.
3. Transportation problems : En problems mein hum determine karte hai a transportation schedule in order to find the cheapest way of transporting a product from plants/factories situated at different locations to different markets.

A firm manufactures two types of products, A and B, and sells them at a profit of 3 per unit of type B product and 5 per unit of type A product. Both product is processed on two machines $M_1$ and $M_2$. One unit of type A requires one minute of processing time on $M_1$ and two minutes of processing time on $M_2$ whereas one unit of type B requires one minute of processing time on $M_1$ and one minute on $M_2$ Machines. $M_1$, and $M_2$, are respectively available for at most $5$ hours and $6$ hours in a day. Find out how many units of each type of product the firm should produce a day in order to maximize the profit. Solve the problem graphically.

Let $x$ units of $A$ and $y$ units of $B$ be produced in order to have a maximum profit.
Then, clearly $x\ge 0$ and $y\ge 0.$ $x$ unit of $A$ and $y$ units of $B$ will take $(x+y)$ minutes on $M_1.$
$\therefore x+y\le 300.$
$x$ units of $A$ and $y$ units of $B$ will take $(2x+y)$ minutes on $M_2.\therefore 2x+y\le 360.$
Let $Z$ be the profit function. Then $Z=5x+3y.$
We have to maximize $Z=5x+3y,$ subject to the constraints
$x\ge 0,y\ge 0,x+y\le 300\text{and}2x+y\le 360.$
Now, $x+y=300\Rightarrow \frac{x}{300}+\frac{y}{300}=1.$
This line meets the axes in $(300,0)\text{and}(0,300).$
Joining these points, we get line $x+y=300.$
Since $(0,0)$ satisfies the inequation $x+y\le 300,$ the region below the line $x+y=300$ containing $O(0,0)$ represents $x+y\le 300.$
Again, $2x+y=360\Rightarrow \frac{x}{180}+\frac{y}{360}=1.$
This line meets the axis in $(180,0)\text{and}(0,360).$
Joining these points, we get the line $2x+y=360.$
Since $(0,0)$ satisfies $2x+y\le 360,$ the region below the line $2x+y=360$ containing $(0,0)$ represents $2x+y\le 360.$
Also $x=0$ is the $\text{y-axis}$ and $y=0$ is the $\text{x-axis}$.
On drawing these lines and shading the feasible region, we obtain a figure, given below.

On solving $x+y=300$ and $2x+y=360,$ we get the point $Q(60,240)$. $\therefore$ the vertices of the feasible region are
$O(0,0),P(180,0),Q(60,240)\text{and}R(0,300).$
Values of $Z=5x+3y$ at $O,P,Q,R$ are $0,900,1020,900$ respectively.
$\therefore$ $Z$ is maximum when $x=60$ and $y=240.$

If a young man rides his motorcycle at $25$ km/hr, he has to spend Rs. $2$ per kilometer on petrol. If he rides it at a faster speed of $40$ km/hr the petrol cost increases to Rs. $5$ per kilometer. He has Rs. $100$ to spend on petrol and wishes to find the maximum distance he can travel within one hour. Express this as an LPP and solve it. graphically.

Let us assume that the man travels $x$ km when the speed is $25$ km/h and $y$ km when the speed is $40$ km/h.
Thus, the total distance travelled is given by $P=x+y$ km and we have to maximize it.
Clearly, $x\ge 0,2x+5y\le 100.$
Since the available time is at most one hour, we have
$\frac{x}{25}+\frac{y}{40}\le 1$ or $8x+5y\le 200.$

Now, we solved the system of the inequations.
$2x+5y=100\Rightarrow \frac{x}{50}+\frac{y}{20}=1.$
This line meets the axes at $(50,0)$ and $(0,20).$ Plot these points and join them to get the line $2x+5y=100.$
Also, $8x+5y=200\Rightarrow \frac{x}{25}+\frac{y}{40}=1.$
This line meets the axes at $(25,0)$ and $(0,40).$ Plot these points and obtain the line $8x+5y=200.$
$x=0$ is the $\text{y-axis}$ and $y=0$ is the $\text{x-axis}$.
We find that the solution set of the above system is the shaded region $OABC$.
The coordinates of $O,A,B,C$ are $(0,0),(25,0),(\frac{50}{3},\frac{40}{3})$ and $(0,20)$ respectively.
So, $P=x+y$ is maximum when $x=\frac{50}{3}$ and $y=\frac{40}{3}.$
Thus the young man can cover the maximum distance of $30$ km, if he rides $\frac{50}{3}$ km/h and $\frac{40}{3}$ km at $40$ km/h.

• A linear programming problem is one that is concerned with finding the optimal value (maximum or minimum) of a linear function of several variables (called objective function) subject to the conditions that the variables are non-negative and satisfy a set of linear inequalities (called linear constraints). Variables are sometimes called decision variables and are non-negative.


• A few important linear programming problems are :
  $\left(i\right)$ Diet problems
  $\left(ii\right)$ Manufacturing problems
  $\left(iii\right)$ Transportation problems


• The common region determined by all the constraints including the non-negative constraints $x\ge 0$, $y\ge 0$ of a linear programming problem is called the feasible region (or solution region) for the problem.


• Points within and on the boundary of the feasible region represent feasible solutions of the constraints. Any point outside the feasible region is an infeasible solution.


• Any point in the feasible region that gives the optimal value (maximum or minimum) of the objective function is called an optimal solution.


• The following Theorems are fundamental in solving linear programming problems :
  Theorem 1 Let $R$ be the feasible region (convex polygon) for a linear programming problem and let $Z=ax+by$ be the objective function. When $Z$ has an optimal value (maximum or minimum), where the variables $x$ and $y$ are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region.


• Theorem 2 Let $R$ be the feasible region for a linear programming problem, and let $Z=ax+by$ be the objective function. If $R$ is bounded, then the objective function $Z$ has both a maximum and a minimum value on $R$ and each of these occurs at a corner point (vertex) of $R$.


• If the feasible region is unbounded, then a maximum or a minimum may not exist However, if it exist, it must occur at a corner point of $R$.


• Corner point method for solving a linear programming problem. The method comprises of the following steps :
  $\left(i\right)$ Find the feasible region of the linear programming problem and determine its corner points (vertices).
  $\left(ii\right)$ Evaluate the objective function $Z=ax+by$ at each corner point. Let $M$ and $m$ respectively be the largest and smallest values at these points.
  $\left(iii\right)$ If the feasible region is bounded, $M$ and $m$ respectively are the maximum and minimum values of the objective function.
  If the feasible region is unbounded, then
  $\left(i\right)$ $M$ is the maximum value of the objective function, if the open half plane determined by $ax+by>M$ has no point in common with the feasible region. Otherwise, the objective function has no maximum value.
  $\left(ii\right)$ $m$ is the minimum value of the objective function, if the open half plane determined by $ax+by<m$ has no point in common with the feasible region. Otherwise, the objective function has no minimum value.


• If two corner points of the feasible region are both optimal solutions of the same type, i.e., both produce the same maximum or minimum, then any point on the line segment joining these two points is also an optimal solution of the same type.

• To bachcho ab hum Linear programming chapter ka quick revision karenge.


• Linear programming problems provide the method of finding an optimized function along with the values which would optimize the required function.


• Formulation of LPP
  Step (1) : Identify the number of decision variables which govern the behaviour of objective function.
  Step (2) : Identify the set of constraints on the decision variables and express them in the form of linear inequations or linear equations.
  Step (3) : Express the objective function in the form of a linear equation in the decision variable.
  Step (4) : Optimize the objective function either graphically or mathematically.



Types of LPP

Type of LPP	Constraints	Objective Function
Diet Problems	The specified nutritional requirement	The cost of food Intake
Manufacturing Problems	Variables like work hour, material availability, production rate, etc.	The cost of production
Transportation Problems	The specific supply demand pattern	The cost of transportation
Optimal Assignment Problems	The number of employees, work hour of each employee, efficiency of employee, etc.	The total assignment done