INDEFINITE INTEGRATIONS for Class 12 MATHS
Introduction
Hello Students , In our earlier theories for y=f(x) we have seen dydx , whose component are dy and dx , had no meaning by themselves. It is now important to modify this point of view and attach meaning to them , so that thereafter we can treat dydx as though it were a fraction in fact as well as in appearance .
Thus , Differential of y=f(x) is dy=f’(x)dx.
For y=x3 , dy=3x2dx and there are so many other examples.
Index
Geometrical representation Integral|Important formulaes|Some techniques for Integration|Standard substitutions|Integration by part|Two classic integrands|Integrating rational function|Algebraic twins|Manipulating integrands|Integration of trigonometric functions|Integration of sin and cos functions having some powers
Definition
In integration , we take anti derivative called as " inverse of a derivative " . For example , Derivative of sinx is cosx then we may say that integral of cosx is sinx. If we consider
(ddx)f(x)=ϕ(x)
then an integral of ϕ(x) with respect to x and we write it as ∫f(x)dx=f(x)
[where the symbol ∫ is known as the sign of integration] .
∫f(x)dx=F(x)+C , where C is called the "constant of integration."
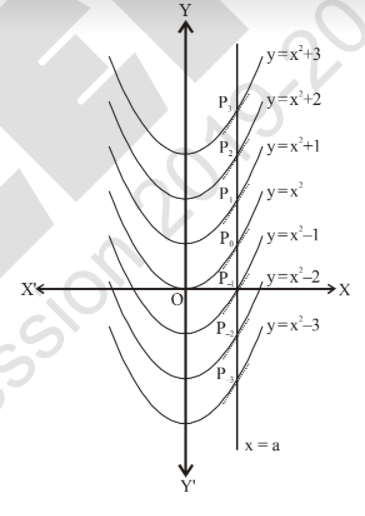
Geometrical representation Integral
We will take a particular function y=f(x) but we will assign different values to the constant C to obtain different family of curves
For example f(x)=2x . Then ∫f(x)dx=x+C . For different values of C , we get different integrals , where C is arbitrary constant. This integral represents a family of integrals. In this case , each integral represents a parabola with its axis along y-axis.
Let line x=a intersects the parabolas y=x2 , y=x2+1 , y=x2+2 at points P0,P1,P2 etc., respectively , then dydx at these points equals 2a.
It means that the tangents to the curves at these points are parallel.
Important formulaes
Some techniques for Integration
Substitution:
Theory : I=∫f(x)dx and let x=ϕ(z)
dIdx=f(x) ; dxdz=ϕ'(z)
⇒dIdz=dIdx⋅dxdz=f(x).ϕ'(z)
Hence I=∫(f(ϕ)(z))ϕ'(z)dz
( b ) If ∫[f(x)]nf'(x)dx OR
∫f'(x)[f(x)]ndx put f(x)=t and proceed
Example 1
∫sinx+cosxsin(x−α)dx is equal to
We have , ∫sinx+cosxsin(x−α)dx
=∫sin(t+α)+cos(t+α)sintdt where t=x−α
=∫(cosα+sinαcott+cosαcott−sinα)dt
=(cosα−sinα)t+(sinα+cosα)log|sint|+C
=(cosα−sinα)(x−α)+(cosα+sinα)log|sin(x−α)|+C
Example 2
∫tanxtan2xtan3xdx is equal to
We have ,
tan3x=tan(2x+x)
⇒tan3x=tan2x+tanx1−tanxtan2x
⇒tanxtan2xtan3x=tan3x−tan2x−tanx
∴∫tanxtan2xtan3xdx
=∫(tan3x−tan2x−tanx)dx
=13log|sec3x|−12log|sec2x|−log|secx|+C
∫f(ϕ(x))ϕ'(x)dx=∫f(ϕ(x))d(ϕ(x))
[(∵ dϕ(x)),(=ϕ'(x)dx)]
⇒∫f(ϕ(x))ϕ'(x)dx=∫f(t)dt , where t =ϕ(x).
Standard substitutions
Example 3
The value of ∫x7(1−x2)5dx is
We have , I=∫x7(1−x2)5dx
⇒I=∫sin7θ(1−sin2θ)5cosθdθ , where x=sinθ
⇒I=∫tan7θsec2θdθ
⇒I=∫(tanθ)7d(tanθ)=18tan8θ+C
⇒I=18x8(1−x2)4+C
Example 4
∫dxx√x2+4
Substitute √x2+4=t
Differentiating it
(2x)dx2√x2+4=dt
dx√x2+4=(dtx)
I=∫(dxx2)
=∫(dtt2−4)
[Use∴∫(dxx2−a2)=12aln∣∣∣x−ax+a∣∣∣+c where a=2]
=(14)ln∣∣∣t−2t+2∣∣∣+c
=(14)ln∣∣∣√x2+4−2√x2+4+2∣∣∣+c
Integration by parts
∫(u⋅v)dx=u∫(vdx)−∫[dudx⋅∫(vdx)]dx where u & v are differentiable functions.
Here u and v are first and second functions respectively and the choice of deciding their order is by ILATE which says that 'former' will be u and 'latter' will be v. Where
I Inverse function
L Logarithmic function
A Algebraic function
T Trigonometric function
E Exponential function
Example 5
Evaluate: ∫ex (logx+1x) dx
∫ex(logx+1x)dx
=∫ex.logxdx+∫ex.1xdx
=[logx∫exdx−∫{ddx.logx∫exdx}dx]
+∫ex.1xdx
=ex.logx−∫ex1xdx+∫ex1xdx+c
=exlogx+c.
Example 6
Evaluate: ∫{1logx−1(logx)2} dx
∫[1logx−1(logx)2]dx
=∫1.1logxdx−∫1(logx)2dx
=1logx.∫1dx−∫{ddx.1logx.∫1dx}dx
−∫1(logx)2dx
=xlogx−∫−1x(logx)2.xdx−∫1(logx)2dx+c
=xlogx+∫1(logx)2dx−∫1(logx)2dx+c
=xlogx+c
Two classic integrands
These are different types of integrands which can be solved by different methods depending on f(x) but the general solutions is given below.
- ∫ex[f(x)+f'(x)]dx=ex.f(x)+c
- ∫[f(x)+x⋅f'(x)]dx=xf(x)+c
Example 7
∫ex(tan−1x+11+x2)dx
Use ∫ex[f(x)+f'(x)]dx=ex.f(x)+c
where f(x)=tan−1x
∴∫ex(tan−1x+11+x2)dx=ex(tan−1x)
Example 8
Solve ∫xex2(sinx2+cosx2)dx
Let x2=t
2xdx=dt
⇒xdx=(12)dt
I=(12)∫[et(sint+cost)dt
[∫ex[f(x)+f'(x)]dx=ex.f(x)+c]
Let f(t)=sint , f'(t)=cost
I=(12)et(sint+cost)dt=(12)etsint+c
⇒I=(12)ex2sinx2+c
Example 9
Evaluate ∫(sinx+xcosx)dx
∫(sinx+xcosx)dx
Using ∫[f(x)+x⋅f'(x)]dx=xf(x)+c
⇒xsinx+c
Integrating rational function
Rational function is defined as the ratio of two polynomials in x which is P(x)Q(x) , where Q(x)≠0. If the degree of P(x) is less than the degree of Q(x) , then the rational function is called 'proper' , otherwise , it is called 'improper'. The improper rational function can be reduced to the proper rational functions by long division process which takes time. Thus we use partial fraction method to write integrand into sum of rational functions which takes less time
Example 10
∫x−2x2−4x+3dx=
Factorising denominator
(x2−4x+3)
⇒x2−3x−x+3
x(x−3)−1(x−3)
⇒(x−3)(x−1)
⇒∫x−2(x−3)(x−1)dx
⇒(12)∫(x−3)+(x−1)(x−3)(x−1)dx
⇒(12)∫(x−3(x−3)(x−1))dx+∫(x−1(x−3)(x−1))dx
⇒(12)[∫(1x−1)dx+∫(1x−3)]dx
⇒(12)ln|x−1|+(12)ln|x−3|+c
ln√x2−4x+3+c
Example 11
Evaluate ∫x2−1(x+1)(x+2)dx
I=∫x2−1(x+1)(x+2)dx
Use a2−b2=(a+b)(a−b)
x2−1=(x+1)(x−1)
I=∫(x−1)(x+1)(x+1)(x+2)dx
I=∫x−1+2−2x+2dx
I=∫(x+2x+2)dx−3∫1x+2dx
I=∫1dx−3∫1x+2dx
I=x−3|log(x+2)|+c
Note:
Integration of ∫dxax2+bx+c , ∫dx√ax2+bx+c , √ax2+bx+c dx make (ax2+bx+c) as a perfect square
Now Integration of type ∫px+qax2+bx+cdx , ∫px+q√ax2+bx+cdx
Now , Express px+q=λ(2ax+b)+μ
Example 12
Evaluate: ∫4x+1x2+3x+2dx
∫4x+1+5−5x2+3x+2dx
∫4x+6−5x2+3x+2dx
2∫2x+3x2+3x+2dx−5∫1x2+3x+2dx
Let A =2∫2x+3x2+3x+2dx
So (x2+3x+2)=t
(2x+3)dx=dt
A=2∫(dtt)
⇒2log∣∣x2+3x+2∣∣
Now consider B=5∫1x2+3x+2dx
So 5∫1x2+3x+2+(94)−(94)dx
⇒5∫⎛⎜
⎜⎝dx(x+32)2−(12)2
⇒5log∣∣
∣∣x+32−12x+32+12∣∣
∣∣
I=A−B
I=2log∣∣x2+3x+2∣∣−5log∣∣
∣∣x+32−12x+32+12∣∣
∣∣+c
Example 13
∫xdxx4+x2+1
I=∫x(x2)2+x2+1
Let x2=t
⇒2xdx=dt
⇒xdx=dt2
I=(12)∫dtt2+t+1
I=(12)∫dt(t+12)2+1−14
(12)∫dt(t+12)2+(√32)2
I=(12)log⎛⎝t+12+√(t+12)2+34⎞⎠+c
Algebraic twins
Integrals of the form ∫x2+1x4+kx2+1
OR
∫x2−1x4+kx2+1 where K is any constant. Divide Nr & Dr by x2 & proceed.
Example 14
∫x2+1x4+x2+1dx
∫x2+1x4+x2+1dx
⇒∫1+1x2x2+1+1x2dx
⇒∫1+1x2(x−1x)2+3dx
Let x−1x=t
⇒(1+1x2)dx=dt
⇒∫dtt2+√32
(1√3)tan−1(t√3)
(1√3)tan−1(x−1√3x)+c
Example 15
Evaluate: ∫1x4+1dx
∫1x4+1dx
⇒∫1x21x2+x2dx
⇒(12)∫2x2x2+1x2
(12)∫(1+1x2)−(1−1x2)x2+1x2dx
I=(12)∫1+1x2x2+1x2dx−(12)∫1−1x2x2+1x2dx
Let ∫1+1x2x2+1x2dx=I1 and ∫1−1x2x2+1x2dx=I2
I1=∫1+1x2x2+1x2−2+2dx
∫1+1x2(x−1x)2+2dx
Let x−1x=t
⇒∫dt(√2)2+t2
[Use ∫dxa2+x2=1atan−1(xa)+c]
⇒1√2tan−1(t√2)+c1
Similarly we can find I2=12√2log∣∣∣x2−√2x+1x2+√2x+1∣∣∣+c2
I=I1+I2
I=1√2tan−1(t√2)+c1+12√2log∣∣∣x2−√2x+1x2+√2x+1∣∣∣+c2
Manipulating integrands:
( i ) ∫dxx(xn+1) , n∈N , takexn common and put 1+x−n=t
( ii ) ∫dxx2(xn+1)n−1n , n∈N , take xn common and put 1+x−n=tn
( iii ) ∫dxxn(xn+1)n−1n , take xn common and put 1+x−n=tn
Example 16
The value of ∫dxxn(1+xn)1n is equal to
Let I=∫1xn(1+xn)1/ndx=∫1xn+1(1+1xn)1/ndx
⇒I=∫(1+x−n)−1/nx−n−1dx
⇒I=∫=−1n(1+x−n)−1/nd(1+x−n)
⇒=−1n(1+x−n)−1n+1(−1n+1)+C=11−n{1+1xn}1−1n+C
Integration of trigonometric functions
Type 1:∫dxa+bsin2x OR ∫dxa+bcos2x OR ∫dxasin2x+bsinxcosx+ccos2x
Divide Nr and Dr by cos2x and put tanx=t
Type 2:∫dxa+bsinx OR ∫dxa+bsinx+ccosx OR∫dxa+bsinx .
Convert sin & cos into their respective tangents of half the angles & put tan(x2)=t
In this case sinx=2t1+t2 and cosx=1−t21+t2
Type 3: ∫acosx+bsinx+cpcosx+qsinx+rdx
Nr=l(Dr)+mddx(Dr)+n
Example 17
Evaluate: ∫12+cosx dx
∫12+cosx dx
=∫12+(2cos2.x2−1)dx
=∫1sin2.x2+cos2.(x2)+2cos2.x2 dx
=∫1sin2.x2+3cos2.x2 dx
=∫sec2.x2tan2.x2+3 dx Let tan.x2=t
⇒sec2.x2 =dtdx
=∫2dtt2+3
=2∫1t2+(√3)2dx
=2√3tan−1(t√3)+c
=2√3tan−1.(tan.x2√3)+c
Example 18
Evaluate: ∫1a2sin2x+b2cos2x dx
∫1a2cos2x+b2sin2xdx
=∫sec2xa2+b2tan2xdx
(Divide Nr and Dr by cos2x)
Let btanx=t
=∫dtb(a2+t2) ⇒bsec2x=dtdx
=1b.1atan−1(ta)+c⇒sec2xdx=dtb
=1abtan−1(btanxa)+c.
Example 19
∫1sinx−3cosx−1dx
∫1sinx−3cosx−1dx
⇒sinx=2tan(x2)1+tan2(x2) and cosx=1−tan2(x2)1+tan2(x2)
∫1(2tan(x2)1+tan2(x2)−31−tan2(x2)1+tan2(x2)−1)dx
∫1+tan2(x2)2tan(x2)−3(1−tan2(x2))−1−tan2(x2)dx
∫sec2(x2)(2tan2(x2)+2tan(x2)−4)dx
Put tanx=t2⇒(12)sec2(x2)dx=dt
∫dtt2+t−2
∫dtt2+2t−t−2
⇒∫dtt−1(t−2)
(13)∫(1t−1−1t+2)dt
(13)ln∣∣∣t−1t+2∣∣∣+c
(13)ln∣tan(x2)−1tan(x2)+2+c
Integration of sin and cos functions having some powers
∫sinmxcosnxdx
Type-I : Let m & n be natural numbers.
- If either m or n is odd , then substitute even power term.
Say ∫(sin2xcos3xdx) where cosx is having even power than substitute sinx=t which is having even power - If both m and n odd , then substitute either of the term.
say ∫(sin1xcos3xdx) where both powers are odd than we can substitute either cosx or sinx as t - If both m and n are even , then use trigonometric identities to convert integrand into cosines.
∫(sin2xcos2xdx) than convert it into the function of cosx function.
Type-II : If m+n is a negative even integer , then substitute tanx=t
Example 20
Evaluate : ∫π/20sin3xcosxdx
Let sinx=t
⇒ cosxdx=dt
Atx=0 t=sin0=0
Atx=π/2,t=sinπ/2=1
∴∫π/20sin3xcosxdx=∫10t3dt=[t44]=14.
Example 21
If ∫sin5xcos4xdx=Acos9x+Bcos7x+Ccos5x+D , then 9A+7B+5C=
I=∫sin5xcos4xdx
⇒I=∫sin4xcos4xsinxdx
⇒I=−∫(1−cos2x)2cos4xd(cosx)
⇒I=−∫(1−t2)2t4dt , where t=cosx
⇒I=−∫(t4−2t6+t8)dt
⇒I=−t99+27t7−15t5+D
⇒I=−19cos9x+27cos7x−15cos5x+D
∴A=−19,B=27andC=−15⇒9A+7B+5C=0