METHODS OF DIFFERENTIATION for Class 12 MATHS
Introduction
Hello Students , Earlier we have seen differentiability in our previous chapter but now we will learn about some methods . Derivative is the instantaneous rate of change of a function with respect to it's variables . We can find the slope of a line with the help of it . Let us find some of the ways to find derivative.
Introduction
Hello Students , Earlier we have seen differentiability in our previous chapter but now we will learn about some methods . Derivative is the instantaneous rate of change of a function with respect to it's variables . We can find the slope of a line with the help of it . Let us find some of the ways to find derivative.
Definition
The value which we get by using formula lim∂x→0∂y∂x=lim∂x→0f(x+∂x)−f(x)∂x
= f'(x) = (dy/dx)<br>iscal≤das<b>derivatebyfirstpr∈cip≤<b>andtheprocessofcalca––t∈gderivativeiscal≤das<b>D⇔erentiation<b>de¬edbyy_1 , y' , Dy , f'(x)
Definition
The value which we get by using formula lim∂x→0∂y∂x=lim∂x→0f(x+∂x)−f(x)∂x
= f'(x) = (dy/dx)<br>iscal≤das<b>derivatebyfirstpr∈cip≤<b>andtheprocessofcalca––t∈gderivativeiscal≤das<b>D⇔erentiation<b>de¬edbyy_1 , y' , Dy , f'(x)
Geometry of derivative
The value which we get by using formula lim∂x→0∂y∂x=lim∂x→0f(x+∂x)−f(x)∂x
= f'(x) = (dy/dx)<br>iscal≤das<b>derivatebyfirstpr∈cip≤<b>andtheprocessofcalca––t∈gderivativeiscal≤das<b>D⇔erentiation<b>de¬edbyy_1 , y' , Dy , f'(x)
Geometry of derivative
The value which we get by using formula lim∂x→0∂y∂x=lim∂x→0f(x+∂x)−f(x)∂x
= f'(x) = (dy/dx)<br>iscal≤das<b>derivatebyfirstpr∈cip≤<b>andtheprocessofcalca––t∈gderivativeiscal≤das<b>D⇔erentiation<b>de¬edbyy_1 , y' , Dy , f'(x)
Example 1
Differentiate e3x from first principle
ddx(f(x)) = limh→0f(x+h)−f(x)h
ddx(e3x) = limh→0e3(x+h)−e3xh
= e3xlimh→0e3h−13h×3
⇒ddx(e3x) = 3e3x
Example 1
Differentiate e3x from first principle
ddx(f(x)) = limh→0f(x+h)−f(x)h
ddx(e3x) = limh→0e3(x+h)−e3xh
= e3xlimh→0e3h−13h×3
⇒ddx(e3x) = 3e3x
Example 2
Differentiate sin3xcos5x w.r.t x at x = 0
Let y=sin3xcos5x=12{2cos5xsin3x}
=12{sin(5x+3x)−sin(5x−3x)}
=12.(sin8x−sin2x)<br≥12.ddx(sin8x−sin2x)
=(12.8cos8x−12×2cos2x)=(4cos8x−cos2x).
Example 2
Differentiate sin3xcos5x w.r.t x at x = 0
Let y=sin3xcos5x=12{2cos5xsin3x}
=12{sin(5x+3x)−sin(5x−3x)}
=12.(sin8x−sin2x)<br≥12.ddx(sin8x−sin2x)
=(12.8cos8x−12×2cos2x)=(4cos8x−cos2x).
Standard derivatives
Standard derivatives
Fundamental theorems
Let f and g be derivable functions , then ,
( a ) ddx(f±g) = dfdx±dgdx
( b )d(cf)dx=cdfdx , where c is a constant
( c )d(fg)dx=f(dg)dx+g(df)dx known as PRODUCT RULE
( d ) d(fg)dx=g(df)dx−f(dg)dx known as QUOTIENT RULE
( e ) If y=f(u) & u=g(x) then dydx=dydu⋅dudx known as CHAIN RULE
Fundamental theorems
Let f and g be derivable functions , then ,
( a ) ddx(f±g) = dfdx±dgdx
( b )d(cf)dx=cdfdx , where c is a constant
( c )d(fg)dx=f(dg)dx+g(df)dx known as PRODUCT RULE
( d ) d(fg)dx=g(df)dx−f(dg)dx known as QUOTIENT RULE
( e ) If y=f(u) & u=g(x) then dydx=dydu⋅dudx known as CHAIN RULE
Example 3
If y=1√a2−x2 , find dydx.
Substituting (a2−x2)=t , we get
y=1√t=t−1/2andt=(a2−x2)
⇒ dydx=−12t−3/2=−12t3/2anddtdx=−2x
⇒ dydx=(dydt×dtdx)=−12t3/2×(−2x)=x(a2−m2)3/2.
Example 3
If y=1√a2−x2 , find dydx.
Substituting (a2−x2)=t , we get
y=1√t=t−1/2andt=(a2−x2)
⇒ dydx=−12t−3/2=−12t3/2anddtdx=−2x
⇒ dydx=(dydt×dtdx)=−12t3/2×(−2x)=x(a2−m2)3/2.
Example 4
If y= 5x(1−x2)13+sin2(2x+3) . Find dydx
We have ,
y=5x(1−x2)−1/3+sin2(2x+3)
⇒ dydx=ddx{5x(1−x2)−1/3}+ddx{sin2(2x+3)}
={5x.(−13)(1−x2)−4/3.(−2x)+(1−x2)−1/3⋅5}+{2sin(2x+3)cos(2x+3).2}
=10x23(1−x2)4/3+5(1−x2)1/3+2sin(4x+6)
=10x2+15(1−x2)3(1−x2)4/3+2sin(4x+6)
=(15−5x2)3(1−x2)4/3+2sin(4x+6).
Example 4
If y= 5x(1−x2)13+sin2(2x+3) . Find dydx
We have ,
y=5x(1−x2)−1/3+sin2(2x+3)
⇒ dydx=ddx{5x(1−x2)−1/3}+ddx{sin2(2x+3)}
={5x.(−13)(1−x2)−4/3.(−2x)+(1−x2)−1/3⋅5}+{2sin(2x+3)cos(2x+3).2}
=10x23(1−x2)4/3+5(1−x2)1/3+2sin(4x+6)
=10x2+15(1−x2)3(1−x2)4/3+2sin(4x+6)
=(15−5x2)3(1−x2)4/3+2sin(4x+6).
Example 5
If y=logtan.x2 , find dydx.
Given: y=logtan.x2.
Putting x2=tandtan.x2=tant=u, we get
y=logu,u=tantandt=x2
⇒dydu=1u,dudt=sec2tanddtdx=12
⇒dydx=(dydu×dudt×dtdx)
=(1u×sec2t×12)=(12tant×sec2t)=1sin2t=1sinx=cosec x.
Hence , dydx=cosec x.
Example 5
If y=logtan.x2 , find dydx.
Given: y=logtan.x2.
Putting x2=tandtan.x2=tant=u, we get
y=logu,u=tantandt=x2
⇒dydu=1u,dudt=sec2tanddtdx=12
⇒dydx=(dydu×dudt×dtdx)
=(1u×sec2t×12)=(12tant×sec2t)=1sin2t=1sinx=cosec x.
Hence , dydx=cosec x.
Logarithmic differentiation
It considers the function which is the product or Quotient of a number of functions
( a ) y=f1(x)⋅f2(x)⋅f3(x).....
OR
y=f1(x)⋅f2(x)⋅f3(x).....g1(x)⋅g2(x)⋅g3(x).....
( b ) It is of the form [f(x)]g(x) where f & g both are derivative
Logarithmic differentiation
It considers the function which is the product or Quotient of a number of functions
( a ) y=f1(x)⋅f2(x)⋅f3(x).....
OR
y=f1(x)⋅f2(x)⋅f3(x).....g1(x)⋅g2(x)⋅g3(x).....
( b ) It is of the form [f(x)]g(x) where f & g both are derivative
Example 6
If y=xx2, then dydx equals
Taking log both sides
logy=logxx2
logy=x2logx [Using product rule]
(1y)⋅(dydx)=x2(1x)+2x⋅logx
=x+2xlogx
⇒(1xx2)dydx=x+2x⋅logx
(dydx)=xx2(x+2x⋅logx)
= xx2⋅x(1+2logx)
=x(x2)+1(1+2logx)
Example 6
If y=xx2, then dydx equals
Taking log both sides
logy=logxx2
logy=x2logx [Using product rule]
(1y)⋅(dydx)=x2(1x)+2x⋅logx
=x+2xlogx
⇒(1xx2)dydx=x+2x⋅logx
(dydx)=xx2(x+2x⋅logx)
= xx2⋅x(1+2logx)
=x(x2)+1(1+2logx)
Example 7
Differentiate (sinx)logx w.r.t. x.
Let y=(sinx)logx .....(i) .
Taking logarithm on both sides of (i) , we get
logy=(logx)(logsinx)......(ii)
On differentiating both sides of (ii) w.r.t. x, we get
1y.dydx=(logx).ddx(logsinx)+(logsinx).ddx(logx)
=log(x).1sinx.cosx+(logsinx).1x
=(logx)cotx+(logsinx)x
⇒ dydx=y.[(logx)cotx+(logsinx)x]
⇒ dydx=(sinx)logx.[(logx)cotx+(logsinx)x].
Example 7
Differentiate (sinx)logx w.r.t. x.
Let y=(sinx)logx .....(i) .
Taking logarithm on both sides of (i) , we get
logy=(logx)(logsinx)......(ii)
On differentiating both sides of (ii) w.r.t. x, we get
1y.dydx=(logx).ddx(logsinx)+(logsinx).ddx(logx)
=log(x).1sinx.cosx+(logsinx).1x
=(logx)cotx+(logsinx)x
⇒ dydx=y.[(logx)cotx+(logsinx)x]
⇒ dydx=(sinx)logx.[(logx)cotx+(logsinx)x].
Example 8
If x=exp{tan−1(y−x2x2)} then dydx equals
x=exp{tan−1(y−x2x2)}
lnx=tan−1(y−x2x2)}
⇒tan(lnx)=(yx2)−1
y=x2[tan(lnx)+1]
⇒y=x2tan(lnx)+x2
(dydx)=2xtan(lnx)+x2⋅sec2(lnx)(1x)+2x
Example 8
If x=exp{tan−1(y−x2x2)} then dydx equals
x=exp{tan−1(y−x2x2)}
lnx=tan−1(y−x2x2)}
⇒tan(lnx)=(yx2)−1
y=x2[tan(lnx)+1]
⇒y=x2tan(lnx)+x2
(dydx)=2xtan(lnx)+x2⋅sec2(lnx)(1x)+2x
Parametric differentiation
If y=f(θ) & x=g(θ) , than (dydx)=dyd(θ)dxd(θ)=f'(θ)g'(θ)
Paramteric differentiation
If y=f(θ) & x=g(θ) , than (dydx)=dyd(θ)dxd(θ)=f'(θ)g'(θ)
Example 9
If x=asec3θandy=atan3θ,find dydx at θ=π3.
We have x=asec3θandy=atan3θ
∴ dxdθ=3asec2θddθ(secθ)=3asec3θtanθ
and dydθ=3atan2θddθ(tanθ)=3atan2θsec2θ
or dydx=dy/dθdx/dθ=3atan2θsec2θ3asec3θtanθ=tanθsecθ=sinθ
or (dydx)θ=π/3=sinπ3=√32
Example 9
If x=asec3θandy=atan3θ,find dydx at θ=π3.
We have x=asec3θandy=atan3θ
∴ dxdθ=3asec2θddθ(secθ)=3asec3θtanθ
and dydθ=3atan2θddθ(tanθ)=3atan2θsec2θ
or dydx=dy/dθdx/dθ=3atan2θsec2θ3asec3θtanθ=tanθsecθ=sinθ
or (dydx)θ=π/3=sinπ3=√32
Example 10
If y=acost and x=a(t−sint) find the value of dydx at t=π2
dydx = −a⋅sinta(1−cost)
(dydx)t=π2 = −1
Example 10
If y=acost and x=a(t−sint) find the value of dydx at t=π2
dydx = −a⋅sinta(1−cost)
(dydx)t=π2 = −1
Derivative of a function w.r.t another function
If y=f(x) & z=g(x) , than (dydx)=dydxdzd(x)=f'(x)g'(x)
Derivative of a function w.r.t another function
If y=f(x) & z=g(x) , than (dydx)=dydxdzd(x)=f'(x)g'(x)
Example 11
Find derivative of (logx)tanx w.r.t. xx
Let u=(logx)tanx and v=xx , than dudv = ?
Taking log in u and v
logu=log((logx)tanx)
logu=tanx⋅log(logx)
(1u)⋅dudx=tanx(1x⋅logx)+log(logx)sec2x
dudx=(logx)tanx[(tanxx⋅logx)+log(logx)sec2x]....(1)
Now , v=xx
logv=logxx=xlogx
(1v)dvdx=logx+x⋅(1x)
=logx+1
dvdx=xx(logx+1).....(2)
Dividing 12 dudv=(logx)tanx(tanxx⋅logx)+log(logx)sec2xxx(logx+1)
Example 11
Find derivative of (logx)tanx w.r.t. xx
Let u=(logx)tanx and v=xx , than dudv = ?
Taking log in u and v
logu=log((logx)tanx)
logu=tanx⋅log(logx)
(1u)⋅dudx=tanx(1x⋅logx)+log(logx)sec2x
dudx=(logx)tanx[(tanxx⋅logx)+log(logx)sec2x]....(1)
Now , v=xx
logv=logxx=xlogx
(1v)dvdx=logx+x⋅(1x)
=logx+1
dvdx=xx(logx+1).....(2)
Dividing 12 dudv=(logx)tanx(tanxx⋅logx)+log(logx)sec2xxx(logx+1)
Example 12
If x=sintcos2t and y=costsin2t , then at t=π4, the value of dydx is equal to :
Given x=sintcos2t
and y=costsin2t
Using product rule , differentiate w.r.t. t
dxdt = costcos2t–2sintsin2t
dydt = −sintsin2t+2costcos2t
dydx = dydtdxdt
= −sintsin2t+2costcos2tcostcos2t–2sintsin2t
At t=π4
dydx=−sin(π4)sin(π2)+2cos(π4)cos(π2)cos(π4)cos(π2)–2sin(π4)sin(π2)
= (−1√2)+(2×1√2⋅0)(1√2)⋅0–2√2
=−1√2−√2=12
Example 12
If x=sintcos2t and y=costsin2t , then at t=π4, the value of dydx is equal to :
Given x=sintcos2t
and y=costsin2t
Using product rule , differentiate w.r.t. t
dxdt = costcos2t–2sintsin2t
dydt = −sintsin2t+2costcos2t
dydx = dydtdxdt
= −sintsin2t+2costcos2tcostcos2t–2sintsin2t
At t=π4
dydx=−sin(π4)sin(π2)+2cos(π4)cos(π2)cos(π4)cos(π2)–2sin(π4)sin(π2)
= (−1√2)+(2×1√2⋅0)(1√2)⋅0–2√2
=−1√2−√2=12
Differentiation of Implicit functions
ϕ(x,y)=0
( a ) In order to find dydx of implicit functions , we differentiate each term w.r.t. x regarding y as a
function of x & then collect terms with dydx to find it's value
( b ) Also the direct formula for dydx
dydx = −∂ϕ∂x∂ϕ∂y , where ∂ϕ∂x
= partial derivative of ϕ(x,y) w.r.t. x taking y as a constant
∂ϕ∂y
= partial derivative of ϕ(x,y) w.r.t. y taking x as a constant .
( c ) For every curve , there exists both implicit and explicit functions but the process of differentiation remains the same.
For example , (ddx)siny=(ddy)siny.(dydx)
= cosy(dydx)
Differentiation of Implicit functions
ϕ(x,y)=0
( a ) In order to find dydx of implicit functions , we differentiate each term w.r.t. x regarding y as a
function of x & then collect terms with dydx to find it's value
( b ) Also the direct formula for dydx
dydx = −∂ϕ∂x∂ϕ∂y , where ∂ϕ∂x
= partial derivative of ϕ(x,y) w.r.t. x taking y as a constant
∂ϕ∂y
= partial derivative of ϕ(x,y) w.r.t. y taking x as a constant .
( c ) For every curve , there exists both implicit and explicit functions but the process of differentiation remains the same.
For example , (ddx)siny=(ddy)siny.(dydx)
= cosy(dydx)
Example 13
If y=x+1x+1x+1x+ . , prove that dydx=y2y−x .
⇒y=x+(1y)
⇒y2=xy+1
⇒2ydydx=y+xdydx+0 [Differentiating both sides w.r.t x]
⇒dydx(2y−x)=y
dydx=y2y−x
Example 13
If y=x+1x+1x+1x+ . , prove that dydx=y2y−x .
⇒y=x+(1y)
⇒y2=xy+1
⇒2ydydx=y+xdydx+0 [Differentiating both sides w.r.t x]
⇒dydx(2y−x)=y
dydx=y2y−x
Example 14
Find dydx , if x+y=sin(x−y)
x+y = sin(x−y)
Differentiate
1+(dydx) = cos(x−y)⋅d(x−y)dx
1+(dydx) = cos(x−y)−(dydx)(cos(x−y))
(dydx)[1+cos(x−y)] = cos(x−y)−1
(dydx)=cos(x−y)−1cos(x−y)+1
Example 14
Find dydx , if x+y=sin(x−y)
x+y = sin(x−y)
Differentiate
1+(dydx) = cos(x−y)⋅d(x−y)dx
1+(dydx) = cos(x−y)−(dydx)(cos(x−y))
(dydx)[1+cos(x−y)] = cos(x−y)−1
(dydx)=cos(x−y)−1cos(x−y)+1
Differentiation by trignometric transformation
Differentiation by trignometric transformation
Example 15
Differentiate sin−1(2x1+x2) w.r.t. cos−1(1−x21+x2)
Let u=sin−1(2x1+x2)andv=cos−1(1−x21+x2)
Putting x=tanθ , we get
u=sin−1(2tanθ1+tan2θ)=sin−1(sin2θ)=2θ
v=cos−1(1−tan2θ1+tan2θ)=cos−1(cos2θ)=2θ
∴u=v⇒dudv=1.
Example 15
Differentiate sin−1(2x1+x2) w.r.t. cos−1(1−x21+x2)
Let u=sin−1(2x1+x2)andv=cos−1(1−x21+x2)
Putting x=tanθ , we get
u=sin−1(2tanθ1+tan2θ)=sin−1(sin2θ)=2θ
v=cos−1(1−tan2θ1+tan2θ)=cos−1(cos2θ)=2θ
∴u=v⇒dudv=1.
Example 16
Differentiate tan−1{√1+x2−√1−x2√1+x2+√1−x2} with respect to cos−1x2
Let u=tan−1{√1+x2−√1−x2√1+x2+√1−x2}andv=cos−1x2.
Then , cos−1x2=v⇒x2=cosv.
Putting x2=cosv, we get
u=tan−1{√1+cosv−√1−cosv√1+cosv+√1−cosv}
⇒tan−1⎧⎪
⎪⎨⎪
⎪⎩√2cos2(v/2)−√2sin2(v/2)√2cos2(v/2)+√2sin2(v/2)⎫⎪
⎪⎬⎪
⎪⎭
=tan−1{cos(v/2)−sin(v/2)cos(v/2)+sin(v/2)}=tan−1{1−tan(v/2)1+tan(v/2)}
[dividing num. and denom. by cos (v/2)]
=tan−1{tan(π4−v2)}=(π4−v2).
∴u=(π4−v2)⇒dudv=−12.
Example 16
Differentiate tan−1{√1+x2−√1−x2√1+x2+√1−x2} with respect to cos−1x2
Let u=tan−1{√1+x2−√1−x2√1+x2+√1−x2}andv=cos−1x2.
Then , cos−1x2=v⇒x2=cosv.
Putting x2=cosv, we get
u=tan−1{√1+cosv−√1−cosv√1+cosv+√1−cosv}
⇒tan−1⎧⎪
⎪⎨⎪
⎪⎩√2cos2(v/2)−√2sin2(v/2)√2cos2(v/2)+√2sin2(v/2)⎫⎪
⎪⎬⎪
⎪⎭
=tan−1{cos(v/2)−sin(v/2)cos(v/2)+sin(v/2)}=tan−1{1−tan(v/2)1+tan(v/2)}
[dividing num. and denom. by cos (v/2)]
=tan−1{tan(π4−v2)}=(π4−v2).
∴u=(π4−v2)⇒dudv=−12.
Inverse and derivative of a function
Let g is inverse of f , then
( a ) g(f(x))=x
g'(f(x))f'(x)=1
( b )f(g(x))=x
f'(g(x))g'(x)=1
Inverse and derivative of a function
Let g is inverse of f , then
( a ) g(f(x))=x
g'(f(x))f'(x)=1
( b )f(g(x))=x
f'(g(x))g'(x)=1
Example 17
If g is the inverse of f and f'(x)=12+xn , then g'(x) is equal to
Given: g(x)=f−1(x)
⇒f(g(x))=x
f'(g(x))⋅g'(x)=1
⇒g'(x)=1f'(g(x))
f'(x)=12+xn
f'(g(x))=12+(g(x))n
⇒g'(x)=(2+(g(x))n)
Example 17
If g is the inverse of f and f'(x)=12+xn , then g'(x) is equal to
Given: g(x)=f−1(x)
⇒f(g(x))=x
f'(g(x))⋅g'(x)=1
⇒g'(x)=1f'(g(x))
f'(x)=12+xn
f'(g(x))=12+(g(x))n
⇒g'(x)=(2+(g(x))n)
Example 18
If y=f(x)=x3+x5 and g is the inverse of f find g′(2)
y=f(x)=x3+x5
Let g(x) be the inverse of f(x) i.e. g(x)=f−1(x)....(1)
f(g(x))=g(f(x))=x
differentiating w.r.t x
f'(g(x))⋅g'(x)=1
⇒g'(x)=1f'(g(2))
From (1) g(2)=f−1(2)=y (say)
f(y)=2 ⇒y3+y5=2 ⇒y=1
g'(2)=1f'(1)
⇒1(3x2+5x4)x=1=18
Example 18
If y=f(x)=x3+x5 and g is the inverse of f find g′(2)
y=f(x)=x3+x5
Let g(x) be the inverse of f(x) i.e. g(x)=f−1(x)....(1)
f(g(x))=g(f(x))=x
differentiating w.r.t x
f'(g(x))⋅g'(x)=1
⇒g'(x)=1f'(g(2))
From (1) g(2)=f−1(2)=y (say)
f(y)=2 ⇒y3+y5=2 ⇒y=1
g'(2)=1f'(1)
⇒1(3x2+5x4)x=1=18
Higher order derivatives
Let a function f(x) be differentiable function and it's first derivative is (dydx) or f'(x) . If we differentiate further we obtain second derivative denoted by d2ydx2 or f''(x) . Now if we differentiate further we obtain third derivative d3ydx3 or f'''(x) and so on.
Note: If x=f(θ) and y=g(θ) where θ is the parameter than ,
dnydxn=dd(θ)dn−1ydxn−1/(dxd(θ))
Higher order derivatives
Let a function f(x) be differentiable function and it's first derivative is (dydx) or f'(x) . If we differentiate further we obtain second derivative denoted by d2ydx2 or f''(x) . Now if we differentiate further we obtain third derivative d3ydx3 or f'''(x) and so on.
Note: If x=f(θ) and y=g(θ) where θ is the parameter than ,
dnydxn=dd(θ)dn−1ydxn−1/(dxd(θ))
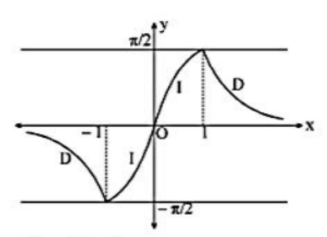
Graphs of some trigonometric functions
( a )y=f(x)=sin−1(2x1+x2) = ⎡⎢
⎢⎣2tan−1x|x|≤1π−2tan−1xx>1−(π+2tan−1x)x<−1⎤⎥
⎥⎦
Points to remember :
( i ) Domain is X∈R & range is [−π2,+π2]
( ii ) f is continuous for all x but not differentiable at x=1 , −1
(iii) (dydx) = (21+x2,|x|<1) , (non existent , |x|=1) , (−21+x2,|x|>1))
(iv) Increasing in [−1,1] & Decreasing in(−∞,−1],[1,∞)
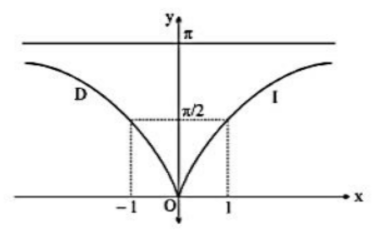
( b )y=f(x)=cos−1(1−x21+x2) = [2tan−1xx=.0−2tan−1xx<0]
Points to remember :
( i ) Domain is X∈R & range is [0,+π]
( ii ) f is continuous for all x but not differentiable at x=0
(iii) (dydx) = (21+x2,x>0) , (non existent , x=0) , (−21+x2,x<0))
(iv) Increasing in [0,∞) & Decreasing in(−∞,0)
General note:
Concavity is decided by the sign of 2nd derivative as:
d2ydx2)≥0⇒ Concave upwards
d2ydx2)≤0⇒ Concave downwards
Graphs of some trigonometric functions
( a )y=f(x)=sin−1(2x1+x2) = ⎡⎢
⎢⎣2tan−1x|x|≤1π−2tan−1xx>1−(π+2tan−1x)x<−1⎤⎥
⎥⎦
Points to remember :
( i ) Domain is X∈R & range is [−π2,+π2]
( ii ) f is continuous for all x but not differentiable at x=1 , −1
(iii) (dydx) = (21+x2,|x|<1) , (non existent , |x|=1) , (−21+x2,|x|>1))
(iv) Increasing in [−1,1] & Decreasing in(−∞,−1],[1,∞)
( b )y=f(x)=cos−1(1−x21+x2) = [2tan−1xx=.0−2tan−1xx<0]
Points to remember :
( i ) Domain is X∈R & range is [0,+π]
( ii ) f is continuous for all x but not differentiable at x=0
(iii) (dydx) = (21+x2,x>0) , (non existent , x=0) , (−21+x2,x<0))
(iv) Increasing in [0,∞) & Decreasing in(−∞,0)
General note:
Concavity is decided by the sign of 2nd derivative as:
d2ydx2)≥0⇒ Concave upwards
d2ydx2)≤0⇒ Concave downwards
Example 19
Find the interval for which f(x)=x2+x+1 is
( i ) concave upwards
( ii ) concave downwards
f(x)=x3+x+1
f'(x)=3x2+1
f''(x)=6x≥0 (Concave upwards)
f''(x)=6x≤0 (Concave downwards)
Example 19
Find the interval for which f(x)=x2+x+1 is
( i ) concave upwards
( ii ) concave downwards
f(x)=x3+x+1
f'(x)=3x2+1
f''(x)=6x≥0 (Concave upwards)
f''(x)=6x≤0 (Concave downwards)
Example 20
y=xex2 Find y''.
y=xex2
y'=1⋅ex2+x⋅ex2⋅2x
= ex2(1+2x2)
y''=ex2⋅2x⋅(1+2x2)+ex2(0+4x)
⇒ex2[2x+4x3+4x]
=(6x+4x3)ex2
Example 20
y=xex2 Find y''.
y=xex2
y'=1⋅ex2+x⋅ex2⋅2x
= ex2(1+2x2)
y''=ex2⋅2x⋅(1+2x2)+ex2(0+4x)
⇒ex2[2x+4x3+4x]
=(6x+4x3)ex2