HYPERBOLA for Class 12 MATHS
Introduction
Hello Students, In today's class we will learn a very interesting topic which is Hyperbola which has a good weightage in the exam of JEE.
These notes are designed keeping in mind the basics and the recent changes in the syllabus and pattern of JEE.
You can follow Doubtnut for all the videos related to JEE 2022.
The Hyperbola is one of the four classic conic sections that is generally created by slicing a cone with a plane. The other conic sections are the parabola, the circle, and the ellipse.
Hyperbola shape is extensively used in the design of bridges. Open orbits of some comets about the Sun follow hyperbolas. Interference pattern produced by two circular waves is hyperbolic in nature. It is the basis for solving trilateration problems.
Index
Basic terminology and Definition|Standard equation of Hyperbola|Tracing of Hyperbola|Facts about Hyperbola|Focal distance of a point|Comparision chart between Hyperbola and Conjugate Hyperbola|Rectangular Hyperbola|Finding all parameters of a Hyperbola|Position of a point with respect to Hyperbola|Equation of tangents|Tangents drawn from outside point|Equation of Normals|Properties
Basic terminology and Definition
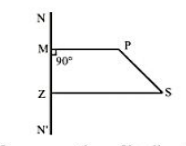
A hyperbola is the locus of a point which moves in a plane such that the ratio of its distance from a fixed point and a given straight line is always constant.
The fixed point is called the focus, the fixed line is called the directrix and the constant ratio is called the eccentricity of the hyperbola and denoted by e.
In the given figure. S is the focus and N’N the directrix.
Let P be any point on the hyperbola, then PSPM=e,e>1.
Equation of a hyperbola can be obtained if the coordinates of its focus, equation of its directrix and eccentricity are given.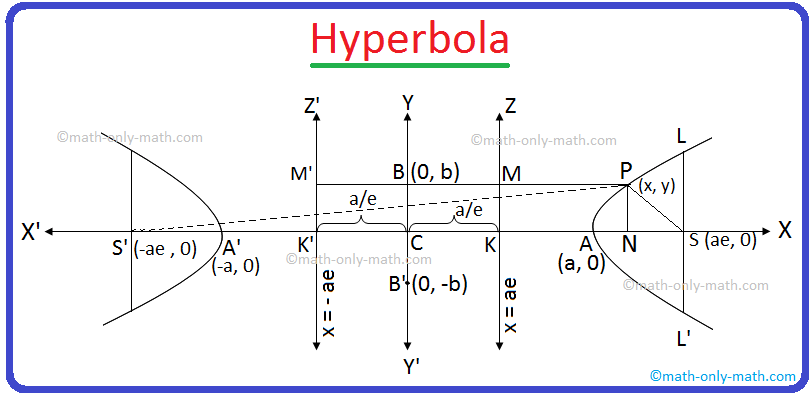
( 1 ) Centre :In the figure, C is the centre of the ellipse. All chords passing through C are called diameter and bisected at C.
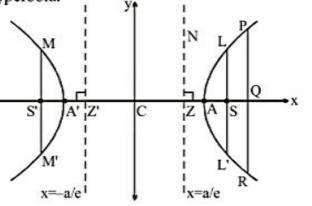
( 2 ) Foci: S(ae,0) and S’(−ae,0) are two foci of hyperbola. Line containing the fixed points S and S’ (called Foci) is called Transverse Axis (TA) or Focal Axis and the distance between S and S’ is called Focal Length.
( 3 ) Axes :The line AA’ is called transverse axis and the line BB’ is perpendicular to it and passes through the centre (0,0) of the hyperbola is called conjugate axis.
The length of transverse and conjugate axes are taken as 2a and 2b respectively.
The transverse and conjugate axes together are called principal axes of hyperbola and their intersection point is called the centre of hyperbola. The points of intersection of the directrix with the transverse axis are known as Foot of the directrix(Z and Z’).
( 4 ) Vertex : The points of intersection (A,A’) of the curve with the transverse axis are called Vertices of the hyperbola.
( 5 ) Double ordiante : Any chord perpendicular to the Transverse axis is called a Double Ordinate.
( 6 ) Latus rectum
When double ordinates passes through the focus of parabola then it is called the latus rectum. In the given figure LL' and MM' are the latus-rectums of the hyperbola.
Let LL'=2k then LS=L’S=k
Let L(ae,k) lie on the hyperbola x2a2−y2b2=1
(a2e2a2)−(k2b2)=1
or k2=b2(e2−1)=b2(b2a2)[:b2=a2(e2−1)]
∴2k=2b2a=LL’
Length of latus rectum=LL'=2b2a=(CA)2TA=2a(e2−1)=2e(ae−ae)=(2e) (distance between the focus and the foot of the corresponding directrix)
( 7 ) Focal chord :
A chord of hyperbola passing through its focus is called a focal chord.
Eccentricity:
For the hyperbola
x2a2−y2b2=1 we have
b2=a2(e2−1)
e=√1+(b2a2)
Eccentricity defines the curvature of the hyperbola and is mathematically spelled as:
e=distance from centre to focus/distance from centre to vertex
Standard equation of Hyperbola
Let S be the focus & ZN is the directrix of an ellipse. Draw perpendicular from S to the directrix which meet it at Z. A moving point is on the hyperbola such that
PS=ePM
Then there is point lies on the line SZ and which divide SZ internally at A and externally at A in the ratio of e:1.
therefore SA=eAZ....(i)
SA’=eA’Z...(ii)
Let AA’=2a & take C as mid point of AA’
CA=CA’=a
Add (i) & (ii)
SA+SA’=e(AZ+A’Z)
(CS−CA)+(CA’+CS)=e[CA−CZ+CA’+CZ]
2CS=2e.CA
CS=ae
Subtract (ii) & (i), we get
SA’−SA=e(A’Z−AZ)
(CA’+CS)−(CS−CA)=e[(CA’+CZ)−(CA−CZ)
2CA=2e⋅CZ⇒CZ=ae
Consider CZ line as x-axis, C as origin & perpendicular to this line & passes through C is considered as
y-axis. Now represent important parameters on coordinates plane. Let P(x,y) is a moving point, then by definition of ellipse.
PS=ePM⇒(PS)2=e2(PM)2
(x−ae)2+(y−0)2=e2(x−ae)2⇒(x−ae)2+y2=(a−ex)2
=x2+a2e2−2xae+y2=a2+e2x2−2xae⇒x2(1−e2)+y2=a2(1−e2)
x2a2+y2a2(1−e2)=1 where b2=a2(e2−1)
Hence equation of hyperbola is = x2a2−y2b2=1 where b2=a2(e2−1)
Tracing of Hyperbola
Equation of given hyperbola is x2a2−y2b2=1.....(i)
( i ) If we put y=0, then we see that hyperbola cuts x-axis at (±a,0)
( ii ) If we put x=0, then y2=−b2. Hence hyperbola does not cut y-axis.
( iii ) When y is replaced by −y, the equation of hyperbola does not change, hence hyperbola is symmetric about x-axis. (Since equation contain even power of y therefore curve will be symmetric about x-axis.
( iv ) When x is replaced by −x, then equation of hyperbola does not change. hence hyperbola is symmetric about y-axis. (Since equation contain even power of x therefore curve will be symmetric about y-axis.
( v ) From (i), y=(±ba)√x2−a2 ,since y is real ⇒x2−a2≥0 or x∈(−∞,−a]∪[a,∞)
curve don’t lie in (−a,a)
For each x≥a or x≤−a there are two values of y symmetrically situated on both side of x-axis.
Hence, the curve denoted by (i) consist of two symmetrical branches. each extending to infinite in two direction.
Facts about Hyperbola
x2a2−y2b2=1
( 1 ) By symmetry of equation of hyperbola, if we take second focus (—ae,0) and second directrix x=−ae and perform same calculation then we get same equation of hyperbola. This suggest that their are two foci arc (ae,0) and (−ae,0) and the two corresponding directrices as x=ae and x=−ae and if focus is (−ae,0), then corresponding directrix is x=−ae
( 2 ) By definition of hyperbola, the distance of any point P on the hyperbola from focus= e(the distance of P from the corresponding directrix)
( 3 ) Distance between foci SS’=2ae & distance between directrix ZZ’=2ae
( 4 ) Two hyperbola are said to be similar if they have same eccentricity.
( 5 ) The hyperbola has two branches neither of them cut the y-axis (conjugate axis).
( 6 ) Since the fundamental equation to the hyperbola only differs from that to the ellipse is having −b2 instead of b2. It is observed that many propositions for the hyperbola are derived from those for the ellipse by simply changing the sign of b2.
( 7 ) Eccentricity e=√1+b2a2. Also b2=a2(e2−1).
The smaller the e, the smaller will be the value of b for a given a. Therefore, as e decreases for a given
a, the branches of the hyperbola would be bending towards x-axis. As e increases, the branches open up.
( 8 ) Equation of hyperbola when its transverse and conjugate axes are x and y-axes respectively is
x2a2−y2(a2)(e2−1) or x2−y2e2−1=a2
If e kept constant and a→0, then hyperbola will tend to pair of straight lines x2−y2e2−1=0, both passing through the origin.
Thus in the situated limiting case of a hyperbola is a pair of straight lines.
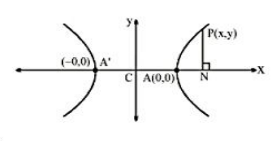
( 9 ) Since x2a2−y2b2=1
∴y2b2=(x2a2)−1=(x−a)(x+a)a2
From figure, AN=CN−CA=x−a
A’N=CN+CA=x+a
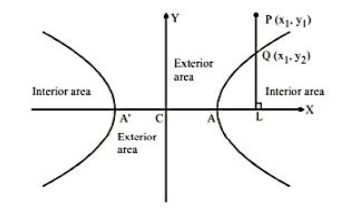
Focal distance of a point
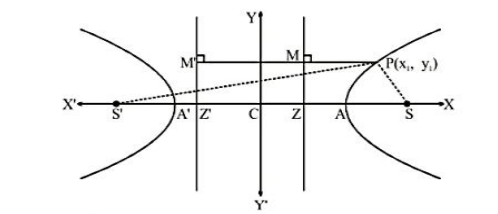
The hyperbola is x2a2−y2b2=1...(1)
The foci S and S’ are (ae,0) and (−ae,0) & corresponded directrix are x=ae and x=−ae respectively.
Let P(x1,y1) be any point on (1).
Now SP=ePM=e(x1−ae)=ex1−a
and S'P=ePM’=e(x1+ae)=ex1+a
S'P−SP=(ex1+a)−(ex1−a)=2a
⇒AA’= Transverse axis
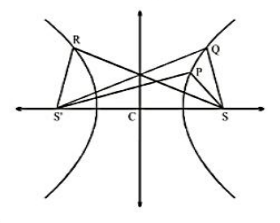
Thus hyperbola is the locus of a point which moves in a plane such that the difference of its distances from two fixed point (foci) is constant and always equal to transverse axis.
Hence, in the given figure
PS’−PS=QS’−QS=RS−RS’= length of transverse axis.
Comparision chart between Hyperbola and Conjugate Hyperbola
Rectangular Hyperbola
If the lengths of transverse and conjugate axes of any hyperbola be equal then it is called rectangular or equilateral hyperbola.
Since length of transverse axis and conjugate axis are same i.e. a=b
then,x2a2−y2b2=1 becomes x2−y2=a2
Eccentricity, e=√1+b2a2=√2
All the results of x2a2−y2b2=1 are applicable to the hyperbola x2−y2=a2 after changing b by a.
Finding all parameters of a Hyperbola
When equation of the hyperbola (x−α)2a2−(Y−β)2b2=1
This equation is the form of X2a2−Y2b2=1, where X=x−h and Y=y−k
( 1 ) Length of semi-transverse axis = a, length of semi-conjugate axis = b
( 2 ) Equation of transverse axis is Y=0, i.e. y−k=0
Equation of conjugate axis is X=0, i.e. x−h=0
( 3 ) Coordinates of centre is given by X=0 and Y=0. i.e. x−h=0 and y−k=0
Therefore, centre is (h,k)
( 4 ) Eccentricity of the hyperbola e=√1+b2a2
( 5 ) Coordinates of vertices of the hyperbola are given by X=±a,Y=0 i.e., x−h=±a,y−k=0.
Hence vertices are (h±a.k).
( 6 ) Coordinate of foci are given by X=±ae,Y=0
i.e., x−h=±ae,y−k=0. Hence foci are (h±ae,k)
( 7 ) Equation of directrices of the hyperbola are X=±ae , i.e., x−h=±ae
Hence directrices are x=h±ae
( 8 ) Length of latus rectum= b2a
( 9 ) Coordinate of ends of latera recta are given by X=ae,Y=±b2a i.e. x−h=±ae,y−h=±b2a
:. and if LR is (h±ae,k±b2a)
Example 1
Find the lengths of the axes, the coordinates of the vertices and the foci, the eccentricity and length of the latus rectum of the hyperbola
x236−y264=1.
The equation of the given hyperbola is x236−y264=1.
Comparing the given equation with x2a2−y2b2=1, we get
a2=36andb2=64.
∴a=6,b=8andc=√a2+b2=√36+64=√100=10.
(i) length of the transverse axis =2a=(2×6) units = 12 units .
Length of the conjugate axis =2b=(2×8) units =16 units.
(ii) The coordinates of the vertices are A(−c,0)andF2(c,0),i.e.,F1(−10,0)andF2(10,0).
(iv) Eccentricity ,e=ca=106=53.
(v) Length of the latus rectum 2b2a=(2×646)units=643units.
Example 2
Find the equations of the hyperbola satisfying the given conditions :Vertices (±2,0),foci(±3,0)
Since the vertices of the given hyperbola are of the form (±a,0) it is a horizontal hyperbola .
Let the required equation be x2a2=y2b2=1.
then , its vertices are (±a,0).
But , it is given that the vertices are (±2,0).
∴a=2
Let its foci be (±c,0)
But , it is given that foci are (±3,0).
∴c=3.
Now,b2=(c2−a2)=(32−22)=(9−4)=5.
Thus ,a2=22=4andb2=5.
Hence , the required equation is x24−y2b2=1.
Example 3
Find the equation of the hyperbola whose vertices are (±7,0) and the eccentricity is 43.
Since the vertices of the given hyperbola are of the form (±a,0),it is a horizontal hyperbola .
Let the requied equation of the hyperbola be x2a2−y2b2=1.
then , its vertices are (±a,0).
But , the vertices are (±7,0)
∴a=7⇔a2=49.
Also ,e=ca⇔c=ae=(7×43)=283.
Now , C2=(a2+b2)⇔b2=(c2−a2)=[(283)2−49]=3439.
Thus,a2=49andb2=3439.
∴ the required equation is
x249−y2(343/9)=1⇔x249−9y2343=1⇔7x2−9y2=343.
Example 4
A hyperbola, having the transverse axis of length 2sinθ, is confocal with the ellipse 3x2+4y2=12. Then its equation is
The equation of the ellipse is x222+y2(√3)2=1.
Let e be its eccentricity. Then,
e=√1−34=12
So, coordinates of its foci are (1,0) and (−1,0).
Let the equation of the hyperbola be x2a2−y2b2=1.
It is given that a=sinθ and the hyperbola is confocal to the ellipse.
∴esinθ=1⇒e=cosecθ
∴b2=a2(e2−1)⇒b=cosθ
Hence, the equation of the hyperbola is
x2cosec2θ−y2sec2θ=1.
Position of a point with respect to Hyperbola
Let S(x,y)≡x2a2−y2b2=1 be the given hyperbola and P(x1,y1) is the given point.
- If S(x1,y1)>0 then P(x1,y1) lie inside the ellipse.
- If S(x1,y1)<0 then P(x1,y1) lie outside the ellipse.
-
If S(x1,y1)=0 then P(x1,y1) lie on the ellipse.
Equation of tangents
( 1 ) Point form: The equation of the tangent to the hyperbola x2a2−y2b2=1 at (x1,y1) is xx1a2−yy1b2=1
Since point (x1,y1) lie on the hyperbola therefore we can use standard substitution to obtain the equation of tangent.
( 2 ) Parametric form: The equation of tangent to the hyperbola x2a2−y2b2=1 at (asec(θ),btan(θ)) is (xa)sec(θ)−(yb)tan(θ)=1.
Note: Point of intersection of the tangents at (θ)1&(θ)2, is x=acos((θ)1−(θ)2)cos((θ)1+(θ)2),y=bsin((θ)1+(θ)2)cos((θ)1+(θ)2)
( 3 ) Slope form:
Given hyperbola is x2a2−y2b2=1
and the given line y=mx+c touches hyperbola then solve (1) and (2) , we get
x2a2−(mx+c)2b2=1 or b2x2−a2(mx+c)2=a2⋅b2 or (b2−a2m2)x2−2a2mcx−a2(c2+b2)=0....(3)
Since line (2) will be tangent to hyperbola (1) if roots of equation (3) are equal i.e. D=0
4a4m2c2+4a2(b2−a2m2)(c2+b2)=0
or a2m2c2+b2c2−a2c2m2+b4−a2b2m2=0
or b2c2+b4−a2b2m2=0
or ç^2+b^2-a^2m^2=0 or c2=a2m2−b2 or c=±a2m2−b2 . This is the required condition of tangency
Note: ( i ) Equation of any tangent to hyperbola x2a2−y2b2=1 may be taken as y=mx+√a2m2−b2 or y=mx+√a2m2−b2 . The co-ordinates of the points of contact are [±(a2m√a2m2−b2),±b2√a2m2−b2]
( ii ) The equation of any tangent to the hyperbola (x−h)2a2(y−k)2b2=1
may be taken as (y−k)=m(x−h)±√a2m2−b2
Tangents drawn from outside point
y=mx±√a2m2−b2....(1) is a tangent to the standard hyperbola.
If above tangent passes through (h,k) then (k−mh)2=a2m2−b2
(h2−a2)m2−2kmh+k2+b2=0....(2)
Above equation is quadratic in m therefore it has two roots m1 and m2.
Hence passing through a given point (h,k) there is a maximum of two tangents can be drawn to the hyperbola
m1+m2=2khh2−a2....(3)
therefore m1⋅m2=k2+b2h2−a2.....(4)
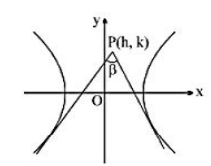
Equations (3) and (4) are used to find the locus of the point of intersection of a pair of tangents which enclose an angle β.
tan2β=(m1+m2)−4m1m2(1+m1m2)2
(substituting the values of m1+m2, and m1m2 to get the locus)
If β=90° then m1m2=1, hence from (4)
k2+b2=a2−h2
x2+y2=a2−b2 which is the equation of director circle
Example 5
The equation of the transvers and conjugate axes of a hyperbola are, respectively, x+2y−3=0 and 2x−y+4=0, and their respective lengths are √2 and 2√3.. The equation of the hyperbola is
The equation of the hyperbola is
(2x−y+4√5)21/2−(x+2y−3√5)1/3=1
or, 25(2x−y+4)2−35(x+2y−3)2=1
Example 6
If the line lx+my+n=0 touches the hyperbola x2a2−y2b2=1. Then
The equation of the line is
lx+my+n=0⇒y=(−lm)x+(−nm)……(i)
We know that the line y=mx+c touches the hyperbola
x2a2−y2b2=1 if c2=a2m2−b2.
So, line (i) will touch x2a2−y2b2=1, if
(−nm)2=a2(−lm)2−b2⇒n2=a2l2−b2m2
Example 7
The equation of the tangent to the hyperbola 3x2−y2−3 which is perpendicular to the line x+3y−2=0 is
Let m to be the slope of the tangent to the given hyperbola. Then,
m×(Slope of the linex+3y=2)=−1
⇒m×(−13)=−1⇒m=3
The equation of the hyperbola is
3x2−y2=3⇒x21−y23=1
This is of the form x2a2−y2b2=1, where a2=1 and b2=3.
So, the equation of the tangents are
y=mx±√a2m2−b2
or, y=3x±√9−3⇒y=3x±√6
Example 8
The line 2x+y=1 is tangent to the hyperbla x2a2−y2b2=1. If this line passes through the point of intersection of the nearest directrix and the x-axis, then the eccentricity of the hyperbola is
It is given that 2x+y=1 passes through the point (a/e,0).
∴2ae=1⇒a=e2
Since 2x+y=1 i.e. y=−2x+1 touches the hyperbola x2a2−y2b2=1.
∴12=a2(−2)2−b2 [Using : c2=a2m2−b2]
⇒4a2−b2=1
⇒4a2−a2(e2−1)=1 [∵b2=a2(e2−1)]
⇒e2−e24(e2−1)=1 [∵a=e2]
⇒5e2−e4=4
⇒e4−5e2+4=0⇒(e2−1)(e2−4)=0⇒e=2
Equation of Normals
( 1 ) Point form:
Equation of normal to a hyperbola = x2a2−y2b2=1 at a point (x1,y1) is
a2xx1−b2yy1=a2+b2
( 2 ) Parametric form:
The equation of normal at (asecϕ,btanϕ) to the hyperbola x2a2−y2b2=1 is
axcosϕ+bycotϕ=a2+b2
Properties
( 1 ) Normal and tangent at any point P(x,y) meet the transverse axis at G and T respectively.The equation of normal at P on the hyperbola x2a2−y2b2=1 is
a2xx1+b2yy1=a2+b2.....(1)
The normal (1) meets the x-axis i.e. then put y=0 in (1) we will get co-ordinates of G((a2+b2a2)x1,0) or (e2x1,0)
CG=e2x1
Now, SG=CG—CS=e2x1−ae=e(ex1−a)=e⋅SP
Similarly, S’G=e⋅S’P
SGS’G=SPS’P
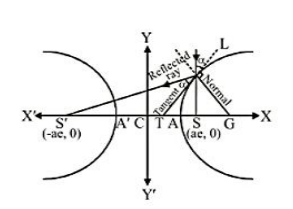
This relation shows that the normal PG is the external bisector of the angle SPS’. The tangent PT (perpendicular to PG) is therefore the internal bisector of the angle SPS’.
The tangent & normal at any point of a hyperbola bisect the angle between the focal radii.
Note : That the ellipse x2a2−y2b2=1 and the hyperboIa x2a2−k2−y2b2−k2=1(a>k>b>0) are confocal and therefore orthogonal.
( 2 ) The tangent & normal at any point of a hyperbola bisect the angle between the focal radii. This spells the reflection property of the hyperbola as “An incoming light ray” aimed towards one focus is reflected from the outer surface of the hyperbola towards the other focus. It follows that if an ellipse and a hyperbola have the same foci, they cut at right angles at any of their common point.
( 3 ) Locus of the feet of the perpendicular drawn from focus of the hyperbola x2a2−y2b2=1 upon any tangent is its auxiliary circle i.e. x2+y2=a2 & the product of the feet of these perpendiculars is b2 i.e., square of semi-conjugate axis.
Similar property exists in ellipse also.
( 4 ) The portion of the tangent between the point of contact & the directrix subtends a right angle at the corresponding focus.
( 5 ) The foci of the hyperbola and the points P and Q in which any tangent meets the tangents at the vertices are concyclic with PQ as diameter of the circle.
Example 9
The equation of the tangent to the hyperbola 3x2−y2−3 which is perpendicular to the line x+3y−2=0 is
Let m to be the slope of the tangent to the given hyperbola. Then,
m×(Slope of the linex+3y=2)=−1
⇒m×(−13)=−1⇒m=3
The equation of the hyperbola is
3x2−y2=3⇒x21−y23=1
This is of the form x2a2−y2b2=1, where a2=1 and b2=3.
So, the equation of the tangents are
y=mx±√a2m2−b2
or, y=3x±√9−3⇒y=3x±√6
Example 10
Let P(asecθ,btanθ)andQ(asecϕ,btanϕ) (where θ+ϕ=π2 be two points on the hyperbola x2a2−y2b2=1 If (h,k) is the point of intersection of the normals at PandQ then k is equal to
The coordinates (h,k) of the point of intersection of the normals at P and Q are given by
h=−(a2+b2a)cos(θ−ϕ2)cosθcosϕcos(θ+ϕ2)
and, k=−(a2+b2a)tan(θ+ϕ2)tanθtanϕ.
We have, θ+ϕ=π2
k=−(a2+b2b)tan.π4tanθcotθ⇒k=−(a2+b2b)
Example 11
If the normal at 'θ' on the hyperbola x2a2−y2b2=1 meets the transverse axis at G, and A and A' are the vertices of the hyperbola , then AC.A'G=
The equation of the normal at (asecθ,btanθ) to the given hyperbola is
axcosθ+bycotθ=(a2+b2)
This meets the transverse axis i.e.x-axis at G. So, the coordinates of G are (a2+b2asecθ,0).
The coordinates of the vertices A and A' are A(a,0) and A'(−a,0) respectively.
∴AG.A'G=(−a+a2+b2asecθ)(a+a2+b2asecθ)
⇒AG.A'G=(−a+ae2secθ)(a+ae2secθ)=a2(e4sec2θ−1)
Example 12
If the tangent and normal to a rectangular hyperbola cut off intercepts a1 and a2 on one axis and b1 and b2 on the other, then
Let the equation of the rectangular hyperbola be
x2−y2=a2
and, let P(asecθ,atanθ) be a point on it.
The equations of the tangent and normal at P are
xsecθ−ytanθ=a……..(i)
and, xcosθ+ycotθ=2a..........(ii)
It is given that the tangent at P cuts off intercepts a1 and b1 on the coordinate axes. Therefore,
a1=acosθ and b1=−acotθ
The normal at P cuts off intercepts a2 and b2 on the coordinate axes. Therefore,
a2=2asecθ and b2=2atanθ
Now,
a1a2+b1b2=acosθ×2asec(θ)+(−acotθ)(2atanθ)
⇒a1a2+b1b2=2a2−2a2=0