APPLICATION OF INTEGRALS for Class 12 MATHS
Introduction
Hello bachcho, ab hum padhenge Application of Integral ke baare mein. To bachcho ye chapter aisa hai jismei apki abhi tak ki sari knowledge use hogi. Aap ne jitna bhi calculus mein padha hai Limits, Continuity and Differentiability, Application of Derivative and Integration sb kuch use hoga. To jaise humne pehle Differentiation padha tha phir uski applications dekhi thi theek usi tarh se abhi humne Integration pdha hai aur ab hum uski applications padhenge jisme humey pta chalega ki integration ka daily life mein use kya hai. To bachcho aapne abhi tak simple curves like circle, rectangle, square, quadrilateral etc. ke hi area padhe hai, lekin ab hum complex figues ka area integration ki help se nikalna sikhenge.
Basic Concepts
To dekho bachcho aap sabhi ne coordinate geometry to padhi hai to chalo hum usko revise kar lete hai.
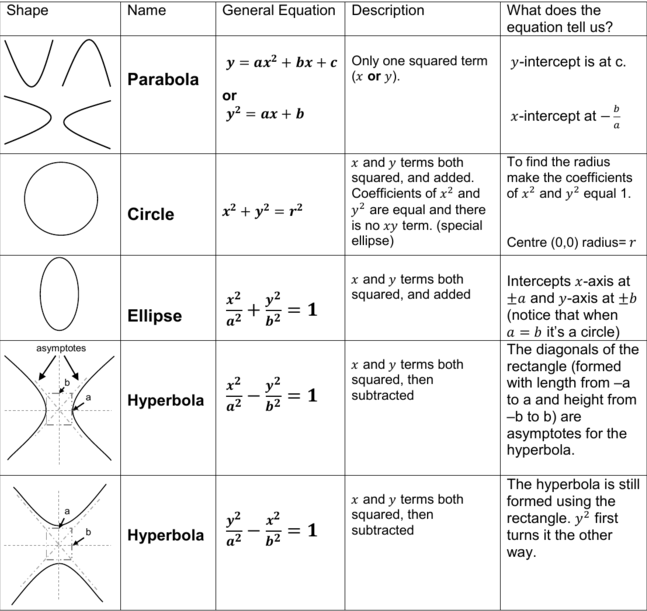
1. Equation of Line
- Slope Form : y=mx+b
- Point Slope :
y−y1=m(x−x1)
where m is the slope (x1,y1) is a point on the line. - Standard Form :
ax+by=c - Intercept Form :
xa+yb=1
a is x-intercept and b is y-intercept
Vertical x=a, vertical line with a as the x-intercept
Horizontal y=b, horizontal line with b as the y-intercept
where m is the slope and b is the y-intercept.
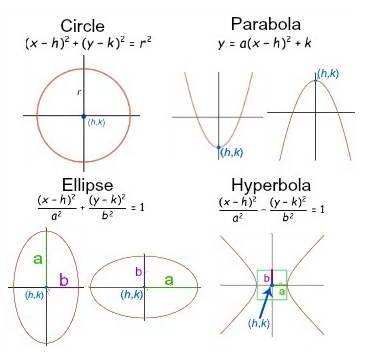
- Centre (h,k)
Radius (r)
Equation of circle :
(x−h)2+(y−k)2=r2
3. Parabola
- Horizontal Axis
x=a(y−k)2+h - Vertical Axis
y=a(x−h)2+k
4. Ellipse
- Horizontal Axis
(x−h)2a2+(y−k)2b2=1
a2>b2
f=√a2−b2
where f is focii of ellipse. - Vertical Axis
(x−h)2b2+(y−k)2a2=1
b2>a2
f=√b2−a2
where f is focii of ellipse.
5. Hyperbola
- (x−h)2a2−(y−k)2b2=1
f=√a2+b2
where f is focii of hyperbola - (y−k)2b2−(x−h)2a2=1
f=√a2+b2, where f is focii of hyperbola.
Area under Simple Curves
To dekho bachcho pichle chapter mein humne area bounded by the curve nikalna sikha tha like for the curve y=f(x), the ordinates x=a, x=b and x-axis, while calculating definite integral as the limit of a sum. To dekho agar bounded area koi specific figure nahi hai to aap kaise nikalenge. Us case mein hum bounded region ko rectangular strips mein divide kar lenge let it's length be y and width dx. To ab hume area nikalna hai. So what is area of rectangle ? i.e. Length×Breadth. So, Area = ydx. To hume to puri figure ka area chahiye to uske liye hum integration ka use karenge because integral mein hum limit as a sum hi to lete hai. 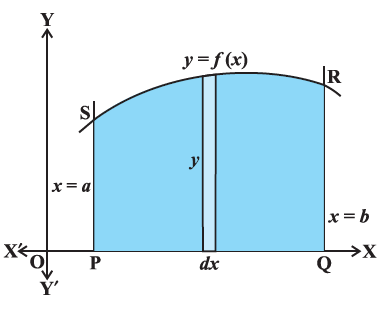
To ab jaise apko es figure mein
PQRSP region ka area nikalna hai to yha pe hum limit consider karenge PS x-axis ko x=a maan
lenge aur QR ko x=b, to ab hum a to b ka area nikalne ke liye area of elementary strip nikalenge.
So, area of PQRSP
A=∫badA = ∫baydx = ∫baf(x)dx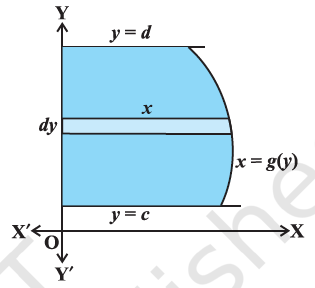
Similarly area A region bounded by curve x=g(y), y-axis and line y=c, y=d given by,
A = ∫dcxdy = ∫dcg(y)dy
To dekho kabhi-kabhi condition asi bhi ho sakti hai jab humara bounded region ye ho 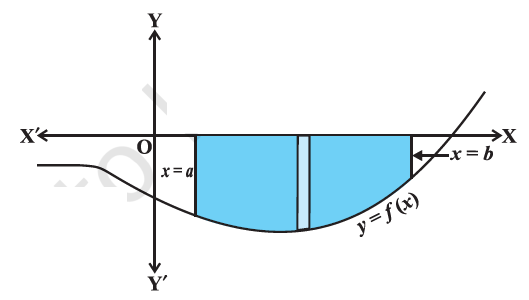
to es case mein area x-axis ke neeche lie kar rha hai that means it would be negative aur area to kabhi negative nahi hota to isliye absolute value nikalne ke liye hum humesha | |
mod consider karenge.
So, see here area is below the x-axis f(x)<0 from x=a to x = b
Thus area is ∣∣∣∫baf(x)dx∣∣∣
Now, consider this figure ismei kuch area x-axis ke upar hai kuch neeche to isko hum do part mein divide kar lete hai let first one be A1 and second one be A2. So, A1<0 and A2>0. Therefore the area A bounded by the curve y=f(x), x-axis from a to b is A=|A1|+A2 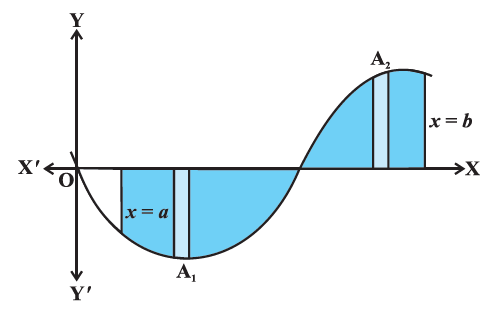
Example 1
Find the area of the circle x2+y2=a2 with radius a.
x2+y2=a2
The center of this circle is (0,0) and radius is 'a'. X - axes and Y - axes divide the circle into 4 symmetric parts.
Now, x2+y2=a2
⇒y=±√a2−x2
In first quadrant,
y=√a2−x2 (because first quadrant mein y positive hota hai)

Co-ordinates of points O and A are (0,0) and (a,0) respectively. Now area of region bounded by the circle, X-axis, x=0 and x=a
= Area of OABO
=∫a0y dx=∫a0√a2−x2dx
=[x2√a2−x2+a22sin−1xa]a0
=(0+a22sin−11)−(0+0)
=a2π2×2=14πa2
∴ Area of circle =4×Area of OABO
=4×14πa2=πa2sq. units.
Note : Bachcho agar circle ka radius a given hai tab area kya hoga by direct formula ?
Area of circle = π×a2
Hence verified.
The area of the region bounded by a curve and a line
Es section mein hum area of region bounded by a line and a circle, a line and a parabola, a line and an ellipse ke baare mein janenge. To dekhiye ab hum complexity ki aur badh rhe hai.
Example 2
Find the area of the region bounded by the parabola x2=4y and the line x=4y−2.
The given curve is x2=4y ...eq(i)
The given line is x=4y−2 ...eq(ii)
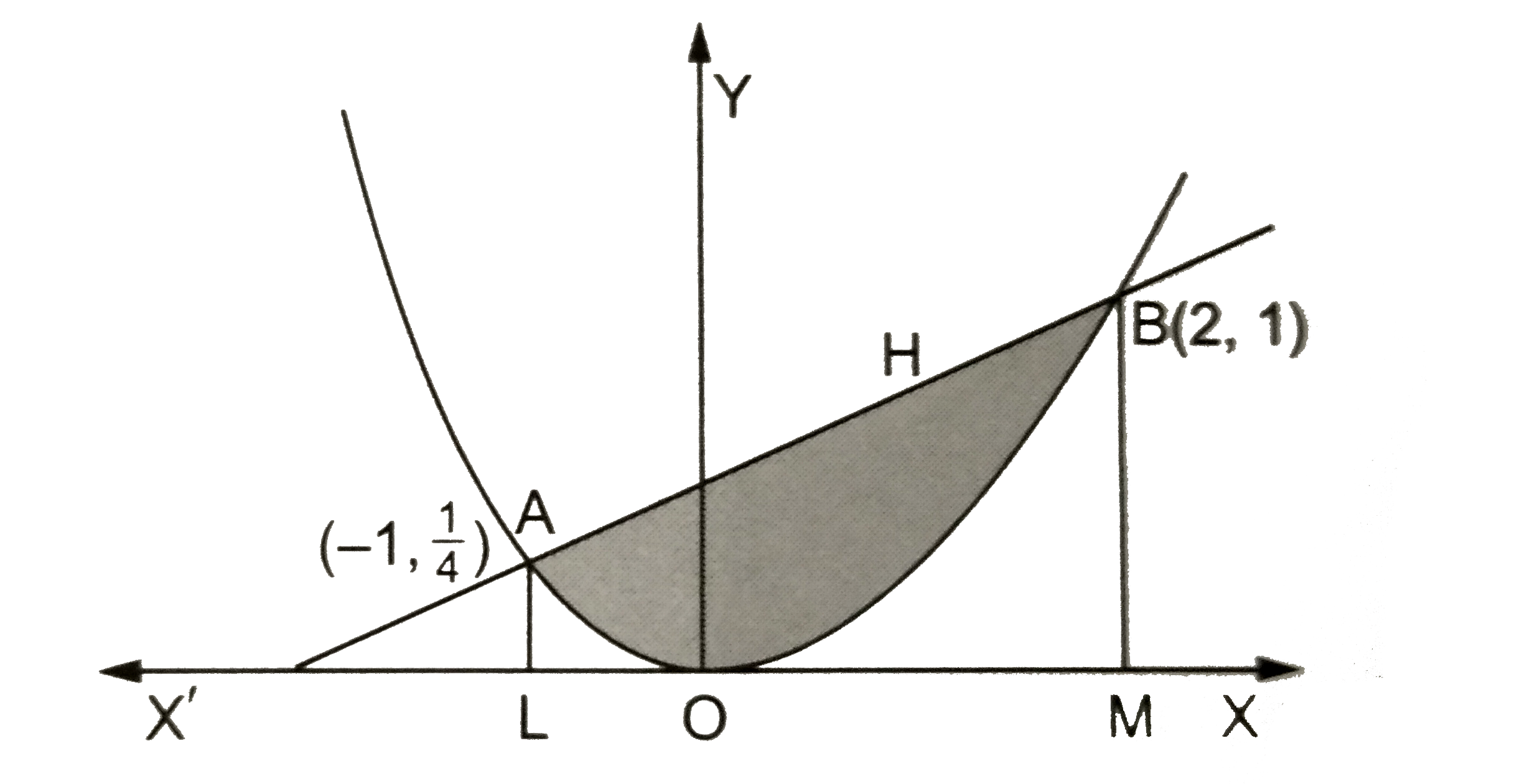
Putting 4y=(x+2) from (ii) into (i) we get
x2=(x+2)⇔(x2−x−2)=0
⇔(x−2)(x+1)=0
⇔x=2orx=−1
Putting x=2 in (i) we get y=1
Putting x=−1 in (i) we get y=14
Thus the points of intersection of the given curve (i) and the line (ii) are A(−1,14) and B(2,1)
Draw AL and BM are perpendiculars on the x−axis
∴ Required area = area AOBA
=(area ALMBA) - (area AOBMLA)
=2∫−1(x−24)dx−2∫−1(x24)dx
=2∫−1{(x+24)−x24}dx=14[x22+2x=x33]2−1
14[(2+4−83)−(12−2+13)]=98 sq units
Example 3
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Sabse phle hum sabhi sides ki equation likhenge. (By using two point formula)
The equation of side AB is
y−0x−2=5−04−2⇒y=52(x−2)
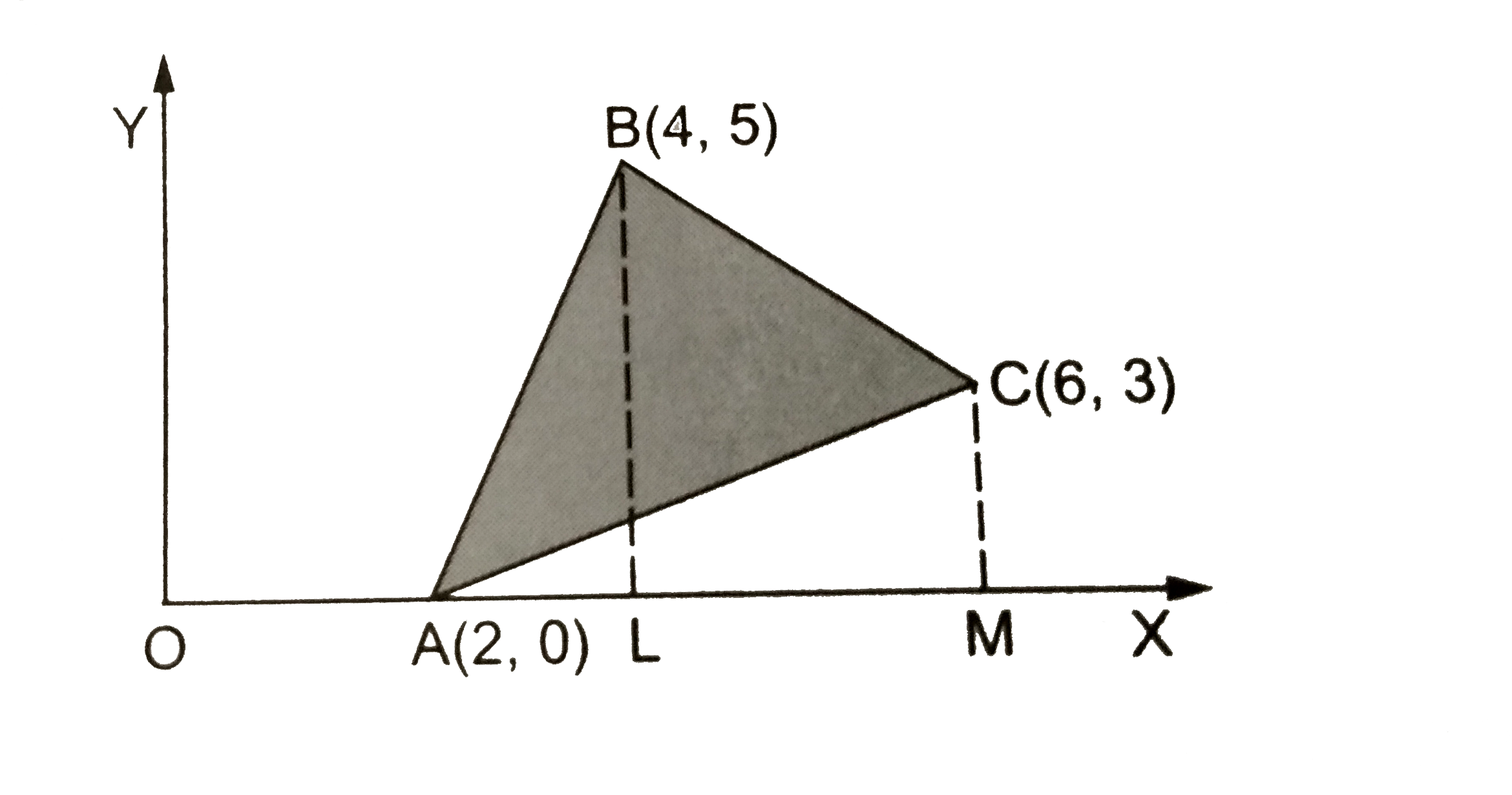
The equation of side BC is
y−5x−4=3−56−4⇒y=−x+9
The equation of side AC is
y−0x−2=3−06−2⇒y=34(x−2)
Draw perpendiculars BL and CM on the x-axis
∴ area of ΔABC
=ar(ΔALB)+ar(trap.BLMC)−ar(ΔAMC)
=4∫2yABdx+6∫4yBCdx−6∫2yACdx
=524∫2(x−2)dx+6∫4(9−x)dx−346∫2(x−2)dx
=52[x22−2x]42+[9x−x22]64−34[x22−2x]62
=52[0−(−2)]+(36−28)−34[6−(2−4)]
= (5+8−6) sq units = 7 sq units.
Example 4
Find the area of the smaller region bounded by the ellipse x2a2+y2b2=1and the line xa+yb=1
The ellipse x2a2+y2b2=1 and the line xa+yb=1 can be drawn as shown in the given figure 
Then, we have of the area of the shaded region.
Required area
= {area between x2a2+y2b2=1 and the x-axis from x=0 to x=a }
- {area between the line xa+yb=1 and the x-axis from x=0 to x=a }
=a∫0(y of the ellipse)dx−a∫0(y of the line x)dx
a∫0ba.√a2−x2dx−a∫0b(a−x)adx
=ba.⎡⎢
⎢⎣x(√a2−x2)2+a22sin−1xa⎤⎥
⎥⎦a0−ba.[ax−x22]a0
=ab2(sin−11−sin−10)−(ab−ab2)=(πab4−ab2)sq units
Hence, the required area is (πab4−ab2)sq units.
Area between Two Curves
Bachcho integration mein kisi large region ka area nikalne ke liye hume usse elementary regions mein divide karna hota hai uske baad kisi region ka area nikalkey unhey add karney se humey uss large region ka area mil jata hai. Now, suppose hume do curve diye gye hai y=f(x), y=g(x) jha f(x)≥g(x) in [a,b] jsa ki figure mein diya gya hai. Ab in dono curve ka intersecting point hai x=a and x=b. To ab humne integral formula set up karna hai. So, uske liye convenient hoga ki hum vertical elementary strip le. To yha pe iska length hum y maan lete hai to yani length kitni ho jayegi upper curve minus lower curve i.e. f(x)−g(x) and width dx.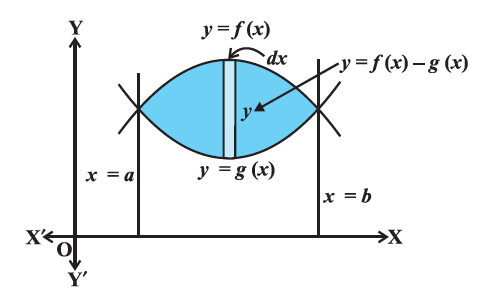
So, elementary area
dA=[f(x)−g(x)]dx and total area A
A=∫ba[f(x)−g(x)]dx
Ab if agar curve es tarh se given ho. 
To yha pe hum dekh sakte hai ki do region aapas mein add ho rhe hai.
See in given figure f(x)≥g(x) in [a,c] and f(x)≤g(x) in [c,d] where a<c<b, then the area of the regions bounded by curves can be written as
Total area = Area of the region ACBDA + Area of the region
BPRQB
=∫ca[f(x)−g(x)]dx+∫bc[g(x)−f(x)]dx
Example 5
Find the area of the region bounded by x2=4y, y=2,y=4and the y-axis in the first quadrant.
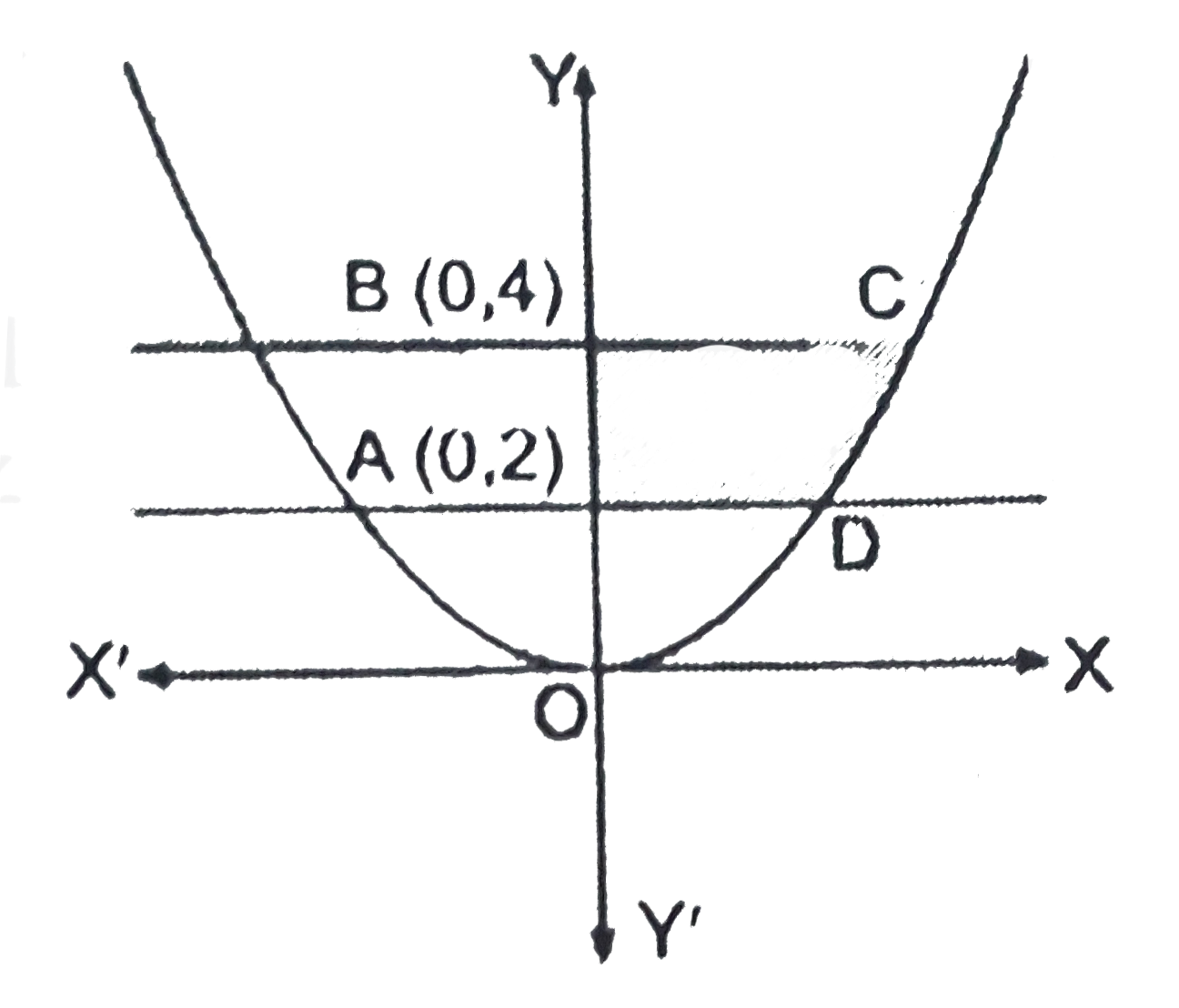
Equation of parabola x2=4y.
Area of region bounded by x2=4y,y=2,y=4 and Y-axis
= Area of ABCDA
=∫42x dy==∫422√y dy
=2.[y3/23/2]42=43[43/2−23/2]
=43(8−2√2)sq. units
=83(4−√2)sq. units
Example 6
Using the method of integration find the area bounded by the curve |x|+|y|=1 [Hint : The required region is bounded by lines x+y=1,x−y=1,x+y=−1 and y−x=1].
Given curve, |x|+|y|=1

In first quadrant (x>0,y>0) then line AB is
x+y=1.
In second quadrant (x<0,y>0) then line BC is
−x+y=1.
In third quadrant (x<0,y<0) then line CD is
−x−y=1.
In fourth quadrant (x>0,y<0) then line DA is
x−y=1.
Since ABCD is a square
Therefore, required area = 4 × (area of shaded region in first quadrant)
=4∫10(1−x)dx
=4[x−x22]10=4[(1−12)−0]
=2 sq. units.
Example 7
Find the area bounded by the curve y=sinx between x=0 and x=2π.
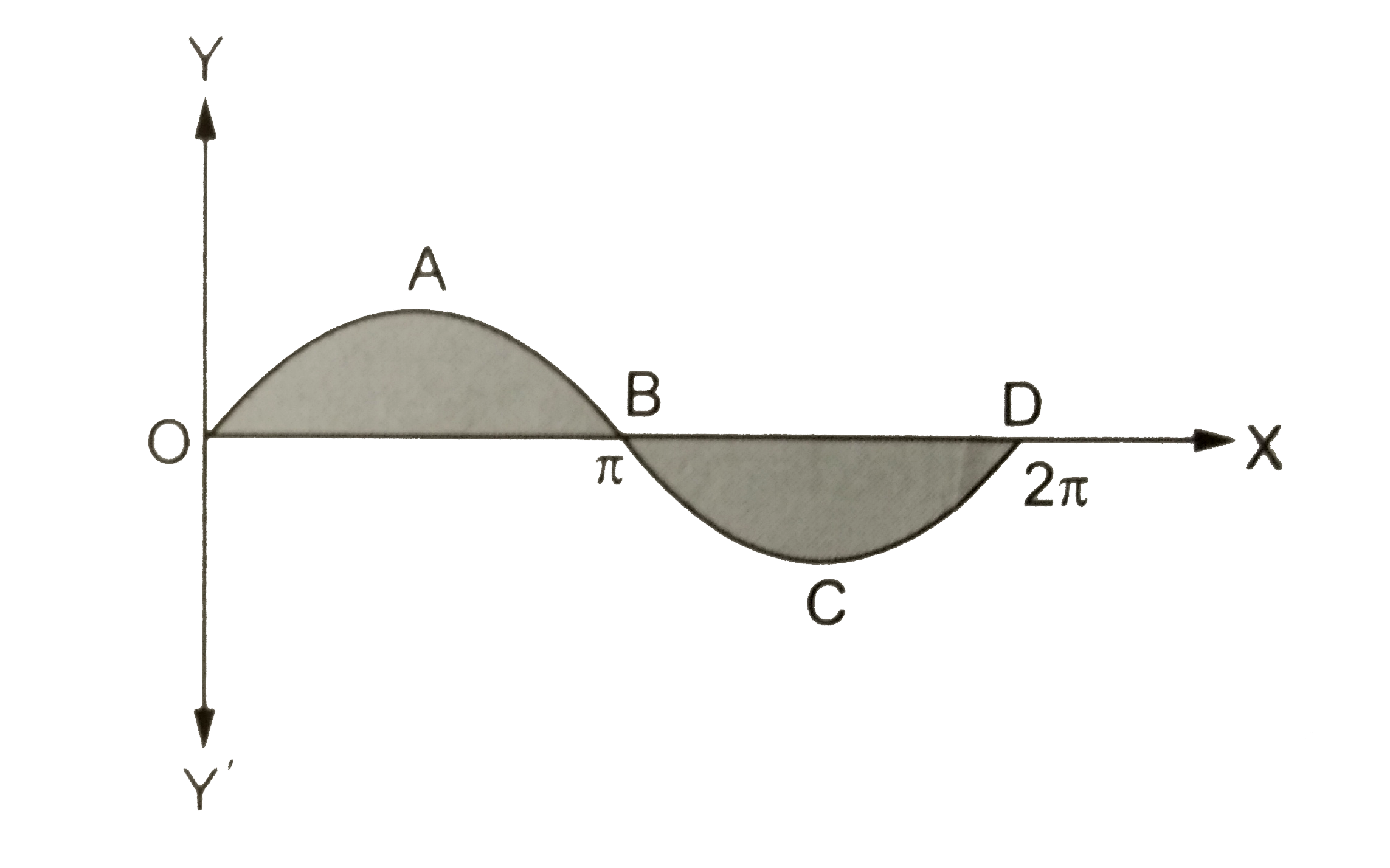
We have to draw the graph of y=sinx
Therefore,
Required area =Area OABO + Area BCDB
=∫π0sinxdx+∣∣∣∫2ππsinxdx∣∣∣
=[−cosx]π0+∣∣[−cosx]2ππ∣∣
=[−cosπ+cos0]+|−cos2π+cosπ|
=1+1+|(−1−1)|
=(2)+|−2|
=4 units.
Example 8
Find the area of region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}.
Let R={(x,y):0≤y≤(x2+1),0≤y≤(x+1),0≤x≤2}
={(x,y):0≤y≤(x2+1)}∩{(x,y):0≤y≤(x+1)}∩{(x,y):0≤x≤2}
=R1∩R2∩R3.
Clearly, R1 is the region consisting of the right-hand side of the y-axis, lying below the parabola y=x2+1.
Also, R2 is the region consisting of the right-hand side of the y-axis, lying below the line y=(x+1)
And R3 is the region above the axis, lying between the ordinates x=0 and x=2
Thus R1∩R2∩R3 is the shaded region.
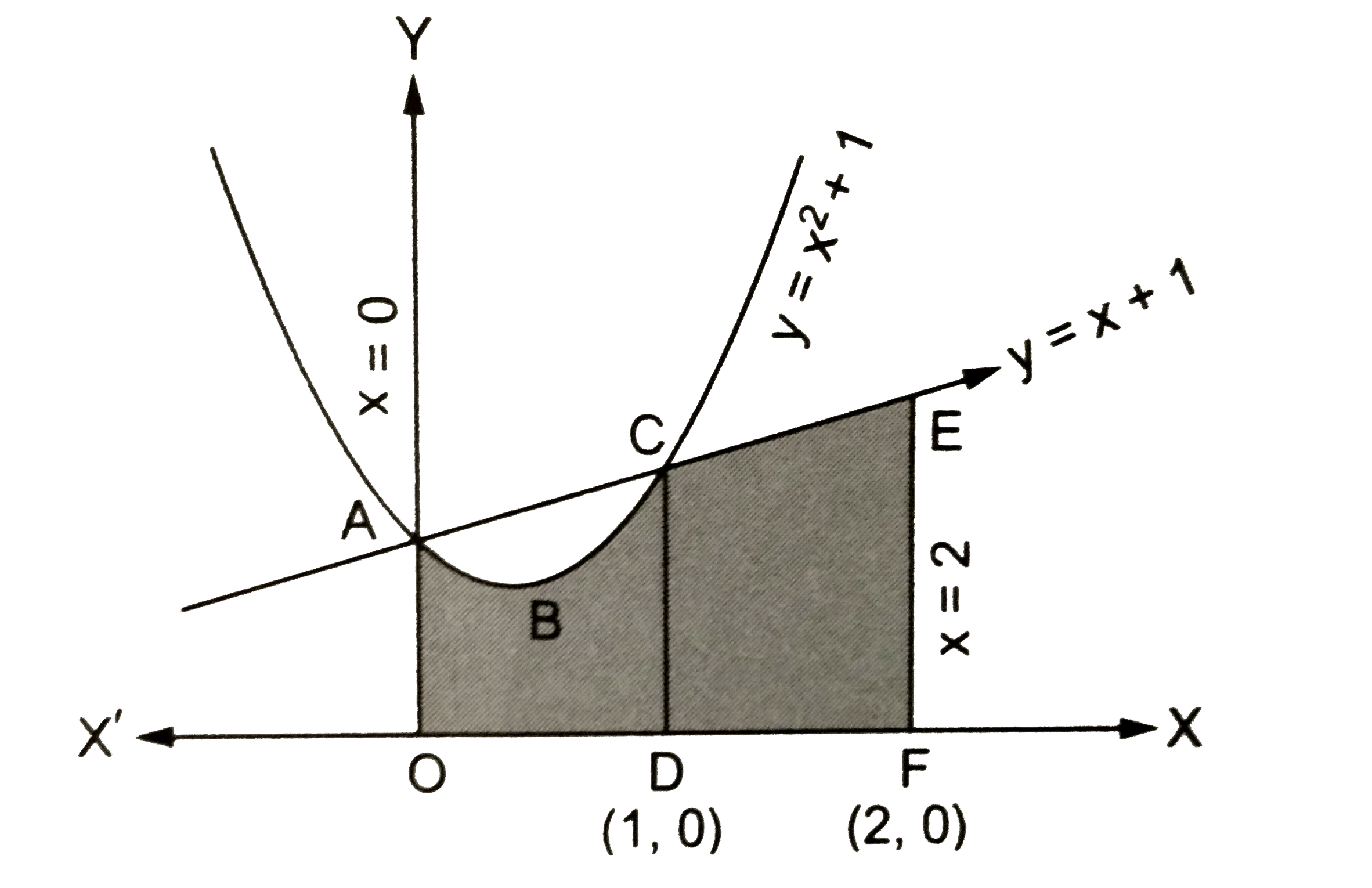
We have, y=x2+1 and y=x+1
⇒x2+1=x+1⇒x(x−1)=0⇒x=0 or x = 1
Now, (x=0⇒y=1) and (x=1⇒y=2).
Thus, the parabola y=(x2+1) and the line y=x+1 intersect at the points A(0,1) and C(1,2) .
∴ Required area = area of the shaded region
= (area ODCBA) + (area CDFEC)
= 1∫0 (y of the parabola ) dx + 2∫1(y of the line ) dx
=1∫0(x2+1)dx+2∫1(x+1)dx
=[x33+x]10+[x22+x]21
=(13+1)+(4−32)=236
sq units .
Hence the required area is 236 sq units.
Summary
1. The area of the region bounded by the curve y=f(x), x-axis and the lines x=a and x=b (b>a) is given by the formula : Area = ∫baydx = ∫baf(x)dx.
2. The area of the region bounded by the curve x=ϕ (y), y-axis and the lines y=c, y=d is given by the formula : Area ∫dcxdy=∫dcϕ(y)dy.
3. The area of the region enclosed between two curves y=f(x), y=g(x) and
the lines x=a, x=b is given by the formula,
Area = ∫ba[f(x)−g(x)]dx, where, f(x)≥g(x) in [a,b].
4. If f(x)≥g(x) in [a,c] and f(x)≤g(x) in [c,d], a<c<b, then
Area = ∫ca[f(x)−g(x)]dx+∫dc[g(x)−f(x)]dx.
Let's Revise
y=mx+c where m(m=y−y1x−x1) and is slope, (x_1, y_1) lies on that line and c is arbitrary constant.
- Bachcho jaisa ki humney padha hai ki kisi curve y=f(x), ordinates x=a, x=b (b>a) aur x−axis ke beech ka area humey definite integral (∫baf(x)dx=∫ba(y)dx) se pta chalta hai. Us region ka area nikalney ke liye hum us region ko elementary areas mein divide kartey hai aur fir sarey elementary areas ka sum karney se humey us region ka area mil jaata hai.
- Elementary area :
- Curve x=f(y), y−axis aur lines y=c, y=d (where d>c) ke beech ka area hum es formula se calculate kartey hai,
Area =∫dc(x)dy=∫dc(f(y))dy
- The area of the region enclosed between two curves y=f(x), y=g(x) and the lines x=a,x=b is given by the formula,
Area =∫ba[f(x)−g(x)]dx
where f(x)≥g(x) in [a,b].
- If f(x)≥g(x) in [a,c] and f(x)≤g(x) in [c,d], a>c>b, then we write the areas as :
Area =∫ca[f(x)−g(x)]dx+∫bc[g(x)−f(x)]dx.