SOUND WAVES for Class 11 PHYSICS

INTRODUCTION

Sound waves ek tarah se disturbance ka pattern hai jo ki energy ke movement ki wajah se hota hai through a medium ( jaise air, water aur koi bhi solid ya liquid matter) jo ki sound source se propagate hote hue aa rhi hai.
Source ek tarah ka object hai humara jo ki vibrations paida krta hai, such as ringing telephone or a person’s vocal chords.Toh jo vibrations paida ho rhe hai uss wajah se uss medium me jo particles hai unme disturbance paida hoga, and ek particle apne bagal waale particle me bhi disturbance create krdega and ye process chlti rahegi, toh baccho jo ye particle me disturbance hone ka jo pattern hai voh hai wave ke form me hota hai.

Baccho sound waves ko medium lgta hai propogate krne ke liye, otherwise ye propagate nhi hongi, isliye baccho sound waves vaccum me travel nhi krti hai.
Sound waves jo ki ek longitudnal waves hai voh reflect, refract, interfere and diffract but cannot be polarised kyunki keval transverse waves hi polarise ho sakti hai.

TYPES OF SOUND WAVES

INFRASONIC WAVES

Voh sound waves jinki frequency 0 se 20 Hz ke beech me lie kregi, use hum infrasonic waves bolte hai.

AUDIABLE WAVES

Voh sound waves jinki frequency 20 se 20000 Hz ke beech me lie kregi, use hum audiable waves bolte hai.

ULTRASONIC WAVES

Voh sound waves jinki frequency greater than 20000 Hz hoti hai, use hum ultrasonic waves bolte hai.
Agr

v_{s}

v_{l}

and

v_{g}

are the speed of sound waves in solid, liquid and gases then,

v_{s} > v_{l} > v_{g}

VELOCITY OF SOUND (LONGITUDNAL) WAVES

Sound waves ki jo velocity hoti hai voh medium ki elasticity and medium ki density prr depend krta hai.
Therefore jo velocity hoti hai sound waves ki voh hoti hai,
$v = \sqrt{\frac{E}{ρ}}$
Where E=coefficient of elasticity of the medium,
$ρ$ =density of medium

NEWTON’S FORMULA

According to newton, kisi bhi gas me longitudnal waves ka propagation ek isothermal process hoti hai.
Therefore ,
Velocity of sound (longitudnal) waves in a gas should be
$v = \sqrt{\frac{E_{T}}{ρ}} = \sqrt{\frac{p}{ρ}}$
Here $E_{T}$ = isothermal coefficient of volume elasticity and it is equal to the pressure of the gas.

LAPLACE’S CORRECTION

Baccho laplace correction me esa kuch nhi hai bss inhone bss newtons ko hi thoda correct kiya, inhone bola ki jo longitudnal waves voh ek adiabatic process hoti hai.
Toh inke hisaab se velocity of sound wave will become,
$v = \sqrt{\frac{E_{S}}{ρ}} = \sqrt{\frac{γ p}{ρ}}$

Where $E_{S}$ = adiabatic coefficient of volume elasticity and it is equal to $γ p$ .

FACTORS AFFECTING VELOCITY OF SOUND WAVE

EFFECT OF PRESSURE

Jaisa ki humne abhi upar dekha velocity of sound wave jo ki newton ne btatya,

v = \frac{\sqrt{p}}{ρ}

, that means

v \propto \sqrt{p}

and we know that

v \propto \sqrt{\frac{R T}{M}}

, therefore

\frac{p}{ρ}

humesha constant rahega kyunki temperature constant hai (isothermal process).
Iska mtlb hai ki sound wave ki velocity prr pressure ka koi effect nhi hota hai.

EFFECT OF TEMPERATURE

Agr laplace se baat ki jaye toh unhone correction kiya tha ki velocity of sound wave,

v = \sqrt{\frac{γ p}{ρ}}

that means

v \propto \sqrt{p}

v \propto \sqrt{\frac{R T}{M}}

Hence,

v \propto \sqrt{T}

Therefore

\frac{v_{1}}{v_{2}} = \sqrt{\frac{T_{1}}{T_{2}}}

EFFECT OF DENSITY

Velocity of sound wave is inversely proportional to square root of density,

v \propto \frac{1}{\sqrt{ρ}}

Therefore ,

\frac{v_{1}}{v_{2}} = \sqrt{\frac{ρ_{2}}{ρ_{1}}}

VIBRATION IN ORGAN PIPES

Jab do longitudinal waves with same frequency and same amplitude ek medium me travel krti hai voh bhi opposite directions me toh by the principle of superposition, standing waves produce hoti hai.
Inn waves ko hum air column me produce krte hai jo ki ek cylindrical tube hota hai with uniform diameter, esi sound producing tubes ko hum organ pipe bolte hai.

VIBRATION OF AIR COLUMN IN CLOSED ORGAN PIPE

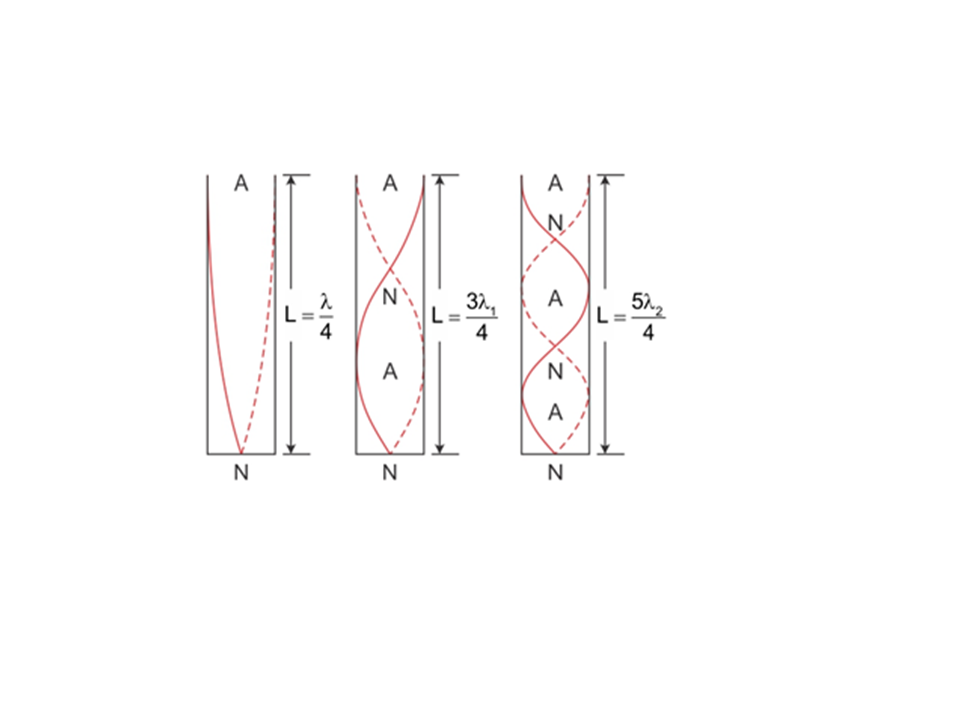
Aisa tube jiska ek end closed ho aur dusra end open ho, uske hum closed organ pipe bolte hai. Ab baccho jab hum open end se air ko blow krwaenge iss organ pipe me toh voh air travel kregi towards the closed end and closed end se reflect hoke vaps open end ki taraf travel kregi and again open end se closed end ke liye reflect ho jaegi. Toh do longitudnal waves opposite directions me travel kr rhi hai toh superposition hoga, and hume standing waves milengi. Closed end prr node banega kyunki waha ke particles ko freedom nhi hai vibrate krne ki and open end prr antinode banega kyunki open end ke particles ke aas sabse jyada freedom hogi vibrate krne ki.

Hence jab hum air blow krte hai closed organ pipe me, toh column vibrate krta hai and free end prr antinode bnata hai and closed end prr node bnata hai.
If

L

is the length of pipe,

λ

be the wavelength and

v

be the velocity of sound in organ pipe then,
Toh jaisa ki aap upar diagram me dekh paa rhe hoge, usme baar ka demo dikhaya hai,

Case 1

L = \frac{λ}{4}

, therefore

λ = 4 L

And frequency hogi,

n_{1} = v e l o c i t \frac{y}{λ}

n_{1} = \frac{v}{λ}

Hence

n_{1} = \frac{v}{4 L}

, baccho

n_{1}

humari frequency hai or ise hum fundamental frequency bolte hai.

Case 2

L = \frac{3 λ}{4}

, therefore

λ = \frac{4 L}{3}

And frequency hogi,

n_{2} = \frac{v}{λ}

n_{2} = \frac{3 v}{4 L}

, ise hum bolte hai First overtone/ 3rd harmonic

Case 3

L = \frac{5 λ}{4}

, therefore

λ = \frac{4 L}{5}

And frequency hogi,

n_{3} = \frac{v}{λ}

n_{2} = \frac{5 v}{4 L}

, ise hum bolte hai Second overtone/ 5th harmonic
Hence jab closed organ pipe mth overtime me vibrate krta hai toh,

L = (2 m + 1) \frac{λ}{4}

So,

λ = \frac{4 L}{2 m + 1}

And

n = (2 m + 1) \frac{v}{4 L}

VIBRATION OF AIR COLUMN IN OPEN ORGAN PIPE

Aisa tube jo dono end se open ho use hum open organ pipe bolte hai.
Jab hum air blow krate hai pipe me kisi ek end se toh ek open end se air travel krti hai toward other open end and then vaps air travel kregi towards first open end and ab inn dono longitudinal waves ka superposition krne prr hume standing waves milengi.
Ab jaisa ki hume pta hai ki dono hi end open hai and open ends rr antinodes bante hai, toh iss case me dono ends prr antinodes banega and beech me node banega.

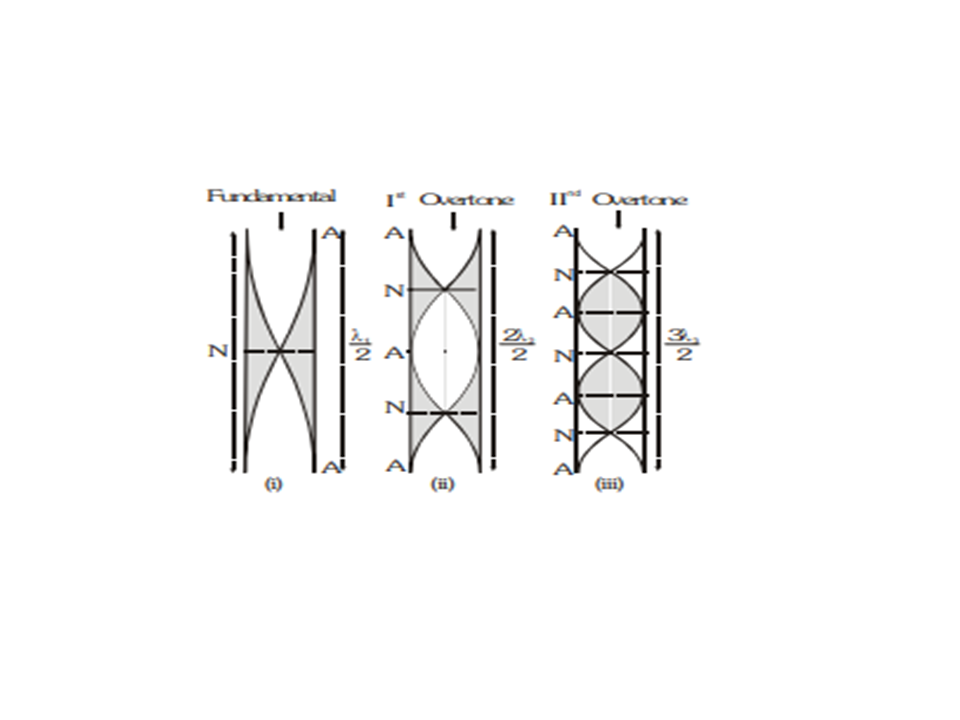
ocr_image

L

is the length of pipe,

λ

be the wavelength and

v

be the velocity of sound in organ pipe then,
Toh jaisa ki aap upar diagram me dekh paa rhe hoge, usme baar ka demo dikhaya hai, Case 1

L = \frac{λ}{2}

, therefore

λ = 2 L

And frequency hogi,

n_{1} = \frac{v e l o c i t y}{λ}

n_{1} = \frac{v}{λ}

Hence

n_{1} = \frac{v}{2 L}

, baccho

n_{1}

humari frequency hai or ise hum fundamental frequency bolte hai.

Case 2

L = \frac{2 λ}{2}

, therefore

λ = \frac{2 L}{2}

And frequency hogi,

n_{2} = \frac{v}{λ}

n_{2} = \frac{2 v}{2 L}

, ise hum bolte hai First overtone

Case 3

L = \frac{3 λ}{2}

, therefore

λ = \frac{2 L}{3}

And frequency hogi,

n_{3} = \frac{v}{λ}

n_{2} = \frac{3 v}{2 L}

, ise hum bolte hai Second overtone
Hence jab closed organ pipe mth overtime me vibrate krta hai toh,

L = (m + 1) \frac{λ}{2}

So,

λ = \frac{2 L}{m + 1}

And

n = (m + 1) \frac{v}{2 L}

BEATS

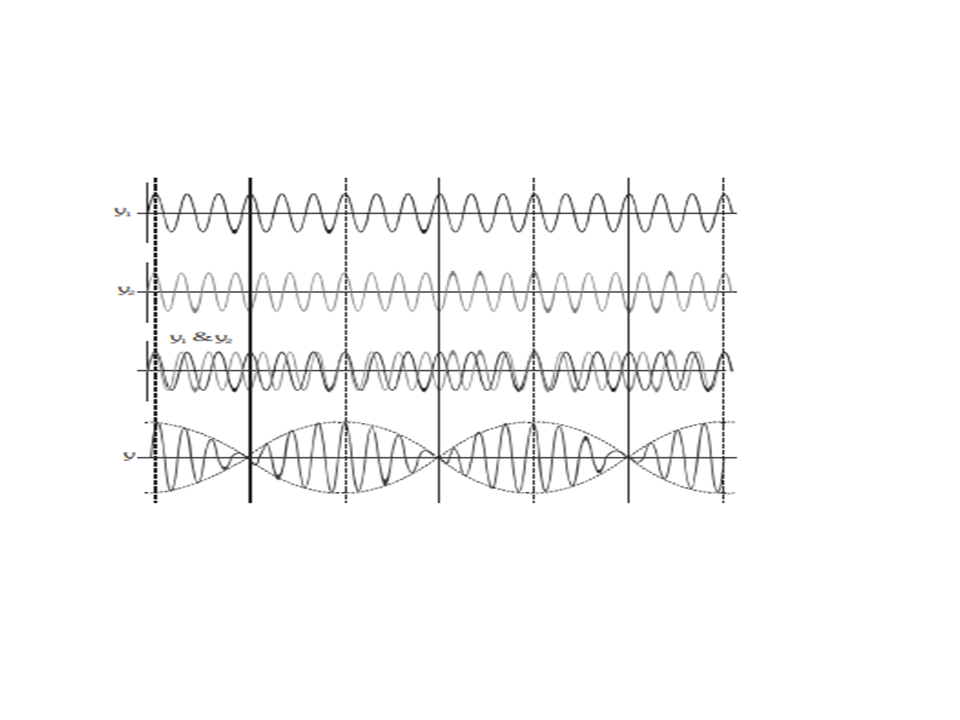
ocr_image

Jab do sound waves jinke amplitude same hai and voh same direction me travel kr rhi hai lekin unki frequencies me thoda sa diffrerence hai, jab inn wave ka superimposition hota hai toh milta hai ki intensity periodically vary kr rhi hai with time, isi effect ko hm beats bolte hai.
Jaisa ki aap diagram me dekh sakte hai, humne do sound waves li, then unka superimpostiion dekha, and them resultant wave aai.

Maan lijiye dono waves ki frequencies $f_{1}$ and $f_{2}$ or voh kisi point prr meet kr rhi hai in space and inka jo corresponding period hai voh $T_{1}$ and $T_{2}$ hai.
Agr dono waves kisi phase me hai at $t = 0$ then after one full cycle voh phirse same phase me honge or esa hoga after $t = T$ jo ki beats a period hai.

Let n be the number of cycles of the first wave in time T, then the number of cycles of the second wave in the same time is (n–1).
Hence $T = n T_{1} = (n - 1) T_{2}$

Now after eliminating n, we will get,
$T = \frac{T_{1} T_{2}}{T_{2} - T_{1}}$
$T = \frac{1}{\frac{1}{T_{1}} - \frac{1}{T_{2}}}$
Or $T = \frac{1}{f_{1}} - \frac{1}{f_{2}}$
And the reciprocal of the beat period is the beat frequency, $f = \frac{1}{T} = f_{1} - f_{2}$

ECHO

Jaisa baccho aapne deha hoga ki jab hum ek khaali room me kuch bolte hai toh aawaz gunjti hai lekin ek room jisme samaan rakha hua hai usme aawaz nhi gunjti hai, aawaz isliye gunjti hai khaali room me baccho kyunki sound waves ka reflection hota hai room ki walls se aur voh bhi multiple times aur isi phenomena ko hum echo bolte hai.
Maan lijiye reflector aur source ke beech ka distance $d$ hai, toh baccho wave kitna travel kregi? Voh $2 d$ distance travel kregi kyunki wave reflector se reflect hoke vaps source tk aaegi tabhi toh hume aawaz sunai degi vaps,
Toh maan lijiye agr v=velocity of sound and t=time of echo,
Therefore, $v = \frac{2 d}{t}$ or $d = \frac{v t}{2}$
Ab baccho agr hum ane ears ki baat krein toh jo ordinary sound ka effect humare ears me $\frac{1}{10}$ seconds ke liye hota hai,
Toh minimum distance of the reflector is $d = \frac{v t}{2}$ ,
$d = (\frac{330}{2}) (\frac{1}{10}) = 16.5 m$

DOPPLER’S EFFECT FOR SOUND WAVES

Baccho jab humara sound ka source, obsever adn medium jab ek relative motion me ho ek dusre ke saath, tab jo frequecy me changes aate hai use hum doppler’s effect bolte hai. Ab baccho hum isko derive krne ke liye kuch assumptions maanenge,

(i) The velocity of the source, the observer and the medium are along the line joining the positions of the source and the observer.
(ii) The velocity of the source and the observer is less than velocity of sound.

CASE I : Source moving, observer stationary

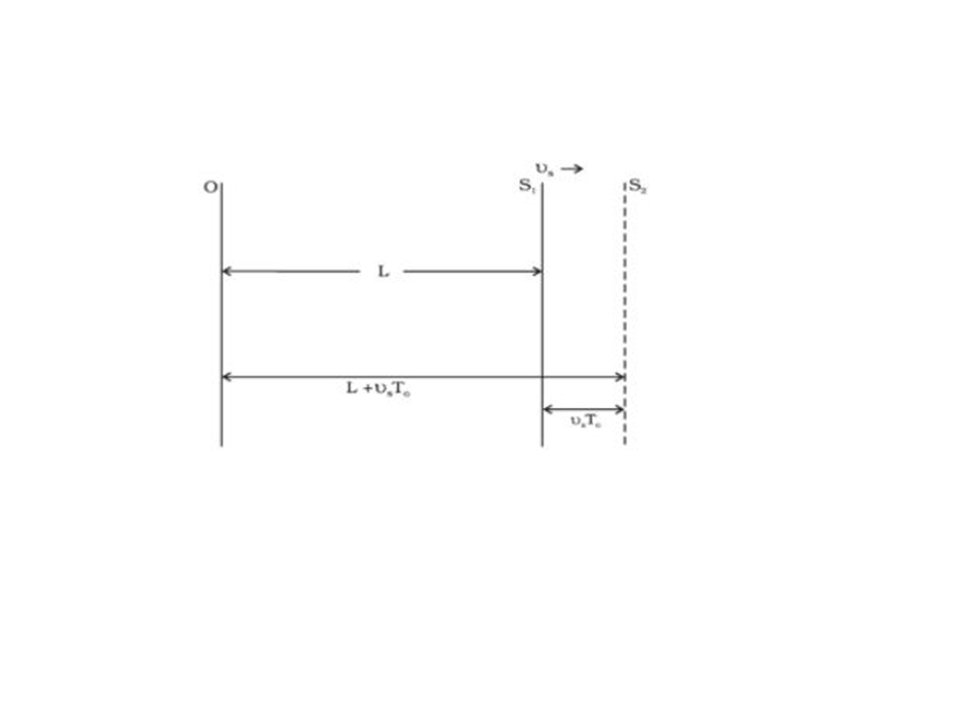
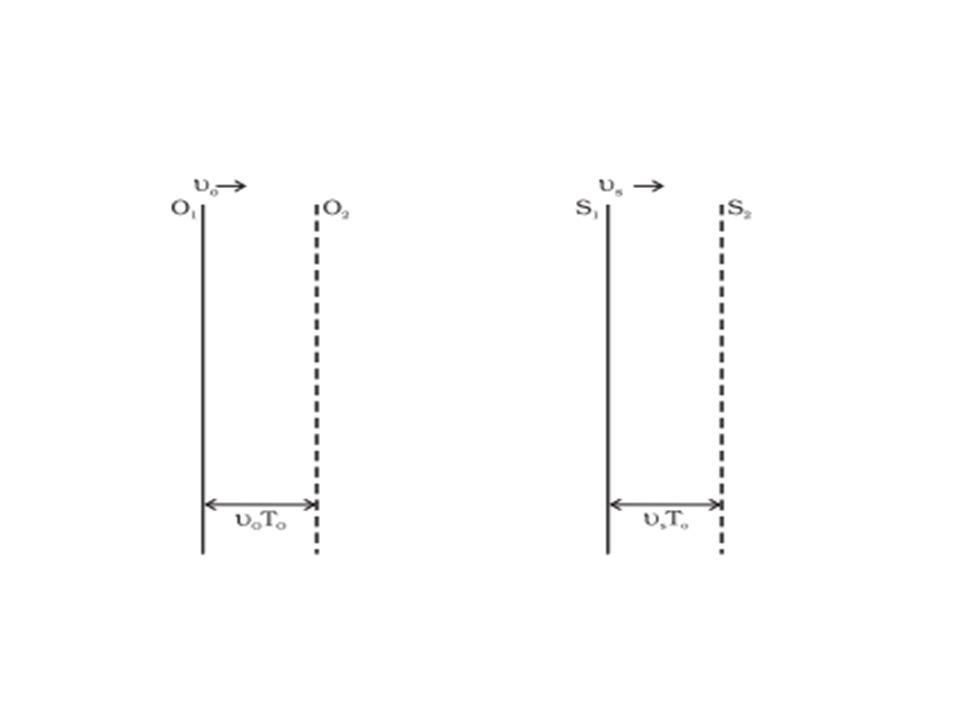
Jaisa ki aapko dikh rha hoga diagram me ki ek observer hai O prr and moving soruce ki initially position jab voh rest prr hai voh hai

S_{1}

and move krne ke baad uski position hai

S_{2}

and observer and

S_{1}

ki distance hai

L

.
And maan lijiye wave ki speed

v

hai jiski angular frequecy

ω

hai and time period

T_{0}

hai.
At

t = 0

humara source

S_{1}

prr hai, toh

t_{1} = \frac{L}{v}

time me wave observer ke pass pahuch jaegi, now source ki velocity

v_{s}

hai and time

t = T_{0}

ke baad voh

v_{s} T_{0}

distance cover krlega. Toh jo observer se distance hoga after moving the source voh hoga

(L + v_{s} T_{0})

. Ab

S_{2}

position prr dusra crest emit hoga, toh vh observer ke pass time

t_{2} = T_{0} + \frac{L + v_{s} T_{0}}{v}

.

And agr hum

n T_{0}

time ki baat krein toh jo source emit krega (n+1)th crest hogi, Toh observer ke pass time

t_{n + 1} = n T_{0} + \frac{L + n v_{s} T_{0}}{v}

me pahuchega.

Iska mtlb hai ki time period

[n T_{0} + \frac{L + n v_{s} T_{0}}{v} - \frac{L}{v}]

me jo observer hai use nth crest milegi and voh time period note krega,

T = [n T_{0} + \frac{L + n v_{s} T_{0}}{v} - \frac{L}{v}] / n

T = T_{0} + \frac{v_{s} T_{0}}{v}

T = T_{0} (1 + \frac{v_{s}}{v})

Ab hum isko frequency ke terms me bhi likh sakte hai,

ν = ν_{0} {(1 + \frac{v_{s}}{v})}^{- 1}

Ab jaisa ki hume pta hai ki

v_{s}

bhut chhota hai as compare to wave velocity, toh hum iska binomial expansion krdenge and higher powers ko neglect krdenge toh jo expression aaega voh hoga,
$ν = ν_{0} (1 - \frac{v_{s}}{v})$ , this is the frequency when source is going away from the observer,
And if we replace the sign of

v_{s}

- v_{s}

, then it will become
$ν = ν_{0} (1 + \frac{v_{s}}{v})$ , this is the frequency when source is approaching the observer.

CASE II : Observer moving, source stationary

Ab iss case me baccho observer move kr rha hai source ki taraf with velocity

v_{0}

, humare saare sign convections and notations same rahenge jo humne upar maana hai, toh iss case me observer approach kr rha hai source ko and uss time velocity hogi

v_{0} + v

, toh baccho jo time interval hoga first and (n+1)th crest me voh hoga,

t_{n + 1} - t_{1} = n T_{0} - \frac{n v_{0} T_{0}}{v_{0} + v}

,
Toh observer time period note krega wave ka voh hoga,
=

T_{0} (1 - \frac{v_{0}}{v_{0} + v})

T_{0} {(1 + \frac{v_{0}}{v})}^{- 1}

And frequency hogi,

ν = ν_{0} (1 + \frac{v_{0}}{v})

CASE III : Both Source and Observer Moving

Baccho iss case me observer and source dono move kr rhe hai with velocity

v_{0}

and

v_{w}

, initially at

t = 0

, huamra observer

O_{1}

prr hai and source

S_{1}

prr hai and source and observe ke beech ki distance

L

hai. Toh ab hum observer se baat krenge toh use wave ki speed

v + v_{0}

dikhegi and time

t_{1}

aaega

t_{1} = \frac{L}{v + v_{0}}

, now after time

t = T_{0}

, dono observer and source apni new position prr pahuch jaenge

O_{2}

and

S_{2}

, toh jo new distance observer and source ke beech me hoga voh hoga

L + (v_{s} - v_{0}) T_{0}

.
Ab source

S_{2}

prr second crest emit krega toh voh observer ke pass time,

t_{2} = \frac{T_{0} + [L + (v_{s} - v_{0}) T_{0}]}{v + v_{0}}

At time

n T_{0}

the source emits its (n+1)th crest and this reaches the observer at time

t_{n + 1} = \frac{n T_{0} + [L + n (v_{s} - v_{0}) T_{0}]}{v + v_{0}}

Hence , time interval

t_{n + 1} - t_{1}

that means,

\frac{n T_{0} + [L + n (v_{s} - v_{0}) T_{0}]}{v + v_{0}} - \frac{L}{v + v_{0}}

Observer count krta hai n crests and time period record krta hai

T = T_{0} (1 + \frac{v_{s} - v_{0}}{v + v_{0}})

T = T_{0} (\frac{v + v_{s}}{v + v_{0}})

Toh jo frequency observe hogi observer ke end prr voh hogi,

ν = ν_{0} (\frac{v + v_{0}}{v + v_{s}})

EXAMPLE 1

Estimate the speed of sound in air at standard temperature and pressure. The mass of 1 mole of air is $29.0 \times 10^{- 3} k g$ , $λ$ for air.

We know that 1 mole of any gas occupies 22.4 litres at STP. Therefore, density of air at STP is:
$ρ_{0}$ =(mass of one mole of air/(volume of one mole of air at STP)
$= \frac{29.0 \times 10^{- 3} k g}{22.4 \times 10^{- 3} m^{3}}$
$= 1.29 k g m^{- 3}$
According to Newton’s formula for the speed of sound in a medium, we get for the speed of sound in air at STP
$v = {[\frac{1.01 \times 10^{5} N m^{- 2}}{1.29 k g m^{- 3}}]}^{1 / 2} = 280 m s^{- 1}$

Learn more

EXAMPLE 2

A pipe 30.0 cm long is open at both ends. Which harmonic mode of the pipe resonates with a 1.1kHz source? Will resonance with the same source be observed if one end of the pipe is closed ? Take the speed of sound in air as $330 m s^{- 1}$ .

The first harmonic frequency is given by
$v_{1} = \frac{v}{λ_{1}} = \frac{v}{2 L}$ (open pipe)
where L is the length of the pipe. The frequency of its nth harmonic is:
$v_{n} = \frac{n v}{2 L}$ , for n=1,2,3,…(open pipe)
First few modes of an open pipe are shown in fig. 15.15
ocr_image

Learn more

EXAMPLE 3

Two sitar strings A and B playing the note 'Dha' are slightly out of tune and produce beats of frequency 5 Hz. The tension of string B is slightly increased and the beat frequency is found to decrease to 3 Hz. What is the original frequency of B, if the frequency of A is 427 Hz?

Increase in the tension of a string increases its frequency. If the original frequency of B ( ν B) were greater than that of $A (ν_{A})$ , further increase in $ν_{B}$ should have resulted in an increase in the beat frequency. But the beat frequency is found to decrease. This shows that $ν_{B} < ν_{A}$ . Since $ν_{A} - ν_{B} = 5 H z$ , and $ν_{A} = 427 H z$ , we get $ν_{B} = 422 H z$

Learn more

EXAMPLE 4

A rocket is moving at a speed of $200 m s^{- 1}$ towards a stationary target. While moving, it emits a wave of frequency 1000 Hz. Some of the sound reaching the target gets reflected back to the racket as an echo. Calculate the frequency of sound as detected by the person at the position of target and frequency of echo as detected by the rocket . Given velocity of sound $= 330 m s^{- 1}$ .

(1) The observer is at rest and the source is moving with a speed of 200 m $s^{- 1}$ . Since this is comparable with the velocity of sound, 330 m $s^{- 1}$ , we must use Eq. (15.50) and not the approximate Eq. (15.51). Since the source is approaching a stationary target, $v_{o} = 0$ , and $v_{s}$ must be replaced by $- v_{s}$ . Thus, we have
$v = v_{0} {(1 - \frac{v_{s}}{v})}^{- 1}$
$v = 1000 H z \times {[1 - 200 m s^{- 1} / 300 m s^{- 1}]}^{- 1}$
$≅ 2540 H z$
(2) The target is now the source (because it is the source of echo) and the rocket’s detector is now the detector or observer (because it detects echo). Thus, $v_{s} = 0$ and $v_{o}$ has a positive value. The frequency of the sound emitted by the source (the target) is v, the frequency intercepted by the target and not $v_{o}$ . Therefore, the frequency as registered by the rocket is
$v' = v (\frac{v + v_{0}}{v})$
$= 2540 H z \times (\frac{200 m s^{- 1} + 330 m s^{- 1}}{330 m s^{- 1}})$
$≅ 4080 H z$

Learn more

SUMMARY

* The speed of a transverse wave on a stretched string is set by the properties of the string. The speed on a string with tension T and linear mass density $μ$ is
$v = \sqrt{\frac{T}{μ}}$

* Sound waves are longitudinal mechanical waves that can travel through solids, liquids, or gases. The speed v of sound wave in a fluid having bulk modulus B and density $ρ$ is
$v = \sqrt{\frac{B}{ρ}}$

* The Doppler effect is a change in the observed frequency of a wave when the source (S) or the observer (O) or both move(s) relative to the medium. For sound the observed frequency ν is given in terms of the source frequency $ν_{0}$ by
$ν = ν_{0} (\frac{v + v_{0}}{v + v_{s}})$ .

Home
Ask Doubt
Profile