UNIT AND DIMENSIONAL ANALYSIS for Class 11 PHYSICS
INTRODUCTION
Sabhi physical quantity ka length, mass, weight, height jaise parameters measurement hai. Aur us physical quantity ko base se compare karne pr hume uska measurement mil jata hai, jiski values numbers (or numerical measures) me hoti hai. Koi bhi object jo apne aap me complete hai us object ko unit kahte hai, or physical quantity ke magnitude ko unit kahte hai. Quantity : Objects ke amount ko quantity kahte hai. Quantity ek property hai jo multitude (counting) or magnitude ko represent karta hai.
Unit of Measurement : Kisi bhi quantity ke definite magnitude ko unit of measurement kahte hai. Jaise length ek physical quantity hai aur uska unit meter hai.
Unit: kisi bhi quantity ko measure karne ya use kisi dusre quantity se compare karne ke liye jo standard hum use karte use Unit kahte hai.
Measurement = Quantity × Unit
kuchh special type ki quantity ko explain karne ke liye unit of measurement ko dimension bhi kahte hai.
Examples:-
- Ram 3 hours padhai karta hai, yaha ‘3’ quantity hai aur ‘Hour’ time ka unit hai.
- Ashok ka weight 80kg hai yaha ‘80’ quantity hai aur ‘kg’ weight ka unit hai.
- Ram 20cm akash se lamba hai yaha ‘20’ quantity hai aur ‘cm’ length ka unit hai.
Sabhi quantity ek dusre ke sath interdependent hote hai, jaise ki unit of length ko meter kahte hai to area ke unit ko hum (meter × meter) likhenge.
Types Of Unit
- Fundamental Unit :
- Yaha bahut sare physical quantity hai lekin hame inhe measure karne ke liye kuchh hi unit ki zarurat hai, kyuki sare quantity ek dusre se kisi na kisi prakar se link hote hai aur aise hi quantity ko measure karne ke liye jo base unit use hota hai wo fundamental unit kehlata hai.
- Derived Units:
- Jo physical quantity kisi aur quantity ke upar nirbhar hota hai, measurement ke liye use Derived quantity kahte hai, aur jo unit in derived quantity ko measure karta hai use Derived Units kahte hai.
System of Units :Base unit aur derived unit ke combine unit ko system of unit kahte hai.
THE INTERNATIONAL SYSTEM OF UNITS
Purane time me alag alag countries ke scientist alag unit system ko follow karte the aur wo system hai CGS, FPS, MKS. Is systems me base unit length, mass & time ko aisa likha jata tha:-
Metric system ke unit aur unit magnitudes ko ab internationally standardized kr diya gaya hai, ab isey International System Of Unit kahte hai jise short me SI unit kahte hai.
Yaha pe 7 basic ya fundamental units hai:-
In & units k alava do aur unit hote hai aur ye angle ko measure karta hai.
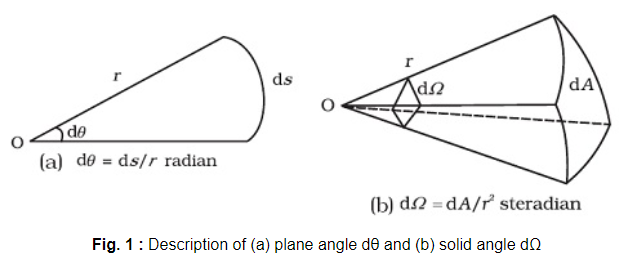
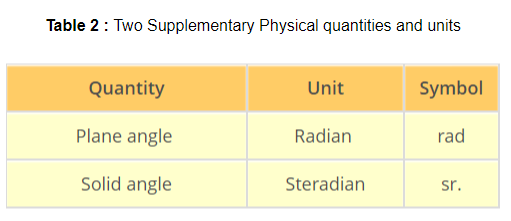
NOTE:
- Jab mole ka use kisi entity ke liye hota hai to us entity ko specific group me hona hoga jaise ki entities kuchh bhi ho sakte atoms, molecules, ions, electrons, other particles or specified groups of such particles.
POINT 1
Unit:
A unit is an internationally accepted standard for measurements of quantities. Measurement consists of a numeric quantity along with a relevant unit. Units for Fundamental or base quantities (like length, time etc.) are called Fundamental units. Units which are combination of fundamental units are called Derived units.MEASUREMENT OF LENGTHT
Length : Koi bhi 2 point ki doori ya kahen ki kisi bhi 2 point ke space koh length kahte hai. For eg. school aur mere ghar ki duri. Iska SI unit hai meter.
Jaise ki lenght ek small unit hai, use hum bade unit me bhi likh sakte hai example :
- Height is measured in 'foot' and 'inches', 1 feet contains 12 inches, and 1 inch means 0.0254 meters.
- Distance is measured in kilometers, 1 kilometer or Km equals 1000 meter.
- Jab Physics lab me hum experiment karte hai tab hum small units like millimeter and centimeter ka use karte hai, 1 meter = 100 centimeters, and 1 centimeter = 10 millimeters, to avoid writing meter, again and again, we write centimeter as ‘cm’, millimeter as ‘mm’ and decimeter as ‘dm’.
Hum length ko apne hisab se measure karte hai ki wo hamesha correct ho aur error free ho.
Hum length ko measure karne ke liye kuchh method jante hai. Eg. jab hum chhoti class me the tab hum line draw ke liye centimeter scale use karte the. Agar object ka nature badalta hai toh hum measuring instrument bhi badalte hai. Some eg:-

Aise bhi bahut se objects hote jinko hum scale se measure nahi kr sakte jaise height of mountain, radius of earth or larger bodies ko measure karne ke liye hum special method use karte hai.
Measurement of large distance
long distance jaise ki sun or earth ke beech ki duri ko measure karne ke liye hum scale use nahi kar skate toh iske liye hum special method use karenge woh hai:-
- Parallax Method
- Echo Method
Parallax is defined as the apparent displacement of an object when the observer's point of view changes.
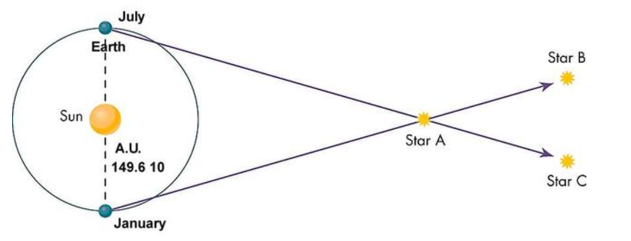
For eg. aap ek pen lijiye aur wall ke samne khade ho jaiye, uske baad apni left eye band kr ke pen ko apne right eye se dekhiye fir right eye band kar left eye se dekhiye. Is experiment se hume ye pata chalega ki distance between pen and wall alag alag hai. Jab humne observe kiya left aur right eye se, is point difference ko hum basis kahte hai. Basis dono eye ke bich ki doori hai. Is method ko hum parallax kahte hai. Is experiment ko niche fig. me show kiya gaya hai.

Echo Method :
Jab sound kisi bhi rukavat(obstacles) se takra kai wapas ata hai tab usay echo kahte hai.
Echo method me hum sound waves ko ek disha ki ore bhejtai hai jaha obstacle hota hai, tab hum ye dekhte hai ki sound waves ko obstacles se wapas ane me kitna samay laga.
Consider kare ki do object jo sound produce kar raha hai unke beech ki duri ‘x’ hai tab, pura distance sound ne travel kiya woh hai ‘2x’(sound ja kar wapas aya).
hum jante hai ki,
Speed=Distance coveredtime taken
Or Speed of sound = 2xTime taken Dusre method hai distance ko measure karne ke liye jo same priciple me kaam karte hai woh hai : Laser method, Sonar method and Radar method.
Estimation Of Very Small Distances - Size of a molecule :
Echo method ka use tab hota jab hume kisi point se koi hill ya building ki duri pata karna ho, duri pata kar ke liye hum radio signal ya fir gun ko fire karte hai aur turant hi echo sunai deta hai.
Ek simple method hai Oleic acid ke molecular size ko find karne ke liye. Oleic acid ek soapy liquid hai jiska larger molecular 10−9m hai.
idea ye hai ki hum pehle pani ki satah me Oleic acid pehla mono molecular ki khoj karenge.
- Pehle hum 1cm3 oleic acid ko, alcohol me mix karenge aur solution ki matra ko 20cm3 rakhenge.
- Tab solution ka concentration barabar hoga [120×20]cm3 of oleic acid per cm3of solution.
- ab hum halke se lycopodium powder ko surface me sprinkle karenge aur iske ek drop ko water surface me dalenge.
- tab oleic acid drop spreads into a thin, large and roughly circular film of molecular thickness on the water surface.
- Consider kijiye humare pas ‘n’ number of drop hai pani me.
- Pehle hum 1 drop ka approximately valu nikalenge (V cm3).
- Toh fir solution ke ‘n’ drop ke volume hoga = nV cm3.
- Amount of oleic acid in this solution = [nV] [120×20] cm3.
- Oleic acid ka solution bahut teji se pani ki satah me faltha hai aur ek patli se layer bana leta hai jiska thickness ‘t’ hai. Agar iske baad ye aur falta hai aur film ka area A cm2 ho tab film ki thickness ye hogi :
t = volume of the filmarea of the film or t = [nV20×20A] cm.
Agar hum assume kare ki film mono molecular thickness hai, tab ye value oleic acid ka diameter hoga. Aur iski thickness ki value 10−9 m nikal kar ati hai.
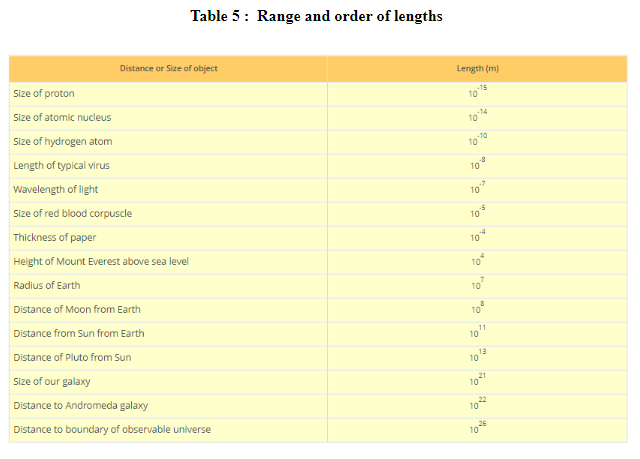
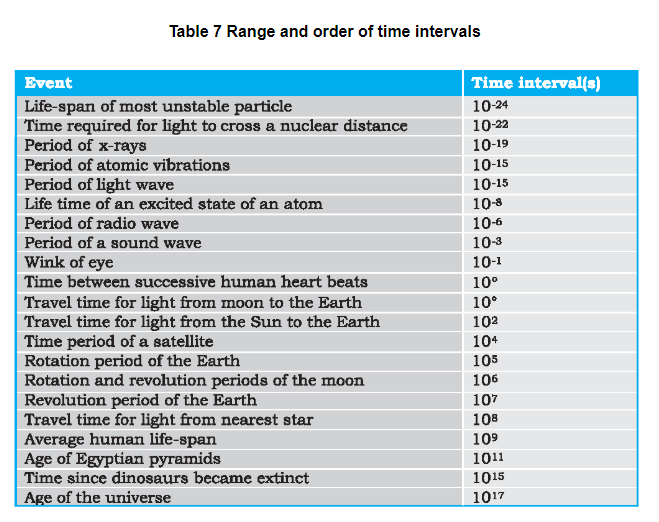
Range Of Length :
Simple objects or heavenly objects ka size me bahut jayda difference hota hai. Aur kisi bhi organism ka length microscopic and macroscopic dono me affect hota hai.For example size of universe is 1026 m ke order me hai aur atom ke chote nucleus ka size 10−14 m hota hai. Hum in dono levels ko define karne ke liye kuch units use karte hai :- 1 fermi or 1f equals to 10−15 m
1 Angstrom or 1Å equals to 10−10 m
1 Astronomical unit or AU ka value 1.496×1011 m hota hai. (yeh sun and earth ka average distance hai).
1 light year or 1ly equals to 9.46×1015 m hai (yeh distance hai jisme light travels karta hai in velocity of 3×108 m/s, 1 year me).
EXAMPLE 1
Calculate the angle of (a) 1∘ (degree) (b) 1′ (minute of arc or arcmin) and (c) 1″(second of arc or arc second) in radians. Use 360∘=2πrad,1∘=60' and 1′ = 60 ″
(a) Humare pas 360∘=2πrad hai
1∘=(π180)rad=1.745×10–2rad
(b) 1∘=60'=1.745×10–2rad
1'=2.908×10–4rad≈2.91×10–4rad
(c) 1'=60''=2.908×10–4rad
1''=4.847×10–4rad≈4.85×10–6rad.
EXAMPLE 2
A man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m, and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO; but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘ (θ is known as ‘parallax’) estimate the distance of the tower C from his original position A.
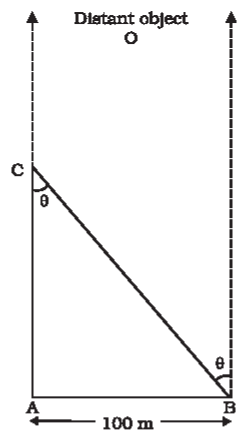
Humare pas jo data dia hua hai vo :
parallax angle θ=40∘
From Fig., AB=ACtanθ
AC=ABtanθ=100mtan400=100m0.8391=119m.
EXAMPLE 3
The moon is observed from two diametrically opposite points A and B on Earth. The angle θ subtended at the moon by the two directions of observation is 1∘54'. Given the diameter of the Earth to be about 1.276×107m, calculate the distance of the moon from the Earth.
We have θ=1∘54'=114'=(114×60)×(4.85×10−6)rad=3.32×10−2rad, since 1=4.85×10−6rad
Also b=AB=1.276×107m
Hence from Eq. (1), we have the earth-moon distance, D=bθ=1.276×1073.32×10−2=3.84×108m.
EXAMPLE 4
Length : Koi bhi 2 point ki doori ya kahen ki kisi bhi 2 point ke space koh length kahte hai. For eg. school aur mere ghar ki duri. Iska SI unit hai meter.
Jaise ki lenght ek small unit hai, use hum bade unit me bhi likh sakte hai example :
- Height is measured in 'foot' and 'inches', 1 feet contains 12 inches, and 1 inch means 0.0254 meters.
- Distance is measured in kilometers, 1 kilometer or Km equals 1000 meter.
- Jab Physics lab me hum experiment karte hai tab hum small units like millimeter and centimeter ka use karte hai, 1 meter = 100 centimeters, and 1 centimeter = 10 millimeters, to avoid writing meter, again and again, we write centimeter as ‘cm’, millimeter as ‘mm’ and decimeter as ‘dm’.
Hum length ko apne hisab se measure karte hai ki wo hamesha correct ho aur error free ho.
Hum length ko measure karne ke liye kuchh method jante hai. Eg. jab hum chhoti class me the tab hum line draw ke liye centimeter scale use karte the. Agar object ka nature badalta hai toh hum measuring instrument bhi badalte hai. Some eg:-

Aise bhi bahut se objects hote jinko hum scale se measure nahi kr sakte jaise height of mountain, radius of earth or larger bodies ko measure karne ke liye hum special method use karte hai.
Measurement of large distance
long distance jaise ki sun or earth ke beech ki duri ko measure karne ke liye hum scale use nahi kar skate toh iske liye hum special method use karenge woh hai:-
- Parallax Method
- Echo Method
Parallax is defined as the apparent displacement of an object when the observer's point of view changes.

For eg. aap ek pen lijiye aur wall ke samne khade ho jaiye, uske baad apni left eye band kr ke pen ko apne right eye se dekhiye fir right eye band kar left eye se dekhiye. Is experiment se hume ye pata chalega ki distance between pen and wall alag alag hai. Jab humne observe kiya left aur right eye se, is point difference ko hum basis kahte hai. Basis dono eye ke bich ki doori hai. Is method ko hum parallax kahte hai. Is experiment ko niche fig. me show kiya gaya hai.

Echo Method :
Jab sound kisi bhi rukavat(obstacles) se takra kai wapas ata hai tab usay echo kahte hai.
Echo method me hum sound waves ko ek disha ki ore bhejtai hai jaha obstacle hota hai, tab hum ye dekhte hai ki sound waves ko obstacles se wapas ane me kitna samay laga.
Consider kare ki do object jo sound produce kar raha hai unke beech ki duri ‘x’ hai tab, pura distance sound ne travel kiya woh hai ‘2x’(sound ja kar wapas aya).
hum jante hai ki,
Speed=Distance coveredtime taken
Or Speed of sound = 2xTime taken Dusre method hai distance ko measure karne ke liye jo same priciple me kaam karte hai woh hai : Laser method, Sonar method and Radar method.
Estimation Of Very Small Distances - Size of a molecule :
Echo method ka use tab hota jab hume kisi point se koi hill ya building ki duri pata karna ho, duri pata kar ke liye hum radio signal ya fir gun ko fire karte hai aur turant hi echo sunai deta hai.
Ek simple method hai Oleic acid ke molecular size ko find karne ke liye. Oleic acid ek soapy liquid hai jiska larger molecular 10−9m hai.
idea ye hai ki hum pehle pani ki satah me Oleic acid pehla mono molecular ki khoj karenge.
- Pehle hum 1cm3 oleic acid ko, alcohol me mix karenge aur solution ki matra ko 20cm3 rakhenge.
- Tab solution ka concentration barabar hoga [120×20]cm3 of oleic acid per cm3of solution.
- ab hum halke se lycopodium powder ko surface me sprinkle karenge aur iske ek drop ko water surface me dalenge.
- tab oleic acid drop spreads into a thin, large and roughly circular film of molecular thickness on the water surface.
- Consider kijiye humare pas ‘n’ number of drop hai pani me.
- Pehle hum 1 drop ka approximately valu nikalenge (V cm3).
- Toh fir solution ke ‘n’ drop ke volume hoga = nV cm3.
- Amount of oleic acid in this solution = [nV] [120×20] cm3.
- Oleic acid ka solution bahut teji se pani ki satah me faltha hai aur ek patli se layer bana leta hai jiska thickness ‘t’ hai. Agar iske baad ye aur falta hai aur film ka area A cm2 ho tab film ki thickness ye hogi :
t = volume of the filmarea of the film or t = [nV20×20A] cm.
Agar hum assume kare ki film mono molecular thickness hai, tab ye value oleic acid ka diameter hoga. Aur iski thickness ki value 10−9 m nikal kar ati hai.
Range Of Length :
Simple objects or heavenly objects ka size me bahut jayda difference hota hai. Aur kisi bhi organism ka length microscopic and macroscopic dono me affect hota hai.For example size of universe is 1026 m ke order me hai aur atom ke chote nucleus ka size 10−14 m hota hai. Hum in dono levels ko define karne ke liye kuch units use karte hai :- 1 fermi or 1f equals to 10−15 m
1 Angstrom or 1Å equals to 10−10 m
1 Astronomical unit or AU ka value 1.496×1011 m hota hai. (yeh sun and earth ka average distance hai).
1 light year or 1ly equals to 9.46×1015 m hai (yeh distance hai jisme light travels karta hai in velocity of 3×108 m/s, 1 year me).

Sun’s angular diameter α=1920=1920×4.85×10−6rad=9.31×10−3rad
Sun’s diameter d=αD=(9.31×10−3)×(1.496×1011)m=1.39×109m.
EXAMPLE 5
If the size of a nucleus (in the range of 10–15 to 10–14 m) is scaled up to the tip of a sharp pin, what roughly is the size of an atom ? Assume the tip of the pin to be in the range 10–5m to 10–4m.
The size of a nucleus is in the range of 10–15 m and 10–14 m. The tip of a sharp pin is taken to be in the range of 10–5 m and 10–4 m. Thus we are scaling up by a factor of 1010. An atom roughly of size 10–10 m will be scaled up to a size of 1 m. Thus a nucleus in an atom is as small in size as the tip of a sharp pin placed at the centre of a sphere of radius about a metre long.
MEASUREMENT OF MASS
Mass matter ki basic property hai. Ye temperature, pressure aur location pr depend nahi karta. Mass ka SI unit Kilogram (Kg) hai. Sabse common way hai object ko mass ko janne ke liye ki is object ko diye hue standard scale me compare kare.
Object ke mass ko determine karne ki liye jo dusra tarika use karte hai usme hum yeh dekhte hai ki kitna force laga object ko accelerate karne me.
kisi body ke mass sai hume yeh pata chalta hai ki kitna strong hai mutual attraction do objects ke beech me.
Consider kijiye ki aap moon per hai aur waha aap apna weight kare toh aap ye dekhenge ki aap ka weight moon me kuch aur hai aur earth per kuch aur. Asa is liye hota hai kyuki moon or earth ki beech me gravitational acceleration hota hai.
OMR (One Minute Revision)
- (i)Agar hume large animal ka weight pata karna ho toh hum kilogram ka use karte hai. Agar hum small object ka weight pata karna chahiye toh hum koi dusra convenient unit use karenge.
(ii) Agar hum jab mass ko microscopic level me measure kare tab jo unit hum use karenge use “ Unified Atomic Mass” kahte hai.
(iii) 1 unified atomic mass unit = 1u = (1/12) of the mass of an atom of carbon-12 isotope (C126) including the mass of electrons =1.66×10−27 kg. Common object ke mass ko hum simply common balance se pata kar sakte hai (tarazu).
(iv) Jab hum heavenly objects jaise planets, star, mountains etc. ka mass pata karna ho tab hum gravitational method jo ki Newton’s Law of Gravitation ko follow karta hai.
(v)Small masses of atomic/subatomic particles etc. ko hum mass spectrograph technique ka use kar sakte hai jisme radius of the trajectory is proportional to the mass of a charged particle moving in uniform electric and magnetic fields.
(vi) Mass or Weight same nahi hota, per yeh equation sai relate karte hai.
W=mg
W = object ka weight
m = object ka mass
g = acceleration due to gravity
Iska matlab ratio of masses of two objects is equal to the ratio of their weights:
W1W2=m1m2
Example : of finding the mass with a scale is to use a simple lever:

The equation to find the mass of the Weight to be Measured is:
m=MdEdL
Where :
Jab kuch aur weight add kare ya kam kare ya fir fulcrum ko move kare toh hum weight ko balance kar sakte hai us se mass ‘m’ pata kar sakte hai.
Modes of Measurement
Hum different mass ko different tarike se measure karte hai. Examples :
- Common objects jaise fruits, vegetables, human weight etc ko hum weight machine se pata kar sakte hai,
- Gravitational formulae ka use hota hai celestial bodies ke liye example: planets, star etc.
Range of Masses
Is universe me bahut sare variety kai objects hai jinke mass ke range me bahut farak hota hai. Nice diye table se hume in alag alag ranjo ke bare me pata chalega.Measurement of Time
Aise period me jaha kuch process, action ya fir kuch bhi hua ho us period ko Time kahte hai. Time is also called the Point or Period when something occurs.- Time physics ka ek internal part hai jaha physical world ki hr ek quantity time pr depend krti hai.
- Time ki wajah se hum universe ke functions ko asani se relate kr sakte hai.
- Aisi aur koi physical quantity nahi hogi jaise acceleration, velocity and electromagnetic waves jo time pr depend hote hai.
- Time interval ko measure karne ke liye hum clock (watch) ka use karte hai.
- In India clock works on the atomic standard of time, which is based on the periodic vibrations produced in a cesium atom
- Indian clocks ko cesium clocks bhi kaha jata hai.
- SI unit of time is : Second.
Aur prakar ke clocks jaise hand watch, pendulum clocks etc. loose aur gain time because of change in temperature, acceleration due to gravity islie ye clocks accurate time nahi show karte.
Second :
Second is the universally accepted unit of time. 1 second is defined as the time taken for 9,192,631,770 vibrations of the radiation relative to the transition between two levels of ground state of Cesium-133 atom.
- The Indian Standard Of Time (IST) is conserved with four Cesium atomic clock se.
- NPL or National Physical Laboratory in New Delhi ne authorized kiya hai cesium atom clock ko use karke IST time maintain karne ke liye.
- IN India NPL manage the standard time and koi improvement hoti hai frequency, time etc me.
- Error in atomic size 10−13, ke order mai hota jo ki bahut hi kam hai.
POINT 2
Parallax :
Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. Distance between the two viewpoints is called Basis.Echo :
An echo is the phenomenon of repetition of sound on reflection from an obstacle. In echo method, a wave (sound or electromagnetic) is sent towards the object and then reflected wave is again received back at the same position.EXAMPLE 6
The radius of a muonic hydrogen atom is 2.5×10−13m. What is the total atomic volume in m3 of a mole of such hydrogen atom.
Here,r=2.5×10−13m
Number of atoms in one mole,
N=6.023×1023
:. Volume of one mole of such hydrogen atoms
V=N×43×227×(2.5×10−13)3
V=3.94×10−14m3.
EXAMPLE 7
Time for 20 oscillations of a pendulum is measured as t1=39.6s,t2=39.9sandt3=39.5s. What is the precision in the measurements?
What is the accuracy of the measurement?
Given t1=39.6s,t2=39.9s and t3=39.5s
Least count of measuring instrument=0.1s
(As measurements have only one decimal place)
Precision in the measurement = Least count of the measuring instrument =0.1s
Mean value of time for 20 oscillations is given by
t=t1+t2+t33
=39.6+39.9+39.53=39.7s
Absolute errors in the measurements
Δt1=t−t1=39.7−39.6=0.1s
Δt2=t−t2=39.7−39.9=−0.2s
Δt3=t−t3=39.7−39.5=0.2s
Mean|o|luteerror=|Δt1|+|Δt2|+|Δt3|3
=0.1+0.2+0.23
=0.53=0.17≈0.2 (rounding off upto one decimal place)
therefore, Accuracy of measurement = ±0.2s.
ACCURACY, PRECISION OF INSTRUMENTS AND ERRORS IN MEASUREMENT
Error : Measurement foundation hai sabhi experiment’s ka jo science and technology ko follow karta hai. Aur har measuring instrument jo hum measure karne ke liye use kare hai experiments me unme kuch uncertainty hoti hai use error kahte hai.
Sabhi calculated quantity jo base karta hai measured values mai , woh sab me error hota hai. We shall distinguish between two terms: accuracy and precision.
Accuracy : Jab kisi bhi quantity ko measure karte hai toh, woh measured value kitne close hai use quantity ke true value se use accuracy kahte hai.
Precision : Precision hume bata hai ki kitna resolution or limit measure hua hain us quantity ka.
Ek experiment, me hum use kar rahe hai measuring instrument of resolution 0.1 cm, tab measured value hume 3.5 cm mila, aur another experiment mai jab hum use kare measuring device of greater resolution, say 0.01 cm, tab jo length hame mila woh to be 3.38 cm tha.
Pehla measurement mai more accuracy hai (kyuki yeh closer hai true value se) per less precision (because it’s resolution is only 0.1 cm), per jo second measurement hai woh less accurate hai per more precise hai.
Isliye every measurement is approximate value due to errors in measurement.
Waise toh errors generally do types ke hote hai :-
- Systematic errors
- Random errors
(a) Instrumental errors : Woh error hai jisme instrument ki design aur instrument ke calibration aur zero error in instrument ke karan.
For example, the temperature graduations of a thermometer may be inadequately calibrated (it may read 104∘C at the boiling point of water at STP whereas it should read 100∘C); in a vernier callipers the zero mark of vernier scale may not coincide with the zero mark of the main scale, or simply an ordinary metre scale may be worn off at one end.
(b) Imperfection in experimental technique or procedure, Personal errors : Jab human body ka temperature pata karne ke thermometer ko armpit me lagate hai jo hamesha original body temperature se kam value show karta hai. (Jaise ke change in temperature, wind velocity, humidity etc.) measurement ke doran systematically effect karta hai measurement ko.
(a) Personal errors : Yeh error self induced hota hai jaise ki measuring instrument ko sahi se place nahi kiya gaya ho ya fir observation ke time me carelessness ki wajah se. For example,agar aap by habit, always hold your head a bit too far to the right while reading the position of a needle on the scale, you will introduce an error due to parallax.
NOTE
- Systematic error ko hum minimise kar sakte hai by selecting proper instrument and removing personal bias as far as possible.
Least Count Error : The smallest value jo instrument measure kar sakta hai use least count kahte hai. Jitni bhi readings measure hoti hai woh srif is value tak hi correct hoti hai.
The least count error is the error associated with the resolution of the instrument. For example, a vernier calliper has the least count as 0.01cm; a spherometer may have a least count of 0.001 cm. Least count error belongs karta hai random errors ke category ko but within a limited size; yeh error occurs in both systematic and random errors. Agar hum metre scale use kare for measurement of length, it may have graduations at 1 mm division scale spacing or interval.
NOTE:
- Higher precision ka measuring instrument use karne se errors ko control kiya ja sakta hai.
- Observation ko hum bar bar Repeat kare aur us value ka mean value le toh woh value us quantity ke bahut close hoga.
Suppose a1,a2,a3....,an values humne obtain kiya by using several measurements. The arithmetic mean values sabse best value ho ga us quantity ka. Is condition measurement asa hoga :
- amean=a1+a2+a3+...+ann....(4)
or,
amean=n∑i=1ain.........(5)
This is denoted by |Δa|. Agar aur koi method nahi hai true value find karne ke liye tab hum arithmetic mean value ko true value consider karte hai. Tab the errors in the individual measurement values from the true value are
Δa1=a1–amean,
Δa2=a2–amean,
.... .... ....
.... .... ....
Δan=an–amean
The Δa calculated above may be positive in certain cases and negative in some other cases. But absolute error |Δa| will always be positive.
(b) The arithmetic mean of all the absolute errors is taken as the final or mean absolute error of the value of the physical quantity a. It is represented by Δamean.
Thus, Δamean=|Δa1|+|Δa2|+|Δa3|+...+|Δan|n..........(6)
=n∑i=1|Δai|n..........(7)
If we do a single measurement, the value we get may be in the range amean±Δamean
i.e. a=amean±Δamean
or,
amean–Δamean≤a≤amean+Δamean...........(8)
This implies that any measurement of the physical quantity a is likely to lie between
(amean+Δamean) and (amean−Δamean).
(c) Instead of the absolute error, we often use the relative error or the percentage error (δa). The relative error is the ratio of the mean absolute error Δamean to the mean value amean of the quantity measured.
Combination of Errors
Agar hume experiment kare by taking several measuring instruments tab errors bhi sare instrument ke combine ho jayenge. For example :
(a) Error of a sum or a difference
Suppose kare ki do physical quantities A and B ke measured values hai A±ΔA, B±ΔB respectively wahi ΔA and ΔB uske absolute errors hai. Tab hum error ko find karne ke liye ΔZ in the sum
Z=A+B.
We have by addition,
Z±ΔZ=(A±ΔA)+(B±ΔB).
The maximum possible error in Z
ΔZ=ΔA+ΔB
For the difference Z=A–B, we have
Z±ΔZ=(A±ΔA)–(B±ΔB)=(A–B)±ΔA±ΔB
or, ±ΔZ=±ΔA±ΔB
The maximum value of the error ΔZ is again ΔA+ΔB. Hence the rule : Jab do quantity ko add ya subtract kare tab, the absolute error in the final result is the sum of the absolute errors in the individual quantities.
(b) Error of a product or a quotient :
Suppose Z=AB and the measured values of A and B are A±ΔA and B±ΔB. Then
Z±ΔZ=(A±ΔA)(B±ΔB)=AB±BΔA±AΔB±ΔAΔB.
Dividing LHS by Z and RHS by AB we have,
1±(ΔZZ)=1±(ΔAA)±(ΔBB)±(ΔAA)(ΔBB).
Since ΔA and ΔB are small, we shall ignore their product.
Hence the maximum relative error
ΔZZ=(ΔAA)+(ΔBB).
Aap isi easily verify kar sakte hai ki yeh division ki liye bhi true hai.
Hence the rule : Jab do quantities ko multiply or divide kare tab, the relative error in the result is the sum of the relative errors in the multipliers.
(c) Error jab measured quantity raised to a power
Suppose Z=A2,
Then,
ΔZZ=(ΔAA)+(ΔAA)=2(ΔAA).
Hence, the relative error in A2 is two times the error in A.
In general, if Z=ApBqCr
Then,
ΔZZ=p(ΔAA)+q(ΔBB)+r(ΔCC).
Hence the rule : Jab relative error in a physical quantity raised to the power k is the k times the relative error in the individual quantity.
POINT 3
Error :
An error is defined as the difference between the actual or true value and the measured value.Systematic error :
Systematic error (also called systematic bias) is consistent, repeatable error associated with faulty equipment or a flawed experiment design.Random error :
Random error (also called unsystematic error, system noise or random variation) has no pattern. One minute your readings might be too small. The next they might be too large. You can’t predict random error and these errors are usually unavoidable.EXAMPLE 8
A physical quantity X is related to four measurable quantities a, b, c and d as follows X=a2b3c5/2d−2. The percentage error in the measurement of a, b, c and d are 1%,2%,3%,and4%, respectively. What is the percentage error in quantity X? If the value of X calculated on the basis of the above relation is 2.763, to what value should you round off the result.
Given, physical quantity is X=a2b3c5/2d−2
Maximum percentage error in X is
ΔXX×100=±[2(Δaa×100)+3(Δbb×100)+52(Δcc×100)+2(Δdd×100)]
=±[2(1)+3(2)+52(3)+2(4)]%
=±[2+6+152+8]=±23.5%
∴ Percentage error in quantity X=±23.5%
Mean absolute error in X=±0.235=±0.24 (rounding -off upto significant digits)
The calculated value of x should be round-off upto two significant digits.
∴X=2.8.
SIGNIFICANT FIGURES
Jaise ki hum jante hai ki hr ek instrument me error hota hai to jab hum result show karte hai to wah result precision show karna chahiye measurement ka. Normally jo measured value hota hai wo numbers me hota hai jisme digits bhi include rehte hai aur in digits ko realibly plus pehle digit ko uncertain kahte hai. Aur the reliable digits plus uncertain digits ko significant figures kahte hai.
NOTE :
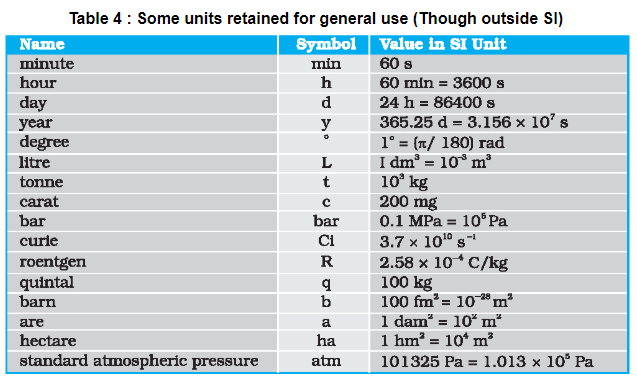
A choice of change of different units does not change the number of significant digits or figures in a measurement.
For example: Ek object ka length hai 2.308 cm yaha pe 4 significant figures hai (2,3,0,8), pr jab isi length ko hum aise likhe 0.02308 tab bhi yaha only 4 significant figures hai. Is se ye proof hota hai ki significant figures me decimal ke location se koi farak nahi padhta.
NOTE :
[The numbers 3.500 or 0.06900 have four significant figures each.]
⇒ Yaha pe kuch confusion ho sakta hai regarding trailing zero(s). Suppose ek length diya 4.700 m. Iska mtlb yaha pe jo zero(s) hai wo precision show karta hai instrument ka. Aisa nahi ho toh 4.700 mko srif 4.7 m likha jata. Then
4.700 m = 470.0 cm = 4700 mm = 0.004700 km.
Yaha pe last numbers mai zero(s) trail kar raha hai toh yeh significant nahi hai yeh observation error hai.
Uper diye gaye number 4 significant number hai aur last me 5 significant number hai. Yaha aap observe kar sakte hai hi a mere change of units cannot change the number of significant figures.
⇒ Significant figures ko define kar ke liye hume kuch ambiguities ko remove karna hota hai aur uske liye sab se best method hai ki measurement ke report ko scientific method me determine kare (in the power of 10) Is notation mai hum sabhi number ko is tarah express kar sakte hai a×10b, yaha ‘a’ number hai 1 to 10 me aur ‘b’ positive aur negative exponent hai 10 ka.
Order Of Magnitude : Agar hai numbers ka approximate value pata karna ho tab decimal ke baad wale number ko nearest digit se round off kar dete hai for numbers ‘a’ 1 (for a≤5) and to 10 (for 5<a≤10). Tab jo number number ko express karte hai approximately as 10b yaha exponent (or power) b of 10 is called order of magnitude of the physical quantity. Jab kabhi srif estimate is requitomato hota tab, the quantity is order mai hota hai 10b.
For example :
Yaha se jo confusion upar tha woh disappear ho ja tata hai :
4.700m=4.700×102cm=4.700×103mm=4.700×10–3km
Power of 10 se irrelevant hai significant figures determine karne ke liye. Jabhi zero(s) base number ‘a’ mai tab woh sare significant figures honge.
Scientific notation for reporting measurement, hum yeh rule follow karte hai :
⇒ Jab bhi hum apni convinent ke liye decimal se pehle zero lagate hai (0.1230) woh significant nahi hote per jo zero end mai hote hai woh significant hote hai. ⇒ Multiplying and dividing number na rounded number or measured value jo ki exact number hai woh sare significant hote hai.
For example in r=d2 or s=2πr, the factor 2 is an exact number and it can be written as 2.0, 2.00 or 2.0000 as required. Similarly, in T=tn, n is an exact number.
Rules for Arithmetic Operations with Significant Figures
Kisi bhi calculated value ka result nearly approximate true value ka hota hai (i.e. values with limited number of significant figures) ye uncertainty reflect karte hai original value se. Yeh aur jayda accurate nahi ho sakte original measured value se. In general, the final result should not have more significant figures than the original data from which it was obtained.
Suppose kare ki mass of an object is measured to be, say, 4.237 g (four significant figures) and its volume is measured to be 2.51 cm3, then its density, by mere arithmetic division, is 1.68804780876 g/cm3 up to 11 decimal places.
Yeh clearly absurd and irrelevant hai to record the calculated value of density ko itne precision me jiske base me yeh value measured h jiska precision is value se kaam hai.
The following rules for arithmetic operations with significant figures ensure that the final result of a calculation is shown with the precision that is consistent with the precision of the input measured values :
Density =4.237g2.51cm−3=1.69gcm−3
Similarly, if the speed of light is given as 3.00×108ms−1 (three significant figures) and one year (1y = 365.25 d) has 3.1557×107s (five significant figures), the light year is 9.47×1015m (three significant figures).
For example, the sum of the numbers 436.32 g, 227.2 g and 0.301 g by mere arithmetic addition, is 663.821 g. But the least precise measurement (227.2 g) is correct to only one decimal place. The final result should, therefore, be rounded off to 663.8 g.
Similarly, the difference in length can be expressed as :
0.307m–0.304m=0.003m=3×10–3m.
Note that we should not use the rule applicable for multiplication and division and write 664 g as the result in the example of addition 3.00×10–3m in the example of subtraction.
They do not convey the precision of measurement properly. For addition and subtraction, the rule is in terms of decimal places.
Rounding off the Uncertain Digits
Kisi bhi computation me result mai hamesha ek ya ek se jyada uncertain digit contain karta hai, yeh digits round off hona chahiye. The rules for rounding off numbers to the appropriate significant figures are obvious in most cases.
A number 2.746 rounded off to three significant figures is 2.75, while the number 2.743 would be 2.74. Rule yeh kehta hai ki preceding digit is raised by 1 if the insignificant digit to be dropped (the underlined digit in this case) is more than 5, and is left unchanged if the latter is less than 5.
In case jab number 2.745 yaha pe 5 insignificant digit hai tab rule yeh hoga ki if the preceding digit is even, the insignificant digit is simply dropped and, if it is odd, the preceding digit is raised by 1.
Then, the number 2.745 rounded off to three significant figures becomes 2.74. On the other hand, the number 2.735 rounded off to three significant figures becomes 2.74 since the preceding digit is odd.
Similarly, jab koi number me bahut sare significant figures ho , such as in 2.99792458×108 m/s is the speed of light in vacuum, is rounded off to an approximate value 3×108 m/s, which is often employed in computations.
Note : Remember that exact numbers that appear in formulae like 2π in T=2π√Lg, have a large (infinite) number of significant figures. The value of π=3.1415926.... is known to a large number of significant figures. You may take the value as 3.142 or 3.14 for π, with limited number of significant figures as required in specific cases.
Rules for Determining the Uncertainty in the Results of Arithmetic Calculations
The rules for determining the uncertainty or error in the number/measured quantity in arithmetic operations can be understood from the following examples.
(1)Agar length and breadth of a thin rectangular sheet are measured, using a metre scale as 16.2 cm and, 10.1 cm respectively, tab yaha pe three significant figures hai each measurement me. Iska mtlb hai ki length ‘l’ ko aisi likh sakte hai as
l=16.2±0.1cm=16.2cm±0.6%.
Similarly, the breadth ‘b’ may be written as
b=10.1±0.1cm=10.1cm±1%
Then, the error of the product of two (or more) experimental values, using the combination of errors rule, will be
lb=163.62cm2+1.6%=163.62+2.6cm2
This leads us to quote the final result as
lb=164+3cm2
Here 3cm2 is the uncertainty or error in the estimation of the area of the rectangular sheet.
(2) Agar set of an experimental data is specified to ‘n’ significant figures,tab jo result milega use combine data bhi valid hoga ‘n’ significant figures ke liye.
However,agar data ko subtract kare, toh significant figures ke number ko reduce kar sakte hai.
For example, 12.9 g – 7.06 g, both specified to three significant figures, cannot properly be evaluated as 5.84 g but only as 5.8 g, as uncertainties in subtraction or addition combine in a different fashion (smallest number of decimal places rather than the number of significant figures in any of the number added or subtracted).
(3) The relative error of a value of a number specified to significant figures depends not only on n but also on the number itself.
For example, the accuracy in measurement of mass 1.02gis±0.01g whereas another measurement 9.89g is also accurate to ±0.01g. The relative error in 1.02g is
=(±0.011.02)×100%=±1%
Similarly, the relative error in 9.89 g is
=(±0.019.89)×100%=±0.1%
Note :
Intermediate results in a multi-step computation should be calculated to one more significant figure in every measurement than the number of digits in the least precise measurement.
Yeh data ko justify karega aur arithmetic operations may be carried out; nahi toh rounding errors build honge.
For example, the reciprocal of 9.58, calculated (after rounding off) to the same number of significant figures (three) is 0.104, but the reciprocal of 0.104 calculated to three significant figures is 9.62. Agar humne aisi likha hota 19.58 = 0.1044 aur uske baad uska reciprocal three significant figures hota, tab hum original value ko retrieve kar lete joki 9.58 hai.
Yeh example justify karta hai ki the idea to retain one more extra digit (than the number of digits in the least precise measurement) in intermediate steps of the complex multi-step calculations in order to avoid additional errors in the process of rounding off the numbers.
POINT 4
Significant Figures :
Every measurement results in a number that includes reliable digits and uncertain digits. Reliable digits plus the first uncertain digit are called significant digits or significant figures. These indicate the precision of measurement which depends on least count of measuring instrument.Accuracy :
The ability of the instrument to measure the accurate value is known as accuracy. In other words, the closeness of the measured value to a standard or true value.Precision :
The closeness of two or more measurements to each other is known as the precision of a substance.EXAMPLE 9
Each side of a cube is measured to be 7.203 m. What are the total surface area and the volume of the cube to appropriate significant figures?
The number of significant figures in the measured length is 4. The calculated area and the volume should therefore be rounded off to 4 significant figures.
Surface area of the cube =6(7.203)2m2=311.299254m2=311.3m2
Volume of the cube =(7.203)3m3=373.714754m3=373.7m3.
DIMENSIONS OF PHYSICAL QUANTITIES
Kisi bhi physical quantity ka nature uke dimension ko describe karta hai. Jab hum kisi bhi object ko observe karte hai toh sab se pehle hum us object ka dimension ko notice karte hai.In fact, we are also defined or observed with respect to our dimensions that is, height, weight, the amount of flesh etc. Dimension of boby ka mtlb hum us body ko base quantity se relate karte hai. Dimension of quantity defined its identity and existence. Yeh clear hai ki jitne bhi physical quantities hai is universe mai sab ka dimension hota hai.
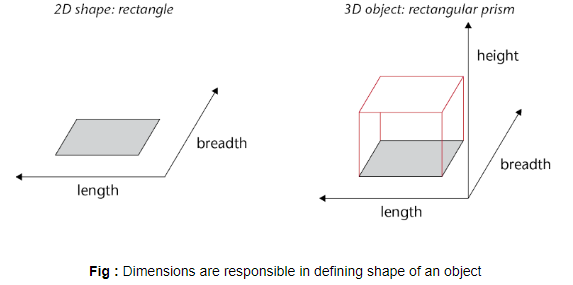

Dimension of physical quantity yeh define karta hai ki the powers to which the fundamental quantities are raised in order to represent that quantity. The seven fundamental quantities are enclosed in square brackets [ ] to represent its dimensions.
For examples :-
Consider a physical quantity Q which depends on base quantities like length, mass, time, electric current, the amount of substance and temperature, when they are raised to powers a, b, c, d, e, and f. Then dimensions of physical quantity Q can be given as:
[Q]=[LaMbTcAdmoleKf].
It is mandatory for us to use [ ] in order to write the dimension of a physical quantity. In real life, everything is written in terms of dimensions of mass, length and time.
For example, the volume occupied by an object is expressed as the product of length, breadth and height, or three lengths. Hence, the dimensions of volume are :
[L]×[L]×[L]=[L]3=[L3].
As the volume is independent of mass and time, it is said to possess zero dimension in mass [M0], zero dimension in time [T0] and three dimensions in length.
Similarly, Force, as the product of mass and acceleration, can be expressed as
Force = mass × acceleration = mass × (length)/(time)2.
The dimensions of force are [M]L[T]2=[MLT–2].
Thus, the force has one dimension in mass, one dimension in length, and –2 dimensions in time. The dimensions in all other base quantities are zero.
Note :
That in this type of representation, the magnitudes are not considered. It is the quality of the type of the physical quantity that enters.
Thus, a change in velocity, initial velocity, average velocity, final velocity, and speed are all equivalent in this context. Since all these quantities can be expressed as length/time, their dimensions are LT or [LT–1].
POINT 5
Dimensions :
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it.DIMENSIONAL FORMULAE AND DIMENSIONAL EQUATION
Dimensional Formulae : Woh hai jo compound expression dikhata hai ki kaun kaun se fundamental quantities involve hai us physical quantity ko banane me.
Dimensional Equation : Yeh aisi equations hai jo represent karte hai physical quantities ke dimension ko equate karte base quantity ke sath.
For example :
The above expressions like [M0L2T0],[M0L3T0],[M0L1T−2] etc are known as dimensional formulae and the equations such as [A]=[M0L2T0], [V]=[M0L3T0], [a]=[M0L1T−2] etc. are known as dimensional equations.
Rules for writing dimensions of a physical quantity
- Force, [F]=[MLT−2]
Velocity. [v]=[LT−1]
Charge, (q)=[AT] Specific heat, (s)=[L2T2K−1]
Gas constant, [R]=[ML2T2K−1mol−1]
- Dimensions are always enclosed in [ ] brackets
- If the body is independent of any fundamental quantity, we take its power to be 0
- When the dimensions are simplified we put all the fundamental quantities with their respective power in single [ ] brackets, for example as in velocity we write [L][T]−1 as [LT−1]
- We always try to get derived quantities in terms of fundamental quantities while writing a dimension.
- Laws of exponents are used while writing dimension of physical quantity so basic requirement is a must thing
- If the dimension is written as it is we take its power to be 1, which is an understood thing
- Plane angle and Solid angle are dimensionless quantity, that is they are independent of fundamental quantities
DIMENSIONAL FORMULAE OF SOME PHYSICAL QUANTITIES
Kisi bhi physical quantity ka dimension formulae hum tabhi likh sakte hai jab hume use quantity ka dusre physical quantity ka relation malum ho. Physical quantities with the dimensional formula table below: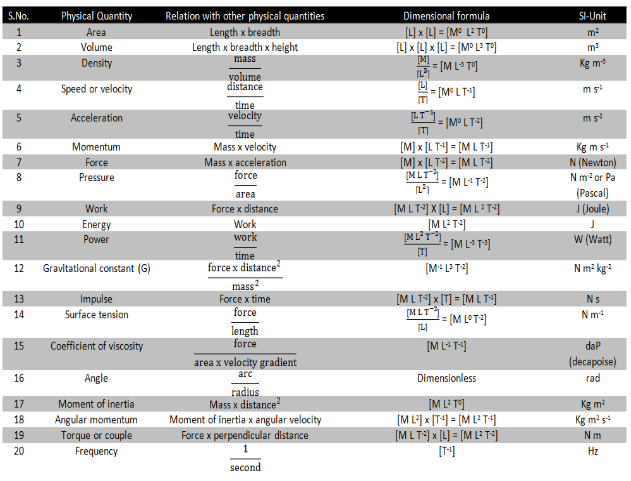
DIMENSIONAL ANALYSIS AND ITS APPLICATIONS
Dimension of base quantities or combination of these dimensions describe karta hai physical quantity ke nature ko. Dimensional Analysis ka use hum, the dimensional consistency of equations, deducing relation among the various physical quantities and checking the derivation, accuracy and dimensional consistency or homogeneity of various mathematical expressions ko check karne me karte hai.Jab magnitudes of two or more physical quantities are multiplied, their units should be treated in the same manner as ordinary algebraic symbols.
Checking the Dimensional Consistency of Equations
Kisi bhi physical quantity ke magnitude ko hum add or subtract kar sakte jab woh done quantity same nature ke ho.In other words, we can add or subtract similar physical quantities. Thus, velocity cannot be added to force, or an electric current cannot be subtracted from the thermodynamic temperature. This simple principle called the principle of homogeneity of dimensions in an equation is extremely useful in checking the correctness of an equation.
Note :
- If the dimensions of all the terms are not the same, the equation is wrong.
- If we derive an expression for the length (or distance) of an object, regardless of the symbols appearing in the original mathematical relation, when all the individual dimensions are simplified, the remaining dimension must be that of length.
- If we derive an equation of speed, the dimensions on both sides of the equation, when simplified, must be of length/ time, or [LT–1].
- Dimensions are customarily used as a preliminary test of the consistency of an equation, when there is some doubt about the correctness of the equation.
- The dimensional consistency does not guarantee correct equations.
- Special functions, jaise ki trigonometric, logarithmic and exponential functions must be dimensionless.
- A pure number, ratio of similar physical quantities, such as angle as the ratio (length/length), refractive index as the ratio (speed of light in vacuum/speed of light in medium) etc., has no dimensions.
Now we can test the dimensional consistency or homogeneity of the equation
x=x0+v0t+12at2
for the distance x travelled by a particle or body in time t which starts from the position x0 with an initial velocity v0 at time t = 0 and has uniform acceleration along the direction of motion. The dimensions of each term may be written as
[x]=[L]
[x^0 ] = [L]<br>[v0t]=[LT–1][T]=[L]
[(12)at2]=[LT–2][T2]=[L].
Uper diye hue equation me aap observe karenge ki jo left me dimension hai wahi right side per bhi hai. Hence this equation is a dimensionally correct equation.
NOTE : A test of consistency of units, but has the advantage that we need not commit ourselves to a particular choice of units, and we need not worry about conversions among multiples and submultiples of the units. It may be borne in mind that if an equation fails this consistency test, it is proved wrong, but if it passes, it is not proved right. Thus, a dimensionally correct equation need not be actually an exact (correct) equation, but a dimensionally wrong (incorrect) or inconsistent equation must be wrong.
Deducing Relation among the Physical Quantities
Kabhi kabhi dimensions ka use hum physical quantity ke relation ko deduce karne me karte hai. For this we should know the dependence of the physical quantity on other quantities (upto three physical quantities or linearly independent variables) and consider it as a product type of the dependence.
Benefits of Dimensions
Benefits of describing a physical quantity are as follows :
- Jab kisi dimensions ko hum describe karte hai, woh hume help karta hai ‘to understand the relation between physical quantities and its dependence on base or fundamental quantities’, i.e, how dimensions of a body rely on mass, time, length, temperature etc.
- Dimensions are used in dimension analysis, where we use them to convert and interchange units
- Dimensions are used in predicting unknown formulae by just studying how a certain body depends on base quantities and up to which extent.
- It makes measurement and study of physical quantities easier
- We are able to identify or observe a quantity just because of its dimensions
- Dimensions define objects and their existence.
Limitations of Dimensions
Are as follows :-
- Dimensions can’t be used for trigonometric and exponential functions
- Dimensions never define exact form of a relation
- We can’t find values of certain constants in physical relations with the help of dimensions
- A dimensionally correct equation may not be the correct equation always
POINT 6
Dimensional formula :
Dimensional formula (equation) : An equation, which gives the relation between fundamental units and derived units in terms of dimensions is called dimensional formula (equation). In mechanics the length, mass and time are taken as three base dimensions and are represented by letters L, M, T respectively.EXAMPLE 10
Let us consider an equation 12mv2=mgh where m is the mass of the body, v its velocity, g is the acceleration due to gravity and h is the height. Check whether this equation is dimensionally correct.
The dimensions of LHS are
[M][LT–1]2=[M][L2T–2]=[ML2T–2]
The dimensions of RHS are
[M][LT–2][L]=[M][L2T–2]=[ML2T–2] The dimensions of LHS and RHS are the same and hence the equation is dimensionally correct.
EXAMPLE 11
The SI unit of energy is J=kgm2s–2; that of speed v is ms–1 and of acceleration a is ms–2. Which of the formula for kinetic energy (K) given below can you rule out on the basis of dimensional arguments (m stands for the mass of the body) : (a) K=m2v3
(b) K=(12)mv2
(c) K=ma
(d) K=(316)mv2
(e) K=(12)mv2+ma
Every correct formula or equation must have the same dimensions on both sides of the equation. Also, only quantities with the same physical dimensions can be added or subtracted.
The dimensions of the quantity on the right side are [M2L3T–3] for (a);
[ML2T–2] for (b) and (d);
[MLT–2] for (c).
The quantity on the right side of (e) has no proper dimensions since two quantities of different dimensions have been added. Since the kinetic energy K has the dimensions of [ML2T–2], formulas (a), (c) and (e) are ruled out.
Note that dimensional arguments cannot tell which of the two, (b) or (d), is the correct formula. For this, one must turn to the actual definition of kinetic energy. The correct formula for kinetic energy is given by (b).
EXAMPLE 12
Consider a simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its time period using a method of dimensions.
The dependence of time period T on the quantities l, g and m as a product may be written as :
T=klxgymz
where k is dimensionless constant and x,y and z are the exponents.
By considering dimensions on both sides, we have
[L0M0T1]=[L1]x[L1T−2]y[M1]z=Lx+yT–2yMz
On equating the dimensions on both sides, we have
x+y=0;–2y=1; and z=0
So that x=½, y=-½, z =0
Then, T=kl½g–½
or, T=k√lg
Note : that value of constant k can not be obtained by the method of dimensions. Here it does not matter if some number multiplies the right side of this formula, because that does not affect its dimensions.
Actually, k=2π so that T=2π√lg
Dimensional analysis is very useful in deducing relations among the interdependent physical quantities. However, dimensionless constants cannot be obtained by this method. The method of dimensions can only test the dimensional validity, but not the exact relationship between physical quantities in any equation. It does not distinguish between the physical quantities having the same dimensions.
A number of exercises at the end of this chapter will help you develop skill in dimensional analysis.
IMPORTANT FORMULAE
Quadratic Equation and its Solution
A second degree equation is called quadratic equation. The equation :
- ax2+bx+c=0
- x=−b±√b2−4ac2a
According to this theorem,
(1+x)n=1+nx+n(n−1)2!x2+n(n−2)3!x3]
Where |x|<1, n is any negative integer or any fraction (positive or negative)
The total number of terms =n+1 i.e.one more than the index of the power of the Binomial,
2≠2x1, 3≠3x2x1 and n≠n(n−1)(n−2)(n−3)..........1],
If |x|⟨1 ,then the terms containing higher power of x can be neglected.
Therefore (1+x)n=1+nx.
Binomial theorem for positive integral index
(x+a)n=xn+nxn−1a1!+n(n−1)xn−12!a2+....+an
where n is any positive integer.
Logarithms
If ax=m ,then x is called the logarithm of m to the base a and is written as logam Thus,if ax=m, then logam=x
Standard Formulae of logarithms
1. logemn=logem+logen<br>2.log_(e)(m)/(n)=log_(e)m-log_(e)n<br>3.log_(e)m^(n)=n log_(e)m<br>TwoSystemsofLogarithms<br><b>1.NaturalLogarithm:<b>Logarithmofaνmber→thebasee(e=2.7182)iscal≤dnaturallogarithm.<br><b>2.CommonLogarithm:<b>Logarithmofaνmber→thebase10iscal≤dcommonlogarithm.Inallpracticalcalca––tions,wealwaysusecommonlogarithms.<br>ConversionofNaturallogarithm→Commonlogarithm<br>Naturallogarithmscanbeconverted∫ocommonlogarithmsasfollows:log_e N = 2.3026 log_10 N<br><b><i>IV.Trigonometry<i><b><br>TrigonometricRatiosofStandard∠sThetrigonometricratiosofstandard∠saregiven∈thefollow∈gtab≤:<br>TrigonometricalRatiosofAlliedAng≤s<br>1.(i)sin(-theta)=-sin theta,<br>(ii)cos(-theta)=cos theta,<br>iii)tan(-theta)=-tan theta]<br>2.(i)sin(90^(@)-theta)=cos theta,<br>(ii)cos(90^(@)-theta)=sin theta,<br>(iii)tan(90^(@)-theta)=cot theta<br>3.(i)sin(90^(@)+theta)=cos theta,<br>(ii)cos(90^(@)+theta)=sin theta,<br>(iii)tan(90^(@)+theta)=-cot theta<br>4.(i)sin (180^(@)-theta)=sin theta,<br>(ii)cos(180^(@)-theta)=-cos theta,<br>(iii)tan(180^(@)-theta)=-tan theta<br>5.(i)sin(180^(@)+theta)=-sin theta,<br>(ii)cos(180^(@)+theta)=-cos theta,<br>(iii)tan(180^(@)+theta)=-tan theta,<br>6.(i)sin(270^(@)-theta)=-cos theta,<br>(ii)cos(270^(@)-theta)=-sin theta,<br>(iii)tan(270^(@)-theta)=cot theta<br>7.(i)(sin)sin(270^(@)+theta)=-cos theta,<br>(ii)cos(270^(@)+theta)=sin theta,<br>(iii)tan(270^(@)+theta)=-cot theta<br>SomeimportantTrigonometricForμlae<br>1.sin(A+B)=sin A cos B+cos A sin B,<br>2.cos(A+B)=cos A cos B-sin A sin B,<br>3.sin(A-B)=sin A cos B-cos A sin B,<br>4.cos(A-B)=cos A cos B+sin A sin B<br>5.sin2A=2sin A cosA,<br>6.sin(A+B)sin(A-B)=sin^(2)A-sin^(2)B,<br>7.cos(A+B)cos(A-B)=cos^(2)A-sin^(2)B,<br>8.tan(A+B)=(tan A+tan B)/(1-tan A tan B),<br>9.sin A+sin B=2sin(A+B)/(2)cos(A-B)/(2),<br>10.sin A-sin B=2cos(A+B)/(2)sin(A-B)/(2),<br>11.cos A+cos B=2cos(A+B)/(2)cos(A-B)/(2),<br>12.cos A-cos B=2sin(A+B)/(2)sin(A-B)/(2)<br>13.cos 2 A = 1 − 2 sin^2 A = 2 cos^2 A −1<br>14.tan 2 A = (2 tan A)/(1- tan^A)<br>15.tan (A-B) =(tan A-tan B)/(1+tan A tan B)<br>16.tan(A+B)=(tan A+tan B)/(1-tan A tan B)<br><b><i>V.D⇔erentiation<b><i><br>TheoremsofD⇔erentiations<br>1.Ify=C,whenCisconstanttherefore (dy)/(dx)=0,<br>2.Ify=x^(n),wherenisan∫e≥rtherefore (dy)/(dx)=nx^(-1)<br>3.Ify=Cu,whereuisthefunctionofxandCisconstant(dy)/(dx)=C(du)/(dx),<br>4.Ify=u+-v+-omega+-......,whereu,vandomegaarethefunctionofx,therefore (dy)/(dx)=(d)/(dx)(u)+-(d)/(dx)(v)+-(d)/(dx)(omega)+-......,<br>5.Ify=u v,whereuandvarethefunctionofx,then(dy)/(dx)=u(dv)/(dx)+(du)/(dx)<br>6.Ify=(v)/(u),whereuandvarethefunctionofx,then(dy)/(dx)=(u(dv)/(dx)-v(du)/(dx))/(u^(2)),<br>7.Ify=u^(n),whereuisthefunctionofxthen(dy)/(dx)=nu^(n-1)(du)/(dx)<br>D⇔erentialcoefficientsofTrigonometricFunctions<br>1.d/(dx) (sin x) = cos x ;andd/(dx) (sin u) = cos u (d (u))/(dx) , u is the function of x
2. ddx(cosx)=−sinx ; ddx(cosu)=−sinud(u)dx
3. ddx(tanx)=sec2x ; ddx(tanu)=sec2uddx(u)<br>4.ddx(cotx)=−cosec2x
5. d/(dx) (sec x) = sec x tan x<br>6.ddx(cosecx)=−cosecxcotx.
Differential Coefficients of Logarithmic and Exponential Functions
Fundamental Formulae of Integration
1. ∫dx=x[∴ddx(x)=1
2. ∫xndx=xn+1n+1 provided n≠−1
3. ∫x−1dx=∫1xdx=logex
4. ∫exdx=ex
5. ∫eaxdx=eaxddx(ax)=eaxa
6. ∫axdx=axlogea
7. ∫sinxdx=−cosx
7a. ∫sinaxdx=−cosaxddx(ax)=−cosaxa
8. ∫cosxdx=sinx
8a. ∫cosaxdx=sinaxa
9. ∫sec2xdx=tanx
10. ∫cosec2xdx=−cotx
11. ∫secxtanxdx=secx
12. ∫cosecxcotxdx=−cosecx
13. ∫tanxdx=∫sinxcosxdx=−∫−sinxcosxdx=−logecosx
14. ∫cotxdx=∫cosxdxsinx=logesinx
15. ∫dx√1−x2=sin−1x : |x|<1
16. ∫dxx√x2−1=sec−1|x| : |x|>1
17. ∫dx1+x2=tan−1x
Theorems of Integration
First Theorem : The integral of the product of a constant and a function is equal to the product of the constant and integral of the function.
i.e. ∫cudx=c∫udx,wherecisconstant.<br><b>SecondTheorem:<b>The∫egralofthe∑ord⇔erenceofaνmberoffunctionsisgivenby<br>int_(u ± v ± ω ± ........) dx = int_udx ± int_v d x ± int_ω d x ± .........