STRING WAVES for Class 11 PHYSICS
INTRODUCTION
Kya aapne kabhi pani me paththar fek ke khela hai? Kya aapne kabhi kisi dori ko jhatak ke dekha hai? Bs yahi to waves hai. Humare charo taraf waves hai jaise ki light ki waves ya phir sound ki waves. Sabhi waves ko hum mathematical terms me bhi describe kr sakte hai jisse different kinds of waves ki study me unhe correlate krne me easy hota hai. Jo dori ka eg. hai wo ek tarah se string hai isiliye usme jo oscillation aur propagation hota hai use hi hum string waves kahate hai. Is chapter me hum isi string waves me focus karenge. Ye string waves mechanical waves ke types me aata hai kyuki mechanical waves ka mtlb hai wo waves jinko travel (propagate) krne ke liye medium ki need hoti hai aur yaha pr dori medium hai.
Ab batao ki pani me paththar fekne se waves generate hona ya phir dori ko jhatakne se waves generate hone ka karan kya hai? Disturbance. Kyuki humne dori ya phir pani me force laga ke disturbance create kiya jiski wajah se wave originate hua. Kyon Ki yaha pani aur dori dono medium hai isliye ye mechanical wave hai. Medium me disturbance ke karan phle atom me motion hua jo next atom se takaraker use bhi motion me le ata hai means motion ko next atom me transmit kr deta hai. Jaise jaise wave pass hoti hai atom aaghe pichhe move krta hai.
INTRODUCTION
Kya aapne kabhi pani me paththar fek ke khela hai? Kya aapne kabhi kisi dori ko jhatak ke dekha hai? Bs yahi to waves hai. Humare charo taraf waves hai jaise ki light ki waves ya phir sound ki waves. Sabhi waves ko hum mathematical terms me bhi describe kr sakte hai jisse different kinds of waves ki study me unhe correlate krne me easy hota hai. Jo dori ka eg. hai wo ek tarah se string hai isiliye usme jo oscillation aur propagation hota hai use hi hum string waves kahate hai. Is chapter me hum isi string waves me focus karenge. Ye string waves mechanical waves ke types me aata hai kyuki mechanical waves ka mtlb hai wo waves jinko travel (propagate) krne ke liye medium ki need hoti hai aur yaha pr dori medium hai.
Ab batao ki pani me paththar fekne se waves generate hona ya phir dori ko jhatakne se waves generate hone ka karan kya hai? Disturbance. Kyuki humne dori ya phir pani me force laga ke disturbance create kiya jiski wajah se wave originate hua. Kyon Ki yaha pani aur dori dono medium hai isliye ye mechanical wave hai. Medium me disturbance ke karan phle atom me motion hua jo next atom se takaraker use bhi motion me le ata hai means motion ko next atom me transmit kr deta hai. Jaise jaise wave pass hoti hai atom aaghe pichhe move krta hai.
INTRODUCTION
Kya aapne kabhi pani me paththar fek ke khela hai? Kya aapne kabhi kisi dori ko jhatak ke dekha hai? Bs yahi to waves hai. Humare charo taraf waves hai jaise ki light ki waves ya phir sound ki waves. Sabhi waves ko hum mathematical terms me bhi describe kr sakte hai jisse different kinds of waves ki study me unhe correlate krne me easy hota hai. Jo dori ka eg. hai wo ek tarah se string hai isiliye usme jo oscillation aur propagation hota hai use hi hum string waves kahate hai. Is chapter me hum isi string waves me focus karenge. Ye string waves mechanical waves ke types me aata hai kyuki mechanical waves ka mtlb hai wo waves jinko travel (propagate) krne ke liye medium ki need hoti hai aur yaha pr dori medium hai.
Ab batao ki pani me paththar fekne se waves generate hona ya phir dori ko jhatakne se waves generate hone ka karan kya hai? Disturbance. Kyuki humne dori ya phir pani me force laga ke disturbance create kiya jiski wajah se wave originate hua. Kyon Ki yaha pani aur dori dono medium hai isliye ye mechanical wave hai. Medium me disturbance ke karan phle atom me motion hua jo next atom se takaraker use bhi motion me le ata hai means motion ko next atom me transmit kr deta hai. Jaise jaise wave pass hoti hai atom aaghe pichhe move krta hai.
TYPES OF MECHANICAL WAVES
Baccho agr hum baat krein mechanical waves ki toh ye 2 type k hoti hai-
(i) Transverse waves
(ii) Longitudinal waves
TRANSVERSE WAVES
Baccho transverse wave voh wave hoti hai jisme particle ke motion ka direction and wave energy ke motion ka direction perpendicular hota hai.Mltb agr particle ke motion ka direction positive y-axis ki taraf hai toh wave ki motion ka direction ya toh negative x-axis hoga ya phir positive x-axis hoga ya phir negative z-axis hoga ya phir positive z-axis hoga, isi ko hum transverse wave bolte hai.
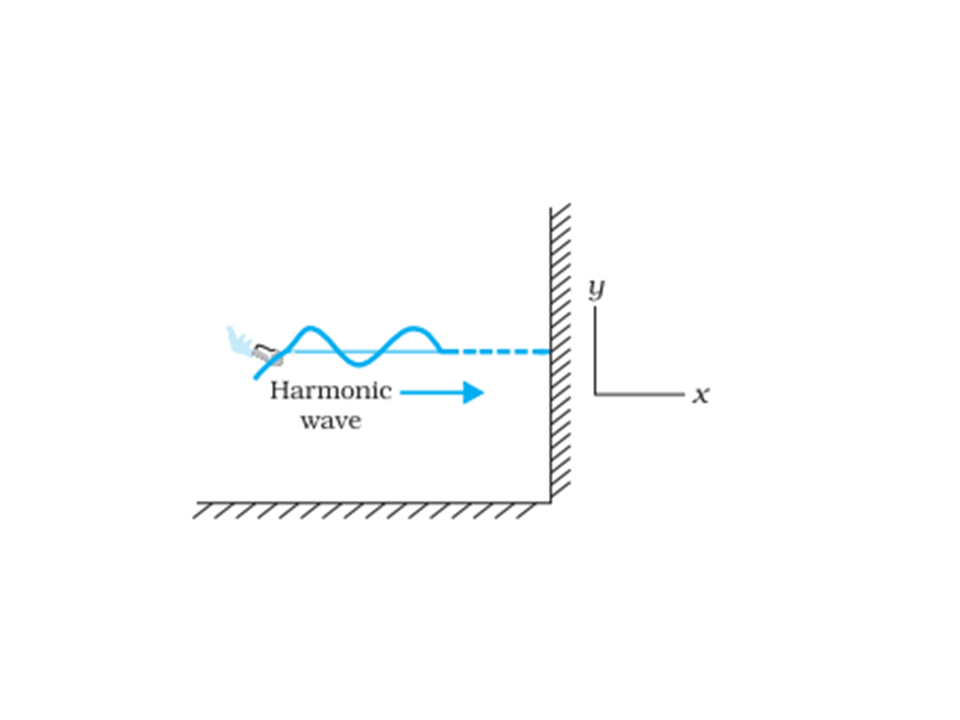
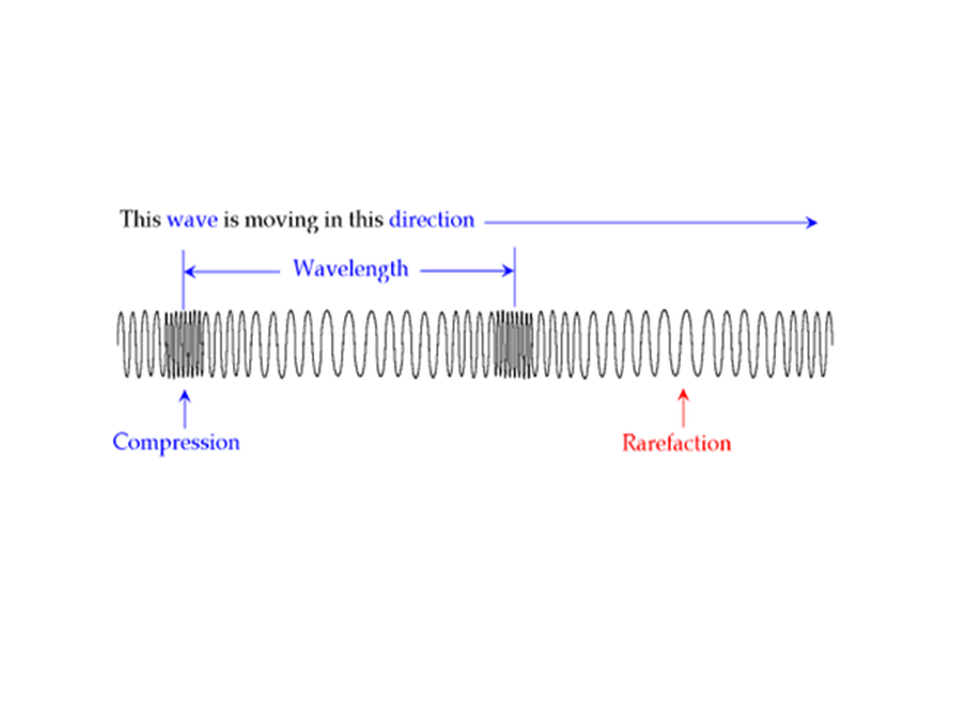
LONGITUDNAL WAVES
Baccho longitudnal wave voh wave hoti hai jisme particle ke motion ka direction and wave energy ke motion ka direction same hota hai hota hai.Mltb agr particle ke motion ka direction positive y-axis ki taraf hai toh wave ki motion ka direction ya toh negative y-axis hoga ya phir positive y-axis hoga.
TYPES OF MECHANICAL WAVES
Baccho agr hum baat krein mechanical waves ki toh ye 2 type k hoti hai-
(i) Transverse waves
(ii) Longitudinal waves
TRANSVERSE WAVES
Baccho transverse wave voh wave hoti hai jisme particle ke motion ka direction and wave energy ke motion ka direction perpendicular hota hai.Mltb agr particle ke motion ka direction positive y-axis ki taraf hai toh wave ki motion ka direction ya toh negative x-axis hoga ya phir positive x-axis hoga ya phir negative z-axis hoga ya phir positive z-axis hoga, isi ko hum transverse wave bolte hai.

LONGITUDNAL WAVES
Baccho longitudnal wave voh wave hoti hai jisme particle ke motion ka direction and wave energy ke motion ka direction same hota hai hota hai.Mltb agr particle ke motion ka direction positive y-axis ki taraf hai toh wave ki motion ka direction ya toh negative y-axis hoga ya phir positive y-axis hoga.

TYPES OF MECHANICAL WAVES
Baccho agr hum baat krein mechanical waves ki toh ye 2 type k hoti hai-
(i) Transverse waves
(ii) Longitudinal waves
TRANSVERSE WAVES Baccho transverse wave voh wave hoti hai jisme particle ke motion ka direction and wave energy ke motion ka direction perpendicular hota hai.
Mltb agr particle ke motion ka direction positive y-axis ki taraf hai toh wave ki motion ka direction ya toh negative x-axis hoga ya phir positive x-axis hoga ya phir negative z-axis hoga ya phir positive z-axis hoga, isi ko hum transverse wave bolte hai.

LONGITUDNAL WAVES Baccho longitudnal wave voh wave hoti hai jisme particle ke motion ka direction and wave energy ke motion ka direction same hota hai hota hai.
Mltb agr particle ke motion ka direction positive y-axis ki taraf hai toh wave ki motion ka direction ya toh negative y-axis hoga ya phir positive y-axis hoga.

GENERAL EQUATION OF A WAVE
Baccho wave ki general equation likhna hai, mtlb hum displacement ki equaiton likhenge, yaha prr hum dekhe toh particle y direction me motion kr rha hai and voh motion kis kis quantity prr depend krega voh hme dekhna hai,
Therefore ,
y depends upons the position of particle on the x-axis, mtlb baccho yaha prr thousads of particles honge ,ab humse displacement ke baare me pucha jaa rha hai toh hume phle btana padega ki kis particle ke motion ke baare me baat ho rhi hai, isliye jis bhi particle ke motion ki baat krenge, uss particle ki position hm btana padegi.
y depends upon time t also, ab bachho hume position pta chl yi hai lekin particle toh SHM kr rha hai uss position in y direction, and time ke saath saath particle ki y direction me position bhi change ho rhi hai, toh baccho y humara time prr bhi depend karega.
Therefore the general equation of wave would be the function of x and t,
y=f(x,t) or we can write,
y=f(ax±bt)
And direction of wave baat krein toh baccho agr ax and bt same sign ke hai mtlb ya toh (ax+bt) ho ya phir (-ax-bt) ho toh wave negative x direction me travel karegi and agr ax and bt opposite sign ke hai mtlb ya toh (ax-bt) ho ya phir (-ax+bt) ho toh wave positive x direction me travel karegi.
And agr baccho yahin humse wave ki speed puche toh voh hoti hai,
Wave speed v=coefficient of tcoefficient of x and yaha prr hum ax and bt ka sign nhi dekhenge.
CONDITION FOR WAVE MOTION
Baccho hume ye toh pta chl gya ki wave ek x and t ka function hoga , lekin kya saari x and t ke functions wave honge?, nhi baccho esa nhi hoga, saare x and t ke function wave nhi ho sakte hai, toh ab baat aati hai ki kon konse x and t ke function wave motion krenge, toh uske liye uss function ko ek condition follow krni padegi, voh hai,∂2y∂t2=K∂2y∂x2 where K is constant which is !=0,
Iss equation me ∂2y∂t2 ka mtlb hai ki partial differentiation of y wrt time t, and same for ∂2y∂x2
And baccho y should be defines for all values of x and t, ye bhi jruri hai baccho, agr y defined nhi hai for the value of x and t, toh voh wave motion nhi hoga.
Toh baccho jab jab ye x and t ka function ye condition ko follow karega, voh voh wave motion ko follow krega,
GENERAL EQUATION OF A WAVE

Baccho wave ki general equation likhna hai, mtlb hum displacement ki equaiton likhenge, yaha prr hum dekhe toh particle y direction me motion kr rha hai and voh motion kis kis quantity prr depend krega voh hme dekhna hai,
Therefore ,
y depends upons the position of particle on the x-axis, mtlb baccho yaha prr thousads of particles honge ,ab humse displacement ke baare me pucha jaa rha hai toh hume phle btana padega ki kis particle ke motion ke baare me baat ho rhi hai, isliye jis bhi particle ke motion ki baat krenge, uss particle ki position hm btana padegi.
y depends upon time t also, ab bachho hume position pta chl yi hai lekin particle toh SHM kr rha hai uss position in y direction, and time ke saath saath particle ki y direction me position bhi change ho rhi hai, toh baccho y humara time prr bhi depend karega.
Therefore the general equation of wave would be the function of x and t,
y=f(x,t) or we can write,
y=f(ax±bt)
And direction of wave baat krein toh baccho agr ax and bt same sign ke hai mtlb ya toh (ax+bt) ho ya phir (-ax-bt) ho toh wave negative x direction me travel karegi and agr ax and bt opposite sign ke hai mtlb ya toh (ax-bt) ho ya phir (-ax+bt) ho toh wave positive x direction me travel karegi.
And agr baccho yahin humse wave ki speed puche toh voh hoti hai,
Wave speed v=coefficient of tcoefficient of x and yaha prr hum ax and bt ka sign nhi dekhenge.
CONDITION FOR WAVE MOTION
Baccho hume ye toh pta chl gya ki wave ek x and t ka function hoga , lekin kya saari x and t ke functions wave honge?, nhi baccho esa nhi hoga, saare x and t ke function wave nhi ho sakte hai, toh ab baat aati hai ki kon konse x and t ke function wave motion krenge, toh uske liye uss function ko ek condition follow krni padegi, voh hai,∂2y∂t2=K∂2y∂x2 where K is constant which is !=0,
Iss equation me ∂2y∂t2 ka mtlb hai ki partial differentiation of y wrt time t, and same for ∂2y∂x2
And baccho y should be defines for all values of x and t, ye bhi jruri hai baccho, agr y defined nhi hai for the value of x and t, toh voh wave motion nhi hoga.
Toh baccho jab jab ye x and t ka function ye condition ko follow karega, voh voh wave motion ko follow krega,
GENERAL EQUATION OF A WAVE

Baccho wave ki general equation likhna hai, mtlb hum displacement ki equaiton likhenge, yaha prr hum dekhe toh particle y direction me motion kr rha hai and voh motion kis kis quantity prr depend krega voh hme dekhna hai,
Therefore ,
y depends upons the position of particle on the x-axis, mtlb baccho yaha prr thousads of particles honge ,ab humse displacement ke baare me pucha jaa rha hai toh hume phle btana padega ki kis particle ke motion ke baare me baat ho rhi hai, isliye jis bhi particle ke motion ki baat krenge, uss particle ki position hm btana padegi.
y depends upon time t also, ab bachho hume position pta chl yi hai lekin particle toh SHM kr rha hai uss position in y direction, and time ke saath saath particle ki y direction me position bhi change ho rhi hai, toh baccho y humara time prr bhi depend karega.
Therefore the general equation of wave would be the function of x and t,
y=f(x,t) or we can write,
y=f(ax±bt)
And direction of wave baat krein toh baccho agr ax and bt same sign ke hai mtlb ya toh (ax+bt) ho ya phir (-ax-bt) ho toh wave negative x direction me travel karegi and agr ax and bt opposite sign ke hai mtlb ya toh (ax-bt) ho ya phir (-ax+bt) ho toh wave positive x direction me travel karegi.
And agr baccho yahin humse wave ki speed puche toh voh hoti hai,
Wave speed v=coefficient of tcoefficient of x and yaha prr hum ax and bt ka sign nhi dekhenge.
CONDITION FOR WAVE MOTION Baccho hume ye toh pta chl gya ki wave ek x and t ka function hoga , lekin kya saari x and t ke functions wave honge?, nhi baccho esa nhi hoga, saare x and t ke function wave nhi ho sakte hai, toh ab baat aati hai ki kon konse x and t ke function wave motion krenge, toh uske liye uss function ko ek condition follow krni padegi, voh hai,
∂2y∂t2=K∂2y∂x2 where K is constant which is !=0,
Iss equation me ∂2y∂t2 ka mtlb hai ki partial differentiation of y wrt time t, and same for ∂2y∂x2
And baccho y should be defines for all values of x and t, ye bhi jruri hai baccho, agr y defined nhi hai for the value of x and t, toh voh wave motion nhi hoga.
Toh baccho jab jab ye x and t ka function ye condition ko follow karega, voh voh wave motion ko follow krega,
DISPLACEMENT IN HARMONIC WAVE

Baccho ab hum baat krenge harmoic wave ki, toh iski displacement ki equation hogi,
y=Asin(wt±kx±ϕ),
Baccho upar diagrem me mene x direction ke along wave maani hai toh iski equation me likhunga,
y=Asin(wt−kx+ϕ)
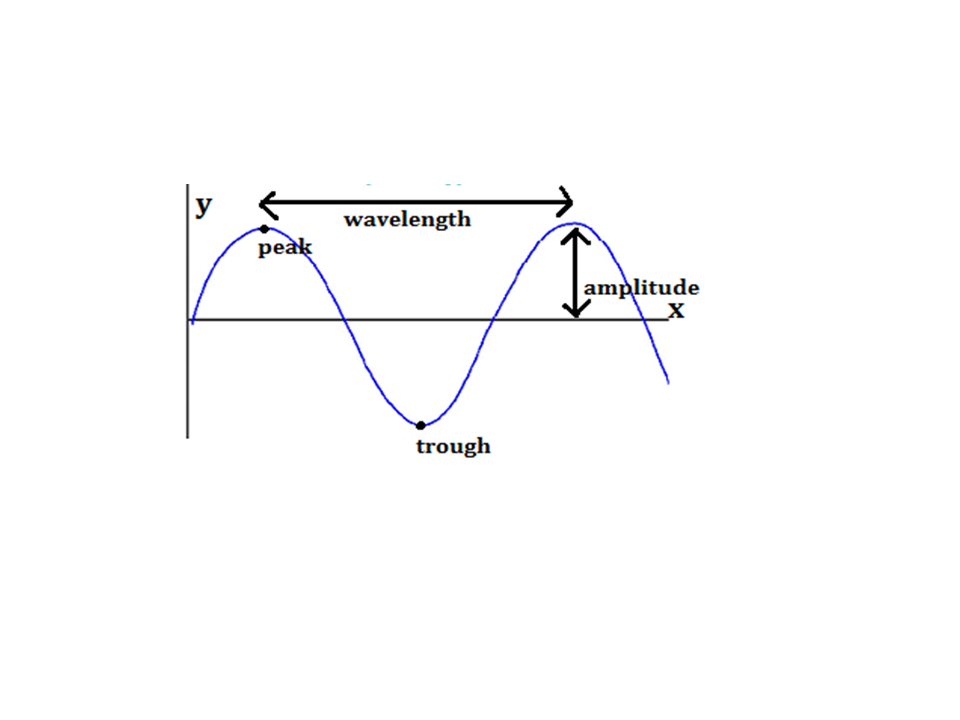
WAVE LENGTH
Baccho wave length ki baat krein toh yeh hoti hai, distance travelled by wave in single time period T,Ab baccho wave ki velocity v hai positove x-axis ki taraf and after single time period T, wave jo distance travel kregi wahi wavelength hogi uski,
Therefore ,
v=λT,
λ=vT where λ is the wave length of wave.
ANGULAR FREQUENCY AND FREQUENCY
Baccho ye toh hum sabko pta hi hai ki frequency ko hum f se denote krte hai adn isko hum define krenge “no. of oscillations per second” ,And frequency f=1T where T is the time period.
Ab baccho hum angular frequency ki baat krein toh use hum ω se denote krte hai and iski SI unit hoti hai rads−1,
Therefore , ω=2πT ,
And relation between ω and f is-
ω=2πf
AMPLITUDE AND PHASE
Baccho humari wave ki equation thi jise hum analyse kar rhe hai voh hai, y=Asin(wt−kx+ϕ)Baccho isme jo A hai voh iss wave ka amplitude hota hai, means particle jab oscillate krega toh uska maximum displacement y direction ke along A hoga.
And baccho yaha prr jo ϕ hai voh phase hai wave ka, mtlb wave start hone se phle kisi x position prr or jis time motion start hua hai, uss time ye particle jis position prr hoga wahi uska phase hoga,
ANGULAR WAVE NUMBER (k)
y=Asin(wt−kx+ϕ)Baccho iss equation me k hota hai use hum angular wave number bolte hai or ya phir propagation constant bolte hai.
Isko humne upar bhi padha hua hai general eqn of wave me,
v=coefficient of tcoefficient of x
Or now we can write,
v=ωk
Hence , k=ωv
And now we know, ω=2πT and v=λT
After putting the values,
k=2πTλT
Therefore k=2πλ
DISPLACEMENT IN HARMONIC WAVE

Baccho ab hum baat krenge harmoic wave ki, toh iski displacement ki equation hogi,
y=Asin(wt±kx±ϕ),
Baccho upar diagrem me mene x direction ke along wave maani hai toh iski equation me likhunga,
y=Asin(wt−kx+ϕ)
WAVE LENGTH
Baccho wave length ki baat krein toh yeh hoti hai, distance travelled by wave in single time period T,Ab baccho wave ki velocity v hai positove x-axis ki taraf and after single time period T, wave jo distance travel kregi wahi wavelength hogi uski,
Therefore ,
v=λT,
λ=vT where λ is the wave length of wave.
ANGULAR FREQUENCY AND FREQUENCY
Baccho ye toh hum sabko pta hi hai ki frequency ko hum f se denote krte hai adn isko hum define krenge “no. of oscillations per second” ,And frequency f=1T where T is the time period.
Ab baccho hum angular frequency ki baat krein toh use hum ω se denote krte hai and iski SI unit hoti hai rads−1,
Therefore , ω=2πT ,
And relation between ω and f is-
ω=2πf
AMPLITUDE AND PHASE
Baccho humari wave ki equation thi jise hum analyse kar rhe hai voh hai, y=Asin(wt−kx+ϕ)Baccho isme jo A hai voh iss wave ka amplitude hota hai, means particle jab oscillate krega toh uska maximum displacement y direction ke along A hoga.
And baccho yaha prr jo ϕ hai voh phase hai wave ka, mtlb wave start hone se phle kisi x position prr or jis time motion start hua hai, uss time ye particle jis position prr hoga wahi uska phase hoga,
ANGULAR WAVE NUMBER (k)
y=Asin(wt−kx+ϕ)Baccho iss equation me k hota hai use hum angular wave number bolte hai or ya phir propagation constant bolte hai.
Isko humne upar bhi padha hua hai general eqn of wave me,
v=coefficient of tcoefficient of x
Or now we can write,
v=ωk
Hence , k=ωv
And now we know, ω=2πT and v=λT
After putting the values,
k=2πTλT
Therefore k=2πλ
DISPLACEMENT IN HARMONIC WAVE

Baccho ab hum baat krenge harmoic wave ki, toh iski displacement ki equation hogi,
y=Asin(wt±kx±ϕ),
Baccho upar diagrem me mene x direction ke along wave maani hai toh iski equation me likhunga,
y=Asin(wt−kx+ϕ)
WAVE LENGTH Baccho wave length ki baat krein toh yeh hoti hai, distance travelled by wave in single time period T,
Ab baccho wave ki velocity v hai positove x-axis ki taraf and after single time period T, wave jo distance travel kregi wahi wavelength hogi uski,
Therefore ,
v=λT,
λ=vT where λ is the wave length of wave.
ANGULAR FREQUENCY AND FREQUENCY Baccho ye toh hum sabko pta hi hai ki frequency ko hum f se denote krte hai adn isko hum define krenge “no. of oscillations per second” ,
And frequency f=1T where T is the time period.
Ab baccho hum angular frequency ki baat krein toh use hum ω se denote krte hai and iski SI unit hoti hai rads−1,
Therefore , ω=2πT ,
And relation between ω and f is-
ω=2πf
AMPLITUDE AND PHASE Baccho humari wave ki equation thi jise hum analyse kar rhe hai voh hai, y=Asin(wt−kx+ϕ)
Baccho isme jo A hai voh iss wave ka amplitude hota hai, means particle jab oscillate krega toh uska maximum displacement y direction ke along A hoga.
And baccho yaha prr jo ϕ hai voh phase hai wave ka, mtlb wave start hone se phle kisi x position prr or jis time motion start hua hai, uss time ye particle jis position prr hoga wahi uska phase hoga,
ANGULAR WAVE NUMBER (k) y=Asin(wt−kx+ϕ)
Baccho iss equation me k hota hai use hum angular wave number bolte hai or ya phir propagation constant bolte hai.
Isko humne upar bhi padha hua hai general eqn of wave me,
v=coefficient of tcoefficient of x
Or now we can write,
v=ωk
Hence , k=ωv
And now we know, ω=2πT and v=λT
After putting the values,
k=2πTλT
Therefore k=2πλ
THE SPEED OF A TRAVELLING WAVE
As we know,
Speed of wave , v=coefficient of tcoefficient of x
Therefore v=ωk
And ω=2πT and k=2πλ
Therefore, v=2πT2πλ
v=λT this is the speed of travelling wave.
SPEED OF A TRANSVERSE WAVE ON STRETCHED STRING
Baccho maan lijiye do strings hai aur dono strings alag alag bandhi hui hai tightly, ab baccho maana ki ek string ka mass dusri string se kam hai,Toh baccho jab humne wave bnai toh dekha ki jis string ka mass kam tha voh jldi travel kr gyi or jis string ka mass jyada tha voh late travel ki, that means,
Wave speed, v∝1mass of string
Ab baccho humne string ki tension ko dekha jaisa humne abhi mass ko dekha hai usi tarah, toh pta chla ki jis string me jitni jyada tension hogi, wave ki speed bhi utni hi jyada hogi.
Therefore , wave speed, v∝tension
Hence , humari string me speed ka formula jo aaya voh aaya,
v=√Tμ where T is the tension in the string
And μ is the mass per unit length of the string.
THE SPEED OF A TRAVELLING WAVE
As we know,
Speed of wave , v=coefficient of tcoefficient of x
Therefore v=ωk
And ω=2πT and k=2πλ
Therefore, v=2πT2πλ
v=λT this is the speed of travelling wave.
SPEED OF A TRANSVERSE WAVE ON STRETCHED STRING
Baccho maan lijiye do strings hai aur dono strings alag alag bandhi hui hai tightly, ab baccho maana ki ek string ka mass dusri string se kam hai,Toh baccho jab humne wave bnai toh dekha ki jis string ka mass kam tha voh jldi travel kr gyi or jis string ka mass jyada tha voh late travel ki, that means,
Wave speed, v∝1mass of string
Ab baccho humne string ki tension ko dekha jaisa humne abhi mass ko dekha hai usi tarah, toh pta chla ki jis string me jitni jyada tension hogi, wave ki speed bhi utni hi jyada hogi.
Therefore , wave speed, v∝tension
Hence , humari string me speed ka formula jo aaya voh aaya,
v=√Tμ where T is the tension in the string
And μ is the mass per unit length of the string.
THE SPEED OF A TRAVELLING WAVE
As we know,
Speed of wave , v=coefficient of tcoefficient of x
Therefore v=ωk
And ω=2πT and k=2πλ
Therefore, v=2πT2πλ
v=λT this is the speed of travelling wave.
SPEED OF A TRANSVERSE WAVE ON STRETCHED STRING Baccho maan lijiye do strings hai aur dono strings alag alag bandhi hui hai tightly, ab baccho maana ki ek string ka mass dusri string se kam hai,
Toh baccho jab humne wave bnai toh dekha ki jis string ka mass kam tha voh jldi travel kr gyi or jis string ka mass jyada tha voh late travel ki, that means,
Wave speed, v∝1mass of string
Ab baccho humne string ki tension ko dekha jaisa humne abhi mass ko dekha hai usi tarah, toh pta chla ki jis string me jitni jyada tension hogi, wave ki speed bhi utni hi jyada hogi.
Therefore , wave speed, v∝tension
Hence , humari string me speed ka formula jo aaya voh aaya,
v=√Tμ where T is the tension in the string
And μ is the mass per unit length of the string.
EXAMPLE 1
Given below are some examples of wave motion. State in each case, if the wave motion is transverse, longitudinal or a combination of both?
(i) Motion of a kink in a long coil spring produced by displacing one end of spring side ways.
(ii) Waves produed in a cylinder containing a liquid by moving its piston back and forth.
(iii) Waves produed by a motor boat sailing in water.
(iv) Light waves travelling from sun to earth.
(v) ultrasonic waves in air produced by a vibrating quartz crystal.
(a) Transverse and longitudinal
(b) Longitudinal
(c) Transverse and longitudinal
(d) Longitudinal
EXAMPLE 1
Given below are some examples of wave motion. State in each case, if the wave motion is transverse, longitudinal or a combination of both?
(i) Motion of a kink in a long coil spring produced by displacing one end of spring side ways.
(ii) Waves produed in a cylinder containing a liquid by moving its piston back and forth.
(iii) Waves produed by a motor boat sailing in water.
(iv) Light waves travelling from sun to earth.
(v) ultrasonic waves in air produced by a vibrating quartz crystal.
(a) Transverse and longitudinal
(b) Longitudinal
(c) Transverse and longitudinal
(d) Longitudinal
EXAMPLE 1
Given below are some examples of wave motion. State in each case, if the wave motion is transverse, longitudinal or a combination of both?
(i) Motion of a kink in a long coil spring produced by displacing one end of spring side ways.
(ii) Waves produed in a cylinder containing a liquid by moving its piston back and forth.
(iii) Waves produed by a motor boat sailing in water.
(iv) Light waves travelling from sun to earth.
(v) ultrasonic waves in air produced by a vibrating quartz crystal.
(a) Transverse and longitudinal
(b) Longitudinal
(c) Transverse and longitudinal
(d) Longitudinal
EXAMPLE 2
A wave travelling along a strong is described by
y(x,t)=0.005sin(80.0x−3.0t)
in which the numerical constants are in SI units (0.005m,80.0radm−1 and 3.0rads−1). Calculate (a) the amplitude. (b) the wavelength (c) the period and frequency of the wave. Also , calculate the displacement y of the wave at a distance x=30.0 cm and time t=20 s?
On comparing this displacement equation with Eq. (15.2),
y(x,t)=asin(kx−ωt).
we find
(a) the amplitude of the wave is 0.005 m = 5 mm.
(b) the angular wave number k and angular frequency ω are
l=80.0m−1 and ω=3.0s−1
We, then, related the wavelength λ to k through Eq. (15.6),
λ=2π/k
=2π80.0m−1
=7.85 cm
(c) Now, we related T to ω by the relation T=2π/ω
=2π3.0s−1
=2.09s
and frequency, v=1/T=0.48 Hz
The displacement y at x=30.0 cm and time t=20 s is given by
y=(0.005m)sin(80×0.3−3.0×20)
=(0.005m)sin(−36+12π)
=(0.005m)sin(1.699)
=(0.005m)sin(97∘)≅5mm
EXAMPLE 2
A wave travelling along a strong is described by
y(x,t)=0.005sin(80.0x−3.0t)
in which the numerical constants are in SI units (0.005m,80.0radm−1 and 3.0rads−1). Calculate (a) the amplitude. (b) the wavelength (c) the period and frequency of the wave. Also , calculate the displacement y of the wave at a distance x=30.0 cm and time t=20 s?
On comparing this displacement equation with Eq. (15.2),
y(x,t)=asin(kx−ωt).
we find
(a) the amplitude of the wave is 0.005 m = 5 mm.
(b) the angular wave number k and angular frequency ω are
l=80.0m−1 and ω=3.0s−1
We, then, related the wavelength λ to k through Eq. (15.6),
λ=2π/k
=2π80.0m−1
=7.85 cm
(c) Now, we related T to ω by the relation T=2π/ω
=2π3.0s−1
=2.09s
and frequency, v=1/T=0.48 Hz
The displacement y at x=30.0 cm and time t=20 s is given by
y=(0.005m)sin(80×0.3−3.0×20)
=(0.005m)sin(−36+12π)
=(0.005m)sin(1.699)
=(0.005m)sin(97∘)≅5mm
EXAMPLE 2
A wave travelling along a strong is described by
y(x,t)=0.005sin(80.0x−3.0t)
in which the numerical constants are in SI units (0.005m,80.0radm−1 and 3.0rads−1). Calculate (a) the amplitude. (b) the wavelength (c) the period and frequency of the wave. Also , calculate the displacement y of the wave at a distance x=30.0 cm and time t=20 s?
On comparing this displacement equation with Eq. (15.2),
y(x,t)=asin(kx−ωt).
we find
(a) the amplitude of the wave is 0.005 m = 5 mm.
(b) the angular wave number k and angular frequency ω are
l=80.0m−1 and ω=3.0s−1
We, then, related the wavelength λ to k through Eq. (15.6),
λ=2π/k
=2π80.0m−1
=7.85 cm
(c) Now, we related T to ω by the relation T=2π/ω
=2π3.0s−1
=2.09s
and frequency, v=1/T=0.48 Hz
The displacement y at x=30.0 cm and time t=20 s is given by
y=(0.005m)sin(80×0.3−3.0×20)
=(0.005m)sin(−36+12π)
=(0.005m)sin(1.699)
=(0.005m)sin(97∘)≅5mm
EXAMPLE 3
A steel wire 0.72 m long has a mass of 5.0×10−3 kg . If the wire is under a tension of 60 N, what is the speed of transverse waves on the wire ?
Mass per unit length of the wire,
μ=5.0×10−3kg0.72m
=6.9×10−3kgm−1
Tension, T=60 N
The speed of wave on the wire is given by
v=√Tμ=√60N6.9×10−3kgm−1=93ms−1
EXAMPLE 3
A steel wire 0.72 m long has a mass of 5.0×10−3 kg . If the wire is under a tension of 60 N, what is the speed of transverse waves on the wire ?
Mass per unit length of the wire,
μ=5.0×10−3kg0.72m
=6.9×10−3kgm−1
Tension, T=60 N
The speed of wave on the wire is given by
v=√Tμ=√60N6.9×10−3kgm−1=93ms−1
EXAMPLE 3
A steel wire 0.72 m long has a mass of 5.0×10−3 kg . If the wire is under a tension of 60 N, what is the speed of transverse waves on the wire ?
Mass per unit length of the wire,
μ=5.0×10−3kg0.72m
=6.9×10−3kgm−1
Tension, T=60 N
The speed of wave on the wire is given by
v=√Tμ=√60N6.9×10−3kgm−1=93ms−1
POWER TRANSMITTED ALONG THE STRING BY A SINE WAVE
Baccho jaisa ki hume ki pta hai ki kinetic energy per unit length and potential energy per unit length same hoti hai string wave me or voh hoti hai,
dKdx=12μA2ω2cos2(ωt−kx), this is the kinetic energy per unit length,
And dPdx=12μA2ω2cos2(ωt−kx), this is the potential energy per unit length.
Therefore total energy per unit length in string wave is-
dEdx=12μA2ω2cos2(ωt−kx)+12μA2ω2cos2(ωt−kx)
Therefore ,
dEdx=μA2ω2cos2(ωt−kx), this is the total energy per unit length of string.
Ab baccho baat krein power transmitted, toh voh hoti hai energy per unit time,
Power P=dEdt, lekin baccho hume toh (dE)/dx pta hai, toh hum kya krenge dx ka multiply and divide krdenge,
Therefore,
P=dEdx×dxdt
Hence, P=μA2ω2cos2(ωt−kx)×v where dxdt=v
Ab baccho ye jo power aayi hai ye instantaneous power hai kisi time t ki,
Pinst=μA2ω2cos2(ωt−kx)×v
Hume ek wave ki poori 1 cycle ki power chahiye toh hum iska average nikalenge,
Therefore ,
Pavg=μA2ω22, this is the average power in 1 cycle.
POWER TRANSMITTED ALONG THE STRING BY A SINE WAVE
Baccho jaisa ki hume ki pta hai ki kinetic energy per unit length and potential energy per unit length same hoti hai string wave me or voh hoti hai,
dKdx=12μA2ω2cos2(ωt−kx), this is the kinetic energy per unit length,
And dPdx=12μA2ω2cos2(ωt−kx), this is the potential energy per unit length.
Therefore total energy per unit length in string wave is-
dEdx=12μA2ω2cos2(ωt−kx)+12μA2ω2cos2(ωt−kx)
Therefore ,
dEdx=μA2ω2cos2(ωt−kx), this is the total energy per unit length of string.
Ab baccho baat krein power transmitted, toh voh hoti hai energy per unit time,
Power P=dEdt, lekin baccho hume toh (dE)/dx pta hai, toh hum kya krenge dx ka multiply and divide krdenge,
Therefore,
P=dEdx×dxdt
Hence, P=μA2ω2cos2(ωt−kx)×v where dxdt=v
Ab baccho ye jo power aayi hai ye instantaneous power hai kisi time t ki,
Pinst=μA2ω2cos2(ωt−kx)×v
Hume ek wave ki poori 1 cycle ki power chahiye toh hum iska average nikalenge,
Therefore ,
Pavg=μA2ω22, this is the average power in 1 cycle.
POWER TRANSMITTED ALONG THE STRING BY A SINE WAVE
Baccho jaisa ki hume ki pta hai ki kinetic energy per unit length and potential energy per unit length same hoti hai string wave me or voh hoti hai,
dKdx=12μA2ω2cos2(ωt−kx), this is the kinetic energy per unit length,
And dPdx=12μA2ω2cos2(ωt−kx), this is the potential energy per unit length.
Therefore total energy per unit length in string wave is-
dEdx=12μA2ω2cos2(ωt−kx)+12μA2ω2cos2(ωt−kx)
Therefore ,
dEdx=μA2ω2cos2(ωt−kx), this is the total energy per unit length of string.
Ab baccho baat krein power transmitted, toh voh hoti hai energy per unit time,
Power P=dEdt, lekin baccho hume toh (dE)/dx pta hai, toh hum kya krenge dx ka multiply and divide krdenge,
Therefore,
P=dEdx×dxdt
Hence, P=μA2ω2cos2(ωt−kx)×v where dxdt=v
Ab baccho ye jo power aayi hai ye instantaneous power hai kisi time t ki,
Pinst=μA2ω2cos2(ωt−kx)×v
Hume ek wave ki poori 1 cycle ki power chahiye toh hum iska average nikalenge,
Therefore ,
Pavg=μA2ω22, this is the average power in 1 cycle.
THE PRINCIPLE OF SUPERPOSITION
Baccho do aur do se jyada wave same medium me travel kar sakti hai without affecting the motion of one another.
Agr kuch waves ek hi medium me propagate krti hai simultaneously, toh jo resultant displacement hoga kisi bhi particle ka uss medium me, voh equal hoga vector sum of each wave jo bhi uss medium me propagate kr rhe hai.
Iski definition likhenge,
“The resultant displacement of a particle at any point of the medium, at any instant of time is the vector sum of the displacements caused to the particle by the individual waves.”
Agr →y1, →y2, →y3............displacement hai particle ka by each wave, toh jo resultant displacement hoga ,
→y=→y1+→y2+→y3+.........
Aur baccho har type ki wave me superposition ka principle lgta hai.
THE PRINCIPLE OF SUPERPOSITION
Baccho do aur do se jyada wave same medium me travel kar sakti hai without affecting the motion of one another.
Agr kuch waves ek hi medium me propagate krti hai simultaneously, toh jo resultant displacement hoga kisi bhi particle ka uss medium me, voh equal hoga vector sum of each wave jo bhi uss medium me propagate kr rhe hai.
Iski definition likhenge,
“The resultant displacement of a particle at any point of the medium, at any instant of time is the vector sum of the displacements caused to the particle by the individual waves.”
Agr →y1, →y2, →y3............displacement hai particle ka by each wave, toh jo resultant displacement hoga ,
→y=→y1+→y2+→y3+.........
Aur baccho har type ki wave me superposition ka principle lgta hai.
THE PRINCIPLE OF SUPERPOSITION
Baccho do aur do se jyada wave same medium me travel kar sakti hai without affecting the motion of one another.
Agr kuch waves ek hi medium me propagate krti hai simultaneously, toh jo resultant displacement hoga kisi bhi particle ka uss medium me, voh equal hoga vector sum of each wave jo bhi uss medium me propagate kr rhe hai.
Iski definition likhenge,
“The resultant displacement of a particle at any point of the medium, at any instant of time is the vector sum of the displacements caused to the particle by the individual waves.”
Agr →y1, →y2, →y3............displacement hai particle ka by each wave, toh jo resultant displacement hoga ,
→y=→y1+→y2+→y3+.........
Aur baccho har type ki wave me superposition ka principle lgta hai.
INTERFERENCE OF WAVES
Baccho aisi do waves jinki frequency same hai and lagbhag same amplitude bhi hai and voh dono waves same direction me propagate kr rhi hai and inn dono wave ka state of polarisation usi medium me bhi same hoga, toh phir baccho inn dono ki intensity different hogi.
Kisi kisi jagah prr intetnsity jyada hogi or kisi kisi jagah prr intensity 0 bhi ho sakti hai.
Let the angular frequency be ω and angular wave number be k,
Consider two waves, y1=A1sin(ωt−kx) and y2=A2sin(ωt−kx+ϕ)
Now by principle of superposition,
y=y1+y2
Therefore , y=Asin(ωt−kx+δ)
Where, A=√A21+A22+2A1A2cosϕ
And tanδ=A2sinϕA1+A2cosϕ
And we know that, intensity I∝A2,
Hence,
I=I1+I2+2√I1I2cosϕ
CONSTRUCTIVE INTERFERENCE (MAXIMUM INTENSITY)
Baccho intensity maximum tab hogi jab cosϕ ki value maximum hogi and cosine ki maximum value 1 hoti hai,Therefore at ϕ=0∘ cosϕ=1,
Hence intensity will become,
Imax=I1+I2+2√I1I2cos0∘
Imax=I1+I2+2√I1I2
Hence, Imax=(√I1+√I2)2
And Amax=A1+A2
DESTRUCTIVE INTERFERENCE (MINIMUM INTENSITY)
Baccho intensity minimum tab hogi jab cosϕki value minimum hogi and cosine ki minimum value −1 hoti hai,Therefore at ϕ=180∘ cosϕ=−1,
Hence intensity will become,
Imin=I1+I2+2√I1I2cos180∘
Imin=I1+I2−2√I1I2
Hence, Imin=(√I1−√I2)2
And Amin=A1−A2
INTERFERENCE OF WAVES
Baccho aisi do waves jinki frequency same hai and lagbhag same amplitude bhi hai and voh dono waves same direction me propagate kr rhi hai and inn dono wave ka state of polarisation usi medium me bhi same hoga, toh phir baccho inn dono ki intensity different hogi.
Kisi kisi jagah prr intetnsity jyada hogi or kisi kisi jagah prr intensity 0 bhi ho sakti hai.
Let the angular frequency be ω and angular wave number be k,
Consider two waves, y1=A1sin(ωt−kx) and y2=A2sin(ωt−kx+ϕ)
Now by principle of superposition,
y=y1+y2
Therefore , y=Asin(ωt−kx+δ)
Where, A=√A21+A22+2A1A2cosϕ
And tanδ=A2sinϕA1+A2cosϕ
And we know that, intensity I∝A2,
Hence,
I=I1+I2+2√I1I2cosϕ
CONSTRUCTIVE INTERFERENCE (MAXIMUM INTENSITY)
Baccho intensity maximum tab hogi jab cosϕ ki value maximum hogi and cosine ki maximum value 1 hoti hai,Therefore at ϕ=0∘ cosϕ=1,
Hence intensity will become,
Imax=I1+I2+2√I1I2cos0∘
Imax=I1+I2+2√I1I2
Hence, Imax=(√I1+√I2)2
And Amax=A1+A2
DESTRUCTIVE INTERFERENCE (MINIMUM INTENSITY)
Baccho intensity minimum tab hogi jab cosϕki value minimum hogi and cosine ki minimum value −1 hoti hai,Therefore at ϕ=180∘ cosϕ=−1,
Hence intensity will become,
Imin=I1+I2+2√I1I2cos180∘
Imin=I1+I2−2√I1I2
Hence, Imin=(√I1−√I2)2
And Amin=A1−A2
INTERFERENCE OF WAVES
Baccho aisi do waves jinki frequency same hai and lagbhag same amplitude bhi hai and voh dono waves same direction me propagate kr rhi hai and inn dono wave ka state of polarisation usi medium me bhi same hoga, toh phir baccho inn dono ki intensity different hogi.
Kisi kisi jagah prr intetnsity jyada hogi or kisi kisi jagah prr intensity 0 bhi ho sakti hai.
Let the angular frequency be ω and angular wave number be k,
Consider two waves, y1=A1sin(ωt−kx) and y2=A2sin(ωt−kx+ϕ)
Now by principle of superposition,
y=y1+y2
Therefore , y=Asin(ωt−kx+δ)
Where, A=√A21+A22+2A1A2cosϕ
And tanδ=A2sinϕA1+A2cosϕ
And we know that, intensity I∝A2,
Hence,
I=I1+I2+2√I1I2cosϕ
CONSTRUCTIVE INTERFERENCE (MAXIMUM INTENSITY) Baccho intensity maximum tab hogi jab cosϕ ki value maximum hogi and cosine ki maximum value 1 hoti hai,
Therefore at ϕ=0∘ cosϕ=1,
Hence intensity will become,
Imax=I1+I2+2√I1I2cos0∘
Imax=I1+I2+2√I1I2
Hence, Imax=(√I1+√I2)2
And Amax=A1+A2
DESTRUCTIVE INTERFERENCE (MINIMUM INTENSITY) Baccho intensity minimum tab hogi jab cosϕki value minimum hogi and cosine ki minimum value −1 hoti hai,
Therefore at ϕ=180∘ cosϕ=−1,
Hence intensity will become,
Imin=I1+I2+2√I1I2cos180∘
Imin=I1+I2−2√I1I2
Hence, Imin=(√I1−√I2)2
And Amin=A1−A2
REFLECTION OF WAVES
REFLECTION FROM RIGID END

Baccho aapko dikh rha hoga ki ek right end humara wall se connected hai jo ki rigid end hai and left end se hum ek pulse paas krenge, jaise hi pulse right end pr pahuchegi, vese hi pulse ek force lgaegi rigid end prr and same equal and opposite force rigid end lgaega pulse prr.
Ab jaisa ki hume pta hai ki right end fixed hai wall prr, toh jo force puse lgaegi rigid end prr uss wajah se wave ka motion hoga and jo force rigid end lgaega pulse ke upar, uss wajah se pulse vaps reflect ho jaegi or voh bhi inverted, ab baccho baat aati hai ki invert kyu hui ring, toh baccho jaisa ki abhi aapne dekha ki pusle bhi ek force lga rhi hai and rigid end bhi force lga rhi hai, same usi tarah pulse rigid end o upar ki taraf move krana chahti hai, toh baccho rigid end as a reaction pulse ko neeche bhejna chahega, ab baccho pulse rigid end ko upar nhi shift kr pata hai kyunki voh end fixed hai but as a reaction force jab rigid end pulse prr lgata hai toh pulse neeche ki taraf move kr jaati hai, isliye baacho ye inverted hoti hai.
Therefore,
Equation of wave propagating in +ve x-axis,
Incident wave, y1=Asin(ωt−kx)
Reflected wave, y2=Asin(ωt+kx+π) or y2=−Asin(ωt+kx)
REFLECTION FROM FREE END
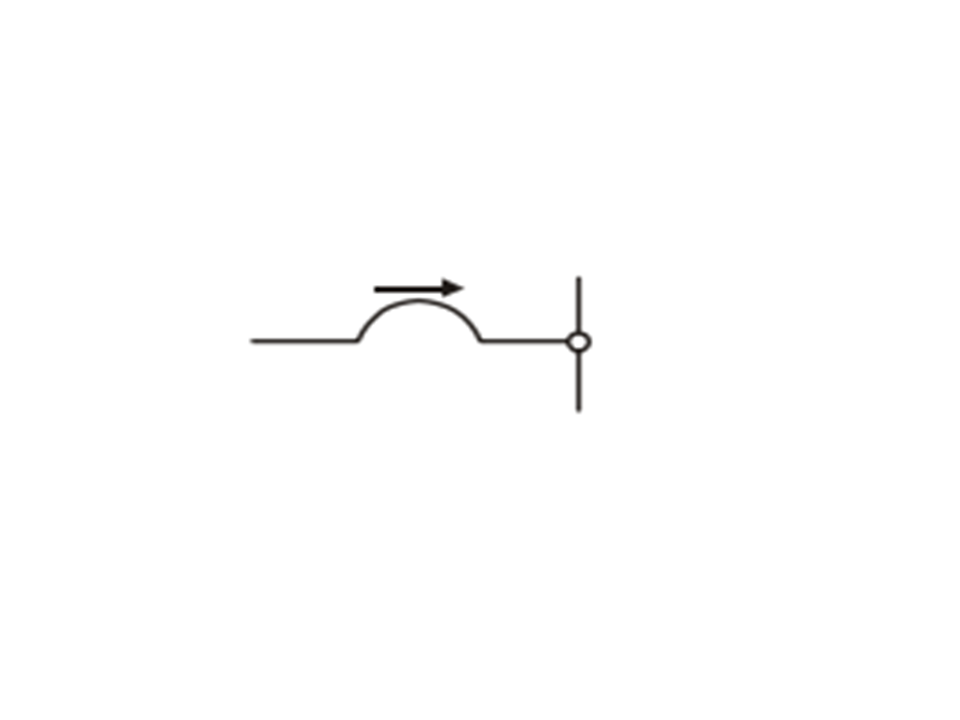
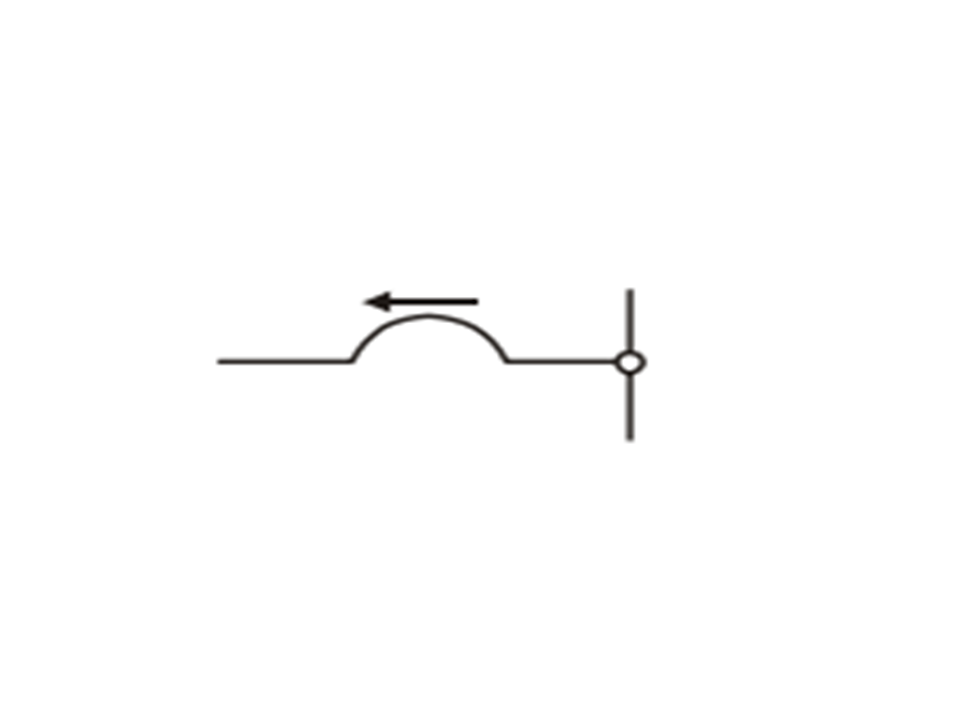
Baccho is case me hum right end ko ek light frictionless ring se attach krdete hai jo ki vertical rod prr freely move kar sakta hai. Ab humne ek pulse transfer ki from left end to right end of the string,
Toh iss case me humara right end free to move hai, iss condition me baccho humari pulse vaps aajaegi without inversion,
Therefore,
Equation of wave propagating in +ve x-axis,
Incident wave, y1=Asin(ωt−kx)
Reflected wave, y2=Asin(ωt+kx)
REFLECTION OF WAVES
REFLECTION FROM RIGID END

Baccho aapko dikh rha hoga ki ek right end humara wall se connected hai jo ki rigid end hai and left end se hum ek pulse paas krenge, jaise hi pulse right end pr pahuchegi, vese hi pulse ek force lgaegi rigid end prr and same equal and opposite force rigid end lgaega pulse prr.
Ab jaisa ki hume pta hai ki right end fixed hai wall prr, toh jo force puse lgaegi rigid end prr uss wajah se wave ka motion hoga and jo force rigid end lgaega pulse ke upar, uss wajah se pulse vaps reflect ho jaegi or voh bhi inverted, ab baccho baat aati hai ki invert kyu hui ring, toh baccho jaisa ki abhi aapne dekha ki pusle bhi ek force lga rhi hai and rigid end bhi force lga rhi hai, same usi tarah pulse rigid end o upar ki taraf move krana chahti hai, toh baccho rigid end as a reaction pulse ko neeche bhejna chahega, ab baccho pulse rigid end ko upar nhi shift kr pata hai kyunki voh end fixed hai but as a reaction force jab rigid end pulse prr lgata hai toh pulse neeche ki taraf move kr jaati hai, isliye baacho ye inverted hoti hai.
Therefore,
Equation of wave propagating in +ve x-axis,
Incident wave, y1=Asin(ωt−kx)
Reflected wave, y2=Asin(ωt+kx+π) or y2=−Asin(ωt+kx)
REFLECTION FROM FREE END


Baccho is case me hum right end ko ek light frictionless ring se attach krdete hai jo ki vertical rod prr freely move kar sakta hai. Ab humne ek pulse transfer ki from left end to right end of the string,
Toh iss case me humara right end free to move hai, iss condition me baccho humari pulse vaps aajaegi without inversion,
Therefore,
Equation of wave propagating in +ve x-axis,
Incident wave, y1=Asin(ωt−kx)
Reflected wave, y2=Asin(ωt+kx)
REFLECTION OF WAVES
REFLECTION FROM RIGID END

Baccho aapko dikh rha hoga ki ek right end humara wall se connected hai jo ki rigid end hai and left end se hum ek pulse paas krenge, jaise hi pulse right end pr pahuchegi, vese hi pulse ek force lgaegi rigid end prr and same equal and opposite force rigid end lgaega pulse prr.
Ab jaisa ki hume pta hai ki right end fixed hai wall prr, toh jo force puse lgaegi rigid end prr uss wajah se wave ka motion hoga and jo force rigid end lgaega pulse ke upar, uss wajah se pulse vaps reflect ho jaegi or voh bhi inverted, ab baccho baat aati hai ki invert kyu hui ring, toh baccho jaisa ki abhi aapne dekha ki pusle bhi ek force lga rhi hai and rigid end bhi force lga rhi hai, same usi tarah pulse rigid end o upar ki taraf move krana chahti hai, toh baccho rigid end as a reaction pulse ko neeche bhejna chahega, ab baccho pulse rigid end ko upar nhi shift kr pata hai kyunki voh end fixed hai but as a reaction force jab rigid end pulse prr lgata hai toh pulse neeche ki taraf move kr jaati hai, isliye baacho ye inverted hoti hai.
Therefore,
Equation of wave propagating in +ve x-axis,
Incident wave, y1=Asin(ωt−kx)
Reflected wave, y2=Asin(ωt+kx+π) or y2=−Asin(ωt+kx)
REFLECTION FROM FREE END


Baccho is case me hum right end ko ek light frictionless ring se attach krdete hai jo ki vertical rod prr freely move kar sakta hai. Ab humne ek pulse transfer ki from left end to right end of the string,
Toh iss case me humara right end free to move hai, iss condition me baccho humari pulse vaps aajaegi without inversion,
Therefore,
Equation of wave propagating in +ve x-axis,
Incident wave, y1=Asin(ωt−kx)
Reflected wave, y2=Asin(ωt+kx)
STANDING OR STATIONARY WAVES
Baccho jab do waves jinka amplitude same ho, unki frequencies bhi same ho, aur voh dono waves opposite direction me travel kar rhi ho, toh inn dono waves ko superimpose krne prr jo wave milti hai use hum standing wavesor stationary waves bolte hai.
Iski defintion hogi,
“The wave propagating in such a medium will be reflected at the boundary and produce a wave of the same kind travelling in the opposite direction. The superposition of the two waves will give rise to a stationary wave. Formation of stationary wave is possible only and only in bounded medium.”.
FROM RIGID END
Baccho hume pta hai ki progressive wave in positive x-direction is given by-y1=Asin(ωt−kx)
And rigid end se reflection ke baad,
y2=Asin(ωt+kx+π) or y2=−Asin(ωt+kx)
Now by the principle of superposition,
ynet=y1+y2
ynet=Asin(ωt−kx)−Asin(ωt+kx)
Therefore ,
ynet=−2Asinkxcosωt, this is the equation of standing wave from the rigid end or fixed end.
Iska amplitude hoga 2Asinkx
Nodes banenge at x=0,λ2,λ,3λ2..........
And antinodes banenge at x=λ4,3λ4.........
FROM FREE END
Baccho hume pta hai ki progressive wave in positive x-direction is given by-y1=Asin(ωt−kx)
And free end se reflection ke baad,
y2=Asin(ωt+kx)
Now by the principle of superposition,
ynet=y1+y2
ynet=Asin(ωt−kx)+Asin(ωt+kx)
Therefore ,
ynet=2Acoskxsinωt, this is the equation of standing wave from the free end. Iska amplitude hoga 2Acoskx
Antiodes banenge at x=0,λ2,λ,3λ2..........
And nodes banenge at x=λ4,3λ4.........
STANDING OR STATIONARY WAVES
Baccho jab do waves jinka amplitude same ho, unki frequencies bhi same ho, aur voh dono waves opposite direction me travel kar rhi ho, toh inn dono waves ko superimpose krne prr jo wave milti hai use hum standing wavesor stationary waves bolte hai.
Iski defintion hogi,
“The wave propagating in such a medium will be reflected at the boundary and produce a wave of the same kind travelling in the opposite direction. The superposition of the two waves will give rise to a stationary wave. Formation of stationary wave is possible only and only in bounded medium.”.
FROM RIGID END
Baccho hume pta hai ki progressive wave in positive x-direction is given by-y1=Asin(ωt−kx)
And rigid end se reflection ke baad,
y2=Asin(ωt+kx+π) or y2=−Asin(ωt+kx)
Now by the principle of superposition,
ynet=y1+y2
ynet=Asin(ωt−kx)−Asin(ωt+kx)
Therefore ,
ynet=−2Asinkxcosωt, this is the equation of standing wave from the rigid end or fixed end.
Iska amplitude hoga 2Asinkx
Nodes banenge at x=0,λ2,λ,3λ2..........
And antinodes banenge at x=λ4,3λ4.........
FROM FREE END
Baccho hume pta hai ki progressive wave in positive x-direction is given by-y1=Asin(ωt−kx)
And free end se reflection ke baad,
y2=Asin(ωt+kx)
Now by the principle of superposition,
ynet=y1+y2
ynet=Asin(ωt−kx)+Asin(ωt+kx)
Therefore ,
ynet=2Acoskxsinωt, this is the equation of standing wave from the free end. Iska amplitude hoga 2Acoskx
Antiodes banenge at x=0,λ2,λ,3λ2..........
And nodes banenge at x=λ4,3λ4.........
STANDING OR STATIONARY WAVES
Baccho jab do waves jinka amplitude same ho, unki frequencies bhi same ho, aur voh dono waves opposite direction me travel kar rhi ho, toh inn dono waves ko superimpose krne prr jo wave milti hai use hum standing wavesor stationary waves bolte hai.
Iski defintion hogi,
“The wave propagating in such a medium will be reflected at the boundary and produce a wave of the same kind travelling in the opposite direction. The superposition of the two waves will give rise to a stationary wave. Formation of stationary wave is possible only and only in bounded medium.”.
FROM RIGID END Baccho hume pta hai ki progressive wave in positive x-direction is given by-
y1=Asin(ωt−kx)
And rigid end se reflection ke baad,
y2=Asin(ωt+kx+π) or y2=−Asin(ωt+kx)
Now by the principle of superposition,
ynet=y1+y2
ynet=Asin(ωt−kx)−Asin(ωt+kx)
Therefore ,
ynet=−2Asinkxcosωt, this is the equation of standing wave from the rigid end or fixed end.
Iska amplitude hoga 2Asinkx
Nodes banenge at x=0,λ2,λ,3λ2..........
And antinodes banenge at x=λ4,3λ4.........
FROM FREE END Baccho hume pta hai ki progressive wave in positive x-direction is given by-
y1=Asin(ωt−kx)
And free end se reflection ke baad,
y2=Asin(ωt+kx)
Now by the principle of superposition,
ynet=y1+y2
ynet=Asin(ωt−kx)+Asin(ωt+kx)
Therefore ,
ynet=2Acoskxsinωt, this is the equation of standing wave from the free end. Iska amplitude hoga 2Acoskx
Antiodes banenge at x=0,λ2,λ,3λ2..........
And nodes banenge at x=λ4,3λ4.........
EXAMPLE 4
The equation of a transverse wave propagating in a string is given by
y=0.02sin(x+30t)
where, xandy are in second.
If linear density of the string is 1.3×10−4kg/m, then the tension in the string is
v=ωk=√Tμ
∴T=μ(ωk)2=(1.3×10−4)(301)2
=0.12N
EXAMPLE 4
The equation of a transverse wave propagating in a string is given by
y=0.02sin(x+30t)
where, xandy are in second.
If linear density of the string is 1.3×10−4kg/m, then the tension in the string is
v=ωk=√Tμ
∴T=μ(ωk)2=(1.3×10−4)(301)2
=0.12N
EXAMPLE 4
The equation of a transverse wave propagating in a string is given by
y=0.02sin(x+30t)
where, xandy are in second.
If linear density of the string is 1.3×10−4kg/m, then the tension in the string is
v=ωk=√Tμ
∴T=μ(ωk)2=(1.3×10−4)(301)2
=0.12N
EXAMPLE 5
A wave moves with speed 300m/s on a wire which is under a tension of 500N. Find how much tension must be changed to increase the speed to 312m/s?
Speed of a transverse wave on a wire is,
v=√Tμ
Differrntiating with respect to tension, we have
dvdT=(12√μT)
Dividing Eq.(ii) by Eq.(i), we have
dvv=12dTT or dT=(2T)dvv
Substituting the proper values, we have
dT=(2)(500)(312−300)300
=40N
i.e. tension should be increased by 40N.
EXAMPLE 5
A wave moves with speed 300m/s on a wire which is under a tension of 500N. Find how much tension must be changed to increase the speed to 312m/s?
Speed of a transverse wave on a wire is,
v=√Tμ
Differrntiating with respect to tension, we have
dvdT=(12√μT)
Dividing Eq.(ii) by Eq.(i), we have
dvv=12dTT or dT=(2T)dvv
Substituting the proper values, we have
dT=(2)(500)(312−300)300
=40N
i.e. tension should be increased by 40N.
EXAMPLE 5
A wave moves with speed 300m/s on a wire which is under a tension of 500N. Find how much tension must be changed to increase the speed to 312m/s?
Speed of a transverse wave on a wire is,
v=√Tμ
Differrntiating with respect to tension, we have
dvdT=(12√μT)
Dividing Eq.(ii) by Eq.(i), we have
dvv=12dTT or dT=(2T)dvv
Substituting the proper values, we have
dT=(2)(500)(312−300)300
=40N
i.e. tension should be increased by 40N.
TRANSMISSION OF WAVES
Baccho abhi tak humne reflection of wave padha, ab hum baat krenge transmission of wave, jese ki baacho reflection me wave jis medium se incident hoti hai, usi medium voh refect hojati hai toh uss wave ki speed same rehti hai, lekin transmission ke case me medium change hota hai,
Isme baccho medium to medium transmission hota hai, means rarer to denser ya phir denser to rarer.

Ab baccho jaisa ki aap deh paa rhe hai diagram me ki wave ko humne rarer medium se denser medium me bheja hai, yaha denser medium mtlb hai baccho ki string ka mass jyada hai,
Ab baccho jaisa ki humne padh liya hai ki velocity in string hota hai,
v=√Tμ
And μ yaha hota hai mass of string per unit length, toh baccho rarer medium ki string ka mass kam hai as compare to denser medium, toh baccho jitna bda mass utna bda μ and jitna bda μ utna bdi uski velocity.
Isliye baccho transmission me velocity change hoti hai,
Agr wave denser to rarer medium me jaegi toh velocity increase kregi and agr wave rarer to denser medium me jaegi toh velocity decrease kregi.
Toh jaisa ki aap diagram me dekh paa rhe hoge ki ye case rarer to denser medium ka hai, toh incident wave ka kuch part reflect hoke vaps aaega and kuch part transmit krega, reflected part invert hoke vaps aajaega, and transmitted part ki velocity kam ho jaegi and voh aage medium me travel kr jaegi.
TRANSMISSION OF WAVES
Baccho abhi tak humne reflection of wave padha, ab hum baat krenge transmission of wave, jese ki baacho reflection me wave jis medium se incident hoti hai, usi medium voh refect hojati hai toh uss wave ki speed same rehti hai, lekin transmission ke case me medium change hota hai,
Isme baccho medium to medium transmission hota hai, means rarer to denser ya phir denser to rarer.

Ab baccho jaisa ki aap deh paa rhe hai diagram me ki wave ko humne rarer medium se denser medium me bheja hai, yaha denser medium mtlb hai baccho ki string ka mass jyada hai,
Ab baccho jaisa ki humne padh liya hai ki velocity in string hota hai,
v=√Tμ
And μ yaha hota hai mass of string per unit length, toh baccho rarer medium ki string ka mass kam hai as compare to denser medium, toh baccho jitna bda mass utna bda μ and jitna bda μ utna bdi uski velocity.
Isliye baccho transmission me velocity change hoti hai,
Agr wave denser to rarer medium me jaegi toh velocity increase kregi and agr wave rarer to denser medium me jaegi toh velocity decrease kregi.
Toh jaisa ki aap diagram me dekh paa rhe hoge ki ye case rarer to denser medium ka hai, toh incident wave ka kuch part reflect hoke vaps aaega and kuch part transmit krega, reflected part invert hoke vaps aajaega, and transmitted part ki velocity kam ho jaegi and voh aage medium me travel kr jaegi.
TRANSMISSION OF WAVES
Baccho abhi tak humne reflection of wave padha, ab hum baat krenge transmission of wave, jese ki baacho reflection me wave jis medium se incident hoti hai, usi medium voh refect hojati hai toh uss wave ki speed same rehti hai, lekin transmission ke case me medium change hota hai,
Isme baccho medium to medium transmission hota hai, means rarer to denser ya phir denser to rarer.

Ab baccho jaisa ki aap deh paa rhe hai diagram me ki wave ko humne rarer medium se denser medium me bheja hai, yaha denser medium mtlb hai baccho ki string ka mass jyada hai,
Ab baccho jaisa ki humne padh liya hai ki velocity in string hota hai,
v=√Tμ
And μ yaha hota hai mass of string per unit length, toh baccho rarer medium ki string ka mass kam hai as compare to denser medium, toh baccho jitna bda mass utna bda μ and jitna bda μ utna bdi uski velocity.
Isliye baccho transmission me velocity change hoti hai,
Agr wave denser to rarer medium me jaegi toh velocity increase kregi and agr wave rarer to denser medium me jaegi toh velocity decrease kregi.
Toh jaisa ki aap diagram me dekh paa rhe hoge ki ye case rarer to denser medium ka hai, toh incident wave ka kuch part reflect hoke vaps aaega and kuch part transmit krega, reflected part invert hoke vaps aajaega, and transmitted part ki velocity kam ho jaegi and voh aage medium me travel kr jaegi.
SONOMETER
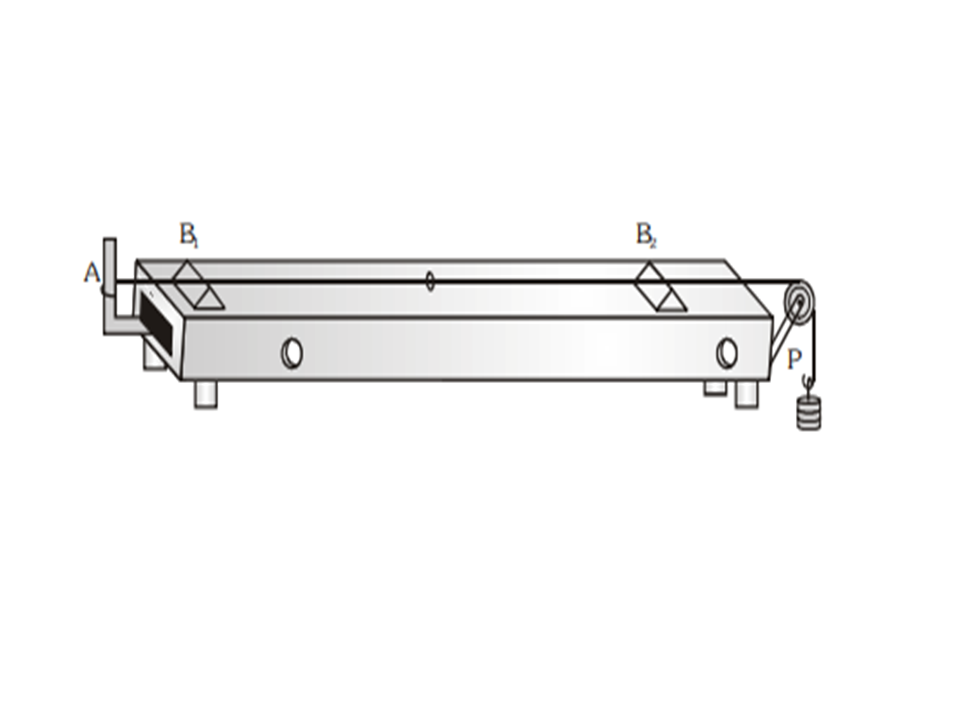
Sonometer consists of a hollow rectangular box of light wood. Isme jo experimental wire hota hai, uske hum ek end ko box ke end se baandh dete hai, phir uss wire ko ek frictionless pulley P ke upar se nikaal kr box ke dusre end tk le jaate hai and uss wire ke end ko hum tension T se stretch krte hai.
Iss box ka kaam ye hota hai ki jab hum iss wire ko vibrate krte hai toh jo sound produce hota hai vibration ki wajah se, uss sound ki loudness ko increase krne ke liye hum box ka use krte hai.
Maan lijiye wire ki length l hai, toh jo frequency of vibration hogi,
f=12l√Tm
Ab humne string me tension ko test krne ke liye ek paper ka chhota sa tuda uske upar rakh diya, aur tuning fork se uss wire ko vibration diya, maan lijiye voh jab humne tuning fork se vibration diya wire ko, toh dono ke paas same frequency aai, toh jo paper hoga voh neeche gir jaega.
SONOMETER

Sonometer consists of a hollow rectangular box of light wood. Isme jo experimental wire hota hai, uske hum ek end ko box ke end se baandh dete hai, phir uss wire ko ek frictionless pulley P ke upar se nikaal kr box ke dusre end tk le jaate hai and uss wire ke end ko hum tension T se stretch krte hai.
Iss box ka kaam ye hota hai ki jab hum iss wire ko vibrate krte hai toh jo sound produce hota hai vibration ki wajah se, uss sound ki loudness ko increase krne ke liye hum box ka use krte hai.
Maan lijiye wire ki length l hai, toh jo frequency of vibration hogi,
f=12l√Tm
Ab humne string me tension ko test krne ke liye ek paper ka chhota sa tuda uske upar rakh diya, aur tuning fork se uss wire ko vibration diya, maan lijiye voh jab humne tuning fork se vibration diya wire ko, toh dono ke paas same frequency aai, toh jo paper hoga voh neeche gir jaega.
SONOMETER

Sonometer consists of a hollow rectangular box of light wood. Isme jo experimental wire hota hai, uske hum ek end ko box ke end se baandh dete hai, phir uss wire ko ek frictionless pulley P ke upar se nikaal kr box ke dusre end tk le jaate hai and uss wire ke end ko hum tension T se stretch krte hai.
Iss box ka kaam ye hota hai ki jab hum iss wire ko vibrate krte hai toh jo sound produce hota hai vibration ki wajah se, uss sound ki loudness ko increase krne ke liye hum box ka use krte hai.
Maan lijiye wire ki length l hai, toh jo frequency of vibration hogi,
f=12l√Tm
Ab humne string me tension ko test krne ke liye ek paper ka chhota sa tuda uske upar rakh diya, aur tuning fork se uss wire ko vibration diya, maan lijiye voh jab humne tuning fork se vibration diya wire ko, toh dono ke paas same frequency aai, toh jo paper hoga voh neeche gir jaega.
EXAMPLE 6
A particle of mass 50g participates in two simple harmonic oscillations simultaneously as given by x1=10(cm)cos[80π(s−1)t] and x2=5(cm)sin[(80π(s−1)t+π/6]. The amplitude of particle's oscillations is given by 'A'. Find the value of A2(in cm2).
A=√A21+A22+2A1A2cosϕ=√102+52+2×5×10×12=√175⇒A2=175.
EXAMPLE 6
A particle of mass 50g participates in two simple harmonic oscillations simultaneously as given by x1=10(cm)cos[80π(s−1)t] and x2=5(cm)sin[(80π(s−1)t+π/6]. The amplitude of particle's oscillations is given by 'A'. Find the value of A2(in cm2).
A=√A21+A22+2A1A2cosϕ=√102+52+2×5×10×12=√175⇒A2=175.
EXAMPLE 6
A particle of mass 50g participates in two simple harmonic oscillations simultaneously as given by x1=10(cm)cos[80π(s−1)t] and x2=5(cm)sin[(80π(s−1)t+π/6]. The amplitude of particle's oscillations is given by 'A'. Find the value of A2(in cm2).
A=√A21+A22+2A1A2cosϕ=√102+52+2×5×10×12=√175⇒A2=175.
EXAMPLE 7
A progressive wave on a string having linear mass density ρ is represented by y=Asin(2πλx−ωt) where y is in mm. Find the total energy (in μJ) passing through origin from t=0 to t=π2ω.
[Take : ρ=3×10−2kg/m,A=1mm,ω=100rad..sec,λ=16cm].
Total energy 12ρA2ω2×λ4.
EXAMPLE 7
A progressive wave on a string having linear mass density ρ is represented by y=Asin(2πλx−ωt) where y is in mm. Find the total energy (in μJ) passing through origin from t=0 to t=π2ω.
[Take : ρ=3×10−2kg/m,A=1mm,ω=100rad..sec,λ=16cm].
Total energy 12ρA2ω2×λ4.
EXAMPLE 7
A progressive wave on a string having linear mass density ρ is represented by y=Asin(2πλx−ωt) where y is in mm. Find the total energy (in μJ) passing through origin from t=0 to t=π2ω.
[Take : ρ=3×10−2kg/m,A=1mm,ω=100rad..sec,λ=16cm].
Total energy 12ρA2ω2×λ4.
SUMMARY
* Mechanical waves can exist in material media and are governed by Newton’s Laws.
* Transverse waves are waves in which the particles of the medium oscillate perpendicular to the direction of wave propagation.
* Longitudinal waves are waves in which the particles of the medium oscillate along the direction of wave propagation.
* Progressive wave is a wave that moves from one point of medium to another.
* The displacement in a sinusoidal wave propagating in the positive x direction is given by y=Asin(kx−ωt+ϕ) where A is the amplitude of the wave, k is the angular wave number, ω is the angular frequency, (kx–ωt+ϕ) is the phase, and ϕ is the phase constant or phase angle.
* Wavelength λ of a progressive wave is the distance between two consecutive points of the same phase at a given time. In a stationary wave, it is twice the distance between two consecutive nodes or antinodes.
* Period T of oscillation of a wave is defined as the time any element of the medium takes to move through one complete oscillation. It is related to the angular frequency ω through the relation T=2πω.
* Frequency f of a wave is defined as 1T and is related to angular frequency by
f=ω2π.
* Speed of a progressive wave is given by
v=ωk=λT=λf.
* The speed of a transverse wave on a stretched string is set by the properties of the string. The speed on a string with tension T and linear mass density μ is
v=√Tμ.
* A travelling wave, at a rigid boundary or a closed end, is reflected with a phase reversal but the reflection at an open boundary takes place without any phase change.
For an incident wave
y=Asin(kx−ωt)
the reflected wave at a rigid boundary is
y=−Asin(kx+ωt)
For reflection at an open boundary
y=Asin(kx+ωt)
* The interference of two identical waves moving in opposite directions produces standing waves. For a string with fixed ends, the standing wave is given by
y=2Asinkxcosωt.
SUMMARY
* Mechanical waves can exist in material media and are governed by Newton’s Laws.
* Transverse waves are waves in which the particles of the medium oscillate perpendicular to the direction of wave propagation.
* Longitudinal waves are waves in which the particles of the medium oscillate along the direction of wave propagation.
* Progressive wave is a wave that moves from one point of medium to another.
* The displacement in a sinusoidal wave propagating in the positive x direction is given by y=Asin(kx−ωt+ϕ) where A is the amplitude of the wave, k is the angular wave number, ω is the angular frequency, (kx–ωt+ϕ) is the phase, and ϕ is the phase constant or phase angle.
* Wavelength λ of a progressive wave is the distance between two consecutive points of the same phase at a given time. In a stationary wave, it is twice the distance between two consecutive nodes or antinodes.
* Period T of oscillation of a wave is defined as the time any element of the medium takes to move through one complete oscillation. It is related to the angular frequency ω through the relation T=2πω.
* Frequency f of a wave is defined as 1T and is related to angular frequency by
f=ω2π.
* Speed of a progressive wave is given by
v=ωk=λT=λf.
* The speed of a transverse wave on a stretched string is set by the properties of the string. The speed on a string with tension T and linear mass density μ is
v=√Tμ.
* A travelling wave, at a rigid boundary or a closed end, is reflected with a phase reversal but the reflection at an open boundary takes place without any phase change.
For an incident wave
y=Asin(kx−ωt)
the reflected wave at a rigid boundary is
y=−Asin(kx+ωt)
For reflection at an open boundary
y=Asin(kx+ωt)
* The interference of two identical waves moving in opposite directions produces standing waves. For a string with fixed ends, the standing wave is given by
y=2Asinkxcosωt.
SUMMARY
* Mechanical waves can exist in material media and are governed by Newton’s Laws.
* Transverse waves are waves in which the particles of the medium oscillate perpendicular to the direction of wave propagation.
* Longitudinal waves are waves in which the particles of the medium oscillate along the direction of wave propagation.
* Progressive wave is a wave that moves from one point of medium to another.
* The displacement in a sinusoidal wave propagating in the positive x direction is given by y=Asin(kx−ωt+ϕ) where A is the amplitude of the wave, k is the angular wave number, ω is the angular frequency, (kx–ωt+ϕ) is the phase, and ϕ is the phase constant or phase angle.
* Wavelength λ of a progressive wave is the distance between two consecutive points of the same phase at a given time. In a stationary wave, it is twice the distance between two consecutive nodes or antinodes.
* Period T of oscillation of a wave is defined as the time any element of the medium takes to move through one complete oscillation. It is related to the angular frequency ω through the relation T=2πω.
* Frequency f of a wave is defined as 1T and is related to angular frequency by
f=ω2π.
* Speed of a progressive wave is given by
v=ωk=λT=λf.
* The speed of a transverse wave on a stretched string is set by the properties of the string. The speed on a string with tension T and linear mass density μ is
v=√Tμ.
* A travelling wave, at a rigid boundary or a closed end, is reflected with a phase reversal but the reflection at an open boundary takes place without any phase change.
For an incident wave
y=Asin(kx−ωt)
the reflected wave at a rigid boundary is
y=−Asin(kx+ωt)
For reflection at an open boundary
y=Asin(kx+ωt)
* The interference of two identical waves moving in opposite directions produces standing waves. For a string with fixed ends, the standing wave is given by
y=2Asinkxcosωt.