OSCILLATIONS for Class 11 PHYSICS
INTRODUCTION
Bacho ham apne daily life mein bhot tarh ke movements dekhte hai. In different types of movements me se kuch simple linear motion hote hai auur kuch projectile motion, jinke baare me aap padh hi chuke ho. Is chapter me ham kuch aise movements ke bare me padhenge jo repeatedly back-and-forth ya ham keh sakte h to-and-fro motion me hota hai. Inme se kuch movements hume amusing lagte hai, ache lagte hai jese ki swing (jhule) ka motion, but kuch to and fro motion hume irritating lagte hai, aur kuch dangerous bhi ho sakte hai. Kya aap jante ho earthquake ke samay buildings oscillatory motion me itna strongly move karte hai that they are shaken apart. The pendulum of the wall-clock also makes a similar motion. This type of motion is called oscillatory motion. Is type ke back-and-forth recurring motion ke bhot sare examples hai bacho, jese koi boat jo river me sink kar rhi ho, kisi steam engine ki piston ko bhi aap dekhoge toh wo bhi backward and forward motion me repeatedly move karta hai. Ye sab oscillatory motion ke examples hai aur is this chapter me hm is motion ke bare me detailed way me padhenge.
PERIODIC AND OSCILLATORY MOTIONS
PERIODIC MOTION
Baccho koi bhi cheez joh regular interval me khud ko repeat kre, use hum periodic motion bolte hai. Isko hum example se samjhte hai, jaise baccho aap logo ka school open hone ka time 8AM hota hai, mtlb har din aapka school 8AM morning me open hojata hai, iska mtlb kya ho rha hai baccho ki ek fixed interval ya regular interval ke baad school open hota hai, toh ise hm periodic motion bolenge.Iski defintion hogi-
“A motion that repeat itself at regular intervals of time is called periodic motion”.
Aao isko hum graphically bhi samjhte hai,
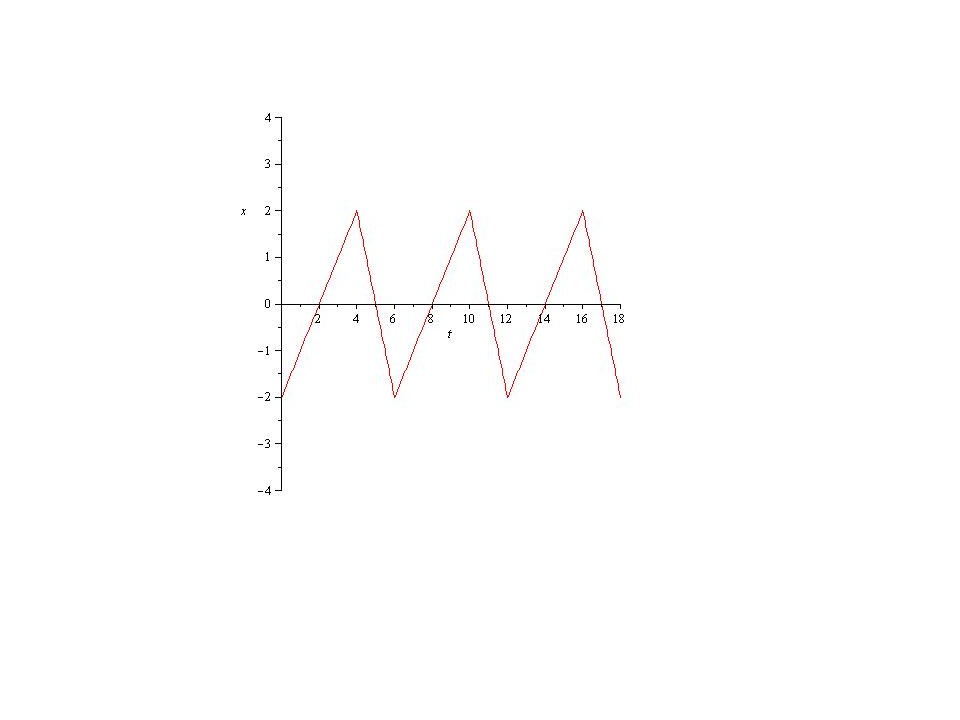
Jaisa ki aap dekh paa rhe honge ki ye graph ek interval ke baad repeat ho rha hai (0-6), (6-12) and (12-18) inn intervals me motion repeat hua hai, or ye periodic hai,mtlb after same interval of time,motion is repeating itself.
OSCILLATORY MOTION
Baccho iske liye hume bss itna janna hai ki jo periodic motion “to and fro motion” krte hai, toh object ya particle oscillation kr rha hai.To and fro ka mtlb hai baccho ki ki ek fixed time interval ke baad voh apni position ko baar baar repeat kre.
Ab uss position ko jisko ye fixed interval ke baad repeat krta hai, use hum mean position bolte hai.
Ab jo simple type ka motion hota hai iss oscillatory motion me, use hum simple harmonic motion bolte hai (SHM).
“All oscillatory motions are periodic motion but all periodic motions are not oscillatory motion”
Kyunki baccho oscillation mtlb hi hota hai ki voh periodic motion jo to and fro motion kr rha ho, but periodic motion me jruri nhi ki voh to and fro motion kre.
And baccho periodic mtlb hi harmonic hota hai, means ek fixed interval ke baad repeat hona. Toh periodic motion ko hum harmonic motion bolte hai.
TIME PERIOD AND FREQUENCY
Abhi humne padha ki aisa motion jo ek regular interval of time me repeat krta hai,use hum periodic motion bolte hai. And sabse chhota interval of time, jiske baad motion repeat krta hai use hum uss periodic motion ka time period bolte hai, and use hum T se denote krte hai.Baccho time period ka reciprocal hi frequency hota hai jisko hum f se denoote krte hai. Therefore ,
f=1T
And iski unit hoti hai sec−1 or isko humne ek special unit se bhi denote krte hai Hertz or Hz.
DISPLACEMENT
Jaise baccho linear motion me displacement hota tha initial and final point ki beech ki doori, prr baccho periodic motion me displacement alag hota hai,Aao ise hum ek spring block diagram se samjhte hai jo ki ek SHM ka example hai,
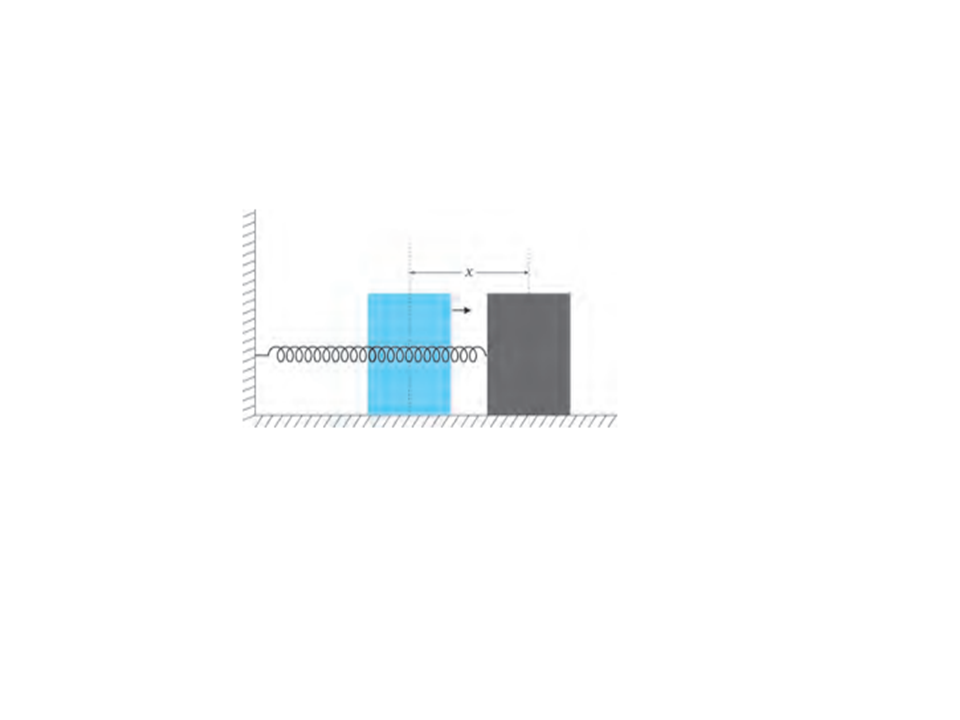
Ye ek spring block system hai and black box show kr rha hai displacment se phle ki baat and blue box show kr rha hai displacement ki baad ki image,
Ab baccho jaisa ki aap dekh paa rhe hai ,initially humara system equilibrium prr hai, ab hum iss block ko x distance displace krenge negative x-axis direction me from its mean position, and isi ko baccho hum displacement bolte hai in periodic motion,
Ab baccho jaise hi hum displace krenge vaise hi spring force lgega block ke displacement ka oppose krega, and voh hota hai F=−kx.
And baccho ye time T ke baad repeat bhi krega,
Therefore ,
Yaha se hume frequency mi jaegi,
ω=2πf
Therefore f=ω2π
And time period T=2πω
SIMPLE HARMONIC MOTION
Maan lijiye ki ek particle hai voh to and fro motion kr rha hai, and dono taraf uska maximum displacement ±A hai.
Toh jab hum ise displace krenge kisi bhi direction me toh iss prr e force lgega jo displacement ka oppose krega,
F=−kx
Maan lijiye particle ka mass m hai and acceleration a hai,
Therefore,
F=ma=−kx,
And isko hum compare krenge a=−ω2x
Hence, ω2=km
So, ω=√km
Toh yaha se hum frequency bta sakte hai,
Frequency f=12π√km
And time period T=2π√mk
Ab hum baccho dekhenge ki actually ho kya rha hai ,
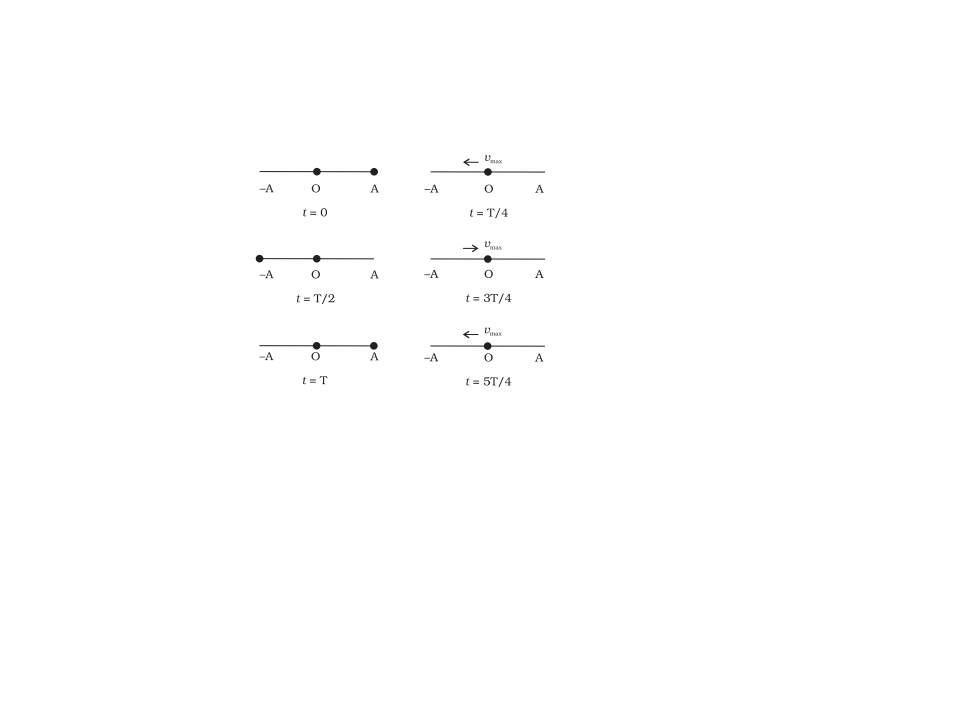
Hum yaha prr analysis krenge ki ek time period me kya kya hua, uske liye hum maan lete hai ki ek spring block system hai and time t=0 prr humara block O ko A distance displace kiya in positive x direction from mean position, ab iss hoga ye ki extreme position A prr humare block prr opposing force moaximum hogi and velocity v=0 hogi, ab hum iss block ko release krdenge.
Ab baccho jaise hi hum iss block ko release krenge, iss block prr ek acceleration lg rha hoga jiski wajah se block vaps mean postion prr aana chahega and velocity bhi increase hoti jaegi,
At time t=T4, particle apni jagah prr vaps aagya because of restoring force and uski velocity 0 se badh kr maximum velocity ho gyi at mean position and mean position prr net force 0 hoga, toh at t=T4 velocity will be maximum and net force on the block will be 0,
Ab baccho block rukega toh nhi, kyunki uski velocity maximum hai,mtlb kinetic energy hai uske pass, toh ab baccho block negative x0axis ki taraf move krega and iske motion ko ab spring force oppose krne lgegi phirse.
At time t=T2, block humara extreme position −A tk pahuch jaega and uss time uski kinetic energy 0 ho jaegi,mtlb velocity 0 ho jaegi and uss time prr jo spring force hai voh maximum hoga, jiski wajah se particle vaps mean position prr aana chahega.
Ye same process t=T tk chlegi,jab iska single time period khatam hoga, and ye usi direction and usi jagah prr hoga jaha se isne t=0 se start kiya tha.
Isi motion ko hum oscillatory motion bhi bolte hai, periodic toh ye hai hi and isi ko hum simple harmonic motion bhi bolte hai.
VELOCITY AND ACCELERATION IN SHM
Baccho SHM me ki force opposing nature ka hota hai,
Maan lete hai ki ek spring block system hai, toh usme force hoga f=−kx
Or f=ma=−kx
Therefore acceleration in SHM a=−kmx
And we can aso write, acceleration a=−ω2x
Ab hum velocity ki baat krenge toh hum acceleration ki equation ki madad se velocity bhi nikaal sakte hai,
Therefore ,
We know that , a=−ω2x
Now we can write, vdvdx=−ω2x
∫vdv=∫−ω2xdx
Now for limits, hme pta hai ki velocity 0 kab hoti hai jab block extreme positions prr hota hai mtlb hai ki at x=±A, v=0
Therefore , v22=−ω2[x22−(±A)22]
v22=−ω2[x22−A22]
Therefore v2=±ω2(A2−x2)
SIMPLE HARMONIC MOTION AND UNIFORM CIRCULAR MOTION
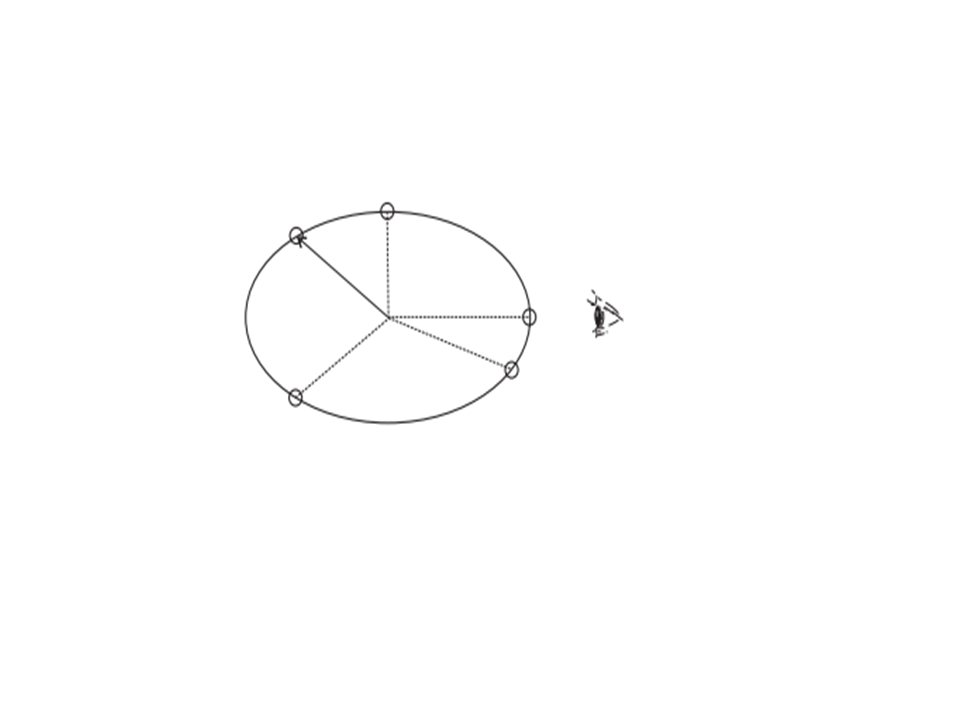
Baccho humne ek experiment kiya, or experiment me humne ek particle ko uniform circular motion krwaya, toh humne ek chhez notice kari ki jab hum iss uniform circular motion ka projection lete hai circle ke diameter ke along, toh dekha ki particle SHM kr rha hai, jaisa ki aap dekh sakte hai ki diameter ke across humne iss motion ko dekha hai.
Ab baccho hum ise thoda detail me samjhenge,
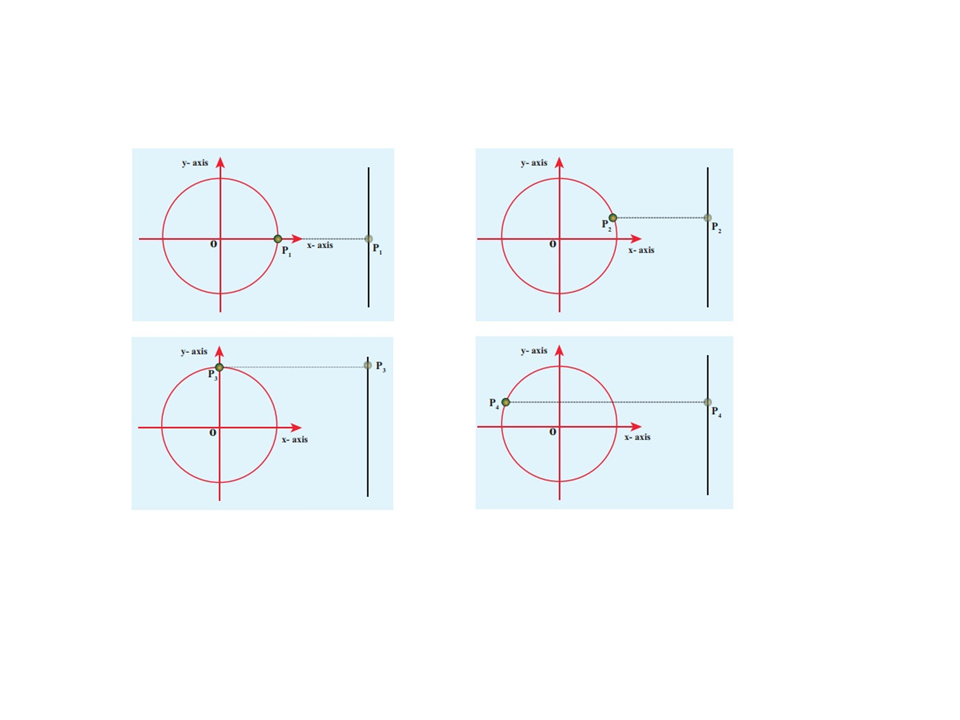
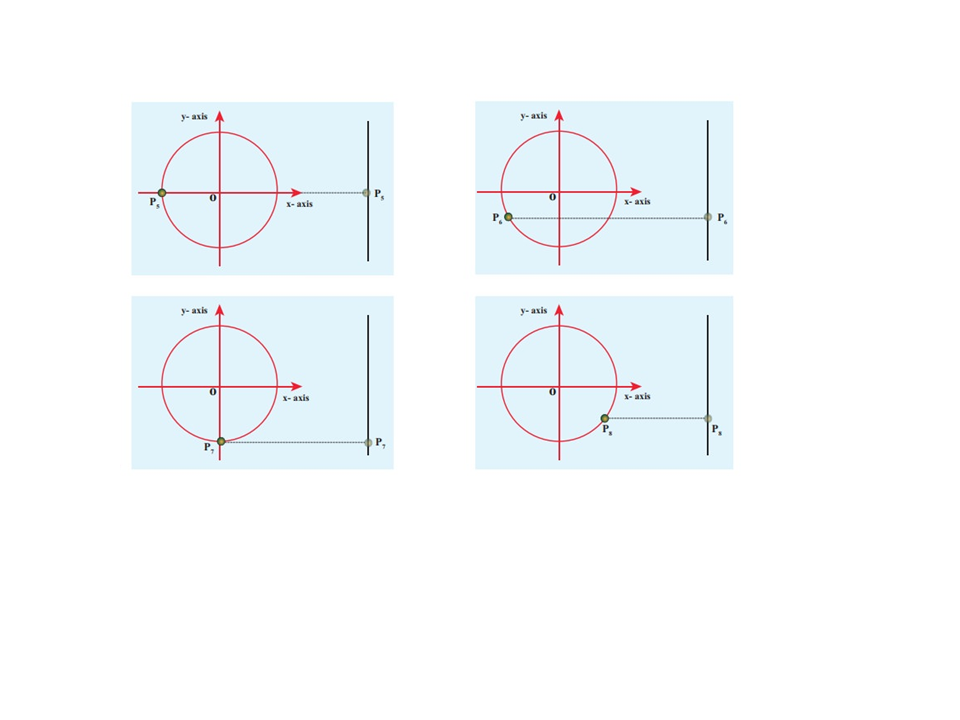
Jaisa ki aap upar graphical representation me dekh sakte ki kaise ek particle P circular motion bhi kr rha hai and uska projection SHM kr rha hai.
Baccho dhyaan rakhne waali baat ye hai ki SHM circular motion nhi hai, hum jo uniform circular motion ka projection lete hai voh SHM krta hai.
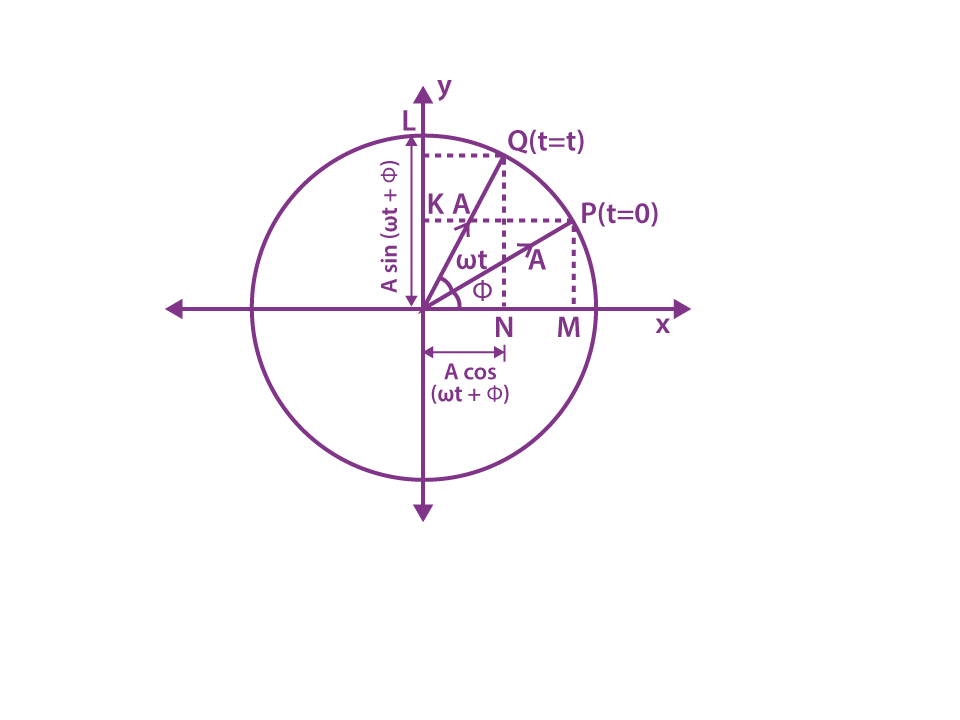
Baccho jaisa ki aap dekh paa rhe hoge diagram me ki particle at t=0 prr P point prr hai and uss time voh x-axis se ϕ angle bna rha hai, baccho hum iska projection diameter ke across dekhenge.
Ab humne dekha ki after time t particle Q position prr pahuch jata hai and uska projection humne diameter ke along dekha hai.
Ab t time me particle jo angle θ chla hoga voh hum nikaal sakte hai, ω=θt,
Therefore θ=ωt
Toh jo total angle hoga voh hoga ωt+ϕ , ab jo y-axis (diameter) ke along projection hoga voh hoga,
Asin(ωt+ϕ) and baccho yhi humara displacement hoga x=Asin(ωt+ϕ) , where A is the radius of circle,
Therefore, this is the displacement eq2 of SHM.
Ab baccho for velocity, hum displacment ko differentiate krdenge wrt time t,
dxdt=d(Asin(ωt+ϕ))dt
v=Aωcos(ωt+ϕ) , this is the velocity in SHM.
And agr hume acceleration chahiye toh hum velocity ko differentiate krdenge wrt to time,
Therefore,
dvdt=d(Aωcos(ωt+ϕ))dt
a=−Aω2sin(ωt+ϕ) , this is the acceleration of particle in SHM.
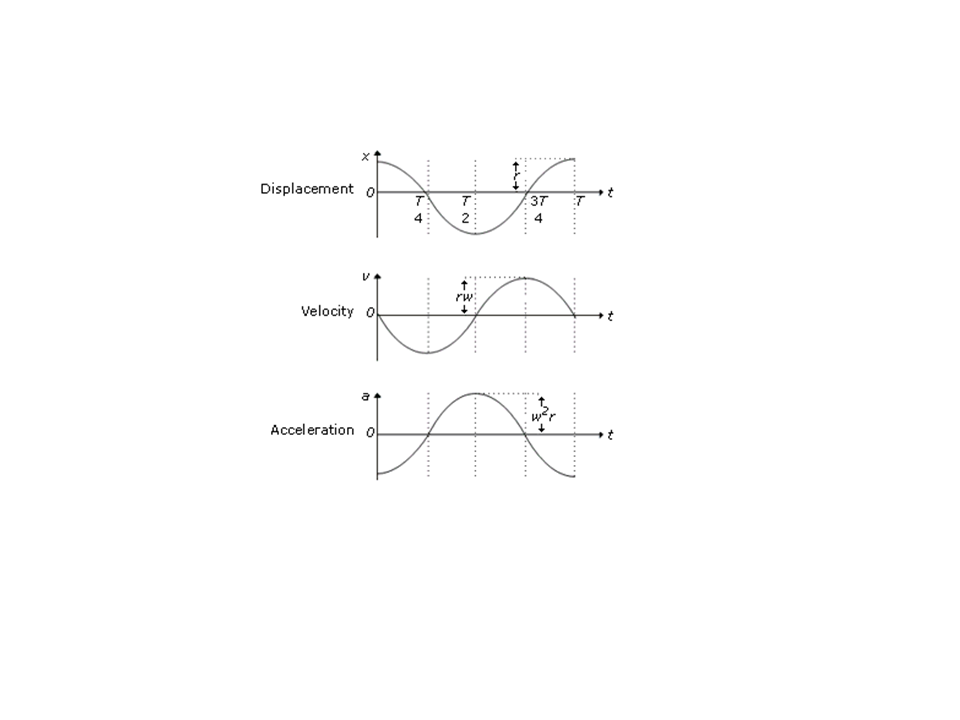
x vs t, v vs t, a vs t GRAPH IN SHM
Now we know the equation of displacement in SHM, that isx=Asin(ωt+ϕ)
And
v=Aωcos(ωt+ϕ)
And
a=−Aω2sin(ωt+ϕ)
Therefore there graph will be of a function of sine and cosine, hence
POINT 1
Periodic motion:A motion that repeat itself at regular intervals of time is called periodic motion.
Time period:The smallest interval of time after which the motion is repeated is called its period.
EXAMPLE 1
Which of the following statements is/are true for a simple harmonic oscillator ?
Let the equation for the SHM is x=asinωt. ltbr gt Clearly, it is a periodic motion because it involves sine functon.
Velocity v=dxdt=ddt(asinωt)=aωcosωt
Velocity is also periodic because of cosine function.
Acceleration, A=dvdt=d2xdt2=−aω2sinωt
[:' Acceleration is a sine function, hence cannot be constant]
=−(ω2a)sinωt=−ω2x
Force, F=massxx acceleration
=mA=−mω2x
Hence, force acting is directly porportioal to displacement from the mean position and oppsite to it.
EXAMPLE 2
The relation between acceleration and displacement of four partical are given below
Which, one of the particle is exempting simple harmonic motion ?
For motion to be be SHM acceleration of the particale must be proportional to negative of displacement.
i.e., a∝−(y or x)
We should be clear that y has to be linear.
EXAMPLE 3
When a mass m is connected individually to two springs S1 and S2, the oscillation frequencies are v1 and v2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be


Consider the diagram, two springs can be considered as parallel.
Hence, keq=Equivalent spring constant
k1+k2
Time period of oscillatin of the spring block-system
T=2π√mkeq=2π√mk1+k2
⇒v=1T=12π×√k1+k2m
Equivalent oscillation frequency.
When the mass is connected to the two springs individually
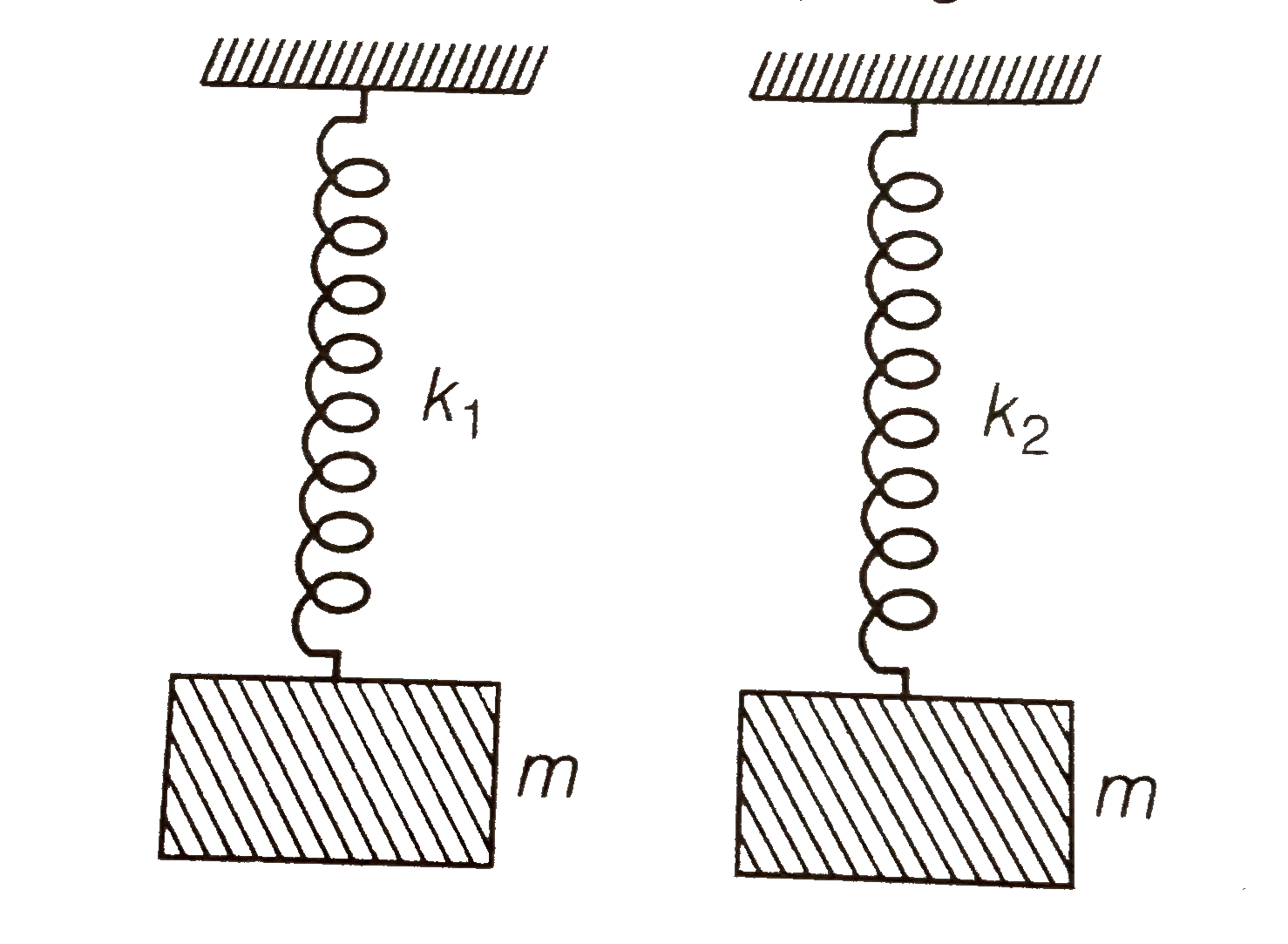
v1=12π√k1m
v2=12π√k2m
From Eqs. (i),(ii) and (iii),
v=12π=[k1m+k2m]1/2 [from Eq. (i)]
12π[4π2v211+4π2v221]
[∵fromEq.(ii)k1m=4π2v21and fromEq.(iii),k2m=4π2v22]
=2π2π[v21+v22]1/2⇒v=√v21+v22]
Not Do not confuse with parallel and series combinations of springs.
EXAMPLE 4
A particle is acted simultaneously by mutally perpendicular simple harmonic motion x=acosωt and y=asinωt. The trajectory of motion of the particle will be
Given, x=acosωt…..(i)
y=asinωt.....(ii)
Squaring and adding Eqs. (i) and (ii),
x2+y2=a2 (cos2ωt+sin2ωt)
=a2⇒x2+y2=a2 [∴cos2ωt+sinωt=1]
This is the equation, of a circle
Clearly, the locus is a circle of constant radius a.
EXAMPLE 5
The displacement of a particle is repersented by the equation y=sin3ωt. The motion is
Given equation of motion is
y=sin3ωt
=(3sinωt−4sin3ωt)/4 [∴sin30=3sin0−4sin30]
⇒dydt=[ddt(3sinωt)−ddt(4sin3ωt)]/4
⇒4dydt=3ωcosωt−4×[3ωcos3ωt]
⇒4×d2ydt2=−3ω2sinωt+12ωsin3ωt
⇒d2ydt2=−3ω2sinω+12ω2sin3ωt4
⇒d2ydt2 is not proportional ot y.
Hence, motion is not SHM.
As the expression is involving sine sine function, hence it will be periodic.
EXAMPLE 6
Motion of an oscillating liquid column in a U-tube is
Consider the diagram in which a liquid column oscillates. In this caes, restoring force acts on the liquid due to gravity. Acceleration of the liquid column, can be calculated in terms of restoring force.

Restoring force f=Weight of liquid column of height 2y
⇒f=−(A×2y×p)×g=−2Apgy [∴η=pv]
⇒f=∝−y⇒ Motion is SHM with force constant k=2Apg.
⇒ Time period T=2π√mk=2π√A×2h×p2Apg=2π√hg
T=2π√lg, where l=h
Which is independent of the density of the liquid.
SHM IN FLUID
OSCILLATION OF A LIQUID COLOUMN IN A U-TUBE
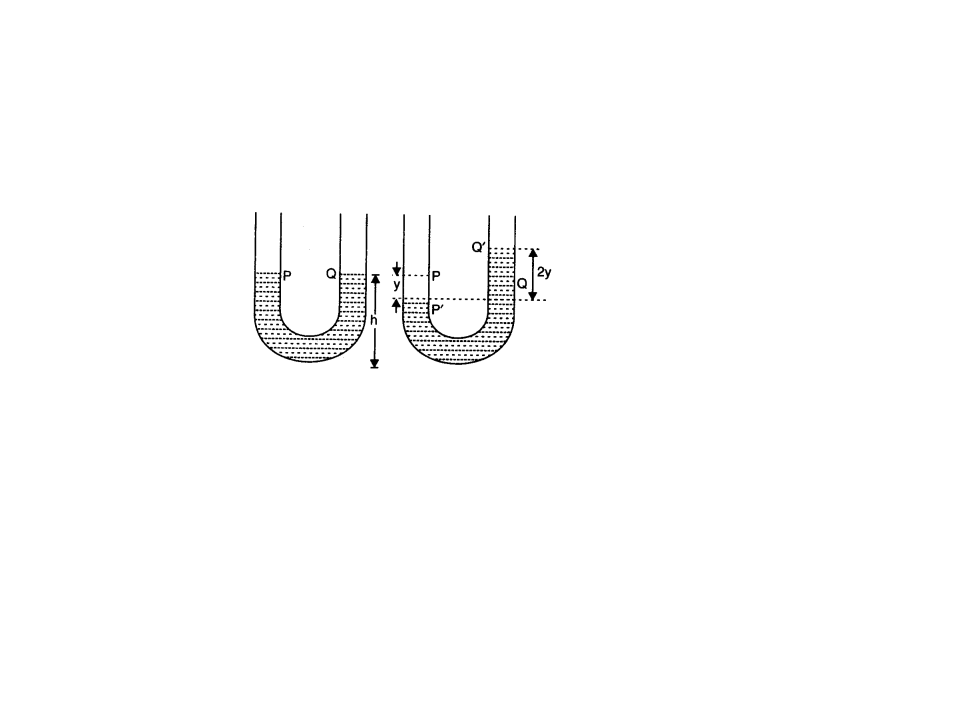
Jesa ki baccho aap dekh paa rhe ho ki ek U-tube liya hai humne jisme ek liquid filled hai, initially dono coloumn me liquid ki height same hai (h) .
Ab humne liquid ke ek side ko y distance displace kiya downwards direction me toh utna hi dusri side me raise hoga liquid.
Ab P’ point prr ek atmospheric pressure (P_0) lgega downwards and liquid ki wajah se upward pressure lgega (P), ab liquid ka pressure jyada hoga atmospheric pressure se ,tabhi liquid upar aaega vaps, and if A is the area of U-tube .
Therefore ,
Fnet=PA−P0A,
Ab hum baccho hume pressure P nikalna hai, toh uske liye hum Q point ka ressure nikaal lete hai and pressure of P’=pressure of Q , kyunki dono ki height same hai.
Ab Q point ka pressure hoga baccha,
Pressure" "at" "Q" "poi nt = P_0+rhog(2y)),
Therefore Fnet=PA−P0A
Fnet=(P0+ρg(2y))A−P0A
Or
Fnet=ρg(2y)A
And we can write, Fnet=−2ρgAy (yaha negative sign isliye lgaya hai kyunki net force ki direction and displacement ki direction, dono opposite hai ek dusre ke.
Now we cam compare this equation with SHM force equation, F=−ky
Therefore, we get
-2rhogAy=-ky
And
k=2ρgA
TIME PERIOD OF A LIQUID COLOUMN IN A U-TUBE
Time period of any SHM is given by- T=2π√mkPutting the value of k in this eqn,
T=2π√m2ρgA
And mass of liquvolume of liquρ
m=ρ×(2Ah)
Again putting the value of m in time period eq^n,
T=2π√2ρAh2ρgA
Therefore,
T=2π√hg , this is the time period of liquid column in a u-tube.
SHM IN GRAVITATION
Bachho isme ek case hota hai tunnel through earth,jisme gravitation chapter ke concept bhi lgte hai,aao hum ise samjhte hai.
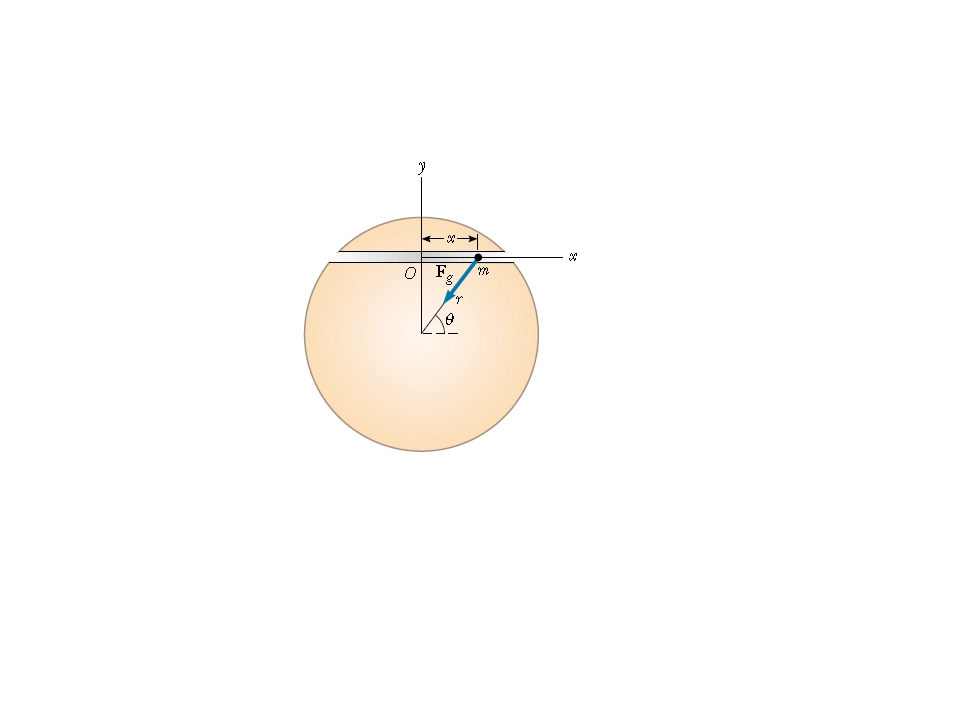
Baccho humne ek tunnel bnai earth ke ek end se dusre end tak, ab humne ek particle liya jiska mass m hai or isko humne mean position (O) prr rakha, uss time particle prr negative y-axis ki taraf ek gravitational force lg rhi hogi, lekin x-axis ki taraf ki force nhi lag rhi hogi.
Ab baccho aapko ye cheez pta hi hogi ki surface prr gravitational acceleration (g) lgta hai and centre prr 0 hota hai, that means jese jese hum centre ki taraf jaate jaaenge vese vese acceleration am hota jaega, and ye vary krta hai,
g’=grR
where R=radius of earth
And r=distance of particle from centre
Ab humne baccho iss particle ko positive x-axis ki taraf bhut chhota sa displacement kiya (x) jesa ki aap diagram me dekh sakte hai, ab iss time gravitational force (Fg’) centre ki taraf lgegi , ab hum iske component break krenge toh ek component Fg’sinθ y direction me lgega and ek component Fg’cosθ particle ke displacement ka oppose krega.
Here ,
Fg’=mg’, therefore jis force ki wajah se SHM hoga voh hogi,
F=Fg’cosθ
F=−mg’cosθ (negative sign show kr rha hai ki displacement and force dono opposite direction me hai)
Ab baccho , cosθ=basehypotenuse,
cosθ=xr where x=displacement of particle
Therefore ,force will become,
F=−mg’(xr)
Now we know, force in SHM is F=−kx,
hence , k=mg’r
k=m(grR)r,
Therefore k=(mgR)
Time period of any Shm is given by- T=2π√mk
Hence, T=2pisqrt((mR)/(mg)),
T=2π√Rg , this is time period of particle .
R=6.4×106m and g=9.8ms2
Toh baccho jo approx time period aata hai tunnel through earth me voh hai, T≈84.6min .
ENERGY IN SHM
Baccho simple harmonic motion me dono tarah ki energies (kinetic energy and potential energy) hoti hai, sabse phle hum padhenge ki kinetic energy SHM me kya hoti hai.
KINETIC ENERGY
Toh ab hum kinetic energy ki baat krein toh voh kya hoti hai baccho,KE=12mv2
And SHM me velocity hoti hai, v=ω√A2−x2,
Ise substitute krenge toh banega,
KE=12m(ω√A2−x2)2
Therefore we can write,
KE=12mω2(A2−x2) where omega=k/m,
This is kinetic energy of a particle performing SHM at position x.
Ab baccho hum baat krenge ki kinetic energy maximum and minimum kab hogi, agr hum baat krein maximum ki baccho toh aap equation me dekh sakte hai ki KE maximum jab hi hogi jab x ki value minimum hogi and x ki value minimum 0 hi ho sakti hai jo ki mean position hoti hai particle ki.
Therefore at mean position (x=0), KE will be maximum,
KEmax=12mω2(A2−02),
KEmax=12mω2A2
And similarly agr hum minimum kinetic energy ki baat krein toh voh jab hogi jab x ki value maximum hogi and x ki value maximum ±A hi ho sakti hai jo ki extreme position hoti hai particle ki.
Therefore at extreme position (x=+-A), KE will be minimum,
KEmin=12mω2(A2−(±A)2),
KEmin=12mω2(A2−A2)
Therefore,
KEmin=0
POTENTIAL ENERGY
Baccho ab baat krenge potential energy ki, toh kya SHM me potential energy hogi?, haan baccho potential energy jrur hogi kyunki SHM me force spring force jesa hota hai, that is F=−kx Jo ki ek conservative force haiToh jo potential energy aati hai voh hum nikaalte hai,
ΔU=−Wconservative, and chhote se workdone ke liye potential energy hogi,
dU=−Wc
Then ∫dU=−∫Fdxcosθ
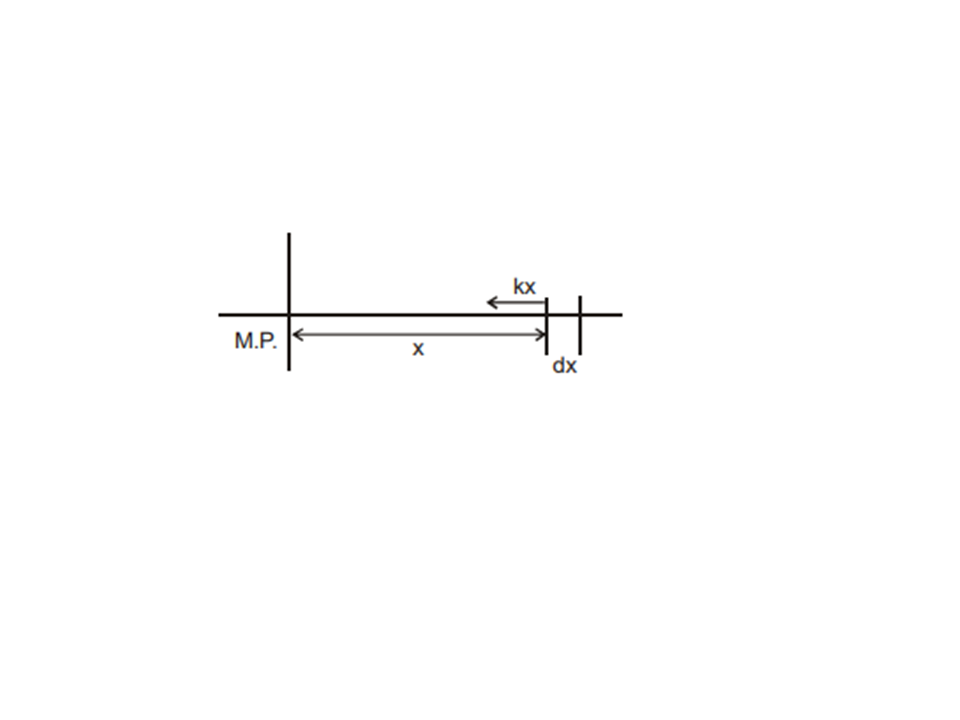
Ab jo force hai voh kisi x position prr hai, toh force displacement ka oppose krega,that means agr hum dx displacement krte hai toh uss displacement ka oppose krega ye force kx, therefore inn dono ke beech ka angle 180∘ , hence
∫dU=−∫Fdxcos180∘
∫dU=−∫kxdxcos180∘
∫dU=−∫kxdx(−1)
[U]=[(kx^2)/2]
Ab hume limits set krni hai, toh hum mean position se kisi position x ke liye integrate krenge, Therefore at initial position x=0, maan lijiye particle ke pass U0 potential energy hai, and jab uski position x ho jaati hai toh maan lete hai ki potential energy uss particle ki U hai. Toh hume expression milega,
U−U0=kx22−0
Therefore, potential energy will be, U=U0+kx22 where k=mω2,
This is potential energy of a particle performing SHM at position x.
Ab baccho hum baat krenge ki potential energy maximum and minimum kab hogi, agr hum baat krein maximum ki baccho toh aap equation me dekh sakte hai ki PE maximum jab hi hogi jab x ki value maximum hogi and x ki value maximum +-A hi ho sakti hai jo ki extreme positions hoti hai particle ki.
Therefore at extreme position (x=+-A), PE will be maximum,
PEmax=U0+k(±A)22
Therefore,
PEmax=U0+kA22
And similarly agr hum minimum potential energy ki baat krein toh voh jab hogi jab x ki value minimum hogi and x ki value minimum 0 hi ho sakti hai jo ki mean position hoti hai particle ki. Therefore at mean position (x=0), PE will be minimum,
PEmax=U0+k02,
PEmin=U0+0
Therefore,
PEmin=U0
TOTAL MECHANICAL ENERGY IN SHM
Agr hum baat krein total mechanical energy ki SHM me toh baccho ye humedha conserve rahegi, mtlb hai ki humesha constant rahegi.Lekin KE and PE constant nhi hongi, ye humesha vary karengi with respect to position of particle, KE and PE x prr depend kr rhi hai ,toh ye humesha change hongi, lekin mechanical energy humesha constant rahegi, aao dekhte hai ki kese constant rahegi.
Total energy= KE + PE,
Therefore, TE=12mω2(A2−x2)+U0+kx22 where k=mω2,
Hence
TE=12mω2(A2−x2)+U0+mω2x22
Or we can write
TE=12mω2A2−12mω2x2+U0+12mω2x2
Atlast, TE=12mω2A2+U0 ,this is total mechanical energy which is conserve (constant).
VARIATION IN SHM ENERGY
Ab jaisa ki aapne dekha ki potential energy and kinetic energy, dono hi variable hai jo ki position of particle prr depend kr rhi hai, ab humne e graph draw kiya, kinetic energy ,potential energy and position of particle ke beech me.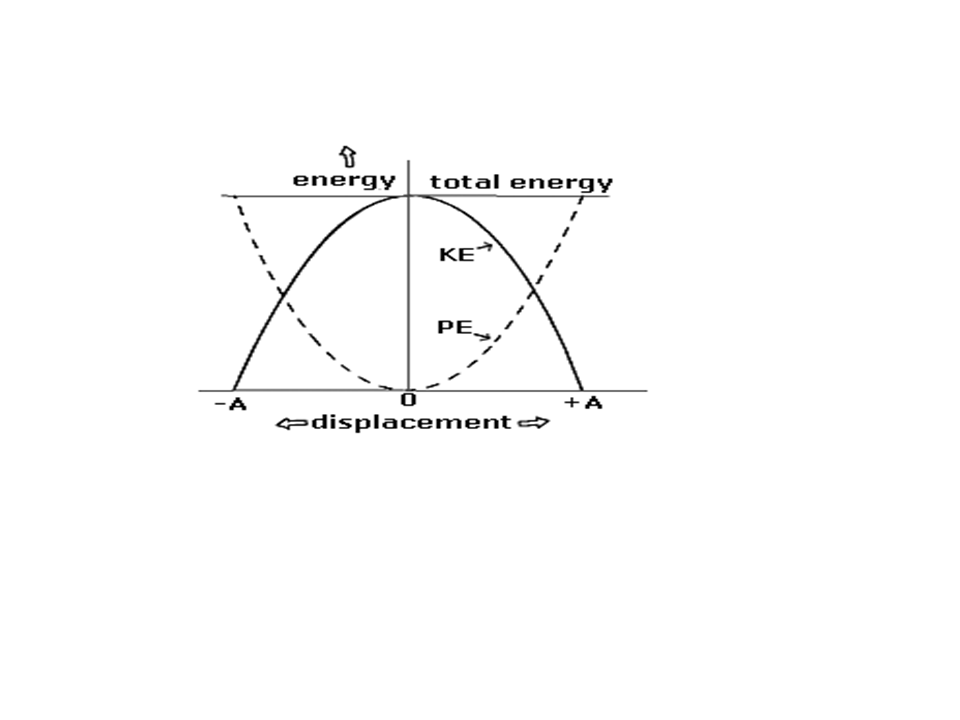
Baccho jaisa ki aap dekh paa rhe hoge graph me ki dotted line PE ko show kr rha hai and dark line KE ko show kr rhi hai and ek jo staright line hai sabse upar voh total energy show kr rhi hai.
Ab jaisa ki aapne dekha ki total enegy humesha conserve rahegi means constant , isliye iska graph ek straight line hai.
Ab baat krein mean position ki toh baccho mean position prr potential energy minimum hoti hai and kinetic energy maximum hoti hai, ye humne upar padha hua hai, baccho yaha prr initial potential energy ko 0 mana hua hai (U_0=0) .
And similarly extreme positions prr dekhe toh potential energy maximum hai and kinetic energy minimum hai.
Isi tarah se energy vary krti hai SHM me.
ANGULAR SHM
Baccho jaisa ki aapne abhi tak linear SHM padha tha, usi jaisa similar hota hai angular SHM, angular SHM me displacement hota hai θ and yaha force ki ajagh torque lgti hai jo ki particle ya pendulum ke motion ka oppose krti hai.
Therefore we can write,
τ=−kθ where k=SHM constant, and θ= angular displacement from mean position.
Yaha SHM ki equation hogi,
d2θdt2+ω2θ=0 and here ω=√KI
SIMPLE PENDULUM
Agr ek heavy point mass ko hum ek weightless string se end prr baandh dete hai and usi string ke dusre end ko ek rigid support prr baandh dete hai, toh iss arrangement ko hum simple pendulum bolte hai.
TIME PERIOD OF A SIMPLE PENDULUM
Ab baccho SHM ki condition hoti hai F=−kx mtlb hai ki itna chhota displacement ki particle ek staright line me SHM kre,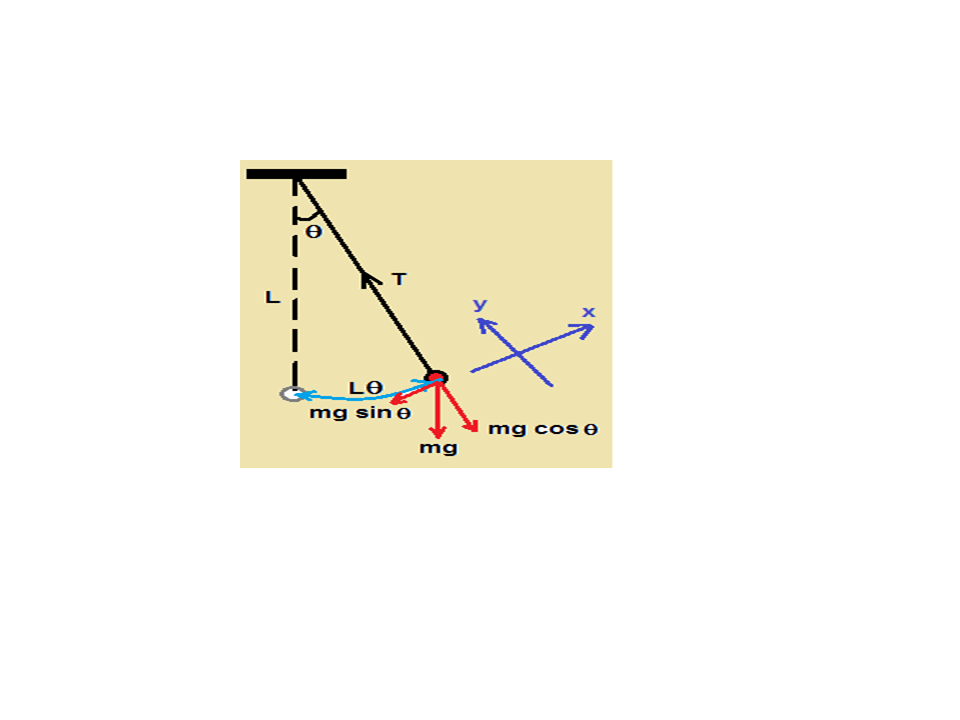
Jaisa ki aap diagram me dekh paa rhe honge ki humne ek ball jiska mass m hai usko ek massless string se baandha hua hai jiski length L hai.
Ab humne iss ball ko mean position se thoda displace krdiya hai angle θ and linear displacement ball ka hua x , ye itna chhota angle hota hai ki jab ball ko chhodenge toh ye ek straight line me SHM krega,
Ab hume pta hai ki
angle=arcradius therefore,
θ=xL
x=Lθ
Tabhi baccho simple pendulum ek linear SHM ka example hai.
After displacement , ball prr gravitational force lgegi mg and hum iss force ke component todenge and voh aaenge mgcosθ and mgsinθ, and ek tesnion force lgegi along the string T ,
Therefore
T=mgcosθ, and baccho jo force iss ball ke displacement ka oppose kregi voh hogi mgsinθ, hence
F=−mgsinθ
Bacchi minus sign isliye lgaya hai kyunki jis direction me displacement hua hai, uske opposite direction me force lg rhi hai .
As displacement θ is small,hence sinθ≈θ
Therefore, F=−mgsinθ
F=−m>hη
F=−mgxL
Now we can compare this equation with F=−kx
Therefore , −mgxL=−kx
k=mgL
And we know that time period of any SHM is T=2π√mk
Hence ,time period of a simple pendulum is given by,
T=2π√mLmg
T=2π√Lg
TIME PERIOD OF A SIMPLE PENDULUM IN ACCELERATING FRAME
Isme bss chhota sa change aaega baccho, accelerating frame ke case me hum gravitational acceleration g ki jagah g_(eff) use krenge, mtlb hai ki hum net gravitational jo pendulum prr lag rha hoga se lenge, hence,T=2π√Lgeff
COMPOUND PENDULUM / PHYSICAL PENDULUM
Jab koi rigid body suspended hoti hai kisi axis se and use hum oscillate krwate hai uss axis ke about toh ise hum compound pendulum ya phir physical pendulum bolte hai.
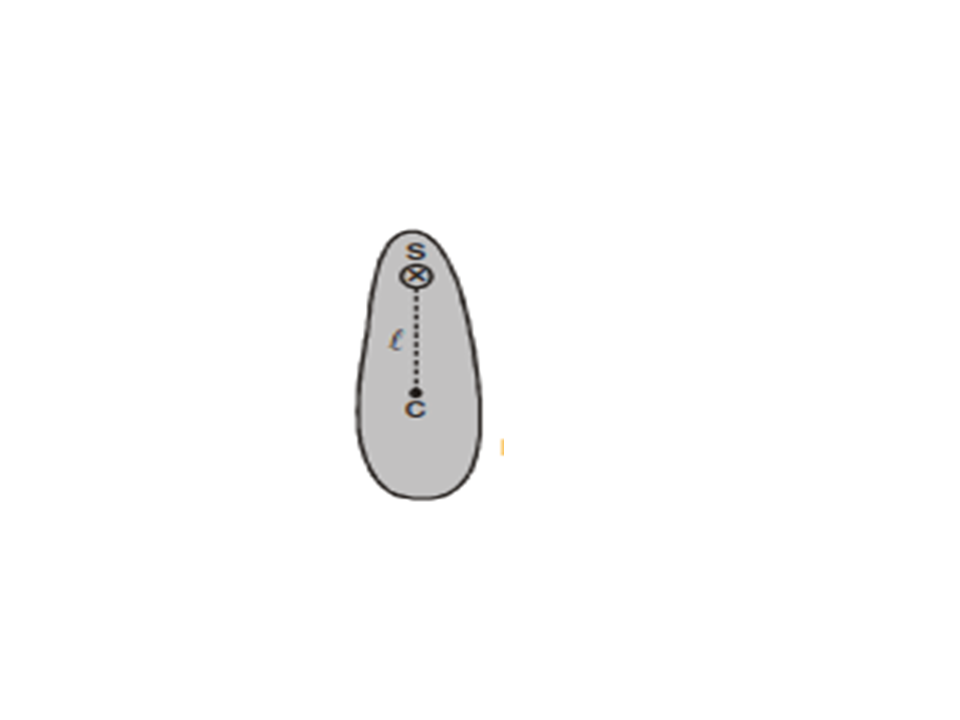
Here
C=position of centre of mass,
S=point of suspension
L=distance between point of suspension and centre of mass
TIME PERIOD OF COMPOUND PENDULUM OR PHYSICAL PENDULUM
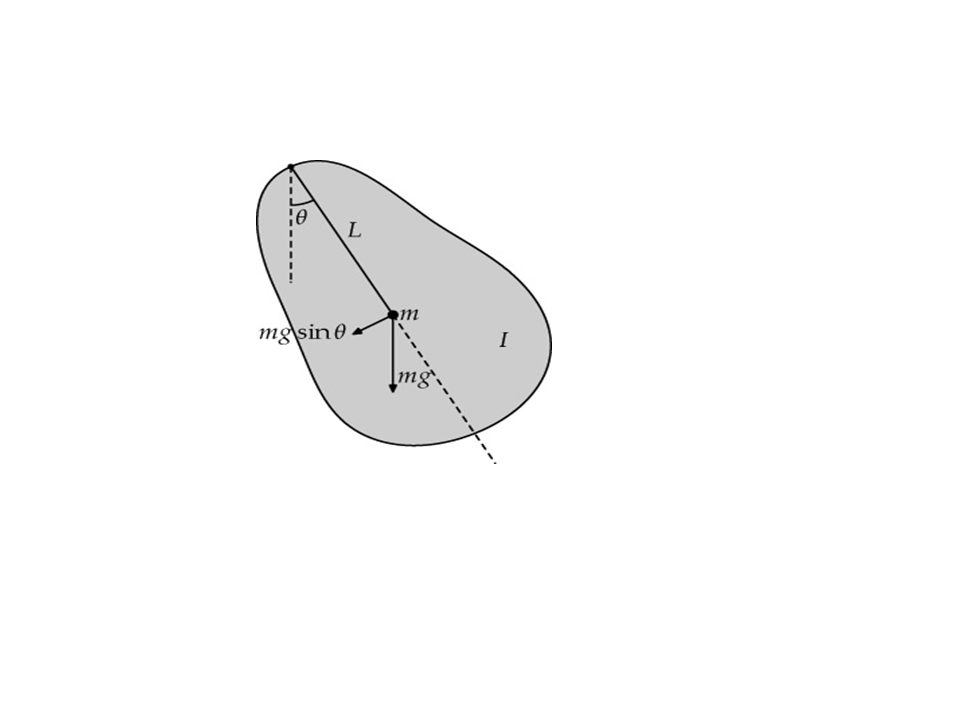
Ab humne rigid body ko suspension point se small angle θ displace kiya, ab baccho centre of mass prr ek gravitational force lg rha hoga mg downwards, ab hum iske component break krenge toh aaenge mgsinθ and mgcosθ , ab baccho humne jis direction me displacement θ kiya hai uske opposite direction me ek torque lgega jo iske motion ka oppose krega and ye torque mgsinθ force ki wajah se lgega.
Therefore , torque=F×R⊥
τ=mgsinθ×L
τ=mgLsinθ
As we know ,θ is so small, therefore sinθ≈θ,
Now torque will be,
τ=−mgLθ
Baccho yaha negative sign isliye lgaya hai kyunki humne displacement anticlockwise kiya hai ,jabki opposing torque clockwise direction me.
Now comparing this torque with angular SHM equation, τ=−kθ
Therefore ,
-ktheta=-mgLtheta<br><br><b>k=mgL<b><br><br>Abtimeperiodofanyanga––rpendu––mhotahai<br>T=2pisqrt(I/k)whereIismomentof∈ertiaaboutp∮ofsuspension.<br><br>Therefore,timeperiodofphysicalpendu––mwod––be,<br><br>T=2pisqrt(I/k)<br><br><b>T=2pisqrt(I/(mgL)
TORSIONAL PENDULUM
Baccho isme ek extended object hota hai jo ki apne centre se suspended hota hai by a light torsion wire. Torsion wire jo hota hai voh inextensible hota hai, but voh apni axis ke about twist ho sakta hai. Jab humne wire ke lower end ko thoda sa rotate krte hai , toh wire ek restoring torque lgata hai jiski wajah se body oscillate krne lgti hai.
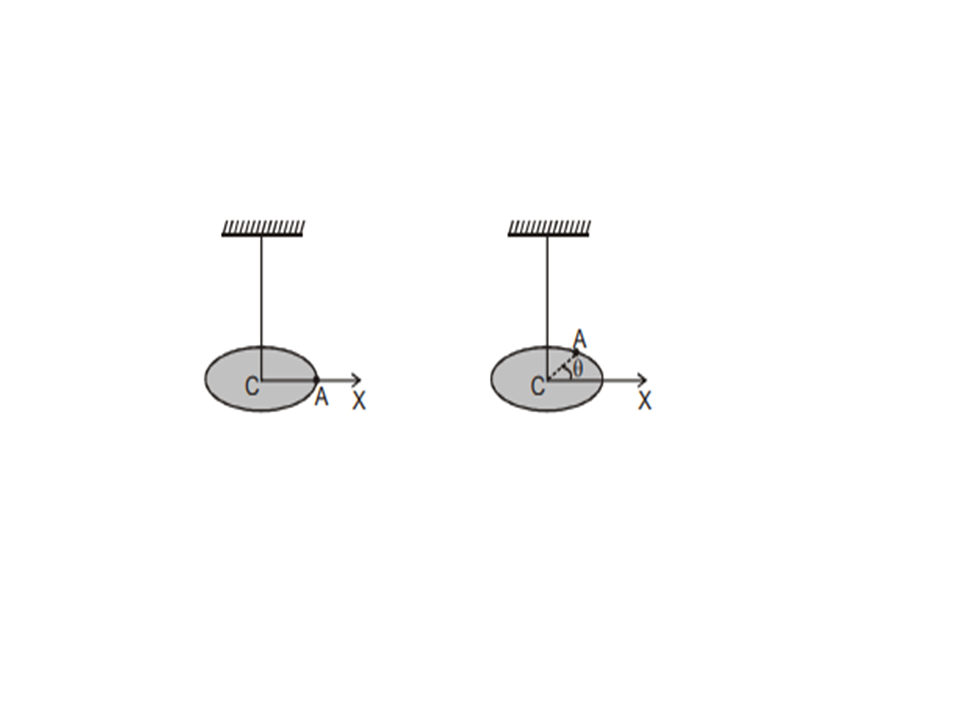
Toh jo restoing torque hota hai voh hota hai,
τ=−Cθ , where C= torsional constant
Or Iα=−Cθ, where I=moment of inertia about the vertical axis.
Or α=−CIθ
TIME PERIOD OF TORSIONAL PENDULUM
Yaha jab aap torque ki equation ko angular SHM ki equation (τ=−kθ)se compare karogeToh milega, k=C,
And time period of any angular SHM is T=2π√Ik,
Therefore
T=2π√IC , this is the time period of torsional pendulum.
COMBINATION OF SHM
Baccho hume SHM ki condition acchese se pta hai ki jab kisi particle prr force lgta hai, toh voh force displacement ke directly proportional hota hai, tabhi SHm hoga.
That means,
F=−kx.
Ab baccho yaha hum ek hi paticle prr do different forces apply krenge, and inn dono forces ki wajah se jo net displacment hoga particle ka,voh bhi SHM krega, isi ko hum combination of SHM bolte hai.
Maan lijiye ek particle hai or uss particle prr do forces lgaye, toh phli force ki wajah se jo displacement hoga voh maanege,
x1=A1sinωt,
And dusri force ki wjaha se jo displacement hoga,
x2=A2sin(ωt+ϕ),
Bachho yaha prr humne same frequency li hui hai, or esa isliye kiya hai kyunki bina same frequency ke SHM nhi hota hai, ye aap log waves chapter me or acchese samjhenge.
Ab baccho jo net displacement hoga voh hoga,
x=x1+x2,
x=A1sinωt+A2sin(ωt+ϕ)
Isko hum ek normal SHm equation me bhi likh sakte hai jaise,
x=Asin(ωt+α)
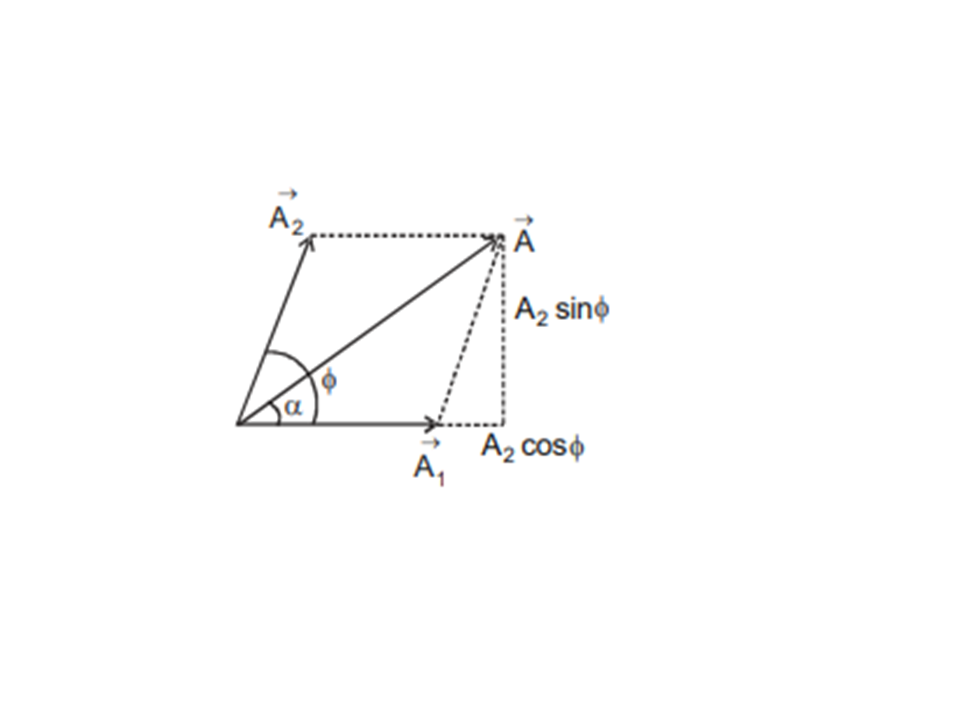
Ab baccho jaisa ki aapko diagram me dikh rha hoga ki do vector →A1 and →A2 diye hue hai or inke beech angle hai ϕ and inka resultant vector hoga →A jo ki α∠bnarhahaivecA_1kesaath.<br><br>Therefore,<br><br>A=sqrt(A_1^2+A_2^2+2A_1A_2cosphi)<br><br>And,tanalpha=(A_2sinphi)/(A_1+A_2cosphi)
Jaisa ki aap dekh sakte ho ki vector addition lgaya hai humne upar, vaise hi combination of SHM me vector addition lgega humesha.
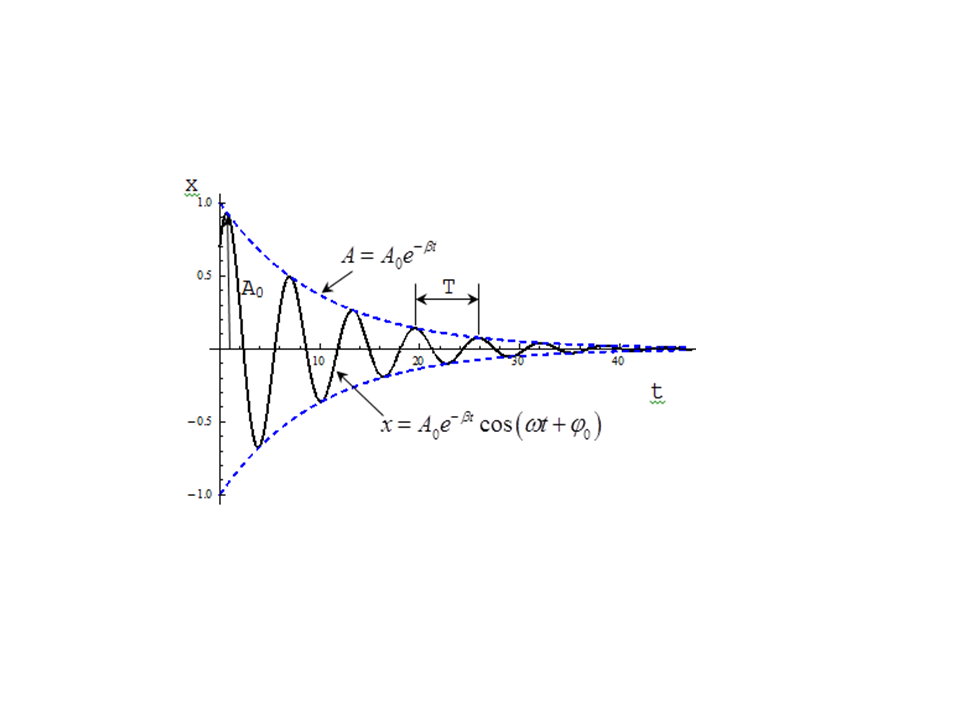
DAMPED OSCILLATION
Baccho aisa kyu hota hai real life me ki jab simple pendulum ka motion hota hai toh voh kuch time baad ruk jata hai?, voh humesha hota hi kyu nhi rehta?, esa isliye hota hai baccho kyunki jo air present hoti hai environment me, voh uss pendulum prr ek resistive force lgati jiski wajah se pendulum ki energy loss hoti rehti hai continuously, and jab tk pendulum rest prr nhi aajata hai, tab tk uss prr air ka force lgata rehta hai and energ loss hoti hi rehti hai.
Aao ise hum or acchese samjhte hai,
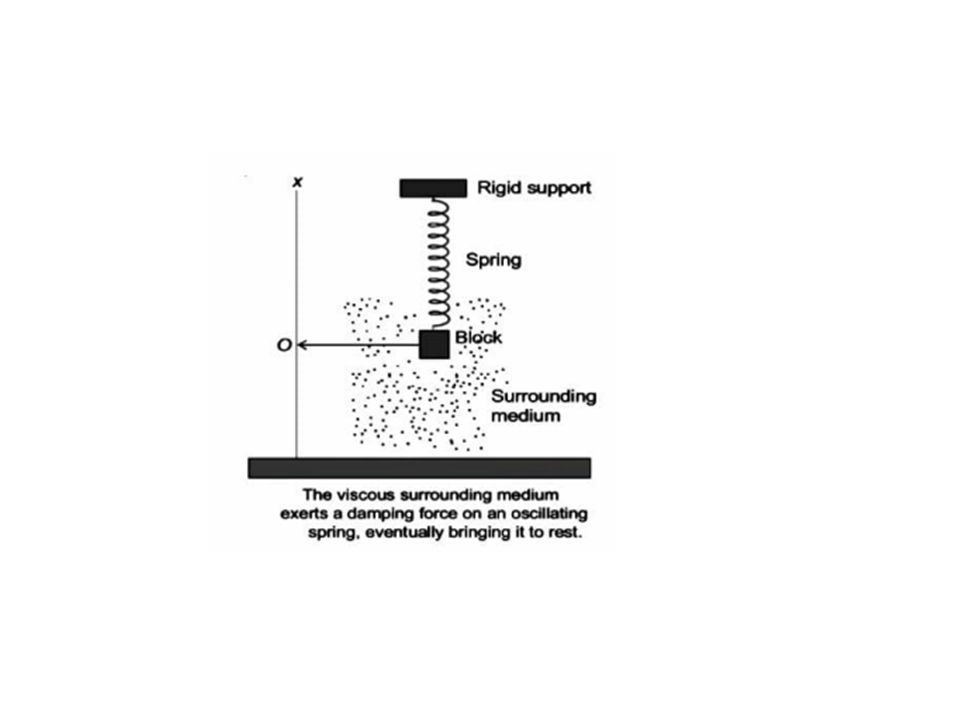
Jaisa ki aap diagram me dekh paa rhe hoge ki humne ek spring block system liya hai and ek surrounding medium bhi hai saath me, humne block ko already uss surrounding medium me rakha hua hai (baccho surrounding medium kuch bhi ho sakta hai jese ki air,water,koi bhi denser ya lighter liquid etc),
Ab jab baccho hum iss block ko thoda sa displace krenge toh ye oscillation krega jaisa ki hum jaante hai , F=−kx se.
Lekin baccho iss baar ye block ek medium me hai or iss prr ek force or lgega jo ki medium ki wajah se hoga jo ki block ki energy ko am krta rahega lgataar, ise hum damping force bolte hai.
Ye force hoga F=−bv ,
Where b=medium constant ( like viscosity for liquid medium)
And v=velocity of block
baccho isme bhi negative sign isliye hai kyunki ye force bhi block ke motion ka oppose krega, mtlb jis taraf velocity hogi block ki, uske opposite ye force lgaega, jiski wajah se block ki energy loss hoti rahegi.
Toh jo net force lgega block prr voh hoga,
F=−kx−bv
Maan lete hai ki block ka acceleration a hai, toh hum likh sakte hai,
ma=−kx−bv
Or md2xdt2=−bdxdt−kx,
Therefore md2xdt2+bdxdt+kx=0 this is the differential equation for damped oscillation
Solution of this damped oscillation differential equation will be,
x=Ae−bt2mcos(w't+ϕ)
Where A is the amplitude and w’ is the angular frequency of the damped oscillation.
And w'=√km−b24m2
Or damped oscillation ka graph kuch iss tarah aata hai.
FORCED OSCILLATION
Maan lijiye ek simple pendulum hai or voh apne equilibrium position prr hai usko humne apni position se thoda displace kiya, toh voh kisi natural frequency se oscillate krega aur ese oscillation ko hum free oscillation kehte hai.
Ab bachho ye oscillation ko khatam damping force krdeta hai, lekin ye oscillation kabhi khatam na ho toh uske liye ek external force ya external agent jruri hai, jo iss oscillation ko continue rakh paye, usi ko hum forced oscillation bolte hai
Maan lijiye ek case hai jisme external force hi periodic hai
Toh mtlb oscillation kabhi nhi rukega, jese ki koi baccha jhhula jhhulta hai toh usko continous chlane ke liye voh apne pero se ek periodic external force lgata hai harr baar.
Toh hum maan lete hai ki F(t) periodic external force hai jiska amplitude F0 hai.
Toh isko hum represent krenge,
F(t)=F0cos(ωd)t
Ab jab hum normal SHM ,damping force and external periodic force ko saath me likhenge toh voh hoga,
ma(t)=−kx(t)−bv(t)+F0cos(ωd)t
Or we can write, md2xdt2+bdxdt+kx=F0cos(ωd)t , this is the differential form of forced oscillation wth angular frequency (ωd).
Phle ye initial natural frequency ω se oscillate rega, then damping ki wajah se iski frequency kam hoti chli jaegi and ek external force ki wajah se ye oscillate krne lgega, and finally voh forced oscillation ki angular frequency (ωd) se oscillation krne lgega.
Iski displacement ki equation hogi,
x(t)=Acos(ωdt+ϕ)
Where t=time measured from the moment, the periodic force is applied.
The amplitude A is a function of a forced frequency ωd and the natural frequency ω .
Therefore
A=F0√m2(ω2−ω2d)+ω2db2
And
tanϕ=−v0ωdx0
EXAMPLE 7
A simple pendulum is taken at a place where its separation from the earth's surface is equal to the radius of the earth. Calculate the time period of small oscillation if the length of the string is 1.0m. Take g=π2m/s2 at the surface of the earth.
g'=g(1+hR)2
Putting h=R
g'=g4
T=2π√l(g/4)
=4π√lg
=4√l=4√1.0 (as g=π2)
=4s
EXAMPLE 8
In the figure shown the time period and the amplitude respectively, when m is left from rest when spring is relaxed are (the inclined plane is smooth)

In equilibrium, let x0 is extention in spring then
kx0=mgsinθ
∴x0=mgsinθk = amplitude of oscillations.
EXAMPLE 9
A solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
T=2π√mk
Here m=(ρ0)(a3)
and K=ρlAg=ρa2g
∴T=2π√ρ0aρg .
EXAMPLE 10
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
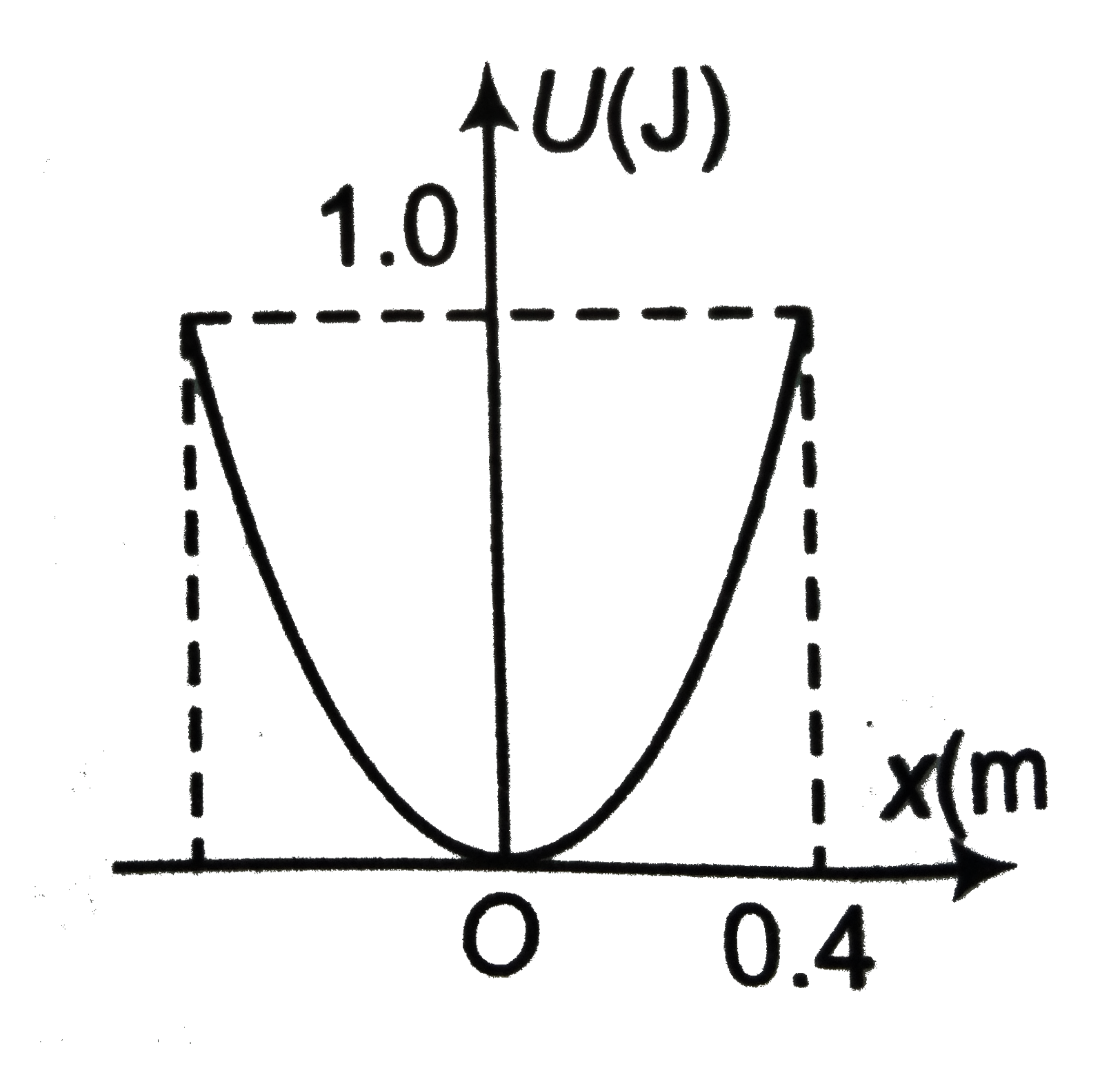
12kA2=1.0
12k(0.4)2=1.0
or k=12.5 or 252N/m
T=2π√mk=2π
⎷2252=4π5s
SUMMARY
* The motion that repeats itself is called periodic motion.
* The period T is the time required for one complete oscillation, or cycle. It is related to the frequency ν by, T=1V.The frequency ν of periodic or oscillatory motion is the number of oscillations per unit time. In the SI, it is measured in hertz : 1hertz=1Hz=1 oscillation per second=1s–1.
* In simple harmonic motion (SHM), the displacement x(t) of a particle from its equilibrium position is given by,
x(t)=Acos(wt+ϕ) (displacement),
in which A is the amplitude of the displacement, the quantity (omegat+phi ) is the phase of the motion, and ϕ is the phase constant. The angular frequency ω is related to the period and frequency of the motion by,
ω=2πT=2πv (angular frequency),
* The particle velocity and acceleration during SHM as functions of time are given by,
v(t)=Aωcos(ωt+ϕ)
And a(t)=−Aω2sin(ωt+ϕ)
* The force acting in a simple harmonic motion is proportional to the displacement and is always directed towards the centre of motion.
* A particle executing simple harmonic motion has, at any time, kinetic energy k=12mv2 and potential energy U=12kx2 . If no friction is present the mechanical energy of the system, E=K+U always remains constant even though K and U change with time.
* A particle of mass m oscillating under the influence of Hooke’s law restoring force given by F=–kx exhibits simple harmonic motion with
ω=√km (angular frequency)
T=2π√mk (period), Such a system is also called a linear oscillator.
* The mechanical energy in a real oscillating system decreases during oscillations because external forces, such as drag, inhibit the oscillations and transfer mechanical energy to thermal energy. The real oscillator and its motion are then said to be damped. If the damping force is given by Fd=−bv, where v is the velocity of the oscillator and b is a damping constant, then the displacement of the oscillator is given by,
x(t)=Ae−bt2mcos(ω't+ϕ)
where ω’, the angular frequency of the damped oscillator, is given by
ω'=√km−b24m2
If the damping constant is small then ω'≈ω, where ω is the angular frequency of the undamped oscillator. The mechanical energy E of the damped oscillator is given by
E(t)=12KA2e−btm.
* If an external force with angular frequency ωd acts on an oscillating system with natural angular frequency ω, the system oscillates with angular frequency ωd . The amplitude of oscillations is the greatest when
ωd=ω
a condition called resonance.