NEWTON’S LAWS OF MOTION for Class 11 PHYSICS
INTRODUCTION
Let us first guess the answer based on our common experience. To move a football at rest, someone must kick it. To throw a stone upwards, one has to give it an upward push. A breeze causes the branches of a tree to swing; a strong wind can even move heavy objects. A boat moves in a flowing river without anyone rowing it. Clearly, some external agency is needed to provide force to move a body from rest. Likewise, an external force is needed also to retard or stop motion. You can stop a ball rolling down an inclined plane by applying a force against the direction of its motion. In these examples, the external agency of force (hands, wind, stream, etc) is in contact with the object. This is not always necessary. A stone released from the top of a building accelerates downward due to the gravitational pull of the earth. A bar magnet can attract an iron nail from a distance. This shows that external agencies (e.g. gravitational and magnetic forces ) can exert force on a body even from a distance.
Newton’s laws of motion, three statements describing the relations between the forces acting on a body and the motion of the body, first formulated by physicist and mathematician Isaac Newton, which are the foundation of classical mechanics.
Some Important Definitions :-Motion
Motion of a body is its movement and is identified by change in either its location or orientation or both, relative to other objects.
Location
Location of a rigid body tells us where it is placed and can be measured by position coordinates of any particle of the body or its mass center. It is also known as position.Orientation
Orientation of a body tells us how it is placed with respect to the coordinate axes. Angles made with the coordinate axes by any linear dimension of the body or a straight line drawn on it, provide suitable measure of orientation.Translation and Rotation Motion
If a body changes its location without change in orientation, it is in pure translational motion and if it changes orientation without change in location, it is in pure rotation motion.Translation Motion
Let us consider the motion of a plate, which involves only change in position without change in orientation. It is in pure translation motion. The plate is shown at two different instants t and t+δt. The coordinate axes shown are in the plane of the plate and represent the reference frame. A careful observation makes the following points obvious.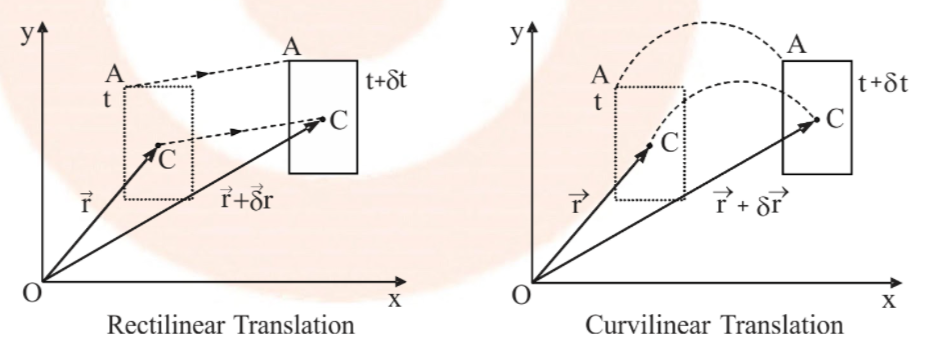
- ∙ None of the linear dimension or any line drawn on the body changes its angles with the coordinate. Therefore, there is no rotation motion.
- All the particles of the body including its mass center move on identical parallel trajectories. Here trajectories of corner A and center C are shown by dashed lines.
- All the particles and mass center of the body cover identical segments of their trajectories in a given time interval. Therefore, at any instant of time all of them have identical velocities and accelerations.
- Pure translation motion of a body can be represented by motion of any of its particle. This is why, we usually consider a body in pure translation motion as a particle.
Momentum: Amount of Motion
Amount of motion in a body depends on its velocity and mass.Linear momentum of a body is defined as product of its mass and velocity. It provides measure of amount of motion.
Linear momentum p of a body of mass m, moving with velocity by →v is expressed by the following equation.
- p=m→v
Dimensions of momentum are [MLT−1]
FORCE AND INERTIA
Everyone has a basic understanding of force from everyday experiences. Although force are not visible, we do see and experiences their effects.
It can be defined as “Force is a push or pull which tries to change or changes the state of rest or uniform motion of a body” or we can say force is the cause of translatory motion.
It is our common observation that an object such as a chain lying a form or a vehicle parked outside the house remains at rest unless a push or a pull is given to it. Such an object cannot move at its own. In other words, force has to be applied in order to move an object at rest. Also, if a body is moving along a straight line with some velocity, it is found that force is required to change the direction of motion or the magnitude of the velocity.
Thus force is an agent which
- Changes or tends to change state of motion
- Changes or tends to change momentum
- Changes or tends to change shape and size of objects.
Inertia :
If you attempt to change the velocity of an object, the object resists this change.
Inertia is solely a property of an individual object; it is a measure of the response of an object to an external force. It can be defined in this way: It is the property of a body by virtue of which it opposes any change in its state rest or uniform motion.
Mass is used to measure inertia. The greater the mass of a body, the less that body changes its state of motion under the action of an applied force.
For example : Consider two large, solid cylinders of equal size, one soft wood and the other steel. If you were to push the cylinders along the horizontal surface, the force required to give the steel cylinder some acceleration would be large than the force needed to give the soft wood cylinder the same acceleration. Therefore, we say that the steel cylinder has more inertia than the soft wood.Mass :
“Mass is an inherent property of a body which is measure of the object’s inertia (Which is a tendency to resist acceleration when a force acts on it) and is independent of body’s surroundings and of the method used to measure it”.
It is a scalar quantity. The SI unit of mass is the kilogram (kg). Mass is the quantity that obeys the rules of ordinary algebra.
For example: If you combine 3 kg, with a 5 kg mass, their total mass will be 8 kg.
Mass should not be confused with weight. Mass and weight are two different quantities. As we will see later, the weight of a body is equal to the magnitude of the force exerted by the earth on the body and varies with location.
For example: A person whose weight is 60 kgf on earth weight only 10 kgf on the moon. On the other hand, the mass of a body is same everywhere, regardless of location. An object having a mass 6 kg on earth also has a mass of 6 kg on the Moon.
NEWTON’S FIRST LAW OR LAW OF INERTIA
Before we state Newton’s first law, consider the following simple experiment. Suppose a book is lying on a table. Obviously, the book remains at rest in the absence of any influences. Now imagine that you push the book with a horizontal force large enough to overcome the force of friction between book and table. The book can then be kept in motion with constant velocity if the force you apply is equal in magnitude to the force of friction and in the direction opposite the friction force.
If the applied force exceeds the force of friction, the book accelerates. If you stop pushing, the book stops sliding after moving a short distance because the force of friction retards its motion. Now imaging pushing the book across a smooth, highly waxed floor. The book again comes to rest after you pushing, but not as quickly as before. Now imaging a floor so highly polished that friction is negligibly small; in this case, the book, once set in motion, slides until it hits the wall. Then force that we have described are external force, that is, forces exerted on the object by other objects.
Before about 1600, scientists felt that the state of matter was the state of rest. Galileo was the first to take a different approach to motion and the natural state of matter. He devised thought experiments, such as the one we just discussed for a book on a frictionless surface, and concluded that it is not the nature of an object to stop ones set in motion: rather, it is its nature to resist changes in its motion. In his words, “Any velocity once imparted to a moving body will be maintained as long as the external causes of retardation are removed”.
The New approach to motion was later formalized by Newton in a form has come to be known as Newton’s first law of motion:
An object at rest remains at rest and an object in motion will continue in motion with a constant velocity (that is, constant speed in a straight line) unless it experiences a net external force.
In simpler terms, we can say that when the net force on a body is zero, its acceleration is zero i.e.,
- ∑F’=0
From the first law, we conclude that an isolated body (a body does not interact with its environment) is either at rest or moving with constant velocity.
APPLICATIONS OF LAW OF INERTIA
When a horse suddenly starts moving, the rider falls backwards. Because the lower part of the body of the rider (which is in contact with the horse) comes in motion but because of inertia the upper part tends to be at rest. Hence the rider falls backwards.
We hit carper with a stick to remove the dust: On hitting with a stick, the carpet comes to motion; but because of inertia, the dust particles remain at rest. Due to this, dust particles get removed from the carpet
NEWTON’S SECOND LAW
Newton’s first explains what happens to an object when the resultant of all external forces on it is zero: it either remains at rest or moves in a straight line with constant speed. Newton’s second law answer the question of what happens to an object has a non-zero resultant force acting on it.
Imagine you are pushing a block of ice across a frictionless horizontal surface. When you exert some horizontal force F, the block moves with some acceleration a. If you apply a force twice as large, the acceleration doubles. Likewise, if the applied force is increased to 3F, the acceleration is tripled, and so on. From such observations we conclude that the acceleration of an object is directly proportional to the resultant force acting on it.
As stated in the preceding section, the acceleration of an object also depends on its mass. This can be understood by considering the following set of experiments. If you apply a force F to a block of ice on a frictionless surface, the block undergoes some acceleration a. If the mass of the block is doubled, the same applied force produces an acceleration a/2. If the mass is tripled, the same applied force produces an acceleration a/3, and so on. According to this observation, we conclude that the acceleration of an object is inversely proportional to its mass.
The observation are summarized in Newton’s second law:
The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
Thus we can relate mass and force through the following mathematical statement of Newton’s second law:
- ∑F’=ma’ ……..(2)
- ∑Fx=max
∑Fy=may
∑Fz=maz
Linear Momentum
It is defined as the total quantity of motion contained in a body and is measured as the product of mass of body and its velocity. It is denoted by p.
It is a vector quantity
Suppose a particle of mass m moves with velocity v.
- p’=mv’
- →F∝d→Pdt or, →F=kd→Pdt
So,
- →F=kddt(m→v) (∵→p=m→v)'
=kmd→vdt
→F=km→a [asd→vdt=→a]
i.e., if m=1,a=1 and F=1
so,
- 1=k×1×1
- F=d→Pdt=m→a ………..(3)
EXAMPLE 1
A force acts for 10 s on a body of mass 10 kg after which the force ceases and the body describes 50 m in the next 5s. Find the magnitude of the force.
After the force ceases, the body covers 50m in 5s
Therefore, final velocity
- v=distancetime=505=10ms−1
- 10=0+a×10
a=1ms−2
F=Ma=10×1=10N
EXAMPLE 2
The driver of three wheeler moving with a speed of 36kmh−1 sees a child standing in the middle of the road and brings his vehicle to rest in 4s, just in time to save the child. What is the average retarding force on the vehicle? The mass of the three wheeler is 400 kg and the mass of the driver is 65 kg.
u=36kmh−1=10 m/s
Now, v=u+at ∴
- 0=10+a×4
a=2.5ms−2
- M=65+400=465kg
- F=−465×2.5=−1162.5N
EXAMPLE 3
A hockey puck with a mass of 200g slides on horizontal frictionless surface of an ice rink. Two force act on the puck as shown in figure. The force F1 has a magnitude of 5.0 N, and F2 has a magnitude of 8.0 N. Determine the magnitude and direction of the puck’s acceleration. [sinα=45,sinβ=32]
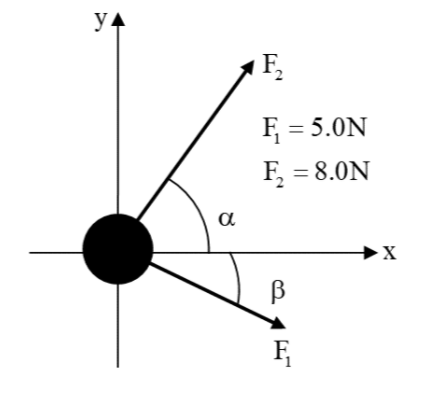
The resultant force in the x direction is
- ∑Fx=F1x+F2x=F1cosβ+F2cosα
=(5.0N)(45)+(8.0N)(35)=8.8N
- ∑Fy=F1y+F2y=−F1sinβ+f2sinα=3.4N
- ax=∑Fxm=8.7N0.20kg=44ms2 , ay=∑Fym=3.4N0.20kg=17ms2
NEWTON’S THIRD LAW
According to Newton’s third law “for every action there is an equal opposite reaction and they act two different bodies”.
It means if two bodies interact, the force exerted on body 1 by body 2 is equal to and opposite the force exerted on body 2 by body 1:
- F12’=−F21’ ……(4)

The action force is equal in magnitude to the reaction force and opposite in direction. In all cases, the action and reaction forces act on different objects.
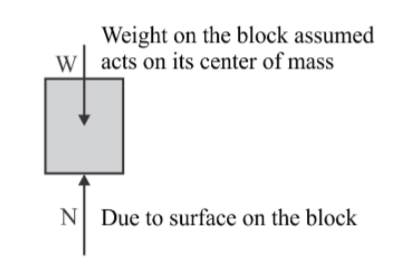
For example, the weight of an object, w, is defined as the force the Earth exerts on the objects. If the object is a box resting on a table, as shown in figure the reaction force to w is the force the box exerts on the earth, w’. The box does not accelerate because it is held up by the table. The table therefore, exerts an upward action force, N, on the box, called the normal force. The normal force is the force that prevents the box from falling through the table and can have any value needed, up to the point of breaking of the table. The normal force balances the force of gravity acting on the box and provides equilibrium. The reaction to N is the force exerted by the box on the table, N’ Therefore, we conclude that
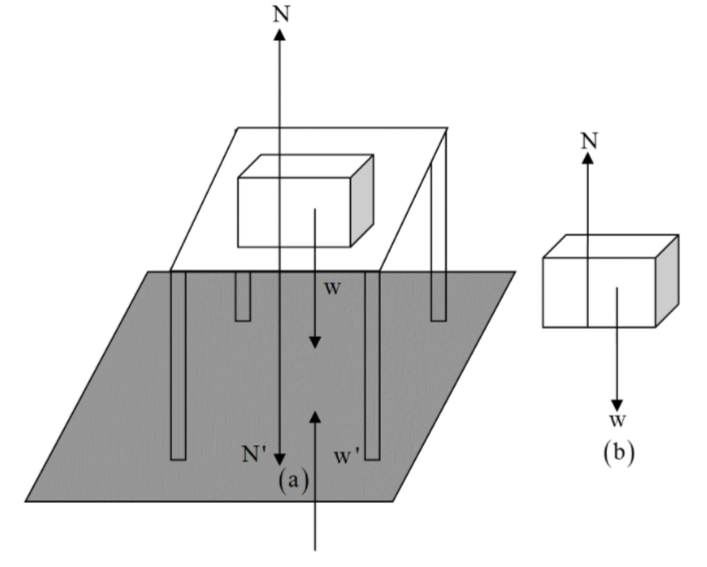
The force N and N’ have the same magnitude, which is the same as w unless the table has broken. Note that the forces acting on the box are w and N, as shown in Figure. The two reaction forces, w’ and N’ are exerted on objects other then the box. Remember, the two forces in an action-reaction pair always act on two different objects.
From the second law, we see that because the box is in equilibrium (a=0) it follows that w=N=mg
Another example, the force acting on a freely falling projectile is its weight, w=mg which is the force exerted by the Earth on the projectile. The reaction to this force is the force of the projectile on the Earth, w’=−w. The reaction force, w’ must accelerate the Earth toward the projectile just as the action w, accelerates the projectile towards the Earth. However, since the Earth has such a large mass, its acceleration due to this reaction force is negligibly small.
NEWTON’S SECOND LAW IS THE REAL LAW OF MOTION
Both Newton’s first law and third law of motion from second law of motion as explained below.
(a)To prove that Newton’s first law is contained in second law. According to Newton’s second law, the external force (→F) applied on a body and the acceleration (→a) produced are related to each other by the relation.
- F’=ma
- Ma’=0 or a=0
Setting a=0, We have v’=u’
It implies that if no external force acts on the body, then a body initially at rest (→u=0) will remain at rest (→v=0) or if it is moving with some velocity (→u) it will keep on moving with the same velocity (→v=→u) This exactly is that Newton’s first law of motion states. Hence, Newton’s first law of motion is contained in the second law.
(b)To prove that Newton’s third law is contained is second law. Consider a system of two bodies A and b mutually interacting with each other, such that no external force acts on the system. Suppose that the body A exerts force FAB’ (action) on body B the body B exerts force FBA’ (action) on body B the body B exerts force FBA’ (reaction) on the body A. If d→p1dt and d→p2dt are rate of change of momentum of the bodies A and b respectively due to the forces →FBA’ and →FAB’ acting on them, then
- →FAB=d→p2dt and →FBA=d→p1dt
- →FBA+→FAB=d→p2dt+d→p2dt=ddt(→p1+→p2)
- FBA’+FAB’=0
FAB’=−FBA’
Concept of Free Body Diagram (FBD)
A force on a body can only exists when there is another body to create it, therefore in every physical situation of concern there must be two or more bodies applying forces on each other. On the other hand the three laws of Newton, describe motion of a single body under action of several forces, therefore, to analyze a given problem, we have to consider each of the bodies separately one by one. This idea provides us with the concept of free body diagram.
A free body diagram is a pictorial representation in which the body under study is assumed free from rest of the system i.e. assumed separated from rest of the interacting bodies and is drawn in its actual shape and orientation and all the forces acting on the body are shown.
How to draw a Free Body Diagram (FBD)
Separate the body under consideration from the rest of the system and draw it separately in actual shape and orientation.
Show all the forces whether known or unknown acting on the body at their respective points of application.
For the purpose count every contact where we separate the body under study from other bodies. At every such point, there may be a contact force. After showing, all the contact forces show all the field forces.
Various Field Forces
Field forces include the gravitational force (weight) electrostatic forces and magnetic forces, which can easily be identified. At present, we consider only gravitational pull from the earth i.e. weight of the body.
Weight: The net gravitational pull of the Earth
The gravitational pull from the earth acts on every particle of the body hence it is a distributed force. The net gravitational pull of the Earth on a body may be considered as weight of the body. It is assumed to act on the center of gravity of the body. For terrestrial bodies or celestial bodies of small size, this force can be assumed uniform throughout its volume. Under such circumstances, center of gravity and center of mass coincide and the weight is assumed to act on them. Furthermore, center of mass of uniform bodies lies at their geometrical center. At present, we discuss only uniform bodies and assume their weight to act on their geometrical center. In the figure weight of a uniform block is shown acting on its geometrical centre that coincides with the center of mass and the centre of gravity of the body.
Various Contact Forces
At every point where a body under consideration is supposed to be separated from other bodies to draw its free-body diagram, there may be a contact force. Most common contact forces, which we usually encounter, are tension force of a string, normal reaction on a surface in contact, friction, spring force etc.
Tension Force of Strings
A string or similar flexible connecting links as a thread or a chain etc. we use to transmit a force. Due to flexibility, a string can be used only to pull a body connected to it by applying a force always along the string. According to the third law, the connected body must also apply an equal and opposite force on the string, which makes the string taut. Therefore, this force is known as tension force T of the string. In the given figure is shown a block pulled by a string, which is being pulled by a person.
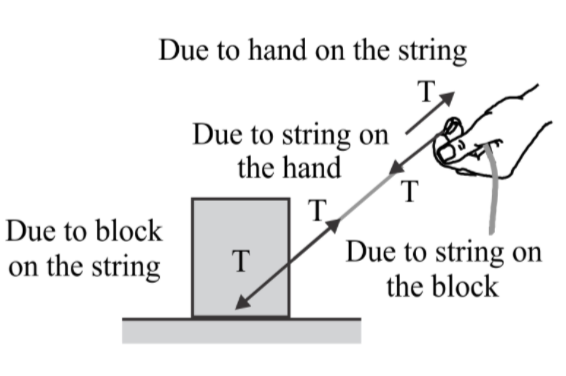
The tension force applied by string on the block and the force applied by the block on the string shown in the figure constitute a third law action-reaction pair. Similarly, tension force applied by the string on hand and force applied by the hand on string is another third law action-reaction pair.
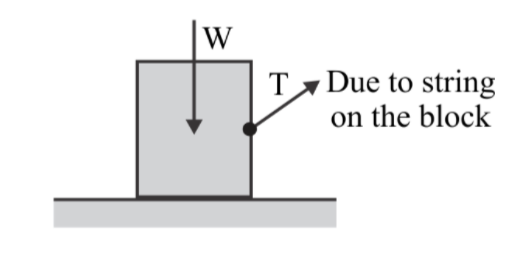
While studying motion of the block, the force applied by the string on it, weight of the block and a reaction from the floor has to be considered. In the figure only weight and tension of string are shown.
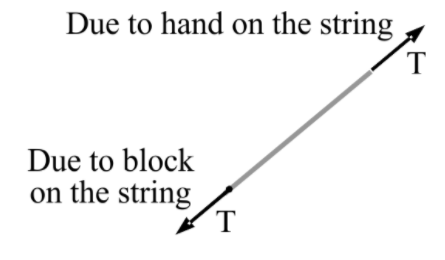
To study motion of the string, the force applied by the block on the string and the force applied by the hand on the string must be considered. These forces are shown in the FBD of string.
To study conditions of motion of the person, the force applied by the string on the hand has to be considered as shown in the figure.

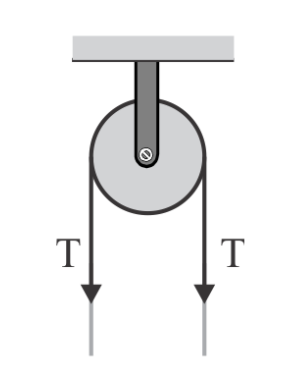
String passing over a pulley
A pulley is a device consisting of a wheel, which can rotate freely on its axel. A single pulley changes direction of tension force. At present for simplicity, we discuss only ideal pulley, which is massless i.e. has negligible mass and rotates on its axel without any friction. An ideal pulley offers no resistance to its rotation, therefore tension force in the string on both sides of it are equal in magnitude. Such a pulley is known as ideal pulley.
Normal Reaction
Two bodies in contact, when press each other, must apply equal and opposite forces on each other. These forces constitute a third law action-reaction pair. If surfaces of the bodies in contact are frictionless, this force acts along normal to the surface at the point of contact. Therefore, it is known as normal reaction.
Consider a block of weight W placed on a frictionless floor. Because of its weight it presses the floor at every point in contact and the floor also applies equal and opposite reaction forces on every point of contact. We show all of them by a single resultant N obtained by their vector addition.
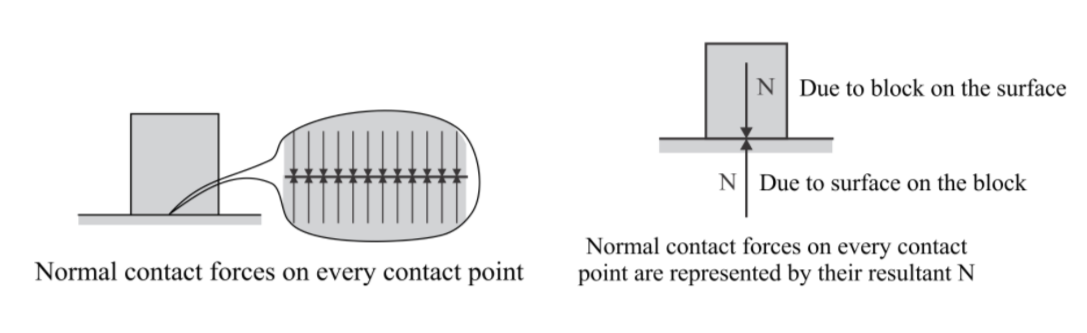
To apply Newton's laws of motion (NLM) on the block, its weight W and normal reaction N applied by the floor on the block must be considered as shown in the following figure. It is the FBD of the block.
Consider a spherical ball of weight W placed on a floor. The normal reaction from the floor on the ball and from the ball on the floor makes third law action-reaction pair. These forces are shown in the left figure.

To apply Newton's laws of motion (NLM) on the ball, its weight W and normal reaction N applied by the floor on the ball must be considered as shown in the above right figure. It is the FBD of the ball.
When two surfaces make contact, the normal reaction acts along the common normal and when a surface and a sharp corner make a contact the normal reaction acts along the normal to the surface. Consider a block placed in a rectangular trough as shown in the figure.
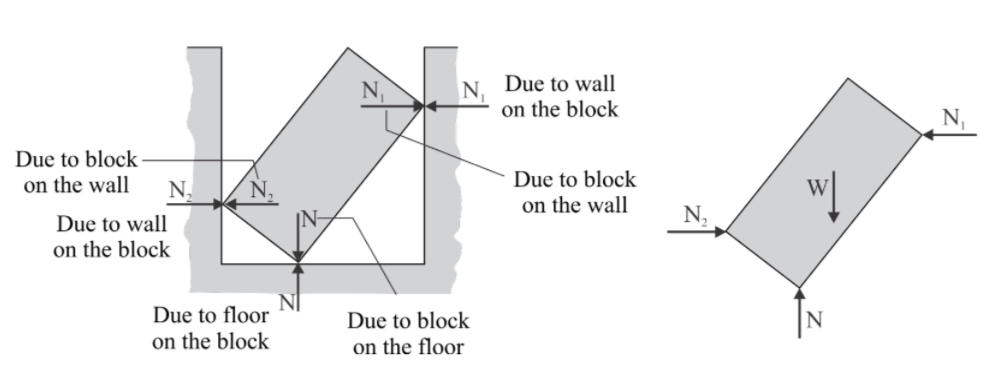
To apply Newton's laws of motion (NLM) on the block, its free body diagram (FBD) is shown in the above right figure.
Spring Force
When no force acts on a spring, it is in relaxed condition i.e. neither compressed nor elongated. Consider a spring attached to a fixed support at one of its end and the other end is free. If we neglect gravity, it remains in relaxed state. When it is pushed by a force F, it is compressed and displacement x of its free end is called compression. When the spring is pulled by a force F, it is elongated and displacement x of its free end is called elongation. Various forces developed in these situations are shown in the following figure.
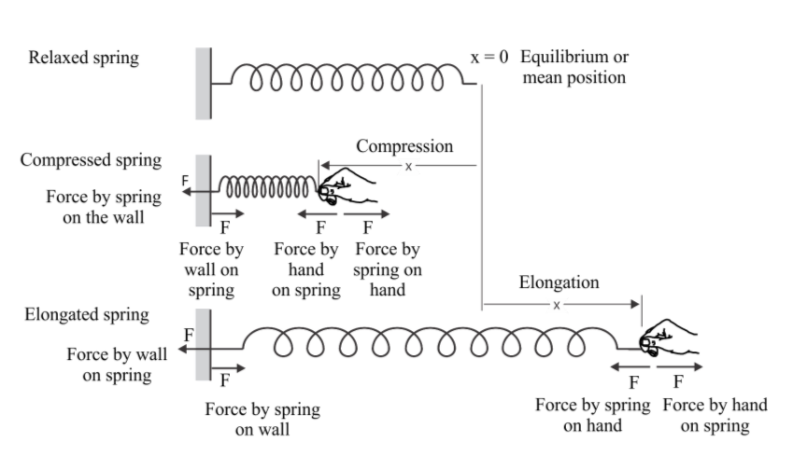
The force applied by the spring on the wall and the force applied by the wall on the spring make a third law action-reaction pair. Similarly, force by hand on the spring and the force by spring on the hand make another third law action-reaction pair.
Hooke's Law:
How spring force varies with deformation in length x of the spring is also shown in the following figure.
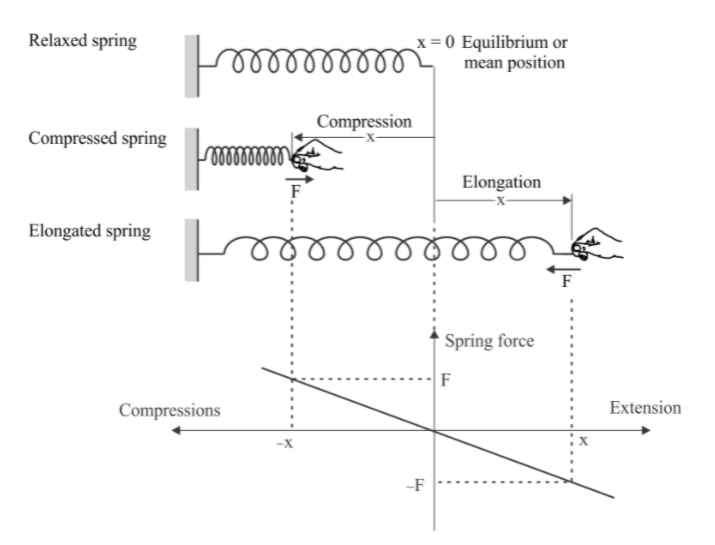
The force F varies linearly with x and acts in a direction opposite to x. Therefore, it is expressed by the following equation
- F=−kx
The constant of proportionality k is known as force constant of the spring or simply as spring constant. The slope modulus of the graph equals to the spring constant.
SI unit of spring constant is newton per meter or (N/m).
Dimensions of spring constant are [MT−2].
Translational Equilibrium
A body in state of rest or moving with constant velocity is said to be in translational equilibrium. Thus if a body is in translational equilibrium in a particular inertial frame of reference, it must have no linear acceleration. When it is at rest, it is in static equilibrium, whereas if it is moving at constant velocity it is in dynamic equilibrium.
Conditions for translational equilibrium
For a body to be in translational equilibrium, no net force must act on it i.e. vector sum of all the forces acting on it must be zero.
If several external forces →F1,→F2…….→Fi,........And→Fn act simultaneously on a body and the body is in translational equilibrium, the resultant of these forces must be zero.
- ∑→Fi=→0
we have:
- ∑Fix=0,∑Fiy=0,∑Fiz=0
If a body is in equilibrium under the action of only two external forces, the forces must be equal and opposite.
If a body is in equilibrium under action of three forces, their resultant must be zero; therefore, according to the triangle law of vector addition they must be coplanar and make a closed triangle.
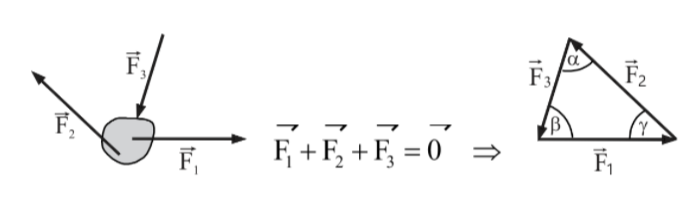
The situation can be analyzed by either graphical method or analytical method.
Graphical method makes use of sine rule or Lami's theorem.

- Sine rule : F1sinα=F2sinβ=F3sinγ
Lami's theorem : F1sinA=F2sinB=F3sinC
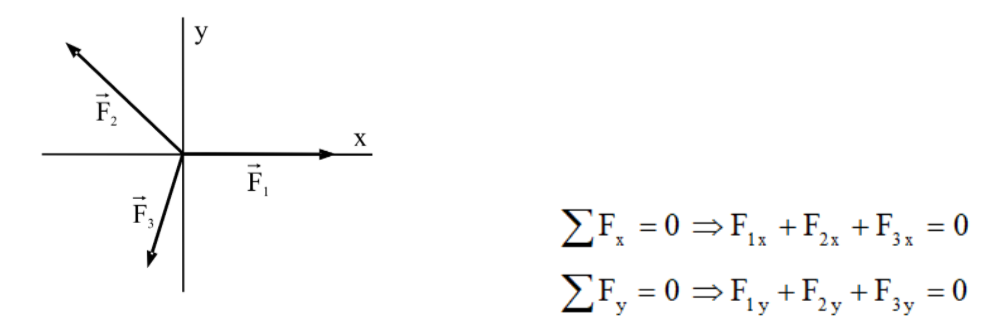
Problems involving more than three forces should be analyzed by analytical method. However, in some situations, there may be some parallel or anti-parallel forces and they should be combined first to minimize the number of forces. This may sometimes lead a problem involving more than three forces to a three-force system.
EXAMPLE 4
Consider a box of mass 10 kg resting on a horizontal table and acceleration due to gravity to be 10ms2.
- Draw the free body diagram of the box.
- Find value of the force exerted by the table on the box.
- Find value of the force exerted by the box on the table.
- Are force exerted by table on the box and weight of the box third law action-reaction pair
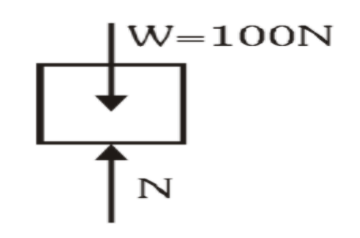
(a) N : Force exerted by table on the box.
(b) The block is in equilibrium.
- ∑→F=0⇒W−N=0⇒N=100N
(d) No
EXAMPLE 5
Consider a spring attached at one of its ends to a fixed support and at other end to a box, which rests on a smooth floor as shown in the figure. Denote mass of the box by m, force constant of the spring by k and acceleration due to gravity by g. The box is pushed horizontally displacing it by distance x towards the fixed support and held at rest.
- Draw free body diagram of the box.
- Find force exerted by hand on the box.
- Write all the third law action-reaction pairs.

(a) F is push by hand.
(b) Since the block is in equilibrium
- ∑Fx=0⇒F=kx
- Force by hand on box and force by box on hand.
- Force by spring on box and force by box on spring.
- Normal reaction by box on floor and normal reaction by floor on box.
- Weight of the box and the gravitational force by which box pulls the earth.
- Force by spring on support and force by support on spring.
EXAMPLE 6
(a) A box of weight 10√3N is held in equilibrium with the help of two strings OA and OB as shown in figure-I. The string OA is horizontal. Find the tensions in both the strings.

(b) If you can change location of the point A on the wall and hence the orientation of the string OA without altering the orientation of the string OB as shown in figure-II. What angle should the string OA make with the wall so that a minimum tension is developed in it?

(a) Free body diagram of the box
Graphical Method: Use triangle law
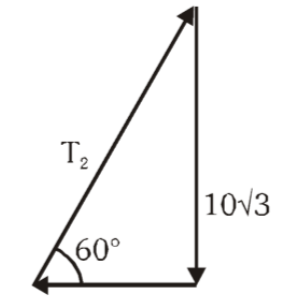
- T2sin60∘−10√3⇒T2−20N
T1tan60∘−10√3⇒T1−10N
- ∑Fx=0⇒T2cos60∘=T ………(i)
∑Fy=0⇒T2sin60∘=10√3 ……….(ii)
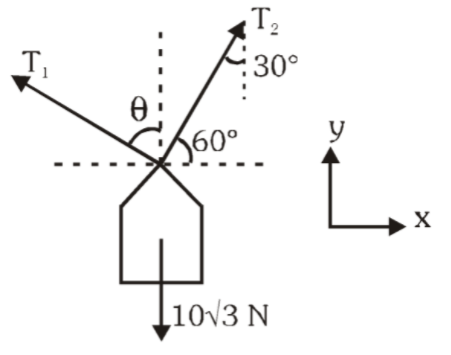
(b) Free body diagram of the box
Graphical Method : Use triangle law
For T1 to be minimum, it must be perpendicular to T2.
- From figure θ=60∘
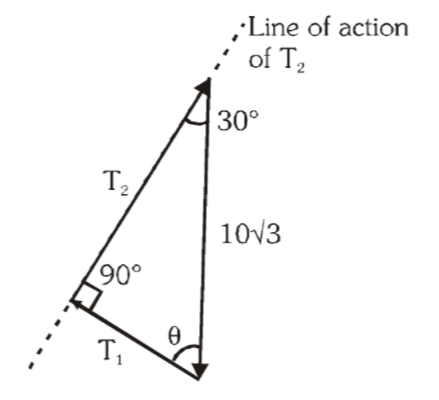
- ∑Fx=0⇒T2cos60∘=T1sinθ …….(i)
∑Fy=0⇒T1cosθ+T2sin602=10√3 ……..(ii)
- T)1=10√3√3sinθ+cosθ
- √3sinθ+cosθ=2
EXAMPLE 7
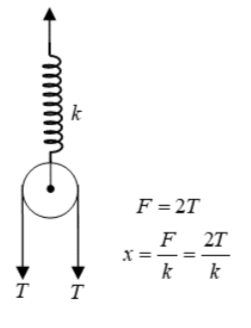
Two boxes A and B of masses m and M are suspended by a system of pulleys are in equilibrium as shown. Express M in terms of m.
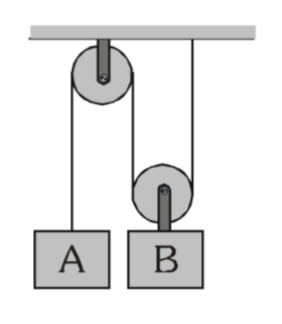
Since tension on both sides of a pulley are equal and string is massless therefore tension everywhere on the string must have same magnitude.

For equilibrium of block A
- ∑→F=→0⇒T=mg ……..(i)
- sun→F=→0⇒F=2T ……..(ii)
- sun→F=→0⇒F=Mg ……..(iii)
- M=2m
EXAMPLE 8
A box of mass m rests on a smooth slope with the help of a thread as shown in the figure. The thread is parallel to the incline plane.

- Draw a free body diagram of the box.
- Find tension in the thread.
- If the thread is replaced by a spring of force constant k, find extension in the spring.
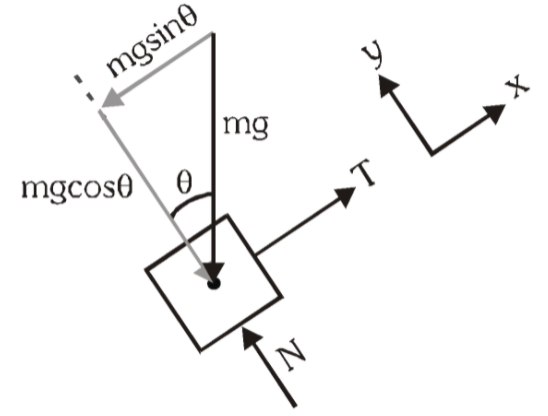
(a) Free body diagram of the block
(b) The block is in equilibrium, therefore
- ∑Fx=0⇒T=mgsinθ ……..(i)
- T=kx ……….(ii)
- x=mgsinθk
EXAMPLE 9
Block A of mass m placed on a smooth slope is connected by a string with another block B of mass M as shown in the figure. If the system is in equilibrium, express M in terms of m.
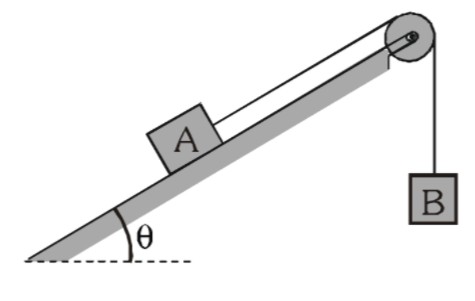
For equilibrium of the block A, net force on it must be zero.
N: Normal reaction from slope
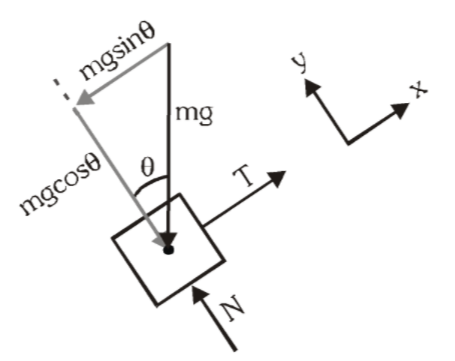
- ∑Fx=0⇒T=mgsinθ ……….(i)
∑Fy=0⇒N=mgcosθ ……….(ii)
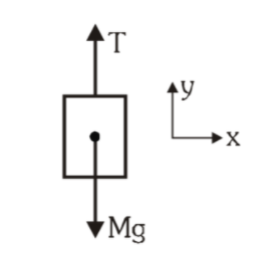
- ∑Fy=0⇒T=mg ……....(ii)
- M=msinθ
EXAMPLE 10
A 70 kg man standing on a weighing machine in a 50 kg lift pulls on the rope, which supports the lift as shown in the figure. Find the force with which the man should pull on the rope to keep the lift stationary and the weight of the man as shown by the weighing machine.

Tension magnitude everywhere in the string is same. For equilibrium of the lift.
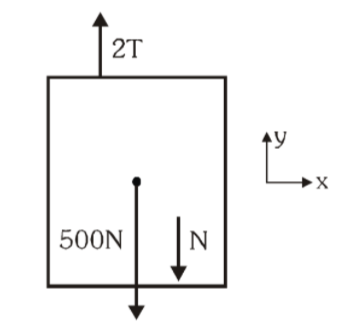
- ∑Fy=0⇒500+N=2T …….(i)

- ∑Fy=0⇒N+T=700 ……….(ii)
Here, T is the pull of mass and N is the reading of the weighing machine.
EXAMPLE 11
A block of mass m placed on a smooth floor is connected to a fixed support with the help of a spring of force constant k. It is pulled by a rope as shown in the figure. Tension force T of the rope is increased gradually without changing its direction, until the block losses contact from the floor. The increase in rope tension T is so gradual that acceleration in the block can be neglected.
- Well before the block loses contact from the floor, draw its free body diagram.
- What is the necessary tension in the rope so that the block loses contact from the floor?
- What is the extension in the spring, when the block loses contact with the floor?
(a) Free body diagram of the block, well before it loses contact with the floor.
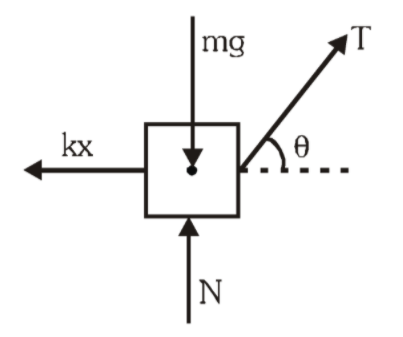
(b) When the block is about to leave the floor, it is not pressing the floor.
Therefore N = 0 and the block is in equilibrium.
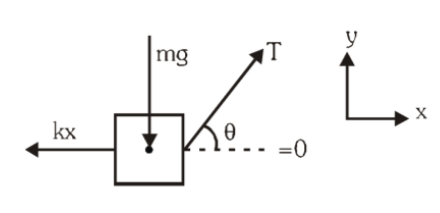
- ∑Fx=0⇒Tcosθ=kx ……….(i)
∑Fy=0⇒Tsinθ=mg ……….(ii)
- T=mgcosecθ
- x=mgcotθk
Dynamics of Particles: Translation motion of accelerated bodies
Newton's laws are valid in inertial frames, which are un-accelerated frames. At present, we are interested in motion of terrestrial bodies and for this purpose; ground can be assumed a satisfactory inertial frame.
In particle dynamics, according to Newton's second law, forces acting on the body are considered as cause and rate of change in momentum as effect. For a rigid body of constant mass, the rate of change in momentum equals to product of mass and acceleration vector. Therefore, forces acting on it are the cause and product of mass and acceleration vector is the effect.

To write the equation of motion it is recommended to draw the free body diagram, put a sign of equality and in front of it draw the body attached with a vector equal to mass times acceleration produced. In the figure is shown a body of mass m on which a single force →F acts and an observer in an inertial frame of reference observes the body moving with acceleration a’.
Acceleration imparted to a body by a force is independent of other forces, therefore when several forces →F1,→F2and→Fa act simultaneously on a body, the acceleration imparted to the body is the same as a single force equal to the vector sum of these forces could produce. The vector sum of these forces is known as the net resultant of these forces.
- →F≠t=→F2+→F2+..............+→Fn=m→a
∑→F=m→a
- ∑Fx=max ∑Fy=may ∑Fz=maz
EXAMPLE 12
Two forces F1 and F2 of magnitudes 50 N and 60 N act on a free body of mass m = 5 kg in directions shown in the figure. What is the acceleration of an object with respect to free space?
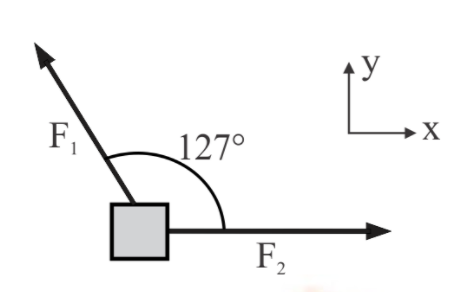
In an inertial frame of reference with its x-axis along the force F2, the forces are expressed in Cartesian components.
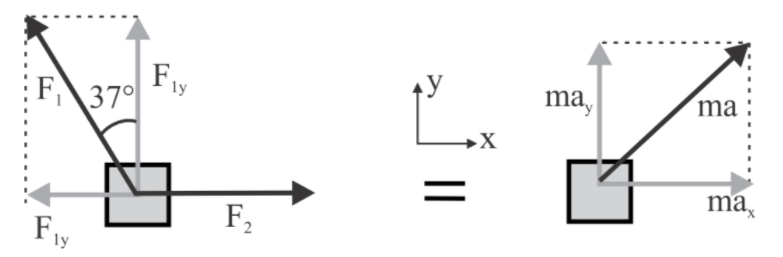
- →F1=(−30ˆi+40ˆj)Nand→F2=60ˆiN
∑Fx=max⇒ax=6ms2
∑Fy=may⇒ay=8ms2
→a=(6ˆi+8ˆj)ms2
EXAMPLE 13
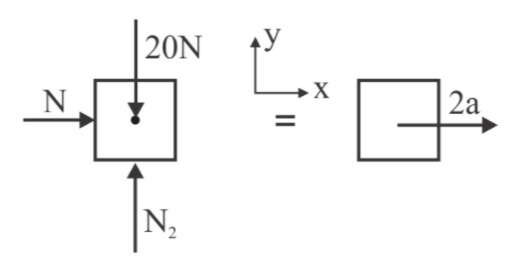
Boxes A and B of mass mA = 1 kg and mB = 2 kg are placed on a smooth horizontal plane. A man pushes horizontally the 1 kg box with a force F = 6 N. Find the acceleration and the reaction force between the boxes.

Since both the blocks move in contact it is obvious that both of them have same acceleration. Say it is 'a'.
Applying NLM to block A
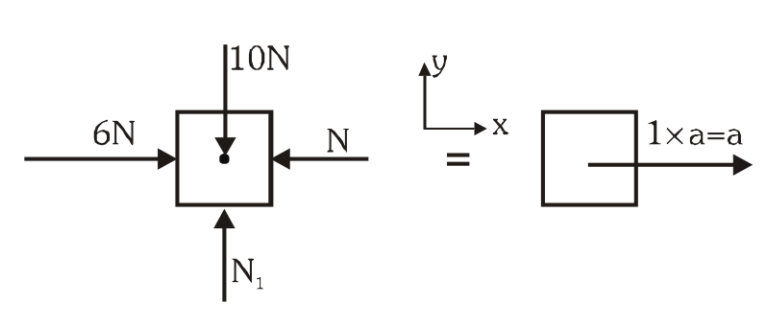
N: Normal reaction from B
N1: Normal reaction from floor
- ∑Fx=max⇒6−N=a ……….(i)
∑Fy=0⇒N1=10N ……….(ii)
N : Normal reaction from A
N2: Normal reaction from ground
- ∑Fx=max⇒N=2a ……….(iii)
∑Fy=0⇒N2=20N ……….(iv)
- a=2ms2 and N=4N
EXAMPLE 14
Two blocks A and B of masses m1 and m2 connected by light strings are placed on a smooth floor as shown in the figure. If the block A is pulled by a constant force F, find accelerations of both the blocks and tension in the string connecting them.
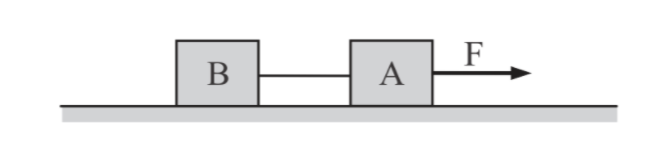
String connecting the blocks remain taut keeping separation between them constant. Therefore it is obvious that both of them move with the same acceleration. Say it is 'a'.
Applying NLM to block A
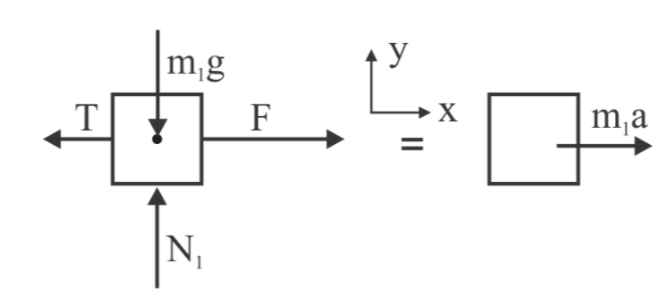
T: Tension of string
N1 : Normal reaction from ground
- ∑Fx=ma⇒F−T=m1a ……….(i)
∑Fy=0⇒N1=m1g ……….(ii)
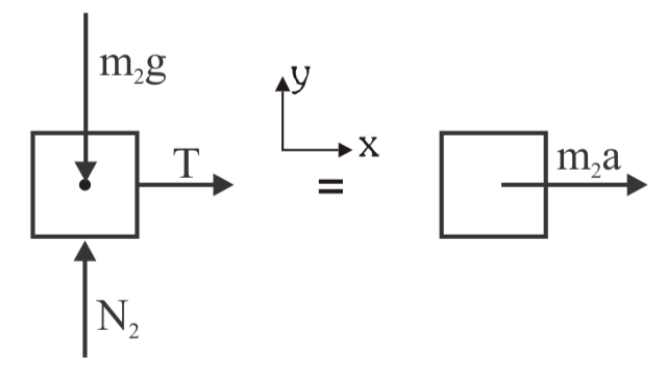
T : Tension of string
N2: Normal reaction from ground.
- ∑Fx=max⇒T=m2a ……….(iii)
∑Fy=0⇒N2=m2g ………..(iv)
- a=Fm1+m2
- T=m2Fm1+m2
EXAMPLE 15
Three identical blocks A, B and C, each of mass 2.0 kg are connected by light strings as shown in the figure. If the block A is pulled by an unknown force F, the tension in the string connecting blocks A and B is measured to be 8.0 N. Calculate magnitude of the force F, tension in the string connecting blocks B and C, and accelerations of the blocks.
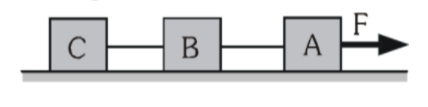
It is obvious that all the three blocks move with the same acceleration. Say it is 'a'.
Applying NLM to the block A.

T1: Tension of string connecting blocks A and B.
N1: Normal reaction from floor.
- ∑Fx=max⇒F−T1=2a ……….(i)
∑Fy=0⇒N1=20N ……….(ii)
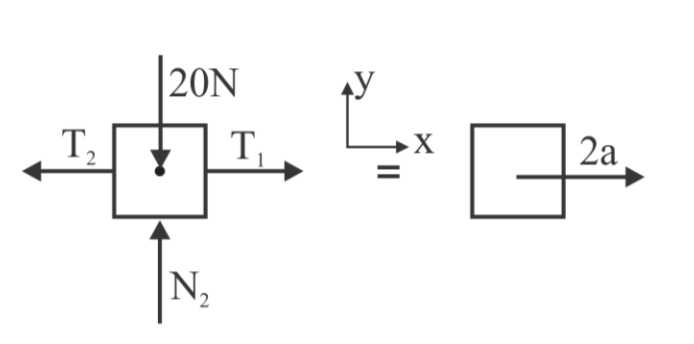
T1: Tension of string connecting blocks A and B.
T2: Tension of string connecting B & C.
N1: Normal reaction from floor.
- ∑Fx=max⇒T1−T2=2a ………..(iii)
∑Fy=0⇒N2=20N ………..(iv)
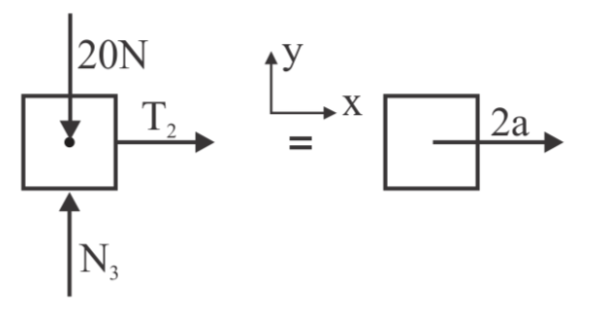
T3: Tension of string connecting B & C.
N3: Normal reaction from floor.
- ∑Fx=max⇒T2=2a …………(v)
∑Fy=0⇒N3=20N ……….(vi)
- F=6a ……....(vii)
- a=2ms2
- F=12N
EXAMPLE 16
Two blocks A and B of masses m1 and m2 connected by uniform string of mass m and length l are placed on smooth floor as shown in the figure. The string also lies on the floor. The block A is pulled by a constant force F.

- Find accelerations a of both the blocks and tensions TA and TB at the ends of the string.
- Find an expression for tension T in the string at a distance x from the rear block in terms of TA,TB,m,l and x.
It is obvious that both the blocks and the whole string move with the same acceleration say it is 'a'. Since string has mass it may have different tensions at different points.
(a) Applying NLM to block A.
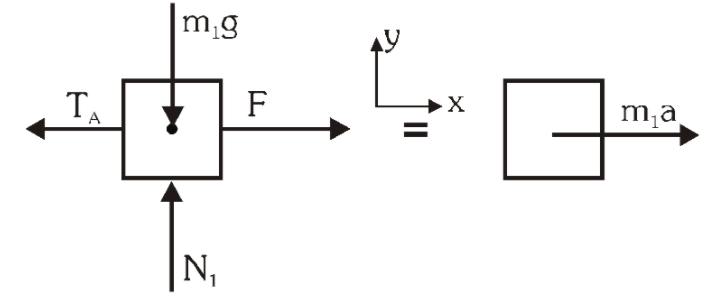
TA: Tension of the string at end connected to block A.
N1 : Normal reaction of floor
- ∑Fx=max⇒F−TA=m1a ………..(i)
∑Fy=0⇒N−1=m1g ……….(ii)
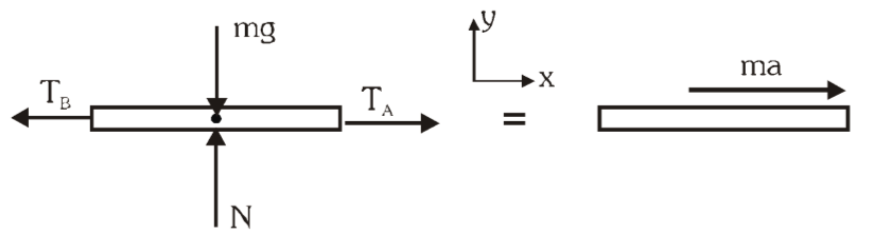
TB : Tension of string at end connected to block B.
N : Normal reaction of floor
- ∑Fx=max⇒TA−TB=ma ……….(iii)
∑Fy=0⇒N=mg ……….(iv)
TB : Tension of string
N2 : Normal reaction from floor
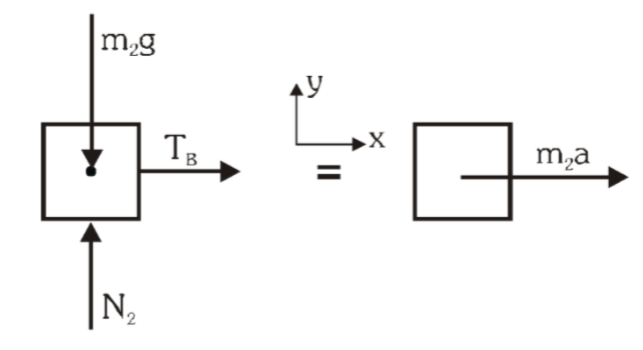
- ∑Fx=max⇒TB=m2a ……….(v)
∑Fy=0⇒N2=m2g ……….(vi)
- a=Fm+m1+m2 ………..(vii)
TA=(m+m2)Fm+m1+m2 ……….(viii)
TB=m2Fm+m1+m2 ……….(ix)
(b) To find tension at a point x distance away from block B, we can consider string of length x or l–x.
Let us consider length of string x and apply NLM.
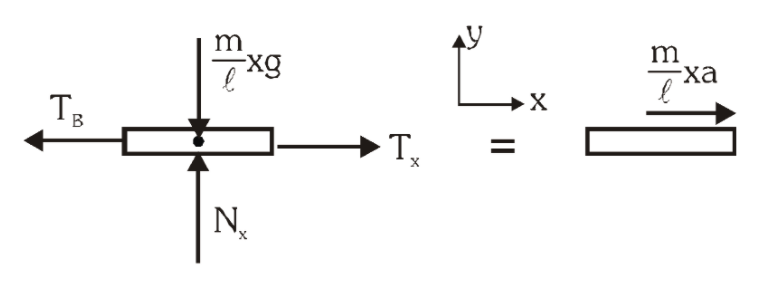
(mx)l : mass of length x.
Tx = Tension at distance x
Nx = Normal reaction of floor
- ∑Fx=max⇒Tx−TB=mxla ……….(x)
- Tx=(mlx+m2)Fm+m1+m2
EXAMPLE 17
The system shown in the figure is released from rest. Assuming mass m2 more than the mass m1, find the accelerations of the blocks and the tension in the string.
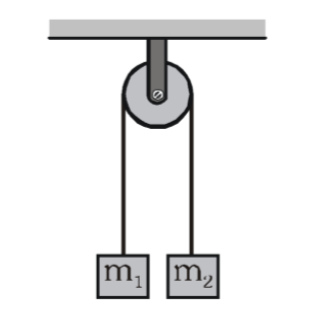
It obvious that both blocks move with same acceleration magnitudes. Say it is 'a'.
Since m2 is heavier, it moves downwards and m1 moves upwards. Tension at both the ends of the string has same magnitude. Say it is 'T'.
Apply NLM to block A of mass m1
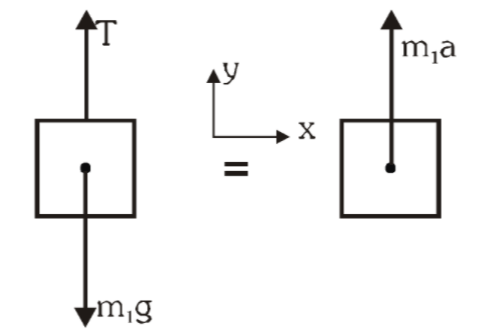
- ∑Fy=may⇒T−m1g=m1a ………..(i)
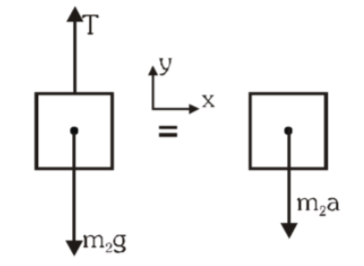
- ∑Fy=may⇒m2g−T=m2a ………..(ii)
- a=(m2−m1m1+m2)g, T=(2m1m2m1+m2)g
EXAMPLE 18
Block A of mass m placed on a smooth slope is connected by a string with another block B of mass M (> msinθ) as shown in the figure. Initially the block A is held at rest and then let free. Find acceleration of the blocks and tension in the string.
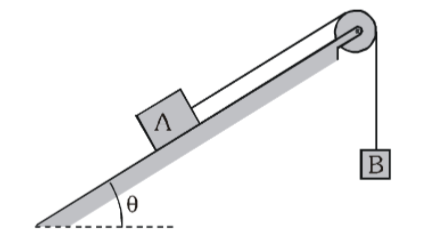
Both the blocks must move with the same magnitude of acceleration.
Since M > m sinθ, block B move downward pulling block A up the plane. Let acceleration magnitude is 'a'.
Tension at both the ends of the string is same. Say it is 'T'.
Apply NLM to block A
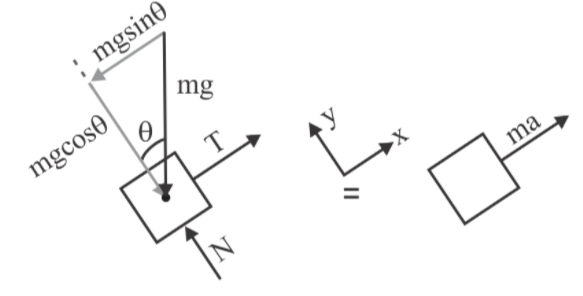
N: Normal reaction from slope
T: Tension of string
- ∑Fx=max⇒T−mgsinθ=ma ……….(i)
∑Fy=0⇒N=mgcosθ …………(ii)
T: Tension of string
- ∑Fy=may⇒Mg−T=ma ………….(iii)
- a=(M−msinθ)gM+m
T=(1+sinθ)mMgM+m
EXAMPLE 19
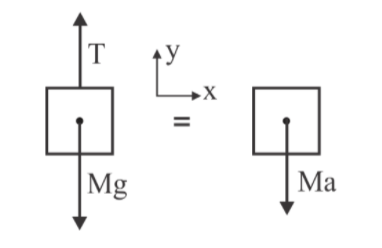
A block of mass ‘m’ is kept on the ground as shown in figure.
- Draw F.B.D. of block.
- Are forces acting on block action–reaction pair.
- If answer is no, draw action reaction pair.
(i)F.B.D. of block
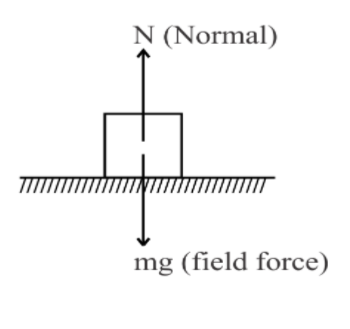
(ii) ‘N’ and Mg are not action-reaction pair. Since pair act on different bodies, and they are of same nature.
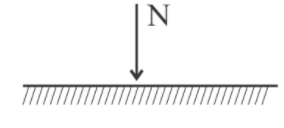
(iii) Pair of ‘mg’ of block acts on earth in opposite direction.

and pair of ‘N’ acts on surface as shown in figure.
EXAMPLE 20
Two spheres A and B are placed between two vertical walls as shown in figure. Draw the free body diagrams of both the spheres.
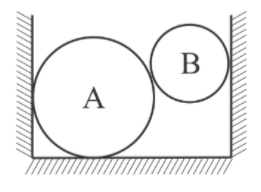
F.B.D. of sphere ‘A’ :
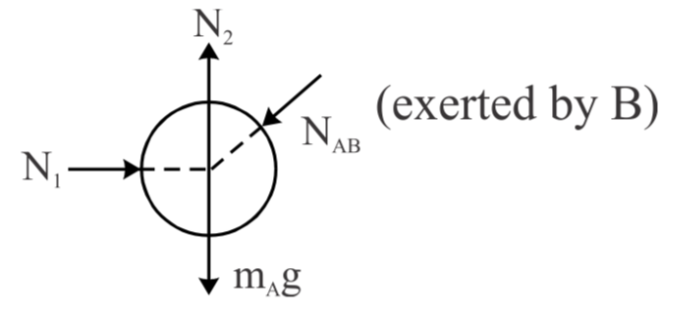
F.B.D. of sphere ‘B’:
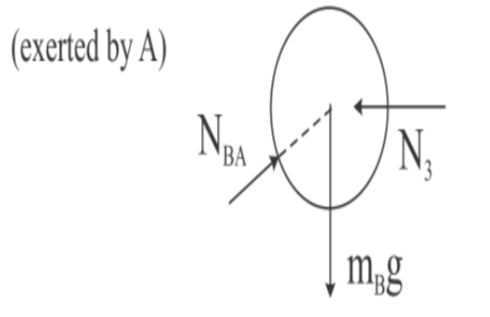
Note : Here NAB and NBA are the action–reaction pair (Newton’s third law).
EXAMPLE 21
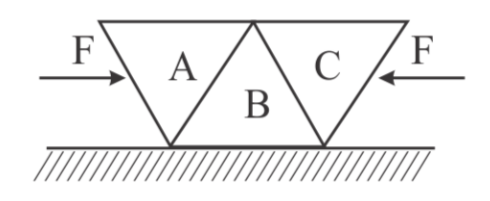
Three triangular blocks A, B and C of equal masses ‘m’ are arranged as shown in figure. Draw F.B.D. of blocks A, B and C. Indicate action–reaction pair between A, B and B, C.
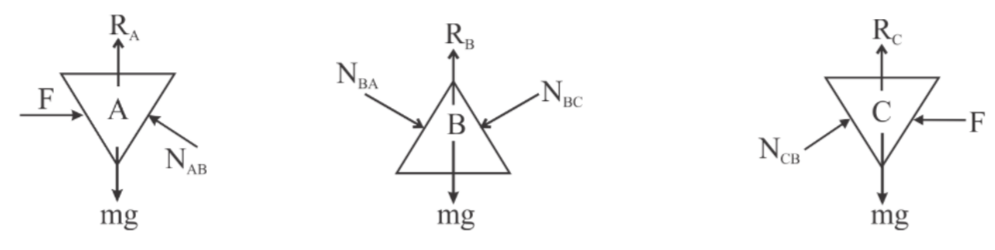
EXAMPLE 22
A ‘block’ of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g = 10 m/s2)
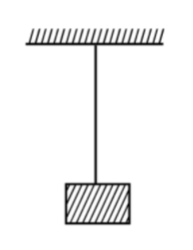
F.B.D. of block
- ∑Fy=0
T−10g=0
- ∴
- T=100N
EXAMPLE 23
The system shown in figure is in equilibrium. Find the magnitude of tension in each string; T1,T2,T3 and T4 (g=10ms2)
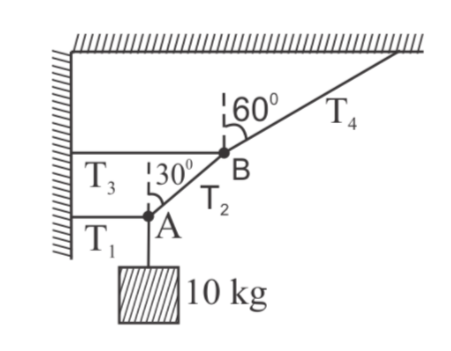
F.B.D. of block 10 kg
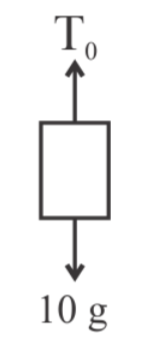
- T0=10g
T0=100N N
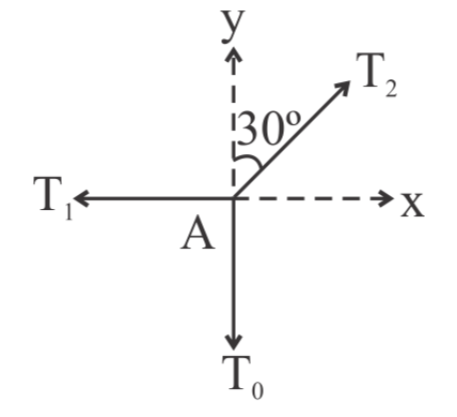
- ∑Fy=0⇒T2cos30∘=T0=100N
T2=200√3N
∑Fx=0⇒T1=T2sin30∘
=200√3×12=100√3N
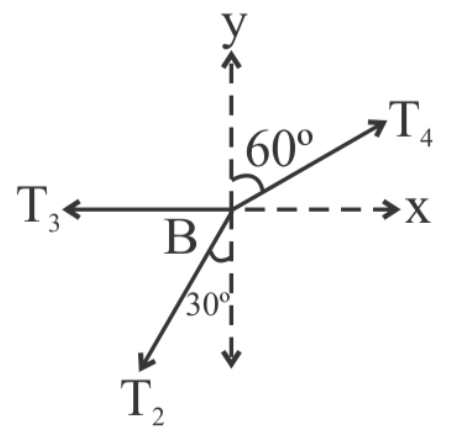
- ∑Fy=0⇒T4cos60∘=T2cos39∘
- ∑Fx=0⇒T3+T2sin30∘=T4sin602
- ∴
- T3=200√3N, T4=200N
EXAMPLE 24
The system shown in figure is in equilibrium, find the tension in each string ; T1,T2,T3,T4 and T5
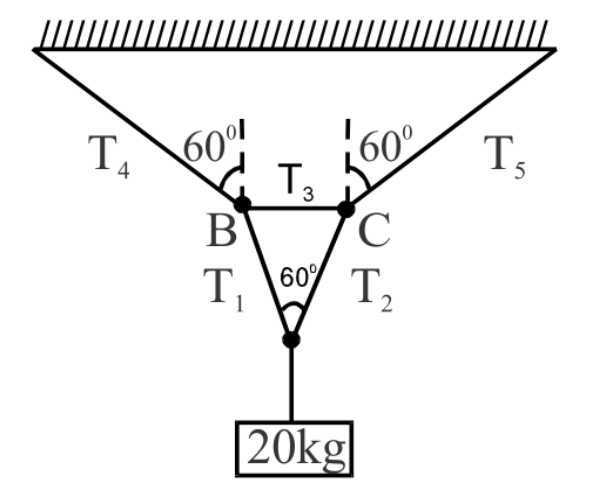
T1=T2=200√3N
T4=T5=200N
T3=200√3N
EXAMPLE 25
Two blocks are kept in contact as shown in figure. Find
- (a)forces exerted by surfaces (floor and wall) on blocks.
(b)contact force between two blocks.
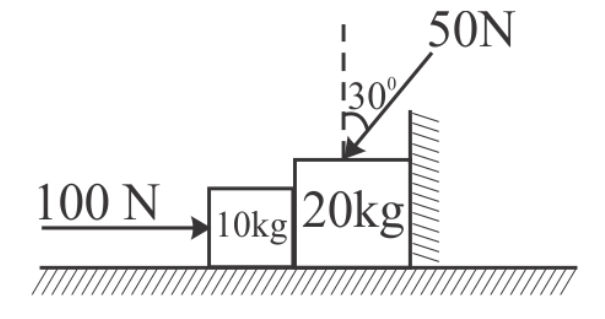
F.B.D. of 10 kg block
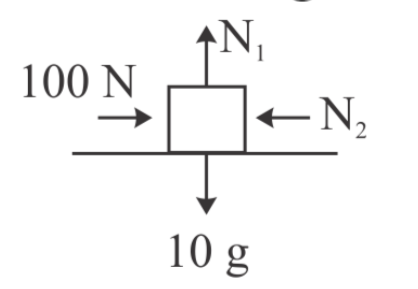
- N1=10g=100N ………..(i)
N2=100N …………(ii)
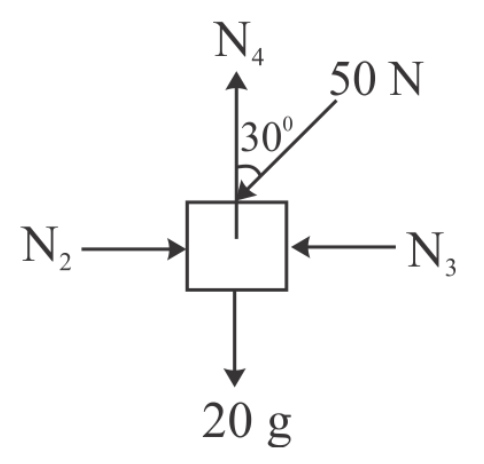
- N2=50sin30∘+N3 ……….(iii)
- N4=243.30N
EXAMPLE 26
The breaking strength of the string connecting wall and block B is 175 N, find the magnitude of weight of block A for which the system will be stationary. The block B weighs 700 N. (g=10ms2)

(175)(√3)N.
EXAMPLE 27
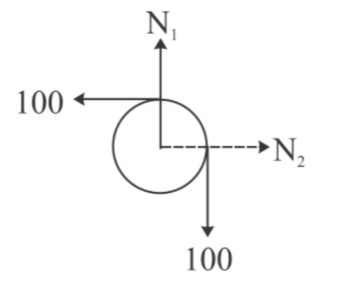
Find the magnitude of force exerted by string on pulley.
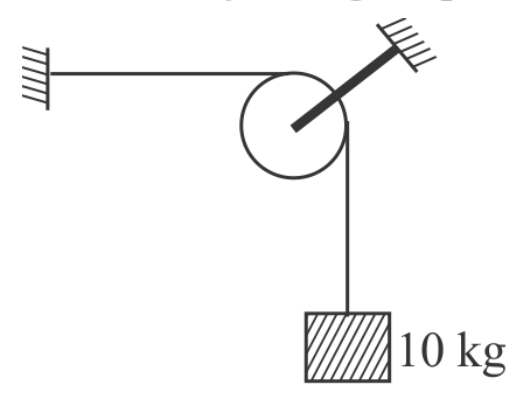
F.B.D. of 10 kg block:
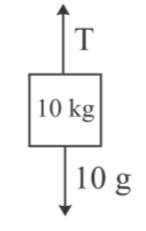
- T=10g=100N
Since string is massless, so tension in both sides of string is same.
Force exerted by string
- +√(100)2+(1002)
=100√2N
EXAMPLE 28
In the arrangement shown in figure, what should be the mass of block A so that the system remains at rest. Also find force exerted by string on the pulley Q. (g=10ms2)
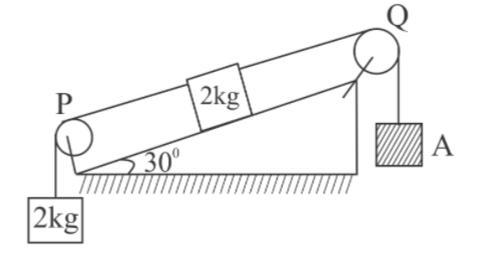
m=3kg,30√3N.
Accelerating Objects
To solve problems involving objects that are in accelerated motion:
Step 1: Make a sketch of the problem.
Step 2: Isolate a single object and then draw the free-body diagram for that object. Label all external forces acting on it. Be sure to include all the forces acting on the chosen body, but be equally carefully not include any force exerted by the body on some other body. Some of the forces may be unknown; label them with algebraic symbols.
Step 3:Choose a convenient coordinate system, show location of coordinate axes explicitly in the free-body diagram, and then determine components of forces with reference to these axes and resolve all forces into x and y components.
Step 4:Apply the equations ∑Fx=max and ∑Fy=may.
Step 5: Step 4 will give two equations with several unknown quantities. If you have only two unknown quantities at this point, you can solve the two equations for those unknown quantities.
Step 6: If step 5 produces two equations with more than two unknowns, go back to step 2 and select another object and repeat these steps. Eventually at step 5 you will have enough equations to solve for all unknown quantities.
EXAMPLE 29
A force F is applied horizontally on mass m1 as shown in figure. Find the contact force between m1 and m2.
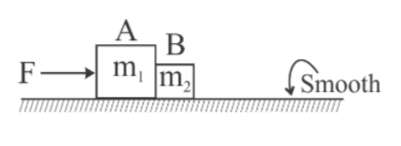
Considering both blocks as a system to find the common acceleration.
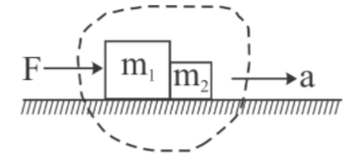
Common acceleration
- a=Fm1+m2 ………..(i)
F.B.D. of mass m2
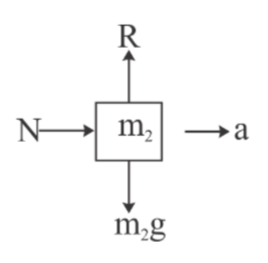
- ∑Fx=max
N+m2.a
N=m2Fm1+m2
EXAMPLE 30
The velocity of a particle of mass 2 kg is given by →v=atˆi+bt2ˆj. Find the force acting on the particle.
From second law of motion:
- →F=dP’dt=ddt(m→v)
=2.ddt(atˆi+bt2ˆj)⇒→F=2aˆi+4btˆj
EXAMPLE 31
A 5 kg block has a rope of mass 2 kg attached to its underside and a 3 kg block is suspended from the other end of the rope. The whole system is accelerated upward at 2 m/s2 by an external force F0.
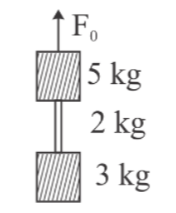
- What is F0?
- What is the net force on rope ?
- What is the tension at middle point of the rope?(g=10ms2)
For calculating the value of F0, consider two blocks with the rope as a system.
F.B.D. of whole system
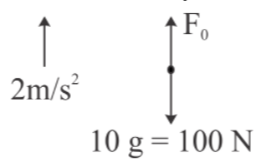
(a)
- F0−100=10×2
F=120N ……….(i)
- F=ma
=(2)(2)
F=4N ……….(ii)

- T−4g=4(2);T=48N
EXAMPLE 32
Two blocks with masses m1 = 0.2 kg and m2 = 0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations: (g=10ms2)
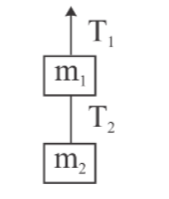
- the blocks are at rest
- they move upward at 5 m/s
- they accelerate upward at 2ms2
- they accelerate downward at 2ms2
- if maximum allowable tension is 10 N.
(a) 5 N, 3 N(b) 5 N, 3 N
(c) 6 N, 3.6 N(d) 4 N, 2.4 N(e) 10ms2
EXAMPLE 33
A block of mass 50 kg is kept on another block of mass 1 kg as shown in figure. A horizontal force of 10 N is applied on the 1kg block. (All surface are smooth). Find (g = 10 m/s2)

- Acceleration of block A and B.
- Force exerted by B on A.
(a) F.B.D. of 50 kg
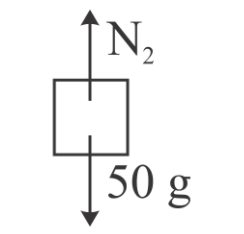
- N2=50g=500N
(b) F.B.D. of 1 kg block:
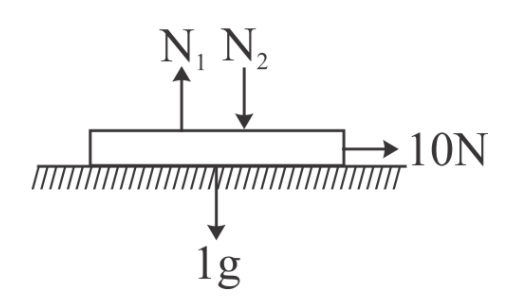
along horizontal direction
- 10=1aA.
aA=10ms2
- N1=N2+1g
=500+10=510N
EXAMPLE 34
Repeat above example if force is applied on 50 kg block rather on the 1kg block.
(a) 2ms2, 0 (b) 510 N
EXAMPLE 35
A horizontal force is applied on a uniform rod of length L kept on a frictionless surface. Find the tension in rod at a distance ‘x’ from the end where force is applied.
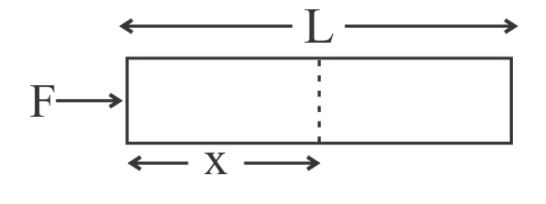
Considering rod as a system, we find acceleration of rod
- a=Fm

Using Newton’s second law
- F−T=(ML)x.a
T=F−MLx.FM
T=F(1−xL)
EXAMPLE 36
Two forces F1 and F2(> F1) are applied at the free ends of uniform rod kept on a horizontal frictionless surface. Find tension in rod at a distance x from end ‘A’.
T=F2−F2−F1L.x
EXAMPLE 37
One end of string which passes through pulley and connected to 10 kg mass at other end is pulled by 100 N force. Find out the acceleration of 10 kg mass. (g = 9.8 ms2)

Since string is pulled by 100 N force. So tension in the string is 100 N.
F.B.D. of 10 kg block
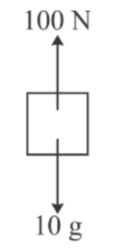
- 100−10g=10a
100−10×9.8=10a
a=0.2ms2.
EXAMPLE 38
Two blocks m1 and m2 are placed on a smooth inclined plane as shown in figure. If they are released from rest. Find:
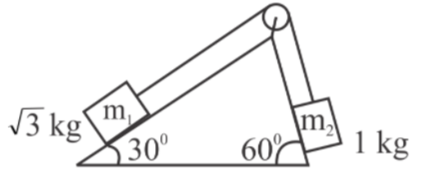
- acceleration of massm1 and m2
- tension in the string
- net force on pulley exerted by string
F.B.D. of m1 :

- M1sinθ−T=m1a
√32g−T=√3a …………(i)
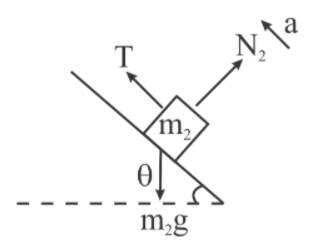
- T−m2gsinθ=m2a
T−1.√32g=1.a ………..(ii)
Putting this value in eq.(i) we get
- T=√3g2
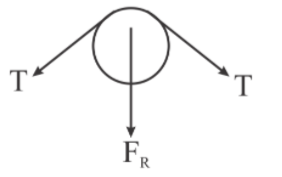
- FR=√2T
FR=√32g
EXAMPLE 39
A 10 kg block kept on an inclined plane is pulled by a string applying 200 N force. A 10 N force is also applied on 10 kg block as shown in figure.
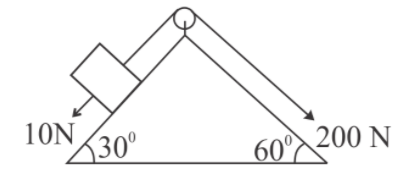
Find:
- tension in the string.
- acceleration of 10 kg block.
- net force on pulley exerted by string
(a) 200 N, (b) 14ms2, (c) 200√2N
EXAMPLE 40
A 60 kg painter stands on a 15 kg platform. A rope attached to the platform and passing over an overhead pulley allows the painter to raise himself along with the platform.
- To get started, he pulls the rope down with a force of 400 N. Find the acceleration of the platform as well as that of the painter.
- What force must he exert on the rope so as to attain an upward speed of 1 m/s in 1s?
- What force should he apply now to -maintain the constant speed of 1 m/s?
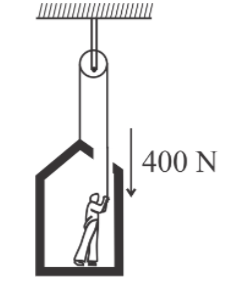
The free body diagram of the painter and the platform as a system can be drawn as shown in the figure.

Note that the tension in the string is equal to the force by which he pulls the rope.
(i) Applying Newton’s Second Law
- 2T−(M+m)g=(M+m)a
- a=2T−(M+m)gM+m
- a=2(400)−(60+15)(10)60+15=0.67ms2
Thus, the applied force is
- F = ½(M+m)(g+a) = ½(60+15)(10+1) = 412.5 N
Thus,
- 2F–(M+m)g=0
- F=(M+m)g2=(60+15)(10)2=375N
System of Interconnected bodies
In system of interconnected bodies, several bodies are interconnected in various manners through some sort of physical links. Sometimes these physical links includes ropes and pulleys and sometimes the bodies under investigation are pushing each other through direct contact. In systems consisting of bodies interconnected through ropes and pulleys, relation between their accelerations depends on the arrangement of the ropes and pulleys. In addition, in system where bodies push each other, they affect relation between their accelerations due to their shapes.
In kinematics while dealing with dependant motion or constrained motion, we have already learnt how to find relations between velocities and accelerations of interconnected bodies.
Analysis of physical situations involving interconnected bodies often demands relation between accelerations of these bodies in addition to the equations obtained by application of Newton’s laws of motion. Therefore, while analyzing problems of interconnected bodies, it is recommended to explore first the relations between accelerations and then apply Newton’s laws of motion.
In following few examples, we learn how to deal with problems of interconnected bodies.
EXAMPLE 41
Two boxes A and B of masses m and M interconnected by an ideal rope and ideal pulleys, are held at rest as shown. When it is released, box B accelerates downwards. Find accelerations of the blocks.
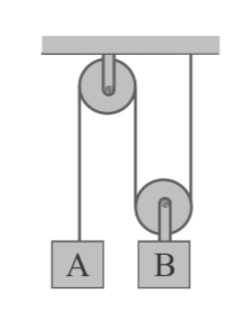
We first show tension forces applied by the string on the box A and the pulley connected to box B. Since the string, as well as the pulleys, both are ideal; the string applies tension force of equal magnitude everywhere. Denoting the tension force by T, we show it in the adjacent figure.

We first explore relation between accelerations aA and aB of the boxes A and B, which can be written either by using constrained relation or method of virtual work or by inspection.
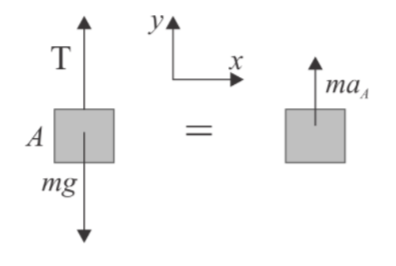
- aA=2ag ………..(i)
- ∑Fy=may→T−mg=maA ………..(ii)
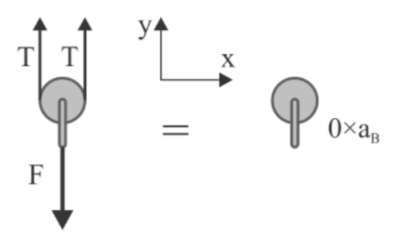
Applying Newton’s Laws of motion to the pulley
- ∑Fy=may→2T−F=0×aB
F=2T ……….(iii)

- ∑Fy=may→Mg−2T=MaB ………….(iv)
- aA=2(M−2mM+4m)gandaB=(M−2mM+4m)g
EXAMPLE 42
In the system shown in figure, block m1 slides down a friction less inclined plane. The pulleys and strings are ideal. Find the accelerations of the blocks.
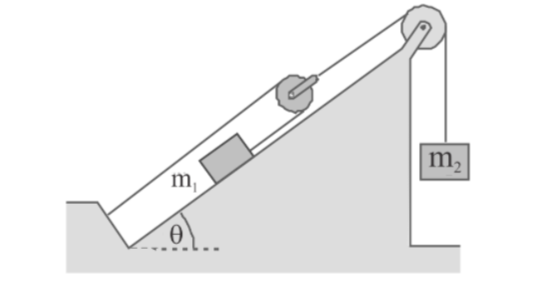
Tension forces applied by the strings are shown in the adjacent figure.
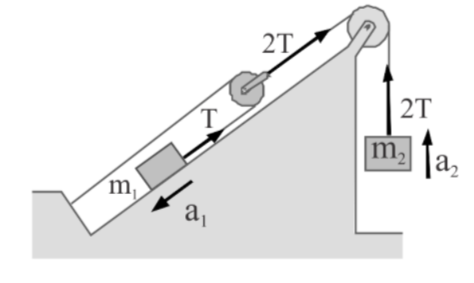
Let the block m1 is moving down the plane with an acceleration a1 and m2 is moving upwards with accelerations a2. Relation between accelerations a1 and a2 of the blocks can be obtained easily by method of virtual work.
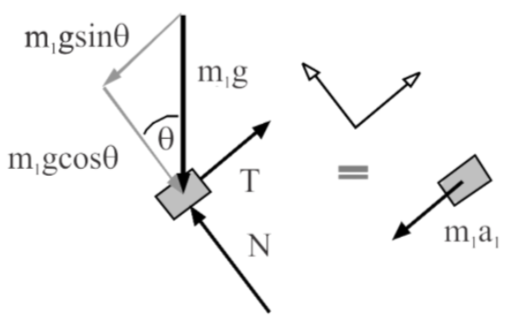
- a1=2a2 ………..(i)
- ∑Fy=max→m1gsinθ−T=m1a1 ……….(ii)
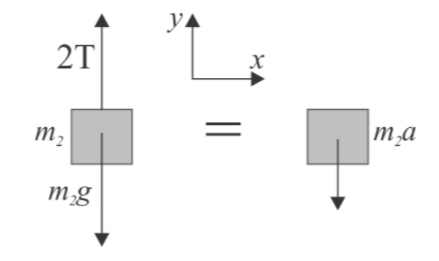
- ∑Fy=may→2T−m2g=m2a2 ………..(iii)
- a1=2(2m1sinθ−m2)4m1+m2g
a2=2m2gsinθ−m2g4m1+m2
CONSTRAINT RELATION
1.Assume the direction of acceleration of each block, e.g., a1 (downward) and a2 (upward) in this case.
2.Locate the position of each block from a fixed point (depending on convenience), e.g., centre of the pulley in this case.
3.Identify the constraint and write down the equation of constraint in terms of the distance assumed.

For example, in the hosen problem, the length of string remains constant is the constraint or restriction.
Thus, x1+x2 = constant
Differentiating both the sides w. r. t. time, we get
- dx1dt+dx2dt=0
Since we have to find a relation between accelerations, therefore, we differentiate it once again w. r. t. Time. Thus
- d2x1dt2+d2x2dt2=0
∴
- d2x1dt2=+a1,a1>0
- d2x2dt2=−a2,a2>0
- a1−a2=0
- a1=a2=a

One can easily see that an expression for length of the string can not be written unless we located the centre of the pulley w. r. t. ground.
If y0 be the distance of the ground from the centre of the pulley then the length of string is
- (y0−y1)+(y0−y2) = constant
2y0−y1−y2 = constant
- 0−d2y1dt2−d2y2dt2=0
Thusa1−a2=0 so
- a1=a2=0
- a=[m1−m2m1+m2]g
- T=[2m1m2m1+m2]g
EXAMPLE 43
A system of the three masses m1,m2 and m3 are shown in the figure. The pulleys are smooth and massless; the strings are massless and inextensible.
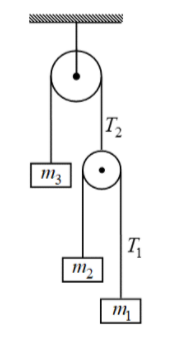
- Find the tension in the strings
- Find the acceleration of each mass
All the blocks are assumed to be moving downward and the free body diagram of each block is known in the figure.
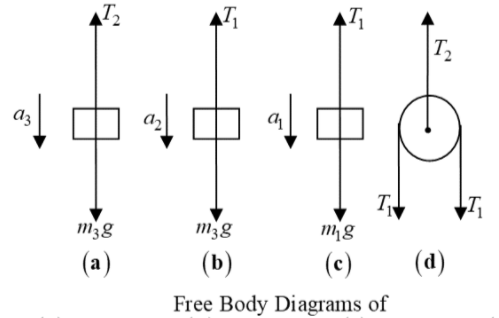
- block m3
- block m2
- block m1
- pulley
Block m1
- m1g−T1=m1a1 ……….(i)
- m2g−T1=m2a2 ………..(ii)
- m3g−T2=m3a3 ………….(iii)
Number of equations: Four
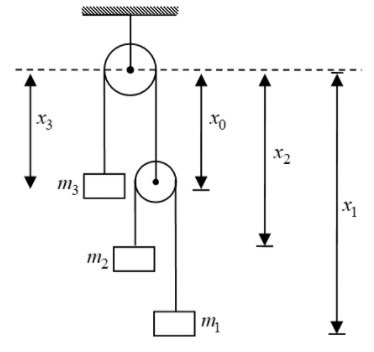
The constraint relation among accelerations can be obtained as follows for upper straight
- x3+x0=c1
- (x2−x0)+(x1−x0)=c2
x2+x1−2x0=c2
- x1+x2+2x3=2c1+c2 = Constant.
- d2x1dt2+d2x2dt2+2d2x3dt2=0
a1+a2+2a3=0 …………….(v)
- T=[4m1m2m34m1m2+m3(m1+m2)]g;T2=2T
a1=[4m1m2+m1m3−3m2m34m1m2+m3(m1+m2)g
a2=[3m1m3−m2m3−4m1m24m1m2+m3(m1+m2)g
a3=[4m1m2−m3(m1+m2)4m1+m2+m3(m1+m2)g
EXAMPLE 44
A 60 kg painter stands on a 15 kg platform. A rope attached to the platform and passing over an overhead pulley allows the painter to raise himself and the platform.

- To get started, he pulls the rope down with force of 400 N. Find the acceleration of the platform as well as that painter.
- What force must he exert on the rope so as to attain an upward speed of 1 m/s in 1 s.
- What force should he apply now to maintain the constant speed of 1 m/s.
The free body diagram of the painter and the platform can be drawn as shown in the figure.
Note that the tension in the string is equal to the force by which he pulls the rope.
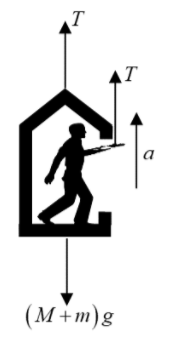
(a)Applying Newton's Second Law
- 2T−(M+m)g=(M+m)a
a=2T−(M+m)gM+m
- a=2(400)−(60+15)(10)60+15=0.67ms2
Thus, the applied force is
- F=12(M+m)(g+a)=½(60+15)(10+1)=412.5N
- 2F−(M+m)g=0
F=(M+m)g2=(60+15)(10)2=375N
Reference Frames : Inertial and Non- Inertial
A reference frame in which Newton's first law is valid is called an inertial reference frame. In an inertial reference frame. In an inertial reference frame, a body subject to no net force will either stay at rest or move at constant velocity.
Any frame moving at constant velocity relative to a known inertial frame is also an inertial frame. If the acceleration of a particle is zero in one inertial frame, it is zero in all inertial frames.
An accelerated frame of reference is called a non –inertial frame. Objects in non-inertial reference frames do not obey Newton's first law.
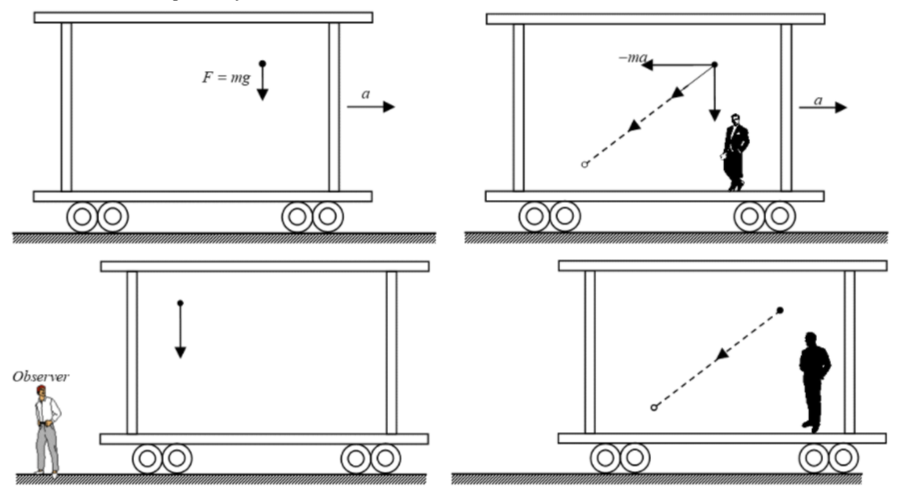
Suppose a ball is on the frictionless floor of a car and the brakes are applied. Since there is no net force on the ball an observer on the ground will see the ball continue to move at the velocity of the car just before the brakes were applied. However, relative to an observer in the car, the ball accelerates in the forward direction, even though there is no net force on it. To explain the acceleration of the ball with respect to the car (non-inertial frame) one has to invent a fictitious force called the pseudo force. It is an imaginary force which acts an all the occupants of an accelerated frame. The direction of the force is opposite to the direction of the acceleration.
- FP=−ma
EXAMPLE 45
Apparent weights in an Accelerating Elevator : A man of mass M stands on a scale in an elevator, as shown in the fig. Find the scale reading when the elevator is accelerating with a0
(i) Upward and (ii) Downward?

(a)Since the man is stationary relative to the elevator, it is also accelerating up with. The forces on the man are reaction N (exerted by the scale platform on which it rests) and mg, the force of gravity. In the reference frame attached to the elevator an additional pseudo force FP=Ma0 acts opposite to the acceleration. The free body diagrams of the man w.r.t. ground and the elevator are shown in figure (a and b)
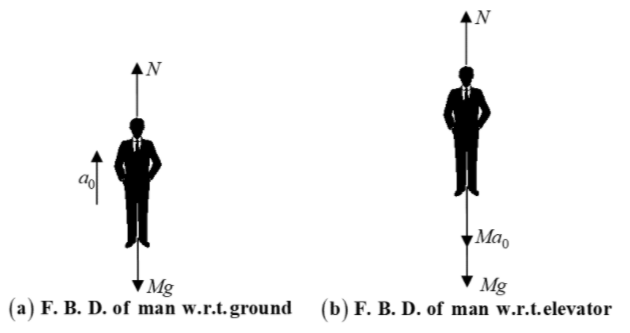
Applying Newton's Second Law
- N−Mg=Ma0
N=M(g+a0)
(b)When the elevator accelerates downward with a0 the free body diagram can be drawn, as shown in the figure
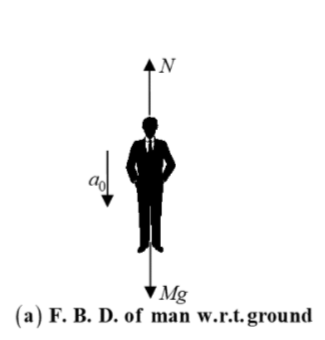
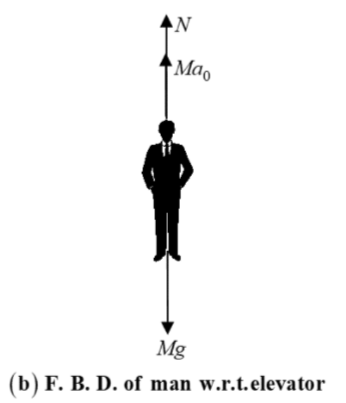
Applying Newton's Second Law With respect to the elevator
- Mg−N=Ma0
N=M(g−a0)
If a0=g as it would if the elevator were in free fall, the man would be apparently weight less.
EXAMPLE 46
Figure shows a pendulum suspended from the roof of a car that has a constant acceleration a relative to the ground.
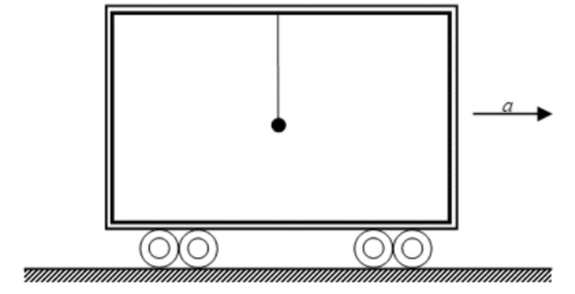
Find the deflection of the pendulum from the vertical as observed from the ground frame and from the frame attached with the car.
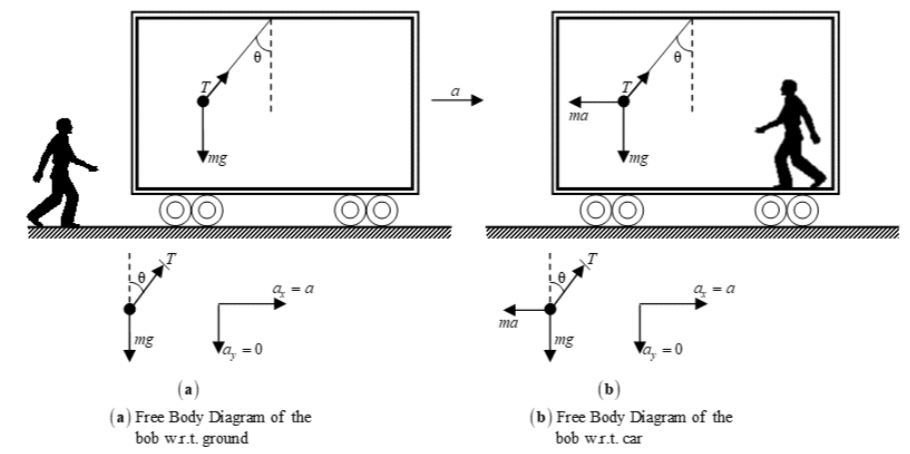
In an inertial frame the suspended bob has acceleration a caused by the horizontal component of the tension T.
- Tsinθ=ma ………….(i)
Tcosθ−mg=0 ………….(ii)
- tanθ=ag
θ=tan−1(ag)
- Tsinθ=ma …………(iii)
Tcosθ=mg ………..(iv)
- tanθ=ag
θ=tan−1(ag)
EXAMPLE 47
A pulley with two blocks system is attached to the ceiling of a lift moving upward with an acceleration a0. Find the deformation in the spring as observed by the inertial and non-inertial reference frame observer.
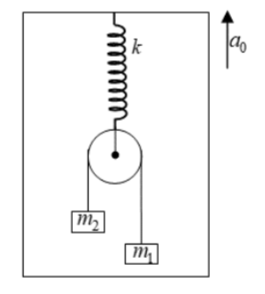

Applying Newton's Second Law
- m1g−T=m1a1 ………..(i)
−m2g+T=m2a2 ………..(ii)
- (x0−x2)+(x0−x1) = constant
2x0−x1−x2 = constant
- 2d2x0dt2−d2x1dt2−d2x2dt2=0
2a0−(−a1)−a2=0
a2=2a0+a1 ………..(iii)
- T=[2m1m2m1+m2](g+a0)
Using Hooke's law F=kx
Where x is the deformation in the spring. Thus,
- x=Fk=[4m1m2m1+m2](g+a0)k
Applying Newton's Second Law
- m1g+m1a0−T=m1arel …………(iv)
−m2g+m2a0+T=m2arel ………….(v)
- arel=(m1−m2m1+m2)(g+a0)
- T=[2m1m2m1+m2](g+a0)
6.WEIGHING MACHINE:
A weighing machine does not measure the weight but measures the force exerted by an object on its upper surface
EXAMPLE 48
A man of mass 60 Kg is standing on a weighing machine placed on ground. Calculate the reading of machine (g=10ms2).

For calculating the reading of weighing machine, we draw F.B.D. of man and machine separately.
F.B.D. of man F.B.D. of weighing machine
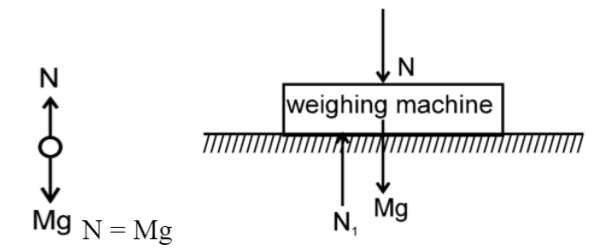
Here force exerted by object on upper surface is N
Reading of weighing machine
- N=Mg=60×10
N=600N.
EXAMPLE 49
A man of mass 60 kg is standing on a weighing machine (2) of mass 5kg placed on ground. Another same weighing machine is placed over man’s head. A block of mass 50kg is put on the weighing machine (1). Calculate the readings of weighing machines (1) and (2) .

500 N, 1150 N.