NEWTON'S LAWS OF MOTION for Class 11 PHYSICS
INTRODUCTION
Hello bachho! Ab hum ek aise zone me enter karenge jisme hum apne aap se question karenge ki why some things behave the way they behave! Kyu ager mera pair fisla to mai neeche hi gira, kyu astronauts ko itni strict training ki zarurat hoti hai kisi bhi space mission ke liye, kyu kisi stone ko hum gulel (slingshot) me lapetkar door tak nishana maar sakte hai pr ek rock ko hum jitna bhi dam laga le, usko hum hila bhi nahi pate. Let’s address these types of questions.
Is chapter me hum Laws of Motion ko study krenge. Hume pata hai ki nature surrounding hai jaha hum rehte hai. Hume ye bhi pata hai ki Physics is the study of nature and natural phenomena. Ager aap nature ko bahut carefully observe kre to aap dekhenge ki kuchh objects rest pr hai aur kuchh motion me. Eg: Niche diye image me buildings rest pr hai aur vehicles move kr rahe hai.

Let's understand Mechanics..
Mechanics is the branch of physics that deals with the study of particles or bodies at rest or in motion. Hum basically objects at rest aur objects in motion ke bare me study krenge. Mechanics ko do branch me divide kiya gya hai. First branch ko statics kehte hai aur second branch ko dynamics kehte hai. Statics is the study of objects at rest. Dynamics is the study of objects in motion. Is chapter ka naam hai Laws of Motion isliye ye chapter dynamics branch ke ander aata hai.
Motion samjhne ke liye hum ek example lete hai. Image me aap dekhenge ek racing car hai jo motion me hai. Jab hum motion ke bare me baat krte hai, humare mind me do questions aata hai. First question: How does an object move? Second question: Why does an object move? In dono question ko answer krne ke liye pehle hum Dynamics ke bare me jante hai.

Dynamics do branch me divided hai. First branch: Kinematics which is the study of the relationship between displacement, velocity, acceleration and time of a given motion, without considering the forces that cause the motion. Isme hum motion ke parameters ko study krte hai bina cause of force ko consider kre. So, Kinematics first question ka answer deta hai, how does an object move. Second branch: Kinetics which is the study of relationship between motion of bodies and forces acting on them. Isme hum cause of motion (force) ko study karte hai. So, Kinetics second question ka answer deta hai, Why does an object move. Is chapter me hum Kinetics ki study karenge.
Humne abhi tak motion ka nature jaana. Humne ek variety of motion dekhe, jaise (i) motion with uniform velocity (ii) accelerated motion. Is chapter me humara main point of discussion “Force” hoga jo ki basic cause hota hai, jiski wajah se motion hota hai aur hum phir us motion ke nature ke baare me discuss karenge ki ye motion aisa hi kyu hoga.
3 basic laws jo ki describe karte hai ki kaise forces govern karte hai unke dwara diye gaye motion ko, un laws ko Sir Isaac Newton ne 1687 me diya tha. In laws ko Newton’s laws kahte hai jo based hai careful aur extensive observations pr. Is laws se aap accurately motion of various objects ko accurately describe kr pane me sakshum ho jayenge.
Is chapter ko achhe se samajhne ke liye hume vectors ki samajh honi chahiye. Ham is chapter me different arrangements ko padhenge, for eg. objects will move along ramps, walls, incline, floor and ceilings. Wo ek string ke madhyam se pulley se hang karenge. hum accelerating aur decelerating lifts ke baare me bhi discuss karenge. In sabhi cases ko samajhne ke liye bs ek key element chahiye: wo hai Newton’s second law. Is basic idea se hum kisi bhi arrangement me is law ko apply kr sakte hai aur motion ko predict kr sakte hai. In laws ko achche se samajhne ke liye hume bahut saare examples solve karne chahiye. So, let’s dive into Newtonian mechanics.
THE CONCEPT OF FORCE
Ek body kaise move krta hai? Ye body ke environment ke saath interaction se determine hota hai. In interactions ko force kehte hai. Force ka concept hume do bodies ke beech ke interactions ka ya body aur environment ke bech ke interactions ka quantitative description deta hai. Jab hum kisi object ko push ya pull krte hai to uspr force exert krte hai. Jab hum ek ball ko throw ya kick krte hai, hum uspr force exert krte hai. In examples me force muscular activity aur object ke state of motion ke change se associated hai. Force hamesha kisi object ko move nahi krata, jaise, example, jab hum baithkr koi book padhte hai, body pr gravitational force act krta hai pr tab bhi hum move nahi krte hai. Hum ek heavy stone ko jab move krte hai to usse move nahi kr pate hai.
As our common experience tells us that to move an object at rest , someone must kick it. Jesa ke hamne abhi kuch daily experience ki bat ki thi..K kisi object pr aap dhakka(push) lagate hai to wo move krne lgti hai. Kisi chalti hui toy car ko rokne ke liye ek external pull ki zarurat hoti hai. Yahi push or pull responsible hota hai kisi object ko move ya stop ya direction badalne ke liye aur use hi ham Force kahte hai. So it's basically..An external force in the form of push or pull which;
1. Produce motion in body at rest
2. Stops a moving body
3. Change the direction of motion of body
CLASSIFICATION OF FORCES
Hamne ye to seekh lia ke kisi body ka state change krne ke liye ek external force ki need hoti hai. Pr kya apne kabhi ye socha hai ke bina touch kiye bhi koi force lgaya ja skta hai ? Ya fr hmesha force lgane ke liye bodies ka contact me hona jaruri hai? Answer hame is section me milega.Do bodies ke beech interactions pr based, force do type ke hote hai.
1. Contact Forces: Tension, normal rcaction, friction, etc. Forces that act between bodies in contact.
2. Field Forces (Non-Contact Forces): Weight, electrostatic forces, etc. Forces that act between bodies separated by a distance without any actual contact.
Hum in forces ke bare me study krenge. Hum each force aur kaise wo do bodies ke beech act krte hai unke bare me study krenge.
Jab hum ek spring ko pull krenge to spring stretch hoga jaisa ki aap niche diye figure me dekhenge. Jab reading lene ke liye spring ko mark krenge to jitna distance spring stretch hoga wo force ke strength ko measure krne me use kiya ja sakta hai. Ager koi bacha ek wagon pull krta hai to wagon move krta hai. Jab ek football kick hota hai to wo deform hot hai aur move bhi krta hai. Ye examples ek type ke forces ka result hai jisse contact force kehte hai. Ye forces do objects ke beech physical contact ke result ke karan hote hai.
Kuchh forces aise bhi hote hai jo do objects ke beech physical contact involve nahi krte hai. In forces ko field forces kehte hai. Gravitational force, electric force aur magnetic force field forces ke examples hai.

FRAME OF REFERENCE (FOR)
Place jaha se hum observations krte hai usse Frame of Reference kehte hai. Frame of reference do type ke hote hai:1. Inertial Frame of Reference: Frame ya observer jo stationary hota hai ya uniform velocity se move krta hai usse inertial frame of reference consider krte hai. Ye FOR ek stationary object ya ek aise object se juda hota hai jo ki ek constant velocity se move kar raha hai, aise frames me Newton ke laws directly applicable hote hai.
Example: Ek aadmi car me baitha hai so, uske liye car frame of reference hoga. Jab car rest pr hoga to inertial frame me hoga. Ek observer hai jo ground pr khada hai so, ground uske liye frame of reference hoga. Ground rest pr hai to observer inertial frame of reference me hoga. Jab car constant velocity se move krega to car inertial frame of reference me hoga.

Newton’s laws of motion inertial frame of reference me valid hote hai. Physics me generally, Earth ko inertial frame consider kiya jata hai aur earth ke rotational effects ko neglect kiya jata hai.
2. Non- Inertial Frame of Reference: Frame ya observer jo inertial frame ke respect me accelerate krta hai usse non- inertial frame of reference kehte hai. Ye FOR ek accelerated object se attached rahta hai. In frames me Newton ke laws directly applicable nahi hote. Yaha par ground of earth ek non-inertial frame of reference tha. Isiliye Newton’s laws yaha apply nahi ho paye.
Example: Suppose ek car move kr raha hai aur uska velocity constantly change ho raha hai matlab car accelerate kr raha hai. So, jo aadmi car me baitha hai uske liye car frame of reference hoga. Car accelerate kr raha hai so, wo non-inertial frame of reference me hoga.

Imagine kijiye ki aap ek station ke platform pr khade hai aur ek train us station ko cross karti hai. Ager aap sochenge to aapko lagega ki wo train aur usme sabhi passengers motion me hai. Lekin ager aap imagine kare ki aap usi train me hai aur apne saamne wale person ko dekhenge to dono hi rest me hai. Iska mtlb motion ho raha hai ya nahi ye observer pr depend karta hai. Wo observer jaha pr bhi hai apne perspective se hi describe kr raha hai ki motion kaisa ho raha hai. Isi observer ko frame of reference kahte hai. Ye frame of reference ground se attached rah sakta hai, ek particular velocity se move kar sakta hai, aur accelerated motion bhi kar sakta hai.
Hum frame of reference ko 2 parts me divide kar sakte hai.
Note: hum apni calculations ke liye ground ko ek inertial frame of reference hi consider karenge. Kyuki ager humne apne ground ko bhi non-inertial frame of reference maan liya to humari calculations kaafi lengthy ho jayengi.
Observations
Imagine kijiye ki ek ice strip earth ke North pole se South pole tak extend karti hai. Ab aap North pole se South pole ki taraf ek ice-hockey puck ko slide kara dijiye. Ab hum 2 frame of reference consider karte hai. Ek frame of reference space me stationary hai aur wo us puck ko ek rotating earth par dekh raha hai. Dusra frame of reference ek point on the ground par hai. Earth ka rotation West to East hota hai. ager hum pehle frame of reference ko consider karte hai jo ki space me stationary hai usko puck kuch aisa jata hua dikhega.

Ager hum durse frame of reference se dekhe jo ki ground par hi ek point par hai to usko puck ka path kuch aisa prateet hoga.

Aisa use isiliye lagega kyuki wo ek rotating frame par hai aur puck ke neeche wali strip ki speed increase hoti rahegi jab tak wo North pole se equator par jayega. (Iske baare me hum vistaar se samjehnge jab hum circular motion discuss karenge). ager hum Newton ke second law ko consider karte hai to ek force laga hoga is puck ko ye westward motion dene ke liye. Lekin aisa koi force hai hi nahi. To hum sochenge ki Newton's law yaha pr fail ho gya. Lekin aisa nahi hai. Newton ke law apply karne ke liye hume apna frame of reference badalna padega ya ek pseudo force lagana padega. Pseudo force par charcha hum aane wale sections me detail me karenge.
Fun fact:
Imagine kijiye aap ek garden me khade hai aur aapke saamne ek Mango tree hai. Ab aap apni aur mango tree ki state ko define kijiye. Aap sochenge ki aap aur mango tree dono hi state of rest me hai. Lekin kya aap jante hai, ki right now, earth apne axis ke about rotate kar rahi hai with a speed of 460 m/s. Earth revolve kar rahi hai apne axis ke about with a speed of 30 km/s. Earth jis solar system ka part hai wo orbit karta hai galactic centre ke with a speed of about 220 km/s. ager hum isme humare galaxy ka motion bhi consider karte hai jo jis universe me hai wo expand at a rate of the speed of light jo ki hai approx. 300,000 km/s. To ab aap samajh sakte hai ki hum kaafi fast move kar rahe hai. However, for all our purposes in understanding laws of motion to do the basic calculations, hum earth ko stationary maan sakte hai. Isse humari calculations me minute sa difference aayege jisko hum neglect kar sakte hai.Proof of the above statement:
Maan lo ki aap kahi aesi state me khade ho jaha se equatorial line pass karti ho, jaise ki Rajasthan. Ye point maan lijiye ki P(red) se show kiya gya hai figure me. ager aap earth ke rotation ko consider karte ho point P par lagne wala centripetal acceleration ki calculations aisi hogi.

Radius of earth, R=6378km
Earth’s period of rotation, T=23.93hr
=23.93×3600s
86164.1s
We know that angular velocity, ω=2πT
and Centripetal acceleration, ac=Rω2
∴ac=R(2πT)2
=6378×103(2π86164.1)2
=0.03m/s2
This is about 300 times smaller than the gravitational acceleration that you experience on the daily basis.
Ab hum ager rotation ke additional factor ko consider kare jisme earth revolve karti hai sun ke around to iska acceleration bas 0.035 % of earth’s gravitational acceleration hi aayega.
Isiliye inspite of these accelerations, humari saari calculations ke liye hum earth ko ek inertial frame hi manenge.
Force aur acceleration ke beech ke relation ke baare me sabse pehle Isaac Newton (1642-1727) ne jaana. Unhone ise study kiya aur present kiya apni book me “Principia Mathematica” me, jinhone classical mechanics ki neev rakhi.
Pehle hum discuss karte hai ki ye laws kaha apply nahi hote:
Ager interacting objects ki speed ek appreciable fraction of speed of light hai, matlab ager hum compare kar sakte hai us speed ko speed of light se, then we have to replace Newtonian mechanics with Einstein’s special theory of relativity. Einstein’s special theory of relativity kisi bhi speed par apply kar sakte hai, including those near the speed of light (c= 299 792 458 m / s).
Ager interacting bodies ka size ek atomic structure ke size se comparable hai, then the Newtonian mechanics is replaced with quantum mechanics. Newtonian mechanics quantum mechanics aur Einstein’s special theory of relativity ka ek special case hota hai.
Newtonian mechanics ke application ka range hota hai, from: motion of objects ranging in size from the very small (almost on the scale of atomic structure) to astronomical (galaxies and clusters of galaxies).
Before Newton mechanics came into prominence, aisa socha jata tha ki ek “force” ki requirement hoti hai kisi bhi body ko ek constant velocity se move karne ke liye. Ek “natural state” wo hoti hai jisme body rest me hoti hai. Ek tarah ka push ya pull ka requirement hota tha body ko ek constant velocity se move karwane ke liye. Ager ye push/pull hum body se hata de to wo body ruk jayegi.
ARISTOTLE'S FALLACY
Kya aap jante hai Inertia kya hai? Aristotle, ek Greek philosopher ne kaha tha ki kisi body ko uniform motion me rakhne ke liye ek external force lagta hai. Isse statement ko hum ek example se samjhenge. Suppose ek car motion me hai. Car ko move krne ke liye engine start krna hota hai phir accelerator press krna hota hai. Jab hum accelerator press krte hai to car move krna start kr deta hai aur ek speed attain krta hai. Phir hum accelerator release kar dete hai aur car slow down hone lagta hai. So, car ko motion me rakhne ke liye hume constantly external force apply krna, tab car uniform motion me rahega aur speed maintain krega.
Phir Galileo ne kaha ki ye assume karna galat hoga ki kisi body ko uniform motion me rakhne ke liye ek net force lagta hai. Jab hum accelerator release krte hai to car slow down hone lagta hai. Galileo ne kaha ki car ko uniform motion me rakhne ke liye hume constantly external force apply krne ki jarurat nahi hai. Car slow down hota hai kyuki car ke tyres aur road ke bich friction hota hai jo car ke motion ko oppose krta hai. Ager friction nahi hota to ek baar hum force apply karte aur agar ham accelerator release karte to car constantly uniform motion me rehta. Hum friction ke bare me is chapter me aage padenge.
NEWTON’S FIRST LAW/ LAW OF INERTIA
Galileo’s First Experiment
Aristotle had a belief ki kisi bhi body ko lagataar move karne ke liye ek force ki requirement hoti hai. Agar hamne force lagana band kar diya to wo object finally stop ho jayega. Isi theory ko aage le jate huye wo is conclusion par aaye ki object ki natural state rest hoti hai aur kisi bhi body ko constant velocity se move karne ke liye hame force ki requirement hoti hai. Thus, constant force = constant velocityGalileo aesa nahi maante the. Unhone a series of experiments kiye. Neeche hamne unke 2 experiments ko explain kiya.
Unhone imagine kiya ki ek aesi duniya ko jisme friction nahi hai. Ye dono ek “thought experiment” hai aur isme hamne friction force ko consider nahi kiya hai.
First experiment ke first case (fig (a))imagine kijiye ki ek object ek slope se roll down kar raha hai. Uski speed isiliye increase ho rahi hai kyuki uspar earth ka gravitational pull lag raha hai.
Fig (b) me ham dekh sakte hai ki object slope par oopar ki taraf roll kar raha hai. Uski velocity ka kam hone ka sirf yahi reason hai ki uspar earth ka gravitational pull neeche ki taraf lag raha hai.
Fig (c) me ham dekh sakte hai ki object horizontal surface par hi roll kar raha hai. Ab us object ki speed na hi kam ho rahi hai aur na hi increase ho rahi hai. Bina kisi acceleration ke ye object ek constant velocity ke saath hi hamesha chalta rahega.

Galileo’s Second Experiment: Double Inclined Experiment
Let’s imagine (fig (a)) ki hamne object ko height h se first inclined plane pr roll kiya. Ye inclined plane smooth hai aur ball dusre side pr same height pr pahunch gya.Fig. (b) me inclined plane ke dusre side ka slope kam tha. Jab ball ko roll kiya to ball longer distance travel krta hai.
Fig (c) me ham dekh sakte hai ki agar friction zero ho to ball infinite distance travel krta hai aur kabhi nahi rukta. Finally, jab ball ke pas koi slope nahi tha, jaise ki aap last image me dekhenge, wo aage hamesha constant velocity me move karta rahega level surface ke along. Galileo ne kaha ki ye object ka natural motion hai.
Conclusion: A body at rest will remain at rest, a body in uniform motion will continue to remain in uniform motion. Phir unhone Inertia ka concept introduce kiya.

The tendency of a body to keep moving (once it is set in motion) or to remain at rest if initially it was at rest results from a property called inertia.
Salient points about inertia:
- Inertia is an inherent property of a material. It is not a physical quantity. Mass of a body is the quantity of matter in an object. Mass of a body is the measure of it’s inertia. Ager kisi body ka mass jyada hai, to usme jyada inertia hoga.

Different types of inertia:
Inertia of rest: The tendency of a body to remain in its position of rest is called inertia of rest.
Examples:
1. Jab hum kisi hanging carpet ko ek stick se beat karte hai, dust particles separate ho jate hai. Aisa isiliye hota hai kyuki carpet ko beat karne pr carpet motion me aa jata hai pr dust particles rest me hi rahte hai. Dust particles phir gravity ki karan gir jate hai.
2. Imagine an arrangement like this. Coin has inertia of rest, means it really want to be in one place. Ager hum uske neeche rakhe hoop ko jaldi se hata de to wo coin bottle me ja girega.

Inertia of motion: The inability of a body to change by itself its state of uniform motion along a straight line.
For example:
Astronauts in space find it more difficult to stop moving because of a lack of gravity acting against them and they keep moving with a constant velocity. Agar space me astronaut ne ek velocity kisi particular direction me gain kar li, to use rokne ke liye uske opposite direction me velocity deni padegi, otherwise wo us direction me hi move karta rahega.

Inertia of direction: The inability of a body to change by itself its direction of motion is called inertia of direction.
For example:
Jab hum ek vehicle ko turn karte hai, to uski tendency rahti hai ki wo us turn ko resist kare- wo vehicle try karega ki wo usi direction me move kare jis direction me wo move kar raha tha. Ise hi inertia of direction kahte hai.

Isi inertia of direction ko counter karne ke liye, tyres ki tread me projections, grooves and sipes provide ki jati hai taaki wo road ko acche se grip kr sake.

Before Newton mechanics came into prominence, aisa socha jata tha ki ek “force” ki requirement hoti hai kisi bhi body ko ek constant velocity se move karne ke liye. Ek “natural state” wo hoti hai jisme body rest me hoti hai. Ek tarah ka push ya pull ka requirement hota tha body ko ek constant velocity se move karwane ke liye. Ager ye push/pull hum body se hata de to wo body ruk jayegi.
Ye ek common observation se bhi hum conclude kr sakte hai. Ager hum ek wooden block ko ek constant velocity dekar force hata de, to wo block kuchh door jakar ruk jata hai. Therefore, it can be assumed that a force should be applied at all times so that the block would not stop and move with a constant velocity. Aristotle argued that a body would move only when subjected to a force, otherwise in the absence of these forces, it would come to rest.
Ab hum ise aise sochte hai ki ager ham us block ko ek slippery surface pr push karke force hata de to wo jyada door tak jayega. Ager hum ground surface ko aur bhi jyada slippery bana de to wo aur bhi jyada doori cover karega. Galileo ne yahi experiments ke dwara Aristotelian approach ko refute kiya. From these observations, hum ye conclude kr sakte hai ki body will keep moving with constant velocity if no force acts on it.
Newton ne Galileo ki hi approach ko aage refine karke apna first law interpret kiya. Is law ko law of inertia bhi kahte hai.
If no force acts on a body, the body’s velocity cannot change; that is, the body cannot accelerate.
“When no net force act on a body the body either remains at rest or moves with constant velocity. Once a body has been set in motion, no net force is needed to keep it moving.”
Isi law ko ager hum vector form me likhe, to hum kah sakte hai ki: “When the vector sum of all the forces acting on a body is zero, or there are no forces acting on a body, it is said to be in equilibrium. That is, if
∑F=0 (Body in equilibrium)
Or
∑Fx=0,∑Fy=0,and∑Fz=0, the body is in equilibrium. Here, equilibrium means the acceleration of the body is zero.
Example:
Hum seat belts kyu pehente hai? Seat belts hume kisi injury se protect krte hai jab car ka accident hota hai. Jab koi car 60 mph pr travel krti hai to driver bhi 60 mph pr travel krta hai. Jab car suddenly ruk jata hai to usko slow down krne ke liye uspr ek external force lgta hai lekin driver pr koi external force nahi lgta so, driver 60 mph pr hi travel kr raha hota hai. Seat belt driver pr ek external force ki tarah kaam krti hai aur usse harm hone se bachati hai.

OMR (One Minute Revision)
- * The first law states that a body at rest will stay at rest until a net external force acts upon it and that a body in motion will remain in motion at a constant velocity until acted on by a net external force.
* Inertia is the tendency of a body in motion to remain in motion. Inertia is dependent on mass, which is why it is harder to change the direction of a heavy body in motion than it is to change the direction of a lighter object in motion.
* The second law explains the relationship between force and motion, as opposed to velocity and motion. It uses the concept of linear momentum to do this.
*The second law states that the net force is equal to the derivative, or rate of change of its linear momentum.
* By simplifying this relationship and remembering that acceleration is the rate of change of velocity, we can see that the second law of motion is where the relationship between force and acceleration comes from.
POINT 1
Inertia: The property of a body that resists any change to its uniform motion; equivalent to its mass.
Friction: A force that resists the relative motion or tendency to such motion of two bodies in contact.
Acceleration: The amount by which a speed or velocity increases (and so a scalar quantity or a vector quantity).
NEWTON’S SECOND LAW
Newton ke second law ko samajhne ke liye pehle let’s understand what “force” is.
Force: Force ek tarah ka interaction hai, jise ager oppose na kiya jaye, to wo object ka motion change kar deta hai. A force can cause an object with mass to change its velocity, i.e to accelerate. Ye ek push ya pull hota hai. Force ka direction aur magnitude dono hota hai, isiliye ise ek vector quantity kahte hai. Iski SI unit newton (N) hoti hai. 
Force jis point pr lagta hai use point of action kahte hai.
The line through the point of application of force and drawn in the direction of force is line of action.
Force ek vector quantity hai iska matlab hai ki ager 2 ya 2 se jyada forces ek body pr act ho rahe hai to hum net force vector addition se nikalenge.
Ager kisi body par net external force act hota hai to wo body accelerate hoti hai. Is acceleration ka direction net force ki direction me hi hota hai. Ye force us body ke mass aur us body ke acceleration ke product ke equal hota hai. That is,
∑F=ma
In xyz coordinate system,
∑Fx=max, ∑Fy=may, ∑Fz=maz
Unit: The SI unit of net force is newton (N), 1 N = 1 kg-m / s.
EXAMPLE 1
A constant force acting on a body of mass 3kg changes its speed from 2ms−1 to 3.5ms−1 in 25 s. The direction of motion of the body remains unchanged. Calculate magnitude and direction of the force.
m = 3.0 kg , u = 2.0 ms−1 v = 3.5 ms−1 , t = 25 g
As F = ma
or F = m(v-u/t) [since a = v-u / t]
implies F = 3.0(3.5 - 2.0) / 25 = 0.18 N .
The force is along the direciton of motion.
EXAMPLE 2
A ball is travelling with uniform translatory motion. This means that it is at rest. The path can be straight line or circular and the ball travels with uniform speed. All parts of the ball have the same velocity (magnitude and direction ) and the velocity is constant. The centre of the ball moves with constant velocity and the ball spins about its centre uniformly
In a uniform translatory motion , all parts of the ball have the same velocity in magnitude and direction and this velocity is constant
The situation is shown in adjacent diagram where a body A is in uniform translatory motion.
EXAMPLE 3
A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N Give the magnitude and direction of the acceleration of the body.
Here m = 5 kg
F1 = 8N and F2 = 6 N
The resultant force on the body
F = √F21+F22 = √82+62 N
⇒ F = √64+36 N = 10 N
The acceleration , a = F / m
⇒ a = 10 / 5 = 2 ms−2 in the same direction as the resultant force.
The direction of acceleration ,
tanβ = 6/8 = 3/4 = 0.75
or, β = tan−1(0.75)
= 37∘ with 8 N force.
NEWTON’S THIRD LAW
Statement: For every action, there is an equal and opposite reaction.
Agar ek body A kisi doosri body B par F force lagati hai to body B bhi A body par equal and opposite -F force lagayegi. Ye dono force F and -F ko ham ‘action-reaction pair’ kahte hai. Dono force me se ham kisi ko bhi action ya reaction force consider kar sakte hai.
Fig me ham dekh sakte hai ki body A body B par →FA force apply kar rahi hai and body B body A par equal and opposite force →FB apply kar rahi hai. Ye dono force hi action-reaction pair hote hai. Ek common question hota hai ki agar ye dono forces equal and opposite hote hai to inka effect cancel out kyu nahi hota hai. Iska answer hai ki ye dono hi forces alag alag body par apply karte hai isiliye ye cancel out nahi hote hai.

Examples:
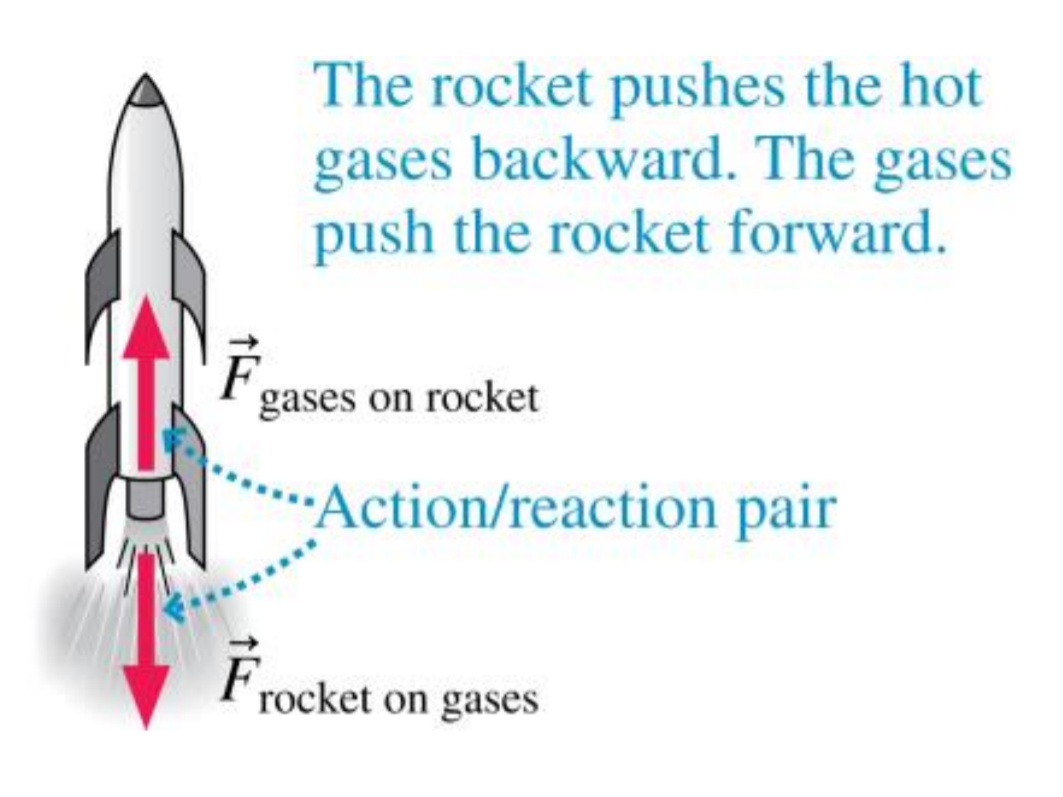
1. Rocket launch: Rocket apna fuel burn karta hai aur burnt fuel niche push hota hai, ye action hoga. Phir rocket automatically upward direction me push hota hai, ye reaction hoga. So, har action ka equal and opposite reaction hota hai.
2. Ek book hai jo table ke across push ho raha hai. Is figure me ham dekh sakte hai ki forces kaise pairs me act hote hai. Book thrust ke karan push ho raha hai jo friction ka opposite reaction hai. Book ka weight downward act krta hai so table bhi equal aur upward force exert krega nahi to table gir jaega. Figure me ham dekh sakte hai ki equal and opposite force book par act ho raha hai jisse wo equilibrium me hai.

3. Jab hum ek air se filled balloon ko release krte hai to equal aur opposite reaction hota hai. Air balloon se nikal jata hai lekin balloon opposite direction me move krta hai.

4. Jab car road pr move krta hai to tyres aur road ke bich equal and opposite force hota hai.

5. Firing a large gun on a skateboard: Ager hum skateboard pr khade hokar ek gun se fire karenge to hum Newton’s third law demonstrate krenge.
Jaise hi bullet aage fire hoga, equal aur opposite force gun par lagega (ise recoiling of gun bhi kahte hai) aur man skateboard ke piche move krega.

6. A cannon firing: Cannon cannonball pr force exert krta hai. Jab bhi koi object force apply krta hai second object pr to second object first object pr equal aur opposite force exert krta hai. So, cannon pr equal aur opposite force hoga lekin uske larger mass aur ground me braced hone ke karan wo jyada piche nahi kick hoga.

OMR (One Minute Revision)
- * Newton’s three laws of physics are the basis for mechanics.
* Newton’s three laws of motion explain the relationship between forces acting on an object and the motion they experience due to these forces. These laws act as the basis for mechanics.
* If an object A exerts a force on object B, object B exerts an equal and opposite force on object A.
* Newton’s third law can be seen in many everyday circumstances. When you walk, the force you use to push off the ground backwards makes you move forward.
IMPULSE
Impulse ek bahut high force hai, jo kisi body pr bahut short time ke liye act krta hai aur uske velocity me change lata hai.
It is defined as the rate of change of momentum of a body during the time of the application of the force.
Denoted by J. Impulse vector quantity hai.
Impulse (J) = (Force)×(time)
→j=→F×t
Impulse ka direction force ke direction me hota hai.
S.I Unit: Ns
Dimensions: M1L1T−1
Impulse Mechanics ka hi small topic hain. Yeh closely related hain Momentum and Force se. Hum is topic me Impulse ka force aur momentum ke sath kya relation hai yeh bhi dekhenge. Impulse ka direct relation motion of the object se hai. Apne daily life mein impulse different situations mein observe kar sakte hai.
For example:
1) jab koi bike kisi wall se takraye(hit)
2) Jab bat se ball ko hit karte hai etc. In short jab bhi kabhi kisi object ke takrane (collision) ki baat hoti hai waha Impulse present hota hai.

Eg: Impulse ke definition se hum yeh kah sakte hai ki jab koi force bahut jor se bahut km time ke liye act krta hai to usse body pr jo effect hota hai usse hi Impulse kah sakte hai.
Figure me ek car ek wall ki tarf some speed se aage ja raha hai. Jaise hi car wall ko hit karta hai to car aur wall dono ek dusre par action reaction force bahot hi small time interval ke liye.
Note:-
1) Jis point aur time par car aur wall collide karte hai ussi point & time me Impulse ka generation hota hai.
2) Iska matlab yeh hai ki bina physical contact ke impulse ka generation nahi ho sakta hai. Aap sabhi kabhi na kabhi cricket khele ho hoge. Cricket me bhi hum kai places par hum anjane me hi impulse ka use karte hai. For example: When we hit the ball with the bat and also when we catch the ball. Ab ye hota kaise hai usko hum diagram se samjhane ki koshish karte hai.
Some Examples of Impulse:
Force Exerted by Liquid Jet on Wall
Liquid Jet Striking a Vertical Wall Normally
Consider krte hai ek liquid jet jiska area A hai aur vertical wall pr velocity v se strike krta hai. Jab liquid wall pr strike krta hai to wall se paralel move krta hai. 
Consider krte hai liquid ka ek small element jiska mass Δm hai.
The change in its momentum after strike is,
[ΔPx]jet=0−Δmv=−Δmv
[Δ→Px]jet+[Δ→Pwall]=0
Transfer of momentum to the wall [ΔPx]wall=Δmv
Ager Δt strike ka duration hai to wall pr jet se force exerted,
F=[ΔPx]wallΔt=ΔmvΔt=(ΔmΔt)v
Δm=ρΔV=(ρΔVΔt)v=ρ(ΔVΔt)v
ρ is the density of the liquid.
If the rate of flow of liquid is ΔVΔt=av,F=ρav2
Liquid Jet Striking the Wall at the Same Angle
Now consider the jet strikes the wall at an angle θ with the normal and rebounds with the same angle.
The transfer of momentum to the wall;
[ΔPx]wall=2Δmvcosθ
[ΔPy]wall=0
Ager Δt strike ka duration hai to wall pr jet se force exerted,
F=[ΔPy]wallΔt=2ΔmvcosθΔt=(ΔmΔt)2vcosθ
=ρ(ΔVΔt)2vcosθ
F=2ρv2cosθ
How to find direction of impulse
Jaisa ki hum ab yeh jaan gaye ki impulse ek vector quantity hai. To iska direction hamesa change in momentum ke direction me hota hai.
Eg. Δp=p2−p1
if p2>p1, then direction of Δp is in the direction of p2.
p2<p1 then direction of Δp is in the direction of p1.
So the direction of impulse will be the same as the direction of impulse.
LINEAR MOMENTUM
Linear momentum is the vector quantity and defined as the product of the mass of an object, m, and its velocity, v. Denoted as P. Momentum describe karta hai ki kisi bhi body me kitna motion contained hai.P=mv
Where,
m = mass and v = velocity
In vector form it is given as →p=m→v
Linear momentum ka direction velocity ke direction me hota hai.
S.I. Unit: kgms−1
Dimensions: M1L1T−1
Suppose do bodies hai jinka masses aur velocities unequal hai pr momentum same hai, then
→P1=→P2
m1→v1=m2→v2
m1m2=→v2→v1
So, m∝1v
Alternate form of Newton’s second law
Kisi bhi body par net force equal hota hai uske momentum ke rate of change ke. That is,
→Fnet=d→pdt
As →p=m→v
d(→p)dt=m(d→v)dt=m→a
As we have already studied, →Fnet=m→a⇒→Fnet=d→pdt Kya aapko pata hai cricket player ball catch krte time apna haath kyu piche krta hai?
Aisa wo isliye krta hai kyunki ek fast moving cricket ball ke pass large momentum hota hai. Jab baller haath piche krta hai to wo moving ball ko rest ki velocity zero karne ka time increase krta hai, aur is time me ball ka velocity bahut high se zero pr aa jata hai. So, ball ka acceleration reduced ho jata hai. Baller par catch krte time impact bhi km ho jata hai aur baller ka haath hurt nahi hota hai.
Ager ball suddenly stop hoga to bahut km time me uski high velocity zero ho jaegi. Thus, rate of change of momentum large hoga aur ball ko catch krne ke liye large force apply krna hota jisse baller ka haath hurt ho sakta hai.

EXAMPLE 4
A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12ms−1 . If the mass of the ball is 0.15 kg , determine the impulse imparted to the ball . (Assume linear motion of the ball).
Charge in momentum
= 0.15 xx 12 - (-0.15 xx 12)
= 3.6 Ns.
Impulse = 3.6 Ns,
in the direction from the batsman to the bowler.
This is an example where the force on the ball by the batsman and the time of constant of the ball and the bat are difficult to know, but the impulse is readily calculated.
EXAMPLE 5
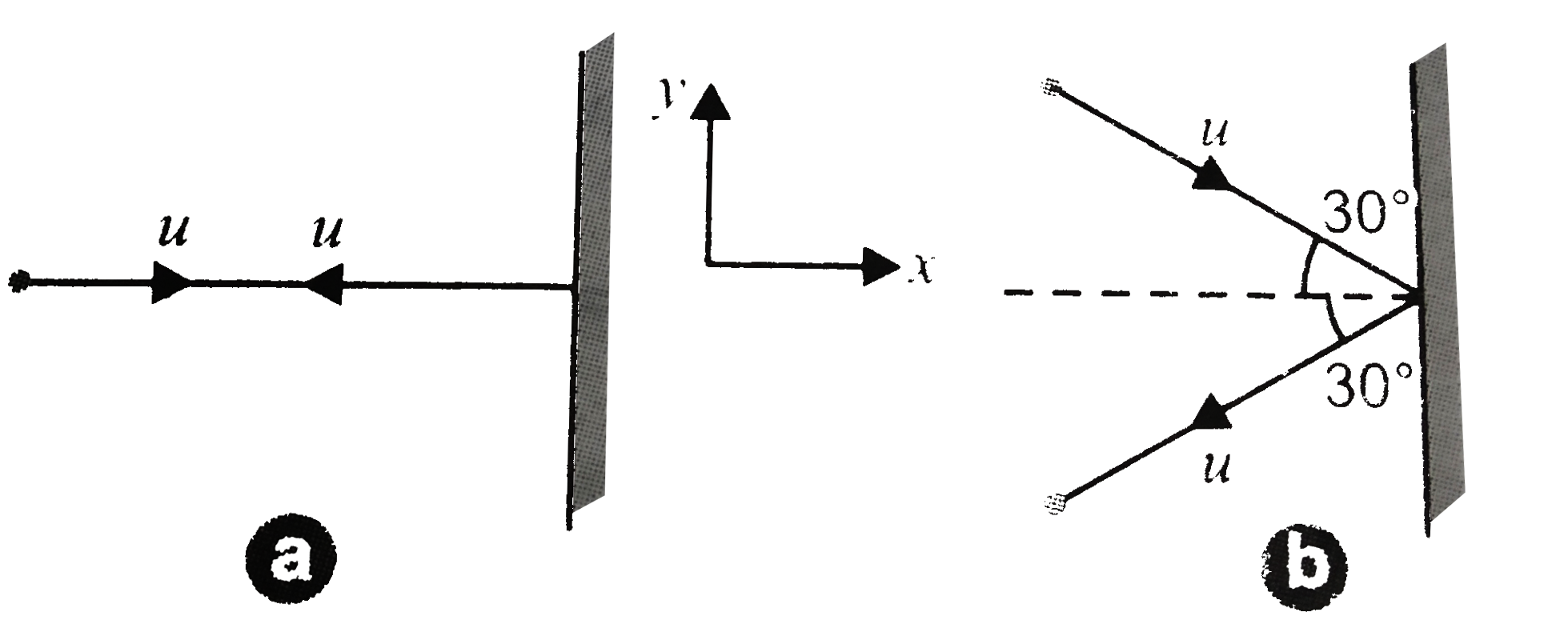
Two identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
An instinctive answer to (i) might be that the force on the wall in case (a) is normal to the wall, while that in case (b) is inclined at 30∘ to the normal. This answer is wrong. The force on the wall is normal to the wall in both cases .
How to find the force on the wall ? The trick is to consider the force (or impulse) on the ball due to the wall using the second law , and then use the third law to answer (i) . Let u be the speed of each ball before and after collision with the wall, and m the mass of each ball . Choose the x and y axes as shown in the figure, and consider the change in momentum of the ball in each case :
Case (a)
(px)initial = mu (py)initial = 0
(px)final = -mu (py)final = 0
Impulse is the change in momentum vector.
Therefore,
x-component of impulse = -2 mu
y-component of impulse = o
Impulse and force are in the same direction. Clearly, fro above , the force on the ball due to the wall is normal to the wall , along the negative x-direction. Using Newton's third law of motion, the force on the wall due to the ball is normal to the wall along the positive x-direction .The magnitude of force cannot be ascertained since the small time taken for the collision has not been specified in the problem.
Case (b)
(px)initial = mucos30∘ , (py)initial = -μsin30∘
(px)final = −μcos30∘ , (py)final = −μsin30∘
Note, while px, changes sign after collision , py does not. Therefore,
x-component of impulse = −2mucos30∘
y-component of impulse = 0
The direction of impulse (and force ) is the same as in (a) and is normal to the wall along the negative x direction . As before , using Newton's third law, the force on the wall due to the ball is normal to the wall along the positive x direction .
The ratio of the magnitudes of the impulses imparted to the balls in (a) and (b) is
2 m u / (2 m u cos30∘ ) = 2 / √3 = 1.2
EXAMPLE 6
A rocket motor consumes one quintal of fuel per secound . The exhaust speed of gases w.r.t roket is 5km/s Calculate the force exerted on the rocket. What is the velocity acquired by the rocket , when its mass reduces to1/100th of its initial mass?
Here , dmdt=1quintal/sec=100kg/s,u=−5km/s=−5×103m/s
As F=−u(dmdt)∴F=−(−5×103)(100)=5×105N
Now υ=?,mm0=1100 or m0m=100
From υ=uloge(m0m)
υ=5×103loge100=(5×103)×2.303log10100=5×103×2.303×2
=2.303×104m/s.
EXAMPLE 7
Two billiard balls each of mass 0.05 kg moving in opposite directions with speed 6ms−1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other ?
Initial momentum of each ball before collision
= 0.05 ×6kgms−1 = 0.3kgms−1
Final momentum of each ball after collision = 0.05 ×6kgms−1 = −0.3kgms−1 Impulse imparted to each ball due to the other = final momentum - initial momentum = 0.3kgms−1- 0.3 kg ms^(-1)<br>=−0.6kg ms^(-1)=0.6kgms^(-1) ( in magnitude)
The two impulse are opposite in direction.
LAW OF CONSERVATION OF LINEAR MOMENTUM
Jab bomb explosion hota hai, bomb pieces har directions me scatter ho jate hai. Bomb ke parts ek particular way me hi scatter honge ye law of conservation of momentum govern karta hai. Let’s understand what this law is all about.
According to the conservation of linear momentum,
If the net external force acting on a system of bodies is zero, then the momentum of the system remains constant or conserved.
Fext=zero
System ka matlab hota hai objects ka collection jiske motion (kinematics ya dynamics) jisme hum interested hote hai. Ager hum ground pr ball ka bounce analyze krte hai to hum ball ke motion me interested hote hai, earth ke motion me nahi. So, ball system hoga. Vaise hi jab hum car crash analyze krenge to dono car system hoga.
Proof of Law of Conservation of linear momentum:
Suppose do spheres A aur B hai jinka mass mA aur mB hai. Sphere A ka velocity uA aur sphere B ka velocity uBhai aur uA uB se greater hai. Thode der baad dono spheres collide hoge. Collision ke baad sphere A ka velocity vA hoga aur sphere B ka velocity vB hoga. Yaha vB vA se greater hoga kyunki sphere A ne sphere B ko push kiya hai and in return uski velocity aur kam hogi kyuki use opposite direction me push B ke dwara mila hai.
Before Collision:

Hum consider krenge sphere A aur sphere B system hai.
Linear momentum, p=mv
Initial linear momentum of the system ⇒→PA=mA→uA+mB→uB....(i)
During collision:
Sphere B sphere A pr →FAB force exert krega. Ye force action force hoga. Sphere A sphere B pr →FBA force exert krega. Ye force reaction force hoga.
Then, according to Newton’s Third Law;
→FAB=−→FBA.....(ii)
After Collision:
Final linear momentum of the system ⇒→PB=mA→vA+mB→vB.....(iii)
As, F=ma and a=v−ut
In formulas ko hum equation (ii) me substitute karenge;
mA→vA−→uAt=mB→uB−→vBt
mA→vA−mA→uA=mB→uB−mB→vB
mA→uA+mB→uB=mA→vA+mB→vB
→PA=→PB
Law of conservation of linear momentum small (microscopic) aur large (macroscopic) dono bodies ke liye applicable hai. Ye system of large number of bodies jo ek dusre se kisi angle pr collide hote hai, unke liye bhi applicable hai.
Humne pehle question dekha tha ki jab bomb explode hota hai to uske pieces har directions me scatter kyu hote hai. Is question ko answer krne liye liye hum bomb ko system consider krte hai. Bomb ka explosion internal force ke karan hota hai. External force jo system pr act krta hai wo zero hoga. Then, law of conservation of linear momentum ke according system ka initial aur final momentum equal hona chahiye.
So, Linear momentum before explosion = Linear momentum after explosion


Explosion se pehle, bomb rest pr tha aur uska velocity zero tha to linear momentum before explosion zero hoga. So, linear momentum after explosion bhi zero hona chahiye.
Hame pata hai ki linear momentum vector quantity hai. So, jab bomb explode hota hai to uske Jab bomb ke pieces sare directions me scatter hoge to sare pieces ke linear momentum ek dusre ko cancel kr denge kyunki linear momentum vector quantity hai. Phir explosion ke baad bomb ka final momentum zero ho jaega.
Relation between Impulse and Linear Momentum:
J=(ma)×tJ=m(v−ut)×t
J=(mv)−(μ)
J=△P
mu is the initial linear momentum and mv is the final linear momentum.
The total change in the momentum of a body during a time interval is equal to the impulse of the force acting during the same interval of time. This is called the principle of impulse and momentum.
OMR (One Minute Revision)
- * Linear momentum (momentum for brevity) is defined as the product of a system’s mass multiplied by its velocity.
* In symbols, linear momentum p is defined to be p=mv, where m is the mass of the system and v is its velocity.
* The SI unit for momentum is kg−ms.
* Newton’s second law of motion in terms of momentum;
The net external force equals the change in momentum of a system divided by the time over which it changes.Fnet=ΔtΔp
POINT 2
Pseudo force: Pseudo force is a force that appears to act on a mass object whose motion is described and observed using a non-inertial frame of reference, such as an accelerating or rotating reference frame.
Uniform motion: Motion at a constant velocity (with zero acceleration). Note that an object in motion will not change its velocity unless an unbalanced force acts upon it.
Net force: The combination of all the forces that act on an object.
Momentum: (of a body in motion) the product of its mass and velocity.
EXAMPLE 8
Two identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
Let m be the mass of the mass of the ball and u be the speed of each ball , before and after collision with the wall. Choosing the x and y axes as shown in Fig .3 (a) . 21 we find
Case (a) (px)initial=μ,(Py)initial=0
(px)final=−mu,(py)final=0
As impulse is change in momentum vector
∴ x component of impulse =mu−mu
=−2μ
As impules and force are in the same direction, therefore , force on the ball due to the wall is along negative x - axis . Using Newton's 3rd law , force on the wall due to the ball is along positive x axis .
Case (b) : (px)initial=mucos30∘,
(py)initial=−musin30∘,
(px)final=−mucos30∘,
(px)final=−musin30∘,
∴ x component of impulse =−μcos30∘−mu
cos30∘=−2μcos30∘,y component of impulse = 0
The direction of force on the wall is same as in case (a) , ie , normal to the wall , along positive x direction the ratio of the magnitude of the impulses imparted to the balls in (a) and (b) is
−2m−2mucos30∘=1√3/2=2√3=1.2
EXAMPLE 9
An impulsive force of 100 N acts on a body for 1 s What is the change in its linear momentum ?
Change in linear momentum = Impulse =F×t=100×1=100Ns .
EXAMPLE 10
What is the principle of the working of a rocket ?
A rocket is based on the principle of conservtion of linear momentum .
EXAMPLE 11
A body is acted upon by a number of external forces . Can it remain at rest ?
Yes , provided vector sum of all the external force acting on the body is zero .
FREE BODY DIAGRAM (FBD)
Suppose ek object hai aur hame uspr act ho rahe forces ke bare me study krna hai to phehle hume forces ko represent krna hoga. Free diagram ka matlab hai kisi body pr act ho rahe sare forces ka diagrammatical ya pictorial representation.
Steps to be followed for FBD:
1. Jo bhi body ya system hame analyze krna hai usse identify krna hoga.2. Sare forces ko act ho rahe unhe vectors se represent krna hoga (with proper magnitude and direction).
3. Ager system me net acceleration present hai to uska direction represent krna hoga.
4. Unknown quantity ko find krne ke liye Newton’s second law apply krna hoga (with proper sign convention).
Newton’s 2nd law: ∑→F=m→anet
Ager force X-axis pr act kr raha hai to total force acting on X-axis: ∑→Fx=m→ax
Ager force Y-axis pr act kr raha hai to total force acting on Y-axis: ∑→Fy=m→ay
Newton’s 2nd law me hame forces ko vector algebra ke according add karna padta hai, kyuki force ek vector quantity hai. Sign convention: forces same direction me act ho rahe to unko add krenge aur ager opposite direction me act ho rahe hai to unko subtract karenge.
Nature me bahut sare forces present hote hai par ham sare forces draw nahi krte. Hume pata hona chahiye ki FBD me hame kaun kaun si forces ko draw karna hai. FBD ka matlab hota hai Free body diagram. Ham kisi bhi system par lagne wale saare forces ko ek diagram banakar show karte hai to ise free body diagram kahte hai. Let’s understand ki wo kaun se forces hai jo generally hame represent karne hai.
COMMON FORCES IN MECHANICS
WEIGHT
Hum sabka weight hota hai. Kya aapko pata hai weight ko kya cause krta hai? Earth ka gravitational force kisi body pr weight cause krta hai. Weight is the gravitational force with which the earth pulls an object.Weight = (mass of the body )× (acceleration due to gravity)
W = mg
Weight vector quantity hai so iska direction hota hai. Weight hamesha downwards towards the centre of earth act krta hai.
Suppose ek block hai jo ground pr rakha hai. Block system hai aur hame block pr act ho rahe forces ko represent krna hai. First force jo hame represent karna hai wo weight hai. Weight represent karne ke liye hum vertically downwards vector draw krenge and mg vector ka magnitude hoga aur ye vector weight represent krta hai. Jab bodies contact me nahi ho tab bhi weight act krta hai kyunki weight non-contact force hai. That simply means ki is force ko act karne ke liye contact ki zarurat nahi hoti hai.

Suppose ek block hai jo inclined plane pr rakha hai aur inclined plane ka angle θ hai. Block ko hum system consider krenge. Hume block par act ho rahe sare forces ko represent krna hai. First force jo hum represent krenge wo hai weight. Weight ko hum vector se represent krenge jo vertically downwards act hota hai aur vector ka magnitude mg hai. Hum weight (mg) ko resolve krenge. Figure me aap dekhenge mg ko hume mgcosθ aur mgsinθ me resolve kiya.

Ager block downward direction me accelerate krta hai to acceleration find krne ke liye Newton’s Second law apply krna hoga. Iske liye hame axes select krne honge. Hum inclined plane ke surface ko x-axis consider krenge aur jo iske perpendicular hai usko y-axis consider krenge.
Total force acting on X-axis: ∑Fx=max
X-axis pr mgsinθ act kr raha hai
Iska sign positive hoga kyunki jab force aur acceleration same direction me hote hai to dono positive hote hai.
So, Mgsinθ=Ma
a=gsinθ
Yaha pr koi friction act nahi ho raha hai.
Jab force acceleration ke direction ke opposite hota hai tab force negative aur acceleration positive rakh sakte hai or vice versa. It all depends on the sign convention.

THE NORMAL FORCE
Normal force is an electromagnetic force that comes into action whenever two bodies are in contact with each other. It is a pushing force in nature. It is always perpendicular to the surface in contact.Imagine kijiye ki ek aap ek chair pr baithe hai. Ab Newton’s second law ke according aap rest pr isiliye hai kyuki aap pr lagne wale sabhi forces ka resultant zero hai. Hum ye sabhi forces ko aapki body ka free body diagram banakar dekh sakte hai.


Aap chair pr rest position me baithe hai. Aap pr ek gravitational pull towards the center of earth lagta hai. Ye aapke weight ke equal hai. Lekin aap earth ki taraf accelerate nahi ho rahe iska kya reason ho sakta hai. Iska matlab chair aap pr utna hi force opposite direction me apply kr rahi hogi. Ab maan lijiye ki aap kuch books ko apne haatho me lekar baithe huye hai, aap tab bhi rest par hi hai. Iska matlab aap par chair ki wajah se lagne wala force bhi badh gya hai. To ye force ek self-adjusting force hai. Weight vertically downward act kar raha hai. Hum maan sakte hai ki ye hamare torso pr act kr raha hai (Actually centre of mass ki position gender aur limbs ki position par depend karta hai, pr hm apni calculations ke liye average position consider kr sakte hai). Hum ye aage chapters me janenge ki hum apne weight ko apne torso pr act hota hua kyu maan sakte hai. Asal me hum apni poori body jo ki ek distributed mass hai use aesa maan sakte hai ki ye saara mass ek point pr concentrated hai. Isi point ko hum center of mass kahte hai. Hum ye consider kr sakte hai ki isi center of mass pr body ke upar lagne wala gravitational force act kr raha hai.
TENSION FORCE
Tension force is the electrostatic force that arises due to interactions between charged particles in a string.Tension force hamesha string ke length ke along act krta hai aur pulling force hota hai. Suppose ek block hai jo string se tied hai aur hum block ko system consider krenge. Hume tension force represent krna hai. Tension force pulling force hai string ke length ke along act krta hai. So, tension force hum →T se represent krenge. Ye upward directed hoga along the length of the string.

Same figure me ager hum ceiling ko system consider krenge. String ceiling se tied hai, hume ceiling pr act ho rahe tension force represent krna hai. Tension force →T se represent krenge. Ye downward directed hoga along the length of the string.

Suppose ek block do strings se attached hai, to do tension force act hoga. T1 first tension force hoga aur T2 second tension force hoga.

Niche diye figure me aap dekhenge ek string se do blocks attached hai. M2 ko system consider krenge to tension T2 hoga jo M2 ko pull karta hai. Ager M1 ko system consider krenge to tension T1 aur T2 hoga jo M1 ko pull krne ka try krta hai. Hume sirf unhi forces ko represent krna hota hai jo system pr act hote hai.

Yaad rakhe:
SPRING FORCE
Jaise ki is force ka naam hai spring force, ye force springs me present hota hai. Hum spring block system consider karenge. Block spring se attached hoga aur mean position me hoga. Mean position ka matlab wo position jaha system pr act ho rahe total force zero hai. Is position ko equilibrium position bhi kehte hai.Jab hum block ko x distance pr right pull karenge to spring stretch hoga kyunki wo elastic hota hai. Phir jab hum block ko release karenge to block wapis apne mean position pr chala jaega. Spring stretch ho raha hai so usme ek force set-up hoga jisse spring force ya elastic force kehte hai. Ye force hamesha mean position ke towards directed hota hai.
Yaha spring force ya restoring force x ke directly proportional hai kyunki F aur x ka direction ek dusre ke opposite me hai.
So, F=−kx
k spring constant ya force constant hai.


Same block ko ager hum left move karenge x distance pr to spring compress hoga. Spring force mean position ke towards act krega.


Yaha spring force ya restoring force -x ke directly proportional hai kyunki F aur x ka direction ek dusre ke opposite me hai.
So, F=−kx
k spring constant ya force constant hai.
k=Fx
SI Unit of k: Nm−1
Dimensions of k: M1L0T−2
FORCE OF FRICTION
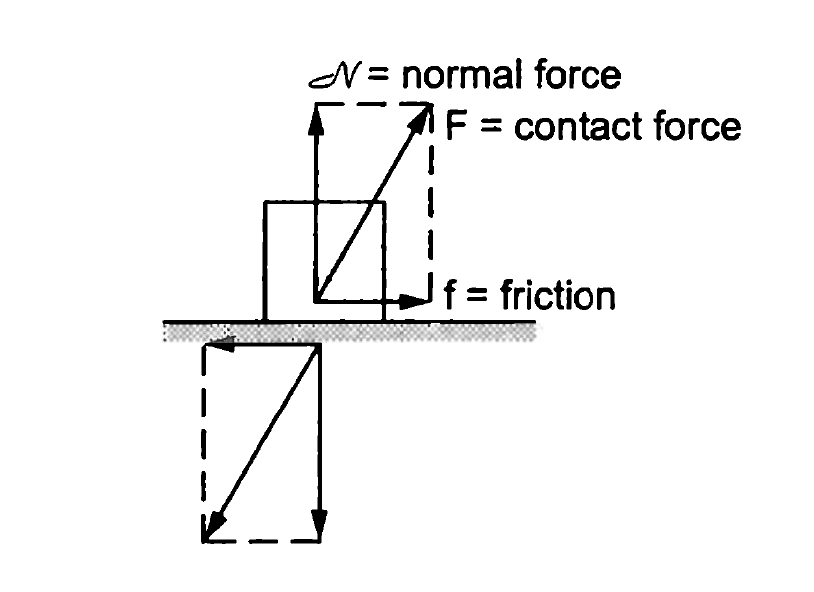
Jab koi force →F kisi body ko ek surface par slide karne ki koshish karta hai, tab ek frictional force us surface ke dwara us body par lagta hai. Ye frictional force parallel hota hai surface ke aur iski direction thodi tricky hoti hai. Iski direction us direction me hoti hai jis direction me wo motion ka oppose kare, ya aesa kah sakte hai ki ye relative motion ke opposite act karta hai. Ye friction force us body aur surface ki bonding ki wajah se lagta hai. Jab koi two bodies contact me hote hai to unke beech electromagnetic force act hota hai jo ki bodies ki surface pr charged particles ke present hone ki wajah se lagta hai. Isi wajah se dono bodies ek doosre par contact force apply karte hai jo ki according to Newton’s Third law equal aur opposite hota hai.
Isi contact force ko ham 2 components me resolve kar sakte hai, ek perpendicular to the contact surface ke aur doosra jo us surface ke parallel ho. Jo component perpendicular hai use hai normal contact force ya normal force kahte hai. Jo component contact surface ke parallel hai use ham friction kahte hai.
Frictional force ek unavoidable force hai. Friction force koi bhi interacting bodies ke beech act karta hai aur us motion ko cease karne ki koshish karta hai. Lagbhag 20% of petrol jo hamare automobiles me use hota hai wo isi friction force (jo ki engine aur drive train me lagta hai), ko khatam karne ke liye use ho jata hai. Ab sochiye aese kitne automobiles honge ek city me, state me aur poori country me jinme sirf friction ko kam karne ke liye fuel use ho jata hai. Isi friction force lagne ke kaaran components me wear and tear hota hai. Ek study ke according industrialized nation (ex: USA, UK) me about 7% of GNP (Gross National Product) isi friction aur wear ko kam karne ke liye use hota hai.
Friction is a necessary evil. Friction ki wajah se hi ham chal pate hai. Car me ek jagah se doosri jagah ja pate hai. Agar friction nahi hota aur hame ek jagah se doosri jagah jana hota to ham kaise ja pate. Hame baar baar apni attain ki huyi velocity ko change karne ke liye ek force ki zarurat hoti. Par wo force hame kaha se milta? Ham apne haatho me pencil nahi pakad pate aur na hi paper par kuch likh pate. Agar hamne kisi tarah pencil ko pakad bhi liya to wo paper par bas slide hi ho jati, kuch likh nahi pati. Hamari car ke tyres aur road ke beech jo friction lagta hai usi wajah se car aage ya peeche move karti hai. Engine to bas wheels ko rotate karta hai. Ye friction hi hai jiski wajah se ham aage ya peeche move kar pate hai. Ab zara sochiye ki agar friction hi present na ho to ham car ko move kaise karwa payenge. Nails aur screws bhi kuch work nahi kar payenge. Wo friction force hi to hai jinki wajah se ek hammered nail apni jagah par hai aur wo aasani se baahar nahi aati.
Friction kisi bhi pair of solids, solid aur fluid, aur pair of fluids ke beech act kar sakta hai. Fluids jo frictional force apply karte hai use ham viscous force(i) kahte hai jise ham aage ke chapters me detail me padhenge.
Experiments:
Kisi block ko kisi surface par push karke leave kar do. Kya hoga? Aapne sahi socha ki wo block kuch doori tay karke ruk jayega. Agar ham us block motion ke baare me soche to usko hamne kuch initial velocity di aur wo finally stop ho gaya. To iska matlab hai ki uspar opposite direction me kuch acceleration act kiya hoga. From Newton’s second law, uspar ek force surface ke parallel zaroor act kiya hoga jiski wajah se velocity kam hote hote zero ho gayi. Isi force ko friction force kahte hai.
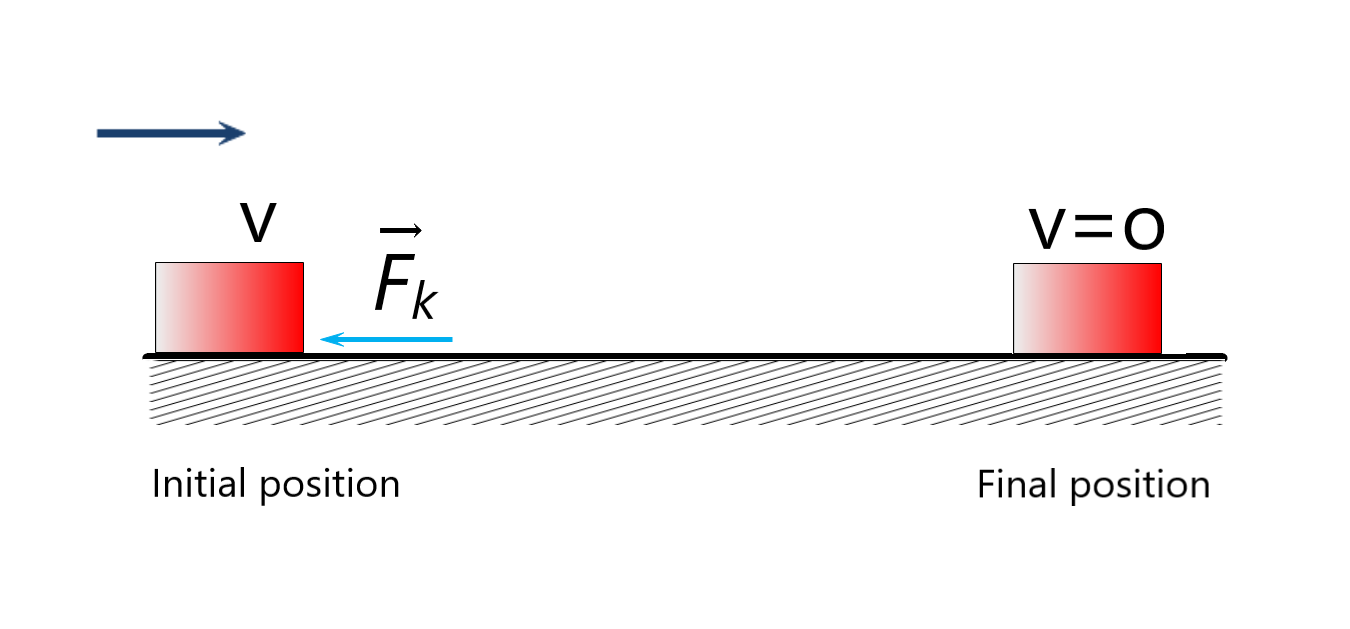
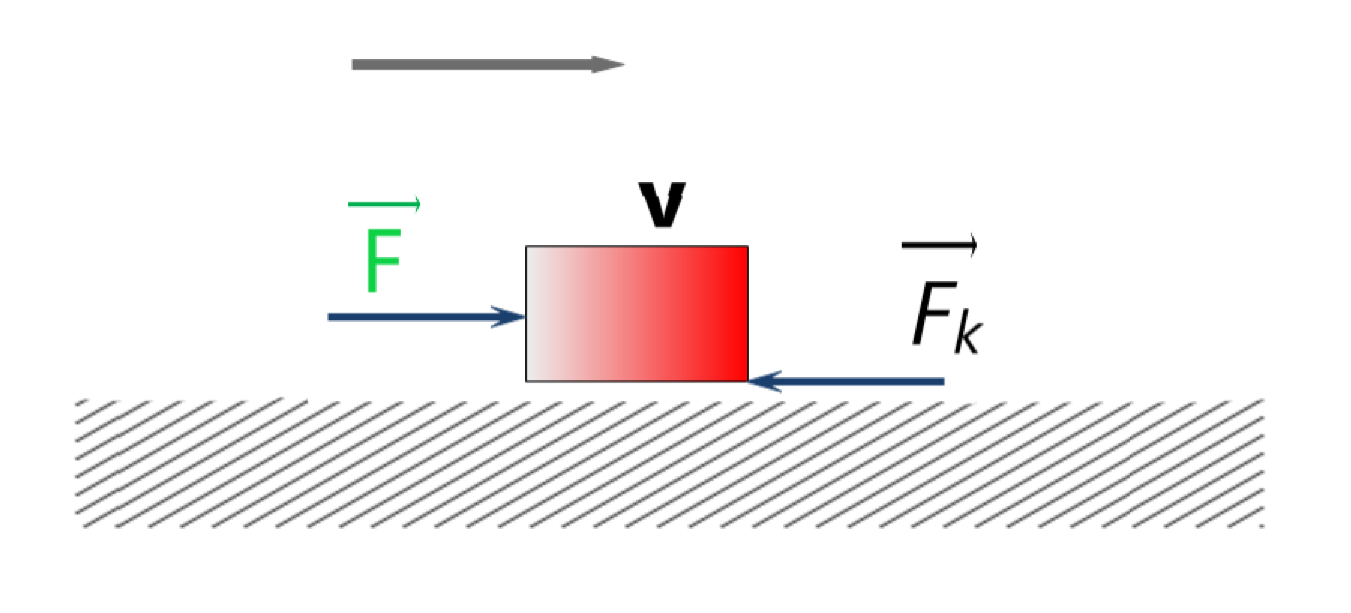
Ab isi block ko usi surface par ek constant velocity se move karane ki koshish karo. Ab aap wo frictional force ko feel kar paoge. Aap jitna bhi force apply kar rahe ho wo frictional force ke effect ko khatam karne ke liye use ho raha hai. Jab block move kar raha hai to uspar lagne wala frictional force kinetic friction force (Fk) hai.
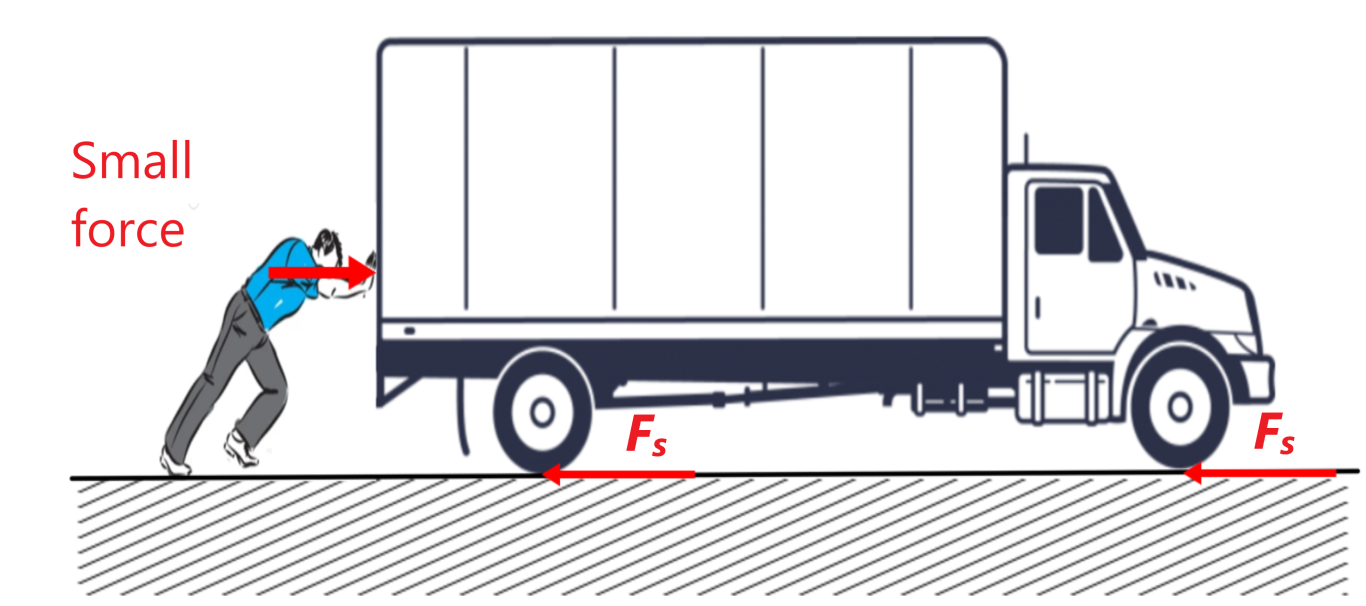
Kisi khade truck ko push karke dekho. Kya hoga? Wo apni jagah par hi rahega, zara bhi move nahi hoga. To Newton’s second law ke according us truck par ek equal and opposite force zaroor lag raha hoga kyuki truck rest pe hi hai. Ye friction force hi hai. Ab aap truck par aur bhi zyada force lagayiye. Kya hua? Truck ab bhi nahi move hua? Iska matlab ye friction force bhi increase ho gya. Utna hi increase hua jitna ki zarurat thi aapke force ke effect ko khatam karne ke liye. Iska matlab ye friction force ek self-adjusting force hai.
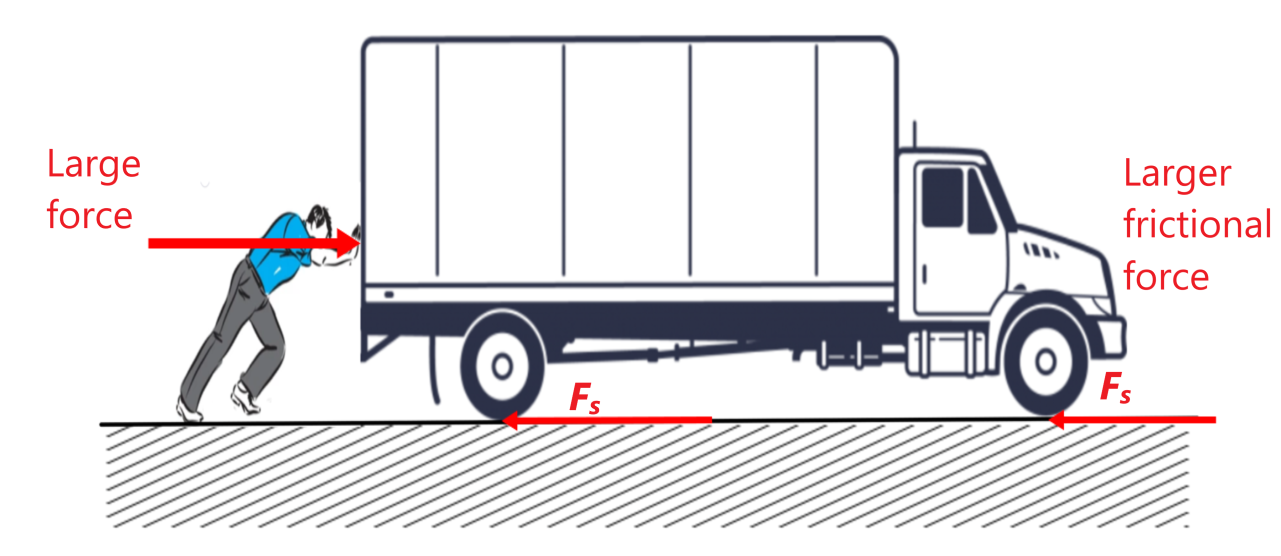
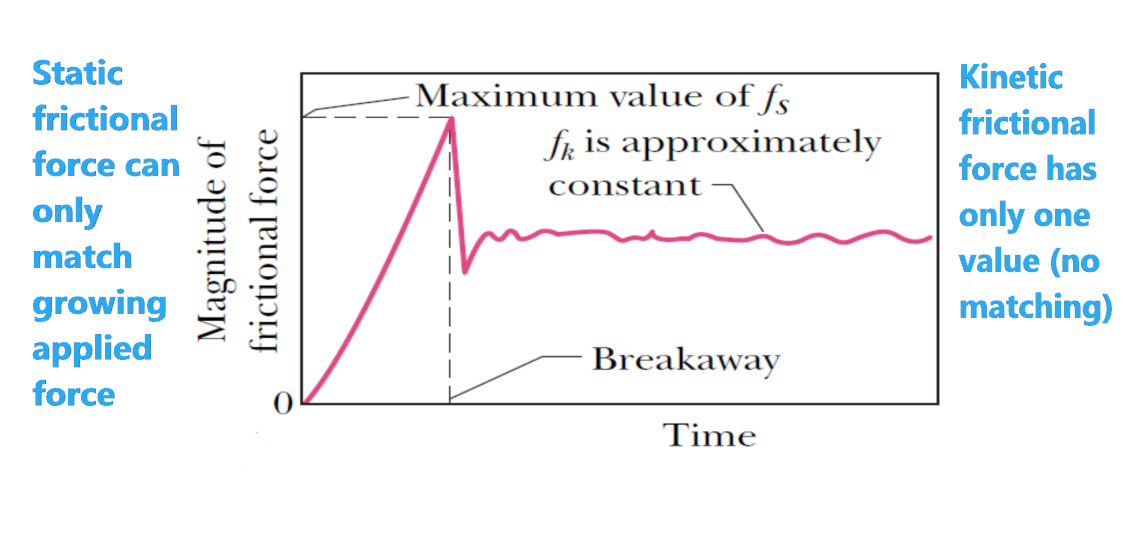
Ek heavy block ko push karne ki koshish karo. Uspar initially ek small push do. Wo nahi move karega. Ab dheere dheere is force ko badhao. Ek point aesa aayega jab ye block move karne lagega. Iska matlab friction force ki ek limit hoti hai. Ye ek particular value tak hi increase ho sakta hai. Ab aapka force is friction force se zyada hai tabhi aap block ko rest se move karwa paye. Ek aur baat. Ab jab aap is block ko move kar pa rahe hai to ab aapko feel hoga ki aapko kam force lagane ki zarurat pad rahi hai. Ye force, jo aapne initially lagaya tha car ko rest se move karne ke liye, us force se kam hai. Jab block rest me tha tab uspar surface dwara aur surface ke parallel jo frictional force lag raha tha wo static frictional force tha. Jab wo block move karne laga to ye force kinetic frictional force hoga. Generally, Kinetic frictional force < Static frictional force
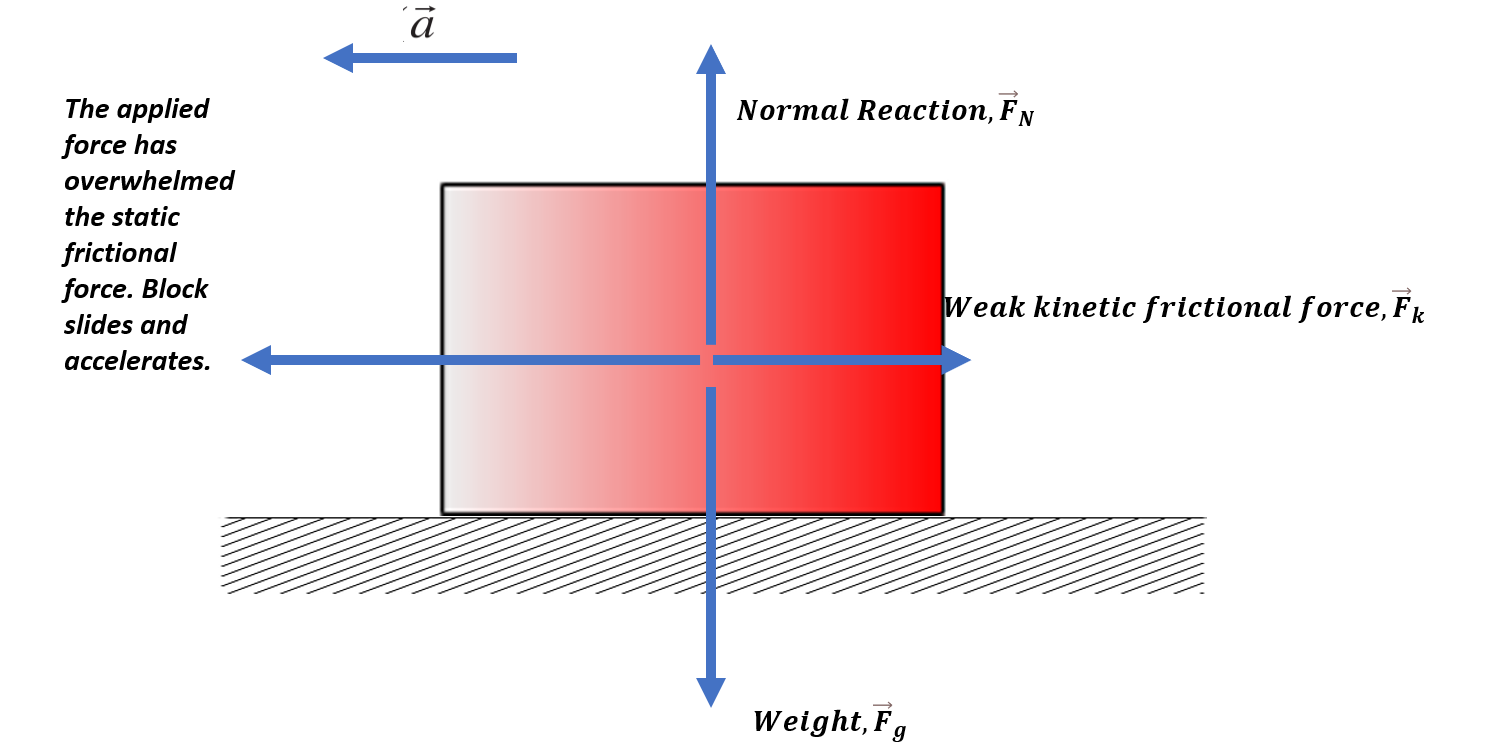
Ager body slide nahi ho rahi hai to is frictional force ko static frictional force fs kahte hai. Agar body slide kar rahi hai to isi frictional force ko kinetic frictional force fk kahte hai. Agar body par lagne wala force just about frictional force ke equal ho jaye aur body bas halka sa force aur lagane par move karne lage to isi frictional force ko limiting frictional force kahte hai fl. Let’s understand the nature of this friction force with the help of a graph.
Let’s consider ki ham ek block par force laga rahe hai. Aur dheere dheere is force ko increase karte hai. Is experiment me ham force tab tak increase karte hai jab tak breakaway nahi ho jata ( meaning block nahi hone lagta). Jaise hi block move karne lagta hai ham ek constant force apply karte hai. Aap graph me dekh sakte hai ki pahle ye force thoda zyada hai comparison me us force ke jo applied hai jab ye block move karne lagta hai.
PROPERTIES OF FRICTION
Agar ek body ek dry and unlubricated ground par rakhi hai aur uspar ham force →Flagaye, to jo frictional force us body par lag raha hai uski ye teen properties hoti hai:
Property 1: Agar wo body move nahi karti hai to uspar static frictional force →fs act karta hai. Ye force →F je equal and opposite direction me act karta hai. Ab agar ham →F ko increase karte hai to static frictional force →fs bhi increase karta hai.
Property 2: Magnitude of →fs ki maximum value hoti hai →fs,max, that is,
→fs,max=μs→FN, where μs is coefficient of static friction and →FN is magnitude of normal force of body from the surface. Agar →F ka surface ke parallel jo component hai wo exceed karta hai →fs,max se to body surface ke along slide hona shuru ho jayegi.
Property 3: Agar body ne slide karna start kar diya hai to frictional force ka magnitude rapidly decrease hone lagta hai aur ek approx. constant value ko attain kar leta hai. Then,
→fk=μk→FN, where μk is coefficient of kinetic friction. Isiliye, sliding ke dauraan →fk hi wo force hai jo relative motion ko oppose karta hai.

POINT 3
Linear momentum: Linear momentum is defined as the product of a system’s mass multiplied by its velocity.
Collision: Collision means two objects coming into contact with each other for a very short period.
EXAMPLE 12
Two bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
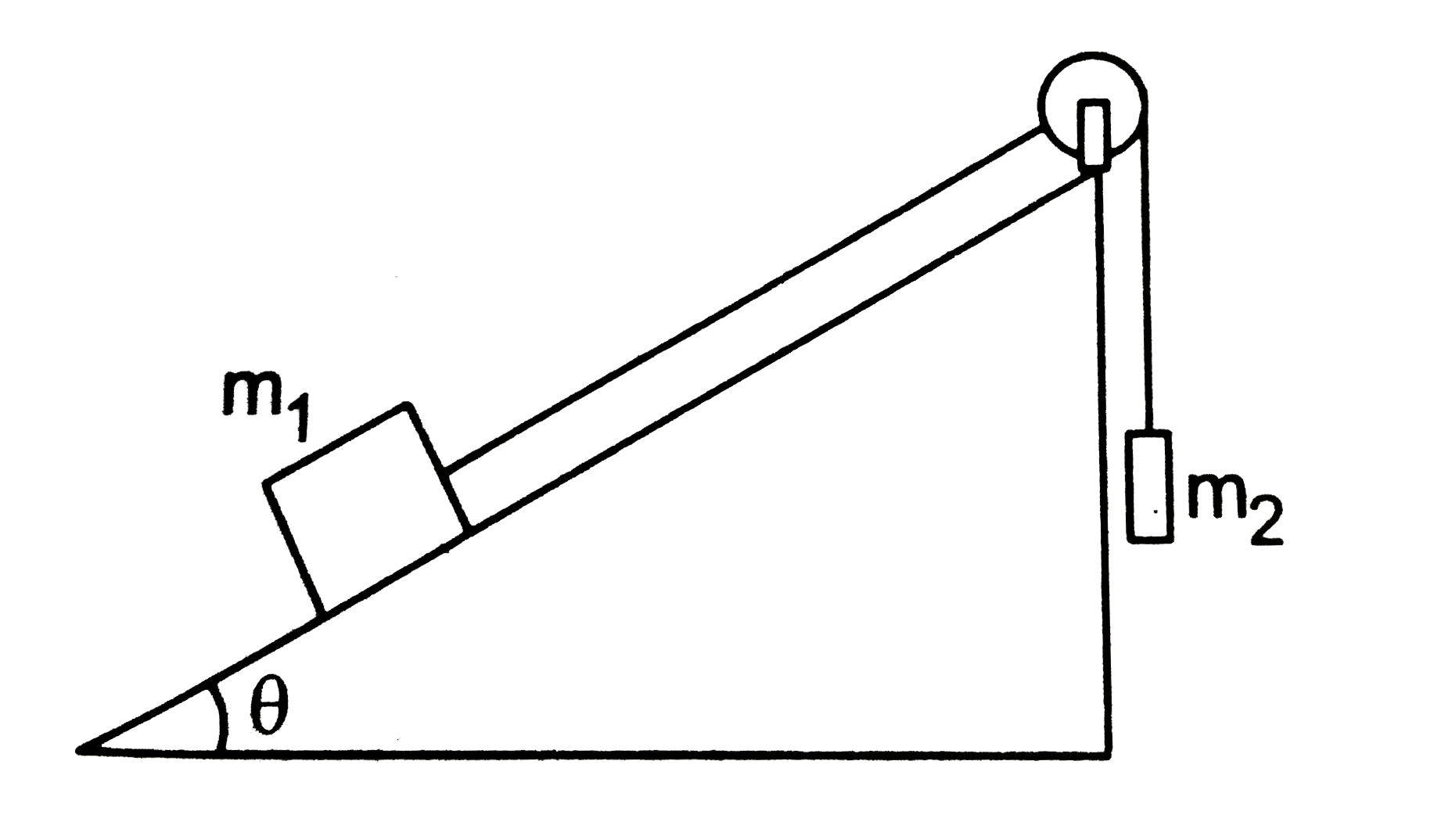
Figure shows the situation with the forces onn m1andm2 shown. Take the body of mass m2 as the system. The forces acting on it are
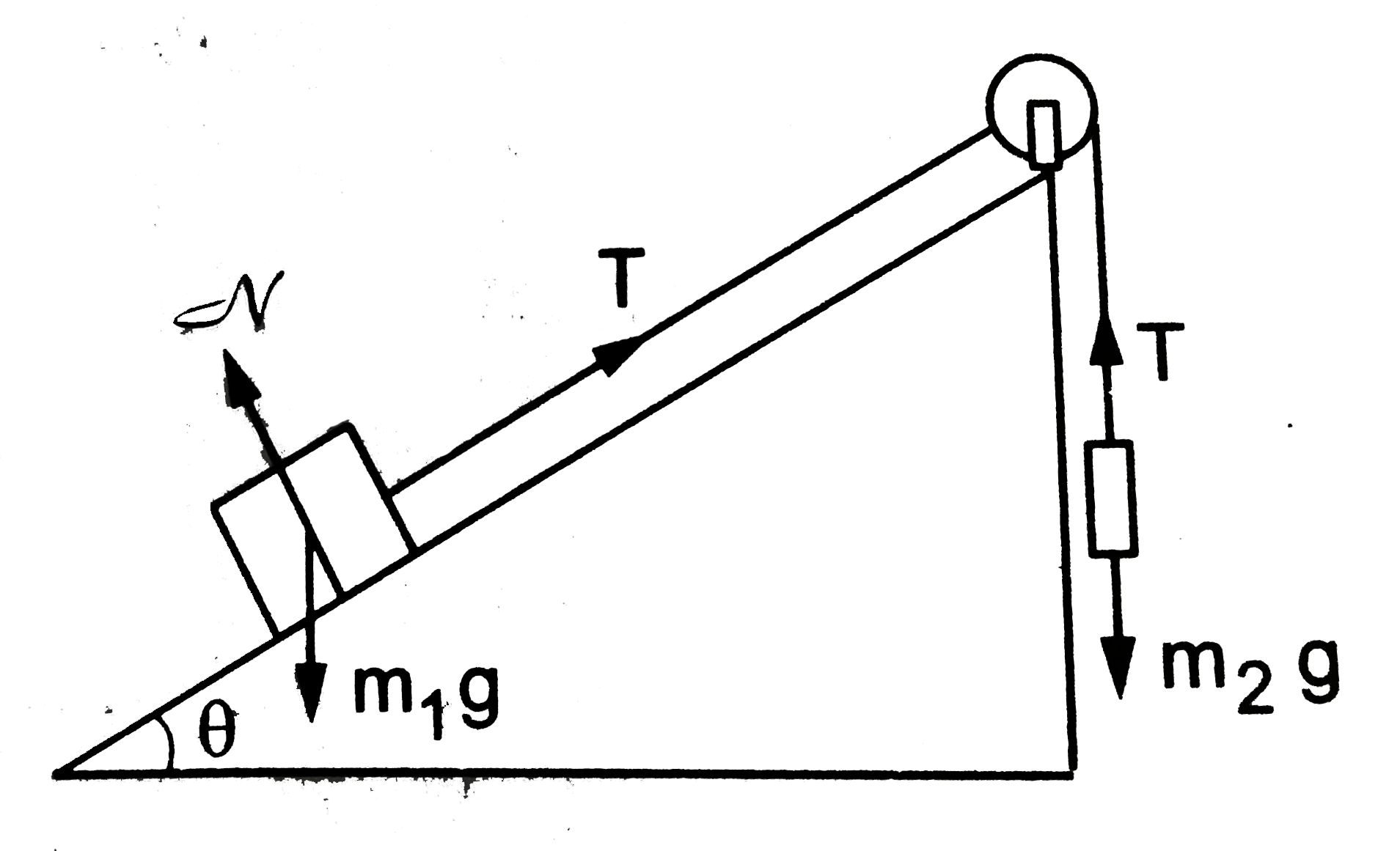
i. m2 g vertically downward (by the earth),
ii. T along the string up the incline (by the string),
N normal to the incline (by the incline).
As the string and the pulley are all light and smooth, the tension in the string is uniform everwhere. Hence, same T is used for the equations of m1andm2.As the system is in equilibrium, these forces should add to zero.
Take components parallel to the incline,
T=m1gcos(π2−θ)=m1gsinθ.........ii
Taking comonents along the normal to the incline,
Taking components along the normal to the incline,
N=m1gcosθ ............iii
Eliminating T from i and ii
m2g=m1gsinθ
or, sinθ=m2m1
giving θ=sin−1(m2m1)
From iii N=m1g√1−(m2m1)2.
EXAMPLE 13
With what acceleration a should the box of figure descends so that the block of mass M exerts a force Mg/4 on the floor of the box?
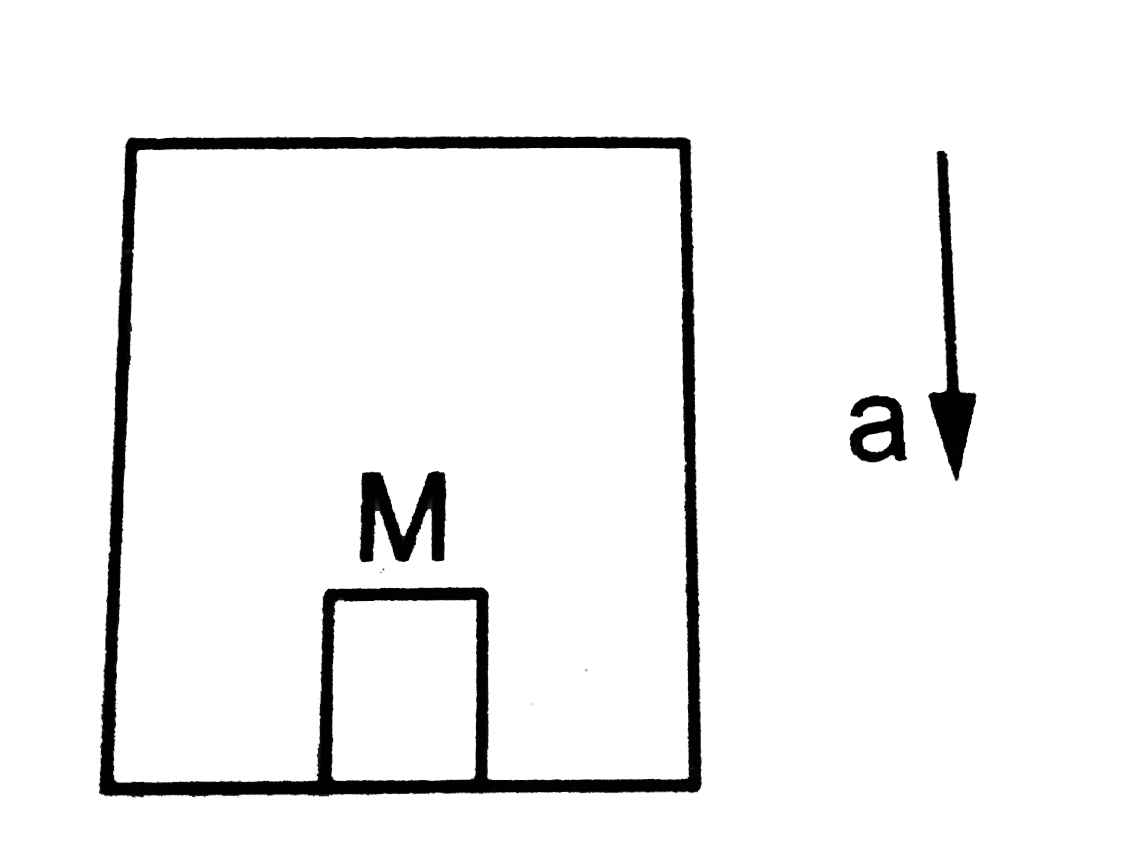
The block is at rest with respect to the box which is accelerated with respect to the ground. Hence, the acceleration of the block with respect to the ground is a downward. The forces on the block are
i. Mg downward (by the earth) and
ii. N upward (by the floor).
The equation of motion of the block is therefore
Mg−N=Ma
If N = Mg/4, the above equation gives a=3g4. The block and hence the box should descend with an acceleration 3g4.
EXAMPLE 14
A stone of of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40rev/min in a horizontal plane What is the tension in the string ? What is the maximum speed with which the stone can be whirled around If the string can withstand a maximum tension of 200 N ?
Here, m = 0.25 kg , r = 1.5 m
n = 40 rpm = 4060rps=23 rps
Now T = mrω2=mr(2πn)2=4π2mrn2
T = 4×227×227×0.25×1.5×(22)2 = 6.6 N
If Tmax = 200 N , then from ,
Tmax = mv2maxr⇒v2max = Tmax×rm
or v2max=200x1.50.25=1200⇒√1200 = 34.6ms−1.
EXAMPLE 15
The block shown in figure has a mass M and descends with an acceleration a. The mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.

Consider the block + the part of the string below A as the system . Let the tension at A be T. The forces acting on this system are
a. (M+mg) g, downward, by the earth
T, upward, by the upper part of the string.
The first is gravitational and the second is electromagnetic. We do not have to write the force by the string on the block. This electromagnetic force is by one part of the system on the other part. Only the forces acting on the system by the objects other than the system are to be included.
The system is descending with an acceleration a. Taking the downward direction as the Y-axis, the total force along the X-axis is (M+m)g−T. Using Newton's law along the X-axis is (M+m)g−T=(M+m)a.
or T=(M+m)(g−a)...........(i)
we have omitted the free body diagram. This you can do if you can draw the free body diagram in your mind and write the equations correctly.
To get the tension T' at the lower end we can put m=0 in i.
Effectively we take the point A at the lower end. Thus, we get T'=M(g−a).
EXAMPLE 16
A block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.

Let us consider the block as the system.
The forces on the block are
a. pull of the earth, Mg, vertically downward,
b. contact force by the table , vertically upward,
c. pull of the string T, along the string.
The free body diagram for the block is shown in figure.
The acceleration of the block is horizontal and towards the right. Take this direction as the X-axis and vertically upward direction as the Y-axis. We have,

component of Mg along the X-axis =0
Component of N along the X-axis =0
component of T along the X-axis = T cosθ
Hence the total force along the X-axis = Tcosθ
Using Newton's law, Tcosθ=Ma......(i)
Component of Mg along the Y-axis =-Mg
Component of N along the Y-axis =N
Component of T along the Y-axis =Tsinθ
Total force along the Y-axis =N+Tsinθ−Mg
Using Newton's law N+Tsinθ−Mg=0 ...........(ii)
From equation (i), T=Macosθ. Putting this in equation ii. N=(Mg−Matanθ)
EXAMPLE 17
A heavy particle of mass 0.50 kg is hanging from a string fixed with the roof. Find the force exerted by the string on the particle. Take g=9.8ms2
 .
.
The forces acting on the particle are
a. pull of the earth 0.50kg×9.8ms2=4.9N vertically downward
b. pull of the string, T (Tension force) acting vertically upward.
The particle is at rest with respect to the earth (which we assume to be an inertial frame). Hence, the sum of the forces should be zero. Therefore, T is 4.9 N acting vertically upward.
EXAMPLE 18
Three blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
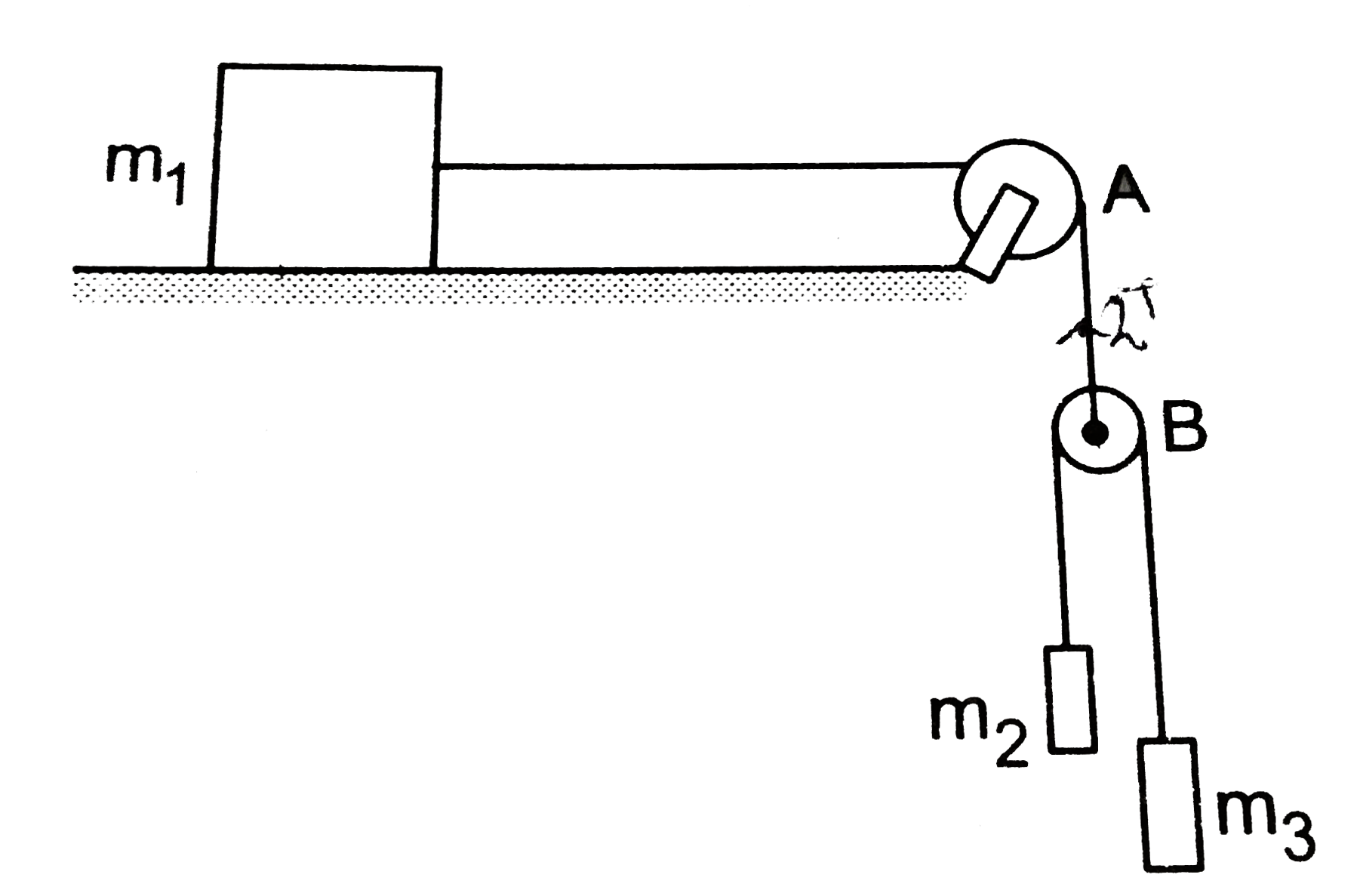
Suppose the acceleration of nq1 is a0 towards right. That will also be the downward acceleration of the pulley B because the string connecting m1andm3 has a constant length. This implies tht the decrease i the separation between m2and B equals the increase in teh separation between m3andB. So, the upward acceleeration of m2 wiht respect to B equals the downward acceleration of m3 with respect of B. Let this acceleration be a
The acceleration of m2 with respect to the ground =a0−a (downward) and the acceleration of m3 with respect to the ground =a0+a (downward).
These accelerations will be used in Newton's laws. Let the tension be T in the upper string and T' in the lower string. consider the motion of the pulley B.

The forces on this light pulley are ltbr> a. T upward by the upper sting and
2T' downwards by thelower string.
As the mass of the pulley is negligible,
2T'−T=0
giving T≡T2............i
Motion m1
THe acceleration is a0 in the horizontal direction. The forces on m1 are
a. T by the string (horizontal)
b. m1 g by theearth (verticlaly downwards) and
N by the table (verrtically upwards).
IN the horizontal direction the equation
T=m1a0
Motion of m2: acceleration is a0−a in the fownward direction. Teh forces on m2 are
a. m2g downward by teh earth and
T'=T2 upward by teh string.
Thus, m2g−T2=m2(a0+a)...........iii
Moton of m3= The aceeleration is (a0+a) downward. The forces on m3 are
a. m3g downward by the earth and
b. T'=T/2 upward by the string. thus,
m3g−T2=m3(a0+0)...........iv.
We want to calculate a0 so we shall elimiN/Ate T and a from ii, iii, and iv.
Putting T from ii in and iii and iv,
a0−a=m2−mI1a02m2=g−m1a02m2
and a0+a+m3g−m−1a02M3=g−m1a02m3
Adding 2a0=2g−m1a02(1m2+1m3)
a0=g−m1a04(1m2+1m3)
or, a0[1+m14(1m−2+1m3)]=g
or,a0=g1+m14(1m2+1m3)
EXAMPLE 19
A monkey is sitting on a tree limb. The limb exerts a
normal force of 48 N and a frictional force of 20 N. Find
the magnitude of the total force exerted by the limb on
the monkey.

The limb exerts a normal force 48 N and frictional force of 20 N.
Resultant magnitude of the force R=√(482+202)
=√2304+400
√2704=52N.
EXAMPLE 20
A particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of the incline has a length L. Find the time taken by the particle to reach the bottom.
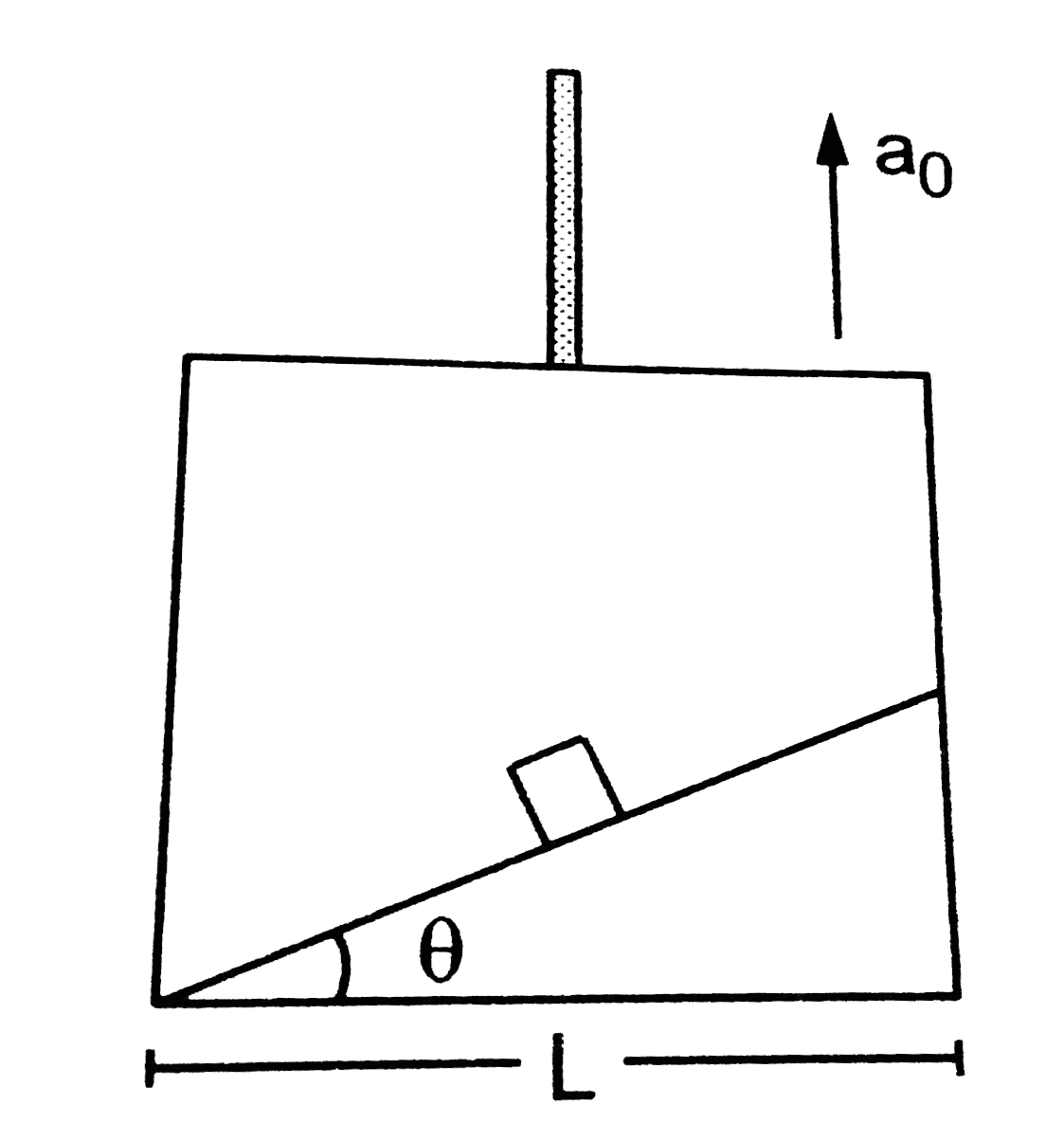
Let us work in the elevator frame. A pseudo force m0 n the downward direction is to be applied on the particle of mass m are.
i. N normal force
ii. mg downward (by the earth),
iii. ma0 downward (pseudo)
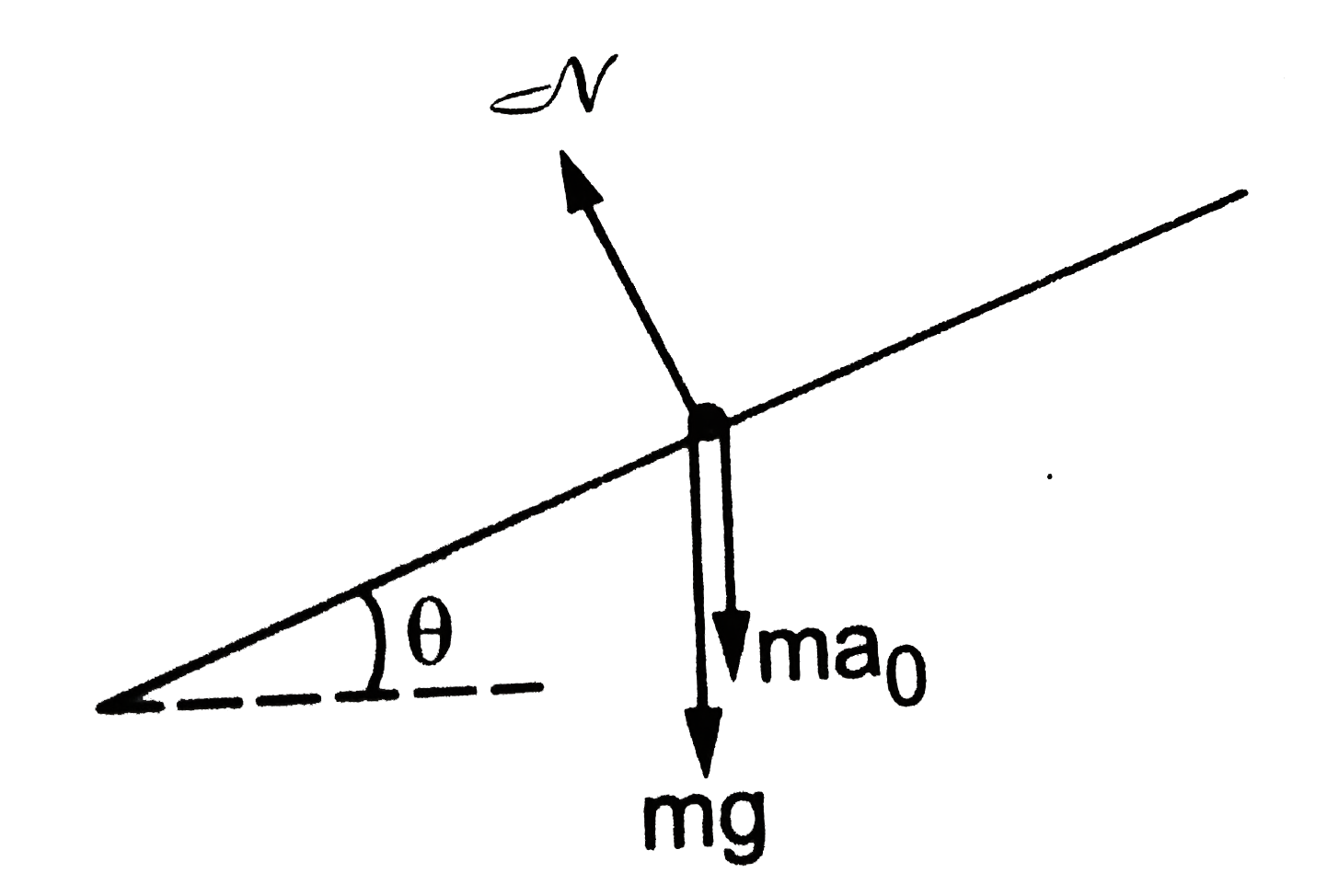 Let a be the acceleration of the partice with respect to the incline. Taking components of the forces parallel to the incline and applying Newton's law,
Let a be the acceleration of the partice with respect to the incline. Taking components of the forces parallel to the incline and applying Newton's law,
mgsinθ+ma0sinθ=ma
or a=(g+a0)sinθ
This is the acceleration with respect to the elevator. In this frame the distance travelled by the particle is Lcosθ. Hence,
Lcosθ=12(g+a0)sinθ.t2,
or, t=[2L(g+a0)sinθcosθ]12⎤⎥⎦.
ANGLE OF REPOSE
Inclined plane ka angle of inclination jispr koi body rakha hota hai aur slide krne wala hota hai us angle ko angle of repose kehte hai.
Suppose inclined plane pr ek block placed hai. Inclined plane ka angle of inclination θ∘hai. Ager block slide hone wala hoga to angle of inclination (θ∘) angle of repose ho jaega. θ∘ find karne ke liye hum block ko system consider karenge aur FBD draw krenge. First force weight hoga jo downward act krega. Hum weight ko resolve krenge to mgsinθ∘ (horizontal component) aur mgcosθ∘ (vertical component) aaega. Next force Normal force hoga jo upward act krta hai. Block slide hone wala hai so uspr upward direction me friction (fL) act krega.
Suppose block equilibrium position me hai. So, X-axis pr act ho rahe total force 0 hoga. Iska matlab left hand force aur right hand force dono equal hona chahiye.
fL=mgsinθ∘
Y-axis pr act ho rahe total force 0 hoga. Iska matlab upward force downward force ko balance krega.
N=mgcosθ∘
mgsinθ∘mgcosθ∘=fLN
fLN=tanθ
⇒μsNN=tanθ
μs=tanθ
θ=tan−1(μs)

PSEUDO FORCE
Pseudo force wo force hai jo hum observer ke frame of reference ke acceleration ke karan non inertial frame of reference me apply krte hai. Ye force matter ke basic interactions ke karan nahi arise hota hai. Pseudo (false) force ko fictitious force bhi kehte hai. Ager koi non inertial frame of reference me hai to wo ek force encounter krega jise pseudo force kehte hai.
Suppose ek block hai jo ground pr rakha hai aur rest pr hai. Ek observer hai jo ground pr khada hai aur ground se observe karta hai. So, observer ke liye ground frame of reference hoga aur ground rest pr hoga. Observer inertia frame me hoga aur uske liye block rest pr hoga.

Suppose ek aadmi apni car me baitha hai to wo car se observation krega. So, aadmi ke liye car frame of reference hoga. Jab car rest pr hoga to wo inertial frame me hoga aur aadmi ke liye block rest pr hoga. Jab car constant velocity se move krega to aadmi ko block backward move krte appear hoga same uniform velocity ke saath.

Ager car forward accelerate krega to aadmi ko block backward accelerate hote appear hoga. Acceleration ke liye force ki requirement hoti hai pr block pr koi force nahi act kr raha hai aur bina force ka block accelerate kr raha hai. So, yaha Newton’s law valid nahi ho raha hai kyunki Newton’s law ke according acceleration ke liye force hona jaruri hai. Non-inertial frame me Newton’s law ko validate krne ke liye pseudo force ke concept ko laya jata hai.
Therefore for the man: Block pr pseudo force act kr raha hai aur pseudo force block ke acceleration ke direction me hoga. Ye force sirf non-inertial frame of reference me aata hai. Direction of pseudo force is opposite to the direction of motion of the non- inertial frame.
Fpseudo=mass of the body×acceleration of non-inertial frame

OMR (One Minute Revision)
- * Net external force is the sum of all of the forcing acting on an object.
* Just because there are forces acting on an object doesn’t necessarily mean that there is a net external force; forces that are equal in magnitude but acting in opposite directions can cancel one another out.
* Friction is the force between an object in motion and the surface on which it moves. Friction is the external force that acts on objects and causes them to slow down when no other external force acts upon them.
* Thrust is an application of the third law of motion. A helicopter uses thrust to push the air under the propeller down, and therefore lift off the ground.
CIRCULAR DYNAMICS
Let’s recapitulate, jo hamne pichle chapter me circular motion me padha tha. Let’s consider ek hockey puck ko string se baandkar ham use rotate kar rahe hai. Wo circular path trace karta hai jiska radius, R hai. Hamne padha tha ki centre ki ore uska acceleration hoga v2r. Is acceleration ko ham centripetal acceleration (“centre-seeking”) acceleration bhi kahte hai.Is chapter me ham padhenge ki kisi bhi object ko circular motion trace karne ke liye ek centripetal force ki requirement hoti hai.
Centripetal force, F=mv2R (magnitude of centripetal force),
where, m is the object's mass. Ye acceleration and force centre ki ore act karte hai.

Here, the puck moves in a uniform circular motion only because of a centripetal force.
Ye centripetal force ek alag tarah ka force nahi hai. Iska naam bas is force ki direction ko define karta hai. Ye force kaise bhi ho sakta hai, viz. Gravitational force, frictional force, tension force, normal reaction, etc.
EQUILIBRIUM
A body is said to be in equilibrium if under the application of forces, it remains in state of rest or in uniform motion.
Equilibrium do type ke hote hai:
1. Translational Equilibrium
2. Rotational Equilibrium
Is chapter me hum sirf Translational equilibrium padenge.
Translational Equilibrium
A body is said to be in translational equilibrium if the resultant force acting on the body is zero.∑→F=0
→F1+→F2+…….+→Fn=0
Force vector quantity. Ager sare forces same plane me nahi hote hai, then;
∑→Fx=0
∑→Fy=0
∑→Fz=0
Complete equilibrium ke liye, body translational aur rotational equilibrium dono me hona chahiye.
CONCURRENT FORCES
If two or more forces act on the same particle, we call them concurrent forces.Lamy's Theorem
If three concurrent forces P,QandR acting on a particle keep the particle in equilibrium, then Lamy's (Lami's) theorem states:
Psinα=Qsinβ=Rsinγ
Here,
α = angle opposite to →P
β = angle opposite to →Q
γ = angle opposite to →R



CONSTRAINT RELATIONS
The equations showing the relation of the motions of a system of bodies, in which one’s motion is constrained by other’s motion, are called the constrained relations.Pehle hum pulleys ke simple cases se analysis start krenge. Consider krte hai situation jaise ki niche image me shown hai. Do bodies ek string se connected hai jo table ke corner se pulley se pass hota hai. Ager yaha string inextensible hai to hum keh sakte hai ki A ka displacement joki downward direction me hai wo B ke displacement joki horizontal direction me hai, uske equal hai. Ager A aur B ka displacement equal time me equal hai, to unka speed aur acceleration ka magnitude bhi equal hona chahiye.

Case (c) me, ager wedge aur block move krne ke liye free hai to block aur wedge ka acceleration related hoge.
Note: Applying Newton's law alone is not sufficient in most cases. If you apply Newton's laws based on the methods shown above, you will get a few equations. You may however find that the number of unknowns is much larger than the number of equations. That is, you will have a situation where, say the number of variables are three but the number of equations are only two. It is, therefore, obvious that you cannot solve the equations to get the value of the variables.
Suppose figure me aapko masses ka acceleration find krna hai.
The number of unknowns will be:
1. tension T,
2. acceleration a1 of the mass, and
3. acceleration of the other body a2.
Yaha teen unknowns hai. Hame sirf do equations milenge- one for one mass and another for the other mass. Clearly aap dekhenge ki problem solve krne ke liye Newton ke laws sufficient nahi hai. In cases me, hume additional equations ki jarurat hoti hai jinhe constraint equations kehte hai.
Constraints mean that two bodies (in this case the bodies which are attached to the pulley) are not free to move the way they want. Inke beech ka acceleration dono pr dependent hota hai.
Constraints geometrical restrictions hote hai jo body ke motion pr imposed hote hai aur body ke trajectory ko bhi govern krte hai. For example, a block placed on the table cannot move normally to the surface, it is bound to move parallel to the surface. We have to use the method of constraint equations to relate the accelerations between the bodies. In many cases you can write down the relation of acceleration by just looking at the situation. In other cases, for complex relationships, we can think of four types of constraints.
1. General constraints
2. Wedge constraint.
3. Pulley constraint
4. Combination of the wedge and pulleys.
PROBLEM SOLVING STRATEGY
EXAMPLE 1Two Blocks on an Inclined Plane
Hum object A aur object B ke liye free-body diagram construct krenge.
Strategy
Hum four steps jo problem-solving strategy me listed hain unko follow krenge.
Solution
Hum start krenge diagram first object ka diagram banakr. Figure (a) me aap dekhenge object A isolated (circled) hai aur dot se represented hai.

Ab hum jo force body pr act krta hai usse include krenge. Object ka weight vertically downwards act krta hai. Cord ka presence tension force indicate krta hai, directed away from the object. Object A ke ps ek interface hai aur wo normal force experience krta hai, directed away from the interface. Object B ke ps niche slide hone ka tendency hai aur object A ke ps upr slide hone ka tendency hai, interface ke respect me. So, friction fBA downward inclined plane ke parallel directed hoga.
Object B do contact surface ke presence ke karan, do normal force aur do friction force experience krta hai. Inclined plane ke saath jo interface hai wo NB aur fB external forces exert krta hai. Object B ke saath jo interface hai wo normal force NAB aur friction force fAB exert krta hai. NAB object B se away direct krta hai aur fAB object B ka object A ke respect me relative motion ke tendency ko oppose krta hai.
Significance:
Jo object consideration me hai humne usse gray se circle kiya hai. Jab hum free body diagrams banana sikhte hai to object pr act ho rahe forces decide krne se pehle object ko circle krna hamare liye helpful hota hai.
EXAMPLE 2
Two Blocks in Contact
Do blocks jo contact me hai unke ek force apply hota hai.
Strategy
Hum each block ke liye free-body diagram draw krenge. Hume Newton’s third law ko consider krna hoga interface pr jaha do blocks touch ho rahe hai.

Solution

Significance
→A21 block 2 ka block 1 pr action force hai aur →A12 block 1 ka block 2 pr reaction force hai.
EXAMPLE 3
Block on the Table (Coupled Blocks)
Figure me aap dekhenge table pr ek block rakha hai. Ek rope ko usse attach krke pulley pr move krate hai. Rope ka dusra end second block se attached hai. Block m2 apne weight ke karan force exert krta hai jisse do blocks aur ek string ka system accelerate hone lgta hai.
Strategy
Hum assume krte hai ki string ka koi mass nahi hai aur wo koi separate object nahi hai. So, each block ke liye hum free body diagram draw krenge.

Solution

Significance
Dono block same rate pr accelerate krte hai. Thus, →a1=→a2. Donom dody m1 aur m2 pr same tension apply hota hai.
OMR (One Minute Revision)
- * To draw a free-body diagram, we draw the object of interest, draw all forces acting on that object, and resolve all force vectors into x– and y-components. We must draw a separate free-body diagram for each object in the problem.
* A free-body diagram is a useful means of describing and analyzing all the forces that act on a body to determine equilibrium according to Newton’s first law or acceleration according to Newton’s second law.
SOME REMANENT TOPICS
Bachho, Rain-man and boat-river problems kaafi popular topics hai relative velocity ke. These topics are to be read as concepts from "Motion in a plane" chapter. Please consider it as part of kinematics but not kinetics as we are not discussing the various forces that are included in these problems:
RIVER-BOAT PROBLEMS
River-boat problems me ham in teen terms ka use karte hai:→vre = →vr = absolute velocity of river or velocity of river with respect to earth (ground).
→vbr = velocity of boatman with respect to river or velocity of boatman is still water. It is the velocity of boatman with which he steers the boat
and
→vbe= →vb = absolute velocity of boatman. It is the actual velocity of boatman relative to earth (ground).
Therefore, →vb=→vbr+→vr
Let’s derive some relations:
Here, a boatman starts from one bank of a river with velocity vbr.

Let’s analyse this in simple figures.

Let’s consider width of river is w. Yaha par boatman width (vertical line) se θ angle subtend kar raha hai.
River is flowing along positive x-direction with velocity →vr. Therefore,
→vb=→vbr+→vr
Therefore, vbx=vrx+vbrx=vr−vbrsinθ
and, vby=vry+vbry
=0+vbrcosθ=vbrcosθ
Now, time taken by the boatman to cross the river is :
t=wvby=wvbrcosθ
or t=wvbrcosθ …… (i)
Further, displacement along x-axis when he reaches on the other bank (also called drift) is : x=vbxt=(vr−vbrsinθ)wvbrcosθ, or
x=(vr−vbrsinθ)wvbrcosθ ….. (ii)
There are three special cases:
(i) Condition when the boatman crosses the river in shortest interval of time
From Eq.(i) we can see that time (t) will be minimum when θ=0∘,
i.e., the boatman should steer his boat perpendicular to the river current.
Also, tmin=wvbr as cosθ=1.

Here, is a simulation for vr=5mmin and vbr=10mmin and θ=0∘



(ii) Condition when the boatman wants to reach point B, i.e., at a point just opposite from where he started
In this case, the drift (x) should be zero.
∴,x=0
or, (vr−vbrsinθ)wvbrcosθ=0
or, (vr=vbrsinθ
or, sinθ=vrvbr
or, θ=sin−1(vrvbr)

Hence, to reach point B the boatman should row at an angle θ=sin−1(vrvbr) upstream from AB.
Further, since sinθ not greater than 1.
So, if vr≥vbr, the boatman can never reach at point B. Because if vr=vbr, sinθ=1 or θ=90∘ and it is just impossible to reach at B if θ=90∘.
Moreover it can be seen that vb=0∘ if vr=vbr and θ=90∘.
Similarly, if vr>vbr, sin theta > 1, i.e., no such angle exists. Practically, it can be realized in this manner that it is not possible to reach at B if river velocity (vr) is too high.
Here, is a simulation for vr=5mmin and vbr=10mmin
vbrsinθ=vr
sinθ=vrvbr=510=0.5
θ=30∘.



RAIN - MAN PROBLEMS
In these type of problems we again come across three terms →vr = = velocity of rain,→vm = velocity of man (it may be velocity of cyclist or velocity of motorist also)
and →vrm = velocity of rain with respect to man. It is the velocity of rain which appears to the man. Here,

vrm=vr−vm
If the man wants to protect himself from the rain, he should hold his umbrella in the direction of the relative velocity of rain with respect to the man. i.e.the umbrella should be held making an angle θ.
and, θ=tan−1∣∣∣vmvr∣∣∣
EXAMPLE 21
A fighter plane is pulling out for a dive at a speed of 900km/h. Assuming its path to be a vertical circle of radius 2000m and its mass to be 16000kg, find the force exerted by the air on it at the lowest point. Take g=9.8m/s2
At the lowest point in the vertical circle, the acceleration is vertically upwards (towards the centre) and its magnitude is v2/r.
The force on the plane are (a) Weight Mg downwards and
(b) force F by the air upward.
Hence, Newton's second law of motion gives
F−Mg=Mv2/r or F=M(g+v2/r)
Here, v=900km/h=9×1053600m/s=250m/s
F=16000(9.8+625002000)N=6.56×105N (upwards)
EXAMPLE 22
Three particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2)
r=a2sec30∘=a√3
F=Gmma2
Fnet=√3F=(Gmma2)(√3)

This will provided the necassary centripetal force.
∴mv2r=√3Gm2a2
T=2πrv=2π(a/√3)√Gm/a=2π√a33Gm
POINT 4
Circular motion Circular motion is described as a movement of an object while rotating along a circular path.
Centripetal: Directed or moving towards a center.
Angular Velocity:Angular velocity is the time rate at which an object rotates, or revolves, about an axis, or at which the angular displacement between two bodies changes. Denoted by ω.
Angular speed Angular speed is the measure of how fast the central angle of a rotating body changes with respect to time. Denoted by ω.
Symmetry: Exact correspondence on either side of a dividing line, plane, center or axis.
Thrust: The force generated by propulsion, as in a jet engine.
EXAMPLE 23
A mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
Figure 5.8(b) and 5.8(c ) are known as free-body diagrams. Figure5.8(b) is the free-body diagram of W and Fig.5.8 (c ) is the free-body diagram of point P .
Consider the equilibrium of the weight aaaaaaaaw.
Clearly , T2 = 6×10= 60 N.
Consider the equilibrium of the point P under the action of three forces - the tensions T1 and T2, and the horizontal force 50 N . The horizontal and vertical components of the resultant force must vanish seperately :
T1 cos θ = T2 = 60 N
T1 sin θ = 50 N
which gives that
tan θ = 5/6 or θ = tan−1(5/6) = 40∘
Note the answer does not depend on the length of the rope (assumed massles ) nor on the point at which the horizontal force is applied.
EXAMPLE 24
All the surfaces shown in figure are assumed to be frictionless. The block of mass m slides on the prism which in turn slides backward on the horizontal surface. Find the acceleration of the smaller block with respect to the prism.

Let the acceleration of the prism be a0 in the backward direction. Consider the motion of the smaller block from the frame of the prism.
The force on the block are

i. N normal force,
mg downward (gravity)
ma0 forward (psuedo). The block slides down the plane. components of the forces parallel to the incline give
ma0cosθ+mgsinθ=ma
or, a=a0cosθ+gsinθ .........i
Components of the force perpendicular to the incline give
N+ma0sinθ=mgcosθ .........ii
Now consider the motion of the prism from the lab frame. No pseudo force is needed as the frame used is inertial. The forces are
i. Mg downward,
ii. N normal to the incline (by the block)
N upward (by the horizontal surface).
Horizontal components give,
Nsinθ=Ma0or,NMa0sinθ ..............iii
Putting in ii.
Ma0sinθ+ma0sinθ=cosθ
or, a0=mgsinθcosθM+msin2θ
From i. a=mgsinθcos2θM+msin2θ+gsinθ
=(M+m)gsinθM+msin2θ.
EXAMPLE 25
The relation →F=m→a , cannot be deduced from Newton's second law, if:
The relation →F=m→a , can only be deduced from Newton's second law, if mass remains constant with time. If mass depends on time then this relation cannot be deduced. Therefore, option (iv) is correct.
EXAMPLE 26
An astronaut accidentally gets separated out his small spaceship accelerating in interstellar space at a constant rate of 100ms−2 . What is the acceleration of the astronaut the instant after he is outside the spaceship? (Assume that there are no nearby stars to exert gravitational force on him)
Since there are no nearby stars to exert gravitational force on him and the small spaceship exerts negligible gravitational attraction on him, the net force acting on the astronaut, once he is out of the spaceship, is zero. In accordance with the first law of motion the acceleration of the astronaut is zero. Therefore, option (i) is correct.
EXAMPLE 27
In which of the following cases the net force acting on the body is not zero?
As the rain drop is falling down with a constant speed, its acceleration, a=0 . Hence, net force on the drop is ma=0 . As the cork is floating on the surface of water, it's weight is balanced by the upthrust. Hence, net force on the cork is zero.
The force exerted by the engine is balanced by the friction due to rough road, as the car is moving with constant velocity, its acceleration a=0 . Hence, net force on the car, F=ma=0 .
Whenever a body is thrown vertically upward gravitational pull of earth gives it a uniform acceleration, a=g in downward direction.
Hence, net force on the pebble=mg ⇒0.05×10=0.5N vertically downwards. Therefore, option (iv) is correct.
EXAMPLE 28
On a stationary sail-boat, air is blown at the sails from a fan attached to the boat. The boat will
The force exerted by the air of fan on the boat is internal and for motion external force is required. Therefore, option (i) is correct.
EXAMPLE 29
A mass of 1kg is suspended by a string A. Another string C is connected to its lower end (see figure). If a sudden jerk is given to C, then
When a sudden jerk is given to C , an impulsive tension exceeding the breaking tension develops in C first, which breaks before this impulse can reach A as a wave through block. Therefore, option (ii) is correct.
EXAMPLE 30
Which of the following statement is not true regarding the Newton's third law of motion?
Action and reaction act on different bodies not on the same body. Therefore, option (ii) is correct.
EXAMPLE 31
Five forces →F1,→F2,→F3,→F4 , and →F5 , are acting on a particle of mass 2.0kg so that is moving with 4m/s2 in east direction. If →F1 force is removed, then the acceleration becomes 7m/s2 in north, then the acceleration of the block if only →F1 is action will be:
→F1+→F2+→F3+→F4+→F5=2(4ˆi) .
and →F2+→F3+→F4+→F5=2(7ˆj) .
From (i) and (ii), →F1=8ˆi−14ˆj .
→a=→F1m=4ˆi−7ˆj .
implies a1=√16+49=√65m/s2 .Therefore, option (ii) is correct.
EXAMPLE 32
A block of metal weighing 2kg is resting on a frictionless plane. It is struck by a jet releasing water at a rate of 1kgs−1 and at a speed of 5ms_1. The initial acceleration of the block is

The water jet striking the block at the rate of 1kg/s at a speed of 5m/s will exert a force on the block
F=vdmdt=5×1=5N .
Under the action of this force of 5N , the block of mass 2kg will move with an acceleration given by
a=Fm=52=2.5m/s2 .Therefore, option (i) is correct.
EXAMPLE 33
Assertion: Friction opposes relative motion and thereby dissipates power in the form of heat.
Reason: Friction is always an undesirable force.
We consider friction as an undesirable force sometimes, not always. In many situation, like in a machine with different moving parts, friction does have a negative role. It opposes relative motion and thereby dissipates power in the from of heat, etc. Therfore, option (iii) is correct.
EXAMPLE 34
Assertion: Force on a body A by body B is equal and opposite to the force on the body B by A .
Reason: Force in nature always occur between pairs of bodies.
By Newton's third law of motion, "to every action, there is always an equal and opposite reaction. Therefore, option (i) is correct.
EXAMPLE 35
Assertion: Force is always in the direction of motion.
Reason: In every case force is not parallel to acceleration.
Force is not always in the direction of motion Depending on the situation, →F may be along →v , opposite to →v , normal to →v . In every case it is parallel to acceleration. Therefore, option (iv) is correct.
EXAMPLE 36
An inclined plane makes an angle 30∘ with the horizontal. A groove (OA) of length 5m cut in the plane makes an angle 30∘ with OX. A short smooth cylinder is free to slide down under the influence of gravity. The time taken by the cylinder to reach from A to O is (g=10ms−2).
Acceleration of cylinder down the plane is
a=(gsin30∘)(sin30∘)=10(12)(12)=2.5m/s2
time taken: t=√(2sa)=√2×52.5=2s. Therefore, option (ii) is correct.
EXAMPLE 37
Two block of masses M1andM2 are connected with a string passing over a pulley as shown in figure The block M1 lies on a horizontal surface friction between the block M1 and the horizontal surface is μ The system accelerates. What additional mass m should be placed on the block M1 so that the system does not accelerate ?
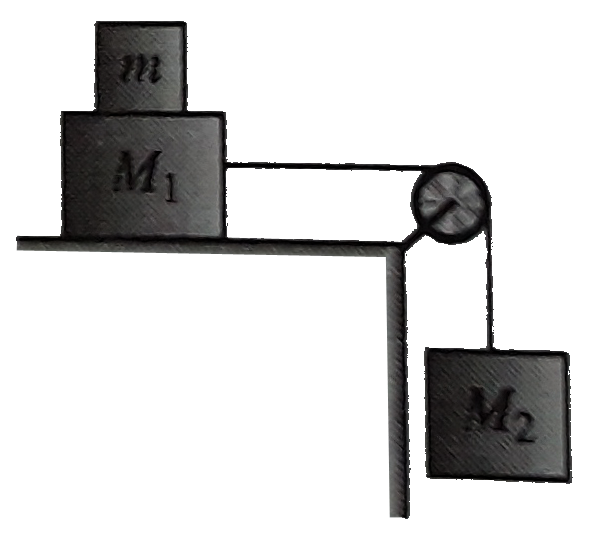
For the equilibrium of block of mass M1 :
Frictional force, f = Tension in the string, T
where T=f
μ(m+M1)g=M2g
T=M2g
From (i) and (ii) μ(m+M1)g=M2g
m=M2μ−M1. Therefore, option (ii) is correct.
EXAMPLE 38
A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

Tsinθ=Mω2R
Tsinθ=Mω2Lsinθ
From (i) and (ii)
T=Mω2L
= M4π2n2L
=M4π2(2π)2L
=16ML. Therefore, option (ii) is correct.
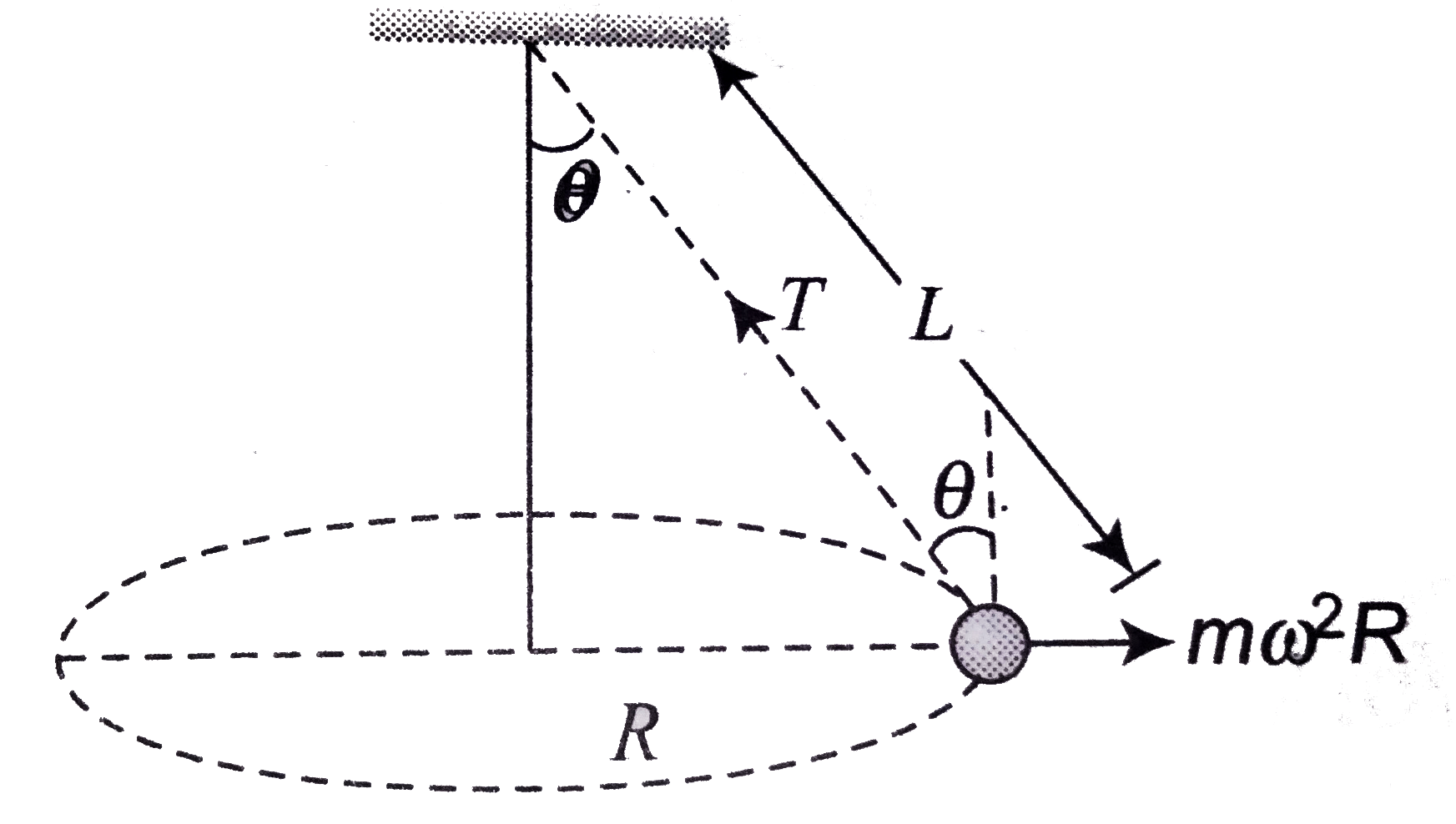
EXAMPLE 39
A balloon of mass M is descending at a constant acceleration α. When a mass m is released from the balloon, it starts rising with the same acceleration α. Assuming that its volume does not change, what is the value of m?
Suppose F = upthrust due to buoyancy
Then while descending, we find
Mg−F=Mα
when ascending, we have F−(M−m)g=(M−m)α
Solving equation (i) and (ii), we get: m=[2αα+g]M. Therefore, option (ii) is correct.
EXAMPLE 40
A plumb bob is hung from the ceiling of a train compartment. The train moves on an inclined track of inclination 30∘ with horizontal. Acceleration of train up the plane is a=g/2 . The angle which the string supporting the bob makes with normal to the ceiling in equilibrium is.
Tsinθ−mgsin30∘=ma implies Tsinθ=mgsin30∘+mg/2
Tcosθ=mgcos30∘
Dividing (i) by (ii), we get
tanθ=2√3. Therefore, option (ii) is correct.

EXAMPLE 41
A body of mass 10kg is acted upon by two perpendicular force, 6N . The resultant acceleration of the body is.
Here, m=10kg
The resultant force acting on the body is
f=√(8N)2+(6N)2=10N
Let the resultant force F makes an angle 6 w.r.t. 8N force.
From figure, tanθ=6N8N=34
The resultant acceleration of the body is
a=Fm=10N10kg=1ms−2
The resultant acceleration is along the direction of the resultant force.
Hence, the resultant acceleration of the body is 1ms−2 at an angle of tan−1 w.r.t. 8N force. Therefore, option (i) is correct.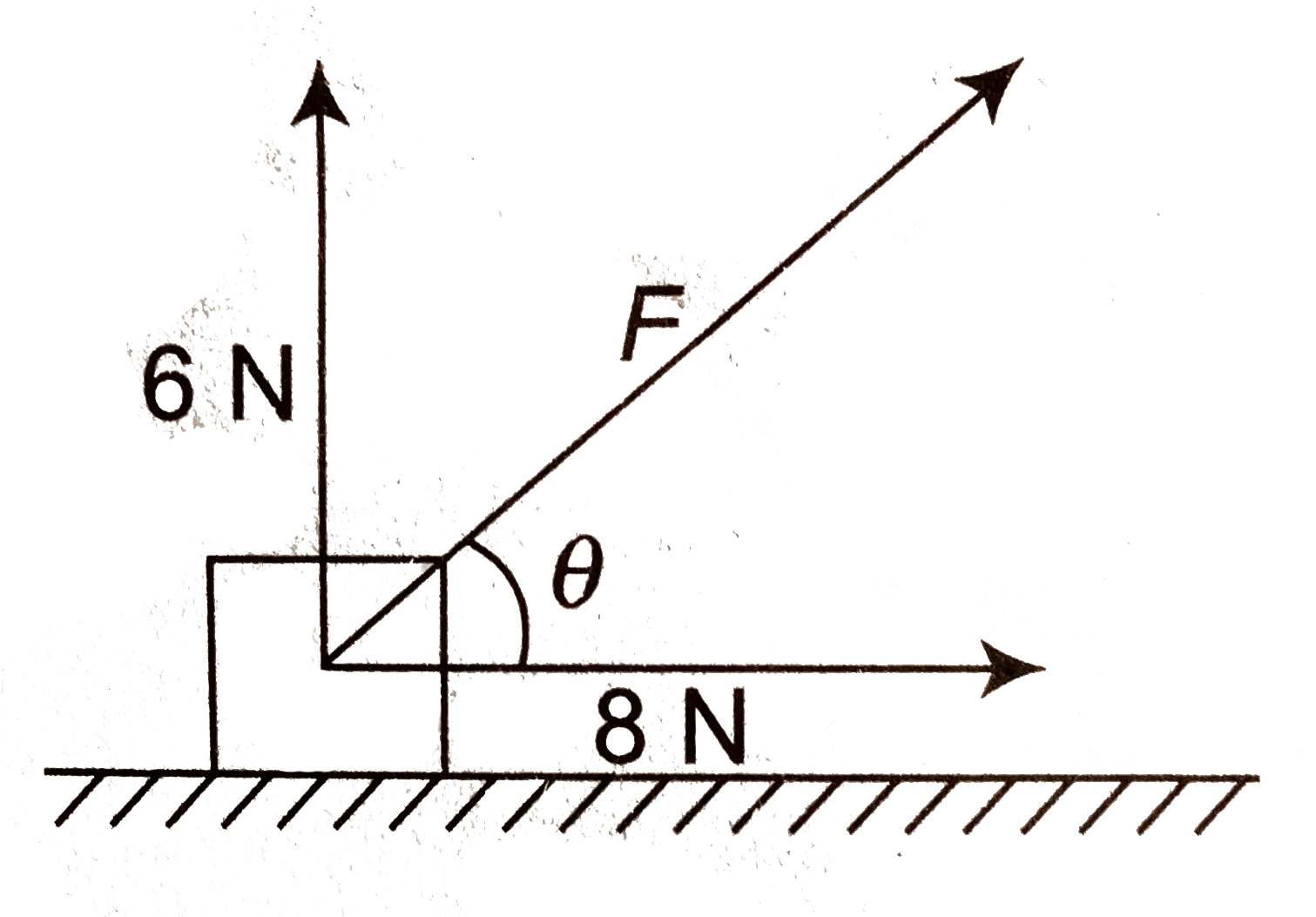
EXAMPLE 42
A rocket is going upward with acceleration motion. A man sitting in it feels his weight increased by 5 times his own weight. If the mass of the rocket including that of the man is 1.0×104kg , how much force is being applied by rocket engine? (Take g=10ms−2).
As the weight of man increased by 5 times, so acceleration of the rocket, a=5g=5×10ms−2
Force applied by rocket engine is
F=ma=1.0×104×50=5×105N. Therefore, answer (ii) is correct.
EXAMPLE 43
A mass of 4kg is suspended by a rope of length 4m from a ceiling. A force of 20N in the horizontal direction is applied at the mid-point of the rope as shown in figure. What is the angle which the rope makes with the vertical in equilibrium? Neglect the mass of the rope. Take g=10ms−2 .
T2=mg=4×10=40N
T1cosθ=40 , T1sinθ=20
tanθ=12 implies θ=tan−1(12) . Therefore, option (ii) is correct. 
EXAMPLE 44
A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it.
R=mgcosθ−mv2r
When θ decreases, coshtη increases i.e., R increases. Therefore, answer (i) is correct. 
EXAMPLE 45
A Rocket having initial mass 5×106kg , which include mass of fuel of mass 4×106kg is ejecting gas with velocity 4000m/s relative to Rocket when entire fuel finishes?
V=uroc.ln(mM)
V=4000.ln(5×1061×106)
V=4000ln(5)
V=6437.75m/s. Therefore, answer (i) is correct.
EXAMPLE 46
Two block A and B of masses 3m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of A and B immediately after the string is cut, are respectively
Before cutting the strip:
After cutting the Strip:
aA=4mg−3mg3m=g3
aB=mgm=g . 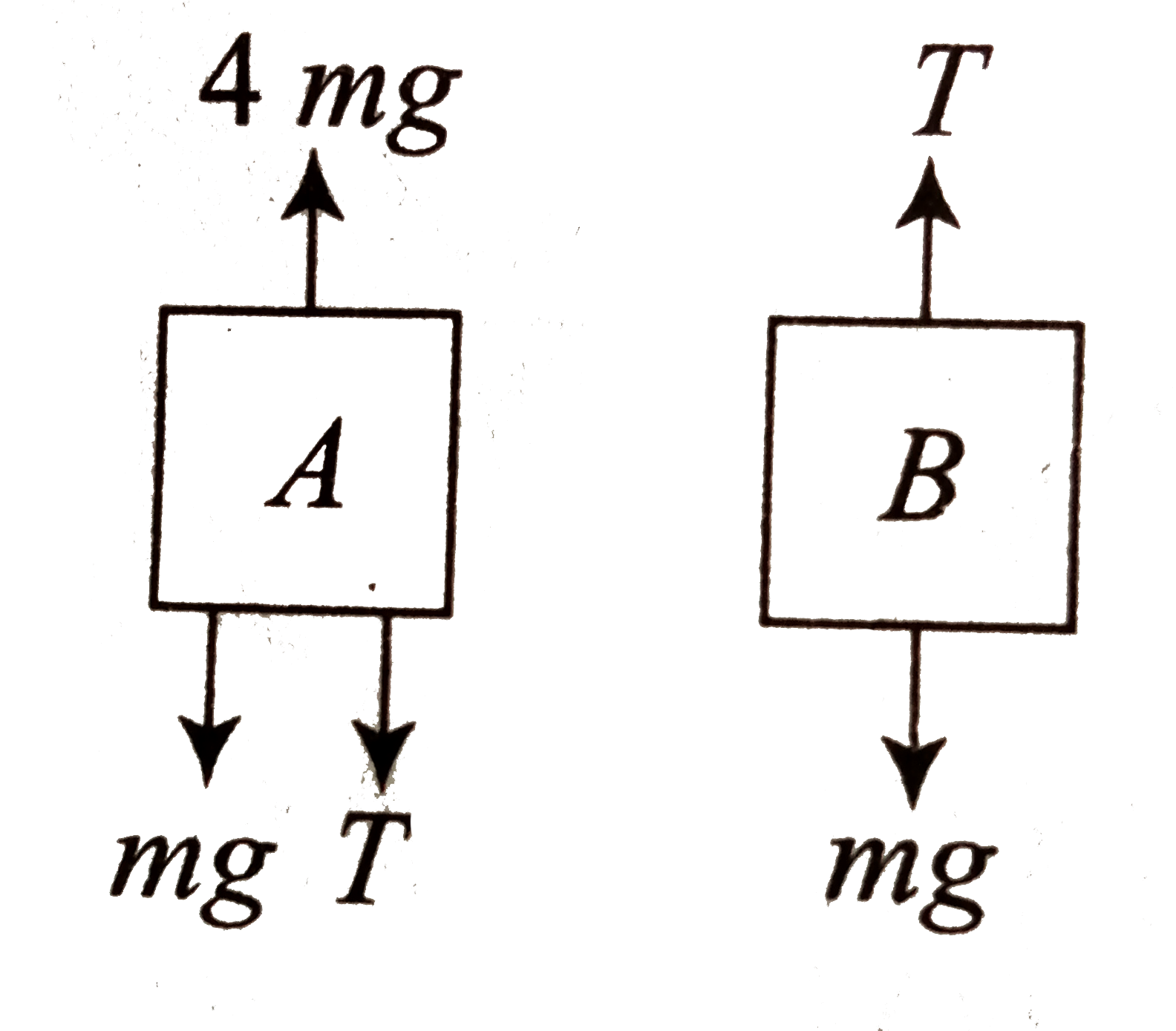 . Therefore, option (i) is correct.
. Therefore, option (i) is correct.
EXAMPLE 47
In the arrangement shown, the pulleys and the string are ideal. The acceleration of block B is.

For B : mg−T=ma
For A : 2T−mg=ma2 implies mg=52ma
a=2g5. Therefore, option (iii) is correct. 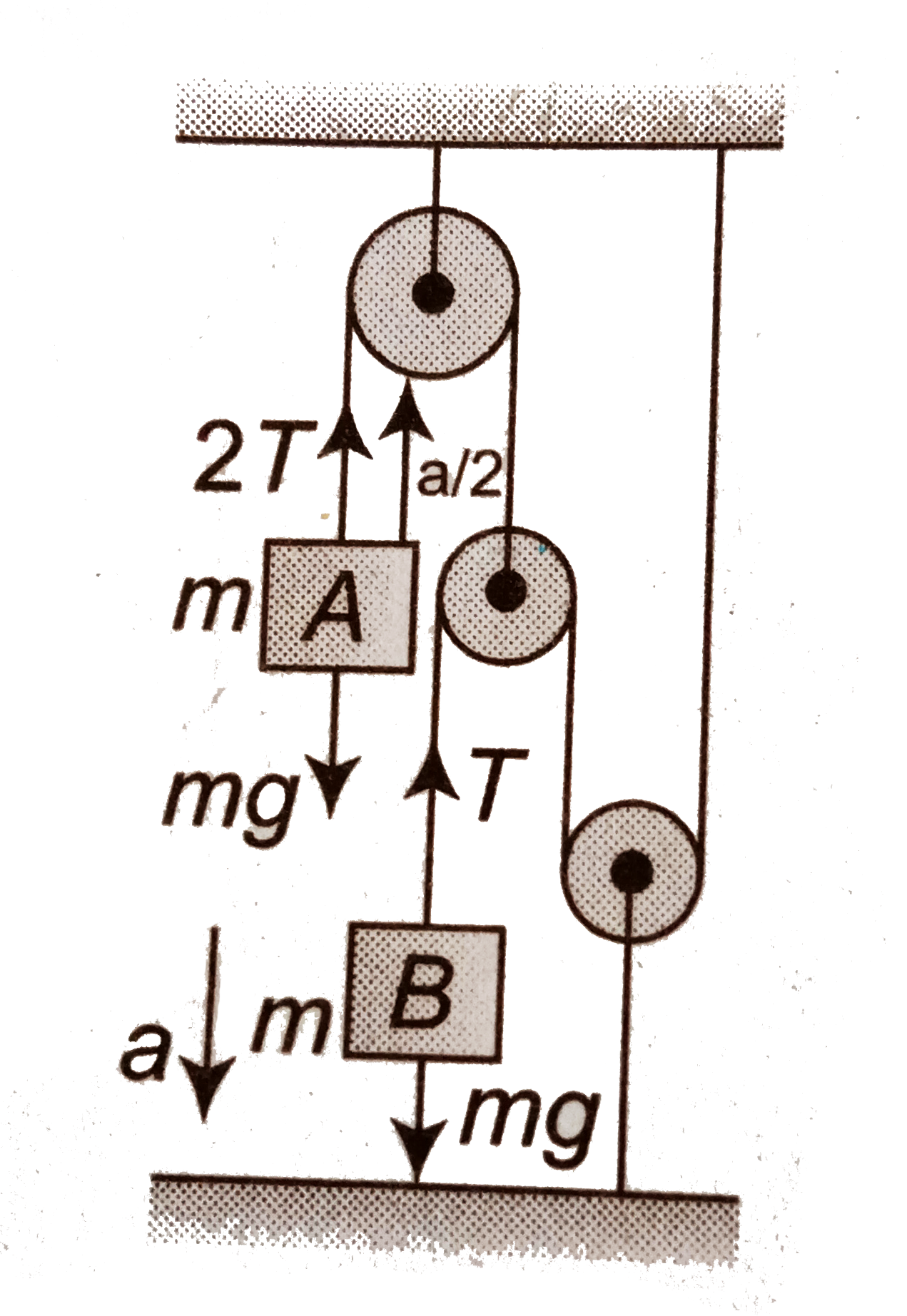
EXAMPLE 48
A smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is at rest w.r.t. the circular ring in the position shown. then ω2 is equal to:

As, cosθ=a2a
θ=60∘
∴ Nsin60∘=mg
Ncos60∘=mω2a2
∴ tan60∘=2gω2a
⇒ ω2=2ga√3 . Therefore, option (ii) is correct.
EXAMPLE 49
A ball is suspended on a thread from the ceiling of a car. The brakes are applied and the speed of car changes from 5 m/sec to 5/3 m/sec during the time interval of 3 seconds. Find the angle that the thread with the ball will deviate from vertical.
The situation is shown in figure. When the car moves toward right with acceleration a and the rope carrying the mass makes an angle theta. Force acting on the body are:
(1) Weight mg downwards.
(2) Tension T in the rope.
(3) Pseudo force ma toward left.
Since the body is in equilibrium under the action of three force, we can apply condition of equilibrium.
Tcosθ−mg=0 , Tsinθ=ma
tanθ=ag or a=gtanθ
Acceleration, a=13(5−53)=109m/sec2
109=10tanθ or tanθ=19⇒θ=tan−1(19). Therefore, option (i) is correct. 
EXAMPLE 50
A block is kept on a frictionless inclined surface with angle of inclination α. The incline is given an acceleration 'a' to keep the block stationary. Then a is equal to
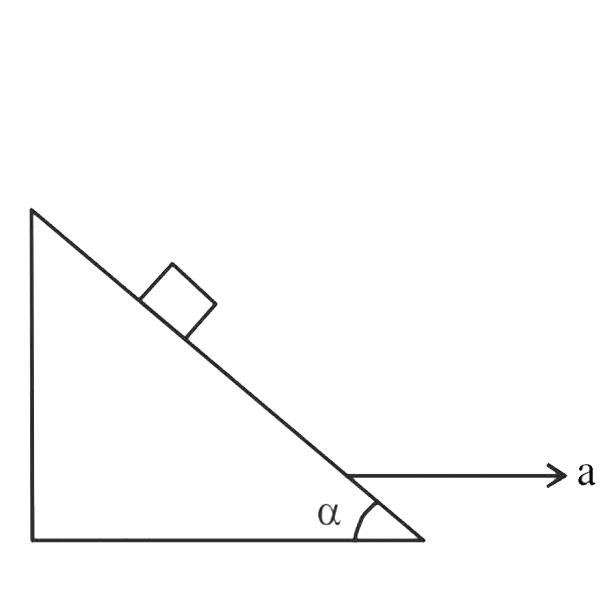
Let the mass of a block is m . It will remain stationary if force acting on it are in equilibrium i.e., macosα=mgsinα⇒a=gtanα
Here mgsinα = Pseudo force on block, mg=weight. Therefore, option (ii) is correct.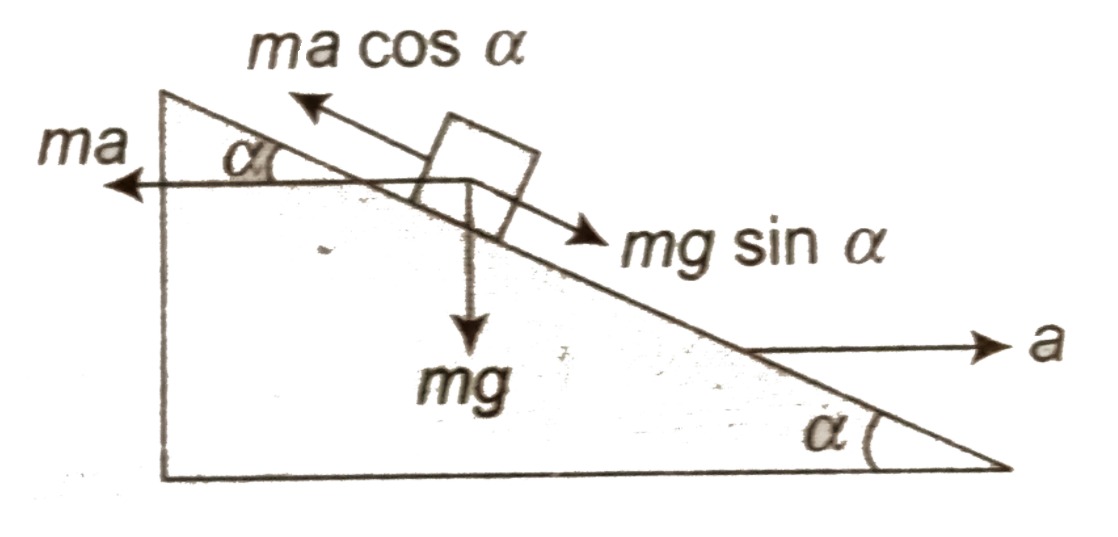
EXAMPLE 51
A box mass m kg is placed on the rear side of an open truck acceleration at 4ms−2 . The coefficient of friction between the box ant the surface below it is 0.4 . The net acceleration of the box with respect to the truck is zero. The value of m is.
Pseudo force on the block
=m×4N (backward)
Force of friction =0.4×m×10N (forward)
Equating, m×4=0.4×m×10
or 4m=4m
Clearly the equation holds good for all values of m. Therefore, option (iv) is correct.
KEY FORMULA
* Net external force: →Fnet=∑→F=→F1+→F2+....
* Newton’s first law: →v= constant when →Fnet=→0N
* Newton’s second law, vector form: →Fnet=∑→F=m→a
* Newton’s second law, scalar form: Fnet=ma
* Newton’s second law, component form: ∑→Fx=m→ax
∑→Fy=m→ay
∑→Fz=m→az
* Newton’s second law, momentum form: →Fnet=d→pdt
* Definition of weight, vector form: →w=m→g
* Definition of weight, scalar form: w=mg
* Newton’s third law: →FAB=−→FBA
* Normal force on an object resting on a horizontal surface, vector form: →N=−m→g
* Normal force on an object resting on a horizontal surface, scalar form: N=mg
* Normal force on an object resting on an inclined plane, scalar form: N=mgcosθ
* Tension in a cable supporting an object of mass m at rest, scalar form: T=w=mg
SUMMARY
1. Aristotle’s view that a force is necessary to keep a body in uniform motion is wrong. A force is necessary in practice to counter the opposing force of friction.
2. Galileo extrapolated simple observations on motion of bodies on inclined planes, and arrived at the law of inertia. Newton’s first law of motion is the same law rephrase thus: “Everybody continues to be in its state of rest or of uniform motion in a straight line, unless compelled by some external force to act otherwise”. In simple terms, the First Law is “If external force on a body is zero, its acceleration is zero”.
3. Momentum (p ) of a body is the product of its mass (m) and velocity (v) : p=mv
4. Newton’s second law of motion : The rate of change of momentum of a body is proportional to the applied force and takes place in the direction in which the force acts. Thus F=k(dpdt)=kma where F is the net external force on the body and its acceleration. We set the constant of proportionality k=1 in SI units. Then F=(dpdt)=ma The SI unit of force is newton : 1N=1kgms−2 .
(a) The second law is consistent with the First Law (F=0 implies a=0)
(b) It is a vector equation
(c) It is applicable to a particle, and also to a body or a system of particles, provided F is the total external force on the system and a is the acceleration of the system as a whole.
(d) F at a point at a certain instant determines a at the same point at that instant. That is the Second Law is a local law; a at an instant does not depend on the history of motion.
5. Impulse is the product of force and time which equals change in momentum. The notion of impulse is useful when a large force acts for a short time to produce a measurable change in momentum. Since the time of action of the force is very short, one can assume that there is no appreciable change in the position of the body during the action of the impulsive force.
6. Newton’s third law of motion: To every action, there is always an equal and opposite reaction In simple terms, the law can be stated thus : Forces in nature always occur between pairs of bodies. Force on a body A by body B is equal and opposite to the force on the body B by A. Action and reaction forces are simultaneous forces. There is no cause-effect relation between action and reaction. Any of the two mutual forces can be called action and the other reaction. Action and reaction act on different bodies and so they cannot be cancelled out. The internal action and reaction forces between different parts of a body do, however, sum to zero.
7. Law of Conservation of Momentum: The total momentum of an isolated system of particles is conserved. The law follows from the second and third law of motion.
8. Friction: Frictional force opposes (impending or actual) relative motion between two surfaces in contact. It is the component of the contact force along the common tangent to the surface in contact. Static friction fs opposes impending relative motion; kinetic friction fk opposes actual relative motion.
9. Force is not always in the direction of motion. Depending on the situation, F may be along v, opposite to v, normal to v or may make some other angle with v. In every case, it is parallel to acceleration.
10. If v=0 at an instant, i.e. if a body is momentarily at rest, it does not mean that force or acceleration are necessarily zero at that instant. For example, when a ball thrown upward reaches its maximum height, v=0 but the force continues to be its weight mg and the acceleration is not zero but g.
11. Force on a body at a given time is determined by the situation at the location of the body at that time. Force is not ‘carried’ by the body from its earlier history of motion. The moment after a stone is released out of an accelerated train, there is no horizontal force (or acceleration) on the stone, if the effects of the surrounding air are neglected. The stone then has only the vertical force of gravity.
12. In the second law of motion F=ma, F stands for the net force due to all material agencies external to the body. a is the effect of the force. ma should not be regarded as yet another force, besides F.
13. The centripetal force should not be regarded as yet another kind of force. It is simply a name given to the force that provides inward radial acceleration to a body in circular motion. We should always look for some material force like tension, gravitational force, electrical force, friction, etc as the centripetal force in any circular motion.
14. Static friction is a self-adjusting force up to its limit µs N (f_s <= µ_s N). Do not put fs=µsN without being sure that the maximum value of static friction is coming into play.
15. The familiar equation mg = R for a body on a table is true only if the body is in equilibrium. The two forces mg and R can be different (e.g. a body in an accelerated lift). The equality of mg and R has no connection with the third law.
16. The terms ‘action’ and ‘reaction’ in the third Law of Motion simply stand for simultaneous mutual forces between a pair of bodies. Unlike their meaning in ordinary language, action does not precede or cause reaction. Action and reaction act on different bodies.
17. The different terms like ‘friction’, ‘normal reaction’ ‘tension’, ‘air resistance’, ‘viscous drag’, ‘thrust’, ‘buoyancy’ ‘weight’ ‘centripetal force’ all stand for ‘force’ in different contexts. For clarity, every force and its equivalent terms encountered in mechanics should be reduced to the phrase ‘force on A by B’.
18. For applying the second law of motion, there is no conceptual distinction between inanimate and animate objects. An animate object such as a human also requires an external force to accelerate. For example, without the external force of friction, we cannot walk on the ground.
19. The objective concept of force in physics should not be confused with the subjective concept of the ‘feeling of force’. On a merry-go-around, all parts of our body are subject to an inward force, but we have a feeling of being pushed outward – the direction of impending motion.