MOTION IN ONE DIMENSION for Class 11 PHYSICS
INTRODUCTION
Is chapter me hum Motion in one dimension ko study krenge. Hume pata hai ki nature surrounding hai jaha hum rehte hai. Hume ye bhi pata hai ki Physics is the study of nature and natural phenomena. Ager aap nature ko bahut carefully observe kre to aap dekhenge ki kuchh objects rest pr hai aur kuchh motion me. Eg: Niche diye image me buildings rest pr hai aur vehicles move kr rahe hai.

Is chapter me hum velocity aur acceleration ke concepts ko samjhenge aur simple situations me apply krenge. One dimension, one ka matlab hai motion along a line ya ek particular direction me motion.
There are three features of motion that we use to describe exactly how an object moves. They are:
1. position jo object ka location ya displacement batata hai.
2. speed jo batata hai ki kitna fast object move kr raha hai ya velocity jo batata hai ki object kitna fast move kr raha batata hai aur object ka direction kya hai.
3. acceleration jo batata hai object ka speed aur velocity kitna fast change ho raha hai.
INTRODUCTION
Is chapter me hum Motion in one dimension ko study krenge. Hume pata hai ki nature surrounding hai jaha hum rehte hai. Hume ye bhi pata hai ki Physics is the study of nature and natural phenomena. Ager aap nature ko bahut carefully observe kre to aap dekhenge ki kuchh objects rest pr hai aur kuchh motion me. Eg: Niche diye image me buildings rest pr hai aur vehicles move kr rahe hai.

Is chapter me hum velocity aur acceleration ke concepts ko samjhenge aur simple situations me apply krenge. One dimension, one ka matlab hai motion along a line ya ek particular direction me motion.
There are three features of motion that we use to describe exactly how an object moves. They are:
1. position jo object ka location ya displacement batata hai.
2. speed jo batata hai ki kitna fast object move kr raha hai ya velocity jo batata hai ki object kitna fast move kr raha batata hai aur object ka direction kya hai.
3. acceleration jo batata hai object ka speed aur velocity kitna fast change ho raha hai.
INTRODUCTION
Is chapter me hum Motion in one dimension ko study krenge. Hume pata hai ki nature surrounding hai jaha hum rehte hai. Hume ye bhi pata hai ki Physics is the study of nature and natural phenomena. Ager aap nature ko bahut carefully observe kre to aap dekhenge ki kuchh objects rest pr hai aur kuchh motion me. Eg: Niche diye image me buildings rest pr hai aur vehicles move kr rahe hai.

Is chapter me hum velocity aur acceleration ke concepts ko samjhenge aur simple situations me apply krenge. One dimension, one ka matlab hai motion along a line ya ek particular direction me motion.
There are three features of motion that we use to describe exactly how an object moves. They are:
1. position jo object ka location ya displacement batata hai.
2. speed jo batata hai ki kitna fast object move kr raha hai ya velocity jo batata hai ki object kitna fast move kr raha batata hai aur object ka direction kya hai.
3. acceleration jo batata hai object ka speed aur velocity kitna fast change ho raha hai.
LET'S UNDERSTAND MECHANICS...
Mechanics is the branch of physics that deals with the study of particles or bodies at rest or in motion. Hum basically objects at rest aur objects in motion ke bare me study krenge. Mechanics ko do branch me divide kiya gya hai. First branch ko statics kehte hai aur second branch ko dynamics kehte hai. Statics is the study of objects at rest. Dynamics is the study of objects in motion. Is chapter ka naam hai Motion in one Dimension isliye ye chapter dynamics branch ke ander aata hai.
Motion samjhne ke liye hum ek example lete hai. Image me aap dekhenge ek racing car hai jo motion me hai. Jab hum motion ke bare me baat krte hai, humare mind me do questions aata hai. First question: How does an object move? Second question: Why does an object move? In dono question ko answer krne ke liye pehle hum Dynamics ke bare me jante hai.

Dynamics do branch me divided hai. First branch: Kinematics which is the study of the relationship between displacement, velocity, acceleration and time of a given motion, without considering the forces that cause the motion. Isme hum motion ke parameters ko study krte hai bina cause of force ko consider kre. So, Kinematics first question ka answer deta hai, how does an object move. Second branch: Kinetics which is the study of relationship between motion of bodies and forces acting on them. Isme hum cause of motion (force) ko study karte hai. So, Kinetics second question ka answer deta hai, Why does an object move. Is chapter me hum Kinematics study karenge. Kinematics is used to relate displacement, velocity, acceleration and time without reference to the cause of motion. We shall discuss about kinematics of the particle here.
LET'S UNDERSTAND MECHANICS...
Mechanics is the branch of physics that deals with the study of particles or bodies at rest or in motion. Hum basically objects at rest aur objects in motion ke bare me study krenge. Mechanics ko do branch me divide kiya gya hai. First branch ko statics kehte hai aur second branch ko dynamics kehte hai. Statics is the study of objects at rest. Dynamics is the study of objects in motion. Is chapter ka naam hai Motion in one Dimension isliye ye chapter dynamics branch ke ander aata hai.
Motion samjhne ke liye hum ek example lete hai. Image me aap dekhenge ek racing car hai jo motion me hai. Jab hum motion ke bare me baat krte hai, humare mind me do questions aata hai. First question: How does an object move? Second question: Why does an object move? In dono question ko answer krne ke liye pehle hum Dynamics ke bare me jante hai.

Dynamics do branch me divided hai. First branch: Kinematics which is the study of the relationship between displacement, velocity, acceleration and time of a given motion, without considering the forces that cause the motion. Isme hum motion ke parameters ko study krte hai bina cause of force ko consider kre. So, Kinematics first question ka answer deta hai, how does an object move. Second branch: Kinetics which is the study of relationship between motion of bodies and forces acting on them. Isme hum cause of motion (force) ko study karte hai. So, Kinetics second question ka answer deta hai, Why does an object move. Is chapter me hum Kinematics study karenge. Kinematics is used to relate displacement, velocity, acceleration and time without reference to the cause of motion. We shall discuss about kinematics of the particle here.
LET'S UNDERSTAND MECHANICS...
Mechanics is the branch of physics that deals with the study of particles or bodies at rest or in motion. Hum basically objects at rest aur objects in motion ke bare me study krenge. Mechanics ko do branch me divide kiya gya hai. First branch ko statics kehte hai aur second branch ko dynamics kehte hai. Statics is the study of objects at rest. Dynamics is the study of objects in motion. Is chapter ka naam hai Motion in one Dimension isliye ye chapter dynamics branch ke ander aata hai.
Motion samjhne ke liye hum ek example lete hai. Image me aap dekhenge ek racing car hai jo motion me hai. Jab hum motion ke bare me baat krte hai, humare mind me do questions aata hai. First question: How does an object move? Second question: Why does an object move? In dono question ko answer krne ke liye pehle hum Dynamics ke bare me jante hai.

Dynamics do branch me divided hai. First branch: Kinematics which is the study of the relationship between displacement, velocity, acceleration and time of a given motion, without considering the forces that cause the motion. Isme hum motion ke parameters ko study krte hai bina cause of force ko consider kre. So, Kinematics first question ka answer deta hai, how does an object move. Second branch: Kinetics which is the study of relationship between motion of bodies and forces acting on them. Isme hum cause of motion (force) ko study karte hai. So, Kinetics second question ka answer deta hai, Why does an object move. Is chapter me hum Kinematics study karenge. Kinematics is used to relate displacement, velocity, acceleration and time without reference to the cause of motion. We shall discuss about kinematics of the particle here.
MOTION
An object is said to be in motion, if it changes its position with the passage of time.
Kisi bhi object ke motion ko describe karne ke liye hume us object ki position ki zaroorat hoti hai. Iske liye hume position coordinate pata hona chahiye. Kuchh cases me hume teen position coordinates, kuchh me do aur ek position coordinates ki zaroorat hoti hai. Iske basis pr hum motion ko classify kr sakte hai:-
One dimensional motion (1-D): Jab particle straight line me move karta hai, us path ko hum 1D motion kahte hai. For eg. motion of a train in a straight line. One dimensional motion is sometimes known as rectilinear or linear motion.
Two dimensional motion (2-D): Jab particle ek plane me move karta hai, tab us 2D motion kahte hai. For eg. carrom board ke coins.
Three dimensional motion (3-D): Jab particle space me move karta hai, us hum 3D motion kahte hai. For eg. motion of kite in the sky.
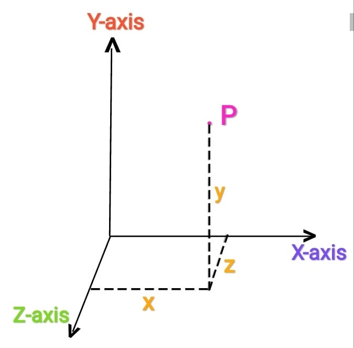
Position
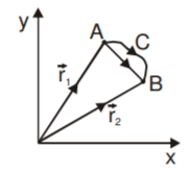
It is defined with respect to some reference point (origin) of a given frame of reference. Consider kare ek particle jo location r1 (at time t1 ) se location r2 (at time t2 ) move kr raha hai ACB path follow karke jaisa ki aap niche diye image me dekhenge.
A frame of reference is an arbitrary set of axes from which the position and motion of an object are described. Earth ko hum jyadatar as frame of reference use krte hai. For example, ek rocket launch ke position ko hum describe krenge in terms of the position of the rocket with respect to Earth, lekin ek cyclist ke position ko hum describe krenge in terms of where she is in relation to the buildings she passes.

MOTION PARAMETERS
There are five basic parameters which are necessary to study a motion:1. Distance
2. Displacement
3. Speed
4. Velocity
5. Acceleration
Hum pehle samjhte hai ki kab ek object ko motion me bataya jata hai. Jab ek object apna position change krta hai with the passage of time, tab kehte hai ki object motion me hai. Ek particle ke motion ko describe krne ke liye jo quantities ki requirement hoti hai unhe basic parameters kehte hai. Ye particle ke motion ko study krne ke liye bahut jaruri hote hai. Hume pata krna hai particle kaha hai ek particle instant of time me to hume distance aur displacement ki requirement hogi. Hume pata krna hai ki particle kitna fast travel kr raha hai to hume speed aur velocity ki requirement hogi aur hume pata krna hai ki particle apna speed change kr raha hai ya nahi, wo accelerate ho raha hai ya decelerate ho raha hai, to hume acceleration ki requirement hogi.
DISTANCE
The length of the actual path traversed by the particle is termed as its distance.Niche diye image me, Distance = length of path ACB.

Its SI unit is metre (m) and it is a scalar quantity. It can never decrease with time.
Dimensions of Distance [M0L1T0]
For example: Image me aap dekhenge professor ka distance 2.0 m hai.

DISPLACEMENT
Displacement is the difference between the final and initial positions of the object in a given interval of time. The change in position vector of the particle for a given time interval is known as its displacement.Kisi particle ke initial aur final position ke bich ke minimum distance ko displacement kehte hai.
Displacement is a vector quantity and its SI unit is metre (m).
Dimensions of Displacement [M0L1T0].
Distance aur displacement ke S.I unit aur dimensions same hai. It can decrease with time.

Jab koi particle path ABC pr point A se point C move krta hai to actual path length ABC uska distance travelled hoga aur S=δr=rc−ra uska displacement hoga.
Displacement ka magnitude aur direction dono hota hai. Isliye displacement ko vectors se represent karte hai. One dimensional motion me, sirf do hi direction hote hai (backward aur forward, upward aur downward) jisme object move karta hai, aur in do direction ko hum + aur − signs se indicate karte hai. Negative sign indicate krta hai displacement ka direction. Isliye one dimension me objects ke motion ko describe krne ke liye vector notation ki zaroorat nahi hoti hai.
Professor wale example me aap dekhenge lecturing ke time, ek professor left right move karti hai. Suppose unka position relative to earth is given by x. +2.0m professor ka displacement relative to Earth hai jo arrow se represented hai aur right point kr raha hai.
For a moving particle in a given interval of time:
DISTINCTION BETWEEN DISTANCE AND DISPLACEMENT
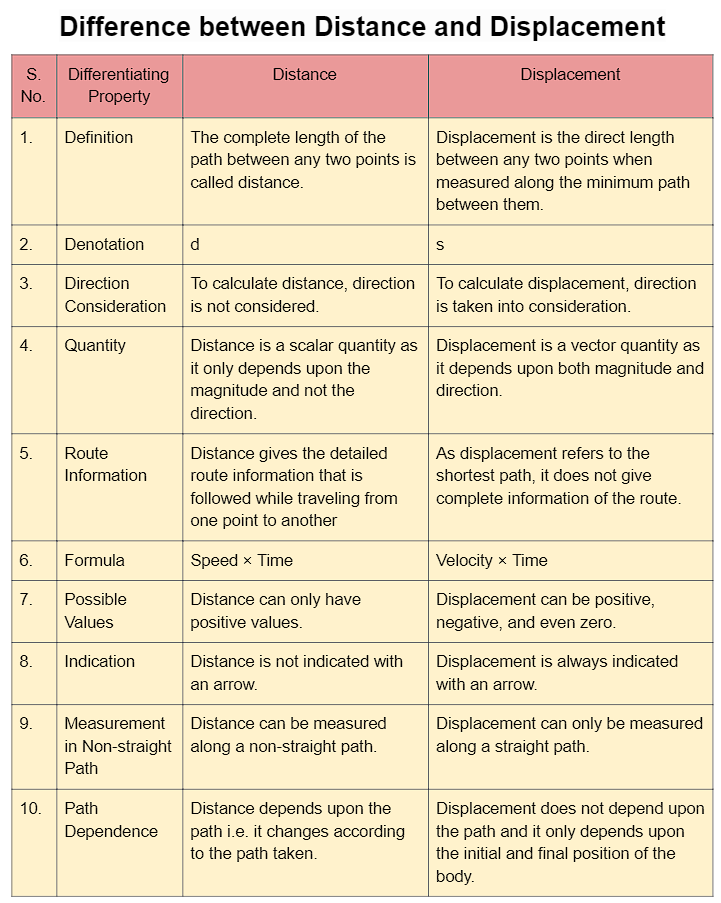
DISTANCE AND DISPLACEMENT OF PARTICLE WHEN IT CHANGES ITS DIRECTION OF MOTION
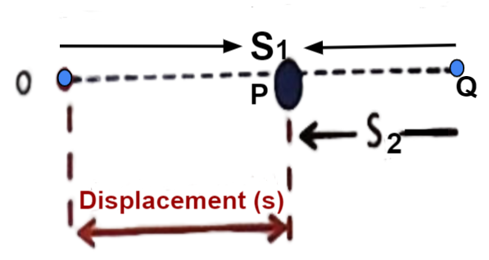
Kya aapko pata hai koi particle jo one dimension me move kr raha hai uske liye kab distance aur displacement different hoga? Ye dono different tab hoge jab particle apna motion ka direction change krega matlab apna motion ka direction reverse krega.Example 1: Suppose ek particle point O se travel krna start krta hai aur point Q reach krta hai jisme distance s1 travel krta hai. Phir particle apna direction reverse krta hai. Point P reach krne me particle s2 distance travel krta hai.
Is case me Displacement, →S=→S1+→S2
Ye n number of changes in direction ke liye apply ho sakta hai.
Note: This can be applied for n number of changes in direction, the net displacement vector sum of all displacements.
→S=→S1+→S2+→S3+........+→Sn
Ab hum same case me distance travelled discuss krenge;
Hum distance travelled calculate krne me, direction ko consider nahi krenge.
The net distance, x=∣∣→S1∣∣+∣∣→S2∣∣
Note: This can be applied for n number of changes in direction, the net distance travelled is equal to the addition of magnitude of all displacements.
x=∣∣→S1∣∣+∣∣→S2∣∣+∣∣→S3∣∣+∣∣→Sn∣∣
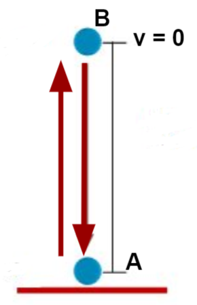
Example 2: Jab ek ball ko hum upr throw krenge, suppose point A se, to highest point, point B, reach krne ke baad wo apne motion ka direction reverse krega aur niche aaega. Koi body (particle) jab kisi point pr apna motion ka direction reverse krta hai to us point pr uska velocity zero hota hai.
MOTION
An object is said to be in motion, if it changes its position with the passage of time.
Kisi bhi object ke motion ko describe karne ke liye hume us object ki position ki zaroorat hoti hai. Iske liye hume position coordinate pata hona chahiye. Kuchh cases me hume teen position coordinates, kuchh me do aur ek position coordinates ki zaroorat hoti hai. Iske basis pr hum motion ko classify kr sakte hai:-
One dimensional motion (1-D): Jab particle straight line me move karta hai, us path ko hum 1D motion kahte hai. For eg. motion of a train in a straight line. One dimensional motion is sometimes known as rectilinear or linear motion.
Two dimensional motion (2-D): Jab particle ek plane me move karta hai, tab us 2D motion kahte hai. For eg. carrom board ke coins.
Three dimensional motion (3-D): Jab particle space me move karta hai, us hum 3D motion kahte hai. For eg. motion of kite in the sky.

Position
It is defined with respect to some reference point (origin) of a given frame of reference. Consider kare ek particle jo location r1 (at time t1 ) se location r2 (at time t2 ) move kr raha hai ACB path follow karke jaisa ki aap niche diye image me dekhenge.

A frame of reference is an arbitrary set of axes from which the position and motion of an object are described. Earth ko hum jyadatar as frame of reference use krte hai. For example, ek rocket launch ke position ko hum describe krenge in terms of the position of the rocket with respect to Earth, lekin ek cyclist ke position ko hum describe krenge in terms of where she is in relation to the buildings she passes.

MOTION PARAMETERS
There are five basic parameters which are necessary to study a motion:1. Distance
2. Displacement
3. Speed
4. Velocity
5. Acceleration
Hum pehle samjhte hai ki kab ek object ko motion me bataya jata hai. Jab ek object apna position change krta hai with the passage of time, tab kehte hai ki object motion me hai. Ek particle ke motion ko describe krne ke liye jo quantities ki requirement hoti hai unhe basic parameters kehte hai. Ye particle ke motion ko study krne ke liye bahut jaruri hote hai. Hume pata krna hai particle kaha hai ek particle instant of time me to hume distance aur displacement ki requirement hogi. Hume pata krna hai ki particle kitna fast travel kr raha hai to hume speed aur velocity ki requirement hogi aur hume pata krna hai ki particle apna speed change kr raha hai ya nahi, wo accelerate ho raha hai ya decelerate ho raha hai, to hume acceleration ki requirement hogi.
DISTANCE
The length of the actual path traversed by the particle is termed as its distance.Niche diye image me, Distance = length of path ACB.

Its SI unit is metre (m) and it is a scalar quantity. It can never decrease with time.
Dimensions of Distance [M0L1T0]
For example: Image me aap dekhenge professor ka distance 2.0 m hai.

DISPLACEMENT
Displacement is the difference between the final and initial positions of the object in a given interval of time. The change in position vector of the particle for a given time interval is known as its displacement.Kisi particle ke initial aur final position ke bich ke minimum distance ko displacement kehte hai.
Displacement is a vector quantity and its SI unit is metre (m).
Dimensions of Displacement [M0L1T0].
Distance aur displacement ke S.I unit aur dimensions same hai. It can decrease with time.

Jab koi particle path ABC pr point A se point C move krta hai to actual path length ABC uska distance travelled hoga aur S=δr=rc−ra uska displacement hoga.
Displacement ka magnitude aur direction dono hota hai. Isliye displacement ko vectors se represent karte hai. One dimensional motion me, sirf do hi direction hote hai (backward aur forward, upward aur downward) jisme object move karta hai, aur in do direction ko hum + aur − signs se indicate karte hai. Negative sign indicate krta hai displacement ka direction. Isliye one dimension me objects ke motion ko describe krne ke liye vector notation ki zaroorat nahi hoti hai.
Professor wale example me aap dekhenge lecturing ke time, ek professor left right move karti hai. Suppose unka position relative to earth is given by x. +2.0m professor ka displacement relative to Earth hai jo arrow se represented hai aur right point kr raha hai.
For a moving particle in a given interval of time:
DISTINCTION BETWEEN DISTANCE AND DISPLACEMENT

DISTANCE AND DISPLACEMENT OF PARTICLE WHEN IT CHANGES ITS DIRECTION OF MOTION
Kya aapko pata hai koi particle jo one dimension me move kr raha hai uske liye kab distance aur displacement different hoga? Ye dono different tab hoge jab particle apna motion ka direction change krega matlab apna motion ka direction reverse krega.Example 1: Suppose ek particle point O se travel krna start krta hai aur point Q reach krta hai jisme distance s1 travel krta hai. Phir particle apna direction reverse krta hai. Point P reach krne me particle s2 distance travel krta hai.
Is case me Displacement, →S=→S1+→S2
Ye n number of changes in direction ke liye apply ho sakta hai.

Note: This can be applied for n number of changes in direction, the net displacement vector sum of all displacements.
→S=→S1+→S2+→S3+........+→Sn
Ab hum same case me distance travelled discuss krenge;
Hum distance travelled calculate krne me, direction ko consider nahi krenge.
The net distance, x=∣∣→S1∣∣+∣∣→S2∣∣
Note: This can be applied for n number of changes in direction, the net distance travelled is equal to the addition of magnitude of all displacements.
x=∣∣→S1∣∣+∣∣→S2∣∣+∣∣→S3∣∣+∣∣→Sn∣∣
Example 2: Jab ek ball ko hum upr throw krenge, suppose point A se, to highest point, point B, reach krne ke baad wo apne motion ka direction reverse krega aur niche aaega. Koi body (particle) jab kisi point pr apna motion ka direction reverse krta hai to us point pr uska velocity zero hota hai.

MOTION
An object is said to be in motion, if it changes its position with the passage of time.
Kisi bhi object ke motion ko describe karne ke liye hume us object ki position ki zaroorat hoti hai. Iske liye hume position coordinate pata hona chahiye. Kuchh cases me hume teen position coordinates, kuchh me do aur ek position coordinates ki zaroorat hoti hai. Iske basis pr hum motion ko classify kr sakte hai:-
One dimensional motion (1-D): Jab particle straight line me move karta hai, us path ko hum 1D motion kahte hai. For eg. motion of a train in a straight line. One dimensional motion is sometimes known as rectilinear or linear motion.
Two dimensional motion (2-D): Jab particle ek plane me move karta hai, tab us 2D motion kahte hai. For eg. carrom board ke coins.
Three dimensional motion (3-D): Jab particle space me move karta hai, us hum 3D motion kahte hai. For eg. motion of kite in the sky.

Position
It is defined with respect to some reference point (origin) of a given frame of reference. Consider kare ek particle jo location r1 (at time t1 ) se location r2 (at time t2 ) move kr raha hai ACB path follow karke jaisa ki aap niche diye image me dekhenge.

A frame of reference is an arbitrary set of axes from which the position and motion of an object are described. Earth ko hum jyadatar as frame of reference use krte hai. For example, ek rocket launch ke position ko hum describe krenge in terms of the position of the rocket with respect to Earth, lekin ek cyclist ke position ko hum describe krenge in terms of where she is in relation to the buildings she passes.

MOTION PARAMETERS
There are five basic parameters which are necessary to study a motion:1. Distance
2. Displacement
3. Speed
4. Velocity
5. Acceleration
Hum pehle samjhte hai ki kab ek object ko motion me bataya jata hai. Jab ek object apna position change krta hai with the passage of time, tab kehte hai ki object motion me hai. Ek particle ke motion ko describe krne ke liye jo quantities ki requirement hoti hai unhe basic parameters kehte hai. Ye particle ke motion ko study krne ke liye bahut jaruri hote hai. Hume pata krna hai particle kaha hai ek particle instant of time me to hume distance aur displacement ki requirement hogi. Hume pata krna hai ki particle kitna fast travel kr raha hai to hume speed aur velocity ki requirement hogi aur hume pata krna hai ki particle apna speed change kr raha hai ya nahi, wo accelerate ho raha hai ya decelerate ho raha hai, to hume acceleration ki requirement hogi.
DISTANCE
The length of the actual path traversed by the particle is termed as its distance.Niche diye image me, Distance = length of path ACB.

Its SI unit is metre (m) and it is a scalar quantity. It can never decrease with time.
Dimensions of Distance [M0L1T0]
For example: Image me aap dekhenge professor ka distance 2.0 m hai.

DISPLACEMENT
Displacement is the difference between the final and initial positions of the object in a given interval of time. The change in position vector of the particle for a given time interval is known as its displacement.Kisi particle ke initial aur final position ke bich ke minimum distance ko displacement kehte hai.
Displacement is a vector quantity and its SI unit is metre (m).
Dimensions of Displacement [M0L1T0].
Distance aur displacement ke S.I unit aur dimensions same hai. It can decrease with time.

Jab koi particle path ABC pr point A se point C move krta hai to actual path length ABC uska distance travelled hoga aur S=δr=rc−ra uska displacement hoga.
Displacement ka magnitude aur direction dono hota hai. Isliye displacement ko vectors se represent karte hai. One dimensional motion me, sirf do hi direction hote hai (backward aur forward, upward aur downward) jisme object move karta hai, aur in do direction ko hum + aur − signs se indicate karte hai. Negative sign indicate krta hai displacement ka direction. Isliye one dimension me objects ke motion ko describe krne ke liye vector notation ki zaroorat nahi hoti hai.
Professor wale example me aap dekhenge lecturing ke time, ek professor left right move karti hai. Suppose unka position relative to earth is given by x. +2.0m professor ka displacement relative to Earth hai jo arrow se represented hai aur right point kr raha hai.
For a moving particle in a given interval of time:
DISTINCTION BETWEEN DISTANCE AND DISPLACEMENT

DISTANCE AND DISPLACEMENT OF PARTICLE WHEN IT CHANGES ITS DIRECTION OF MOTION
Kya aapko pata hai koi particle jo one dimension me move kr raha hai uske liye kab distance aur displacement different hoga? Ye dono different tab hoge jab particle apna motion ka direction change krega matlab apna motion ka direction reverse krega.Example 1: Suppose ek particle point O se travel krna start krta hai aur point Q reach krta hai jisme distance s1 travel krta hai. Phir particle apna direction reverse krta hai. Point P reach krne me particle s2 distance travel krta hai.
Is case me Displacement, →S=→S1+→S2
Ye n number of changes in direction ke liye apply ho sakta hai.

Note: This can be applied for n number of changes in direction, the net displacement vector sum of all displacements.
→S=→S1+→S2+→S3+........+→Sn
Ab hum same case me distance travelled discuss krenge;
Hum distance travelled calculate krne me, direction ko consider nahi krenge.
The net distance, x=∣∣→S1∣∣+∣∣→S2∣∣
Note: This can be applied for n number of changes in direction, the net distance travelled is equal to the addition of magnitude of all displacements.
x=∣∣→S1∣∣+∣∣→S2∣∣+∣∣→S3∣∣+∣∣→Sn∣∣
Example 2: Jab ek ball ko hum upr throw krenge, suppose point A se, to highest point, point B, reach krne ke baad wo apne motion ka direction reverse krega aur niche aaega. Koi body (particle) jab kisi point pr apna motion ka direction reverse krta hai to us point pr uska velocity zero hota hai.

EXAMPLE 1
A particle starts from the origin, goes along the X-axis to the pont (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
Distance = |OA| + |AC|
= 20 + 40 = 60 m
Displacement = OA + AC
=20ˆi+(−40ˆi)=(−20ˆi)m

EXAMPLE 1
A particle starts from the origin, goes along the X-axis to the pont (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
Distance = |OA| + |AC|
= 20 + 40 = 60 m
Displacement = OA + AC
=20ˆi+(−40ˆi)=(−20ˆi)m

EXAMPLE 1
A particle starts from the origin, goes along the X-axis to the pont (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
Distance = |OA| + |AC|
= 20 + 40 = 60 m
Displacement = OA + AC
=20ˆi+(−40ˆi)=(−20ˆi)m

EXAMPLE 2
A car moves from O to D along the path OABCD shown in fig.
What is distance travelled and net displacement.
Distance =∣∣∣−−→OA∣∣∣+∣∣∣−−→AB∣∣∣+∣∣∣−−→BC∣∣∣+∣∣∣−−→CD∣∣∣
=8+4+4+1=17km
Displacement =−−→OA+−−→AB+−−→BC+−−→CD
=8ˆi+(−4ˆj)+(−4ˆi)+ˆj=4ˆi−3ˆj
⇒|displacement|=√(4)2+(3)2=5
So, Displacement = 5km, 37∘ S of E
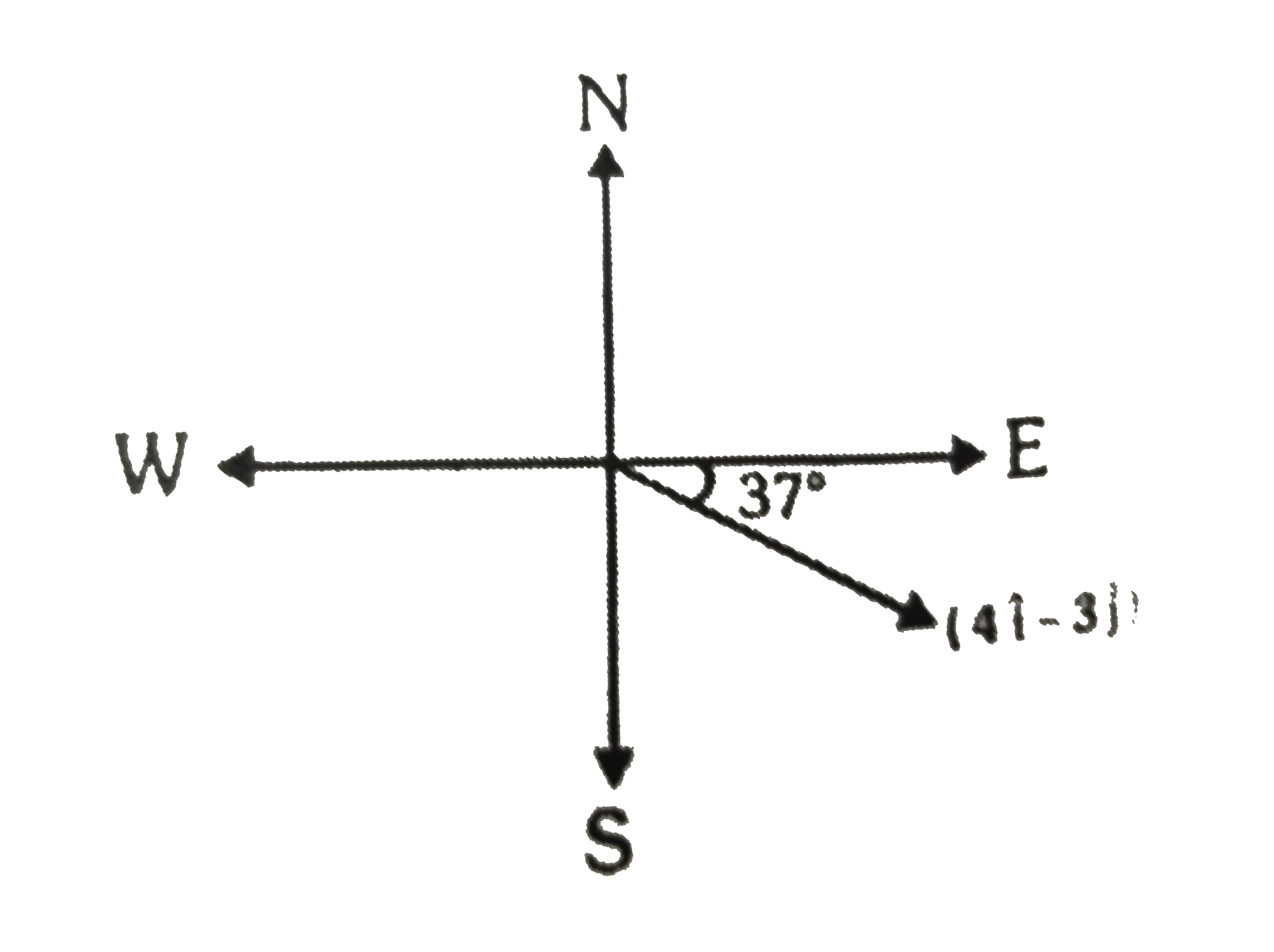
EXAMPLE 2
A car moves from O to D along the path OABCD shown in fig.
What is distance travelled and net displacement.
Distance =∣∣∣−−→OA∣∣∣+∣∣∣−−→AB∣∣∣+∣∣∣−−→BC∣∣∣+∣∣∣−−→CD∣∣∣
=8+4+4+1=17km
Displacement =−−→OA+−−→AB+−−→BC+−−→CD
=8ˆi+(−4ˆj)+(−4ˆi)+ˆj=4ˆi−3ˆj
⇒|displacement|=√(4)2+(3)2=5
So, Displacement = 5km, 37∘ S of E

EXAMPLE 2
A car moves from O to D along the path OABCD shown in fig.
What is distance travelled and net displacement.
Distance =∣∣∣−−→OA∣∣∣+∣∣∣−−→AB∣∣∣+∣∣∣−−→BC∣∣∣+∣∣∣−−→CD∣∣∣
=8+4+4+1=17km
Displacement =−−→OA+−−→AB+−−→BC+−−→CD
=8ˆi+(−4ˆj)+(−4ˆi)+ˆj=4ˆi−3ˆj
⇒|displacement|=√(4)2+(3)2=5
So, Displacement = 5km, 37∘ S of E

EXAMPLE 3
A particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
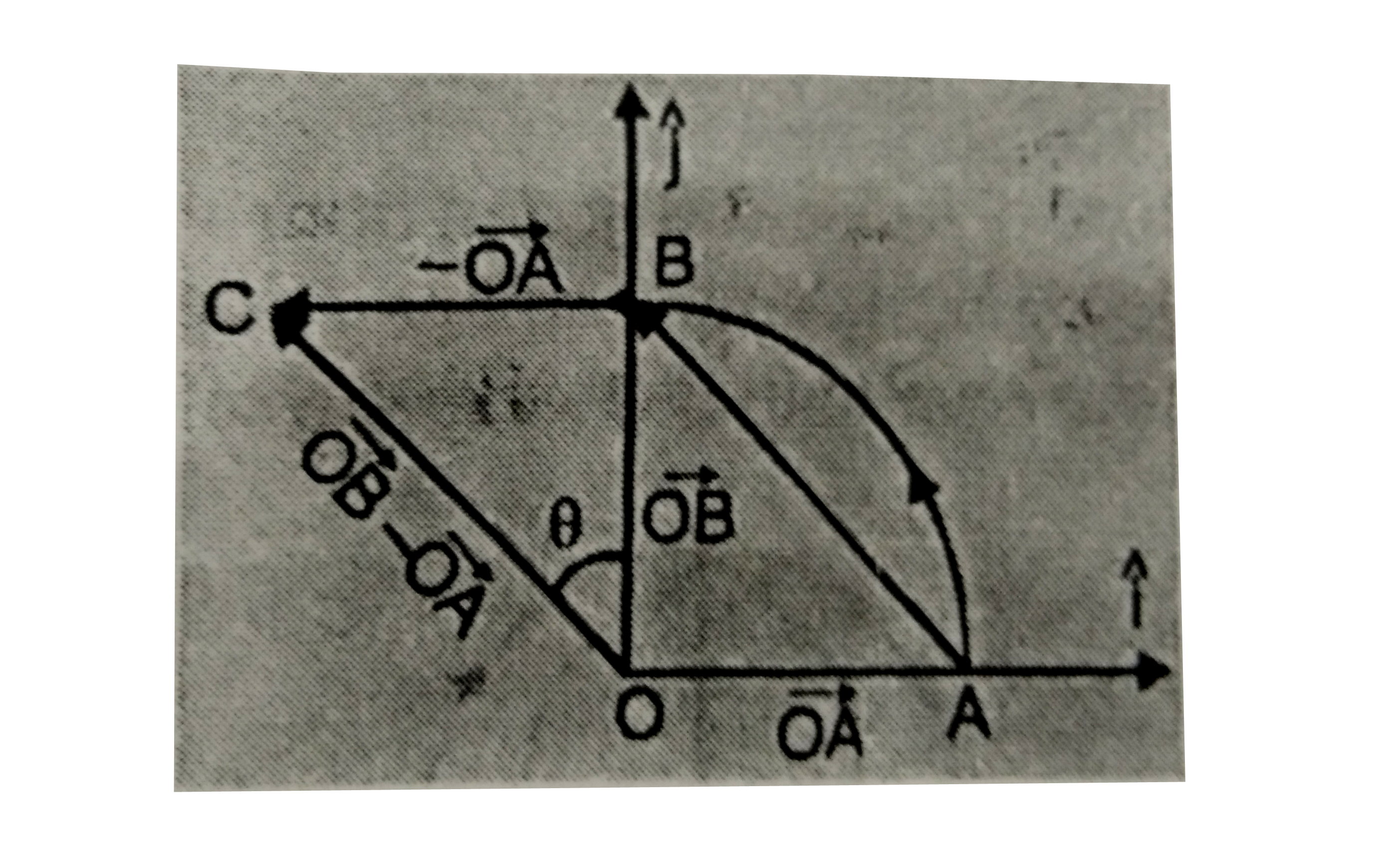
Displacement −−→AB=−−→OB−−−→OA=(10ˆj−10ˆi) m
∣∣∣−−→AB∣∣∣=√102+102=10√2m
From ΔOBCtanθ=OAOB=1010=1⇒θ=45∘
Angle between displacement vector −−→OC and x-axis = 90∘+45∘=135∘
Distance of path AB = 14 (circumference) = 14(2πR)m=(5π)m
EXAMPLE 3
A particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?

Displacement −−→AB=−−→OB−−−→OA=(10ˆj−10ˆi) m
∣∣∣−−→AB∣∣∣=√102+102=10√2m
From ΔOBCtanθ=OAOB=1010=1⇒θ=45∘
Angle between displacement vector −−→OC and x-axis = 90∘+45∘=135∘
Distance of path AB = 14 (circumference) = 14(2πR)m=(5π)m
EXAMPLE 3
A particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?

Displacement −−→AB=−−→OB−−−→OA=(10ˆj−10ˆi) m
∣∣∣−−→AB∣∣∣=√102+102=10√2m
From ΔOBCtanθ=OAOB=1010=1⇒θ=45∘
Angle between displacement vector −−→OC and x-axis = 90∘+45∘=135∘
Distance of path AB = 14 (circumference) = 14(2πR)m=(5π)m
AVERAGE SPEED
Average speed for the given motion is defined as the ratio of the total distance travelled by the object to the total time taken.
Average speed (Vav) = total distance travelled/ total time taken =ΔSΔt
Average speed aur velocity ka same unit hota hai (m/s).
In M.K.S. = m/s
In C.G.S = cm/s
Speed scalar quantity hai.
Dimension [M0L1T−1]
Average speed moving object ka direction nahi batata hai. Isliye, ye hamesha positive (in contrast to the average velocity which can be positive or negative) hota hai. Jab object ka motion straight line me hai aur uska direction bhi same hai, tab displacement ka magnitude aur total path length dono equal hota hai. Is case me, average velocity ka magnitude aur average speed equal hota hai. Maximum cases me, motion change in direction involve krta hai taki path length displacement ke magnitude se greater ho. Ye show krta hai ki speed velocity ke magnitude se greater hai.
For a moving particle in a given interval of time
AVERAGE VELOCITY
Average velocity is defined ‘as the ratio of total displacement to the total time interval in the given displacement.’Average velocity = total displacement/total time
Ager x2 kisi object ka position hai time t2 pr aur x1 object ka position hai time t1 pr, to average velocity (vav) hoga;
¯v=x2−x1t2−t1=δxδt
Yaha pe jo bar hai velocity symbol ke upar wo standard notation hai jo average quantity indicate krta hai. Velocity ka S.i unit ms or ms−1 hai lekin kmh−1 roj ke applications use hota hai.
Displacement ke jaise hi, average velocity bhi vector quantity hai. Average velocity positive ya negative ho sakta hai, depending upon the sign of the displacement. Jab displacement zero hota hai to average velocity bhi zero hota hai.
Instantaneous Velocity
Instantaneous velocity is defined as Rate of change of displacement.→v=→dSdt
Velocity vector quantity hai.
In M.K.S. = m/s
In C.G.S. = cm/s
Dimension = [M0L1T−1]
For a very small time, the value of displacement in magnitude would be equal to distance.
Therefore, ∣∣∣→dSdt∣∣∣=dxdt
dxdt instantaneous speed hai.
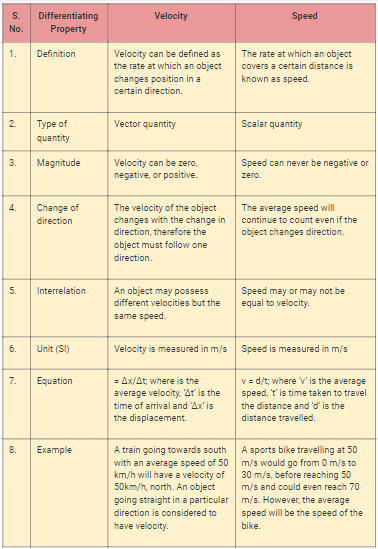
DISTINCTION BETWEEN SPEED AND VELOCITY
OMR (One Minute Revision)
- * Kinematics is the description of motion without considering its causes. In this chapter, it is limited to motion along a straight line, called one-dimensional motion.
* Displacement is the change in position of an object. The SI unit for displacement is the meter. Displacement has direction as well as magnitude.
* Distance traveled is the total length of the path traveled between two positions.
ACCELERATION
The acceleration of the object at a given instant of time or at a given point of motion.Acceleration = change in velocity/time taken
Acceleration vector quantity hai. Ye positive, negative ya zero ho sakta hai. Jab acceleration ka direction body ke movement ek taraf ho, i.e., the velocity of a body is increasing with time, tab acceleration hoga.
Jab acceleration ka direction body ke movement ke direction me hoga, i.e., the velocity of a body is increasing with time, tab acceleration +ve hoga.
Jab acceleration ka direction body ke movement ke opposite direction me hoga, i.e., the velocity of a body is decreasing with time, tab acceleration −ve hoga. Negative acceleration ko retardation ya deceleration kehte hai.
Jab body constant velocity me ho, tab body ka acceleration zero hoga.
Acceleration ka unit MKS system ya S.I me m/s2 hai aur CGS system me cm/s2 hai.
Uniform Acceleration
Jab object ka velocity equally change hota hai equal interval of time me, tab usse uniform acceleration kahte hai.
Variable Acceleration
Jab object ka velocity unequal amount me change hota equal intervals of time me, tab usse variable acceleration ya non-uniform acceleration kahte hai.
Average Acceleration
Average acceleration is defined as the ratio of the total change in the velocity of the object during motion to the total time taken.
Average acceleration, →a(av) = total change in velocity/ total time taken = Δ→vΔt
Instantaneous Acceleration
Jab object variable acceleration me move kr raha hota hai, to different instants of time pr different acceleration possess krta hai, tab us acceleration ko Instantaneous acceleration kahte hai. Instantaneous acceleration is a continuous function of time and gives the acceleration at any specific time during the motion.
Thus, the instantaneous acceleration of an object:
(i) Is equal to the first time derivative of velocity at the given instant.
(ii) Is equal to the second time derivative of position of the object at the given instant.
AVERAGE SPEED
Average speed for the given motion is defined as the ratio of the total distance travelled by the object to the total time taken.
Average speed (Vav) = total distance travelled/ total time taken =ΔSΔt
Average speed aur velocity ka same unit hota hai (m/s).
In M.K.S. = m/s
In C.G.S = cm/s
Speed scalar quantity hai.
Dimension [M0L1T−1]
Average speed moving object ka direction nahi batata hai. Isliye, ye hamesha positive (in contrast to the average velocity which can be positive or negative) hota hai. Jab object ka motion straight line me hai aur uska direction bhi same hai, tab displacement ka magnitude aur total path length dono equal hota hai. Is case me, average velocity ka magnitude aur average speed equal hota hai. Maximum cases me, motion change in direction involve krta hai taki path length displacement ke magnitude se greater ho. Ye show krta hai ki speed velocity ke magnitude se greater hai.
For a moving particle in a given interval of time
AVERAGE VELOCITY
Average velocity is defined ‘as the ratio of total displacement to the total time interval in the given displacement.’Average velocity = total displacement/total time
Ager x2 kisi object ka position hai time t2 pr aur x1 object ka position hai time t1 pr, to average velocity (vav) hoga;
¯v=x2−x1t2−t1=δxδt
Yaha pe jo bar hai velocity symbol ke upar wo standard notation hai jo average quantity indicate krta hai. Velocity ka S.i unit ms or ms−1 hai lekin kmh−1 roj ke applications use hota hai.
Displacement ke jaise hi, average velocity bhi vector quantity hai. Average velocity positive ya negative ho sakta hai, depending upon the sign of the displacement. Jab displacement zero hota hai to average velocity bhi zero hota hai.
Instantaneous Velocity
Instantaneous velocity is defined as Rate of change of displacement.→v=→dSdt
Velocity vector quantity hai.
In M.K.S. = m/s
In C.G.S. = cm/s
Dimension = [M0L1T−1]
For a very small time, the value of displacement in magnitude would be equal to distance.
Therefore, ∣∣∣→dSdt∣∣∣=dxdt
dxdt instantaneous speed hai.
DISTINCTION BETWEEN SPEED AND VELOCITY

OMR (One Minute Revision)
- * Kinematics is the description of motion without considering its causes. In this chapter, it is limited to motion along a straight line, called one-dimensional motion.
* Displacement is the change in position of an object. The SI unit for displacement is the meter. Displacement has direction as well as magnitude.
* Distance traveled is the total length of the path traveled between two positions.
ACCELERATION
The acceleration of the object at a given instant of time or at a given point of motion.Acceleration = change in velocity/time taken
Acceleration vector quantity hai. Ye positive, negative ya zero ho sakta hai. Jab acceleration ka direction body ke movement ek taraf ho, i.e., the velocity of a body is increasing with time, tab acceleration hoga.
Jab acceleration ka direction body ke movement ke direction me hoga, i.e., the velocity of a body is increasing with time, tab acceleration +ve hoga.
Jab acceleration ka direction body ke movement ke opposite direction me hoga, i.e., the velocity of a body is decreasing with time, tab acceleration −ve hoga. Negative acceleration ko retardation ya deceleration kehte hai.
Jab body constant velocity me ho, tab body ka acceleration zero hoga.
Acceleration ka unit MKS system ya S.I me m/s2 hai aur CGS system me cm/s2 hai.
Uniform Acceleration
Jab object ka velocity equally change hota hai equal interval of time me, tab usse uniform acceleration kahte hai.
Variable Acceleration
Jab object ka velocity unequal amount me change hota equal intervals of time me, tab usse variable acceleration ya non-uniform acceleration kahte hai.
Average Acceleration
Average acceleration is defined as the ratio of the total change in the velocity of the object during motion to the total time taken.
Average acceleration, →a(av) = total change in velocity/ total time taken = Δ→vΔt
Instantaneous Acceleration
Jab object variable acceleration me move kr raha hota hai, to different instants of time pr different acceleration possess krta hai, tab us acceleration ko Instantaneous acceleration kahte hai. Instantaneous acceleration is a continuous function of time and gives the acceleration at any specific time during the motion.
Thus, the instantaneous acceleration of an object:
(i) Is equal to the first time derivative of velocity at the given instant.
(ii) Is equal to the second time derivative of position of the object at the given instant.
AVERAGE SPEED
Average speed for the given motion is defined as the ratio of the total distance travelled by the object to the total time taken.
Average speed (Vav) = total distance travelled/ total time taken =ΔSΔt
Average speed aur velocity ka same unit hota hai (m/s).
In M.K.S. = m/s
In C.G.S = cm/s
Speed scalar quantity hai.
Dimension [M0L1T−1]
Average speed moving object ka direction nahi batata hai. Isliye, ye hamesha positive (in contrast to the average velocity which can be positive or negative) hota hai. Jab object ka motion straight line me hai aur uska direction bhi same hai, tab displacement ka magnitude aur total path length dono equal hota hai. Is case me, average velocity ka magnitude aur average speed equal hota hai. Maximum cases me, motion change in direction involve krta hai taki path length displacement ke magnitude se greater ho. Ye show krta hai ki speed velocity ke magnitude se greater hai.
For a moving particle in a given interval of time
AVERAGE VELOCITY
Average velocity is defined ‘as the ratio of total displacement to the total time interval in the given displacement.’Average velocity = total displacement/total time
Ager x2 kisi object ka position hai time t2 pr aur x1 object ka position hai time t1 pr, to average velocity (vav) hoga;
¯v=x2−x1t2−t1=δxδt
Yaha pe jo bar hai velocity symbol ke upar wo standard notation hai jo average quantity indicate krta hai. Velocity ka S.i unit ms or ms−1 hai lekin kmh−1 roj ke applications use hota hai.
Displacement ke jaise hi, average velocity bhi vector quantity hai. Average velocity positive ya negative ho sakta hai, depending upon the sign of the displacement. Jab displacement zero hota hai to average velocity bhi zero hota hai.
Instantaneous Velocity
Instantaneous velocity is defined as Rate of change of displacement.→v=→dSdt
Velocity vector quantity hai.
In M.K.S. = m/s
In C.G.S. = cm/s
Dimension = [M0L1T−1]
For a very small time, the value of displacement in magnitude would be equal to distance.
Therefore, ∣∣∣→dSdt∣∣∣=dxdt
dxdt instantaneous speed hai.
DISTINCTION BETWEEN SPEED AND VELOCITY

OMR (One Minute Revision)
- * Kinematics is the description of motion without considering its causes. In this chapter, it is limited to motion along a straight line, called one-dimensional motion.
* Displacement is the change in position of an object. The SI unit for displacement is the meter. Displacement has direction as well as magnitude.
* Distance traveled is the total length of the path traveled between two positions.
ACCELERATION
The acceleration of the object at a given instant of time or at a given point of motion.Acceleration = change in velocity/time taken
Acceleration vector quantity hai. Ye positive, negative ya zero ho sakta hai. Jab acceleration ka direction body ke movement ek taraf ho, i.e., the velocity of a body is increasing with time, tab acceleration hoga.
Jab acceleration ka direction body ke movement ke direction me hoga, i.e., the velocity of a body is increasing with time, tab acceleration +ve hoga.
Jab acceleration ka direction body ke movement ke opposite direction me hoga, i.e., the velocity of a body is decreasing with time, tab acceleration −ve hoga. Negative acceleration ko retardation ya deceleration kehte hai.
Jab body constant velocity me ho, tab body ka acceleration zero hoga.
Acceleration ka unit MKS system ya S.I me m/s2 hai aur CGS system me cm/s2 hai.
Uniform Acceleration
Jab object ka velocity equally change hota hai equal interval of time me, tab usse uniform acceleration kahte hai.
Variable Acceleration
Jab object ka velocity unequal amount me change hota equal intervals of time me, tab usse variable acceleration ya non-uniform acceleration kahte hai.
Average Acceleration
Average acceleration is defined as the ratio of the total change in the velocity of the object during motion to the total time taken.
Average acceleration, →a(av) = total change in velocity/ total time taken = Δ→vΔt
Instantaneous Acceleration
Jab object variable acceleration me move kr raha hota hai, to different instants of time pr different acceleration possess krta hai, tab us acceleration ko Instantaneous acceleration kahte hai. Instantaneous acceleration is a continuous function of time and gives the acceleration at any specific time during the motion.
Thus, the instantaneous acceleration of an object:
(i) Is equal to the first time derivative of velocity at the given instant.
(ii) Is equal to the second time derivative of position of the object at the given instant.
EXAMPLE 4
A particle travels first half of the total distance with constant speed v1 and second half with constant speed v2. Find the average speed during the complete journey.
vmv=s+st1+t2=2ssv1+sv2=2v1v2v1+v2

Note : - Here vav is the harmonic mean of two speeds.
EXAMPLE 4
A particle travels first half of the total distance with constant speed v1 and second half with constant speed v2. Find the average speed during the complete journey.
vmv=s+st1+t2=2ssv1+sv2=2v1v2v1+v2

Note : - Here vav is the harmonic mean of two speeds.
EXAMPLE 4
A particle travels first half of the total distance with constant speed v1 and second half with constant speed v2. Find the average speed during the complete journey.
vmv=s+st1+t2=2ssv1+sv2=2v1v2v1+v2

Note : - Here vav is the harmonic mean of two speeds.
EXAMPLE 5
If a particle travels with speed v1 during first half time interval and with speed v2 during second half time interval. Find its average speed during its journey.
s1=v1tands2=v2t
Total distance = s1+s2=(v1+v2)t
total time = t+t=2t then vav=s1+s2t+t=(v1+v2)t2t=v1+v22
Note : - here vav is arithmetic mean of two speeds.

EXAMPLE 5
If a particle travels with speed v1 during first half time interval and with speed v2 during second half time interval. Find its average speed during its journey.
s1=v1tands2=v2t
Total distance = s1+s2=(v1+v2)t
total time = t+t=2t then vav=s1+s2t+t=(v1+v2)t2t=v1+v22
Note : - here vav is arithmetic mean of two speeds.

EXAMPLE 5
If a particle travels with speed v1 during first half time interval and with speed v2 during second half time interval. Find its average speed during its journey.
s1=v1tands2=v2t
Total distance = s1+s2=(v1+v2)t
total time = t+t=2t then vav=s1+s2t+t=(v1+v2)t2t=v1+v22
Note : - here vav is arithmetic mean of two speeds.

EXAMPLE 6
A car moves with a velocity 2.24 km/h in first minute, with 3.60 km/h in the second minute and with 5.18 km/h in the third minute. Calculate the average velocity in these three minutes.
Distance travelled in first minute s1=v1×t1=2.24×160 km
Distance travelled in second minute s2=v2×t2=3.60×160 km
Distance travelled in third minute s3=v3×t3=5.18×160 km
Total distance travelled, s=s1+s2+s3=2.2460+3.6060+5.1860=11.0260 km
Total time taken, t=1+1+1=3min=120 h
∴ average velocity =st=11.0260×201=3.67 km/h
EXAMPLE 6
A car moves with a velocity 2.24 km/h in first minute, with 3.60 km/h in the second minute and with 5.18 km/h in the third minute. Calculate the average velocity in these three minutes.
Distance travelled in first minute s1=v1×t1=2.24×160 km
Distance travelled in second minute s2=v2×t2=3.60×160 km
Distance travelled in third minute s3=v3×t3=5.18×160 km
Total distance travelled, s=s1+s2+s3=2.2460+3.6060+5.1860=11.0260 km
Total time taken, t=1+1+1=3min=120 h
∴ average velocity =st=11.0260×201=3.67 km/h
EXAMPLE 6
A car moves with a velocity 2.24 km/h in first minute, with 3.60 km/h in the second minute and with 5.18 km/h in the third minute. Calculate the average velocity in these three minutes.
Distance travelled in first minute s1=v1×t1=2.24×160 km
Distance travelled in second minute s2=v2×t2=3.60×160 km
Distance travelled in third minute s3=v3×t3=5.18×160 km
Total distance travelled, s=s1+s2+s3=2.2460+3.6060+5.1860=11.0260 km
Total time taken, t=1+1+1=3min=120 h
∴ average velocity =st=11.0260×201=3.67 km/h
EXAMPLE 7
A bird files due north at velocity 20 ms−1 for 15s it rests for 5s and then files due south at velocity 24ms−1 for 10s. For the whole trip find the average speed and magnitude of average velocity
Average speed = Total DistanceTotal Time=20×15+24×1015+5+10=54030=18m/s
Average velocity = DisplacementTotal Time=(20×15)ˆj+(24×10)(−ˆj)15+510=60ˆj30=2ˆj
Magnitude of average velocity = ∣∣2→j∣∣=2m/s
EXAMPLE 7
A bird files due north at velocity 20 ms−1 for 15s it rests for 5s and then files due south at velocity 24ms−1 for 10s. For the whole trip find the average speed and magnitude of average velocity
Average speed = Total DistanceTotal Time=20×15+24×1015+5+10=54030=18m/s
Average velocity = DisplacementTotal Time=(20×15)ˆj+(24×10)(−ˆj)15+510=60ˆj30=2ˆj
Magnitude of average velocity = ∣∣2→j∣∣=2m/s

EXAMPLE 7
A bird files due north at velocity 20 ms−1 for 15s it rests for 5s and then files due south at velocity 24ms−1 for 10s. For the whole trip find the average speed and magnitude of average velocity
Average speed = Total DistanceTotal Time=20×15+24×1015+5+10=54030=18m/s
Average velocity = DisplacementTotal Time=(20×15)ˆj+(24×10)(−ˆj)15+510=60ˆj30=2ˆj
Magnitude of average velocity = ∣∣2→j∣∣=2m/s

POSITION-TIME GRAPH
Ab hum samajhte hai motion parameters ko kaise time ke respect me graphically represent kr sakte hai.
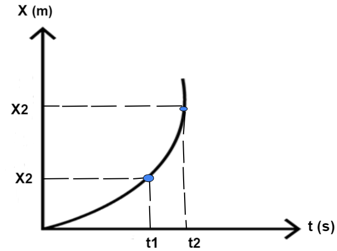
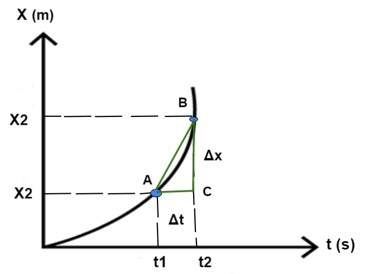
Ek particle ke motion ke liye, hume particle ke distance ya displacement ki requirement hoti hai jo position-time graph se easily samjha ja sakta hai. For example: Ager do time instances (t1 aur t2) hai aur positions x1 aur x2 hai to displacement t1 se t2 tak x2 - x1 me given hoga.
Average Velocity
→vavg=→x2−→x1t2−t1
=→ΔxΔt
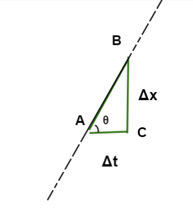
Jab humΔx aur Δt ko graph me represent krenge to hume triangle ABC milega. Is triangle ABC me ΔxΔt tan θ hai.
Note: Slope of chord between any two points on position-time graph gives us average velocity.
Instantaneous Velocity

Ab hum same graph se instantaneous value find krenge. Instantaneous value bahut km time ke liye hota hai. Iska matlab dt ko graph me reduce krna hoga. Jab ye bahut small value me reduce hoga to ye ek point ho jaega aur chord tangent ho jaega jaise ki aap niche graph me dekhenge. Hamne padha hai average value of velocity is given by the slope of the chord. Is case me chord tangent ho gya hai so, instantaneous value of velocity will be given by tan θ. tan θ tangent ka slope hai.
→v=→dSdt = tan θ

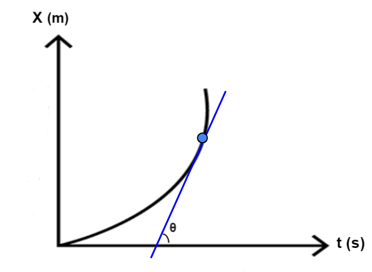
Note: Slope of tangent to position-time graph at any instant gives us instantaneous velocity at that instant.
VELOCITY-TIME GRAPH
Ab hum samajhte hai kaise velocity-time graph draw krenge.Hamne padha hai ek particle ke motion ke liye, hume particle ke distance ya displacement ki requirement hoti hai. Hum samjhenge kaise hum velocity-time graph se displacement ka value pata kr sakte hai. Hame particle ki velocity ki requirement hai. t1 pr velocity v1 hai aur t2 pr v2 hai. Displacement aur velocity ke alawa hame particle ke acceleration ki bhi requirement hai.
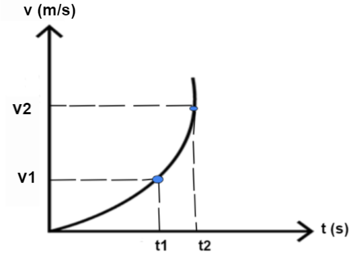
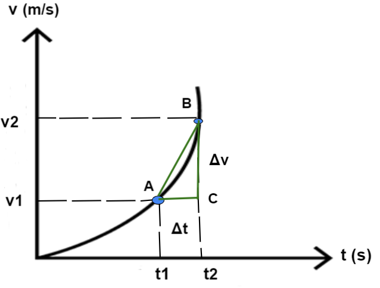
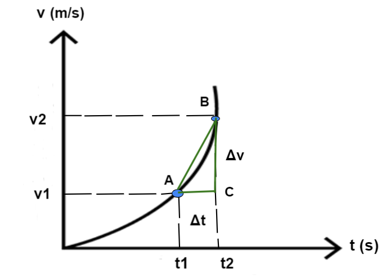
Average acceleration
(→aavg)=→v2−→v1t2−t1
=→ΔvΔt
Jab humΔv aur Δt ko graph me represent krenge to hume triangle ABC milega. Is triangle ABC me ΔvΔt tan θ hai.
Note: Slope of chord between any two points on velocity-time graph gives us average acceleration.
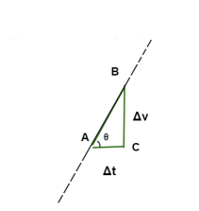
Instantaneous acceleration
Ab hum same graph se instantaneous value find krenge. Instantaneous value bahut km time ke liye hota hai. Iska matlab dt ko graph me reduce krna hoga jaisa hume velocity-time graph me kiya. Jab ye bahut small value me reduce hoga to ye ek point ho jaega aur chord tangent ho jaega jaise ki aap niche graph me dekhenge. Hamne padha hai average value of acceleration is given by the slope of the chord. Is case me chord tangent ho gya hai so, instantaneous value of acceleration will be given by tan θ. tan θ tangent ka slope hai.
→a=→dvdt = tan θ
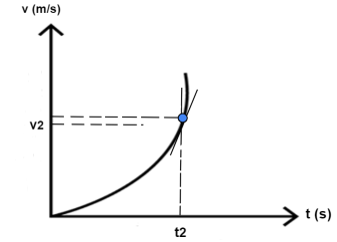
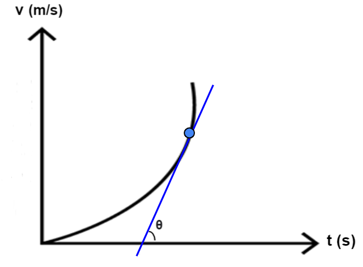
Note: Slope of tangent to velocity-time graph at any instant gives us instantaneous acceleration at that instant.
Displacement

→v=→dSdt
⇒→dS=→v(dt)
Total displacement
⇒∫→dS=∫→v(dt)=→ΔS
Curve aur time-axis ke bich ka area particle ka displacement represent krta hai.
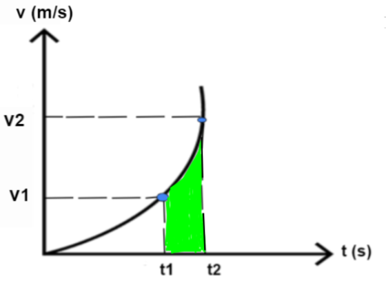
Note: The area between the curve and time axis represents the displacement of the particle during the given time interval in the velocity-time graph.
POSITION-TIME GRAPH
Ab hum samajhte hai motion parameters ko kaise time ke respect me graphically represent kr sakte hai.

Ek particle ke motion ke liye, hume particle ke distance ya displacement ki requirement hoti hai jo position-time graph se easily samjha ja sakta hai. For example: Ager do time instances (t1 aur t2) hai aur positions x1 aur x2 hai to displacement t1 se t2 tak x2 - x1 me given hoga.
Average Velocity
→vavg=→x2−→x1t2−t1
=→ΔxΔt
Jab humΔx aur Δt ko graph me represent krenge to hume triangle ABC milega. Is triangle ABC me ΔxΔt tan θ hai.
Note: Slope of chord between any two points on position-time graph gives us average velocity.


Instantaneous Velocity

Ab hum same graph se instantaneous value find krenge. Instantaneous value bahut km time ke liye hota hai. Iska matlab dt ko graph me reduce krna hoga. Jab ye bahut small value me reduce hoga to ye ek point ho jaega aur chord tangent ho jaega jaise ki aap niche graph me dekhenge. Hamne padha hai average value of velocity is given by the slope of the chord. Is case me chord tangent ho gya hai so, instantaneous value of velocity will be given by tan θ. tan θ tangent ka slope hai.
→v=→dSdt = tan θ


Note: Slope of tangent to position-time graph at any instant gives us instantaneous velocity at that instant.
VELOCITY-TIME GRAPH
Ab hum samajhte hai kaise velocity-time graph draw krenge.Hamne padha hai ek particle ke motion ke liye, hume particle ke distance ya displacement ki requirement hoti hai. Hum samjhenge kaise hum velocity-time graph se displacement ka value pata kr sakte hai. Hame particle ki velocity ki requirement hai. t1 pr velocity v1 hai aur t2 pr v2 hai. Displacement aur velocity ke alawa hame particle ke acceleration ki bhi requirement hai.

Average acceleration
(→aavg)=→v2−→v1t2−t1
=→ΔvΔt
Jab humΔv aur Δt ko graph me represent krenge to hume triangle ABC milega. Is triangle ABC me ΔvΔt tan θ hai.
Note: Slope of chord between any two points on velocity-time graph gives us average acceleration.


Instantaneous acceleration

Ab hum same graph se instantaneous value find krenge. Instantaneous value bahut km time ke liye hota hai. Iska matlab dt ko graph me reduce krna hoga jaisa hume velocity-time graph me kiya. Jab ye bahut small value me reduce hoga to ye ek point ho jaega aur chord tangent ho jaega jaise ki aap niche graph me dekhenge. Hamne padha hai average value of acceleration is given by the slope of the chord. Is case me chord tangent ho gya hai so, instantaneous value of acceleration will be given by tan θ. tan θ tangent ka slope hai.
→a=→dvdt = tan θ


Note: Slope of tangent to velocity-time graph at any instant gives us instantaneous acceleration at that instant.
Displacement

→v=→dSdt
⇒→dS=→v(dt)
Total displacement
⇒∫→dS=∫→v(dt)=→ΔS
Curve aur time-axis ke bich ka area particle ka displacement represent krta hai.

Note: The area between the curve and time axis represents the displacement of the particle during the given time interval in the velocity-time graph.
POSITION-TIME GRAPH
Ab hum samajhte hai motion parameters ko kaise time ke respect me graphically represent kr sakte hai.

Ek particle ke motion ke liye, hume particle ke distance ya displacement ki requirement hoti hai jo position-time graph se easily samjha ja sakta hai. For example: Ager do time instances (t1 aur t2) hai aur positions x1 aur x2 hai to displacement t1 se t2 tak x2 - x1 me given hoga.
Average Velocity
→vavg=→x2−→x1t2−t1
=→ΔxΔt
Jab humΔx aur Δt ko graph me represent krenge to hume triangle ABC milega. Is triangle ABC me ΔxΔt tan θ hai.
Note: Slope of chord between any two points on position-time graph gives us average velocity.


Instantaneous Velocity

Ab hum same graph se instantaneous value find krenge. Instantaneous value bahut km time ke liye hota hai. Iska matlab dt ko graph me reduce krna hoga. Jab ye bahut small value me reduce hoga to ye ek point ho jaega aur chord tangent ho jaega jaise ki aap niche graph me dekhenge. Hamne padha hai average value of velocity is given by the slope of the chord. Is case me chord tangent ho gya hai so, instantaneous value of velocity will be given by tan θ. tan θ tangent ka slope hai.
→v=→dSdt = tan θ


Note: Slope of tangent to position-time graph at any instant gives us instantaneous velocity at that instant.
VELOCITY-TIME GRAPH
Ab hum samajhte hai kaise velocity-time graph draw krenge.Hamne padha hai ek particle ke motion ke liye, hume particle ke distance ya displacement ki requirement hoti hai. Hum samjhenge kaise hum velocity-time graph se displacement ka value pata kr sakte hai. Hame particle ki velocity ki requirement hai. t1 pr velocity v1 hai aur t2 pr v2 hai. Displacement aur velocity ke alawa hame particle ke acceleration ki bhi requirement hai.

Average acceleration
(→aavg)=→v2−→v1t2−t1
=→ΔvΔt
Jab humΔv aur Δt ko graph me represent krenge to hume triangle ABC milega. Is triangle ABC me ΔvΔt tan θ hai.
Note: Slope of chord between any two points on velocity-time graph gives us average acceleration.


Instantaneous acceleration

Ab hum same graph se instantaneous value find krenge. Instantaneous value bahut km time ke liye hota hai. Iska matlab dt ko graph me reduce krna hoga jaisa hume velocity-time graph me kiya. Jab ye bahut small value me reduce hoga to ye ek point ho jaega aur chord tangent ho jaega jaise ki aap niche graph me dekhenge. Hamne padha hai average value of acceleration is given by the slope of the chord. Is case me chord tangent ho gya hai so, instantaneous value of acceleration will be given by tan θ. tan θ tangent ka slope hai.
→a=→dvdt = tan θ


Note: Slope of tangent to velocity-time graph at any instant gives us instantaneous acceleration at that instant.
Displacement

→v=→dSdt
⇒→dS=→v(dt)
Total displacement
⇒∫→dS=∫→v(dt)=→ΔS
Curve aur time-axis ke bich ka area particle ka displacement represent krta hai.

Note: The area between the curve and time axis represents the displacement of the particle during the given time interval in the velocity-time graph.
EXAMPLE 8
The displacement of a point moving along a straight line is given by
s=4t2+5t−6
Here s is in cm and t is in seconds calculate
(i) Initial speed of particle
(ii) Speed at t=4s
(i) Speed, v=dsdt=8t+5 Initial speed (i.e at t=0), v=5cm/s
(ii) At t=4s,v=8(4)+5=37cm/s
EXAMPLE 8
The displacement of a point moving along a straight line is given by
s=4t2+5t−6
Here s is in cm and t is in seconds calculate
(i) Initial speed of particle
(ii) Speed at t=4s
(i) Speed, v=dsdt=8t+5 Initial speed (i.e at t=0), v=5cm/s
(ii) At t=4s,v=8(4)+5=37cm/s
EXAMPLE 8
The displacement of a point moving along a straight line is given by
s=4t2+5t−6
Here s is in cm and t is in seconds calculate
(i) Initial speed of particle
(ii) Speed at t=4s
(i) Speed, v=dsdt=8t+5 Initial speed (i.e at t=0), v=5cm/s
(ii) At t=4s,v=8(4)+5=37cm/s
ACCELERATION-TIME GRAPH
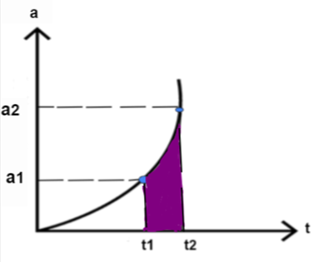
Niche diye graph se hum displacement ka value find nahi kr paenge lekin y-axis ko read karke acceleration ka value find kr sakte hai. Hum hum discuss krte hai do time instances (t1 aur t2) ke bich change in velocity ko kaise find kr sakte hai. Acceleration ka value a1 aur a2 given hai.

→a=→dvdt
⇒→dv=→a(dt)
⇒∫→dv=∫→a(dt)=→Δv
=→v2−→v1
Note: The area between the curve and time axis represents the change in velocity of the particle during the given time interval in acceleration time graph.
VELOCITY-DISPLACEMENT GRAPH
Ab hum velocity versus displacement graph ko samjhenge. Niche diye graph me aap dekhenge ek particle ka velocity variation displacement ke respect me diya hai. Hame particle ka acceleration find karna hai. Humne previous graphs me padha hai ki graph ka slope change in y-axis ko change in x-axis se divide krke calculate kr sakte hai.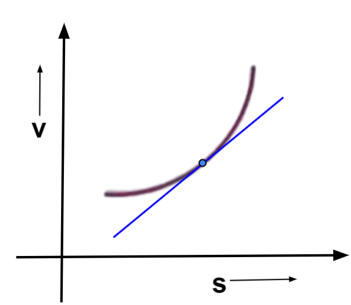
Is case me, Slope = dvds
Using, a=v(dvds)
⇒dvds=av
Slope =av
EQUATIONS OF MOTION
3 equations of motion for a particle in straight line:v=u+at ......(i)
S = ut +½ at^2 ......(ii)
v2=u2+2aS ......(iii)
Where, u = initial velocity; v = final velocity; a = acceleration; t = time; S = displacement
* Ye equations tab hi applicable hoge jab object ka acceleration constant hoga. Iska matlab acceleration magnitude aur direction dono me constant hoga. i.e. →a = constant.
* In equations ko vectorially apply krna hai. Iska matlab hume direction use krna hai, ek side +ve hoga aur dusra side −ve hoga. In equations se hame sirf displacement ka value pata chalega distance ka nahi.
Let’s try to derive them one by one;
Derivation of v=u+at, using velocity-time graph
Teeno equations ke liye condition hai ki acceleration constant hoga. Thus slope ka value velocity-time graph ke liye constant hoga. Iska matlab straight line hoga. Suppose particle apna motion velocity u se start krta hai aur velocity v se end krta hai. u initial velocity hai aur v final velocity hai. Ager hum A ko line BC se perpendicularly join kr denge jo intersect hoga D pr, to hume BD ka value milega jo (v−u) ke equal hoga aur OC ka value t ke equal hoga.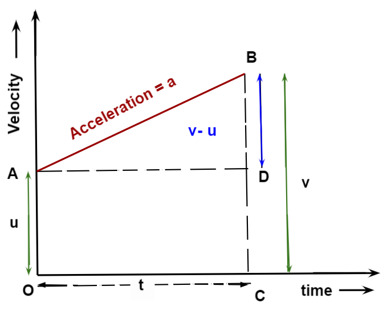
→a = constant
From triangle ABD,
Slope = BD/AD
Therefore, a=v−ut
at=(v−u)
v=u+at
Derivation of S=ut+½at2, using velocity-time graph
Hum same velocity-time graph aur same acceleration A se B tak lenge. Initial velocity u hai aur final velocity v hai aur time t hoga. Is case me hum displacement find krenge. Hame pata hai ki area between the curve aur time access particle ka displacement ka value batata hai.
We know that area under v−t graph gives displacement.
S=½× height × sum of parallel sides
S=½×OC×(OA+BC)
=½t(u+v)
Substituting, v=u+at
=½t(u+u+at)
½t(2u+at)
S=ut+½at2
Derivation of v2=u2+2aS or v2−u2=2aS,usingvelocity−timegraph<h2><span>Humsamevelocity−timegraphaursameae≤rationAseBtak≤n≥.Initialvelocityuhaiaurf∈alvelocityvhaiaurtimethoga.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_025.pngwh=80%mx-autosty≤=background:white;><br><br>Weknowtˆareaunderv-tgraphgivesdisplacement.<br>S = ½ xxheightxx∑ofparal≤lss<br>S = ½ xx OC xx (OA +BC)<br>½ t(v + u)<br><br>Weknow,v = u +at<br>t = (v-u)/a<br>S = ½ [(v-u)/a] (v+u)<br>S = ½ [(v^2 - u^2)/a]<br><b>2aS = v^2 - u^2<b><h2>VERTICALMOTION<h2>A≥rhumkisiobjectkouprthrowkren≥→wostraightl∈efollowkregaaurwapasnicheaaega.Isitypekemotionke¯emeabhumstudykren≥.Supposeekballhaijissehumvelocityusethrowkren≥aurheighthpruskavelocityvhoga.Humyahatime∈stantke¯emebaatnahikrraheisliyemotionketeenoequationsmesehumewoequationusekrnahaijismetimenahiaatahai.So,humyaha3rdequationusekren≥.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_026.pngwh=80%mx-autosty≤=background:white;><br><br>Verticalmotionkeliye,ae≤rationdue→gravityhameshadownwardactkrtahai.Humupwardmotionko+veconsrkrrahehaisoae≤rationdue→gravity(g)-vehoga.Partic≤upwardmovekrrahahaisodisplacement+hhoga.<br><br>Tak∈gupwardas+ve,∈itialvelocity=u,ae≤ration=-g<br>Displacement(S)is+hasbodyhasmovedupward.<br>Abhumequationmevaluesputkren≥;<br>v^2 = u^2 + 2as<br>=> v^2 = u^2 + 2(-g) (h)<br>=> v = ±sqrt(u^2 - 2gh)<br>+vevaluede¬e,partic≤isgo∈gup(+ve)<br>-vevaluede¬e,partic≤iscomingdown.<br><br>Humyeconcludekrsaktehaikiballnichejayegayaupjayegauskaspeedekpartica––rheightprsamehoga.<br><br>Abhmsameheighthseballkeupraurnicheja≠katimepatakrtehai.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_027.pngwh=80%mx-autosty≤=background:white;><br><br><b>Whi≤go∈gup;<b><br>{Timeofascent(t_a)}<br>Hum≠upward+verakhahai,<br>So,Initialvelocity=uandAe≤ration=-g<br><br>Usingv = u + at<br>sqrt(u^2 - 2gh) = u - g t_a<br>Since,v = sqrt(u^2 - 2gh)ataheighth<br><b>t_a = u - sqrt(u^2 - 2gh)/g<b><br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_028.pngwh=80%mx-autosty≤=background:white;><br><br><b>Whi≤comingdown;<b><br>{Timeofdecent(t_d)}<br>Hum≠downward-verakhahai,<br>So,F∈alvelocity=-uandAe≤ration=-g<br>Usingv = u + at<br><br>-u = sqrt(u^2 - 2gh) - g t_d<br><b>t_d = u - sqrt(u^2 - 2gh)/g
In dono equations se hum ye conclude kr sakte hai ki same height ke liye ascent (the act of ascending; a motion upwards) aur decent (an instance of descending; act of coming down) ka time same hota hai. Ek particular height pr particle ka speed upr ya niche jane me same hota hai. Ek particular height reach me aur us same height se niche aane me same time lgta hai.
ACCELERATION-TIME GRAPH
Niche diye graph se hum displacement ka value find nahi kr paenge lekin y-axis ko read karke acceleration ka value find kr sakte hai. Hum hum discuss krte hai do time instances (t1 aur t2) ke bich change in velocity ko kaise find kr sakte hai. Acceleration ka value a1 aur a2 given hai.

→a=→dvdt
⇒→dv=→a(dt)
⇒∫→dv=∫→a(dt)=→Δv
=→v2−→v1

Note: The area between the curve and time axis represents the change in velocity of the particle during the given time interval in acceleration time graph.
VELOCITY-DISPLACEMENT GRAPH
Ab hum velocity versus displacement graph ko samjhenge. Niche diye graph me aap dekhenge ek particle ka velocity variation displacement ke respect me diya hai. Hame particle ka acceleration find karna hai. Humne previous graphs me padha hai ki graph ka slope change in y-axis ko change in x-axis se divide krke calculate kr sakte hai.
Is case me, Slope = dvds
Using, a=v(dvds)
⇒dvds=av
Slope =av
EQUATIONS OF MOTION
3 equations of motion for a particle in straight line:v=u+at ......(i)
S=ut+½at2 ......(ii)
v2=u2+2aS ......(iii)
Where, u = initial velocity; v = final velocity; a = acceleration; t = time; S = displacement
* Ye equations tab hi applicable hoge jab object ka acceleration constant hoga. Iska matlab acceleration magnitude aur direction dono me constant hoga. i.e. →a = constant.
* In equations ko vectorially apply krna hai. Iska matlab hume direction use krna hai, ek side +ve hoga aur dusra side −ve hoga. In equations se hame sirf displacement ka value pata chalega distance ka nahi.
Let’s try to derive them one by one;
Derivation of v=u+at, using velocity-time graph
Teeno equations ke liye condition hai ki acceleration constant hoga. Thus slope ka value velocity-time graph ke liye constant hoga. Iska matlab straight line hoga. Suppose particle apna motion velocity u se start krta hai aur velocity v se end krta hai. u initial velocity hai aur v final velocity hai. Ager hum A ko line BC se perpendicularly join kr denge jo intersect hoga D pr, to hume BD ka value milega jo (v−u) ke equal hoga aur OC ka value t ke equal hoga.
→a = constant
From triangle ABD,
Slope = BD/AD
Therefore, a=v−ut
at=(v−u)
v=u+at
Derivation of S=ut+½at2, using velocity-time graph
Hum same velocity-time graph aur same acceleration A se B tak lenge. Initial velocity u hai aur final velocity v hai aur time t hoga. Is case me hum displacement find krenge. Hame pata hai ki area between the curve aur time access particle ka displacement ka value batata hai.
We know that area under v−t graph gives displacement.
S=½× height × sum of parallel sides
S=½×OC×(OA+BC)
=½t(u+v)
Substituting, v=u+at
=½t(u+u+at)
½t(2u+at)
S=ut+½at2
Derivation of v2=u2+2aS or v2−u2=2aS,usingvelocity−timegraph<h2><span>Humsamevelocity−timegraphaursameae≤rationAseBtak≤n≥.Initialvelocityuhaiaurf∈alvelocityvhaiaurtimethoga.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_025.pngwh=80%mx-autosty≤=background:white;><br><br>Weknowtˆareaunderv-tgraphgivesdisplacement.<br>S = ½ xxheightxx∑ofparal≤lss<br>S = ½ xx OC xx (OA +BC)<br>½ t(v + u)<br><br>Weknow,v = u +at<br>t = (v-u)/a<br>S = ½ [(v-u)/a] (v+u)<br>S = ½ [(v^2 - u^2)/a]<br><b>2aS = v^2 - u^2<b><h2>VERTICALMOTION<h2>A≥rhumkisiobjectkouprthrowkren≥→wostraightl∈efollowkregaaurwapasnicheaaega.Isitypekemotionke¯emeabhumstudykren≥.Supposeekballhaijissehumvelocityusethrowkren≥aurheighthpruskavelocityvhoga.Humyahatime∈stantke¯emebaatnahikrraheisliyemotionketeenoequationsmesehumewoequationusekrnahaijismetimenahiaatahai.So,humyaha3rdequationusekren≥.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_026.pngwh=80%mx-autosty≤=background:white;><br><br>Verticalmotionkeliye,ae≤rationdue→gravityhameshadownwardactkrtahai.Humupwardmotionko+veconsrkrrahehaisoae≤rationdue→gravity(g)-vehoga.Partic≤upwardmovekrrahahaisodisplacement+hhoga.<br><br>Tak∈gupwardas+ve,∈itialvelocity=u,ae≤ration=-g<br>Displacement(S)is+hasbodyhasmovedupward.<br>Abhumequationmevaluesputkren≥;<br>v^2 = u^2 + 2as<br>=> v^2 = u^2 + 2(-g) (h)<br>=> v = ±sqrt(u^2 - 2gh)<br>+vevaluede¬e,partic≤isgo∈gup(+ve)<br>-vevaluede¬e,partic≤iscomingdown.<br><br>Humyeconcludekrsaktehaikiballnichejayegayaupjayegauskaspeedekpartica––rheightprsamehoga.<br><br>Abhmsameheighthseballkeupraurnicheja≠katimepatakrtehai.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_027.pngwh=80%mx-autosty≤=background:white;><br><br><b>Whi≤go∈gup;<b><br>{Timeofascent(t_a)}<br>Hum≠upward+verakhahai,<br>So,Initialvelocity=uandAe≤ration=-g<br><br>Usingv = u + at<br>sqrt(u^2 - 2gh) = u - g t_a<br>Since,v = sqrt(u^2 - 2gh)ataheighth<br><b>t_a = u - sqrt(u^2 - 2gh)/g<b><br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_028.pngwh=80%mx-autosty≤=background:white;><br><br><b>Whi≤comingdown;<b><br>{Timeofdecent(t_d)}<br>Hum≠downward-verakhahai,<br>So,F∈alvelocity=-uandAe≤ration=-g<br>Usingv = u + at<br><br>-u = sqrt(u^2 - 2gh) - g t_d<br><b>t_d = u - sqrt(u^2 - 2gh)/g
In dono equations se hum ye conclude kr sakte hai ki same height ke liye ascent (the act of ascending; a motion upwards) aur decent (an instance of descending; act of coming down) ka time same hota hai. Ek particular height pr particle ka speed upr ya niche jane me same hota hai. Ek particular height reach me aur us same height se niche aane me same time lgta hai.
ACCELERATION-TIME GRAPH
Niche diye graph se hum displacement ka value find nahi kr paenge lekin y-axis ko read karke acceleration ka value find kr sakte hai. Hum hum discuss krte hai do time instances (t1 aur t2) ke bich change in velocity ko kaise find kr sakte hai. Acceleration ka value a1 aur a2 given hai.

→a=→dvdt
⇒→dv=→a(dt)
⇒∫→dv=∫→a(dt)=→Δv
=→v2−→v1

Note: The area between the curve and time axis represents the change in velocity of the particle during the given time interval in acceleration time graph.
VELOCITY-DISPLACEMENT GRAPH
Ab hum velocity versus displacement graph ko samjhenge. Niche diye graph me aap dekhenge ek particle ka velocity variation displacement ke respect me diya hai. Hame particle ka acceleration find karna hai. Humne previous graphs me padha hai ki graph ka slope change in y-axis ko change in x-axis se divide krke calculate kr sakte hai.
Is case me, Slope = dvds
Using, a=v(dvds)
⇒dvds=av
Slope =av
EQUATIONS OF MOTION
3 equations of motion for a particle in straight line:v=u+at ......(i)
S=ut+½at2 ......(ii)
v2=u2+2aS ......(iii)
Where, u = initial velocity; v = final velocity; a = acceleration; t = time; S = displacement
* Ye equations tab hi applicable hoge jab object ka acceleration constant hoga. Iska matlab acceleration magnitude aur direction dono me constant hoga. i.e. →a = constant.
* In equations ko vectorially apply krna hai. Iska matlab hume direction use krna hai, ek side +ve hoga aur dusra side −ve hoga. In equations se hame sirf displacement ka value pata chalega distance ka nahi.
Let’s try to derive them one by one;
Derivation of v=u+at, using velocity-time graph
Teeno equations ke liye condition hai ki acceleration constant hoga. Thus slope ka value velocity-time graph ke liye constant hoga. Iska matlab straight line hoga. Suppose particle apna motion velocity u se start krta hai aur velocity v se end krta hai. u initial velocity hai aur v final velocity hai. Ager hum A ko line BC se perpendicularly join kr denge jo intersect hoga D pr, to hume BD ka value milega jo (v−u) ke equal hoga aur OC ka value t ke equal hoga.
→a = constant
From triangle ABD,
Slope = BD/AD
Therefore, a=v−ut
at=(v−u)
v=u+at
Derivation of S=ut+½at2, using velocity-time graph
Hum same velocity-time graph aur same acceleration A se B tak lenge. Initial velocity u hai aur final velocity v hai aur time t hoga. Is case me hum displacement find krenge. Hame pata hai ki area between the curve aur time access particle ka displacement ka value batata hai.
We know that area under v−t graph gives displacement.
S=½× height × sum of parallel sides
S=½×OC×(OA+BC)
=½t(u+v)
Substituting, v=u+at
=½t(u+u+at)
½t(2u+at)
S=ut+½at2
Derivation of v2=u2+2aS or v2−u2=2aS,usingvelocity−timegraph<h2><span>Humsamevelocity−timegraphaursameae≤rationAseBtak≤n≥.Initialvelocityuhaiaurf∈alvelocityvhaiaurtimethoga.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_025.pngwh=80%mx-autosty≤=background:white;><br><br>Weknowtˆareaunderv-tgraphgivesdisplacement.<br>S = ½ xxheightxx∑ofparal≤lss<br>S = ½ xx OC xx (OA +BC)<br>½ t(v + u)<br><br>Weknow,v = u +at<br>t = (v-u)/a<br>S = ½ [(v-u)/a] (v+u)<br>S = ½ [(v^2 - u^2)/a]<br><b>2aS = v^2 - u^2<b><h2>VERTICALMOTION<h2>A≥rhumkisiobjectkouprthrowkren≥→wostraightl∈efollowkregaaurwapasnicheaaega.Isitypekemotionke¯emeabhumstudykren≥.Supposeekballhaijissehumvelocityusethrowkren≥aurheighthpruskavelocityvhoga.Humyahatime∈stantke¯emebaatnahikrraheisliyemotionketeenoequationsmesehumewoequationusekrnahaijismetimenahiaatahai.So,humyaha3rdequationusekren≥.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_026.pngwh=80%mx-autosty≤=background:white;><br><br>Verticalmotionkeliye,ae≤rationdue→gravityhameshadownwardactkrtahai.Humupwardmotionko+veconsrkrrahehaisoae≤rationdue→gravity(g)-vehoga.Partic≤upwardmovekrrahahaisodisplacement+hhoga.<br><br>Tak∈gupwardas+ve,∈itialvelocity=u,ae≤ration=-g<br>Displacement(S)is+hasbodyhasmovedupward.<br>Abhumequationmevaluesputkren≥;<br>v^2 = u^2 + 2as<br>=> v^2 = u^2 + 2(-g) (h)<br>=> v = ±sqrt(u^2 - 2gh)<br>+vevaluede¬e,partic≤isgo∈gup(+ve)<br>-vevaluede¬e,partic≤iscomingdown.<br><br>Humyeconcludekrsaktehaikiballnichejayegayaupjayegauskaspeedekpartica––rheightprsamehoga.<br><br>Abhmsameheighthseballkeupraurnicheja≠katimepatakrtehai.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_027.pngwh=80%mx-autosty≤=background:white;><br><br><b>Whi≤go∈gup;<b><br>{Timeofascent(t_a)}<br>Hum≠upward+verakhahai,<br>So,Initialvelocity=uandAe≤ration=-g<br><br>Usingv = u + at<br>sqrt(u^2 - 2gh) = u - g t_a<br>Since,v = sqrt(u^2 - 2gh)ataheighth<br><b>t_a = u - sqrt(u^2 - 2gh)/g<b><br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_NEET_C03_028.pngwh=80%mx-autosty≤=background:white;><br><br><b>Whi≤comingdown;<b><br>{Timeofdecent(t_d)}<br>Hum≠downward-verakhahai,<br>So,F∈alvelocity=-uandAe≤ration=-g<br>Usingv = u + at<br><br>-u = sqrt(u^2 - 2gh) - g t_d<br><b>t_d = u - sqrt(u^2 - 2gh)/g
In dono equations se hum ye conclude kr sakte hai ki same height ke liye ascent (the act of ascending; a motion upwards) aur decent (an instance of descending; act of coming down) ka time same hota hai. Ek particular height pr particle ka speed upr ya niche jane me same hota hai. Ek particular height reach me aur us same height se niche aane me same time lgta hai.
EXAMPLE 9
(a) If s=2t3+3t2+2t+8 then find time at which acceleration is zero.
(b) Velocity of a particle (starting at t =0) varies with time as v= 4t. Calculate the displacement of part between t = 2 to t = 4 s
(a) v=dsdt=6t2+6t+2⇒a=dvdt=12t=6=0⇒t=−12 which is impossible. There acceleration can never be zero.
(b) ∵dxdt=v∴x=∫vdt=4∫24tdt=[2t2]42=2(4)2−2(2)2=32−8=24 m
EXAMPLE 9
(a) If s=2t3+3t2+2t+8 then find time at which acceleration is zero.
(b) Velocity of a particle (starting at t =0) varies with time as v= 4t. Calculate the displacement of part between t = 2 to t = 4 s
(a) v=dsdt=6t2+6t+2⇒a=dvdt=12t=6=0⇒t=−12 which is impossible. There acceleration can never be zero.
(b) ∵dxdt=v∴x=∫vdt=4∫24tdt=[2t2]42=2(4)2−2(2)2=32−8=24 m
EXAMPLE 9
(a) If s=2t3+3t2+2t+8 then find time at which acceleration is zero.
(b) Velocity of a particle (starting at t =0) varies with time as v= 4t. Calculate the displacement of part between t = 2 to t = 4 s
(a) v=dsdt=6t2+6t+2⇒a=dvdt=12t=6=0⇒t=−12 which is impossible. There acceleration can never be zero.
(b) ∵dxdt=v∴x=∫vdt=4∫24tdt=[2t2]42=2(4)2−2(2)2=32−8=24 m
EXAMPLE 10
The velocity of a particle is given by v=(2t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=2 second.
Acceleration (a) =dvdt=ddt(2t2−4t+3)=4t−4
Therefore acceleration at t=2s is equal to, a=(4×2)−4=4m/s2
EXAMPLE 10
The velocity of a particle is given by v=(2t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=2 second.
Acceleration (a) =dvdt=ddt(2t2−4t+3)=4t−4
Therefore acceleration at t=2s is equal to, a=(4×2)−4=4m/s2
EXAMPLE 10
The velocity of a particle is given by v=(2t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=2 second.
Acceleration (a) =dvdt=ddt(2t2−4t+3)=4t−4
Therefore acceleration at t=2s is equal to, a=(4×2)−4=4m/s2
EXAMPLE 11
A particle is moving along a straight line OX, At a time t (in seconds) the distance x (in metres) of particle from point O is given by x=10+6t−3t2. How long would the particle travel before coming to rest?
Initial value of x, at t=0, x1=10 m
Velocity v = dxdt=6−6t When v =0, t = 1s
Final value of x, at t = 1s, x2=10+6×1−3(12)=13 m
Distance travelled =x2−x1=13−10= 3m
EXAMPLE 11
A particle is moving along a straight line OX, At a time t (in seconds) the distance x (in metres) of particle from point O is given by x=10+6t−3t2. How long would the particle travel before coming to rest?
Initial value of x, at t=0, x1=10 m
Velocity v = dxdt=6−6t When v =0, t = 1s
Final value of x, at t = 1s, x2=10+6×1−3(12)=13 m
Distance travelled =x2−x1=13−10= 3m
EXAMPLE 11
A particle is moving along a straight line OX, At a time t (in seconds) the distance x (in metres) of particle from point O is given by x=10+6t−3t2. How long would the particle travel before coming to rest?
Initial value of x, at t=0, x1=10 m
Velocity v = dxdt=6−6t When v =0, t = 1s
Final value of x, at t = 1s, x2=10+6×1−3(12)=13 m
Distance travelled =x2−x1=13−10= 3m
EXAMPLE 12
The acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
a=2s+1⇒dvdt=2s+1⇒dvds⋅dsdt=2s+1⇒dvds⋅v=2s+1
⇒v∫0vdv=2s∫0sds+s∫0ds
⇒(v22)v0=2(s22)s0+[s]s0 ⇒v22=s2+s⇒v=√2s(s+1)
EXAMPLE 12
The acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
a=2s+1⇒dvdt=2s+1⇒dvds⋅dsdt=2s+1⇒dvds⋅v=2s+1
⇒v∫0vdv=2s∫0sds+s∫0ds
⇒(v22)v0=2(s22)s0+[s]s0 ⇒v22=s2+s⇒v=√2s(s+1)
EXAMPLE 12
The acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
a=2s+1⇒dvdt=2s+1⇒dvds⋅dsdt=2s+1⇒dvds⋅v=2s+1
⇒v∫0vdv=2s∫0sds+s∫0ds
⇒(v22)v0=2(s22)s0+[s]s0 ⇒v22=s2+s⇒v=√2s(s+1)
EXAMPLE 13
For a particle moving with constant acceleration, prove that the displacement in the nth second is given by
snth=u+a2(2n−1)
From s=ut+12at2
sn=un+12an2……….(1)
sn−1=u(n−1)+12a(n−1)2……….(2)
By equation (1) & (2)
sn−sn−1=snth=u+a2(2n−1)
EXAMPLE 13
For a particle moving with constant acceleration, prove that the displacement in the nth second is given by
snth=u+a2(2n−1)
From s=ut+12at2
sn=un+12an2……….(1)
sn−1=u(n−1)+12a(n−1)2……….(2)
By equation (1) & (2)
sn−sn−1=snth=u+a2(2n−1)
EXAMPLE 13
For a particle moving with constant acceleration, prove that the displacement in the nth second is given by
snth=u+a2(2n−1)
From s=ut+12at2
sn=un+12an2……….(1)
sn−1=u(n−1)+12a(n−1)2……….(2)
By equation (1) & (2)
sn−sn−1=snth=u+a2(2n−1)
EXAMPLE 14
Two cars start off a race with velocities 2m/s and 4m/s travel in straight line with uniform acceleration 2m/s2and1m/s2 respectively. What is the length of the path if they reach the final point at the same time ?
Let both particles reach at same position in same time t then from s = ut+12at2
For 1st particle : s=4(t)+12(1)t2=4t+t22, For 2nd particle : s=2(t)+12(2)t2=2t+t2
Equation above equation we get 4t+t22=2t+t2⇒t=4s
Subsituting value of t in above equation s = 4(4)+12(1)(4)2=16+8=24m
EXAMPLE 14
Two cars start off a race with velocities 2m/s and 4m/s travel in straight line with uniform acceleration 2m/s2and1m/s2 respectively. What is the length of the path if they reach the final point at the same time ?
Let both particles reach at same position in same time t then from s = ut+12at2
For 1st particle : s=4(t)+12(1)t2=4t+t22, For 2nd particle : s=2(t)+12(2)t2=2t+t2
Equation above equation we get 4t+t22=2t+t2⇒t=4s
Subsituting value of t in above equation s = 4(4)+12(1)(4)2=16+8=24m
EXAMPLE 14
Two cars start off a race with velocities 2m/s and 4m/s travel in straight line with uniform acceleration 2m/s2and1m/s2 respectively. What is the length of the path if they reach the final point at the same time ?
Let both particles reach at same position in same time t then from s = ut+12at2
For 1st particle : s=4(t)+12(1)t2=4t+t22, For 2nd particle : s=2(t)+12(2)t2=2t+t2
Equation above equation we get 4t+t22=2t+t2⇒t=4s
Subsituting value of t in above equation s = 4(4)+12(1)(4)2=16+8=24m
EXAMPLE 15
A train, travelling at 20km/hr is approaching a platform. A bird is sitting on a pole on the platform. When the train is at a distance of 2 km from pole, breakes are applied which produce auniform deceleration in it. At that instant the bird flies towards the train at 60km/hr and after touching the nearest point on the train flies back to the pole and then flies towards the train and continues repeating itself. Calculate how much distance will the bird have flown before the train stops?
For retardation of train,
a=∣∣∣v2−u22s∣∣∣ = (20 × 20)/(2 × 2) = 100 km/hr2,
Time to reach platform = 20/ 100 =(⅕ )hr,
Total distance travelled by the bird = vt = 60 × ⅕ = 12 km.
EXAMPLE 15
A train, travelling at 20km/hr is approaching a platform. A bird is sitting on a pole on the platform. When the train is at a distance of 2 km from pole, breakes are applied which produce auniform deceleration in it. At that instant the bird flies towards the train at 60km/hr and after touching the nearest point on the train flies back to the pole and then flies towards the train and continues repeating itself. Calculate how much distance will the bird have flown before the train stops?
For retardation of train,
a=∣∣∣v2−u22s∣∣∣ = (20 × 20)/(2 × 2) = 100 km/hr2,
Time to reach platform = 20/ 100 =(⅕ )hr,
Total distance travelled by the bird = vt = 60 × ⅕ = 12 km.
EXAMPLE 15
A train, travelling at 20km/hr is approaching a platform. A bird is sitting on a pole on the platform. When the train is at a distance of 2 km from pole, breakes are applied which produce auniform deceleration in it. At that instant the bird flies towards the train at 60km/hr and after touching the nearest point on the train flies back to the pole and then flies towards the train and continues repeating itself. Calculate how much distance will the bird have flown before the train stops?
For retardation of train,
a=∣∣∣v2−u22s∣∣∣ = (20 × 20)/(2 × 2) = 100 km/hr2,
Time to reach platform = 20/ 100 =(⅕ )hr,
Total distance travelled by the bird = vt = 60 × ⅕ = 12 km.
KEY EQUATIONS
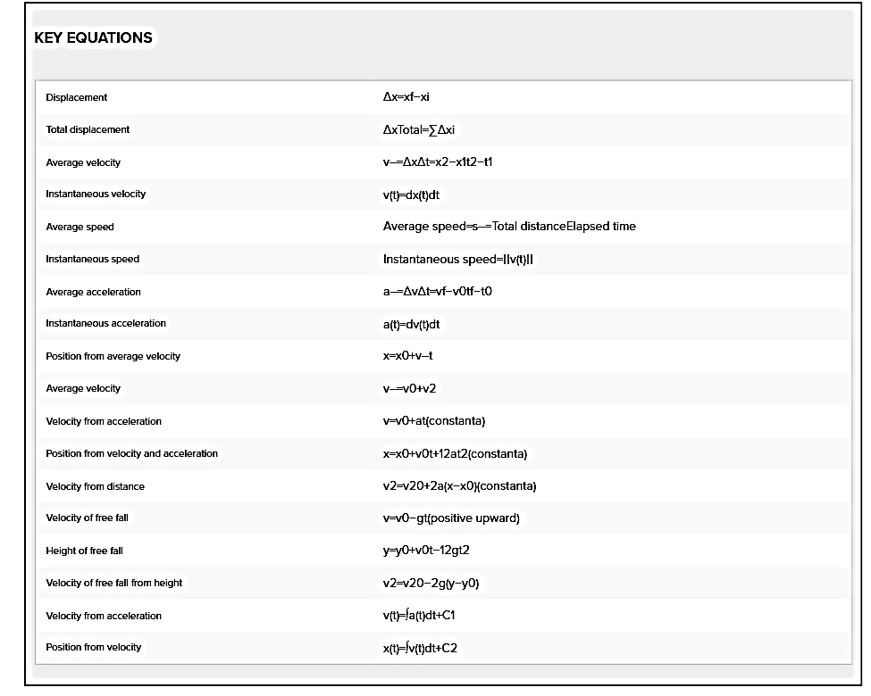
KEY EQUATIONS

KEY EQUATIONS

DEFINITIONS
1. Point Object : If the length covered by the objects are very large in comparison to the size of the objects, the objects are considered point objects.
2. Reference System : The motion of a particle is always described with respect to a reference system. A reference system is made by taking an arbitrary point as origin and imagining a co-ordinate system to be attached to it. This co-ordinate system chosen for a given problem constitutes the reference system for it.
3. Motion: An object is said to be in motion, if it changes its position with the passage of time.
4. Total Path Length (Distance) : For a particle in motion the total length of the actual path traversed between initial and final positions of the particle is known as the ‘total path length’ or distance covered by it.
5. Displacement : Displacement of a particle in a given time is defined as the change in the position of particle in a particular direction during that time. It is given by a vector drawn from its initial position to its final position.
6. Position: It is defined with respect to some reference point (origin) of a given frame of reference.
7. Acceleration: The acceleration of the object at a given instant of time or at a given point of motion.
8. Instantaneous acceleration: Instantaneous acceleration is a continuous function of time and gives the acceleration at any specific time during the motion. It is calculated from the derivative of the velocity function.
9. Instantaneous velocity: Instantaneous velocity is the type of velocity of an object in motion. This can be determined as the average velocity, but we may narrow the period of time so that it approaches zero.
10. Average speed: Average speed for the given motion is defined as the ratio of the total distance travelled by the object to the total time taken.
11. Average Velocity: Average Velocity is defined as the ratio of total displacement to the total time interval in the given displacement.
12. Vertical Motion: Vertical motion is generally defined as motion that is normal to some defined horizontal surface.
DEFINITIONS
1. Point Object : If the length covered by the objects are very large in comparison to the size of the objects, the objects are considered point objects.
2. Reference System : The motion of a particle is always described with respect to a reference system. A reference system is made by taking an arbitrary point as origin and imagining a co-ordinate system to be attached to it. This co-ordinate system chosen for a given problem constitutes the reference system for it.
3. Motion: An object is said to be in motion, if it changes its position with the passage of time.
4. Total Path Length (Distance) : For a particle in motion the total length of the actual path traversed between initial and final positions of the particle is known as the ‘total path length’ or distance covered by it.
5. Displacement : Displacement of a particle in a given time is defined as the change in the position of particle in a particular direction during that time. It is given by a vector drawn from its initial position to its final position.
6. Position: It is defined with respect to some reference point (origin) of a given frame of reference.
7. Acceleration: The acceleration of the object at a given instant of time or at a given point of motion.
8. Instantaneous acceleration: Instantaneous acceleration is a continuous function of time and gives the acceleration at any specific time during the motion. It is calculated from the derivative of the velocity function.
9. Instantaneous velocity: Instantaneous velocity is the type of velocity of an object in motion. This can be determined as the average velocity, but we may narrow the period of time so that it approaches zero.
10. Average speed: Average speed for the given motion is defined as the ratio of the total distance travelled by the object to the total time taken.
11. Average Velocity: Average Velocity is defined as the ratio of total displacement to the total time interval in the given displacement.
12. Vertical Motion: Vertical motion is generally defined as motion that is normal to some defined horizontal surface.
DEFINITIONS
1. Point Object : If the length covered by the objects are very large in comparison to the size of the objects, the objects are considered point objects.
2. Reference System : The motion of a particle is always described with respect to a reference system. A reference system is made by taking an arbitrary point as origin and imagining a co-ordinate system to be attached to it. This co-ordinate system chosen for a given problem constitutes the reference system for it.
3. Motion: An object is said to be in motion, if it changes its position with the passage of time.
4. Total Path Length (Distance) : For a particle in motion the total length of the actual path traversed between initial and final positions of the particle is known as the ‘total path length’ or distance covered by it.
5. Displacement : Displacement of a particle in a given time is defined as the change in the position of particle in a particular direction during that time. It is given by a vector drawn from its initial position to its final position.
6. Position: It is defined with respect to some reference point (origin) of a given frame of reference.
7. Acceleration: The acceleration of the object at a given instant of time or at a given point of motion.
8. Instantaneous acceleration: Instantaneous acceleration is a continuous function of time and gives the acceleration at any specific time during the motion. It is calculated from the derivative of the velocity function.
9. Instantaneous velocity: Instantaneous velocity is the type of velocity of an object in motion. This can be determined as the average velocity, but we may narrow the period of time so that it approaches zero.
10. Average speed: Average speed for the given motion is defined as the ratio of the total distance travelled by the object to the total time taken.
11. Average Velocity: Average Velocity is defined as the ratio of total displacement to the total time interval in the given displacement.
12. Vertical Motion: Vertical motion is generally defined as motion that is normal to some defined horizontal surface.
SUMMARY
The velocity at a particular instant is equal to the slope of the tangent drawn on position-time graph at that instant.
¯a=ΔvΔt
a=limΔt→0¯a=limΔt→0ΔvΔt=dvdt
The acceleration of an object at a particular time is the slope of the velocity-time graph at that instant of time. For uniform motion, acceleration is zero and the x-t graph is a straight line inclined to the time axis and the v-t graph is a straight line parallel to the time axis. For motion with uniform acceleration, x-t graph is a parabola while the v-t graph is a straight line inclined to the time axis.
v=v0+at
x=x0+v0t+12at2
v2=(v0)2+2ax
if the position of the object at time t = 0 is 0. If the particle starts at x=x0 , x in above equations is replaced by (x–x0).
SUMMARY
The velocity at a particular instant is equal to the slope of the tangent drawn on position-time graph at that instant.
¯a=ΔvΔt
a=limΔt→0¯a=limΔt→0ΔvΔt=dvdt
The acceleration of an object at a particular time is the slope of the velocity-time graph at that instant of time. For uniform motion, acceleration is zero and the x-t graph is a straight line inclined to the time axis and the v-t graph is a straight line parallel to the time axis. For motion with uniform acceleration, x-t graph is a parabola while the v-t graph is a straight line inclined to the time axis.
v=v0+at
x=x0+v0t+12at2
v2=(v0)2+2ax
if the position of the object at time t = 0 is 0. If the particle starts at x=x0 , x in above equations is replaced by (x–x0).
SUMMARY
The velocity at a particular instant is equal to the slope of the tangent drawn on position-time graph at that instant.
¯a=ΔvΔt
a=limΔt→0¯a=limΔt→0ΔvΔt=dvdt
The acceleration of an object at a particular time is the slope of the velocity-time graph at that instant of time. For uniform motion, acceleration is zero and the x-t graph is a straight line inclined to the time axis and the v-t graph is a straight line parallel to the time axis. For motion with uniform acceleration, x-t graph is a parabola while the v-t graph is a straight line inclined to the time axis.
v=v0+at
x=x0+v0t+12at2
v2=(v0)2+2ax
if the position of the object at time t = 0 is 0. If the particle starts at x=x0 , x in above equations is replaced by (x–x0).