PROJECTILE MOTION for Class 11 PHYSICS
INTRODUCTION
Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration of gravity. The object is called a projectile, and its path is called its trajectory. The motion of falling objects, as covered in Problem-Solving Basics for One-Dimensional Kinematics, is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In this section, we consider two-dimensional projectile motion, such as that of a football or other object for which air resistance is negligible.
In a Projectile Motion, there are two simultaneous independent rectilinear motions:
- Along the x-axis: uniform velocity, responsible for the horizontal (forward) motion of the particle.
Along y-axis: uniform acceleration, responsible for the vertical (downwards) motion of the particle.
MOTION IN A PLANE
Two-dimensional (2D) motion means motion that takes place in two different directions (or coordinates) at the same time. The simplest motion would be an object moving linearly in one dimension. An example of linear movement would be a car moving along a straight road or a ball thrown straight up from the ground. If an object is moving in one direction with a constant velocity while accelerating in another direction, calculating the motion is more complicated. An example of 2D movement would be throwing a football or hitting a home run in baseball. In the following examples in this chapter, motion in the Earth’s gravitational field is explored.
POSITION VECTOR AND DISPLACEMENT
The displacement of a particle is the difference between its final position, and initial position. Therefore, the displacement vector for the particle as shown in figure equals the difference between its final position vector and its initial position vector.
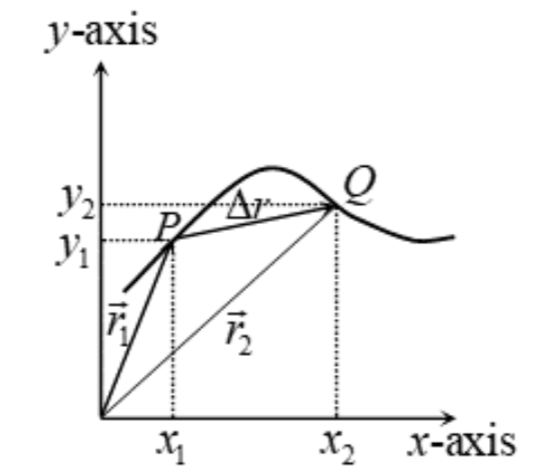
Suppose a particle moves in a plane along the curve as shown in figure. At time t1 the particle is at point P, and at some later time t2, the particle is at Q, where the indices 1 and 2 refer to initial and final values. As the particle moves from P to Q in the time interval Δt=t2−t1 the position vector changes from r1 to r2
- Δr=r2−r1 &nbs0 (from triangle law of vector addition) … (16)
Let the co-ordinate of the particle at points P and Q are x1,y1) and (x2,y2) respectively. Then,
- →r1=x1ˆi+y1ˆj
→r2=x2ˆi+y2ˆj
→r2−→r1=(x2ˆi+y2ˆj)−(x1ˆi+y1ˆj)
Δ→r=(x2−x1)ˆi+y2−y1)ˆj
Δ→r=Δxˆi+Δyˆj
As we see from figure the magnitude of the displacement vector is less than the distance traveled along the curve path.
VELOCITY
We define the average velocity of the particle during the time interval Δt as the ratio of the displacement to that time interval :
- →v=Δ→rΔt ……..(1)
Δ→r=Δxˆi+Δyˆj
Δ→rΔt=ΔxˆiΔt+ΔyˆjΔt⇒→v=vxˆi+vyˆj
∙ The average velocity between points P and Q is independent of the path between the two points. This is because the average velocity is proportional to the displacement, which in turn depends only on the initial and final position vectors and not on the path taken between those two points.
As we did with one-dimensional motion, we conclude that if a particle starts its motion at some point and returns to this point via any path, its average velocity is zero for this trip since its displacement is zero.
Instantaneous velocity
The instantaneous velocity →v, is defined as the limit of the average velocity, ΔrΔt, as Δt approaches zero : i.e.- →v=limΔt→0Δ→rΔt=d→rdt …….(2)
Consider again the motion of a particle between two points in the plane, as shown in figure. As the time intervals over which we observe the motion become smaller and smaller, the direction of the displacement approaches that of the line tangent to the path at the point
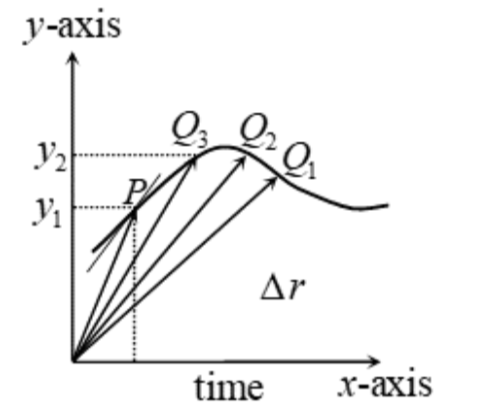
- →v=limΔt→0Δ→xˆi+Δ→yˆjΔt=dxdtˆi+dydtˆj=vxˆi+vyˆj
- The magnitude of the instantaneous velocity vector is called the speed.
ACCELERATION
(a)Average acceleration
The average acceleration of a particle as it moves from P to Q is defined as the ratio of the change in the instantaneous velocity vector, Δv, to the elapsed time, Δt i.e.,- →a=Δ→vΔt=→v2−→v1t2−t1 ……….(1)
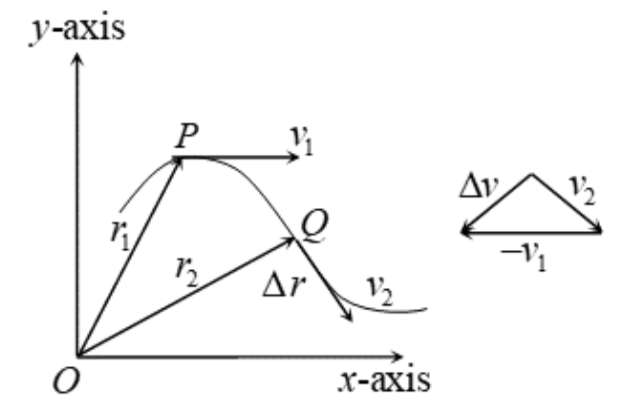
- Δ→v=→v2−→v1
→a=Δ→vΔt=Δ(→vxˆi+→vyˆj)t2−t1=axˆi+ayˆj
(b)Instantaneous acceleration
The instantaneous acceleration →a, is defined as the limiting value of the ratio Δ→vΔt as Δt approaches zero :- →a=limΔt→0ΔvΔt=d→vdt ……….(2)
TWO DIMENSIONAL MOTION WITH CONSTANT ACCELERATION
Let us consider two-dimensional motion during which the acceleration remains constant. That is, we assume that the magnitude and direction of the acceleration remain unchanged during the motion.
As we learned, in cause of the motion a particle can be determined by its position vector →r. The position vector for a particle moving in the xy plane can be written
- →r=xˆi+yˆj ………..(1)
- →v=d→rdt=dxdtˆi+dydtˆj
→v=vxˆi+vyˆj ……….(2)
- →a=d→vdt=dvxdtˆi+dvydtˆj
→a=axˆi+ayˆj ……….(3)
- →v=→v0+a→t{vx=vx0+axtvy=vy0+ayt} ……….(4)
→v=→v0+½→at2{x=vx0t+½axt2y=vy0t+12ayt} ………..(5)
v2=v20+2as{v2x=v2x0+2axsxv2y=v2y0+2aysy} ……….(6)
Examples of motion in plane are projectile motion and circular motion.
PROJECTILE MOTION
Projectile refers to an object that is in flight after being thrown or projected. In a projectile motion, the only acceleration acting is in the vertical direction which is acceleration due to gravity (g). Equations of motion, therefore, can be applied separately in X-axis and Y-axis to find the unknown parameters.
Some examples of Projectile Motion are Football, A baseball, A cricket ball, or any other object. The projectile motion consists of two parts - one is the horizontal motion of no acceleration and the other vertical motion of constant acceleration due to gravity. The projectile motion is always in the form of a parabola.
Assumptions of projectile motion
- The acceleration due to gravity (‘g’) is constant over the motion of projectile
- The effect of air resistances is negligible
- The effect due to rotation of earth and curvature of the earth is negligible

We can study the two-dimensional motion as one-dimensional motion along x-axes and y-axis since its superposition gives the resultant motion.
Let us assume that at t=0, projectile leaves the origin (x=0,y=0) with velocity u, which makes an angle θ with the horizontal.
Motion along horizontal direction (x-axis) :
In this direction initial velocity will be horizontal component of initial velocity with which the object is projected i.e.,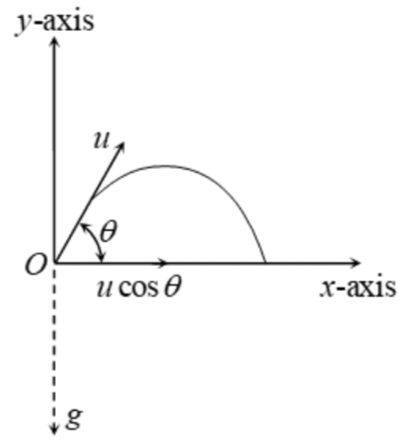
- ux=ucosθ
- ax=0
- vx=v0x+axt
vx=ux
vx=ucosθ
- x=v0t+½axt2
x=uxt
x=(ucosθ)t
Motion in vertical direction (y-axis)
In this direction initial velocity will be vertical component of initial velocity with which the object is projected.- uy=usinθ
- ay=−g (which is constant)
- vy=uy−gt
vy=usinθ−gt
- y=uyt−12gt2
y=(usinθ)t−12gt2
- v2y=u2y−2gy
v2y=(usinθ)2−2gy
EQUATION OF TRAJECTORY
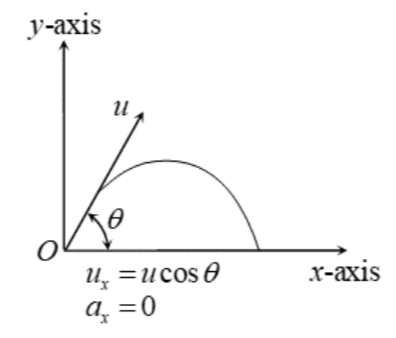
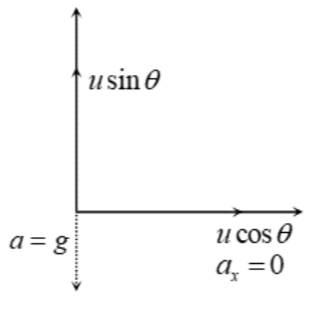
Let projected body be in motion for t second.
Consider motion in x-direction
- ux=ucosθ
ax=0
x=(ucosθ)t
t=xucosθ
- uy=usinθ and ay=−g
y=(usinθ)t−12gt2 ……….(1)
- y=(usinθ)xucosθ−12gx2u2cos2θ
y=(tanθ)x−12gx2u2cos2θ ……….(2)
The above equation represents a parabola. So we can say that equation of trajectory is parabola.
VELOCITY OF PROJECTILE IN SPACE
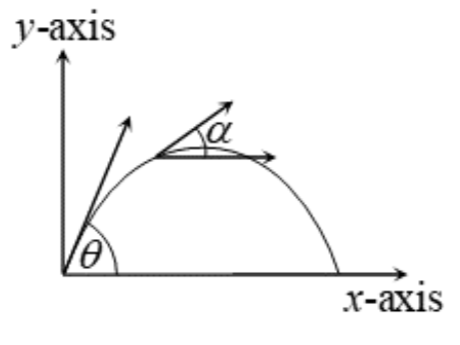
Now to obtain the speed v of the projectile as a function of time, first we calculate speed along x-axis and y-axis vx and vy respectively as a function of time
- v=√v2x+v2y
- vx=(ucosθ)
- vy=usinθ−>
|v|=√(ucosθ2)+(usinθ−gt)2
v=√u2−2u>sinθ+g2t2 ……….(1)
- tanα=(vyvx)
TIME OF ASCENT
Time of ascent is the time when the projectile will attain the maximum height. At this position the vertical component of velocity vector will become zero.

As shown in figure P is point of maximum height. Now to find the time taken from initial point of projection upto maximum height, we consider motion in y-direction
- vy=uy−gt
0=usinθ−gt
t=usinθg
t=usinθg
TIME OF FLIGHT
When a particle is projected in air after some time it hits the ground again, time taken in this process is called time of flight or we can say time of flight is time of motion of projectile when it is in air. It is denoted by T.
Let a particle be projected from O and again it hits the ground at point Q. In this motion distance traveled in y-direction is zero.
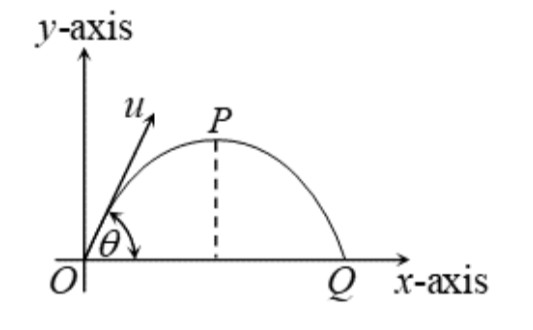
On applying equation of motion in y-direction.
- y=ut−12gt2
0=usinθT−12gT2
0=(usinθ−12gT)T
T=0 or T=2usinθg
T=2usinθg ……….(1)
The total time of flight is consists of two parts
- Time taken by the particle to go from O to highest point P, it is called time of ascent.
- Time taken by the particle to go from the highest point P to Q where it hits the ground again. It is called time of descent.
As motion from O to P and P to Q are symmetrical.- ∴ time of ascent = time of descent = usinθg
- T=2usinθg
MAXIMUM HEIGHT OF PROJECTILE
It is the maximum vertical height attained by the particle above the point of projection during its flight. It is denoted by
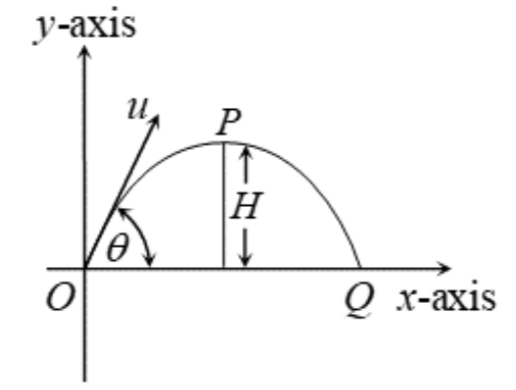
When the projectile is at maximum height, its vertical component of velocity will be zero.
Initial velocity
- vy=usinθ
- v2=u2−2gs
0=u2sin2θ−2gH
H=u2sin2θ2g
HORIZONTAL RANGE
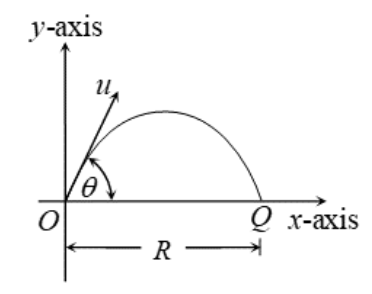
Range of projectile is horizontal distance traveled by the particle during the time of flight
Motion along x-axis is with constant velocity
So distance traveled in this direction will be
- x=(ucosθ)t
R=(ucosθ)T
- T=2usinθg
- R=(ucosθ)(2usinθg)
R=u2sin2θg ………..(1)
- R=u2sin2θg
- sin2θ=1=sin90∘⇒2θ=90∘⇒θ=45∘
- Rmax=u2g ……….(2)
When range is maximum, the maximum height H reached by the projectile
- H=u2sin245^22g=u22g=Rmax4
- θ1+θ2=90∘
If θ1=45∘+α,then θ2=45∘−α
Important formulae/points
Projectile on horizontal plane
Time of flight,
- T=2usinθg
- R=u2sin2θg
- H=u2sin2θ2g
- y=xtanθ−12gx2u2sec2θ=xtanθ(1−xR)
- θ=45∘
EXAMPLE 1
A ball is thrown from a field with a speed of 12.0 m/s at an angle of 45∘ with the horizontal. At what distance will it hit the field again? Take g=10.0ms2
The horizontal range = u2sin2θg
=(12ms2)×sin(2×45∘)10ms2
=144m2s210ms2=14.4m
Thus, the ball hits the field at 14.4 m from the point of projection
EXAMPLE 2
Find the maximum horizontal range when the velocity of projection is 30 m/s. Find the two directions of projection to give a range of 45 m. Take g=10ms2.
(i) Maximum range
- Rm=u2g=30210=90m
- sin2α=45×1030×30=12
2α=30∘ or 2α=150∘ [∵(180−θ)=sinθ]
α=15∘ or α=75∘
EXAMPLE 3
What is the least velocity with which a cricket ball can be thrown through a distance of 100 m?
Since the range is given, the least velocity of projection is that value when the angle of projection is 45°. For velocity u to be least
- u2sin2αg=100
- u2=100×9.8=980
u=√980=31.3ms
EXAMPLE 4
From a point on the ground at a distance 10 m from the foot of a vertical wall, a ball is thrown at an angle of 45° which just clears the top of the wall and afterwards strikes the ground at a distance 5 m on the other side. Find the height of the wall.

Let u be the velocity of projection at an angle α=45∘ with the horizontal.
Horizontal range = u2sin2αg=15
- u2g=15
- y=xtanα−12gx22u2cos2α
y=x×1−12gx2u2×12=xgx2u2=xx215
- h=10−10215=5015=313m