FLUID MECHANICS for Class 11 PHYSICS
INTRODUCTION
Baccho fluids mtlb hota hai koi aisi cheez jo flow kre, jaise ki liquid and gases, iss chapter me hum sab liquid ke motin ki baat kreinge, jaise abhi tk hum solid ke motion ki baat krte hue aaye hai, same usi tarah ab hum fluid ke motion ki baat krenge.
Isme bhi hum do tarah ke liquid ki baat krenge, jaise ki ek liquid jo flow ho rha hai or ek liquid jo ki ruka hua hai, aur inn dono fluids ki poori ki poori mechanics ki aaj hum study krne waale hai.
INTRODUCTION
Baccho fluids mtlb hota hai koi aisi cheez jo flow kre, jaise ki liquid and gases, iss chapter me hum sab liquid ke motin ki baat kreinge, jaise abhi tk hum solid ke motion ki baat krte hue aaye hai, same usi tarah ab hum fluid ke motion ki baat krenge.
Isme bhi hum do tarah ke liquid ki baat krenge, jaise ki ek liquid jo flow ho rha hai or ek liquid jo ki ruka hua hai, aur inn dono fluids ki poori ki poori mechanics ki aaj hum study krne waale hai.
INTRODUCTION
Baccho fluids mtlb hota hai koi aisi cheez jo flow kre, jaise ki liquid and gases, iss chapter me hum sab liquid ke motin ki baat kreinge, jaise abhi tk hum solid ke motion ki baat krte hue aaye hai, same usi tarah ab hum fluid ke motion ki baat krenge.
Isme bhi hum do tarah ke liquid ki baat krenge, jaise ki ek liquid jo flow ho rha hai or ek liquid jo ki ruka hua hai, aur inn dono fluids ki poori ki poori mechanics ki aaj hum study krne waale hai.
PRESSURE
Bachho agr me pressure ki baat krun toh ise hum ek example se samjhte hai, maan lijiye me apni ek finger se apne haath ko kisi force se press krta hun, toh mujhe kuch nhi hoga bss aisa lgega ki koi cheez hai jo force lga rhi hai, and same agr me finger ki jagah ek safety pin ya needle ko apne haath prr usi same force se press karun toh blood nikal jata hai, toh aisa kya hua yaha , jabki dono jagah forcs toh same the, toh baccho yaha term introduce hoga ek voh hai pressure.
Baccho pressure hota hai ,
P=F⊥A,
Unit of pressure is Nm2 or Pascal Pa
Perpendicular component humne isliye liya baccho kyunki agr force kisi angle prr lgegi toh uske perpendicular component ki wajah se hi pressure generate hoga, tangential component se pressure generate nhi hoga.
PRESSURE
Bachho agr me pressure ki baat krun toh ise hum ek example se samjhte hai, maan lijiye me apni ek finger se apne haath ko kisi force se press krta hun, toh mujhe kuch nhi hoga bss aisa lgega ki koi cheez hai jo force lga rhi hai, and same agr me finger ki jagah ek safety pin ya needle ko apne haath prr usi same force se press karun toh blood nikal jata hai, toh aisa kya hua yaha , jabki dono jagah forcs toh same the, toh baccho yaha term introduce hoga ek voh hai pressure.
Baccho pressure hota hai ,
P=F⊥A,
Unit of pressure is Nm2 or Pascal Pa
Perpendicular component humne isliye liya baccho kyunki agr force kisi angle prr lgegi toh uske perpendicular component ki wajah se hi pressure generate hoga, tangential component se pressure generate nhi hoga.
PRESSURE
Bachho agr me pressure ki baat krun toh ise hum ek example se samjhte hai, maan lijiye me apni ek finger se apne haath ko kisi force se press krta hun, toh mujhe kuch nhi hoga bss aisa lgega ki koi cheez hai jo force lga rhi hai, and same agr me finger ki jagah ek safety pin ya needle ko apne haath prr usi same force se press karun toh blood nikal jata hai, toh aisa kya hua yaha , jabki dono jagah forcs toh same the, toh baccho yaha term introduce hoga ek voh hai pressure.
Baccho pressure hota hai ,
P=F⊥A,
Unit of pressure is Nm2 or Pascal Pa
Perpendicular component humne isliye liya baccho kyunki agr force kisi angle prr lgegi toh uske perpendicular component ki wajah se hi pressure generate hoga, tangential component se pressure generate nhi hoga.
VARIATION OF PRESSURE IN DEPTH
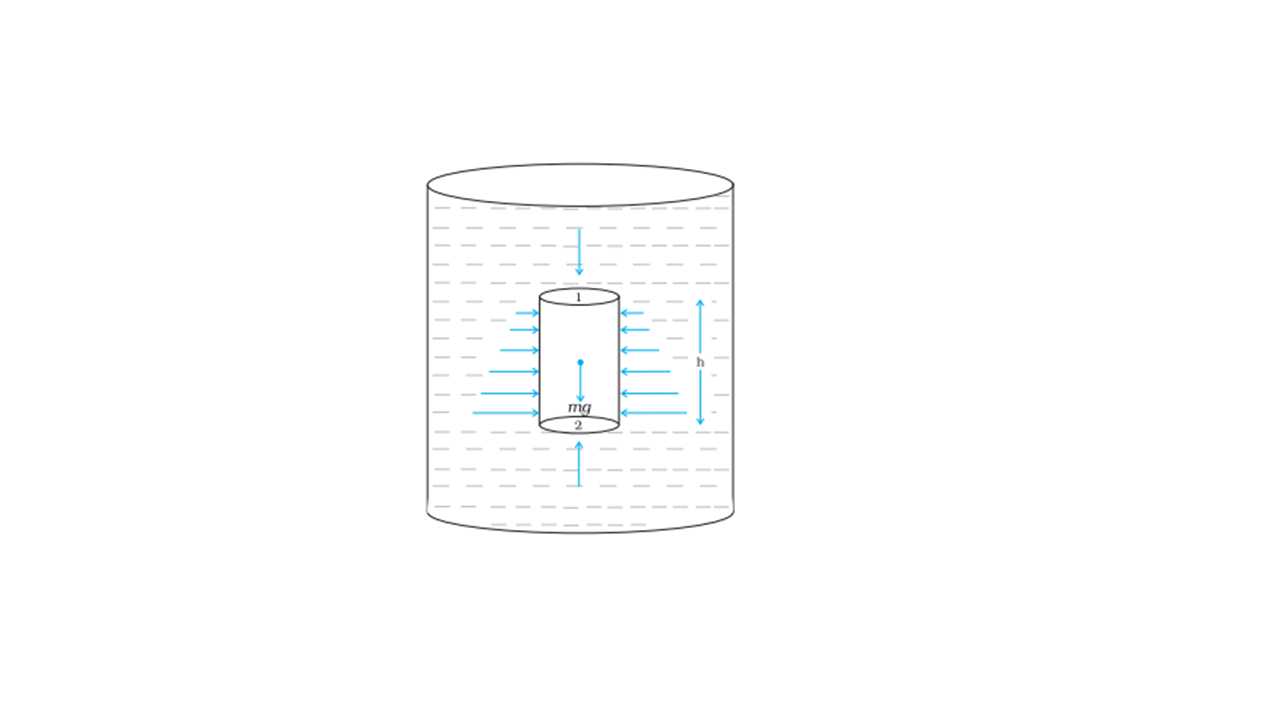
Baccho hume ek container liya hai and uss container me humne koi liquid fill kiya hua jiski density ρ hai. Ab me iss water me do points maanunga and unko mark krdunga 1 and 2 jaisa ki aap diagram me dekh sakte hai.
Baccho jaisa ki hum sab jaante hai ki jese jese hum depth me jaenge vese vese liquid ki layers increase hoti jaaengi means liquid a weight increase hota jaega and iski wajah se jaise jaise neeche jaenge pressure bhi increase hota jata hai.
Ab baccho jaisa ki liquid ruka ha hai toh iska mtlb liquid equlilibrium prr hai, means net force of liquid should be 0.
Point 1 prr force downwards lgega or voh hoga P1A and point 2 prr force uwards lgega or voh hoga P2A and ek gravitational force lgega liquid ke m mass prr downwards directions me,
Now F≠t=0,
Therefore, P1A+mg=P2A and m=ρV where V=volume of liquid,
Therefore we can write, P2A−P1A=ρVg
If the height of liquid column is h, then V=Ah
P2−P1=ρgh
This is the pressure difference of liquid columnar point 1 and 2.
VARIATION OF PRESSURE IN DEPTH

Baccho hume ek container liya hai and uss container me humne koi liquid fill kiya hua jiski density ρ hai. Ab me iss water me do points maanunga and unko mark krdunga 1 and 2 jaisa ki aap diagram me dekh sakte hai.
Baccho jaisa ki hum sab jaante hai ki jese jese hum depth me jaenge vese vese liquid ki layers increase hoti jaaengi means liquid a weight increase hota jaega and iski wajah se jaise jaise neeche jaenge pressure bhi increase hota jata hai.
Ab baccho jaisa ki liquid ruka ha hai toh iska mtlb liquid equlilibrium prr hai, means net force of liquid should be 0.
Point 1 prr force downwards lgega or voh hoga P1A and point 2 prr force uwards lgega or voh hoga P2A and ek gravitational force lgega liquid ke m mass prr downwards directions me,
Now F≠t=0,
Therefore, P1A+mg=P2A and m=ρV where V=volume of liquid,
Therefore we can write, P2A−P1A=ρVg
If the height of liquid column is h, then V=Ah
P2−P1=ρgh
This is the pressure difference of liquid columnar point 1 and 2.
VARIATION OF PRESSURE IN DEPTH

Baccho hume ek container liya hai and uss container me humne koi liquid fill kiya hua jiski density ρ hai. Ab me iss water me do points maanunga and unko mark krdunga 1 and 2 jaisa ki aap diagram me dekh sakte hai.
Baccho jaisa ki hum sab jaante hai ki jese jese hum depth me jaenge vese vese liquid ki layers increase hoti jaaengi means liquid a weight increase hota jaega and iski wajah se jaise jaise neeche jaenge pressure bhi increase hota jata hai.
Ab baccho jaisa ki liquid ruka ha hai toh iska mtlb liquid equlilibrium prr hai, means net force of liquid should be 0.
Point 1 prr force downwards lgega or voh hoga P1A and point 2 prr force uwards lgega or voh hoga P2A and ek gravitational force lgega liquid ke m mass prr downwards directions me,
Now F≠t=0,
Therefore, P1A+mg=P2A and m=ρV where V=volume of liquid,
Therefore we can write, P2A−P1A=ρVg
If the height of liquid column is h, then V=Ah
P2−P1=ρgh
This is the pressure difference of liquid columnar point 1 and 2.
BAROMETER

Baccho barometer ek device hota hai jis ki help se hum kisi bhi jagah prr atmospgeric pressure ki value bta sakte hai.
Aao jaante hai ki ye kese work krta hai,
Baccho hum log liquid mercury ko ek container me daal dete hai then uske andr ek capillary tube mercury bhar kar use hum ulta kr dete hai mercury container me, toh hum ye notice krte hai ki kuch part mercury ka capillary tube mese container me flow krjata hai and upar kuch vaccum create hojata hai capillary tube me.
Toh baccho ab maan lete hai ki capillary tube me mercury kuch h height tak fill hai and hume pta hai ki same horizontal layer prr pressure same hota hai.
Ab hum container me liqud ki sabse top layer ki baat krenge toh-
Pressure by liquid column would be equal to pressure exerting on surface of liquid container that is equal to Patm where Patm means atmospheric pressure.
So we can write,
Phg=Patm
Pvaccum+ρgh=Patm
Where Pvaccum=0
therefore , Patm=ρgh
Form this we can find the atmospheric pressure by knowing the value of h.
BAROMETER

Baccho barometer ek device hota hai jis ki help se hum kisi bhi jagah prr atmospgeric pressure ki value bta sakte hai.
Aao jaante hai ki ye kese work krta hai,
Baccho hum log liquid mercury ko ek container me daal dete hai then uske andr ek capillary tube mercury bhar kar use hum ulta kr dete hai mercury container me, toh hum ye notice krte hai ki kuch part mercury ka capillary tube mese container me flow krjata hai and upar kuch vaccum create hojata hai capillary tube me.
Toh baccho ab maan lete hai ki capillary tube me mercury kuch h height tak fill hai and hume pta hai ki same horizontal layer prr pressure same hota hai.
Ab hum container me liqud ki sabse top layer ki baat krenge toh-
Pressure by liquid column would be equal to pressure exerting on surface of liquid container that is equal to Patm where Patm means atmospheric pressure.
So we can write,
Phg=Patm
Pvaccum+ρgh=Patm
Where Pvaccum=0
therefore , Patm=ρgh
Form this we can find the atmospheric pressure by knowing the value of h.
BAROMETER

Baccho barometer ek device hota hai jis ki help se hum kisi bhi jagah prr atmospgeric pressure ki value bta sakte hai.
Aao jaante hai ki ye kese work krta hai,
Baccho hum log liquid mercury ko ek container me daal dete hai then uske andr ek capillary tube mercury bhar kar use hum ulta kr dete hai mercury container me, toh hum ye notice krte hai ki kuch part mercury ka capillary tube mese container me flow krjata hai and upar kuch vaccum create hojata hai capillary tube me.
Toh baccho ab maan lete hai ki capillary tube me mercury kuch h height tak fill hai and hume pta hai ki same horizontal layer prr pressure same hota hai.
Ab hum container me liqud ki sabse top layer ki baat krenge toh-
Pressure by liquid column would be equal to pressure exerting on surface of liquid container that is equal to Patm where Patm means atmospheric pressure.
So we can write,
Phg=Patm
Pvaccum+ρgh=Patm
Where Pvaccum=0
therefore , Patm=ρgh
Form this we can find the atmospheric pressure by knowing the value of h.
MANOMETER
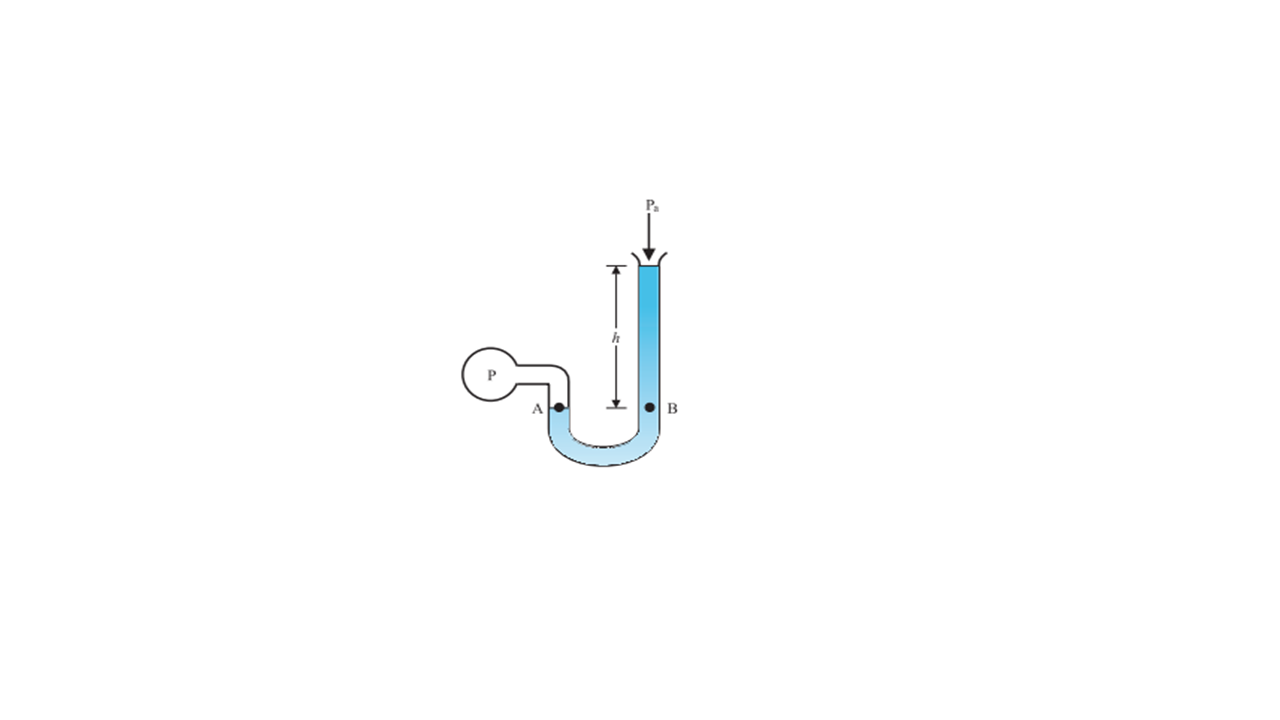
Manometer ek aisa device hai jis ki hep se hum kisi bhi gas ka pressure nikaal sakte hai, aao isko samjhte hai hum.
Jaisa ki aap sabhi diagram me dekh paa rhe hoge ki humne ek tube liya hua hai and usme already ek gas filled hai, then humne upar se ek liquid fill kya hai uss tube me and then usko chhod diya hai, humne chhodne ke baad ye notice kiya ki liquid column euillibrium prr aa jata hai and liquid A point prr aake ruk jata hai,
Toh baccho PA=PB
And PA=Pgas and PB=P0+ρgh
Therefore, Pgas=P0+ρgh
This is how we can find the pressure of gas by manometer.
MANOMETER

Manometer ek aisa device hai jis ki hep se hum kisi bhi gas ka pressure nikaal sakte hai, aao isko samjhte hai hum.
Jaisa ki aap sabhi diagram me dekh paa rhe hoge ki humne ek tube liya hua hai and usme already ek gas filled hai, then humne upar se ek liquid fill kya hai uss tube me and then usko chhod diya hai, humne chhodne ke baad ye notice kiya ki liquid column euillibrium prr aa jata hai and liquid A point prr aake ruk jata hai,
Toh baccho PA=PB
And PA=Pgas and PB=P0+ρgh
Therefore, Pgas=P0+ρgh
This is how we can find the pressure of gas by manometer.
MANOMETER

Manometer ek aisa device hai jis ki hep se hum kisi bhi gas ka pressure nikaal sakte hai, aao isko samjhte hai hum.
Jaisa ki aap sabhi diagram me dekh paa rhe hoge ki humne ek tube liya hua hai and usme already ek gas filled hai, then humne upar se ek liquid fill kya hai uss tube me and then usko chhod diya hai, humne chhodne ke baad ye notice kiya ki liquid column euillibrium prr aa jata hai and liquid A point prr aake ruk jata hai,
Toh baccho PA=PB
And PA=Pgas and PB=P0+ρgh
Therefore, Pgas=P0+ρgh
This is how we can find the pressure of gas by manometer.
EXAMPLE 1
The two thigh bones (femur bones) each of cross-sectional area 10cm2 support the upper part of a human body of mass 40 kg . Estimate the average pressure sustained by the femurs. g=10m/s2
Total cross-sectional area of the femurs is A=2×10cm2=20×10−4m2. The force acting on them is F=40kg wt=400N (taking g=10ms−2). This force is acting vertically down and hence, normally on the femurs. Thus the average pressure is
Pav=FA=2×105Nm−2
EXAMPLE 1
The two thigh bones (femur bones) each of cross-sectional area 10cm2 support the upper part of a human body of mass 40 kg . Estimate the average pressure sustained by the femurs. g=10m/s2
Total cross-sectional area of the femurs is A=2×10cm2=20×10−4m2. The force acting on them is F=40kg wt=400N (taking g=10ms−2). This force is acting vertically down and hence, normally on the femurs. Thus the average pressure is
Pav=FA=2×105Nm−2
EXAMPLE 1
The two thigh bones (femur bones) each of cross-sectional area 10cm2 support the upper part of a human body of mass 40 kg . Estimate the average pressure sustained by the femurs. g=10m/s2
Total cross-sectional area of the femurs is A=2×10cm2=20×10−4m2. The force acting on them is F=40kg wt=400N (taking g=10ms−2). This force is acting vertically down and hence, normally on the femurs. Thus the average pressure is
Pav=FA=2×105Nm−2
EXAMPLE 2
What is the pressure on a swimmer 10m below the surface of lake? g=10ms−2, atmospheric pressure = 1.01×105Pa
Here
h=10m and ρ=1000kg m−3. Take g=10ms−2
P=Pa+ρgh
=1.01×105Pa+1000kgm−3×10ms−2×10m
=2.01×105Pa
≈2atm
This is a 100% increase in pressure from surface level. At a depth of 1 km, the increase in pressure is 100 atmm! submarines are designed to withstand such enormous pressures.
EXAMPLE 2
What is the pressure on a swimmer 10m below the surface of lake? g=10ms−2, atmospheric pressure = 1.01×105Pa
Here
h=10m and ρ=1000kg m−3. Take g=10ms−2
P=Pa+ρgh
=1.01×105Pa+1000kgm−3×10ms−2×10m
=2.01×105Pa
≈2atm
This is a 100% increase in pressure from surface level. At a depth of 1 km, the increase in pressure is 100 atmm! submarines are designed to withstand such enormous pressures.
EXAMPLE 2
What is the pressure on a swimmer 10m below the surface of lake? g=10ms−2, atmospheric pressure = 1.01×105Pa
Here
h=10m and ρ=1000kg m−3. Take g=10ms−2
P=Pa+ρgh
=1.01×105Pa+1000kgm−3×10ms−2×10m
=2.01×105Pa
≈2atm
This is a 100% increase in pressure from surface level. At a depth of 1 km, the increase in pressure is 100 atmm! submarines are designed to withstand such enormous pressures.
EXAMPLE 3
The density of the atmosphere at sea level is 1.29kg/m3. Assume that it does not change with altitude. Then how high would the atmosphere extend ? g=9.8ms−2. Atmospheric pressure =1.013×105Pa.
ρgh=1.29kgm−3×9.8ms2×hm=1.01×105Pa
∴h=7989m≈8km
In reality the density of air decreases with height. So does the value of g. the atmospheric cover extends with decreasing pressure over 100 km. We should also note that the sea level atmospheric pressure is not always 760 mm of Hg. A drop in the Hg level by 100 or more is a sign of an approaching storm.
EXAMPLE 3
The density of the atmosphere at sea level is 1.29kg/m3. Assume that it does not change with altitude. Then how high would the atmosphere extend ? g=9.8ms−2. Atmospheric pressure =1.013×105Pa.
ρgh=1.29kgm−3×9.8ms2×hm=1.01×105Pa
∴h=7989m≈8km
In reality the density of air decreases with height. So does the value of g. the atmospheric cover extends with decreasing pressure over 100 km. We should also note that the sea level atmospheric pressure is not always 760 mm of Hg. A drop in the Hg level by 100 or more is a sign of an approaching storm.
EXAMPLE 3
The density of the atmosphere at sea level is 1.29kg/m3. Assume that it does not change with altitude. Then how high would the atmosphere extend ? g=9.8ms−2. Atmospheric pressure =1.013×105Pa.
ρgh=1.29kgm−3×9.8ms2×hm=1.01×105Pa
∴h=7989m≈8km
In reality the density of air decreases with height. So does the value of g. the atmospheric cover extends with decreasing pressure over 100 km. We should also note that the sea level atmospheric pressure is not always 760 mm of Hg. A drop in the Hg level by 100 or more is a sign of an approaching storm.
STREAMLINE FLOW
Baccho abhi tk humne aise fluid ki study ki joh ruka hua tha means static tha or bol sakte hai fluid equilibrium prr tha, lekin ab hum baat krne waale hai dynamic fluid ki baccho, iska mtlb hai aisa fluid ya liquid jo ki flow krega, jaise ki waterfall hum sabne dekh rakha hoga, usme jo water flow kr rha hai usi ko dynamic fluid bolte hai toh ab hum behte hue liquid ki baat krenge,
Iss dynamic fluid ki study ke liye humne sabse phle streamline flow ko janna hoga, baccho streamline flow ek assumption hai jiski wajah se hum dynamic fliud ki study kr paate hai, 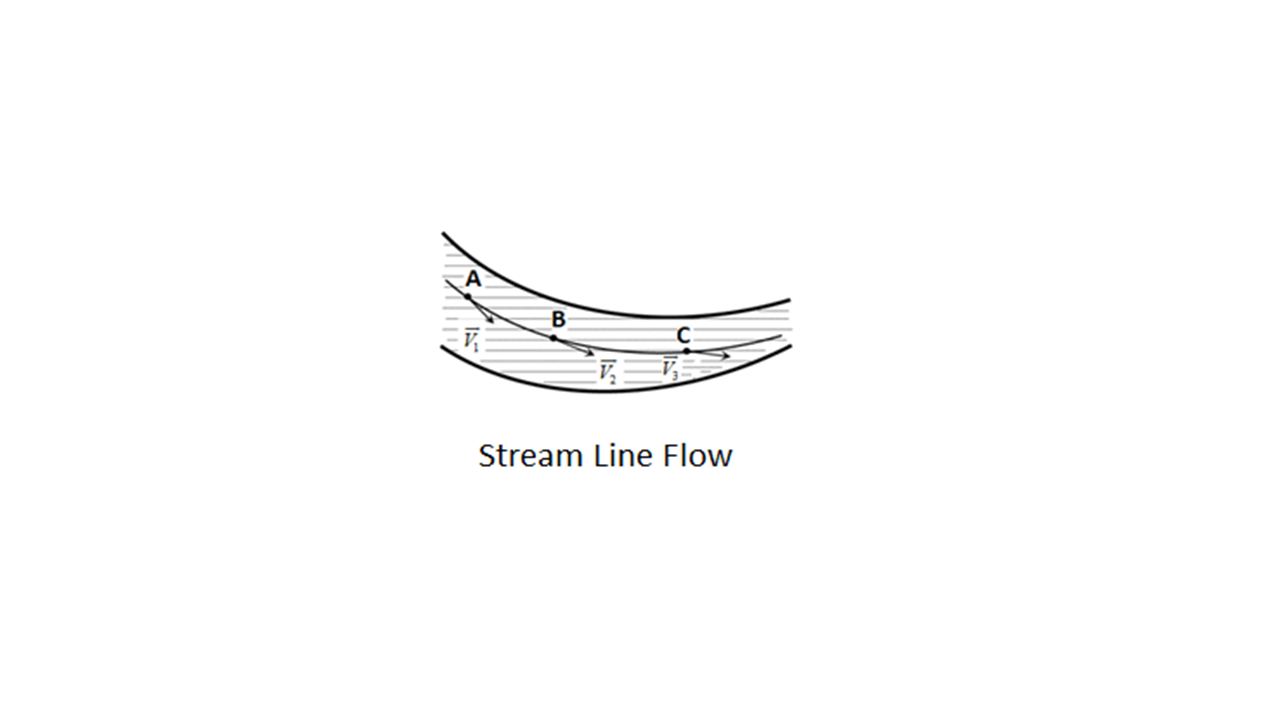
Jaisa ki aap diagram me dekh paa rhe hoge ki ek pipe me liquid flow kr rha hai and usme hume teen points maane hai A, B and C.
Sabse phli statement hum dete hai ki “ velocity of fluid molecules at any point in the pipe would be constant with time” iska mtlb hai baccho ki A point prr agr kuch velocity hai vA toh jitna bi ya jo bhi fluid ke molecules iss point A se pass honge voh sab ke sab vA velocity se pass honge same se for B point and same is for C point, prr iska mtlb ye nhi hai vA, vB ya vC same honge, baccho ye alag alag hongi lekin A point prr jo velocity vA hai voh humesha same rahegi usi point prr with time.
Dusri baat hum ye bolte hai ki “ All fluid molecules follows previous molecules path”, mtlb hai ki agr hum teem molecules maan lete hai a, b, c toh jis path se a gya hoga usi path se b jaega uski same path se c jaega.
STREAMLINE FLOW
Baccho abhi tk humne aise fluid ki study ki joh ruka hua tha means static tha or bol sakte hai fluid equilibrium prr tha, lekin ab hum baat krne waale hai dynamic fluid ki baccho, iska mtlb hai aisa fluid ya liquid jo ki flow krega, jaise ki waterfall hum sabne dekh rakha hoga, usme jo water flow kr rha hai usi ko dynamic fluid bolte hai toh ab hum behte hue liquid ki baat krenge,
Iss dynamic fluid ki study ke liye humne sabse phle streamline flow ko janna hoga, baccho streamline flow ek assumption hai jiski wajah se hum dynamic fliud ki study kr paate hai,

Jaisa ki aap diagram me dekh paa rhe hoge ki ek pipe me liquid flow kr rha hai and usme hume teen points maane hai A, B and C.
Sabse phli statement hum dete hai ki “ velocity of fluid molecules at any point in the pipe would be constant with time” iska mtlb hai baccho ki A point prr agr kuch velocity hai vA toh jitna bi ya jo bhi fluid ke molecules iss point A se pass honge voh sab ke sab vA velocity se pass honge same se for B point and same is for C point, prr iska mtlb ye nhi hai vA, vB ya vC same honge, baccho ye alag alag hongi lekin A point prr jo velocity vA hai voh humesha same rahegi usi point prr with time.
Dusri baat hum ye bolte hai ki “ All fluid molecules follows previous molecules path”, mtlb hai ki agr hum teem molecules maan lete hai a, b, c toh jis path se a gya hoga usi path se b jaega uski same path se c jaega.
STREAMLINE FLOW
Baccho abhi tk humne aise fluid ki study ki joh ruka hua tha means static tha or bol sakte hai fluid equilibrium prr tha, lekin ab hum baat krne waale hai dynamic fluid ki baccho, iska mtlb hai aisa fluid ya liquid jo ki flow krega, jaise ki waterfall hum sabne dekh rakha hoga, usme jo water flow kr rha hai usi ko dynamic fluid bolte hai toh ab hum behte hue liquid ki baat krenge,
Iss dynamic fluid ki study ke liye humne sabse phle streamline flow ko janna hoga, baccho streamline flow ek assumption hai jiski wajah se hum dynamic fliud ki study kr paate hai,

Jaisa ki aap diagram me dekh paa rhe hoge ki ek pipe me liquid flow kr rha hai and usme hume teen points maane hai A, B and C.
Sabse phli statement hum dete hai ki “ velocity of fluid molecules at any point in the pipe would be constant with time” iska mtlb hai baccho ki A point prr agr kuch velocity hai vA toh jitna bi ya jo bhi fluid ke molecules iss point A se pass honge voh sab ke sab vA velocity se pass honge same se for B point and same is for C point, prr iska mtlb ye nhi hai vA, vB ya vC same honge, baccho ye alag alag hongi lekin A point prr jo velocity vA hai voh humesha same rahegi usi point prr with time.
Dusri baat hum ye bolte hai ki “ All fluid molecules follows previous molecules path”, mtlb hai ki agr hum teem molecules maan lete hai a, b, c toh jis path se a gya hoga usi path se b jaega uski same path se c jaega.
EQUATION OF CONTINUITY
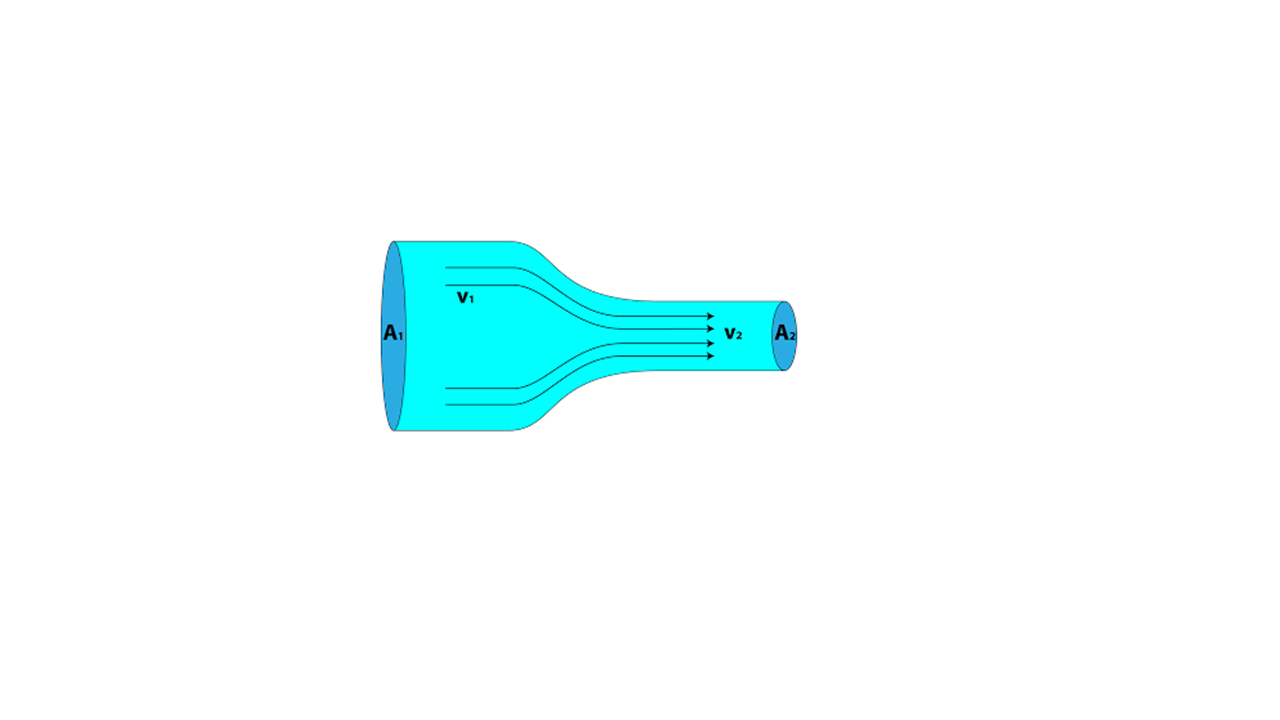
Baccho maan lijiye humare pass e pipe hai or usme koi fluid flow kr rha hai from left to right and pipe me koi bhi kisi bhi type ka gap bilkul nhi hai means poora pipe fluid se filled hai.
As we are studying fluid mechanics, hum starting me dekh chuke hai ki hum ideal fluid ki study krte hai, and baccho jaisa ki aap sabhi ko pta hai ideal fluid means “incompressible” means humara fluid ab or jyada compress nhi ho sakta hai, toh mujhe ek baat btao baccho ki jitna mass of fluid enter krega left side se toh kya utna hi amount of fluid bahar nikal jaega right side se?, bilkul baccho, aisa isliye hoga kyu humara fluid incompressible hai, ab or jyada voh compress toh ho nhi sakta, isliye jitna fluid left side se aaega utne amount oa fluid bahar nikal jaega.
Bachho equation of continuity “law of conservation of mass” per based hai.
Let the density of the fluid be ρ and Let m1 mass is entering from left side with area A1 and velocity v1 and m2 mass is coming out from right side with area A2 and velocity v2
Maan lijiye kuch Δt time ke liye humne flow ko dekha toh mila ki left side se kuch fluid andr aa gya hai, toh kitna volume andr aaya hoga,
Volume of fluid entered in time Δt = A1×(v1Δt)
Means mass(m1) of liquid entered in time Δt = rhoxxV
Or m1=ρ×A1×(v1Δt)
Similarly,
Volume of fluid coming out in time Δt = A2×(v2Δt)
Means mass(m2) of liquid coming out in time Δt = rhoxxV
Or m2=ρ×A2×(v2Δt)
Now by conservation of mass,
m1=m2
ρ×A1×(v1Δt)=ρ×A2×(v2Δt)
Hence, A1v1=A2v2, this is the continuity equation.
EQUATION OF CONTINUITY

Baccho maan lijiye humare pass e pipe hai or usme koi fluid flow kr rha hai from left to right and pipe me koi bhi kisi bhi type ka gap bilkul nhi hai means poora pipe fluid se filled hai.
As we are studying fluid mechanics, hum starting me dekh chuke hai ki hum ideal fluid ki study krte hai, and baccho jaisa ki aap sabhi ko pta hai ideal fluid means “incompressible” means humara fluid ab or jyada compress nhi ho sakta hai, toh mujhe ek baat btao baccho ki jitna mass of fluid enter krega left side se toh kya utna hi amount of fluid bahar nikal jaega right side se?, bilkul baccho, aisa isliye hoga kyu humara fluid incompressible hai, ab or jyada voh compress toh ho nhi sakta, isliye jitna fluid left side se aaega utne amount oa fluid bahar nikal jaega.
Bachho equation of continuity “law of conservation of mass” per based hai.
Let the density of the fluid be ρ and Let m1 mass is entering from left side with area A1 and velocity v1 and m2 mass is coming out from right side with area A2 and velocity v2
Maan lijiye kuch Δt time ke liye humne flow ko dekha toh mila ki left side se kuch fluid andr aa gya hai, toh kitna volume andr aaya hoga,
Volume of fluid entered in time Δt = A1×(v1Δt)
Means mass(m1) of liquid entered in time Δt = rhoxxV
Or m1=ρ×A1×(v1Δt)
Similarly,
Volume of fluid coming out in time Δt = A2×(v2Δt)
Means mass(m2) of liquid coming out in time Δt = rhoxxV
Or m2=ρ×A2×(v2Δt)
Now by conservation of mass,
m1=m2
ρ×A1×(v1Δt)=ρ×A2×(v2Δt)
Hence, A1v1=A2v2, this is the continuity equation.
EQUATION OF CONTINUITY

Baccho maan lijiye humare pass e pipe hai or usme koi fluid flow kr rha hai from left to right and pipe me koi bhi kisi bhi type ka gap bilkul nhi hai means poora pipe fluid se filled hai.
As we are studying fluid mechanics, hum starting me dekh chuke hai ki hum ideal fluid ki study krte hai, and baccho jaisa ki aap sabhi ko pta hai ideal fluid means “incompressible” means humara fluid ab or jyada compress nhi ho sakta hai, toh mujhe ek baat btao baccho ki jitna mass of fluid enter krega left side se toh kya utna hi amount of fluid bahar nikal jaega right side se?, bilkul baccho, aisa isliye hoga kyu humara fluid incompressible hai, ab or jyada voh compress toh ho nhi sakta, isliye jitna fluid left side se aaega utne amount oa fluid bahar nikal jaega.
Bachho equation of continuity “law of conservation of mass” per based hai.
Let the density of the fluid be ρ and Let m1 mass is entering from left side with area A1 and velocity v1 and m2 mass is coming out from right side with area A2 and velocity v2
Maan lijiye kuch Δt time ke liye humne flow ko dekha toh mila ki left side se kuch fluid andr aa gya hai, toh kitna volume andr aaya hoga,
Volume of fluid entered in time Δt = A1×(v1Δt)
Means mass(m1) of liquid entered in time Δt = rhoxxV
Or m1=ρ×A1×(v1Δt)
Similarly,
Volume of fluid coming out in time Δt = A2×(v2Δt)
Means mass(m2) of liquid coming out in time Δt = rhoxxV
Or m2=ρ×A2×(v2Δt)
Now by conservation of mass,
m1=m2
ρ×A1×(v1Δt)=ρ×A2×(v2Δt)
Hence, A1v1=A2v2, this is the continuity equation.
BERNOULLI’S PRINCIPLE
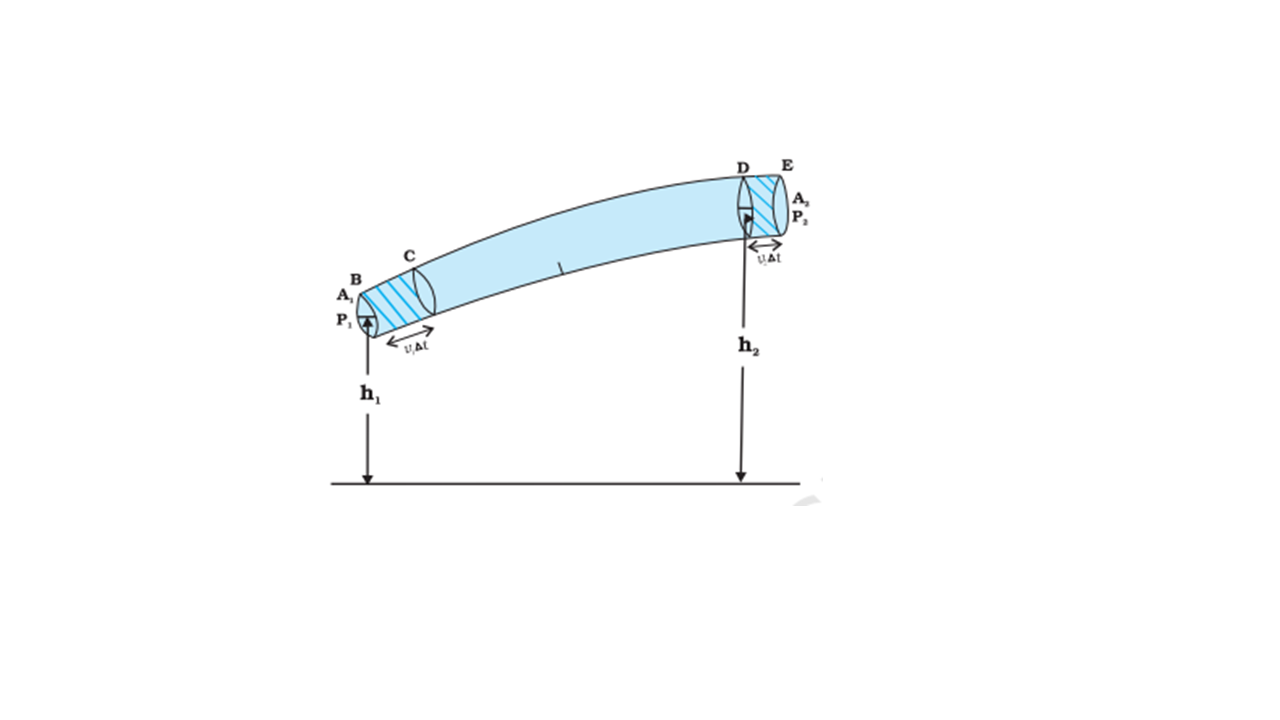
Baccho jaise hume abhi continuity equation dekhi vese hi hume bernoulli’s theorem bhi dekhni hai, ab baacho dekha jaye toh hum static fluid me pressure difference nikaalte the toh voh aata tha, P2−P1=ρgh where ρ is the density of fluid.
Lekin ab baccho fluid humara static nhi hai, ye fluid flow kr rha hai pipe me toh ye dynamic fuid hua, toh aise fluid me do point ka pressure difference kese nikala jaye, ye cheez hume bernoulli’s principle se pta chlegi.
Bernoulli’s principle “conservation of energy” prr based hai.
Jaisa ki aap diagram me dekh sakte hai ki humne ek pipe liya hai jisme fluid flow kr rha hai and ye pipe ka ek end which is point A, ye humara h1 height upar hai surface se and point B h2 height upar hai surface se, point A and B ka area A1 and A2 hai and dono points prr fluid ki velocity v1 and v2 hai.
Ab baccho hume pta hai ki work-energy theorem hoti hai,
Workdone by all the forces = change in kinetic energy,
Means Wall forces = ΔKE
Yaha prr work humari gravity bhi kr rhi hai jiski wajah se potential energy aaegi, pressure ke work ki wajah se pressure energy aaegi and velocity ki wajah se kinetic energy aaegi.
Voh hoti hai,
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
This is the bernoulli’s equation.
Isko aap check bhi kr sakte ho, static fluid ke case me fluid ki velocity hoti nhi thi means, v1=v2=0
Put the value of velocities in bernoullis equation, we will get,
P1+ρgh1=P2+ρgh2
that is P2−P1=ρg(h1−h2) , this is the equation for pressure difference in static fluid.
BERNOULLI’S PRINCIPLE

Baccho jaise hume abhi continuity equation dekhi vese hi hume bernoulli’s theorem bhi dekhni hai, ab baacho dekha jaye toh hum static fluid me pressure difference nikaalte the toh voh aata tha, P2−P1=ρgh where ρ is the density of fluid.
Lekin ab baccho fluid humara static nhi hai, ye fluid flow kr rha hai pipe me toh ye dynamic fuid hua, toh aise fluid me do point ka pressure difference kese nikala jaye, ye cheez hume bernoulli’s principle se pta chlegi.
Bernoulli’s principle “conservation of energy” prr based hai.
Jaisa ki aap diagram me dekh sakte hai ki humne ek pipe liya hai jisme fluid flow kr rha hai and ye pipe ka ek end which is point A, ye humara h1 height upar hai surface se and point B h2 height upar hai surface se, point A and B ka area A1 and A2 hai and dono points prr fluid ki velocity v1 and v2 hai.
Ab baccho hume pta hai ki work-energy theorem hoti hai,
Workdone by all the forces = change in kinetic energy,
Means Wall forces = ΔKE
Yaha prr work humari gravity bhi kr rhi hai jiski wajah se potential energy aaegi, pressure ke work ki wajah se pressure energy aaegi and velocity ki wajah se kinetic energy aaegi.
Voh hoti hai,
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
This is the bernoulli’s equation.
Isko aap check bhi kr sakte ho, static fluid ke case me fluid ki velocity hoti nhi thi means, v1=v2=0
Put the value of velocities in bernoullis equation, we will get,
P1+ρgh1=P2+ρgh2
that is P2−P1=ρg(h1−h2) , this is the equation for pressure difference in static fluid.
BERNOULLI’S PRINCIPLE

Baccho jaise hume abhi continuity equation dekhi vese hi hume bernoulli’s theorem bhi dekhni hai, ab baacho dekha jaye toh hum static fluid me pressure difference nikaalte the toh voh aata tha, P2−P1=ρgh where ρ is the density of fluid.
Lekin ab baccho fluid humara static nhi hai, ye fluid flow kr rha hai pipe me toh ye dynamic fuid hua, toh aise fluid me do point ka pressure difference kese nikala jaye, ye cheez hume bernoulli’s principle se pta chlegi.
Bernoulli’s principle “conservation of energy” prr based hai.
Jaisa ki aap diagram me dekh sakte hai ki humne ek pipe liya hai jisme fluid flow kr rha hai and ye pipe ka ek end which is point A, ye humara h1 height upar hai surface se and point B h2 height upar hai surface se, point A and B ka area A1 and A2 hai and dono points prr fluid ki velocity v1 and v2 hai.
Ab baccho hume pta hai ki work-energy theorem hoti hai,
Workdone by all the forces = change in kinetic energy,
Means Wall forces = ΔKE
Yaha prr work humari gravity bhi kr rhi hai jiski wajah se potential energy aaegi, pressure ke work ki wajah se pressure energy aaegi and velocity ki wajah se kinetic energy aaegi.
Voh hoti hai,
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
This is the bernoulli’s equation.
Isko aap check bhi kr sakte ho, static fluid ke case me fluid ki velocity hoti nhi thi means, v1=v2=0
Put the value of velocities in bernoullis equation, we will get,
P1+ρgh1=P2+ρgh2
that is P2−P1=ρg(h1−h2) , this is the equation for pressure difference in static fluid.
VENTURIMETER
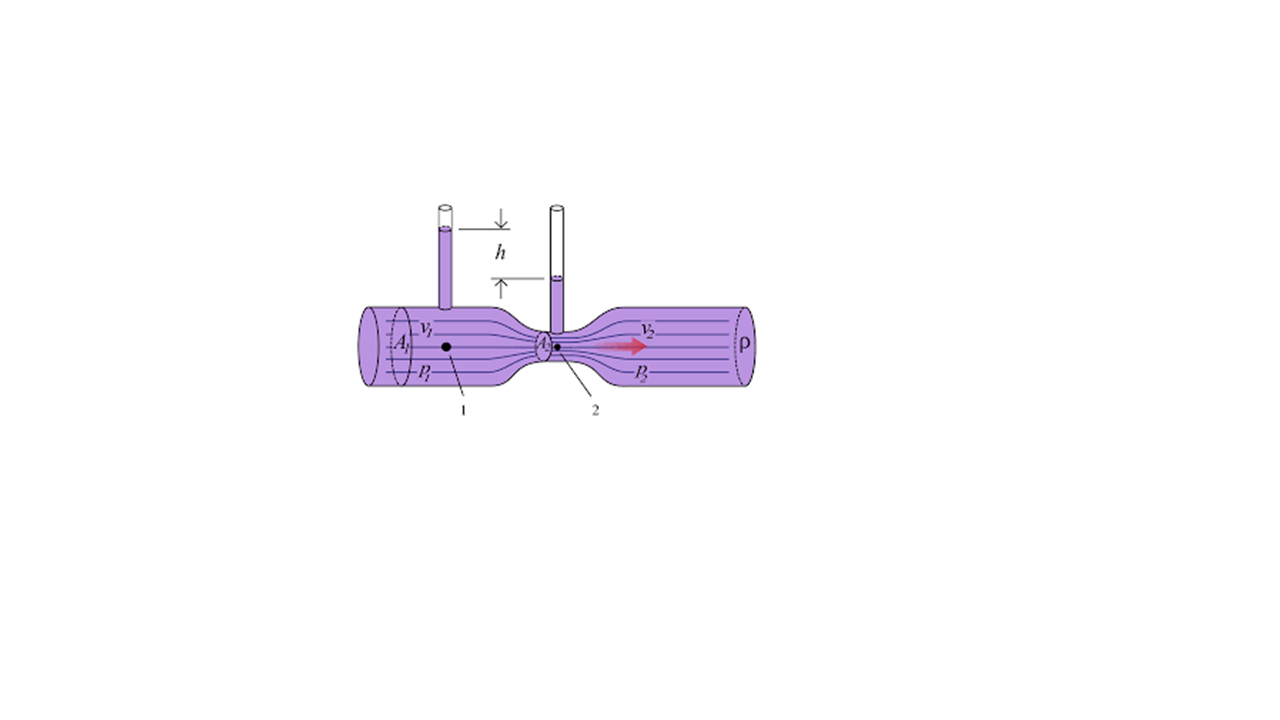
Baccho jaisa ki humne continuity equation me dekha tha ki A1v1=A2v2 hota hai.
Toh baccho hum ab kisi bhi cheez ka area of cross-section toh dekh kr calculate krke bta sakte hai prr main dikkat aati hai ki fluid ki velocity kya hogi, voh kese btaya jaye, toh veocity of fluid nikaalne ke liye hi concept aata hai venturimeter ka,
Jaisa ki aap diagram me dekh sakte hai ki ek humare paas system hai jisme fluid flow kr rha hai and iss system me do capillary tubes hai or unn dono me fluid kuch na kuch heights prr and inn dono fluids ki height ka difference h hai, dono tubes ke neeche hi humne do points maane hai point 1 and point 2 and point 1 prr fluid ki velocity v1 hai and area A1 hai and kuch pressure hoga jo ki lquid column ki wajah se hoga and same cheez point 2 prr hogi, waha prr velocity v2 hogi and area A1 hoga and pressure hoga liquid column ki wajah se,
Toh baccho ek relation toh continuity equation se milega,
A1v1=A2v2............eqn(1)
And dusra relation bernoulli’s equation se milega and baccho humne iss system ki height surface se same rakhi hai, that means h1=h1=0,
Now we will write,
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
Putting h1=h1=0,
Will get,
P1+12ρv21=P2+12ρv22
And,
Point 1 ke liquid column ki wajah se pressure hoga kuch and point 2 ki wajah se liquid column hoga , voh aaega P1−P2=ρgh
Therefore, equation will become P1−P2=12ρv22−12ρv21
Hence, 12ρ(v22−v21)=ρgh
Therefore, v22−v21=2gh....................eqn(2)
After solving eqn(1) and eqn(), we will get,
v2=A1√2ghA21−A22
And v1=A2√2ghA21−A22
Hume dono velocity mil gyi venturimeter ki help se.
VENTURIMETER

Baccho jaisa ki humne continuity equation me dekha tha ki A1v1=A2v2 hota hai.
Toh baccho hum ab kisi bhi cheez ka area of cross-section toh dekh kr calculate krke bta sakte hai prr main dikkat aati hai ki fluid ki velocity kya hogi, voh kese btaya jaye, toh veocity of fluid nikaalne ke liye hi concept aata hai venturimeter ka,
Jaisa ki aap diagram me dekh sakte hai ki ek humare paas system hai jisme fluid flow kr rha hai and iss system me do capillary tubes hai or unn dono me fluid kuch na kuch heights prr and inn dono fluids ki height ka difference h hai, dono tubes ke neeche hi humne do points maane hai point 1 and point 2 and point 1 prr fluid ki velocity v1 hai and area A1 hai and kuch pressure hoga jo ki lquid column ki wajah se hoga and same cheez point 2 prr hogi, waha prr velocity v2 hogi and area A1 hoga and pressure hoga liquid column ki wajah se,
Toh baccho ek relation toh continuity equation se milega,
A1v1=A2v2............eqn(1)
And dusra relation bernoulli’s equation se milega and baccho humne iss system ki height surface se same rakhi hai, that means h1=h1=0,
Now we will write,
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
Putting h1=h1=0,
Will get,
P1+12ρv21=P2+12ρv22
And,
Point 1 ke liquid column ki wajah se pressure hoga kuch and point 2 ki wajah se liquid column hoga , voh aaega P1−P2=ρgh
Therefore, equation will become P1−P2=12ρv22−12ρv21
Hence, 12ρ(v22−v21)=ρgh
Therefore, v22−v21=2gh....................eqn(2)
After solving eqn(1) and eqn(), we will get,
v2=A1√2ghA21−A22
And v1=A2√2ghA21−A22
Hume dono velocity mil gyi venturimeter ki help se.
VENTURIMETER

Baccho jaisa ki humne continuity equation me dekha tha ki A1v1=A2v2 hota hai.
Toh baccho hum ab kisi bhi cheez ka area of cross-section toh dekh kr calculate krke bta sakte hai prr main dikkat aati hai ki fluid ki velocity kya hogi, voh kese btaya jaye, toh veocity of fluid nikaalne ke liye hi concept aata hai venturimeter ka,
Jaisa ki aap diagram me dekh sakte hai ki ek humare paas system hai jisme fluid flow kr rha hai and iss system me do capillary tubes hai or unn dono me fluid kuch na kuch heights prr and inn dono fluids ki height ka difference h hai, dono tubes ke neeche hi humne do points maane hai point 1 and point 2 and point 1 prr fluid ki velocity v1 hai and area A1 hai and kuch pressure hoga jo ki lquid column ki wajah se hoga and same cheez point 2 prr hogi, waha prr velocity v2 hogi and area A1 hoga and pressure hoga liquid column ki wajah se,
Toh baccho ek relation toh continuity equation se milega,
A1v1=A2v2............eqn(1)
And dusra relation bernoulli’s equation se milega and baccho humne iss system ki height surface se same rakhi hai, that means h1=h1=0,
Now we will write,
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
Putting h1=h1=0,
Will get,
P1+12ρv21=P2+12ρv22
And,
Point 1 ke liquid column ki wajah se pressure hoga kuch and point 2 ki wajah se liquid column hoga , voh aaega P1−P2=ρgh
Therefore, equation will become P1−P2=12ρv22−12ρv21
Hence, 12ρ(v22−v21)=ρgh
Therefore, v22−v21=2gh....................eqn(2)
After solving eqn(1) and eqn(), we will get,
v2=A1√2ghA21−A22
And v1=A2√2ghA21−A22
Hume dono velocity mil gyi venturimeter ki help se.
SPEED OF EFFLUX
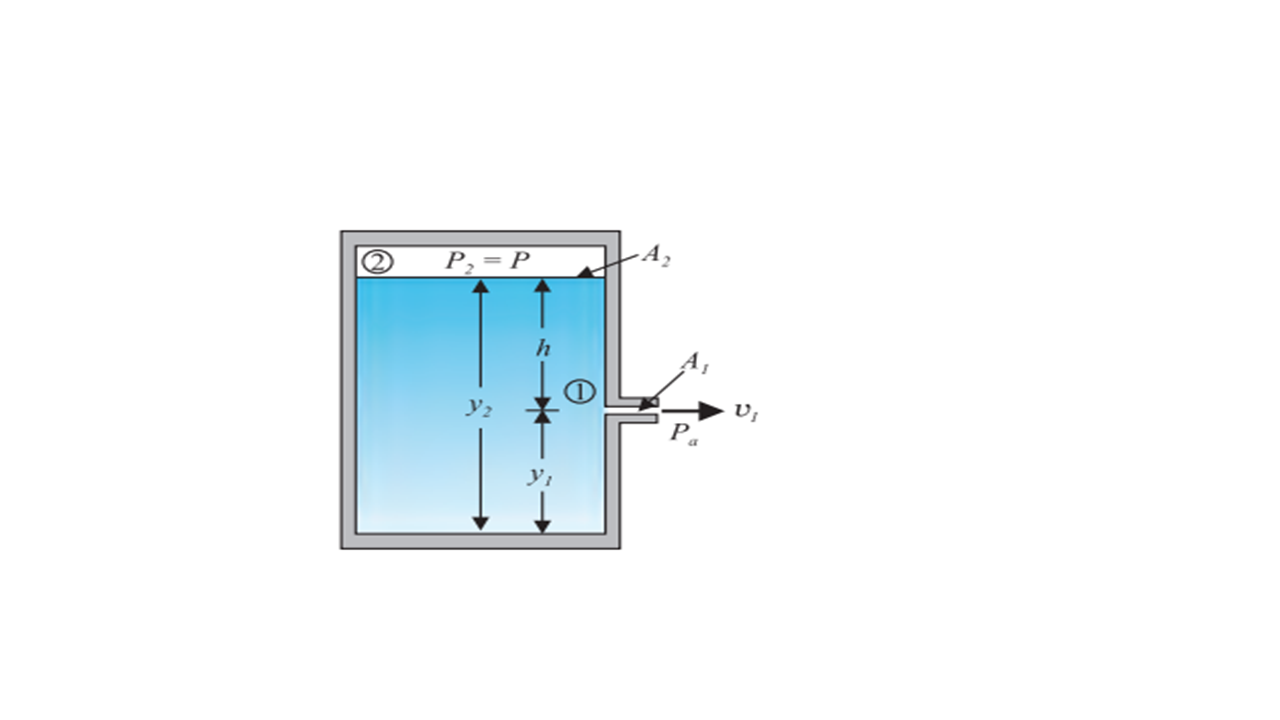
Baccho jaisa ki daigram me diya hua hai, humne ek container me fluid fill kiya hua hai and kahi ek jagah humne hole kiya hua hai, iss hole se nikalne waale fluid ki speed ko hi hum speed of efflux bolte hai.
Toh baccho isme bhi same concept lgta hai voh hai bernoulli’s equation, jaisa ki hum jaante hai ki huamra fluid incompressible hai means jitna fluid bahar niklega hole se utna hi fluid upar se neeche ki taraf shift hoga, toh hmne do point maane hai point 1 and point 2, ab baccho point 1 ki speed ko hum vf se denote krenge and area ko A1se and point 2 ki speed ko v se denote krenge and area ko A2, now by continuity equation,
A1vf=A2v,
Baccho yaha prr hum assume krte hai ki point 2 a area bhut bda hai as compare to hole ka area, therefore, vf>>>>>>v,
Hence we can take v=0,
Now baccho humne venturimeter me ek cheez dekhi thi,
v22−v21=2gh,
Here v2 is speed of hole and v1 is the speed of point A,
Therefore, we can write,
v2f−0=2gh
vf=√2gh, this is the speed of efflux.
SPEED OF EFFLUX

Baccho jaisa ki daigram me diya hua hai, humne ek container me fluid fill kiya hua hai and kahi ek jagah humne hole kiya hua hai, iss hole se nikalne waale fluid ki speed ko hi hum speed of efflux bolte hai.
Toh baccho isme bhi same concept lgta hai voh hai bernoulli’s equation, jaisa ki hum jaante hai ki huamra fluid incompressible hai means jitna fluid bahar niklega hole se utna hi fluid upar se neeche ki taraf shift hoga, toh hmne do point maane hai point 1 and point 2, ab baccho point 1 ki speed ko hum vf se denote krenge and area ko A1se and point 2 ki speed ko v se denote krenge and area ko A2, now by continuity equation,
A1vf=A2v,
Baccho yaha prr hum assume krte hai ki point 2 a area bhut bda hai as compare to hole ka area, therefore, vf>>>>>>v,
Hence we can take v=0,
Now baccho humne venturimeter me ek cheez dekhi thi,
v22−v21=2gh,
Here v2 is speed of hole and v1 is the speed of point A,
Therefore, we can write,
v2f−0=2gh
vf=√2gh, this is the speed of efflux.
SPEED OF EFFLUX

Baccho jaisa ki daigram me diya hua hai, humne ek container me fluid fill kiya hua hai and kahi ek jagah humne hole kiya hua hai, iss hole se nikalne waale fluid ki speed ko hi hum speed of efflux bolte hai.
Toh baccho isme bhi same concept lgta hai voh hai bernoulli’s equation, jaisa ki hum jaante hai ki huamra fluid incompressible hai means jitna fluid bahar niklega hole se utna hi fluid upar se neeche ki taraf shift hoga, toh hmne do point maane hai point 1 and point 2, ab baccho point 1 ki speed ko hum vf se denote krenge and area ko A1se and point 2 ki speed ko v se denote krenge and area ko A2, now by continuity equation,
A1vf=A2v,
Baccho yaha prr hum assume krte hai ki point 2 a area bhut bda hai as compare to hole ka area, therefore, vf>>>>>>v,
Hence we can take v=0,
Now baccho humne venturimeter me ek cheez dekhi thi,
v22−v21=2gh,
Here v2 is speed of hole and v1 is the speed of point A,
Therefore, we can write,
v2f−0=2gh
vf=√2gh, this is the speed of efflux.
EXAMPLE 4
At a depth of 1000 m in an ocean (a) what is the absolute pressure? (b) what is the gauge pressure? (c ) Find the force acting on the window of area 20cm×20cm of a submarine at this depth, the interior of which is maintained at sea-level atmospheric pressure. The density of sea water is 1.03×103kgm−3, g=10ms−2. Atmospheric pressure = 1.01×105Pa.
Here h=100m and ρ=1.03×103kgm−3 P=Pa+ρgh ltb rgt =1.01×105Pa
+1.03×103kgm−3×10ms−2×1000m
=104.01×105Pa
≈104atm
(b). Gauge pressure is P−P=ρgh=P
Pg=1.03×103kgm−3×10ms2×1000m
=103×105Pa
≈103atm
(c). The pressure outside the submarine is P=Pa+ρgh and the pressure inside it is Pa. Hence, the net pressure acting on the window is gauge pressure Pg=ρgh. Since the area of the window is A=0.04m2, the force acting on it is
F=PgA=103×105Pa×0.04m2=4.12×105N
EXAMPLE 4
At a depth of 1000 m in an ocean (a) what is the absolute pressure? (b) what is the gauge pressure? (c ) Find the force acting on the window of area 20cm×20cm of a submarine at this depth, the interior of which is maintained at sea-level atmospheric pressure. The density of sea water is 1.03×103kgm−3, g=10ms−2. Atmospheric pressure = 1.01×105Pa.
Here h=100m and ρ=1.03×103kgm−3 P=Pa+ρgh ltb rgt =1.01×105Pa
+1.03×103kgm−3×10ms−2×1000m
=104.01×105Pa
≈104atm
(b). Gauge pressure is P−P=ρgh=P
Pg=1.03×103kgm−3×10ms2×1000m
=103×105Pa
≈103atm
(c). The pressure outside the submarine is P=Pa+ρgh and the pressure inside it is Pa. Hence, the net pressure acting on the window is gauge pressure Pg=ρgh. Since the area of the window is A=0.04m2, the force acting on it is
F=PgA=103×105Pa×0.04m2=4.12×105N
EXAMPLE 4
At a depth of 1000 m in an ocean (a) what is the absolute pressure? (b) what is the gauge pressure? (c ) Find the force acting on the window of area 20cm×20cm of a submarine at this depth, the interior of which is maintained at sea-level atmospheric pressure. The density of sea water is 1.03×103kgm−3, g=10ms−2. Atmospheric pressure = 1.01×105Pa.
Here h=100m and ρ=1.03×103kgm−3 P=Pa+ρgh ltb rgt =1.01×105Pa
+1.03×103kgm−3×10ms−2×1000m
=104.01×105Pa
≈104atm
(b). Gauge pressure is P−P=ρgh=P
Pg=1.03×103kgm−3×10ms2×1000m
=103×105Pa
≈103atm
(c). The pressure outside the submarine is P=Pa+ρgh and the pressure inside it is Pa. Hence, the net pressure acting on the window is gauge pressure Pg=ρgh. Since the area of the window is A=0.04m2, the force acting on it is
F=PgA=103×105Pa×0.04m2=4.12×105N
EXAMPLE 5
Two syringes of different cross-sections (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0cm and 3.0 cm respectively.
(a) Find the force on the larger piston when a force of 10N is applied to the smaller piston.
(b) The smaller piston is paused in through 6.0 cm, much does the larger piston move out?
(a). Since pressure is transmitted undiminished throughout the fluid,
F2=A2A1F1=π(3/2×10−2m)2π(1/2×10−2m)2×10N
=90N
(b). Water is considered to be perfectly incompressible. Volume covered by the movement of smaller piston inwards is equal to volume moved outwards due to the larger piston
L1A1=L2A2
L2=A1A2L1=π(1/2×10−2m)2π(3/2×10−2m)2×6×10−2m
≅0.67×10−2m=0.67cm
Note, atmospheric pressure is common to both pistons and has been ignored.
EXAMPLE 5
Two syringes of different cross-sections (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0cm and 3.0 cm respectively.
(a) Find the force on the larger piston when a force of 10N is applied to the smaller piston.
(b) The smaller piston is paused in through 6.0 cm, much does the larger piston move out?
(a). Since pressure is transmitted undiminished throughout the fluid,
F2=A2A1F1=π(3/2×10−2m)2π(1/2×10−2m)2×10N
=90N
(b). Water is considered to be perfectly incompressible. Volume covered by the movement of smaller piston inwards is equal to volume moved outwards due to the larger piston
L1A1=L2A2
L2=A1A2L1=π(1/2×10−2m)2π(3/2×10−2m)2×6×10−2m
≅0.67×10−2m=0.67cm
Note, atmospheric pressure is common to both pistons and has been ignored.
EXAMPLE 5
Two syringes of different cross-sections (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0cm and 3.0 cm respectively.
(a) Find the force on the larger piston when a force of 10N is applied to the smaller piston.
(b) The smaller piston is paused in through 6.0 cm, much does the larger piston move out?
(a). Since pressure is transmitted undiminished throughout the fluid,
F2=A2A1F1=π(3/2×10−2m)2π(1/2×10−2m)2×10N
=90N
(b). Water is considered to be perfectly incompressible. Volume covered by the movement of smaller piston inwards is equal to volume moved outwards due to the larger piston
L1A1=L2A2
L2=A1A2L1=π(1/2×10−2m)2π(3/2×10−2m)2×6×10−2m
≅0.67×10−2m=0.67cm
Note, atmospheric pressure is common to both pistons and has been ignored.
VISCOSITY
Baccho ek liquid ki layer dusri liquid ki layer prr jo tangential force lgati hai use hu viscous force bote hai and this force is also called as liquid frictional force and iss phenomena is called as viscosity.
Viscous force do type ke hote hai, ek jab lgta hai jab body surface of fluid ke contact me ho aur ek viscous force jab lgta hai jab body poori fluid me immerge ho.
VISOCUS FORCE (WHEN BODY IS IN CONTACT WITH SURFACE OF FLUID)
Baccho yaha prr humne dekha ki jab jab there is a relative velocity in body and fluid, tab tab lgta hai viscous force (Fv),Ab humne dekha ki ,
FV∝dvdx, where dvdx is the velocity gradient ,
And viscous force Fv∝A, where A is the area of body which is in contact with fluid surface.
Therefore jab humne inn dono proportionality ko combine kiya toh ek constant aaya,
Fv=−ηAdvdx, where η is the coefficient of viscosity, which different for different fluids,
STOKE’S LAW
Baccho jab body fully immerged ho liquid me toh uss time jo viscous force lgta hai use hi hum stoke’s law bolte hai,Ab aapne syllabus me kevl spherical body ka immerge hona hi hai,
Toh maan lete hai ki ek sphere immerged hai kisi liquid me jiska coefficient of viscosity η hai
Toh baccho, Fv∝r where r is the radius of sphere, baccho jitna jyada radius hoga, utna jyada area sphere cover krega, or utna jyada hi viscous force lgega,
Phir humne dekha Fv∝v, where v is the velocity of sphere and Fv∝η
Jab inn sabko ek saath likha toh mila,
Fv=6πηrv, this is the viscous force when full body is immerged in the liquid.
VISCOSITY
Baccho ek liquid ki layer dusri liquid ki layer prr jo tangential force lgati hai use hu viscous force bote hai and this force is also called as liquid frictional force and iss phenomena is called as viscosity.
Viscous force do type ke hote hai, ek jab lgta hai jab body surface of fluid ke contact me ho aur ek viscous force jab lgta hai jab body poori fluid me immerge ho.
VISOCUS FORCE (WHEN BODY IS IN CONTACT WITH SURFACE OF FLUID)
Baccho yaha prr humne dekha ki jab jab there is a relative velocity in body and fluid, tab tab lgta hai viscous force (Fv),Ab humne dekha ki ,
FV∝dvdx, where dvdx is the velocity gradient ,
And viscous force Fv∝A, where A is the area of body which is in contact with fluid surface.
Therefore jab humne inn dono proportionality ko combine kiya toh ek constant aaya,
Fv=−ηAdvdx, where η is the coefficient of viscosity, which different for different fluids,
STOKE’S LAW
Baccho jab body fully immerged ho liquid me toh uss time jo viscous force lgta hai use hi hum stoke’s law bolte hai,Ab aapne syllabus me kevl spherical body ka immerge hona hi hai,
Toh maan lete hai ki ek sphere immerged hai kisi liquid me jiska coefficient of viscosity η hai
Toh baccho, Fv∝r where r is the radius of sphere, baccho jitna jyada radius hoga, utna jyada area sphere cover krega, or utna jyada hi viscous force lgega,
Phir humne dekha Fv∝v, where v is the velocity of sphere and Fv∝η
Jab inn sabko ek saath likha toh mila,
Fv=6πηrv, this is the viscous force when full body is immerged in the liquid.
VISCOSITY
Baccho ek liquid ki layer dusri liquid ki layer prr jo tangential force lgati hai use hu viscous force bote hai and this force is also called as liquid frictional force and iss phenomena is called as viscosity.
Viscous force do type ke hote hai, ek jab lgta hai jab body surface of fluid ke contact me ho aur ek viscous force jab lgta hai jab body poori fluid me immerge ho.
VISOCUS FORCE (WHEN BODY IS IN CONTACT WITH SURFACE OF FLUID)
Baccho yaha prr humne dekha ki jab jab there is a relative velocity in body and fluid, tab tab lgta hai viscous force (Fv),Ab humne dekha ki ,
FV∝dvdx, where dvdx is the velocity gradient ,
And viscous force Fv∝A, where A is the area of body which is in contact with fluid surface.
Therefore jab humne inn dono proportionality ko combine kiya toh ek constant aaya,
Fv=−ηAdvdx, where η is the coefficient of viscosity, which different for different fluids,
STOKE’S LAW
Baccho jab body fully immerged ho liquid me toh uss time jo viscous force lgta hai use hi hum stoke’s law bolte hai,Ab aapne syllabus me kevl spherical body ka immerge hona hi hai,
Toh maan lete hai ki ek sphere immerged hai kisi liquid me jiska coefficient of viscosity η hai
Toh baccho, Fv∝r where r is the radius of sphere, baccho jitna jyada radius hoga, utna jyada area sphere cover krega, or utna jyada hi viscous force lgega,
Phir humne dekha Fv∝v, where v is the velocity of sphere and Fv∝η
Jab inn sabko ek saath likha toh mila,
Fv=6πηrv, this is the viscous force when full body is immerged in the liquid.
SURFACE TENSION
Baccho abhi tak humne jo bhi baat ki voh fluid ke andr ki kari, ab hum liquid ke surface ki baat krenge.
Baccho liquid ki surface ki ek property hoti hai ki voh apne surface area ko minimum rakhna chahte hai, isi property ko hum surface tension bolte hai.
Liquid surface ke saare molecules ek dusre ko pull kr rhe hai or ek dusre molecules ko apni taraf pull kar rhe hai.
Maan lijiye ek liquid ki surface prr humne ek massless thin wire daal diya hai, toh baccho uss rassi ko surface ke moleucles kuch forces se pull kr rhe honge,
Toh baccho surface tension hogi, S=FL where S is the surface tension and it is defined as “the force acting on per unit length of wire is called as its surface tension”.
SURFACE TENSION
Baccho abhi tak humne jo bhi baat ki voh fluid ke andr ki kari, ab hum liquid ke surface ki baat krenge.
Baccho liquid ki surface ki ek property hoti hai ki voh apne surface area ko minimum rakhna chahte hai, isi property ko hum surface tension bolte hai.
Liquid surface ke saare molecules ek dusre ko pull kr rhe hai or ek dusre molecules ko apni taraf pull kar rhe hai.
Maan lijiye ek liquid ki surface prr humne ek massless thin wire daal diya hai, toh baccho uss rassi ko surface ke moleucles kuch forces se pull kr rhe honge,
Toh baccho surface tension hogi, S=FL where S is the surface tension and it is defined as “the force acting on per unit length of wire is called as its surface tension”.
SURFACE TENSION
Baccho abhi tak humne jo bhi baat ki voh fluid ke andr ki kari, ab hum liquid ke surface ki baat krenge.
Baccho liquid ki surface ki ek property hoti hai ki voh apne surface area ko minimum rakhna chahte hai, isi property ko hum surface tension bolte hai.
Liquid surface ke saare molecules ek dusre ko pull kr rhe hai or ek dusre molecules ko apni taraf pull kar rhe hai.
Maan lijiye ek liquid ki surface prr humne ek massless thin wire daal diya hai, toh baccho uss rassi ko surface ke moleucles kuch forces se pull kr rhe honge,
Toh baccho surface tension hogi, S=FL where S is the surface tension and it is defined as “the force acting on per unit length of wire is called as its surface tension”.
SURFACE ENERGY

Ab baccho hum surface ki energy ki baat krenge, toh iske liye aap diagram me dekh paa rhe honge ki humne ek soap film bnai hai jiske ek end prr massless wire of length L rakha hua hai, ab baccho ek important baat, hum jab bhi soap film ki baat krenge toh iske paas do layers hoti hai, ek upar waali surface and ek neeche waali surface, toh jo yaha prr jo wire prr force lag rha hoga voh F+F=2F hoga.
Toh is wire ko humne ek external force lga kr dx displace kiya jo ki equal hoga surface tension ki wajha se lgne waali force ke,
Therefore, workdone by external force= change in potential energy
W=ΔU
force×displacement=ΔU
Here we will take force=2F and displacement dx
ΔU=2Fdx where F=SL (surface tension),
Now, change in area would be ΔA=2L(x+dx)−2Lx
Therefore, ΔA=2Ldx
Therefore after comparing,
ΔU=SΔA , this is the surface energy of soap film.
SURFACE ENERGY

Ab baccho hum surface ki energy ki baat krenge, toh iske liye aap diagram me dekh paa rhe honge ki humne ek soap film bnai hai jiske ek end prr massless wire of length L rakha hua hai, ab baccho ek important baat, hum jab bhi soap film ki baat krenge toh iske paas do layers hoti hai, ek upar waali surface and ek neeche waali surface, toh jo yaha prr jo wire prr force lag rha hoga voh F+F=2F hoga.
Toh is wire ko humne ek external force lga kr dx displace kiya jo ki equal hoga surface tension ki wajha se lgne waali force ke,
Therefore, workdone by external force= change in potential energy
W=ΔU
force×displacement=ΔU
Here we will take force=2F and displacement dx
ΔU=2Fdx where F=SL (surface tension),
Now, change in area would be ΔA=2L(x+dx)−2Lx
Therefore, ΔA=2Ldx
Therefore after comparing,
ΔU=SΔA , this is the surface energy of soap film.
SURFACE ENERGY

Ab baccho hum surface ki energy ki baat krenge, toh iske liye aap diagram me dekh paa rhe honge ki humne ek soap film bnai hai jiske ek end prr massless wire of length L rakha hua hai, ab baccho ek important baat, hum jab bhi soap film ki baat krenge toh iske paas do layers hoti hai, ek upar waali surface and ek neeche waali surface, toh jo yaha prr jo wire prr force lag rha hoga voh F+F=2F hoga.
Toh is wire ko humne ek external force lga kr dx displace kiya jo ki equal hoga surface tension ki wajha se lgne waali force ke,
Therefore, workdone by external force= change in potential energy
W=ΔU
force×displacement=ΔU
Here we will take force=2F and displacement dx
ΔU=2Fdx where F=SL (surface tension),
Now, change in area would be ΔA=2L(x+dx)−2Lx
Therefore, ΔA=2Ldx
Therefore after comparing,
ΔU=SΔA , this is the surface energy of soap film.
ANGLE OF CONTACT
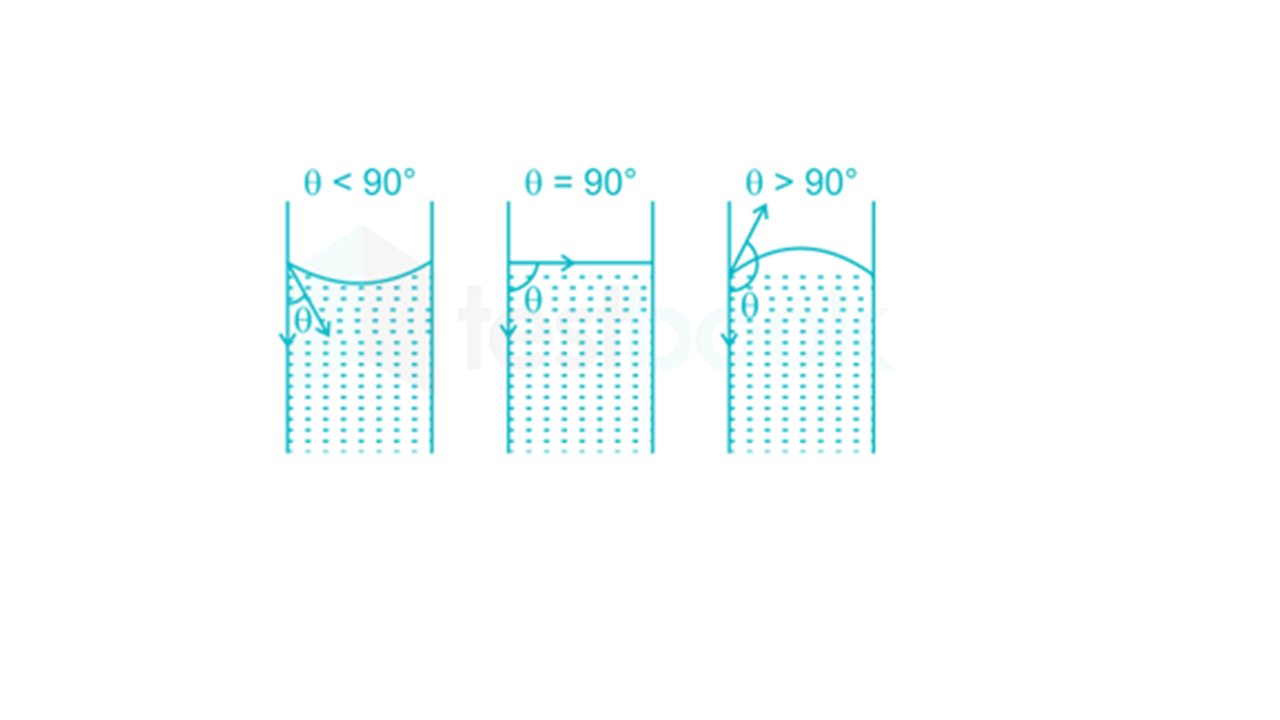
Baccho different different liquid ke liye different different meniscus bante hai, toh jaise impure water humara concave meniscus bnata hai jaisa ki aapko first tube me θ<90∘ dikh rha hoga and jisme θ>90∘ dikh rha hai use hum convex meniscus bolte hai ye jab banta hai jab isme mercury ho.
Angle of contact dekhne se phle hume sabse phle point of contach dekhna padega fluid ka glass tube ke saath,
Then uske baad hum tangent draw krte hai uss point of contact se, ek tangent bnate hai fluid ko consider krke and uski direction rakhte hai away from the glass tube and along the fluid and ek tangent bnate hai glass prr and uski direction towards the fluid hoti hai, inn dono directions ke beech me banne waale angle ko angle of contact bolte hai.
ANGLE OF CONTACT

Baccho different different liquid ke liye different different meniscus bante hai, toh jaise impure water humara concave meniscus bnata hai jaisa ki aapko first tube me θ<90∘ dikh rha hoga and jisme θ>90∘ dikh rha hai use hum convex meniscus bolte hai ye jab banta hai jab isme mercury ho.
Angle of contact dekhne se phle hume sabse phle point of contach dekhna padega fluid ka glass tube ke saath,
Then uske baad hum tangent draw krte hai uss point of contact se, ek tangent bnate hai fluid ko consider krke and uski direction rakhte hai away from the glass tube and along the fluid and ek tangent bnate hai glass prr and uski direction towards the fluid hoti hai, inn dono directions ke beech me banne waale angle ko angle of contact bolte hai.
ANGLE OF CONTACT

Baccho different different liquid ke liye different different meniscus bante hai, toh jaise impure water humara concave meniscus bnata hai jaisa ki aapko first tube me θ<90∘ dikh rha hoga and jisme θ>90∘ dikh rha hai use hum convex meniscus bolte hai ye jab banta hai jab isme mercury ho.
Angle of contact dekhne se phle hume sabse phle point of contach dekhna padega fluid ka glass tube ke saath,
Then uske baad hum tangent draw krte hai uss point of contact se, ek tangent bnate hai fluid ko consider krke and uski direction rakhte hai away from the glass tube and along the fluid and ek tangent bnate hai glass prr and uski direction towards the fluid hoti hai, inn dono directions ke beech me banne waale angle ko angle of contact bolte hai.
CAPILLARY RISE
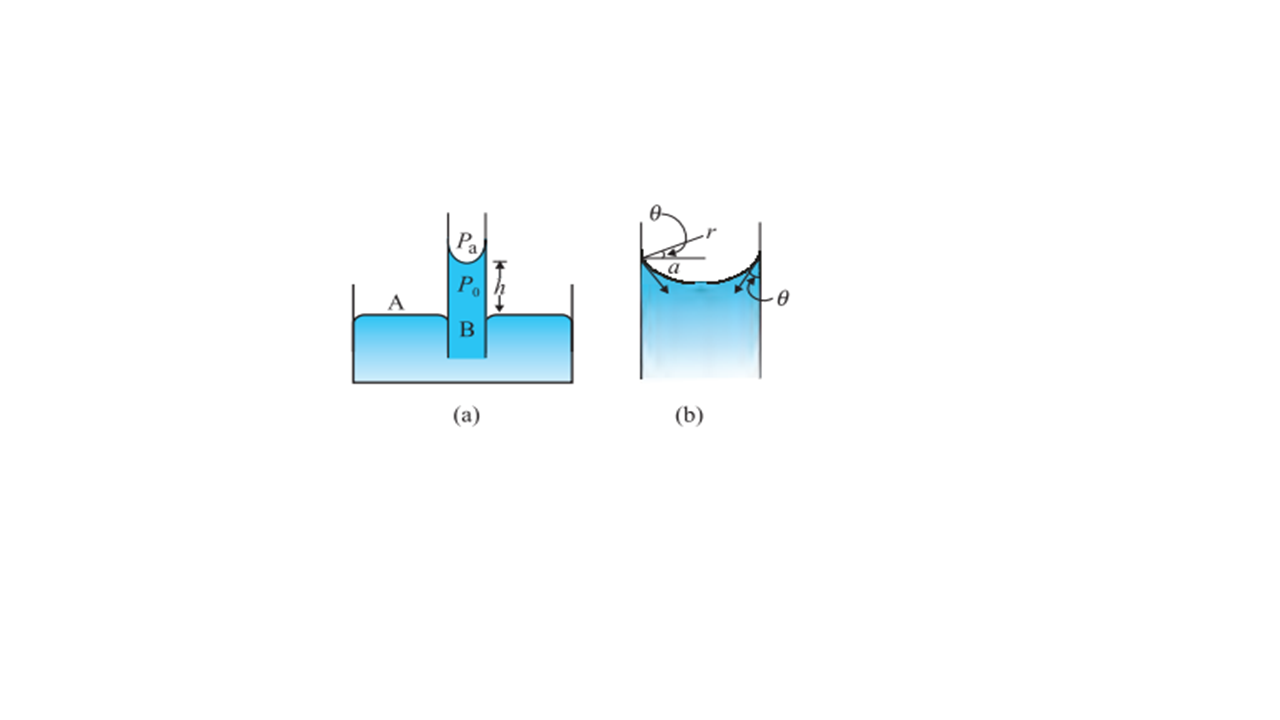
Baccho hum cappilary rise concave meniscus ke liye dekhenge jisme angle of contact θ<90∘ hota hai.
Jaisa ki aap sab diagram me dekh sakte ho ki e capillary tune hai jise humne ek fluid me dip kiya hua hai, and uska meniscus concave bna hua hai, toh baccho, PA=PB
Therefore, P0=(P0−2Sr)+ρgh where h is the height of fluid in capillary tube and ρ is the density of fluid and r is the radius of meniscus.
Therefore, r=2Sρgh
Now as you all can see in the (b) part of the diagram, a is the radius of tube, so by calculating,
a=rcosθ
Therefore, we can also write, a=2Scosθρgh
CAPILLARY RISE

Baccho hum cappilary rise concave meniscus ke liye dekhenge jisme angle of contact θ<90∘ hota hai.
Jaisa ki aap sab diagram me dekh sakte ho ki e capillary tune hai jise humne ek fluid me dip kiya hua hai, and uska meniscus concave bna hua hai, toh baccho, PA=PB
Therefore, P0=(P0−2Sr)+ρgh where h is the height of fluid in capillary tube and ρ is the density of fluid and r is the radius of meniscus.
Therefore, r=2Sρgh
Now as you all can see in the (b) part of the diagram, a is the radius of tube, so by calculating,
a=rcosθ
Therefore, we can also write, a=2Scosθρgh
CAPILLARY RISE

Baccho hum cappilary rise concave meniscus ke liye dekhenge jisme angle of contact θ<90∘ hota hai.
Jaisa ki aap sab diagram me dekh sakte ho ki e capillary tune hai jise humne ek fluid me dip kiya hua hai, and uska meniscus concave bna hua hai, toh baccho, PA=PB
Therefore, P0=(P0−2Sr)+ρgh where h is the height of fluid in capillary tube and ρ is the density of fluid and r is the radius of meniscus.
Therefore, r=2Sρgh
Now as you all can see in the (b) part of the diagram, a is the radius of tube, so by calculating,
a=rcosθ
Therefore, we can also write, a=2Scosθρgh
EXAMPLE 6
In a car lift, compressed air exerts a force F1 on a small piston having a radius of 0.5cm. This pressure is transmitted to a second piston of radius 10.0 cm . If the mass of the car to be lifted is 1350 kg. calculate F1. What is the pressure necessary to accomplish this task?
Since pressure is transmitted undiminished throughout the fluid,
F1=A1A2=F2=π(5×10−2m)2π(15×10−2m)2(1350kg×9.8ms−2)
=1470N
≈1.5×103N
The air pressure that will produce this force is
P=F1A1=1.5×103Nπ(5×10−2)2m=1.9×105Pa
This is almost double the atmospheric pressure. Hydraulic brakes in automobiles also work on the same principle. when we apply a little force on the pedal with our foot the master piston moves inside the master cylider. and the pressure caused is transmitted through the brake oil to act on a piston of larger area. A large force acts on the piston and is pushed down expanding the brake shoes against brake lining. In this way, a small force on the pedal produces a large retarding force on the wheel. An important advantage of the system is that the pressure set up by pressing pedal is transmitted equally to all cylinders attached to the four wheels so that the braking effort is equal on all wheels.
EXAMPLE 6
In a car lift, compressed air exerts a force F1 on a small piston having a radius of 0.5cm. This pressure is transmitted to a second piston of radius 10.0 cm . If the mass of the car to be lifted is 1350 kg. calculate F1. What is the pressure necessary to accomplish this task?
Since pressure is transmitted undiminished throughout the fluid,
F1=A1A2=F2=π(5×10−2m)2π(15×10−2m)2(1350kg×9.8ms−2)
=1470N
≈1.5×103N
The air pressure that will produce this force is
P=F1A1=1.5×103Nπ(5×10−2)2m=1.9×105Pa
This is almost double the atmospheric pressure. Hydraulic brakes in automobiles also work on the same principle. when we apply a little force on the pedal with our foot the master piston moves inside the master cylider. and the pressure caused is transmitted through the brake oil to act on a piston of larger area. A large force acts on the piston and is pushed down expanding the brake shoes against brake lining. In this way, a small force on the pedal produces a large retarding force on the wheel. An important advantage of the system is that the pressure set up by pressing pedal is transmitted equally to all cylinders attached to the four wheels so that the braking effort is equal on all wheels.
EXAMPLE 6
In a car lift, compressed air exerts a force F1 on a small piston having a radius of 0.5cm. This pressure is transmitted to a second piston of radius 10.0 cm . If the mass of the car to be lifted is 1350 kg. calculate F1. What is the pressure necessary to accomplish this task?
Since pressure is transmitted undiminished throughout the fluid,
F1=A1A2=F2=π(5×10−2m)2π(15×10−2m)2(1350kg×9.8ms−2)
=1470N
≈1.5×103N
The air pressure that will produce this force is
P=F1A1=1.5×103Nπ(5×10−2)2m=1.9×105Pa
This is almost double the atmospheric pressure. Hydraulic brakes in automobiles also work on the same principle. when we apply a little force on the pedal with our foot the master piston moves inside the master cylider. and the pressure caused is transmitted through the brake oil to act on a piston of larger area. A large force acts on the piston and is pushed down expanding the brake shoes against brake lining. In this way, a small force on the pedal produces a large retarding force on the wheel. An important advantage of the system is that the pressure set up by pressing pedal is transmitted equally to all cylinders attached to the four wheels so that the braking effort is equal on all wheels.
EXAMPLE 7
The flow of blood in a large artery of an anaeshetized dog is diverted through a venturimeter. The wider part of the meter has a cross sectional area equal to that of the artery i.e. 8mm2. The narrower parts has an are 4mm2. The pressure dorp in the artery is 24Pa. what is the speed of the blood in the artery ? Given that density of the blood = 1.06×103kg/m3
We take the density of blood from table 1.06×103kgm−3. The ratio of the areas is (Aa)=2.
we obtain
υ1=√2×24Pa1060kgm−2×(22−1)=0.123ms−1
EXAMPLE 7
The flow of blood in a large artery of an anaeshetized dog is diverted through a venturimeter. The wider part of the meter has a cross sectional area equal to that of the artery i.e. 8mm2. The narrower parts has an are 4mm2. The pressure dorp in the artery is 24Pa. what is the speed of the blood in the artery ? Given that density of the blood = 1.06×103kg/m3
We take the density of blood from table 1.06×103kgm−3. The ratio of the areas is (Aa)=2.
we obtain
υ1=√2×24Pa1060kgm−2×(22−1)=0.123ms−1
EXAMPLE 7
The flow of blood in a large artery of an anaeshetized dog is diverted through a venturimeter. The wider part of the meter has a cross sectional area equal to that of the artery i.e. 8mm2. The narrower parts has an are 4mm2. The pressure dorp in the artery is 24Pa. what is the speed of the blood in the artery ? Given that density of the blood = 1.06×103kg/m3
We take the density of blood from table 1.06×103kgm−3. The ratio of the areas is (Aa)=2.
we obtain
υ1=√2×24Pa1060kgm−2×(22−1)=0.123ms−1
SUMMARY
* The basic property of a fluid is that it can flow. The fluid does not have any resistance to change of its shape. Thus, the shape of a fluid is governed by the shape of its container
* A liquid is incompressible and has a free surface of its own. A gas is compressible and it expands to occupy all the space available to it.
* If F is the normal force exerted by a fluid on an area A then the average pressure Pav is defined as the ratio of the force to area
P=FA
* Pascal’s law states that: Pressure in a fluid at rest is same at all points which are at the same height. A change in pressure applied to an enclosed fluid is transmitted undiminished to every point of the fluid and the walls of the containing vessel.
* The pressure in a fluid varies with depth h according to the expression P=Pa+ρgh where ρ is the density of the fluid, assumed uniform.
* The volume of an incompressible fluid passing any point every second in a pipe of non uniform crossection is the same in the steady flow
* Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of interface between the liquid and the bounding surface. It is the extra energy that the molecules at the interface have as compared to the interior.
SUMMARY
* The basic property of a fluid is that it can flow. The fluid does not have any resistance to change of its shape. Thus, the shape of a fluid is governed by the shape of its container
* A liquid is incompressible and has a free surface of its own. A gas is compressible and it expands to occupy all the space available to it.
* If F is the normal force exerted by a fluid on an area A then the average pressure Pav is defined as the ratio of the force to area
P=FA
* Pascal’s law states that: Pressure in a fluid at rest is same at all points which are at the same height. A change in pressure applied to an enclosed fluid is transmitted undiminished to every point of the fluid and the walls of the containing vessel.
* The pressure in a fluid varies with depth h according to the expression P=Pa+ρgh where ρ is the density of the fluid, assumed uniform.
* The volume of an incompressible fluid passing any point every second in a pipe of non uniform crossection is the same in the steady flow
* Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of interface between the liquid and the bounding surface. It is the extra energy that the molecules at the interface have as compared to the interior.
SUMMARY
* The basic property of a fluid is that it can flow. The fluid does not have any resistance to change of its shape. Thus, the shape of a fluid is governed by the shape of its container
* A liquid is incompressible and has a free surface of its own. A gas is compressible and it expands to occupy all the space available to it.
* If F is the normal force exerted by a fluid on an area A then the average pressure Pav is defined as the ratio of the force to area
P=FA
* Pascal’s law states that: Pressure in a fluid at rest is same at all points which are at the same height. A change in pressure applied to an enclosed fluid is transmitted undiminished to every point of the fluid and the walls of the containing vessel.
* The pressure in a fluid varies with depth h according to the expression P=Pa+ρgh where ρ is the density of the fluid, assumed uniform.
* The volume of an incompressible fluid passing any point every second in a pipe of non uniform crossection is the same in the steady flow
* Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of interface between the liquid and the bounding surface. It is the extra energy that the molecules at the interface have as compared to the interior.