KINETIC THEORY for Class 11 PHYSICS

INTRODUCTION

Baccho iss chapter me hum jaanenge molecule hota kya hai uska nature kya hota hai,behaviour kaisa hota hai vagerah vagerah.phir uss basis prr hum inki applications prr baat krenge,molecules kese collide krte hai uss baare me bhi baat krenge.
Jaise ki newton, boyles and or bhi scientist logo ne milkr btaya ki gases jo hoti hai voh small tiny atomic particles se bani hoti hai. Phir isi basis prr kinetic theory aai jo explain krti hai gases ka behaviour.
Phir humne dekha ki inter atomic motion solid and liquid me kaafi am hota hai,mtlb collision kaafi kam hota hai kyunki molecules apni jagah ko nhi chhodte hai, lekin gases me aisa nhi hota hai,waha inter atomic motion hota hai, jis wajah se hum kinetic theory of gases padhte hai.

MOLECULAR NATURE OF MATTER

Baccho jab John Dalton ne atom ki discovery ki 1803 mein toh duniya ne samjha ki ye atom mila hai ye bhut bdi cheez hai “matter is made up of small particles called atom”.
Yaha tk ki iss time ke ek bhut acche scientist Richard Feynman (in 20th century), inhone kaha ki atom ki discovery se badi ki discovery nhi hai science me,agr humari ye poori generation marr jati hai like dinasaurs ka aana ya environment ka disaster anything jis se humari generation marr jaati hai, to jo ek information me aage pass krna chahunga voh hogi atom ki information. Phir hume lga hum sab padh sakte hai, prr esa hua nhi.
Phir 1873 me ek theory aai kinetic theory, isme inhone kaha ki ye jo atoms hai ya ye jo molecules hote hai, ye sirf hote nhi hai balki saath me constantly motion krte hai, motion krte hai toh mtb konsi energy baccho?, voh hogi kinetic energy.
Ab ek important baat ye hai ki hum kinetic theory of “gases” hi kyu padhte hai, kyunki baccho gases ke molecules hi sabse jyada motion krte hai as compare to solid and liquid.
Toh “kinetic theory of gases” kya kehti hai baccho ki gases ki jitni bhi properties hai voh sab iss wajah se hai kyunki gases ke molecules ya atoms constantly motion kr rhe hai.
Ab hum kinetic theory of gases ka sabse bda assumption ki baat krenge-”intermolecular force is absent in ideal gases”.iss assumption ki wajah se ye hua baccho ki hum study krte hai “ average properties of gases ”. Ab aap log soch rhe honge ki hum exact proerties kyu nhi padhte hai, hum average hi kyu padhte hai?, toh kya molecules ki property change ho rhi hai kahi na kahi?, toh baccho kinetic theory kehti hai ki jab motion hota hai molecules ka toh motion krte krte voh collide kar jaate hai, collide hone ke baad ye hota hai ki ek molecule apna momentum dusre ko transfer krdeta hai, and dusra phle ko transfer kar deta hai. Iss collision ki wajah se inke momentum mein and speed mein changes aate hai jis wajah se inki properties change hoti rehti hai aur lagataar properties change hoti rehti hai isliye hum study krte hai average properties of gases.

MEAN FREE PATH

Jaisa ki baccho aap upar diye hue diagram me dekh paa rhe hoge ki ek black colour ka molecule hai and baaki white colour ke molecules given hai,yaha prr hum black molecule ki baat krenge toh black molecule ki path given hai and voh kis kis molecule ke saath collision krta hua gya hai voh bhi aap diagram me dekh sakte hai.
Baccho free path mtlb hota hai ki 2 successive collisions ke beech me molecule ne kitna distance travel kiya, ise hum bolte hai free path. Ab baccho saare collision ek jaise toh honge nhi,kuch colisions ke beech me distance kam hogi or kuch collisions ke beech me distance jyada hogi, toh isi wajah se ki sabki distance alag alag hai, hum log mean free path ki study krte hai.
Mean free path ko hum define krenge average distance travelled by a molecule between two successive collisions .
Maan lijiye ki molecule ki free path

λ_{1}

λ_{2}

λ_{3}

and so on

λ_{n}

hai toh, Mean free path,

$λ_{m} = \frac{λ_{1} + λ_{2} + λ_{3} + ... . λ_{n}}{n}$ .

BEHAVIOUR OF GASES

Bachho abhi aapne upar padha ki ek throey hai kinetic theory, ab hum baat krenge ki kese aai ye theory, or phle gases ke laws kya rhe and kya ye kinetic theory purane gases ke laws ko sahi prove kar paa rha hai?, ye sab hum behaviour of gases me dekhenge.

BOYLE’S LAW

In 1661, boyle’s ka law aaya, ye bolte hai ki agr gas ka temperature constant ho, toh jo gas ka mass given hoga, uske liye pressure inversly proportional hoga to its volume.
Means "Provided temperature of gas is constant, then for a given mass of gas, the pressure is inversely proportional to its volume” .

P \propto \frac{1}{V}

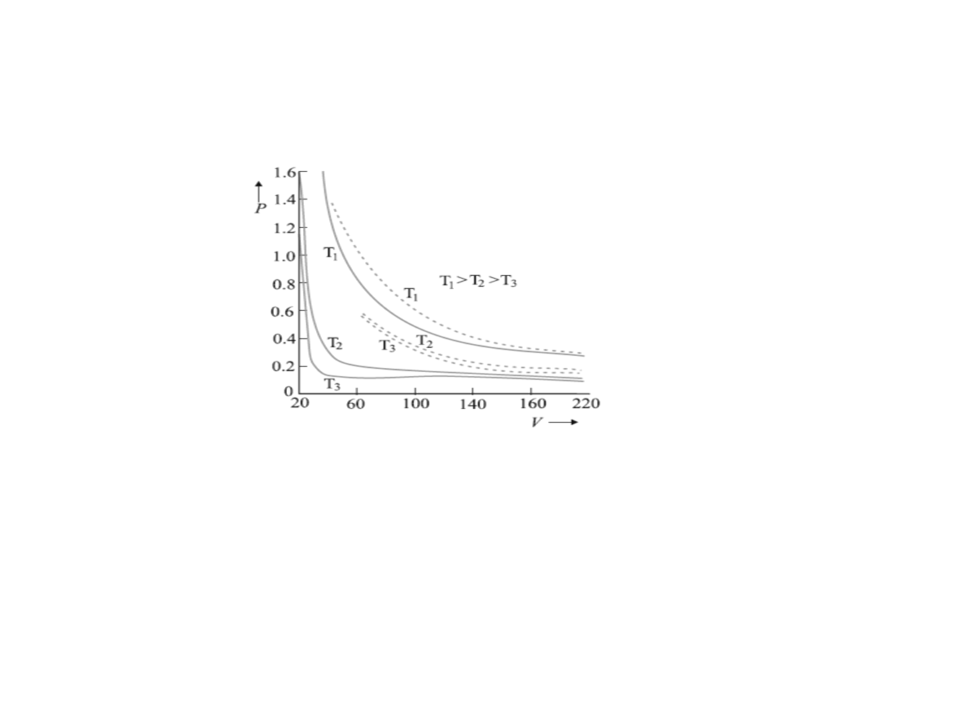
Baccho ab humne ek graph plot kiya

P \propto \frac{1}{V}

ka for different temperatures

T_{1}

T_{2}

and

T_{3}

.
Dark line indicate kr rhi hai jo humne gas law diya uska graph at a given temperature and dotted line show kr rhi hai experimental graph at a given temperature.

Ab baccho humne dekha ki jab temperature

T_{1}

(high temperature) hai toh iss case me dark line and dotted line kaafi close hai, mtlb gas law agree kar rha hai eperimental. Lekin same cheez agr humne

T_{2}

(less than

T_{1}

) temperature ke liye dekhi toh dono lines me doori thi, mtlb hai ki gas law agree nhi kr rha tha experimental se. And same humne

T_{3}

(less than

T_{2}

) ke liye dekha toh doori or jyada ho gyi dono lines me, mtlb ye bilkul bhi agree nhi krta gas law ko.

Toh yaha se hume conclusion mila ki ye jo boyle’s law hai voh kevl or kevl high temperature prr valid hai sabhi gases ke liye.
We can also say this,

P V = c o n s t a n t

Therefore,

P_{1} V_{1} = P_{2} V_{2}

CHARLE’S LAW

In 1783, charle’s a law aaya, inhone bola ki agr gas ka pressure constant rakhe, toh jo gas ka mass given hoga, uske liye volume directly porportional hoga to its absolute temperature.
Means "Provided pressure of gas is constant, then for a given mass of gas, the volume is directly proportional to its absolute temperature " .

V \propto T

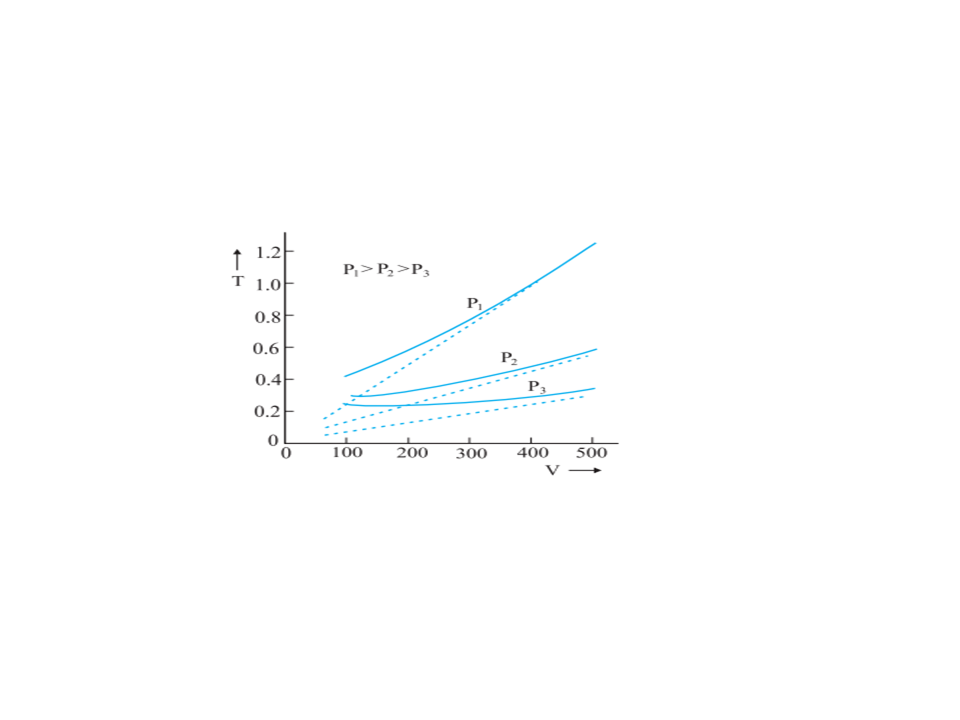
Baccho ab humne ek graph plot kiya

V \propto T

ka for different pressures

P_{1}

P_{2}

and

P_{3}

. Dark line indicate kr rhi hai jo humne gas law diya uska graph at a given pressure and dotted line show kr rhi hai experimental graph at a given pressure.

Ab baccho humne dekha ki jab pressure

P_{1}

hai toh iss case me jaise jaise temperature increase ho rha hai vese hi vese dark line and dotted line close aati jaa rhi hai, mtlb gas law agree kar rha hai eperimental at high temperature only. And similarly for pressure

P_{2}

and pressure

P_{3}

.

Toh yaha se hume conclusion mila ki ye jo charle’s law hai voh kevl or kevl high temperature prr valid hai sabhi gases ke liye.
We can also say this,

\frac{V}{T} = c o n s t a n t

Therefore,

\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}

AVAGADRO’S HYPOTHESIS

At constant temperature and pressure “ Equal volume of all gases contains equal no. of molecules ”. Mtlb hai baccho ki agr do gases ke volume equal hai toh jo no. of molecules honge voh bhi equal honge dono ke.

V ∝ no. of molecules (provided pressure and temperature to be constant)

Ab baccho jitne jyada no. of molecules honge utne jyada no. of moles hone, toh hum keh sakte hai,

V ∝ no. of moles,
Therefore

V \propto μ

Ab baccho jab hume ye teeno laws (boyle’s law, charle’s law and avagadro hypothesis) ko combine kiya toh hume mila,

V \propto \frac{μ T}{P}

Therefore we can say,

V = R \frac{μ T}{P}

or $P V = μ R T$ , where

R = 8.314 J m o l^{- 1} K^{- 1}

(gas constant)

This is ideal gas equation .

Ab baat ye hai ki kya saari gas ideal gas hoti hai?, ya phir hoti bhi hai toh kab hoti hai, toh iske liye humne phirse ek graph banaya for 1 mole of any gas, that means

μ = 1

,
Therefore

P V = R T

\frac{P V}{R T} = 1

and pressure ke beech me.

ocr_image

Baccho aapko jo straight line dikh rhi haivoh ideal gas follow kr rhi hai and for ideal gas

\frac{P V}{R T} = 1

ye humesha follow hoga, phir humne experiment kiya for different temperatures and use plot kiya, toh dekha ki at low pressure and high temperature, real gas behaves as an ideal gas.

KINETIC THEORY OF AN IDEAL GAS

Kinetic theory padhne se phle kya kya assumptions kiye gye hai, hum unn baare me jaanege phle,

Molecules identical honge phir chahe voh size, shape ya mass ki baat ho.
Molecules are constantly in random motion along straight line.
All the collisions of gas molecules among themselves and with the wall of container is elastic in nature.
Gas ka pressure jo hoga voh molecules ke colisions ki wajah se hoga with wall of container, that means
P $\propto$ No.of collisions of molecules per unit area.

PRESSURE OF AN IDEAL GAS

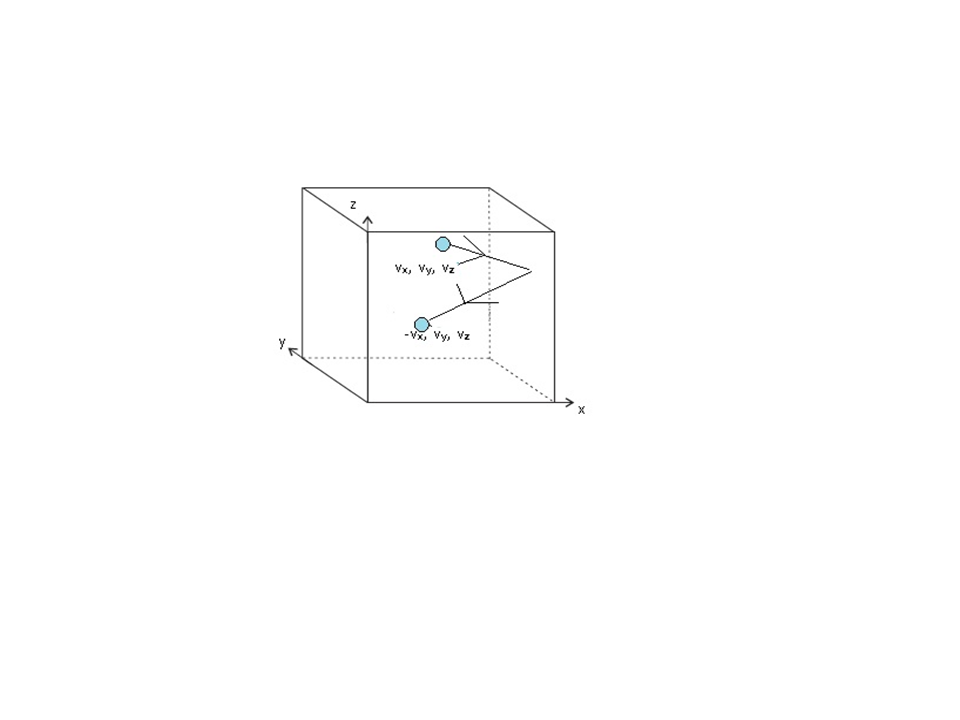
Maan lijiye humne ek cube shaped container liya hai jiski side ki length L hai or usme n no. of molecules hai and ek molecule ka mass m hai.
Yaha hum x-axis waali wall prr collision maan kr challenge. Toh jaisa ki aap sabhi ko diagram me dikh rha hoga ki molecule x-axis waali wall prr collision krta hai and palat kr vaps aajata hai. Baccho molecule ke pass teeno direction me velocity hogi, humne ek molecule liya hai toh uski velocity hum maan lete hai u , toh ye equal hogi,

u = (u_{x}) ˆ i + (u_{y}) ˆ j + (u_{z}) ˆ k

, and u ke magnitude ki baat krein toh voh hoga,

u = \sqrt{{(u_{x})}_{x}^{2} + {(u_{y})}_{y}^{2} + {(u_{z})}_{z}^{2}}

, ab jaisa ki hum jaante hai ki teeno direction me velocities same hongi toh hum x direction ki velocity ke terms me likhenge toh aaega,

u = \sqrt{3 u_{x}^{2}}

(this is the velocity of 1 molecule in the container in terms of x direction).

Ab jaisa ki hum dekh paa rhe hai ki molecule x-axis waali wall se collision krta hai, toh Initial momentum hoga,

P_{i} = m u_{x}

and jab wall se collide krke molecule vaps aaega toh final momentum hoga,

P_{f} = - m u_{x}

, toh change in momentum hoga,

Δ P = P_{i} - P_{f}

Δ P = m u_{x} - (- m u_{x})

$Δ P = 2 m u_{x}$

Ab baccho, iss collision ko hone me kitna time lga hoga ye hum nikaal sakte hai,

Time

t = \frac{2 L}{u_{x}}

,

Ab baccho humare paas time bhi aa gya,

Ab force kitna lga hoga,

F = \frac{Δ P}{t}

,
Therefore,

F = \frac{2 m u_{x}^{2}}{2 L}

F = \frac{m (\frac{1}{3} u^{2})}{L}

Hence, force $F = \frac{1}{3} \frac{m u^{2}}{L}$ ,

Ab baccho ye jo force aai hai ye ek molecule ki aai hai and box me

n

no. of molecules hai, therefore,
Force due to

n

no. of molecules will be-

F = \frac{1}{3} \frac{m u_{1}^{2}}{L} + \frac{1}{3} \frac{m u_{2}^{2}}{L} + \frac{1}{3} \frac{m u_{3}^{2}}{L} + ... ... ... ... ... ... ... ... ... ... ... + \frac{1}{3} \frac{m u_{n}^{2}}{L}

F = \frac{1}{3} \frac{m}{L} (u_{1}^{2} + u_{2}^{2} + u_{3}^{2} + ... ... ... ... ... ... ... ... ... . + u_{n}^{2})

Ab baccho hume pta hai ,

u_{r m s} = \sqrt{\frac{u_{1}^{2} + u_{2}^{2} + u_{3}^{2} + ... ... + u_{n}^{2}}{n}}

Therefore we can write,

F_{n e t} = \frac{1}{3} (\frac{m}{L}) n u_{r m s}

Ye humari net force aaaegi.

Ab baccho hume pta hai ki

p r e s s u r e = \frac{f o r c e}{a r e a}

,

Therefore, pressure of an ideal gas aaega,

P = \frac{1}{3} (\frac{m}{L}) (\frac{n u_{r m s}}{A})

where area

A = L^{2}

Therefore ,

P = \frac{1}{3} (\frac{m}{L}) (\frac{n u_{r m s}}{L^{2}})

P = \frac{1}{3} \frac{m n u_{r m s}}{L^{3}}

,
Hence ,

$P = \frac{1}{3} \frac{m n u_{r m s}}{V}$ where

V = L^{3}

(volume of cube), this is the pressure of an ideal gas.

Or we can write,

P V = \frac{1}{3} m n u_{r m s}

KINETIC ENERGY OF AN IDEAL GAS

Baccho kinetic energy hoti hai,

KE=1/2m u^2,
Therefore for 1 molecule,

K E = \frac{1}{2} m u_{1}^{2}

Hence for

n

no. of molecules,

K E = \frac{1}{2} m u_{1}^{2} + \frac{1}{2} m u_{2}^{2} + \frac{1}{2} m u_{3}^{2} + ... ... ... ... . . + \frac{1}{2} m u_{n}^{2}

K E = \frac{1}{2} m (u_{1}^{2} + u_{2}^{2} + u_{3}^{2} + ... ... ... ... ... ... ... + u_{n}^{2})

$K E = \frac{1}{2} m n u_{r m s}^{2}$ , this is the kinetic energy for

n

no. of molecules.

Now if we divide the pressure equation and kinetic energy equation, we will get,

\frac{K E}{P V} = \frac{\frac{1}{2} m n u_{r m s}^{2}}{\frac{1}{3} m n u_{r m s}}

this will become,

$K E = \frac{3}{2} P V$

For 1 mole of ideal gas, PV=RT
Therefore,

K E = \frac{3}{2} R T

And for 1 molecule,

K E = \frac{3}{2} \frac{R}{N_{A}} T

Or $K E = \frac{3}{2} K_{b} T$ where K_b=boltzman constant and the value of

K_{b} = 1.38 \times 10^{- 23}

POINT 1

Mean free path:average distance travelled by a molecule between two successive collisions.

Boyle's law:Provided temperature of gas is constant, then for a given mass of gas, the pressure is inversely proportional to its volume.

Charle's law:Provided pressure of gas is constant, then for a given mass of gas, the volume is directly proportional to its absolute temperature.

Avagadro's hypothesis:Equal volume of all gases contains equal no. of molecules.

EXAMPLE 1

The density of water is $1000 k g m^{- 3}$ . The density of water vapour at $100^{\circ} C$ and 1 atmospheric pressure is $0.6 k g m^{- 3}$ . The volume of a molecule multiplied by the total number gives what is called, molecular volume. Estimate the ratio (or fraction) of the molecular volume to the total volume occupied by the water vapour under the above conditions of temperature and pressure.

For a given mass of water molecules, the density is less if volume is large. So the volume of the vapour is $1000 / 0.6 = 1 / (6 \times 10^{- 4})$ times larger. If densities of bulk water and water molecules are same, then the fraction of molecular volume to the total volume in liquid state is 1. As volume in vapour state has increased, the fractional volume is less by the same amount, i.e. $6 \times 10^{- 4}$ .

Learn more

EXAMPLE 2

Estimate the volume of a water molecule using the data in above example. What is its approximate size?

In the liquid (or solid) phase, the molecules of water are quite closely packed. The density of water molecule may therefore, be regarded as roughly equal to the density of bulk water $= 1000 k g m^{- 3}$ . To estimate the volume of a water molecule, we need to know the mass of a single water molecule. We know that 1 mole of water has a mass approximately equal to (2 + 16)g = 18 g = 0.018 kg. Since 1 mole contains about $6 10^{23}$ molecules (Avogadro’s number), the mass of a molecule of water is $(0.018) / (6 10^{23}) k g = 3 10^{- 26} k g$ . Therefore, a rough estimate of the volume of a water molecule is as follows : Volume of a water molecule $= (3 10^{- 26} k g) / (1000 k g m^{- 3})$
$= 3 10^{- 29} m^{3}$
$(4 / 3) π {(Radius)}^{3}$
Hence,Radius ~~ 2" "10^(-10) m= 2 Å

Learn more

EXAMPLE 3

What is the average distance between atoms (interatomic distance) in water ? Using the data from above examples.

A given mass of water in vapour state has ${1.6710}^{3}$ times the volume of the same mass of water in liquid state (Ex. 13.1). This is also the increase in the amount of volume available for each molecule of water. When volume increases by $10^{3}$ times the radius increases by $V^{\frac{1}{3}}$ or 10 times, i.e., 10 2 Å = 20 Å. So the average distance is 2 20 = 40 Å.

Learn more

EXAMPLE 4

A vessel contains two non-reactive gases neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of
(i) number of molecules, and
(ii) mass density of neon and oxygen in the vessel.
Atomic mass of neon = 20.2 u, and molecular mass of oxygen = 32.0 u.

Answer Partial pressure of a gas in a mixture is the pressure it would have for the same volume and temperature if it alone occupied the vessel. (The total pressure of a mixture of non-reactive gases is the sum of partial pressures due to its constituent gases.) Each gas (assumed ideal) obeys the gas law. Since V and T are common to the two gases, we have $P_{1} V = μ_{1} R T and P_{2} V = μ_{2} R T, i e . (P_{1} / P_{2}) = (μ_{1} / μ_{2})$ .Here 1 and 2 refer to neon and oxgen respectively.Since $(P_{1} / P_{2}) = (3 / 2) (g i v e n), (μ_{1} / μ_{2}) = 3 / 2$ . (i) by definitaion $μ_{1} = (N_{1} / N_{A}) and μ_{2} = (N_{2} / N_{A}) w h e r e N_{1} and N_{2}$ are the number of molecules of 1 and 2 $N_{A}$ is the Avogardo's number. therefore $(\frac{N_{1}}{N_{2}}) = (μ_{1} / μ_{2})$ =3/2. (ii) we can also write $μ_{1} = (m_{1} / M_{1}) and μ_{2} = (m_{2} / M_{2}) where m_{1} and m_{2}$ are thier molecular masses.(both $M_{1} and M_{2} as well as m_{2} and M_{2}$ should be expressed in the same untis. if $ρ_{1} and ρ_{2}$ are the mass densities of 1 and 2 respectively, we have $\frac{ρ_{1}}{ρ_{2}} = \frac{m_{1} / V}{m_{2} / V} = \frac{m_{1}}{m_{2}} = \frac{μ_{1}}{μ_{2}} \times (\frac{M_{1}}{M_{2}})$
$= 3 / 2 \times 20.2 / 32.0 = 0.947$

Learn more

EXAMPLE 5

A flask contains argon and chlorine in the ratio 2:1 by mass. The temperature of the mixture is $27^{\circ} C$ . Obtain the ratio of
$(i)$ average kinetic energy per molecule, and
$(i i)$ root mean square speed of the molecules of two gases.
Atomic mass of argon = 39.9 u, Molecular mass of chlorine = 70.9 u.

The important point to remember is that the average kinetic energy (per molecule) of any (ideal) gas (be it monatomic like argon, diatomic like chlorine or polyatomic) is always equal to $(3 / 2) k_{B} T$ . It depends only on temperature, and is independent of the nature of the gas. (i) Since argon and chlorine both have the same temperature in the flask, the ratio of average kinetic energy (per molecule) of the two gases is 1:1.
(ii) Now lt $1 / 2 m v_{r m s} 2$ = average kinetic energy per molecule = (3/2) ) kBT where m is the mass of a molecule of the gas. Therefore,
$= \frac{{(V_{r m s}^{2})}_{A r}}{{(V_{r m s}^{2})}_{C l}} = \frac{{(m)}_{c l}}{{(m)}_{A r}} = \frac{70.9}{39.9} = 1.77$
where M denotes the molecular mass of the gas. (For argon, a molecule is just an atom of argon.) Taking square root of both sides, $\frac{{(V_{r m s})}_{A r}}{{(V_{r m s})}_{C l}} = 1.33$ You should note that the composition of the mixture by mass is quite irrelevant to the above calculation. Any other proportion by mass of argon and chlorine would give the same answers to (i) and (ii), provided the temperature remains unaltered.

Learn more

EXAMPLE 6

Uranium has two isotopes of masses 235 and 238 units. If both are present in uranium hexa fluoride gas, which would have the larger average speed ? If atomic mass of fluorine is 19 units, estimate the percentage difference in speed at any temperature.

Answer At a fixed temperature the average energy = lt m ltv2 gt is constant. So smaller the mass of the molecule, faster will be the speed. The ratio of speeds is inversely proportional to the square root of the ratio of the masses. The masses are 349 and 352 units. So
$v_{349} / v_{352} = {(352 / 349)}^{1 / 2} = 1.0044 .$
Hence difference $\frac{Δ V}{V} = 0.44 %$ [ $^{235} U$ is the isotope needed for nuclear fission. To separate it from the more abundant isotope $^{235} U$ , the mixture is surrounded by a porous cylinder. The porous cylinder must be thick and narrow, so that the molecule wanders through individually, colliding with the walls of the long pore. The faster molecule will leak out more than the slower one and so there is more of the lighter molecule (enrichment) outside the porous cylinder (Fig. 13.5). The method is not very efficient and has to be repeated several times for sufficient enrichment.].

Learn more

EXAMPLE 7

(a) When a molecule (or an elastic ball) hits a (massive) wall, it rebounds with the same speed. When a ball hits a massive bat held firmly, the same thing happens However, when the bat is moving towards the ball, the ball rebounds with a different speed. Does the ball move faster or slower?
(b) When gas in a cylinder is compressed by pushing in a piston. Its temperature rises. Guess at an explanation of this in terms of kinetic theory using (a) above
(c) What happens when a compressed gas pushes a piston out and expands. What would you observe?
(d) Sachin Tendulkar uses a heavy cricket bat while playing. Does it help him in any way?

(a) Let the speed of the ball be u relative to the wicket behind the bat. If the bat is moving towards the ball with a speed V relative to the wicket, then the relative speed of the ball to bat is V + u towards the bat. When the ball rebounds (after hitting the massive bat) its speed, relative to bat, is V + u moving away from the bat. So relative to the wicket the speed of the rebounding ball is V + (V + u) = 2V + u, moving away from the wicket. So the ball speeds up after the collision with the bat. The rebound speed will be less than u if the bat is not massive. For a molecule this would imply an increase in temperature.You should be able to answer (b) (c) and (d) based on the answer to (a). (Hint: Note the correspondence, piston $\to$ bat ,cylinder $\to$ wicket ,molecule $\to$ ball.

Learn more

LAW OF EQUIPARTITION OF ENERGY

Baccho jaisa ki hume pta hai ki1 molecule ki kinetic energy in a free space hoti hai,
$K E = \frac{1}{2} m u_{x}^{2} + \frac{1}{2} m u_{y}^{2} + \frac{1}{2} m u_{z}^{2}$
And humne abhi upar dekha ki kinetic energy of 1 molecule aati hai, $K E = \frac{3}{2} K_{b} T$ ,
Agr hum ise compare krein toh aaega,
$K E = \frac{3}{2} K_{b} T = \frac{1}{2} m u_{x}^{2} + \frac{1}{2} m u_{y}^{2} + \frac{1}{2} m u_{z}^{2}$
And hume ye bhi pta hai ki x ke along ki velocity ho ya y ke along ki ho, sab ek jesi hogi,
Toh iska mtlb hai ki agr three direction ki energy $\frac{3}{2} K_{b} T$ hai, toh ek direction me $\frac{1}{2} K_{b} T$ hogi, mtlb hai ki har direction me equally divide krdenge hum kinetic energy ko, baccho isi ko hum equipartition of energy bolte hai.
Ab baccho isme ek cheez or aati hai voh hai, degree of freedom , and isko hum $f$ se denote krte hai, iska mtlb hota hai ki voh molecule kitne type ke motion kr rha hai, jese ki abhi humare molecule ke paas three directional velocity hai toh iska mtlb degree of freedom 3 hogi.

Baccho abhi tk humne monoatomic gases ki baat ki, ab hum agr diatomic ki baat krein like $O_{2}$ , $N_{2}$ toh baccho iss case me degree of freedom 5 hota hai, iska mtlb hai ki yaha 5 type ke motion honge,

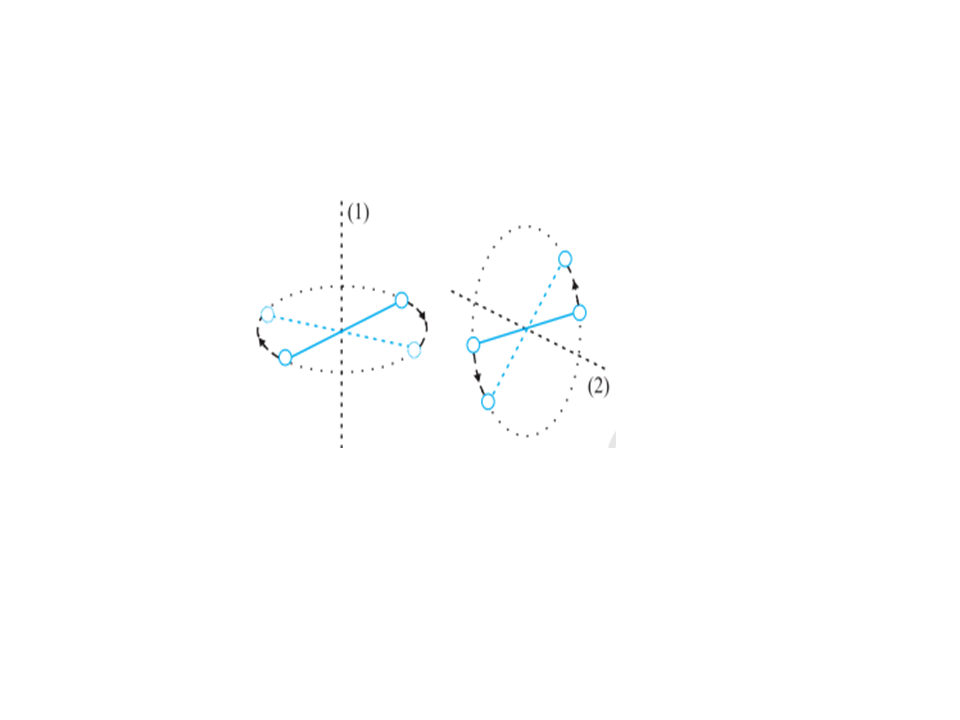
Ab baccho iss diatomic ke case me 3 motion toh hume pta hai ki veocity x ke along,y ke along and z ke along hogi, lekin isme 2 type ke motion or add ho jaenge kyunki 2 axis ke abount ye rotational motion bhi kr rha hai with angular velocity $ω_{1}$ and $ω_{2}$ , Toh bacchi jo ab total KE aaegi voh hogi,

$K E = \frac{1}{2} m u_{x}^{2} + \frac{1}{2} m u_{y}^{2} + \frac{1}{2} m u_{z}^{2} + \frac{1}{2} I_{1} ω_{1}^{2} + \frac{1}{2} I_{2} ω_{2}^{2}$
Toh iss case me bhi equipartition hoga energy ka, and ek motion ke liye energy hoti hai 1/2K_bT, toh 5 motions ke liye energy hogi $\frac{5}{2} K_{b} T$

Toh baccho hum jo kinetic energy ko likh sakte hai voh hoga, $K E = \frac{f}{2} K_{b} T$ , where f is degree of freedom,

For monoatomic gases, f=3
For diatomic gases, f=5,
For triatomic linear gases ,f=7
For triatomic non linear gases, f=6

SPECIFIC HEAT CAPACITY

MONOATOMIC GASES

Monoatomic gas ke molecule ke paas kevl three translational degree of freedom hoti hai $f = 2$ , therefore, average energy of a molecule of an monoatomic gas at temperature T is $\frac{3}{2} K_{b} T$ .

Therefore, for 1 mole for gas,

$U = \frac{3}{2} N_{A} K_{b} T$
$U = \frac{3}{2} R T$
The molar specific heat at constant volume, $C_{v}$ is

$C_{v} = \frac{d U}{d T}$
Therefore , $C_{v} = \frac{3}{2} R$

For an ideal gas,
$C_{p} - C_{v} = R$
Therefore , $C_{p} = \frac{5}{2} R$
And the ratio of specific heats $γ = \frac{C_{p}}{C_{v}} = \frac{5}{3}$

DIATOMIC GASES
Diatomic gas ke molecule ke paas three translational degree of freedom and two rotational degree of freedom hoti hai $f = 3 + 2 = 5$ , therefore, average energy of a molecule of an diatomic gas at temperature T is $\frac{5}{2} K_{b} T$ .

Therefore, for 1 mole for gas,

$U = \frac{5}{2} N_{A} K_{b} T$
$U = \frac{5}{2} R T$

The molar specific heat at constant volume, $C_{v}$ is

$C_{v} = \frac{d U}{d T}$
Therefore , $C_{v} = \frac{5}{2} R$

For an ideal gas,

$C_{p} - C_{v} = R$
Therefore , $C_{p} = \frac{7}{2} R$
And the ratio of specific heats $γ = \frac{C_{p}}{C_{v}} = \frac{7}{5}$

POLYATOMIC GASES
polyatomic gas means jiski degree of freedom $f$ hai, iske ke molecule ke paas $n$ degree of freedom hogi $f$ , therefore, average energy of a molecule of an polyatomic gas at temperature T is $\frac{f}{2} K_{b} T$ .
Iss case me C_v ki value aati hai,
$C_{v} = (3 + f) R$
For an ideal gas,
$C_{p} - C_{v} = R$
Therefore , $C_{p} = (4 + f) R$
And the ratio of specific heats $γ = \frac{C_{p}}{C_{v}} = \frac{4 + f}{3 + f}$

SPECIFIC HEAT CAPACITY OF SOLIDS
Hum law of equipartition of energy use kr sakte hai yaha specific heat capacity of solids ko butane ke liye.
Maan lo ek solid hai jiske paas N atoms hai, and sab apni mean position ke about vibrate kr rhe hai, toh jo average energy hogi ek oscillation ki in one dimension is given by,
$2 \times \frac{1}{2} K_{b} T = K_{b} T$ , and in three dimensions, it will be $3 K_{b} T$ and for 1 mole of solid,
$N = N_{A}$ ,
Therefore the total energy will be,
$U = 3 K_{b} T \times N_{A}$

Now at constant pressure,
$Δ Q = Δ U + P Δ V = Δ U$ (since for a solid $Δ V = 0$ )

Therefore , $C = \frac{Δ Q}{Δ T} = \frac{Δ U}{Δ T} = 3 R$

MEAN FREE PATH

Baccho humne iss chapter ke starting me dekh rha hai ki mean free path kya hota hai “the distance between two successive collisions is called the mean free path” and isko hum define krte the,

$λ_{m} = \frac{λ_{1} + λ_{2} + λ_{3} + ... . λ_{n}}{n}$

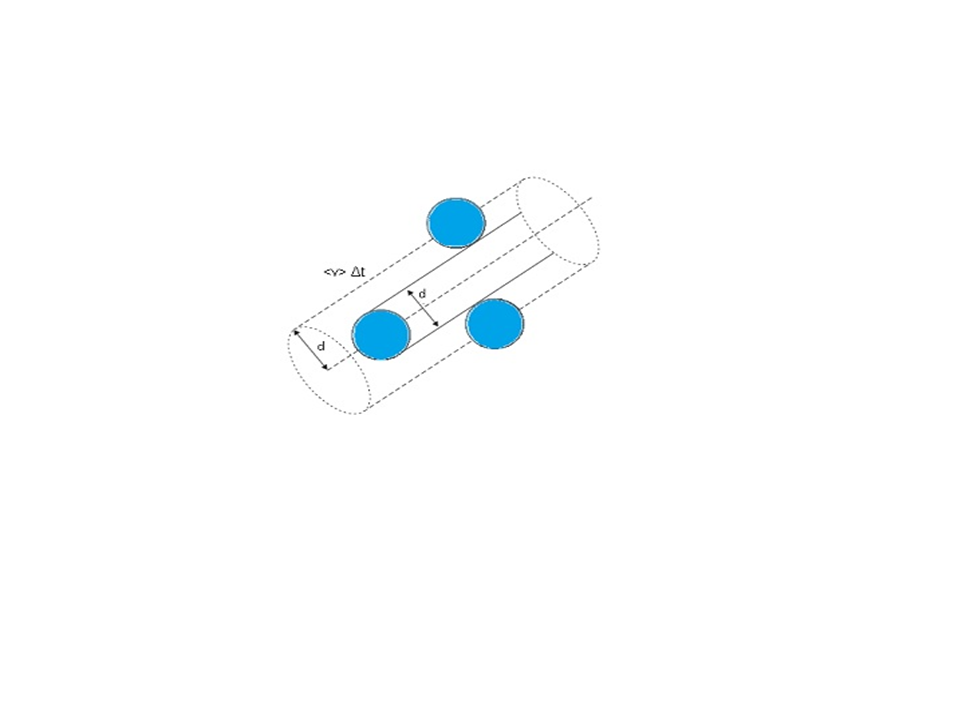
Ab baccho hum maan lete hai ki ek molecue hai jiska diameter $d$ hai, or ese kaafi moleucles honge,ab humne mana hai ki ek cylinder hai jiska diameter $2 d$ and length $1 m$ hai or iss cylinder ke andr kuch molecules poore honge,kuch aadhe hi honge or kuch molecules ke thoda part andr hoga,

Toh hum maan lete hai ki no. of molecules per unit volume jo iss cylinder me collision krenge voh $n$ hai.
Therefore ,
No. of molecules inside cylinder
= $(v o l u m e o f c y l i n d e r) \times n$
= $π d^{2} (1) \times n$

Therefore ,
No. of collisions in $1 m$ travelling distance = $π d^{2} n$
Toh baccho ab hume dikh rha hai ki,

pid^2(1)n collision $\to$ 1m distance

Toh baccho 1 collision ke liye kitna distance cover krega?

So for 1 collision $\to \frac{1}{π d^{2} n}$ distance
Or baccho yhi toh hota hai mean free path,
Toh hum likhenge, mean free path= $\frac{1}{π d^{2} n}$ .

POINT 2

Law of equipartition of energy:According to the law of equipartition of energy, for any dynamic system in thermal equilibrium, the total energy for the system is equally divided among the degree of freedom.

Mean free path:average distance travelled by a molecule between two successive collisions.

EXAMPLE 8

A cylinder of fixed capacity 44.8 litre contains helium gas at standard temperature and pressure. What is the amount of heat needed to raise the temperature of the gas in the cylinder by ${15.0}^{\circ} C ? [R = 8.31 J m o l^{- 1} K (- 1)]$

Using the gas law PV = $μ R T$ , you can easily show that 1 mol of any (ideal) gas at standard temperature (273 K) and pressure $(1 a t m = 1.01 10^{5} Pa)$ occupies a volume of 22.4 litres. This universal volume is called molar volume. Thus the cylinder in this example contains 2 mol of helium. Further, since helium is monatomic, its predicted (and observed) molar specific heat at constant volume, $C_{v}$ = (3//2) R, and molar specific heat at constant pressure, $C_{p}$ = (3/2) R + R = (5/2) R . Since the volume of

Learn more

EXAMPLE 9

Estimate the mean free path for a water molecule in water vapour at 373 K. Given diameter of water molecule $= 2 Å$ and number density of water molecule (at NTP) $= 2.7 \times 10^{25} m^{- 3}$ . Compare it with interatomic distance for water $= 40 Å$ .

The d for water vapour is same as that of air. The number density is inversely proportional to absolute temperature. SO $n = 2.7 \times 10^{25} \times \frac{273}{373} = 2 \times 10^{25} m^{- 25}$ Note that the mean free path is 100 times the interatomic distance ~ 40 Å $= 4 10^{- 9}$ m calculated earlier. It is this large value of mean free path that leads to the typical gaseous behaviour. Gases can not be confined without a container. Using, the kinetic theory of gases, the bulk measurable properties like viscosity, heat conductivity and diffusion can be related to the microscopic parameters like molecular size. It is through such relations that the molecular sizes were first estimated.

Learn more

SUMMARY

* The ideal gas equation connecting pressure (P), volume (V) and absolute temperature (T ) is $P V = μ R T = k_{b} N T$ where $μ$ is the number of moles and N is the number of molecules. R and $k_{b}$ are universal constants. $R = 8.314 J m o l^{- 1} K^{- 1}$ , $k_{b} = \frac{R}{N_{A}} = 1.38 \times 10^{- 23} J K^{- 1}$

* Kinetic theory of an ideal gas gives the relation $P = \frac{1}{3} n m u^{2}$ where n is number density of molecules, m the mass of the molecule and $u^{2}$ is the mean of squared speed. Combined with the ideal gas equation it yields a kinetic interpretation of temperature. $\frac{1}{2} m u^{2} = \frac{3}{2} k_{b} T$
$u_{r m s} = \sqrt{u^{2}} = \sqrt{\frac{3 k_{b} T}{m}}$ .
This tells us that the temperature of a gas is a measure of the average kinetic energy of a molecule, independent of the nature of the gas or molecule. In a mixture of gases at a fixed temperature the heavier molecule has the lower average speed.

. * The translational kinetic energy
$E = \frac{3}{2} k_{b} N T$
This leads to a relation $P V = \frac{3}{2} E$

* The law of equipartition of energy states that if a system is in equilibrium at absolute temperature T, the total energy is distributed equally in different energy modes of absorption, the energy in each mode being equal to $\frac{1}{2} k_{b} T$ . Each translational and rotational degree of freedom corresponds to one energy mode of absorption and has energy $\frac{1}{2} k_{b} T$ . Each vibrational frequency has two modes of energy (kinetic and potential) with corresponding energy equal to
$2 \times \frac{1}{2} k_{b} T = k_{b} T$

* Using the law of equipartition of energy, the molar specific heats of gases can be determined and the values are in agreement with the experimental values of specific heats of several gases. The agreement can be improved by including vibrational modes of motion.

* The mean free path l is the average distance covered by a molecule between two successive collisions :
$L = \frac{1}{\sqrt{2} n π d^{2}}$
where n is the number density and d the diameter of the molecule.

Home
Ask Doubt
Profile