FRICTION for Class 11 PHYSICS
INTRODUCTION
Friction ek aisa force hai jo hamesha harame around hota hai. Jo bodies contact me hote hai, unke relative motion ko oppose krta hai. Friction hame move krne ko allow bhi krta hai. Ager do bodies contact me ho aur ek dure ke relative move kr rahe ho to unke beech ke friction ko kinetic friction kehte hai. Eg: Friction ek hockey puck ko slow kr deta hai jo ice pr slide kr raha hota hai. Jab objects stationary hote hai to unke beech static friction act krta hai. Usually do objects ke beech static friction kinetic friction se jyada hota hai.
THE FRICTION FORCE
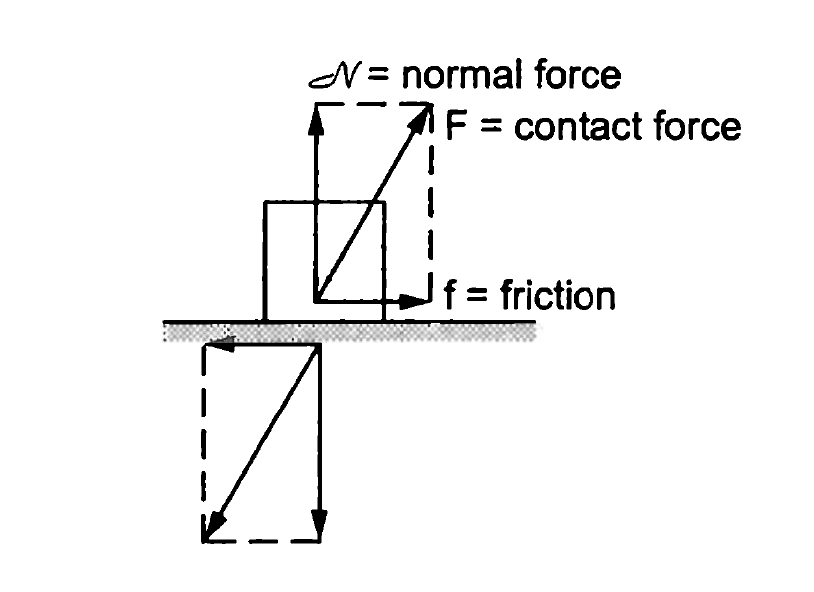
Jab koi force →F kisi body ko ek surface par slide karne ki koshish karta hai, tab ek frictional force us surface ke dwara us body par lagta hai. Ye frictional force parallel hota hai surface ke aur iski direction thodi tricky hoti hai. Iski direction us direction me hoti hai jis direction me wo motion ka oppose kare, ya aesa kah sakte hai ki ye relative motion ke opposite act karta hai. Ye friction force us body aur surface ki bonding ki wajah se lagta hai.Jab koi two bodies contact me hote hai to unke beech electromagnetic force act hota hai ji ki bodies ki surface par charged particles ke present hone ki wajah se lagta hai. Isi wajah se dono bodies ek doosre par contact force apply karte hai jo ki according to Newton’s Third law equal aur opposite hota hai.
Isi contact force ko ham 2 components me resolve kar sakte hai, ek perpendicular to the contact surface ke aur doosra jo us surface ke parallel ho. Jo component perpendicular hai use hai normal contact force ya normal force kahte hai. Jo component contact surface ke parallel hai use ham friction kahte hai.
EXPERIMENTS
Kisi block ko kisi surface par push karke leave kar do. Kya hoga? Aapne sahi socha ki wo block kuch doori tay karke ruk jayega. Ager ham us block motion ke baare me soche to usko hamne kuch initial velocity di aur wo finally stop ho gaya. To iska matlab hai ki uspar opposite direction me kuch acceleration act kiya hoga. From Newton’s second law, uspar ek force surface ke parallel zaroor act kiya hoga jiski wajah se velocity km hote hote zero ho gayi. Isi force ko friction force kahte hai. 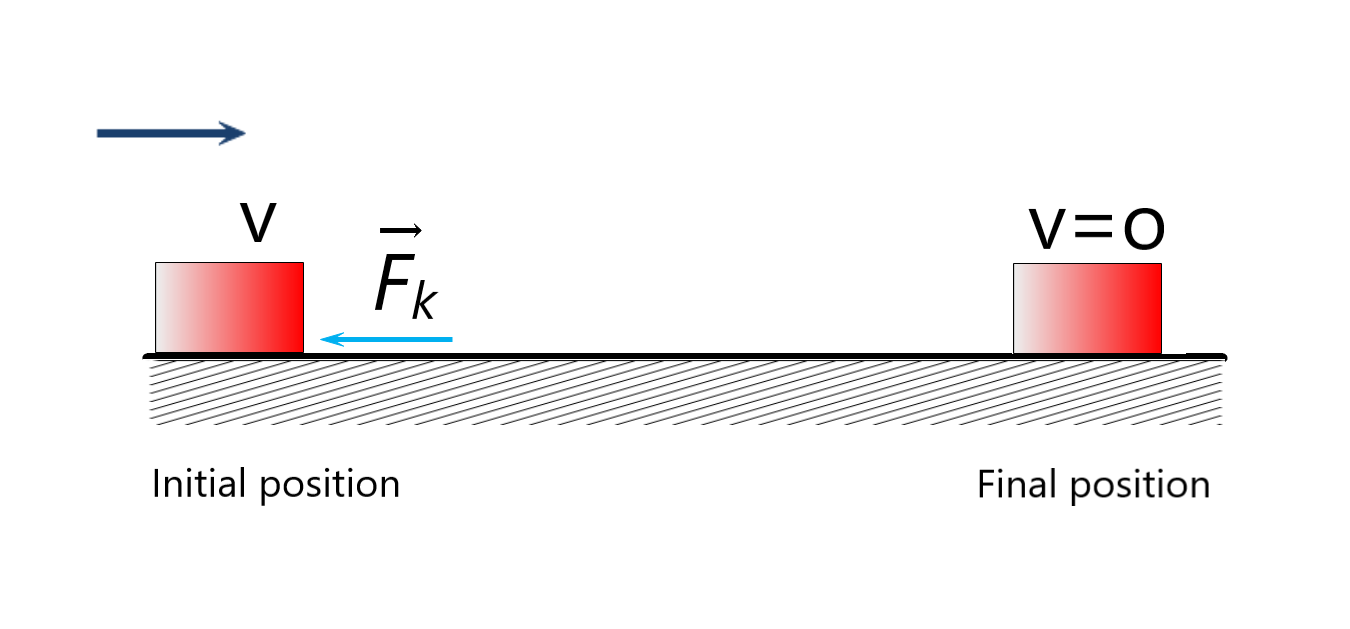
Ab isi block ko usi surface pr ek constant velocity se move karane ki koshish karo. Ab aap wo frictional force ko feel kr paoge. Aap jitna bhi force apply kr rahe ho wo frictional force ke effect ko khatam karne ke liye use ho raha hai. Jab block move kr raha hai to uspr lagne wala frictional force kinetic friction force (Fk) hai.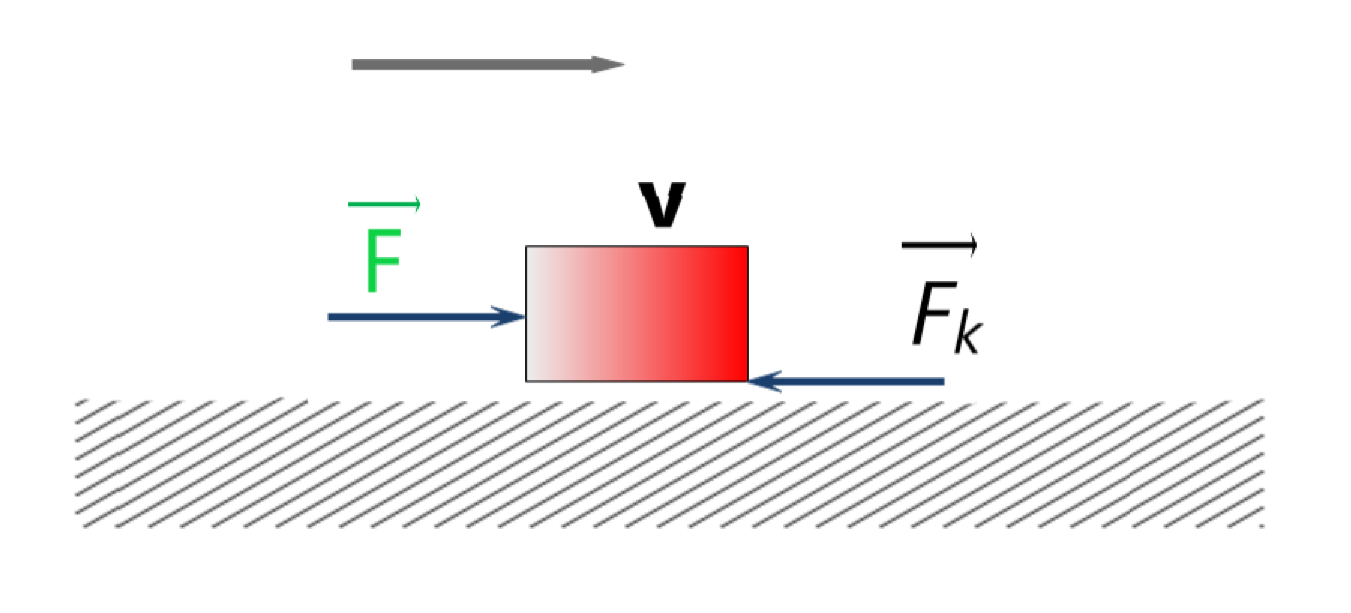
Kisi khade truck ko push karke dekho. Kya hoga? Wo apni jagah par hi rahega, zara bhi move nahi hoga. To Newton’s second law ke according us truck pr ek equal and opposite force zaroor lag raha hoga kyuki truck rest pr hi hai. Ye friction force hi hai. Ab aap truck pr aur bhi jyada force lagayiye. Kya hua? Truck ab bhi nahi move hua? Iska matlab ye friction force bhi increase ho gya. Utna hi increase hua jitna ki zarurat thi aapke force ke effect ko khatam karne ke liye. Iska matlab ye friction force ek self-adjusting force hai.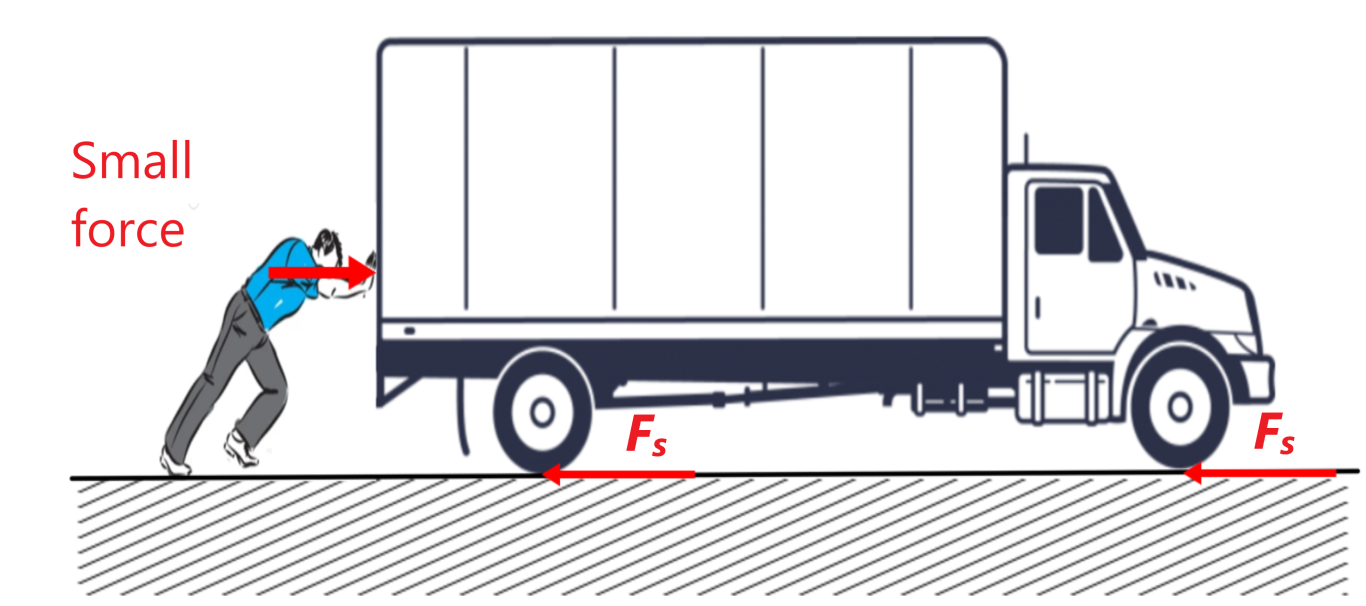
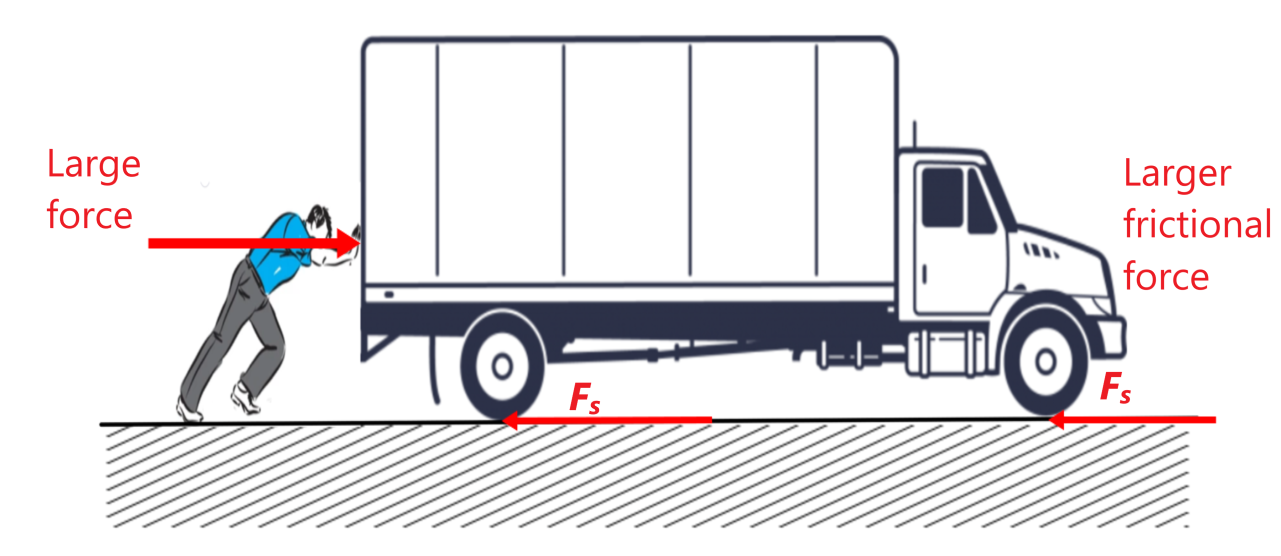
Ek heavy block ko push karne ki koshish karo. Uspar initially ek small push do. Wo nahi move karega. Ab dheere dheere is force ko badhao. Ek point aesa aayega jab ye block move karne lagega. Iska matlab friction force ki ek limit hoti hai. Ye ek particular value tak hi increase ho sakta hai. Ab aapka force is friction force se zyada hai tabhi aap block ko rest se move karwa paye. Ek aur baat. Ab jab aap is block ko move kar pa rahe hai to ab aapko feel hoga ki aapko kam force lagane ki zarurat pad rahi hai. Ye force, jo aapne initially lagaya tha car ko rest se move karne ke liye, us force se km hai. Jab block rest me tha tab uspar surface dwara aur surface ke parallel jo frictional force lag raha tha wo static frictional force tha. Jab wo block move karne laga to ye force kinetic frictional force hoga.
Generally, Kinetic frictional force < Static frictional force
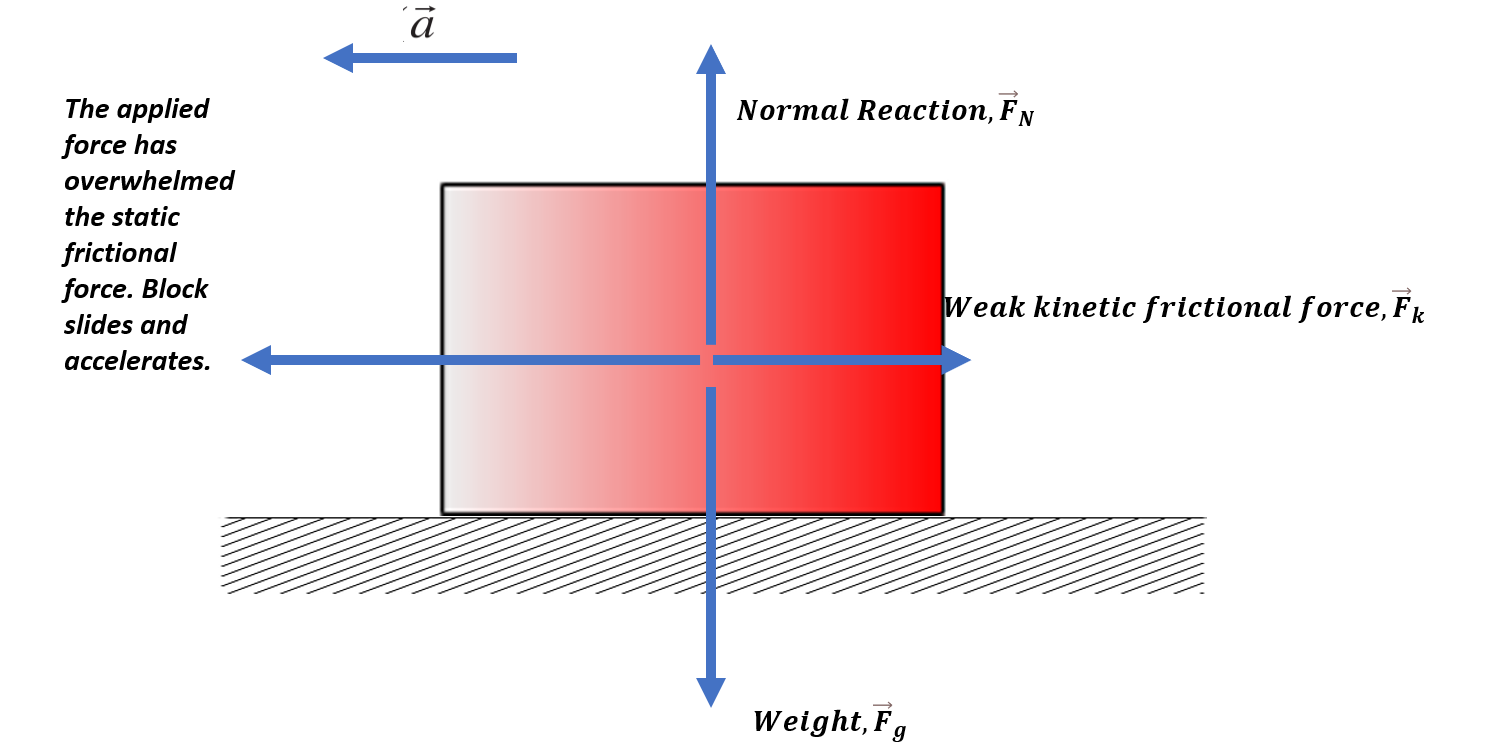
Ager body slide nahi ho rahi hai to is frictional force ko static frictional force fs kahte hai. Agar body slide kar rahi hai to isi frictional force ko kinetic frictional force fk kahte hai.
Agar body par lagne wala force just about frictional force ke equal ho jaye aur body bas halka sa force aur lagane par move karne lage to isi frictional force ko limiting frictional force kahte hai fl.
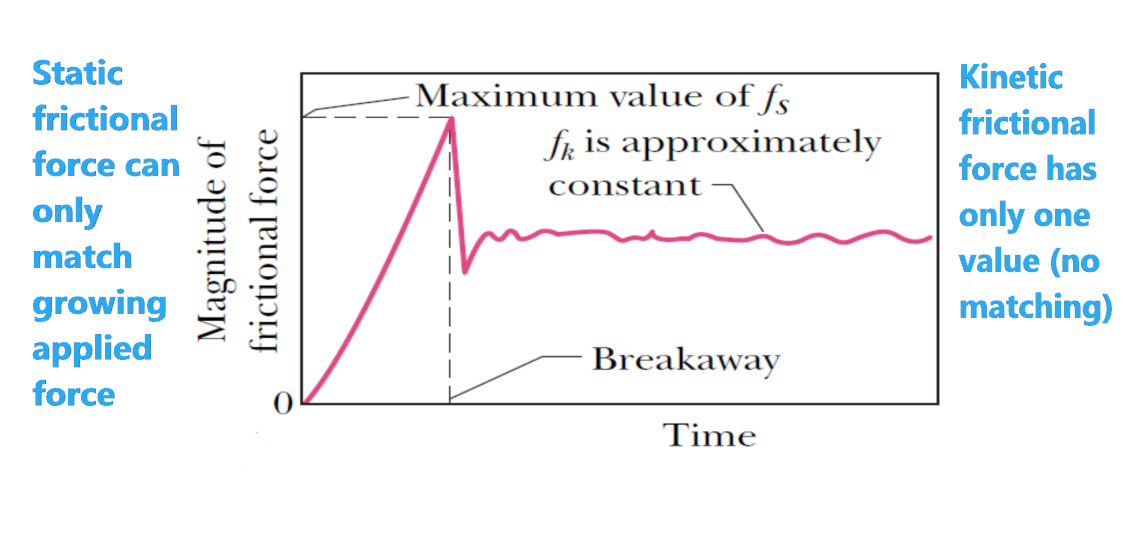
Let’s understand the nature of this friction force with the help of a graph. Let’s consider ki ham ek block par force laga rahe hai. Aur dheere dheere is force ko increase karte hai. Is experiment me ham force tab tak increase karte hai jab tak breakaway nahi ho jata ( meaning block nahi hone lagta). Jaise hi block move karne lagta hai ham ek constant force apply karte hai. Aap graph me dekh sakte hai ki pahle ye force thoda jyada hai comparison me us force ke jo applied hai jab ye block move karne lagta hai.
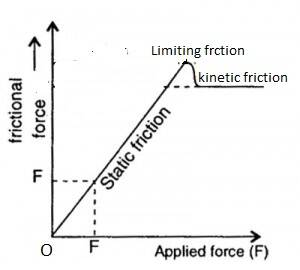
PROPERTIES OF FRICTION
Ager ek body ek dry and unlubricated ground par rakhi hai aur uspar ham force →Flagaye, to jo frictional force us body par lag raha hai uski ye teen properties hoti hai:
Property 1: Agar wo body move nahi karti hai to uspar static frictional force →fs act karta hai. Ye force →F je equal and opposite direction me act karta hai. Ab agar ham →F ko increase karte hai to static frictional force →fs bhi increase karta hai.
Property 2: Magnitude of →fs ki maximum value hoti hai →fs,max, that is,
→fs,max=μs→FN, where μs is coefficient of static friction and →FN is magnitude of normal force of body from the surface. Agar →F ka surface ke parallel jo component hai wo exceed karta hai →fs,max se to body surface ke along slide hona shuru ho jayegi.
Property 3: Agar body ne slide karna start kar diya hai to frictional force ka magnitude rapidly decrease hone lagta hai aur ek approx. constant value ko attain kar leta hai. Then,
→fk=μk→FN, where μk is coefficient of kinetic friction. Isiliye, sliding ke dauraan →fk hi wo force hai jo relative motion ko oppose karta hai. 
GRAPH OF FRICTION
POINT
Friction: A force that resists the relative motion or tendency to such motion of two bodies in contact.
Kinetic Friction: If two systems are in contact and moving relative to one another, then the friction between them is called kinetic friction.
Static Friction: Static friction is the frictional force between the surfaces of two substances when they are not in motion with respect to each other.
Normal Force: The normal force is the support force exerted upon an object that is in contact with another stable object.
PROBLEM SOLVING STRATEGY
EXAMPLE: SKIING EXERCISE
Ques: A skier with a mass of 62 kg is sliding down a snowy slope. Find the coefficient of kinetic friction for the skier if friction is known to be 45.0 N.
Strategy
The magnitude of kinetic friction was given in to be 45.0 N. Kinetic friction is related to the normal force N as fk=μkN; thus, the coefficient of kinetic friction can be found if we can find the normal force of the skier on a slope. The normal force is always perpendicular to the surface, and since there is no motion perpendicular to the surface, the normal force should equal the component of the skier’s weight perpendicular to the slope.
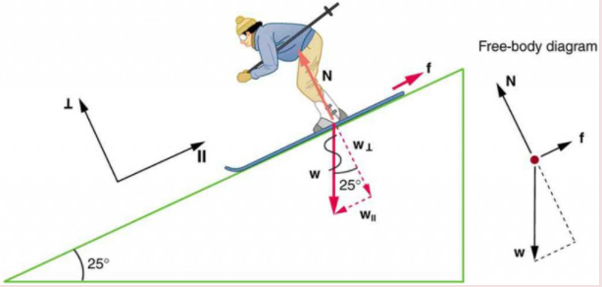
The motion of the skier and friction are parallel to the slope and so it is most convenient to project all forces onto a coordinate system where one axis is parallel to the slope and the other is perpendicular (axes shown to the left of skier). N (the normal force) is perpendicular to the slope, and f (the friction) is parallel to the slope, but w (the skier’s weight) has components along both axes, namely w⊥ and W/. N is equal in magnitude to w⊥, so there is no motion perpendicular to the slope. However, f is less than W/ in magnitude, so there is acceleration down the slope (along the x-axis).
That is, N = w_⊥ = w cos 25º = mg cos 25º.
Substituting this into our expression for kinetic friction, we get fk=μkmgcos25º, which can now be solved for the coefficient of kinetic friction μk.
Solution
Solving for μk gives
μk=fkN=fkwcos25∘=fkmgcos25∘
Substituting known values on the right-hand side of the equation,
μk=45.0(62kg)(9.80ms2)(0.906)=0.082
Discussion
In situations like this, where an object of mass m slides down a slope that makes an angle θ with the horizontal, friction is given by fk=μkmgcosθ. All objects will slide down a slope with constant acceleration under these circumstances.
EXAMPLE 1
A cyclist speeding at 18km/h on a level road takes a sharp circular turn of radius 3 m without reducing the speed . The coefficient of static friction between the tyres and the road is 0.1 Will the cyclist slip while taking the turn ?
On an unbanked road, frictional force alone can provide the centripetal force needed to keep the cyclist moving on a circular turn without slipping. If the speed is too large , or if the turn is too sharp (i.e. of too small a radius ) or both , the frictional force is not suffecient to provide the necessary centripetal force, and the cyclist slips . The condition for the cyclist not to slip is given by Eq. (5.18) :
ν2 ≤ μsRg
Now, R = 3 m , g = 9.8 ms−2 , μs = 0.01. That is μsRg = 2.94 m2s−2 , ν = 18 km/h = 5 ms−1, i.e., ν2 = 25 m2s−2 . The condition is not obeyed . The cycllist will slip while taking the circular turn.
EXAMPLE 2
Assertion: Friction opposes relative motion and thereby dissipates power in the form of heat.
Reason: Friction is always an undesirable force.
We consider friction as an undesirable force sometimes, not always. In many situation, like in a machine with different moving parts, friction does have a negative role. It opposes relative motion and thereby dissipates power in the from of heat, etc. Therfore, option (iii) is correct.
EXAMPLE 3
A box mass m kg is placed on the rear side of an open truck acceleration at 4ms−2 . The coefficient of friction between the box ant the surface below it is 0.4 . The net acceleration of the box with respect to the truck is zero. The value of m is.
Pseudo force on the block
=m×4N (backward)
Force of friction =0.4×m×10N (forward)
Equating, m×4=0.4×m×10
or 4m=4m
Clearly the equation holds good for all values of m. Therefore, option (iv) is correct.
EXAMPLE 4
Two block of masses M1andM2 are connected with a string passing over a pulley as shown in figure The block M1 lies on a horizontal surface friction between the block M1 and the horizontal surface is μ The system accelerates. What additional mass m should be placed on the block M1 so that the system does not accelerate ?
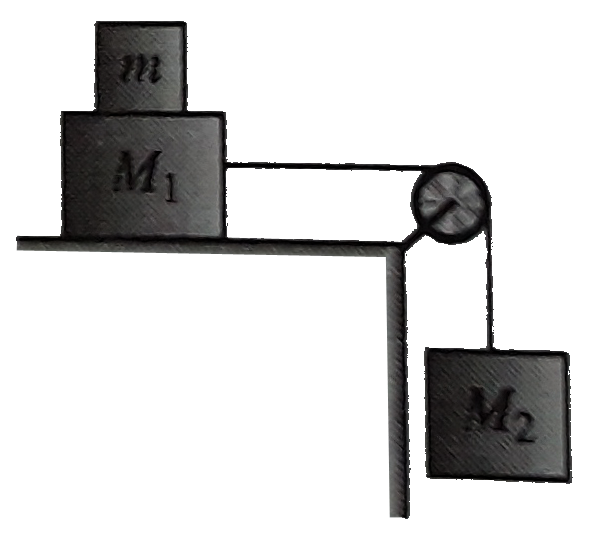
For the equilibrium of block of mass M1 :
Frictional force, f = Tension in the string, T
where T=f
μ(m+M1)g=M2g
T=M2g
From (i) and (ii) μ(m+M1)g=M2g
m=M2μ−M1. Therefore, option (ii) is correct.
EXAMPLE 5
A car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyre and the road is mu, the shortest distance in which the car can be stopped is.
Let R be the normal reaction.
Retarding force F=ma=μR=μmg
∴ a=μg
Now from equation of motion v2=u2−2as
implies 0=u2−2as implies s=u22a=u22μg implies s=v202μg . Therfore, answer (i) is correct.
EXAMPLE 6
Determine the maximum acceleration of the train in which a box lying on the floor will remain stationary given that the coefficient of static friction between the box and the train is floor is 0.15 given g=10m/s2 .
Since the acceleration of the box is due to the static friction.
ma = fs ≤ μsN = μsmg
i.e. a ≤ μsg
∴ amax = μsg = 0.15 × 10 m s−2
= 1.5ms−2
EXAMPLE 7
A mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
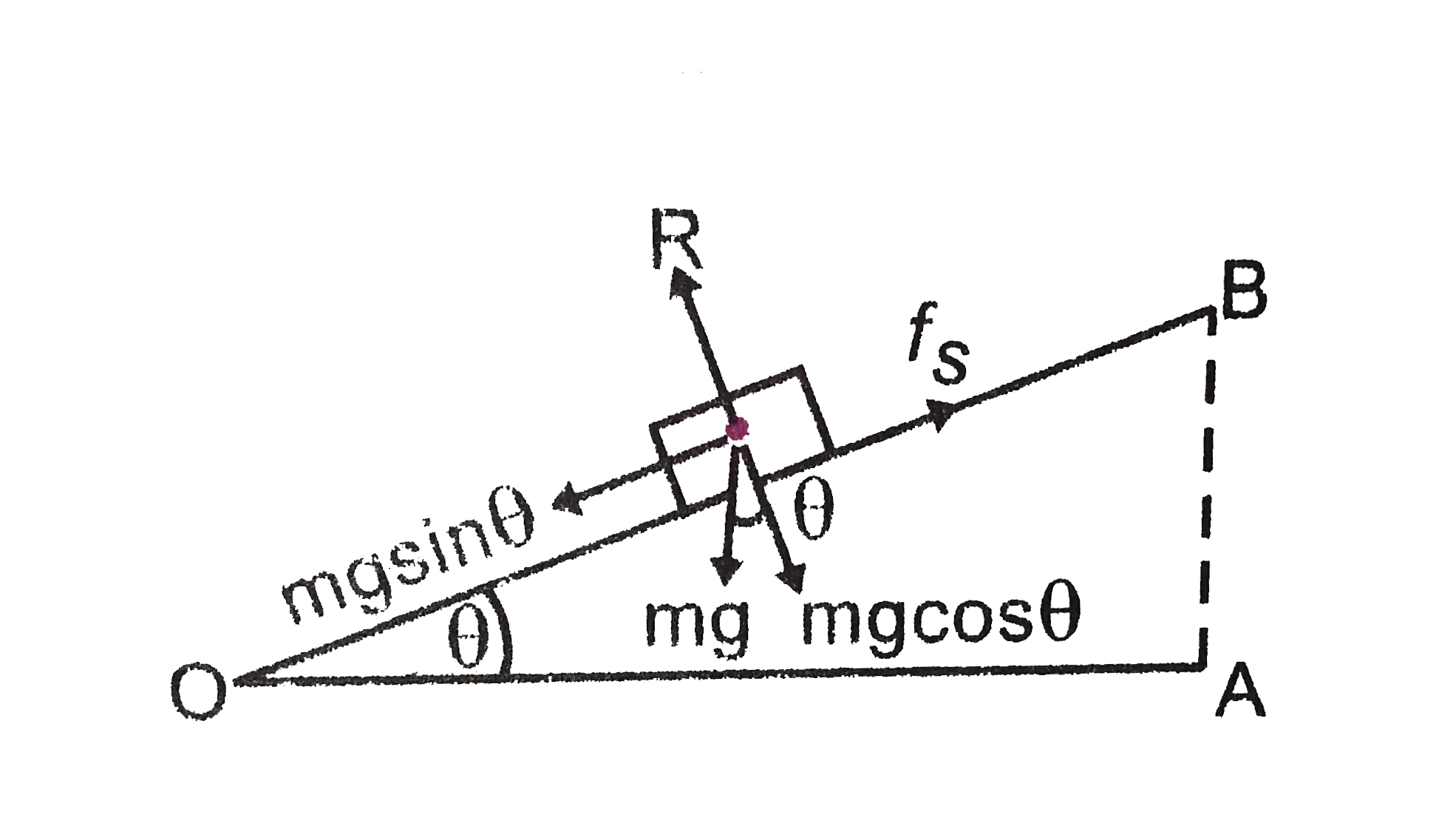
The forces acting on a block of mass m at rest on an inclined plane are (i) the weight mg acting vertically downwards (ii) the normal force N of the plane on the block , and (iii) the static frictional force fs opposing the impending motion. In equilibrium , the resulatant of these forces must be zero. Resolving the weight mg along the two directions shown, we have
m g sin θ = fs , m g cosθ = N
As θ increases , the self-adjusting frictional force fs increases until at θ = θmax, fs achieves its maximum value , (fs)max = μsN.
Therefore , tan<θmax=μs or θmax = tan−1μs
When θ becomes just a little more than θmax , there is a small net force on the block and it begins to slide. Note that θmax depends only on μs and is independent of the mass of the block.
For θmax = 15∘
μs = tan 15∘
= 0.27
EXAMPLE 8
Two bodies A and B of mass 5 kg and 10 kg contact with each other rest on a table against a rigid The coefficient of friction between the bodies and the table is 0.15 A force of 200 N is applied horizontal on A What are (a) the reaction of thee wall (b) the the action , reaction forces between A & B ? What happens when the wall is removed ? Does the answer to (b) Change, when the bodies are in motion ? Ignore difference between μs and μk

(i) When the wall exists and blocks A and B are pushing the wall, there can't be any motion i.e., blocks are at rest . Hence, (a) reaction of the partition = - ( force applied on A) = 200 N towards left. ltbRgt (b) action reaction forces between A and B are 200 N each. A presses B towards right with an action force 200 N and B exerts a reaction force on A towards left having magnitude 200 N .
(ii) When the wall is removed, motion can take place such that net pushing force provides the acceleration to the block system. Hence, taking kinetic friction into account, we have
200 - μ (m1+m2)g = (m1+m2) a
⇒ a = 200 - μ(m1+m2)g / (m1+m2) = 200−0.15×(5+10)×10/ ( 5 + 10 )
= 200 - 22.5 / 15 = 177.5 / 15 = 11.8 ms−2
∴ If force excerted by A and B be FBA ,then considering equilibrium ( or free body diagram ) of only block A ,we have
200 - f1 = m1a + FBA or 200 - (μ)m1g = m1g + FBA
⇒ FBA = 200 - μm1g - m1a = 200 - (0.15 ×5×10) - (5×11.8)
= 200 - 7.5 -59
= 200 - 66.5 =133.5N=1.3×102N towards right
~therefore Force excerted on A by B FAB = −FBA = 1.3 xx 10 ^(2) N towards left.
EXAMPLE 9
Figure shown a man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1m/s−2 . What is the net force on the man? If the coefficient of static friction between the man's shoes and the belt is 0.2 up to what maximum acceleration of the belt can the man continue to be stationary relative to the belt? Mass of the man=65kg(g=9.8m/s2)

Here acceleration of conveyor belt a = 1ms−2 , μs = 0.02 and mass of man m = 65 kg. As the man is in an accelerating frame, he experiences a pseudo force Fs= ma as shown
in fig (a) Hence to maintain his equilibrium , he exerts a force F = Fs = ma = 65×1= 65 N in forward direction i.e direction of motion of belt .
∴ Net force acting on man = 65 N (forward)
As shown in fig(b) , the man can continue to be stationary with respect to belt ,if force of friction μsN = μsmg = mamax
amax = μs .g = 0.2 × 10 = 2ms−2
SUMMARY
1. Friction Frictional force opposes (impending or actual) relative motion between two surfaces in contact. It is the component of the contact force along the common tangent to the surface in contact.
2. Static friction fs opposes impending relative motion; kinetic friction fk opposes actual relative motion.
3. A normal force is always perpendicular to the contact surface between systems.
4. Friction depends on both of the materials involved.
5. Magnitude of static friction fs is fs≤μsN, where μs is the coefficient of static friction and N is the magnitude of the normal force.
6. The magnitude of kinetic friction fk is given by fk=μkN, where μk is the coefficient of kinetic friction.