ELASTICITY AND VISCOSITY for Class 11 PHYSICS
INTRODUCTION
Hum pehle basics samjhte hai jisse hume ye chapter samjhne me easy hoga. Physics kya hai? Physics is the branch of science which deals with the study of energy and matter. Energy is the capacity to do work and matter is anything in this universe which has mass and occupies space. Matter teen types me classified hai: Solid, liquid and gases. Is chapter me solid ka ek property “Elasticity” hum depth me padhenge.
Applications of Elasticity of Material
Bridge pr jo cables hote hai unke proper calculations karke unka diameters decide kiya jata hai. Same calculations construction sites pr bhi hote hai.
INTRODUCTION
Hum pehle basics samjhte hai jisse hume ye chapter samjhne me easy hoga. Physics kya hai? Physics is the branch of science which deals with the study of energy and matter. Energy is the capacity to do work and matter is anything in this universe which has mass and occupies space. Matter teen types me classified hai: Solid, liquid and gases. Is chapter me solid ka ek property “Elasticity” hum depth me padhenge.
Applications of Elasticity of Material
Bridge pr jo cables hote hai unke proper calculations karke unka diameters decide kiya jata hai. Same calculations construction sites pr bhi hote hai.
Let's understand Deforming Force..
Is chapter me hum solids aur unke ander ke mechanical properties ke bare me study krenge. Abhi tak humne jin bodies ke bare me padha hai wo rigid bodies the. Rigid bodies wo bodies hoti hai jinpr ager hum deforming force ya koi external force lagate hai to uske ander koi deformation nahi aata hai.
Deforming force
When force is applied in such a way that the body has no translation motion, but molecules of body are forced to undergo a change in their relative motion, but molecules of body are forced to undergo a change in their relative position is called deforming force. As a result of this force, the body may undergo a change in length, volume and shape.
S.I Unit: Newton
Dimensions: [MLT−2]
Deforming force ko hum do ways se apply kr sakte hai:
1. When the body is subjected to two equal and opposite forces.
2. When one end of the body is connected to a fixed support and the other end subjected to a force. In this case there develops an equal amount of reaction force on a fixed end.
3. When force is applied at one end of the body, the inertia plays a significant role to stretch the body.
Let's understand Deforming Force..
Is chapter me hum solids aur unke ander ke mechanical properties ke bare me study krenge. Abhi tak humne jin bodies ke bare me padha hai wo rigid bodies the. Rigid bodies wo bodies hoti hai jinpr ager hum deforming force ya koi external force lagate hai to uske ander koi deformation nahi aata hai.
Deforming force
When force is applied in such a way that the body has no translation motion, but molecules of body are forced to undergo a change in their relative motion, but molecules of body are forced to undergo a change in their relative position is called deforming force. As a result of this force, the body may undergo a change in length, volume and shape.
S.I Unit: Newton
Dimensions: [MLT−2]
Deforming force ko hum do ways se apply kr sakte hai:
1. When the body is subjected to two equal and opposite forces.
2. When one end of the body is connected to a fixed support and the other end subjected to a force. In this case there develops an equal amount of reaction force on a fixed end.
3. When force is applied at one end of the body, the inertia plays a significant role to stretch the body.
ELASTICITY
The property of matter by virtue of which a body tends to regain its original shape and size after deforming forces are removed is called elasticity.
Elastic properties pr based objects 4 categories me categorized hote hai.
Rigid: Ye objects external force apply krne pr bilkul bhi deform nahi hote hai. Practically koi bhi object perfectly rigid nahi hota hai.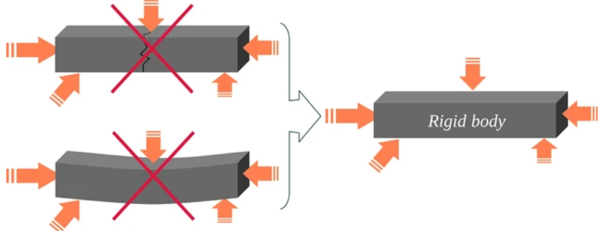
Elastic: Aise bodies jo deforming force ke remove hone ke baad apna shape aur size completely regain kr lete hai unhe elastic bodies kehte hai. Deforming me jo work done lagta hai wo body me internally store hota hai aur usse elastic potential energy kehte hai.
Partially elastic: Jo bodies deforming force ke remove hone ke baad apna original shape aur size completely regain nahi kr pate unhe partially elastic bodies kehte hai. Deforming me jo work done hota hai usme se kuchh lost hota hai aur baki elastic potential energy ke form me store hota hai.
Inelastic/Plastic: Jo bodies deforming force ke remove hone ke baad apna original shape aur size regain nahi kr pate unhe inelastic ya plastic body kehte hai.
Important facts about elasticity
Jis body ko dimension me certain change ke liye jyada deforming force lagta hai wo jyada elastic hota hai. Example: Steel ya iron balls rubber se jyada elastic hai.
Jab do bodies pr equal deforming force lagta hai tab jis body me km deformation hota hai wo body jyada elastic hota hai. Example: For the same load, more elongation is produced in rubber wire than in steel wire hence steel is more elastic than rubber. Similarly, water is more elastic than air as volume change in water is less for the same applied pressure.
Elasticity ko samjhne ke liye stress aur strain ko samajhna bahut easy hai.
ELASTICITY
The property of matter by virtue of which a body tends to regain its original shape and size after deforming forces are removed is called elasticity.
Elastic properties pr based objects 4 categories me categorized hote hai.
Rigid: Ye objects external force apply krne pr bilkul bhi deform nahi hote hai. Practically koi bhi object perfectly rigid nahi hota hai.
Elastic: Aise bodies jo deforming force ke remove hone ke baad apna shape aur size completely regain kr lete hai unhe elastic bodies kehte hai. Deforming me jo work done lagta hai wo body me internally store hota hai aur usse elastic potential energy kehte hai.
Partially elastic: Jo bodies deforming force ke remove hone ke baad apna original shape aur size completely regain nahi kr pate unhe partially elastic bodies kehte hai. Deforming me jo work done hota hai usme se kuchh lost hota hai aur baki elastic potential energy ke form me store hota hai.
Inelastic/Plastic: Jo bodies deforming force ke remove hone ke baad apna original shape aur size regain nahi kr pate unhe inelastic ya plastic body kehte hai.
Important facts about elasticity
Jis body ko dimension me certain change ke liye jyada deforming force lagta hai wo jyada elastic hota hai. Example: Steel ya iron balls rubber se jyada elastic hai.
Jab do bodies pr equal deforming force lagta hai tab jis body me km deformation hota hai wo body jyada elastic hota hai. Example: For the same load, more elongation is produced in rubber wire than in steel wire hence steel is more elastic than rubber. Similarly, water is more elastic than air as volume change in water is less for the same applied pressure.
Elasticity ko samjhne ke liye stress aur strain ko samajhna bahut easy hai.
STRESS
Internal restoring force per unit area is called stress. Ek body pr stress ke effect ko strain kehte hai. Stress body ko deform kr sakta hai.
Jab kisi body pr deforming force lagta hai to object deform ho jata hai aur usko wapis apne original shape aur size me lane ke liye ek opposing force hota hai jo object ke ander generate hota hai. Ye restoring force deforming force ke equal hoga magnitude me aur direction me opposite hoga.
The measure of this restoring force generated per unit area of the material is called stress.
Thus, Stress is defined as “The restoring force per unit area of the material”. It is a tensor quantity. Denoted by the Greek letter σ. Measured using Pascal or Nm2. Mathematically expressed as –
Stress (σ) = (Restoring force(F))/(Cross-sectional area(A))
Note 1:This restoring force may or may not be equal to external deforming force.
Note 2: Restoring force may or may not be uniform throughout the body.
Types of stress
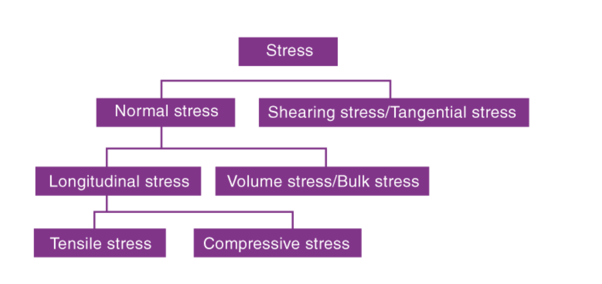
Tensile/ Longitudinal/ Normal Stress
It is the perpendicular restoring force (perpendicular to area) per unit area. When two cross-sectional areas of the cylinder are subjected to equal and opposite forces the stress experienced by the cylinder is called longitudinal stress.
Longitudinal Stress = Deforming Force / Area of cross-section =FA
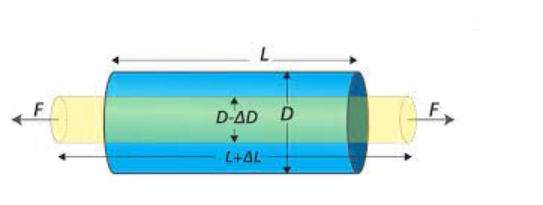
Jab koi body longitudinal stress ke ander hota hai to deforming force body ke length ke along act krta hai. Longitudinal stress body ke length me change lata hai. Isliye diameter me bhi slight change aata hai. Longitudinal Stress ya to object ko uske length ke along ya to stretch ya compress krta hai. Thus, it can be further classified into two types based on the direction of deforming force-
Tensile stress
If the deforming force or applied force results in the increase in the object’s length then the resulting stress is termed as tensile stress. For example: When a rod or wire is stretched by pulling it with equal and opposite forces (outwards) at both ends.
Compressive stress
If the deforming force or applied force results in the decrease in the object’s length then the resulting stress is termed as compressive stress. For example: When a rod or wire is compressed/squeezed by pushing it with equal and opposite forces (inwards) at both ends.
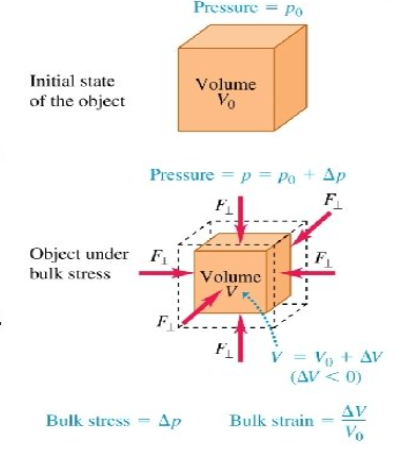
Bulk Stress or Volume Stress
When the deforming force or applied force acts from all dimensions resulting in the change of volume of the object then such stress is called volumetric stress or Bulk stress. In short, when the volume of the body changes due to the deforming force it is termed as Volume stress. Bulk stress is the pressure change Δp.
Tangential/ Shearing Stress
When the direction of the deforming force or external force is parallel to the cross-sectional area, the stress experienced by the object is called shearing stress or tangential stress. This results in the change in the shape of the body.
Tangential Stress (σT) = Tangential restoring force/Cross-section area

STRAIN
Strain is the amount of deformation experienced by the body in the direction of force applied, divided by the initial dimensions of the body.Niche diye equation solid ke terms me deformation ka relation batata hai:
ε=δlL
where, ε is the strain due to stress applied, δl is the change in length and L is the original length of the material.
Strain dimensionless quantity hai aur ye relative change in shape ko define krta hai.
Types of Strain
Kisi body pr stress application pr based strain do types ke hote hai:Tensile Strain
Tensile strain is the change in length (or area) of a body due to the application of tensile stress. Ek body pr tensile strain tab produce hota hai jab uspr applied forces usse strecth krne ki kosish krte hai aur body ka length increase hota hai. Tensile stain ko hum mathematically aise express krte hai: ε=ΔLL
Yaha, ε tensile strain hai; ΔL change in length hai aur L original length hai.
Compressive Strain
Compressive Strain is the change in length (or area) of a body due to the application of compressive strain. Ek body pr compressive strain tab produce hota hai jab uspr applied forces ke karan body ka length decrease hota hai.
Shear Strain
This type of strain is produced when a shearing stress is present over a section.
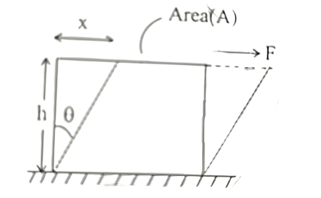
Shearing strain = xh⇒tanθ
=θ; if θ is very small
Yaha x upper surface ka displacement hai aur h upper surface aur lower surface ke bich ka height hai.
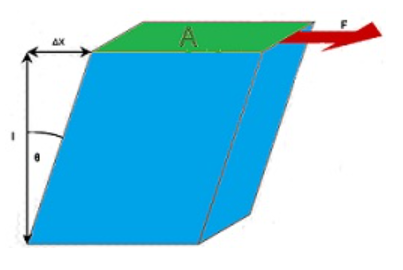
Volume strain
When a body is subjected to a volume stress, its volume changes. Volume strain is defined as fractional change in volume.
Volume strain = (change in volume)/(original volume) =ΔVV
Yaha, ΔV change in volume hai aur V original volume hai.
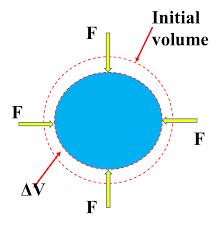
STRESS
Internal restoring force per unit area is called stress. Ek body pr stress ke effect ko strain kehte hai. Stress body ko deform kr sakta hai.
Jab kisi body pr deforming force lagta hai to object deform ho jata hai aur usko wapis apne original shape aur size me lane ke liye ek opposing force hota hai jo object ke ander generate hota hai. Ye restoring force deforming force ke equal hoga magnitude me aur direction me opposite hoga.
The measure of this restoring force generated per unit area of the material is called stress.
Thus, Stress is defined as “The restoring force per unit area of the material”. It is a tensor quantity. Denoted by the Greek letter σ. Measured using Pascal or Nm2. Mathematically expressed as –
Stress (σ) = (Restoring force(F))/(Cross-sectional area(A))
Note 1:This restoring force may or may not be equal to external deforming force.
Note 2: Restoring force may or may not be uniform throughout the body.
Types of stress

Tensile/ Longitudinal/ Normal Stress
It is the perpendicular restoring force (perpendicular to area) per unit area. When two cross-sectional areas of the cylinder are subjected to equal and opposite forces the stress experienced by the cylinder is called longitudinal stress.
Longitudinal Stress = Deforming Force / Area of cross-section =FA

Jab koi body longitudinal stress ke ander hota hai to deforming force body ke length ke along act krta hai. Longitudinal stress body ke length me change lata hai. Isliye diameter me bhi slight change aata hai. Longitudinal Stress ya to object ko uske length ke along ya to stretch ya compress krta hai. Thus, it can be further classified into two types based on the direction of deforming force-
Tensile stress
If the deforming force or applied force results in the increase in the object’s length then the resulting stress is termed as tensile stress. For example: When a rod or wire is stretched by pulling it with equal and opposite forces (outwards) at both ends.
Compressive stress
If the deforming force or applied force results in the decrease in the object’s length then the resulting stress is termed as compressive stress. For example: When a rod or wire is compressed/squeezed by pushing it with equal and opposite forces (inwards) at both ends.
Bulk Stress or Volume Stress
When the deforming force or applied force acts from all dimensions resulting in the change of volume of the object then such stress is called volumetric stress or Bulk stress. In short, when the volume of the body changes due to the deforming force it is termed as Volume stress. Bulk stress is the pressure change Δp.

Tangential/ Shearing Stress
When the direction of the deforming force or external force is parallel to the cross-sectional area, the stress experienced by the object is called shearing stress or tangential stress. This results in the change in the shape of the body.
Tangential Stress (σT) = Tangential restoring force/Cross-section area

STRAIN
Strain is the amount of deformation experienced by the body in the direction of force applied, divided by the initial dimensions of the body.Niche diye equation solid ke terms me deformation ka relation batata hai:
ε=δlL
where, ε is the strain due to stress applied, δl is the change in length and L is the original length of the material.
Strain dimensionless quantity hai aur ye relative change in shape ko define krta hai.
Types of Strain
Kisi body pr stress application pr based strain do types ke hote hai:Tensile Strain
Tensile strain is the change in length (or area) of a body due to the application of tensile stress. Ek body pr tensile strain tab produce hota hai jab uspr applied forces usse strecth krne ki kosish krte hai aur body ka length increase hota hai. Tensile stain ko hum mathematically aise express krte hai: ε=ΔLL
Yaha, ε tensile strain hai; ΔL change in length hai aur L original length hai.
Compressive Strain
Compressive Strain is the change in length (or area) of a body due to the application of compressive strain. Ek body pr compressive strain tab produce hota hai jab uspr applied forces ke karan body ka length decrease hota hai.
Shear Strain
This type of strain is produced when a shearing stress is present over a section.
Shearing strain = xh⇒tanθ
=θ; if θ is very small
Yaha x upper surface ka displacement hai aur h upper surface aur lower surface ke bich ka height hai.

Volume strain
When a body is subjected to a volume stress, its volume changes. Volume strain is defined as fractional change in volume.
Volume strain = (change in volume)/(original volume) =ΔVV
Yaha, ΔV change in volume hai aur V original volume hai.

POINT 1
Elasticity: When we stretch an object, it changes its shape and when we leave, it regains its shape. Or we can say it is the property to regain the original shape once the external force is removed. Example: Spring.
Plasticity: When an object changes its shape and never comes back to its original shape even when external force is removed. It is the property of permanent deformation. Example: Plastic materials.
Ductility: When an object can be pulled in thin sheets, wires or plates, it has the ductile properties. It is the property of being drawn into thin wires/sheets/plates. Example: Gold or Silver.
Strength: The ability to withstand applied stress without failure. Many categories of objects have higher strength than others.
Tangential or Shearing Stress: It is the restoring force per unit area when the force applied is parallel to the cross-sectional area of the body.
Hydraulic Stress: It is the restoring force per unit area when the force is applied by a fluid like water on the body or object.
Strain: It is a measure of the deformation that can represent the displacement between particles in the body relative to a reference length.
Longitudinal Strain: It is the change in length to the original length of the body due to the applied longitudinal stress. It is a change in length divided by the original length.
Shearing Strain: It is the measure of the relative displacement of the opposite faces of the body due to the shearing stress. Shearing strain can be represented by tan θ.
Volume Strain: It is the ratio of change in volume to the original volume as a result of the hydraulic stress. It is the change in volume divided by the initial or original volume.
Tensile stress: The restoring force per unit area is when a body is stretched by two equal and opposite forces acting perpendicularly to the cross-sectional area.
Compressive stress: The restoring force per unit area is when the body is compressed by opposing forces.
POINT 1
Elasticity: When we stretch an object, it changes its shape and when we leave, it regains its shape. Or we can say it is the property to regain the original shape once the external force is removed. Example: Spring.
Plasticity: When an object changes its shape and never comes back to its original shape even when external force is removed. It is the property of permanent deformation. Example: Plastic materials.
Ductility: When an object can be pulled in thin sheets, wires or plates, it has the ductile properties. It is the property of being drawn into thin wires/sheets/plates. Example: Gold or Silver.
Strength: The ability to withstand applied stress without failure. Many categories of objects have higher strength than others.
Tangential or Shearing Stress: It is the restoring force per unit area when the force applied is parallel to the cross-sectional area of the body.
Hydraulic Stress: It is the restoring force per unit area when the force is applied by a fluid like water on the body or object.
Strain: It is a measure of the deformation that can represent the displacement between particles in the body relative to a reference length.
Longitudinal Strain: It is the change in length to the original length of the body due to the applied longitudinal stress. It is a change in length divided by the original length.
Shearing Strain: It is the measure of the relative displacement of the opposite faces of the body due to the shearing stress. Shearing strain can be represented by tan θ.
Volume Strain: It is the ratio of change in volume to the original volume as a result of the hydraulic stress. It is the change in volume divided by the initial or original volume.
Tensile stress: The restoring force per unit area is when a body is stretched by two equal and opposite forces acting perpendicularly to the cross-sectional area.
Compressive stress: The restoring force per unit area is when the body is compressed by opposing forces.
RELATION BETWEEN STRESS AND STRAIN
Jab kisi body se deforming force remove hota hai to wo apna actual size regain krta hai. Lekin ager deforming force high hota hai to body apna size 100% regain nahi kr pata hai. The maximum stress on whose removal, the bodies regain their original dimensions, is called the elastic limit. Iska matlab ager stress elastic limit ke ander hai to deforming forces ya stress remove krne ke baad body apna size 100% regain kr paega.
The different regions in the stress-strain diagram are:
(i) Proportional Limit
Stress-strain curve me ye region Hooke’s Law obey krta hai. Is limit me, stress-strain ratio proportionality constant batata hai jisse Young’s modulus kehte hai. Graph me point OA proportional limit represent krta hai.
(ii) Elastic Limit
It is the point in the graph up to which the material returns to its original position when the load acting on it is completely removed. Is limit ke beyond material apne original position me return nahi krte hai aur plastic deformation yaha appear hona start ho jata hai.
(iii) Yield Point
The yield point is defined as the point at which the material starts to deform plastically. After the yield point is passed, permanent plastic deformation occurs. There are two yield points (i) upper yield point (ii) lower yield point.
(iv) Ultimate Stress Point
It is a point that represents the maximum stress that a material can endure before failure. Beyond this point, failure occurs.
(v) Fracture or Breaking Point
It is the point in the stress-strain curve at which the failure of the material takes place.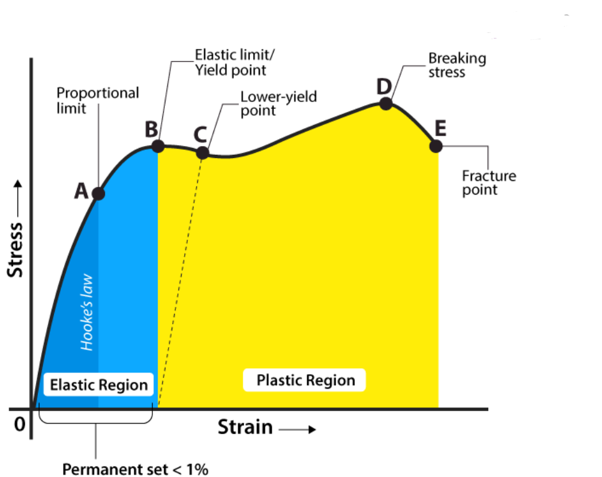
Few terms related to elasticity
Elastic after effect: Kuchh material bodies apna original configuration regain krne me thoda time leta hai. Deforming force ke removal ke baad original configuration ko regain krne me jo delay hota hai usse elastic after effect kehte hai.
Elastic Fatigue: Repeated strains ke karan material apna strength kho deta hai, isse elastic fatigue kehte hai.
HOOKE’S LAW
Hooke’s law ko law of elasticity bhi kehte hai. Isse English scientist named Robert Hooke ne 1660 me kiya tha. Hooke’s law basically states that “when an object has a relatively small deformation the size of the deformation is directly proportional to the deforming load or force.”Hooke’s law science aur engineering ke bahut sare branches me use hota hai kyunki ye mainly forces aur deformations pr depend krta hai ager wo bahut kam hue to. Ye bahut disciples jaise ki molecular mechanics, seismology aur acoustics ka foundation hai. Ye law galvanometer, spring scale, manometer aur balance wheel of a mechanical clock ka fundamental principle hai.
Hooke’s law Statement: When a material behaves elastically and exhibits a linear relationship between stress and strain, it is called linearly elastic material. In this case, stress is directly proportional to strain.
Graph me aapne dekha ki elastic region OA me stress strain ke directly proportional hai. Stress ∝ strain
Stress = E (Strain)
E = (Stress(sigma))/ (strain(epsilon))
E ko modulus of elasticity kehte hai.
Types of strain pr based, modulus of elasticity teen types ke hote hai:
1. Young’s modulus of elasticity (Y)
Y = (Longitudinal stress)/(Longitudinal strain)
Stress =FA
F= internal restoring force or tension force
Strain =ΔLL
Y=FAΔLL
FLAΔL
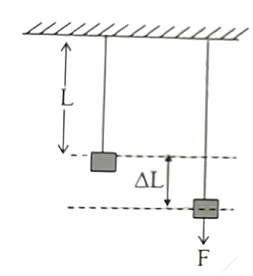
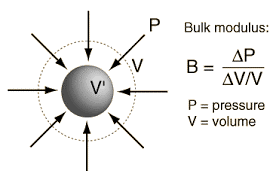
2. Bulk modulus of elasticity (K)
K= (volume stress)/(volume strain)
B=−ΔPΔVV
{ΔV =-ve}
‘-’ sign makes B positive as volume generally decreases on applying pressure
3. Shear Modulus or Modulus of Rigidity (η)
Shear modulus (eta) = (Shear stress)/ (Shear strain)
η=FAxh
(tanθ=xh)
η=FAθ
Compressibility of a material (β)
It is the reciprocal of the bulk modulus.
β=1B
β=−ΔVVΔP
BREAKING STRESS (σB)
Jab koi wire ek certain limit ke beyond loaded ho to wo break kr jata hai. The maximum stress corresponding to which it breaks, is the breaking stress (σB) . Corresponding force ko breaking force kehte hai.
RELATION BETWEEN STRESS AND STRAIN
Jab kisi body se deforming force remove hota hai to wo apna actual size regain krta hai. Lekin ager deforming force high hota hai to body apna size 100% regain nahi kr pata hai. The maximum stress on whose removal, the bodies regain their original dimensions, is called the elastic limit. Iska matlab ager stress elastic limit ke ander hai to deforming forces ya stress remove krne ke baad body apna size 100% regain kr paega.
The different regions in the stress-strain diagram are:
(i) Proportional Limit
Stress-strain curve me ye region Hooke’s Law obey krta hai. Is limit me, stress-strain ratio proportionality constant batata hai jisse Young’s modulus kehte hai. Graph me point OA proportional limit represent krta hai.
(ii) Elastic Limit
It is the point in the graph up to which the material returns to its original position when the load acting on it is completely removed. Is limit ke beyond material apne original position me return nahi krte hai aur plastic deformation yaha appear hona start ho jata hai.
(iii) Yield Point
The yield point is defined as the point at which the material starts to deform plastically. After the yield point is passed, permanent plastic deformation occurs. There are two yield points (i) upper yield point (ii) lower yield point.
(iv) Ultimate Stress Point
It is a point that represents the maximum stress that a material can endure before failure. Beyond this point, failure occurs.
(v) Fracture or Breaking Point
It is the point in the stress-strain curve at which the failure of the material takes place.
Few terms related to elasticity
Elastic after effect: Kuchh material bodies apna original configuration regain krne me thoda time leta hai. Deforming force ke removal ke baad original configuration ko regain krne me jo delay hota hai usse elastic after effect kehte hai.
Elastic Fatigue: Repeated strains ke karan material apna strength kho deta hai, isse elastic fatigue kehte hai.
HOOKE’S LAW
Hooke’s law ko law of elasticity bhi kehte hai. Isse English scientist named Robert Hooke ne 1660 me kiya tha. Hooke’s law basically states that “when an object has a relatively small deformation the size of the deformation is directly proportional to the deforming load or force.”Hooke’s law science aur engineering ke bahut sare branches me use hota hai kyunki ye mainly forces aur deformations pr depend krta hai ager wo bahut kam hue to. Ye bahut disciples jaise ki molecular mechanics, seismology aur acoustics ka foundation hai. Ye law galvanometer, spring scale, manometer aur balance wheel of a mechanical clock ka fundamental principle hai.
Hooke’s law Statement: When a material behaves elastically and exhibits a linear relationship between stress and strain, it is called linearly elastic material. In this case, stress is directly proportional to strain.
Graph me aapne dekha ki elastic region OA me stress strain ke directly proportional hai. Stress ∝ strain
Stress = E (Strain)
E = (Stress(sigma))/ (strain(epsilon))
E ko modulus of elasticity kehte hai.
Types of strain pr based, modulus of elasticity teen types ke hote hai:
1. Young’s modulus of elasticity (Y)
Y = (Longitudinal stress)/(Longitudinal strain)
Stress =FA
F= internal restoring force or tension force
Strain =ΔLL
Y=FAΔLL
FLAΔL

2. Bulk modulus of elasticity (K)
K= (volume stress)/(volume strain)
B=−ΔPΔVV
{ΔV =-ve}
‘-’ sign makes B positive as volume generally decreases on applying pressure

3. Shear Modulus or Modulus of Rigidity (η)
Shear modulus (eta) = (Shear stress)/ (Shear strain)
η=FAxh
(tanθ=xh)
η=FAθ

Compressibility of a material (β)
It is the reciprocal of the bulk modulus.
β=1B
β=−ΔVVΔP
BREAKING STRESS (σB)
Jab koi wire ek certain limit ke beyond loaded ho to wo break kr jata hai. The maximum stress corresponding to which it breaks, is the breaking stress (σB) . Corresponding force ko breaking force kehte hai.
CHANGE IN DENSITY DUE TO CHANGE IN VOLUME
Jab koi object bulk stress ke ander hota hai to uska density change ho jata hai.
ρ=mV
ρ=mV−1
Differentiating the expression;
dρ=m(−1V−2dV)
dρ=mdVV2
dρ=ρdVV
dρρ−−dVV
B=−ΔPΔVV=dPdVV
dρρ=dPB
Δρ=ρΔPB
Yaha, Δρ change in density hai; ρ pressure change se density hai; ΔP change in pressure hai aur B bulk modulus hai.
CHANGE IN RADIUS DUE TO BULK STRESS
Volume of the spherical bodyV=43πR3
dV=43π3R2dR
dV=43πR3(dRR)
dVV=3(dRR)
ΔVV=3(ΔRR)
(DeltaR)/R = ⅓ ((DeltaV)/V)
Bulk modulus B=−ΔPΔVV
ΔRR=−ΔP3B
ΔR=−RΔP3B
For Linear Springs
Mathematically Hooke’s law state krta hai ki applied force F spring constant k into displacement ya change in length ke equal hota hai. F=kx. k ka value sirf elastic material ke uper hi nahi balki material ke dimension aur shape pr bhi depend krta hai.Sare materials me elasticity ka kuchh degree hota hai. Is elastic property ke karan restoring force aata hai concept me. Is elasticity property ko hum restoring force ke form me measure kr sakte hai. Ye restoring force deformation force oppose krta hai aur material ka original dimension ko maintain krna ka try krta hai.
F=–kx
This expression for Hooke’s Law is also known as the spring constant formula.
Here,
F is restoring force.
x represents the magnitude of the distortion or displacement from equilibrium as exhibited in the stretching of a spring or rubber band.
k is the proportionality constant, also known as the spring constant.
Note:– Here the direction of the force is in the direction opposite that of the displacement, so consider minus sign.
Applications of Hooke’s Law
The applications of Hooke’s Law is as given below:Most commonly, in everyday life, Hooke’s Law is applied in springs because of their elasticity.
They are used not only in the engineering field but also used in the field of medical science.
It is used in breathing (lungs), skin, spring beds, diving boards and cars suspension systems.
It is used as a fundamental principle behind the manometer, spring scale and balance wheel of the clock.
It is also used as the foundation for seismology, acoustics and molecular mechanics.
Disadvantages of Applying Hooke’s Law
The disadvantages of Hooke’s Law is as follows:Hooke’s Law is applied only in the elastic region.
Hooke’s Law gives accurate results only for solid bodies if the forces and deformations are small.
Hooke’s Law is not a universal law.
CHANGE IN DENSITY DUE TO CHANGE IN VOLUME
Jab koi object bulk stress ke ander hota hai to uska density change ho jata hai.
ρ=mV
ρ=mV−1
Differentiating the expression;
dρ=m(−1V−2dV)
dρ=mdVV2
dρ=ρdVV
dρρ−−dVV
B=−ΔPΔVV=dPdVV
dρρ=dPB
Δρ=ρΔPB
Yaha, Δρ change in density hai; ρ pressure change se density hai; ΔP change in pressure hai aur B bulk modulus hai.
CHANGE IN RADIUS DUE TO BULK STRESS
Volume of the spherical bodyV=43πR3
dV=43π3R2dR
dV=43πR3(dRR)
dVV=3(dRR)
ΔVV=3(ΔRR)
ΔRR=⅓(ΔVV)
Bulk modulus B=−ΔPΔVV
ΔRR=−ΔP3B
ΔR=−RΔP3B
For Linear Springs
Mathematically Hooke’s law state krta hai ki applied force F spring constant k into displacement ya change in length ke equal hota hai. F=kx. k ka value sirf elastic material ke uper hi nahi balki material ke dimension aur shape pr bhi depend krta hai.Sare materials me elasticity ka kuchh degree hota hai. Is elastic property ke karan restoring force aata hai concept me. Is elasticity property ko hum restoring force ke form me measure kr sakte hai. Ye restoring force deformation force oppose krta hai aur material ka original dimension ko maintain krna ka try krta hai.
F=–kx
This expression for Hooke’s Law is also known as the spring constant formula.
Here,
F is restoring force.
x represents the magnitude of the distortion or displacement from equilibrium as exhibited in the stretching of a spring or rubber band.
k is the proportionality constant, also known as the spring constant.
Note:– Here the direction of the force is in the direction opposite that of the displacement, so consider minus sign.
Applications of Hooke’s Law
The applications of Hooke’s Law is as given below:Most commonly, in everyday life, Hooke’s Law is applied in springs because of their elasticity.
They are used not only in the engineering field but also used in the field of medical science.
It is used in breathing (lungs), skin, spring beds, diving boards and cars suspension systems.
It is used as a fundamental principle behind the manometer, spring scale and balance wheel of the clock.
It is also used as the foundation for seismology, acoustics and molecular mechanics.
Disadvantages of Applying Hooke’s Law
The disadvantages of Hooke’s Law is as follows:Hooke’s Law is applied only in the elastic region.
Hooke’s Law gives accurate results only for solid bodies if the forces and deformations are small.
Hooke’s Law is not a universal law.
POINT 2
Intermolecular Forces: As we know, solids are made up of atoms and molecules packed close to each other. The arrangement is such that each molecule exerts a force on its neighbouring molecule. These forces are known as intermolecular forces.
Plasticity: It is the ability of a body to undergo permanent deformation (in shape, size, or volume) when the deforming forces are removed. Bodies that show attributes of plasticity are called plastic bodies. Examples of plastic bodies: Wax, Clay, Plasticine.
Young’s Modulus: Within the elastic limits of a thin wire or rod, it is defined as the ratio of longitudinal stress to longitudinal strain.
Bulk Modulus: Measures the ability of a substance to withstand compression from all sides. It is defined as the ratio of normal stress to volumetric strain.
Shear Modulus/ Modulus of Rigidity: According to the mechanical properties of solids chapter, it is defined as the ratio of shear stress to shear strain.
Poisson’s Ratio: It is defined as the ratio between lateral strain (change in diameter) and longitudinal strain (change in length).
POINT 2
Intermolecular Forces: As we know, solids are made up of atoms and molecules packed close to each other. The arrangement is such that each molecule exerts a force on its neighbouring molecule. These forces are known as intermolecular forces.
Plasticity: It is the ability of a body to undergo permanent deformation (in shape, size, or volume) when the deforming forces are removed. Bodies that show attributes of plasticity are called plastic bodies. Examples of plastic bodies: Wax, Clay, Plasticine.
Young’s Modulus: Within the elastic limits of a thin wire or rod, it is defined as the ratio of longitudinal stress to longitudinal strain.
Bulk Modulus: Measures the ability of a substance to withstand compression from all sides. It is defined as the ratio of normal stress to volumetric strain.
Shear Modulus/ Modulus of Rigidity: According to the mechanical properties of solids chapter, it is defined as the ratio of shear stress to shear strain.
Poisson’s Ratio: It is defined as the ratio between lateral strain (change in diameter) and longitudinal strain (change in length).
POISSON’S RATIO
Jab kisi rod ya wire pr longitudinal stress hota hai to:
- Uska length tensile force (longitudinal length) ke along increase krta hai
- Uska length tensile force (transverse/lateral length) ke perpendicular me decrease ho jata hai
μ =- (Lateral stress)/ (Longitudinal stress)
=−ΔddΔLL
=−ΔrrΔLL
Note: Minus sign ensures that μ is positive.
RELATION BETWEEN VARIOUS MODULUS (Y,η,B,ν)
Y: Young’s Modulusη: Shear Modulus
B: Bulk Modulus
ν: Poisson’s Ratio
1. 3Y=13B+1η
2. B=Y3(1−2ν)
3. η=Y2(1+ν)
POISSON’S RATIO
Jab kisi rod ya wire pr longitudinal stress hota hai to:
- Uska length tensile force (longitudinal length) ke along increase krta hai
- Uska length tensile force (transverse/lateral length) ke perpendicular me decrease ho jata hai
μ =- (Lateral stress)/ (Longitudinal stress)
=−ΔddΔLL
=−ΔrrΔLL
Note: Minus sign ensures that μ is positive.
RELATION BETWEEN VARIOUS MODULUS (Y,η,B,ν)
Y: Young’s Modulusη: Shear Modulus
B: Bulk Modulus
ν: Poisson’s Ratio
1. 3Y=13B+1η
2. B=Y3(1−2ν)
3. η=Y2(1+ν)
ELASTIC POTENTIAL ENERGY
Deforming me jo work done lagta hai wo body me internally store hota hai aur usse elastic potential energy kehte hai.
Finding work done in increasing the length by ΔL
At an instant, let the elongation be x
T=F
Y=FLAx
F=AYxL
Work done in further dx elongation
dW=Fdx
∫dW=AYL∫ΔL0xdx
W=AY(ΔL)22L
Ye work done
In elongation ΔL rod me elastic potential energy ke form me stored rahega. W=U
U=½AYL(ΔL)2
On comparing with spring energy (½kx2)
The rod behaves like a spring of spring constant k=AYL
U=½(YΔLL)(ΔLL)(AL)
U=½Y(strain)2×(volume)
Since Y = stress/strain
U=½(stress)(strain)(volume)
U=12(stress)2Y(volume)
Elastic Potential Energy Density
It is the elastic potential energy per unit volume.
u=½Y(strain)2
Since Y = stress/strain
u=½ (stress)(strain)
u=½(stress)2Y
ANALOGY OF ROD AS SPRING
Ek case analyze krte hai yaha hum ek rod ko spring analyze krenge. Suppose rod pr force F apply krte hai.
Then Y = (Stress)/(Strain)
F=(YAL)x...........(i)
Same extension x ke liye suppose spring constant k hai ek spring ka aur uspr force F apply krte hai to F=kx................(ii)
Comparing equation (i) and (ii);
k=YAL
So the rod can be assumed to behave as spring or spring constant.
INTERATOMIC FORCE CONSTANT
When an external force is applied on a solid, the distance between its atoms changes and interatomic force works to restore the original dimension.F=KΔr
K is the interatomic force constant.
K=Yr0 yaha Y young’s modulus hai aur r0 normal distance between the atoms of wire hai.
Note:
* The number of atoms having interatomic distance r0 in length l of a wire, N=lr0
* The number of atoms in area A of wire having interatomic separation r0,N=Ar20
ELASTIC POTENTIAL ENERGY
Deforming me jo work done lagta hai wo body me internally store hota hai aur usse elastic potential energy kehte hai.
Finding work done in increasing the length by ΔL
At an instant, let the elongation be x
T=F
Y=FLAx
F=AYxL
Work done in further dx elongation
dW=Fdx
∫dW=AYL∫ΔL0xdx
W=AY(ΔL)22L
Ye work done
In elongation ΔL rod me elastic potential energy ke form me stored rahega. W=U
U=½AYL(ΔL)2
On comparing with spring energy (½kx2)
The rod behaves like a spring of spring constant k=AYL
U=½(YΔLL)(ΔLL)(AL)
U=½Y(strain)2×(volume)
Since Y = stress/strain
U=½ (stress)(strain)(volume)<br>U = 1/2 ("stress")^2/Y ("volume")<b><br><br>El∗icPotentialE≠rgyDensity<br>Itistheel∗icpotentiale≠rgyperunitvolume.<br>u = ½ Y ("strain")^2<br>SinceY=stressstra∈<br>u =½(stress)(stra∈)<br>u = ½ ("stress")^2/Y<h2>ANALOGYOFRODASSPRING<h2>Ekcaseanalyzekrtehaiyahahumekrodkospr∈ganalyzekren≥.SupposerodprforceFapplykrtehai.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/LN_SELF_PHY_XI_ENG_PAID_C09_17.pngwh=80%mx-autosty≤=background:white;><br><br>ThenY=StressStra∈<br>F=((YA)/L)x...........(i)<br>Sameextensionxkeliye⊃posespr∈gconstantkhaiekspr∈gkaaurusprforceFapplykrtehai→F =kx................(ii)<br>Compar∈gequation(i)and(ii);<br>k=(YA)/L<b><br>Sotherodcanbeas∑ed→behaveasspr∈gorspr∈gconstant.<h2>INTERATOMICFORCECONSTANT<h2><b>Whenanexternalforceisappliedonasolthedistancebetweenitsa→mschan≥sand∫era→micforceworks→res→retheorig∈aldimension.<br>F=KDeltar<b><br>Kisthe∫era→micforceconstant.<br><b>K = Yr_0<b>yahaYyoung’smodu––shaiaurr_0∥a∥ldistancebetweenthea→msofwirehai.<br><br><b>Note:<b><br>⋅Theνmberofa→mshav∈g∫era→micdistancer_0∈≤n>hlofawire,N =l/r_0<br>⋅Theνmberofa→ms∈areaAofwirehav∈g∫era→micseparationr_0, N=A/r_0^2
VISCOSITY
Baccho ek liquid ki layer dusri liquid ki layer prr jo tangential force lgati hai use hu viscous force bote hai and this force is also called as liquid frictional force and iss phenomena is called as viscosity.
Viscous force do type ke hote hai, ek jab lgta hai jab body surface of fluid ke contact me ho aur ek viscous force jab lgta hai jab body poori fluid me immerge ho.
VISOCUS FORCE (WHEN BODY IS IN CONTACT WITH SURFACE OF FLUID)
Baccho yaha prr humne dekha ki jab jab there is a relative velocity in body and fluid, tab tab lgta hai viscous force (Fv),Ab humne dekha ki ,
FV∝dvdx, where dvdx is the velocity gradient ,
And viscous force Fv∝A, where A is the area of body which is in contact with fluid surface.
Therefore jab humne inn dono proportionality ko combine kiya toh ek constant aaya,
Fv=−ηAdvdx, where η is the coefficient of viscosity, which different for different fluids,
STOKE’S LAW
Baccho jab body fully immerged ho liquid me toh uss time jo viscous force lgta hai use hi hum stoke’s law bolte hai,Ab aapne syllabus me kevl spherical body ka immerge hona hi hai,
Toh maan lete hai ki ek sphere immerged hai kisi liquid me jiska coefficient of viscosity η hai
Toh baccho, Fv∝r where r is the radius of sphere, baccho jitna jyada radius hoga, utna jyada area sphere cover krega, or utna jyada hi viscous force lgega,
Phir humne dekha Fv∝v, where v is the velocity of sphere and Fv∝η
Jab inn sabko ek saath likha toh mila,
Fv=6πηrv, this is the viscous force when full body is immerged in the liquid.
VISCOSITY
Baccho ek liquid ki layer dusri liquid ki layer prr jo tangential force lgati hai use hu viscous force bote hai and this force is also called as liquid frictional force and iss phenomena is called as viscosity.
Viscous force do type ke hote hai, ek jab lgta hai jab body surface of fluid ke contact me ho aur ek viscous force jab lgta hai jab body poori fluid me immerge ho.
VISOCUS FORCE (WHEN BODY IS IN CONTACT WITH SURFACE OF FLUID)
Baccho yaha prr humne dekha ki jab jab there is a relative velocity in body and fluid, tab tab lgta hai viscous force (Fv),Ab humne dekha ki ,
FV∝dvdx, where dvdx is the velocity gradient ,
And viscous force Fv∝A, where A is the area of body which is in contact with fluid surface.
Therefore jab humne inn dono proportionality ko combine kiya toh ek constant aaya,
Fv=−ηAdvdx, where η is the coefficient of viscosity, which different for different fluids,
STOKE’S LAW
Baccho jab body fully immerged ho liquid me toh uss time jo viscous force lgta hai use hi hum stoke’s law bolte hai,Ab aapne syllabus me kevl spherical body ka immerge hona hi hai,
Toh maan lete hai ki ek sphere immerged hai kisi liquid me jiska coefficient of viscosity η hai
Toh baccho, Fv∝r where r is the radius of sphere, baccho jitna jyada radius hoga, utna jyada area sphere cover krega, or utna jyada hi viscous force lgega,
Phir humne dekha Fv∝v, where v is the velocity of sphere and Fv∝η
Jab inn sabko ek saath likha toh mila,
Fv=6πηrv, this is the viscous force when full body is immerged in the liquid.
SURFACE TENSION
Baccho abhi tak humne jo bhi baat ki voh fluid ke andr ki kari, ab hum liquid ke surface ki baat krenge.
Baccho liquid ki surface ki ek property hoti hai ki voh apne surface area ko minimum rakhna chahte hai, isi property ko hum surface tension bolte hai.
Liquid surface ke saare molecules ek dusre ko pull kr rhe hai or ek dusre molecules ko apni taraf pull kar rhe hai.
Maan lijiye ek liquid ki surface prr humne ek massless thin wire daal diya hai, toh baccho uss rassi ko surface ke moleucles kuch forces se pull kr rhe honge,
Toh baccho surface tension hogi, S=FL where S is the surface tension and it is defined as “the force acting on per unit length of wire is called as its surface tension”.
SURFACE TENSION
Baccho abhi tak humne jo bhi baat ki voh fluid ke andr ki kari, ab hum liquid ke surface ki baat krenge.
Baccho liquid ki surface ki ek property hoti hai ki voh apne surface area ko minimum rakhna chahte hai, isi property ko hum surface tension bolte hai.
Liquid surface ke saare molecules ek dusre ko pull kr rhe hai or ek dusre molecules ko apni taraf pull kar rhe hai.
Maan lijiye ek liquid ki surface prr humne ek massless thin wire daal diya hai, toh baccho uss rassi ko surface ke moleucles kuch forces se pull kr rhe honge,
Toh baccho surface tension hogi, S=FL where S is the surface tension and it is defined as “the force acting on per unit length of wire is called as its surface tension”.
SURFACE ENERGY

Ab baccho hum surface ki energy ki baat krenge, toh iske liye aap diagram me dekh paa rhe honge ki humne ek soap film bnai hai jiske ek end prr massless wire of length L rakha hua hai, ab baccho ek important baat, hum jab bhi soap film ki baat krenge toh iske paas do layers hoti hai, ek upar waali surface and ek neeche waali surface, toh jo yaha prr jo wire prr force lag rha hoga voh F+F=2F hoga.
Toh is wire ko humne ek external force lga kr dx displace kiya jo ki equal hoga surface tension ki wajha se lgne waali force ke,
Therefore, workdone by external force= change in potential energy
W=ΔU
force×displacement=ΔU
Here we will take force=2F and displacement dx
ΔU=2Fdx where F=SL (surface tension),
Now, change in area would be ΔA=2L(x+dx)−2Lx
Therefore, ΔA=2Ldx
Therefore after comparing,
ΔU=SΔA , this is the surface energy of soap film.
SURFACE ENERGY

Ab baccho hum surface ki energy ki baat krenge, toh iske liye aap diagram me dekh paa rhe honge ki humne ek soap film bnai hai jiske ek end prr massless wire of length L rakha hua hai, ab baccho ek important baat, hum jab bhi soap film ki baat krenge toh iske paas do layers hoti hai, ek upar waali surface and ek neeche waali surface, toh jo yaha prr jo wire prr force lag rha hoga voh F+F=2F hoga.
Toh is wire ko humne ek external force lga kr dx displace kiya jo ki equal hoga surface tension ki wajha se lgne waali force ke,
Therefore, workdone by external force= change in potential energy
W=ΔU
force×displacement=ΔU
Here we will take force=2F and displacement dx
ΔU=2Fdx where F=SL (surface tension),
Now, change in area would be ΔA=2L(x+dx)−2Lx
Therefore, ΔA=2Ldx
Therefore after comparing,
ΔU=SΔA , this is the surface energy of soap film.
ANGLE OF CONTACT
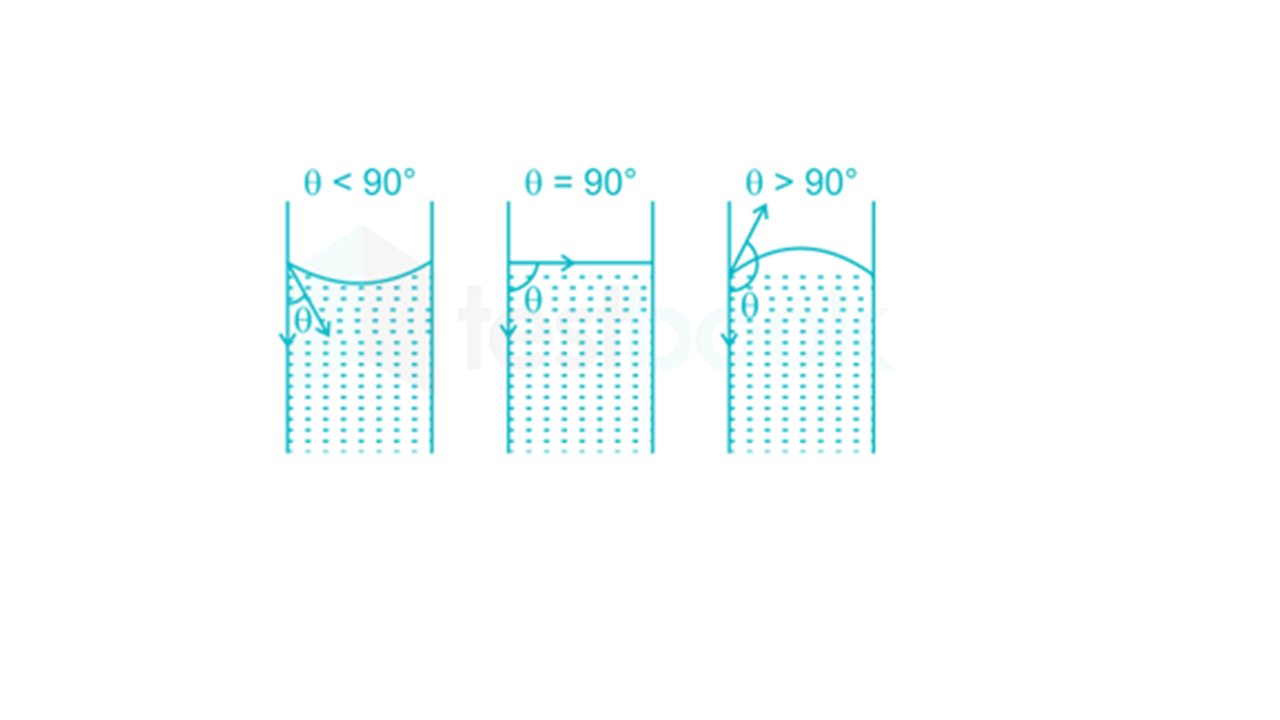
Baccho different different liquid ke liye different different meniscus bante hai, toh jaise impure water humara concave meniscus bnata hai jaisa ki aapko first tube me θ<90∘ dikh rha hoga and jisme θ>90∘ dikh rha hai use hum convex meniscus bolte hai ye jab banta hai jab isme mercury ho.
Angle of contact dekhne se phle hume sabse phle point of contach dekhna padega fluid ka glass tube ke saath,
Then uske baad hum tangent draw krte hai uss point of contact se, ek tangent bnate hai fluid ko consider krke and uski direction rakhte hai away from the glass tube and along the fluid and ek tangent bnate hai glass prr and uski direction towards the fluid hoti hai, inn dono directions ke beech me banne waale angle ko angle of contact bolte hai.
ANGLE OF CONTACT

Baccho different different liquid ke liye different different meniscus bante hai, toh jaise impure water humara concave meniscus bnata hai jaisa ki aapko first tube me θ<90∘ dikh rha hoga and jisme θ>90∘ dikh rha hai use hum convex meniscus bolte hai ye jab banta hai jab isme mercury ho.
Angle of contact dekhne se phle hume sabse phle point of contach dekhna padega fluid ka glass tube ke saath,
Then uske baad hum tangent draw krte hai uss point of contact se, ek tangent bnate hai fluid ko consider krke and uski direction rakhte hai away from the glass tube and along the fluid and ek tangent bnate hai glass prr and uski direction towards the fluid hoti hai, inn dono directions ke beech me banne waale angle ko angle of contact bolte hai.
CAPILLARY RISE
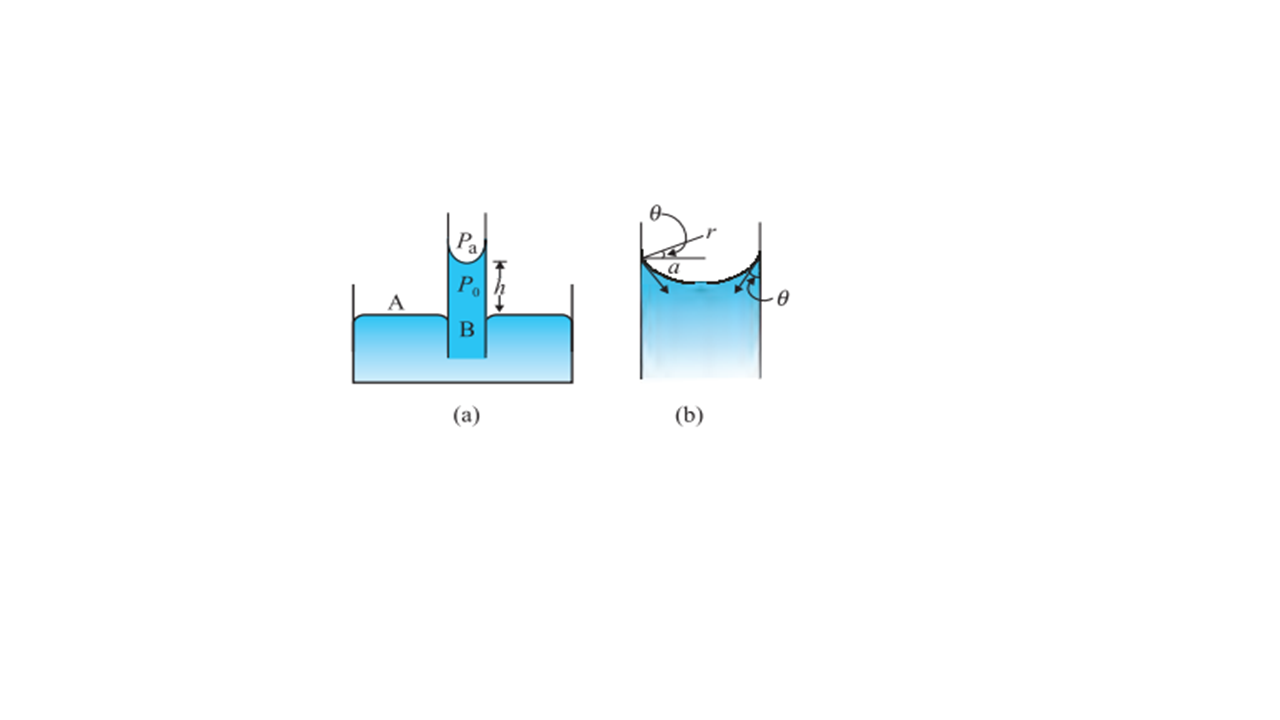
Baccho hum cappilary rise concave meniscus ke liye dekhenge jisme angle of contact θ<90∘ hota hai.
Jaisa ki aap sab diagram me dekh sakte ho ki e capillary tune hai jise humne ek fluid me dip kiya hua hai, and uska meniscus concave bna hua hai, toh baccho, PA=PB
Therefore, P0=(P0−2Sr)+ρgh where h is the height of fluid in capillary tube and ρ is the density of fluid and r is the radius of meniscus.
Therefore, r=2Sρgh
Now as you all can see in the (b) part of the diagram, a is the radius of tube, so by calculating,
a=rcosθ
Therefore, we can also write, a=2Scosθρgh
CAPILLARY RISE

Baccho hum cappilary rise concave meniscus ke liye dekhenge jisme angle of contact θ<90∘ hota hai.
Jaisa ki aap sab diagram me dekh sakte ho ki e capillary tune hai jise humne ek fluid me dip kiya hua hai, and uska meniscus concave bna hua hai, toh baccho, PA=PB
Therefore, P0=(P0−2Sr)+ρgh where h is the height of fluid in capillary tube and ρ is the density of fluid and r is the radius of meniscus.
Therefore, r=2Sρgh
Now as you all can see in the (b) part of the diagram, a is the radius of tube, so by calculating,
a=rcosθ
Therefore, we can also write, a=2Scosθρgh
EXAMPLE 1
A steel rod of length 1 m and radius 10 mm is stretched by a force 100 kN along its length. The stress produced in the rod is YSteel=2×1011Nm−2
Here r=2 cm =2×10−2m
L=1m, F= 100 kN=100×10−3N=105N
Stress produced in the rod is
stress =FA=Fπr2=100×103N3.14×(10−2m)2=3.18×108Nm−2
EXAMPLE 1
A steel rod of length 1 m and radius 10 mm is stretched by a force 100 kN along its length. The stress produced in the rod is YSteel=2×1011Nm−2
Here r=2 cm =2×10−2m
L=1m, F= 100 kN=100×10−3N=105N
Stress produced in the rod is
stress =FA=Fπr2=100×103N3.14×(10−2m)2=3.18×108Nm−2
EXAMPLE 2
The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will
Breaking force = Breaking stress × Area of cross-section . When the wires is cut to half, there is no change in the area of the area of cross-section of their wire. Therefore , there is not change in the area of the maximum load (i.e., braking force ) the wire can support.
EXAMPLE 2
The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will
Breaking force = Breaking stress × Area of cross-section . When the wires is cut to half, there is no change in the area of the area of cross-section of their wire. Therefore , there is not change in the area of the maximum load (i.e., braking force ) the wire can support.
EXAMPLE 3
A square lead slab of side 50 cm and thickness 10 cm is subjected to a shearing force (on its narrow face) of 9×104N. The lower edge is riveted to the floor. How much will the upper edge be displaced? (Shear modulus of lead=5.6×109Nm−2)
The lead slab is fixed and force fixed and force is applied parallel to the narrow face as shown in the figure. Area of the face parrallel to which this force is applied is

A=50cm×10cm=0.5m×0.1m=0.05m2
If ΔL is the displacement of the upper edge of the slab due to tangential force F, then
η=F/AΔL/LorΔL=FLηA
Substituting the given value,
ΔL=(9×104N)(0.5m)5.6×109Nm−2×0.05m3
=−1.6×10−4m=0.16mm
EXAMPLE 3
A square lead slab of side 50 cm and thickness 10 cm is subjected to a shearing force (on its narrow face) of 9×104N. The lower edge is riveted to the floor. How much will the upper edge be displaced? (Shear modulus of lead=5.6×109Nm−2)
The lead slab is fixed and force fixed and force is applied parallel to the narrow face as shown in the figure. Area of the face parrallel to which this force is applied is

A=50cm×10cm=0.5m×0.1m=0.05m2
If ΔL is the displacement of the upper edge of the slab due to tangential force F, then
η=F/AΔL/LorΔL=FLηA
Substituting the given value,
ΔL=(9×104N)(0.5m)5.6×109Nm−2×0.05m3
=−1.6×10−4m=0.16mm
EXAMPLE 4
If the volume of a wire remains constant when subjected to tensile stress, the value of Poisson's ratio of the material of the wire is
Let L be the length, r be the radius of the wire. Volume of the wire is V=πr2L
Differentiating both side, we get ΔV=π(2rΔr)L+πr2ΔL
As the volume of the wire remains unchanged when it gets stretched, so AV = 0. Hence
0=2πrLΔ+πr2ΔL)
∴Δr/rΔL/L=−12
Poisson's ratio=Lateral strainLongitudinal strain=−Δr/rΔL/L=12=0.5
EXAMPLE 4
If the volume of a wire remains constant when subjected to tensile stress, the value of Poisson's ratio of the material of the wire is
Let L be the length, r be the radius of the wire. Volume of the wire is V=πr2L
Differentiating both side, we get ΔV=π(2rΔr)L+πr2ΔL
As the volume of the wire remains unchanged when it gets stretched, so AV = 0. Hence
0=2πrLΔ+πr2ΔL)
∴Δr/rΔL/L=−12
Poisson's ratio=Lateral strainLongitudinal strain=−Δr/rΔL/L=12=0.5
EXAMPLE 5
One end of a horizontal thick copper wire of length 2L and radius 2R is welded to an end fo another horizontal thin copper wire of lenth L and radius R. When the arrangement is stretched by applying forces at two ends, the ratio of the elongation in the thin wire to that in the thick wire is

Both the rods are made up of the same kind of meteria, i.e., their young's modulus is same.
k1=π4R2y2L,K2=πR2yL
Force constants of two rods are ,
∴F=k1x=k2y
⇒yx=k1y
EXAMPLE 5
One end of a horizontal thick copper wire of length 2L and radius 2R is welded to an end fo another horizontal thin copper wire of lenth L and radius R. When the arrangement is stretched by applying forces at two ends, the ratio of the elongation in the thin wire to that in the thick wire is

Both the rods are made up of the same kind of meteria, i.e., their young's modulus is same.
k1=π4R2y2L,K2=πR2yL
Force constants of two rods are ,
∴F=k1x=k2y
⇒yx=k1y
EXAMPLE 6
Two blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?

T=2m1m2m1+m2g=2×1×21+2×10N=403N
If r is the minimum radius, then
Breaking stress =403(πr2)or403π×106=403πr2
or r2=1106orr=1103m=1mm
EXAMPLE 6
Two blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?

T=2m1m2m1+m2g=2×1×21+2×10N=403N
If r is the minimum radius, then
Breaking stress =403(πr2)or403π×106=403πr2
or r2=1106orr=1103m=1mm
EXAMPLE 7
A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of 2rev./s at the bottom of the circle. The cross-sectional area of the wire is 0.065cm2 . Calculate the elongaton of the wire when the mass is at the lowest point of its path Ysteel=2×1011Nm−2.
Here, m = 15 kg , r = L = 1 m
v=2rev s−1,A=0.05cm2=0.05×10−4m2
When the mass is the lowest point of the vertical circle, the stretching force is
F=mg+mrω2=mg+mr(2πv)2
=15×10+15×(1)×(2π×2)2=2516N
As Y=F/AΔL/L∴ΔL=FLAY
ΔL=2526N×1m0.05×10−4m2×2×1011=2.52×10−3m=2.52mm
EXAMPLE 7
A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of 2rev./s at the bottom of the circle. The cross-sectional area of the wire is 0.065cm2 . Calculate the elongaton of the wire when the mass is at the lowest point of its path Ysteel=2×1011Nm−2.
Here, m = 15 kg , r = L = 1 m
v=2rev s−1,A=0.05cm2=0.05×10−4m2
When the mass is the lowest point of the vertical circle, the stretching force is
F=mg+mrω2=mg+mr(2πv)2
=15×10+15×(1)×(2π×2)2=2516N
As Y=F/AΔL/L∴ΔL=FLAY
ΔL=2526N×1m0.05×10−4m2×2×1011=2.52×10−3m=2.52mm
EXAMPLE 8
A material has Poisson's ratio 0.50. If a uniform rod of it suffers a longitudinal strain of 2×10−3, then the percentage change in volume is
As the Poisson's ratio of a material is 0.5, so there is no change in volume.
EXAMPLE 8
A material has Poisson's ratio 0.50. If a uniform rod of it suffers a longitudinal strain of 2×10−3, then the percentage change in volume is
As the Poisson's ratio of a material is 0.5, so there is no change in volume.
EXAMPLE 9
The compressibility of water is 5×10−10m2/N . If it is subjected to a pressure of 15 MPa, the fractional decrease in volume will be-
Bulk modulus , B=−P(ΔV/V) -ve sign shows that with an increase in pressure, a decrease in volume occurs.
Compressibility, K=1B=−ΔVPV
Decrease in volume, ΔV=PVK
=4×107×1×6×10−10=24×10−3 litre
=24×10−3×103cm3=24cc
EXAMPLE 9
The compressibility of water is 5×10−10m2/N . If it is subjected to a pressure of 15 MPa, the fractional decrease in volume will be-
Bulk modulus , B=−P(ΔV/V) -ve sign shows that with an increase in pressure, a decrease in volume occurs.
Compressibility, K=1B=−ΔVPV
Decrease in volume, ΔV=PVK
=4×107×1×6×10−10=24×10−3 litre
=24×10−3×103cm3=24cc
EXAMPLE 10
The area of a cross-section of steel wire is 0.5cm−2 and Young's modulus of steel is 2×1011Nm−2. The force required to stretch by 0.5% of its length is
Here, A=0.5cm2=0.5×10−4m2,
Y=2×1011Nm2
ΔLL=0.3%=0.3100=0.1×10−2
As Y=F/AΔL/L∴F=YΔLLA
=2×1011Nm−2×0.5×10−2×0.5×10−4m2
=5×103N=5000N
EXAMPLE 10
The area of a cross-section of steel wire is 0.5cm−2 and Young's modulus of steel is 2×1011Nm−2. The force required to stretch by 0.5% of its length is
Here, A=0.5cm2=0.5×10−4m2,
Y=2×1011Nm2
ΔLL=0.3%=0.3100=0.1×10−2
As Y=F/AΔL/L∴F=YΔLLA
=2×1011Nm−2×0.5×10−2×0.5×10−4m2
=5×103N=5000N
EXAMPLE 11
A spherical ball of density ρ and radius0.003m is dropped into a tube containing a viscous fluid up to the 0 cm mark as shown in the figure. Viscosity of the fluid =1.26N−s/m2 and its density ρL=ρ2=1260kg/m3. Assume that the ball reaches a terminal speed at 10cm mark. The time taken by the ball to travel the distance between the 10cm and 20cm mark is (g=10m/s2)

vT=29r2(ρ−σ)gη
=2×(0.003)2(1260×2−1260)×109×1.26
=0.02m/s
t=dvT=10×10−20.02=5s.
EXAMPLE 11
A spherical ball of density ρ and radius0.003m is dropped into a tube containing a viscous fluid up to the 0 cm mark as shown in the figure. Viscosity of the fluid =1.26N−s/m2 and its density ρL=ρ2=1260kg/m3. Assume that the ball reaches a terminal speed at 10cm mark. The time taken by the ball to travel the distance between the 10cm and 20cm mark is (g=10m/s2)

vT=29r2(ρ−σ)gη
=2×(0.003)2(1260×2−1260)×109×1.26
=0.02m/s
t=dvT=10×10−20.02=5s.
EXAMPLE 12
A body floats in water with its one-third volume above the surface. The same body floats in a liquid with one-third volume immersed. The density of the liquid is
Fraction of volume immersed
f=ρsρl or r∝1ρl
f1f2=ρl2ρl1 or ρl2=(f1f2)ρl1
=(V−V/3)(V/3)ρl1
=2ρl1.
EXAMPLE 12
A body floats in water with its one-third volume above the surface. The same body floats in a liquid with one-third volume immersed. The density of the liquid is
Fraction of volume immersed
f=ρsρl or r∝1ρl
f1f2=ρl2ρl1 or ρl2=(f1f2)ρl1
=(V−V/3)(V/3)ρl1
=2ρl1.
SUMMARY
1. Stress is the restoring force per unit area and strain is the fractional change in dimension. In general there are three types of stresses (a) tensile stress — longitudinal stress (associated with stretching) or compressive stress (associated with compression), (b) shearing stress, and (c) hydraulic stress.
2. For small deformations, stress is directly proportional to the strain for many materials. This is known as Hooke’s law. The constant of proportionality is called modulus of elasticity. Three elastic moduli viz., Young’s modulus, shear modulus and bulk modulus are used to describe the elastic behaviour of objects as they respond to deforming forces that act on them. A class of solids called elastomers does not obey Hooke’s law.
3. When an object is under tension or compression, the Hooke’s law takes the form FA=YΔLL where ΔLL is the tensile or compressive strain of the object, F is the magnitude of the applied force causing the strain, A is the cross-sectional area over which F is applied (perpendicular to A) and Y is the Young’s modulus for the object. The stress is FA.
4. A pair of forces when applied parallel to the upper and lower faces, the solid deforms so that the upper face moves sideways with respect to the lower. The horizontal displacement ΔL of the upper face is perpendicular to the vertical height L. This type of deformation is called shear and the corresponding stress is the shearing stress. This type of stress is possible only in solids. In this kind of deformation the Hooke’s law takes the form FA=G×ΔLL where ΔL is the displacement of one end of object in the direction of the applied force F, and G is the shear modulus.
5. When an object undergoes hydraulic compression due to a stress exerted by a surrounding fluid, the Hooke’s law takes the form p=B(ΔVV), where p is the pressure (hydraulic stress) on the object due to the fluid, ΔVV (the volume strain) is the absolute fractional change in the object’s volume due to that pressure and B is the bulk modulus of the object.
6. In the case of a wire, suspended from ceiling and stretched under the action of a weight (F) suspended from its other end, the force exerted by the ceiling on it is equal and opposite to the weight. However, the tension at any cross-section A of the wire is just F and not 2F. Hence, tensile stress which is equal to the tension per unit area is equal to FA.
7. Hooke’s law is valid only in the linear part of the stress-strain curve.
8. The Young’s modulus and shear modulus are relevant only for solids since only solids have lengths and shapes.
9. Bulk modulus is relevant for solids, liquid and gases. It refers to the change in volume when every part of the body is under the uniform stress so that the shape of the body remains unchanged.
10. Metals have larger values of Young’s modulus than alloys and elastomers. A material with a large value of Young’s modulus requires a large force to produce small changes in its length.
11. In daily life, we feel that a material which stretches more is more elastic, but it is a misnomer. In fact material which stretches to a lesser extent for a given load is considered to be more elastic.
12. In general, a deforming force in one direction can produce strains in other directions also. The proportionality between stress and strain in such situations cannot be described by just one elastic constant. For example, for a wire under longitudinal strain, the lateral dimensions (radius of cross section) will undergo a small change, which is described by another elastic constant of the material (called Poisson ratio).
13. Stress is not a vector quantity since, unlike a force, the stress cannot be assigned a specific direction. Force acting on the portion of a body on a specified side of a section has a definite direction.
14. Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of interface between the liquid and the bounding surface. It is the extra energy that the molecules at the interface have as compared to the interior.
SUMMARY
1. Stress is the restoring force per unit area and strain is the fractional change in dimension. In general there are three types of stresses (a) tensile stress — longitudinal stress (associated with stretching) or compressive stress (associated with compression), (b) shearing stress, and (c) hydraulic stress.
2. For small deformations, stress is directly proportional to the strain for many materials. This is known as Hooke’s law. The constant of proportionality is called modulus of elasticity. Three elastic moduli viz., Young’s modulus, shear modulus and bulk modulus are used to describe the elastic behaviour of objects as they respond to deforming forces that act on them. A class of solids called elastomers does not obey Hooke’s law.
3. When an object is under tension or compression, the Hooke’s law takes the form FA=YΔLL where ΔLL is the tensile or compressive strain of the object, F is the magnitude of the applied force causing the strain, A is the cross-sectional area over which F is applied (perpendicular to A) and Y is the Young’s modulus for the object. The stress is FA.
4. A pair of forces when applied parallel to the upper and lower faces, the solid deforms so that the upper face moves sideways with respect to the lower. The horizontal displacement ΔL of the upper face is perpendicular to the vertical height L. This type of deformation is called shear and the corresponding stress is the shearing stress. This type of stress is possible only in solids. In this kind of deformation the Hooke’s law takes the form FA=G×ΔLL where ΔL is the displacement of one end of object in the direction of the applied force F, and G is the shear modulus.
5. When an object undergoes hydraulic compression due to a stress exerted by a surrounding fluid, the Hooke’s law takes the form p=B(ΔVV), where p is the pressure (hydraulic stress) on the object due to the fluid, ΔVV (the volume strain) is the absolute fractional change in the object’s volume due to that pressure and B is the bulk modulus of the object.
6. In the case of a wire, suspended from ceiling and stretched under the action of a weight (F) suspended from its other end, the force exerted by the ceiling on it is equal and opposite to the weight. However, the tension at any cross-section A of the wire is just F and not 2F. Hence, tensile stress which is equal to the tension per unit area is equal to FA.
7. Hooke’s law is valid only in the linear part of the stress-strain curve.
8. The Young’s modulus and shear modulus are relevant only for solids since only solids have lengths and shapes.
9. Bulk modulus is relevant for solids, liquid and gases. It refers to the change in volume when every part of the body is under the uniform stress so that the shape of the body remains unchanged.
10. Metals have larger values of Young’s modulus than alloys and elastomers. A material with a large value of Young’s modulus requires a large force to produce small changes in its length.
11. In daily life, we feel that a material which stretches more is more elastic, but it is a misnomer. In fact material which stretches to a lesser extent for a given load is considered to be more elastic.
12. In general, a deforming force in one direction can produce strains in other directions also. The proportionality between stress and strain in such situations cannot be described by just one elastic constant. For example, for a wire under longitudinal strain, the lateral dimensions (radius of cross section) will undergo a small change, which is described by another elastic constant of the material (called Poisson ratio).
13. Stress is not a vector quantity since, unlike a force, the stress cannot be assigned a specific direction. Force acting on the portion of a body on a specified side of a section has a definite direction.
14. Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of interface between the liquid and the bounding surface. It is the extra energy that the molecules at the interface have as compared to the interior.