STRAIGHT LINES for Class 11 MATHS

Bachcho jaisa ki aap logo ne class 10th mai coordinate geometry chapter padha tha. Toh abh class 11th mai straight line bhi uska broad concept hai. Yeh algebra aur geometry ka combination hai. Earlier classes mai humne padha tha coordinate axes, coordinate plane, plotting of points in a plane, section formula, distance formula, etc. Hum ye sab bhi padhenge par inke sath hi hum aur bhi new aur interesting concept padhenge. Ye sare concept coordinate geometry ke basics hai. Abh hum aage interesting examples ke saath iss chapter ko padhenge.
Kya aapko pta hai ki straight lines kya hai?
Agar aapko nahi pta toh koi baat nahi hum aage ise detail mai padhenge. Bachcho jaisa ki aap logo ne class 10th mai coordinate geometry chapter padha tha. Toh abh class 11th mai straight line bhi uska broad concept hai. Yeh algebra aur geometry ka combination hai. Earlier classes mai humne padha tha coordinate axes, coordinate plane, plotting of points in a plane, section formula, distance formula, etc. Hum ye sab bhi padhenge par inke sath hi hum aur bhi new aur interesting concept padhenge. Ye sare concept coordinate geometry ke basics hai. Abh hum aage interesting examples ke saath iss chapter ko padhenge.

A straight line is a curve such that every points on the line segment joining any two points on it lies on it.

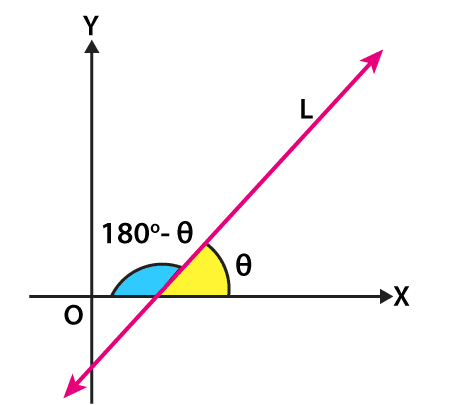
Ek coordinate plane par ek line $x$-axis par do angles banati hai jo ki supplementary angles hote hai.
Supplementary angles are those angles whose sum is equal to ${180}^{\circ }$.
One is $\theta$ other is ${180}^{\circ }$-$\theta$.
Slope kya hai?
Slope ek slant height ki tarah hota hai yani ki ek stair ki tarah.
The slope of a line is denoted by $m$.
Thus, $m=\tan \theta$.

If the area of the triangle $ABC$ is zero, then three points $A$, $B$ and $C$ lie on a line, i.e., they are collinear.

At which point should the origin be shifted so that co-ordinates of point $(2,5)$ become $(1,-4)$ ?

Let required point be $(h,k)$
Here $x=2$, $y=5$, $X=1$, $Y=-4$
Now, $x=X+h$ and $y=Y+k$
$\Rightarrow 2=1+h$ and $5$= $\pm$ $k$
$\Rightarrow h=1$ and $k=9$
$\therefore \text{Origin will be shifted to the point}(1,9)$

Find the value of $x$ so that the inclination of the line joining the points $(x,-3)$ and $(2,5)$ is ${135}^{\circ }$

Let $A(x,-3)$ and $B(2,5)$ be the given points. Then slope of $AB$ =$\frac{5-(-3)}{2-x}=\frac{8}{(2-x)}$
But slope of $AB$ = ${\tan 135}^{\circ }$
$=\tan ({180}^{\circ }-{45}^{\circ })$
$=-{\tan 45}^{\circ }$
$=-1$
$\therefore \frac{8}{2-x}$ $=-1$
$\Rightarrow x-2=8$
$x=10$
Hence, $x=10$

Let $P$ $(x_1,y_1)$ and $Q$ $(x_2,y_2)$ two points on non - vertical line on $x$-axis jiska angle $\theta$ hai.
The inclination of line $l$ may be acute or obtuse.
Case $1$ : When angle ($\theta$) is acute:
Slope of line = $l$ = $m$ = $\tan \theta$
$\tan \theta$ = $\frac{y_2-y_1}{x_2-x_1}$

Case $2$ : When angle ($\theta$) is obtuse.
$m=\tan \theta$
$m$ = $\frac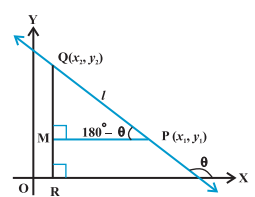{y_2-y_1}{x_2-x_1}$

Conditions for parallelism and perpendicularity of lines in terms of their slopes.
Abh suppose kare koi do non - vertical line parallel hai $l_1$ and $l_2$ aur unke slopes $m_1$ and $m_2$ hai.
Let their inclination be $\alpha$ and $\beta$.
i.e. $m_1$ = $\alpha$ and $m_2$ = $\beta$ jo ki $m_1$ = $m_2$ hai.
$\tan \alpha =\tan \beta$

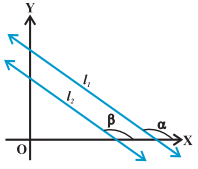
Agar koi do line equal hai toh uske inclinations (angles) bhi equal honge.
Agar koi do line $l_1$ and $l_2$ ek dusre ke perpendicular hai toh unke slopes negative hote hai.
$m_1$ $m_2$ = $-1$

Angle between two lines
Jab hum ek plane par ek line se zyada line ke bare mai sochte hai to ya to hume wo lines intersecting ya parallel milti hai.
Hum jante hai ki jab do lines intersect karti hai to wo do pair vertically opposite angles banati hai aur jisme se kisi do adjacent angles ka ${180}^{\circ }$ hota hai.
Let $\theta$ and $\varphi$ be the adjacent angles.
$m_1$ = ${\tan \alpha }_1$ and $m_2$ = ${\tan \alpha }_2$
$\theta ={\alpha }_2-{\alpha }_1$ and ${\alpha }_1$, ${\alpha }_2$ = ${90}^{\circ }$
$\tan \theta$ = $\frac{m_2-m_1}{1+m_1{m}_2}$, as $1+m_1{m}_2$ $\ne$ $0$

Case I : If $\frac{m_2-m_1}{1+m_1{m}_2}$ is positive, then $\tan \theta$ will be positive and $\tan \phi$ will be negative, which means $\theta$ will be acute and $\phi$ will be obtuse.
Case II : If $\frac{m_2-m_1}{1+m_1{m}_2}$ is positive, then $\tan \theta$ will be positive and $\tan \phi$ will be negative, which means $\theta$ will be acute and $\phi$ will be obtuse.
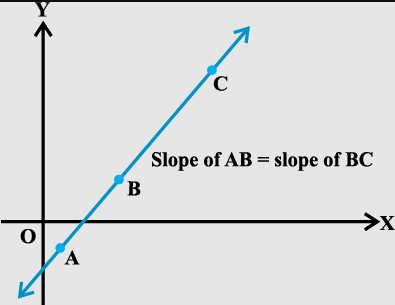
Collinearity of three points
Hum jante hai ki two parallel lines ka slope equal hota hai.
Agar do lines ka slope same hai toh wo ek common point se pass ho rahi hain. Then two lines will coincide.
Agar $A$, $B$ and $C$ ye tino point $XY$ plane par lie karte hai aur inka slope bhi same hai toh ye tino points collinear hai.
Three points are collinear if and only if slope of AB = slope of BC with lie on a same line.

If three points $A(h,0),P(a,b)$ and $B(0,k)$ lie on a line, show that: $\frac{a}{h}+\frac{b}{k}=1.$

Slope of line $AB=\frac{0-b}{h-a}=\frac{-b}{h-a}$
Slope of line $BC=\frac{k-0}{0-h}=\frac{-k}{h}$
Now, $A$ , $B$ and $C$ are collinear.
$\therefore$ Slope of $AB=$ Slope of $BC$
$\Rightarrow \frac{-b}{h-a}=\frac{-k}{h}$
$\Rightarrow -hb=-kh+ak$
Divide both sides by $kh$
$\Rightarrow \frac{-b}{k}=-1+\frac{a}{h}$
$\Rightarrow \frac{a}{h}+\frac{b}{k}=1$

Find the equation of line which passes through the point $(2,3)$ and the sum of whose intercepts on axes is $10$.

Let the equation of straight line be $\frac{x}{a}+\frac{y}{b}=1$.
It passes through the point $(2,3)$
$\frac{2}{a}+\frac{3}{b}=1$…..$\left(1\right)$
Given that $a+b=10$
$\Rightarrow b=10-a$
From eq. $\left(1\right)$
$\frac{2}{a}+\frac{3}{10-a}=1$
$\Rightarrow \frac{20-2a+3a}{a(10-a)}=1$
$\Rightarrow 20+a=10a-a^2$
$\Rightarrow a^2-9a+20=0$
$\Rightarrow (a-4)(a-5)=0$
$\Rightarrow a=4$ or $a=5$
If $a=4$ then $b=10-4=6$
If $a=5$ then $b=10-5=5$
$\therefore$ Equation of line is
$\frac{x}{4}+\frac{y}{6}=1$ or $\frac{x}{5}+\frac{y}{5}=1$
$\Rightarrow 3x+2y=12$ or $x+y=5$

Hum jante hai ki ek line plane par bahot sare points contain karti hai.
Now, we will discuss the equation of a line under different conditions.
Horizontal line

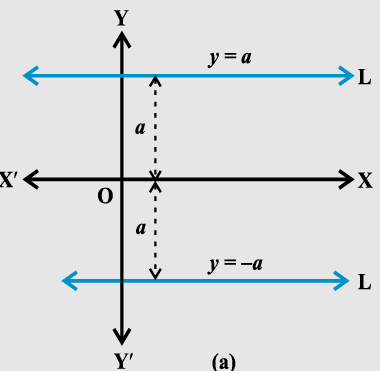
Humne ek horizontal line $L$ draw kari.
Agar line $L$ above the $x$ - axis hai to uski equation $y=a$ hogi.
Agar line $L$ below the $x$ - axis hai to uski equation $y=-a$ hogi.
Vertical line

Humne ek vertical line $L$ draw kari hai.
Agar vertical line $L$, plane $XY$ mai lie karti hai toh uski equation $x=b$ hogi.
Agar vertical line $L$, plane $X\text{'}Y$ mai lie karti hai toh uski equation $x=-b$ hogi
Point - slope form
Suppose kare ki ek fixed point $P_0$ $(x_0,y_0)$ ek non - vertical line $L$ par lie karta hai whose slope is $m$
Let $P(x,y)$ be an arbitrary point on $L$.
So the equation we get,
$m$ = $\frac{y-y_0}{x-x_0}$, i.e., $y-y_0$ = m$(x-x_0)$
Two - point form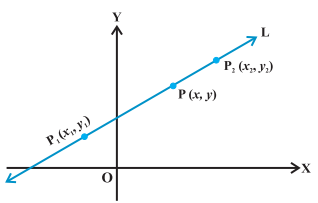

Let the line $L$ passes through two given points $P_1$ $(x_1,y_1)$ and $P_2$ $(x_2,y_2)$.
Let $P$ $(x,y)$ be a general point on $L$.
Ye tino points $P_1$, $P_2$, $P$ collinear hai.
$\therefore$ Slope of $P_{1}P$ = Slope of $P_1$, $P_2$
So the equation we get,
$y-y_1$ = $\frac{y_2-y_1}{x_2-x_1}$ $(x-x_1)$.
Slope - intercept form

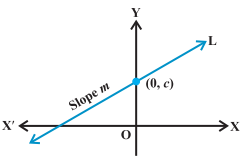
Intercepts are the point at which the graph intersects the axes.
Case 1 : Suppose a line $L$ with slope m cuts the $y$ - axis at a distance $c$ from the origin.
The distance $c$ is called the $y$ - intercept of the line $L$.
So the equation we get, $y=mx+c$, by the using formula $(y-y_1)$ = m $(x-x_1)$
where,
$y=y$ coordinate
$m=$ slope
$x=x$ coordinate
$c=y$ intercept.
Case $2$ : Suppose line $L$ with slope m $x$ - axis ko $d$ point par intercept karti hai.
So the equation we get, $y=m(x-d).$
Intercept - form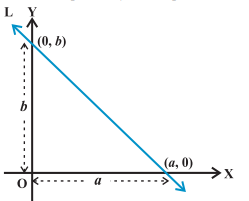

Suppose a line $L$ makes intercept on $x$ - axis and $y$ - axis
So point on $x$ - axis is $(a,0)$ and on $y$ - axis is $(0,b).$
So the equation we get, $y-0$ = $\frac{b-0}{0-a}(x-a)$
i.e., $\frac{x}{a}+\frac{y}{b}=1$
Normal form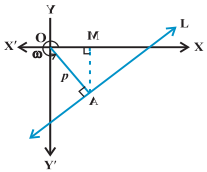


Length of perpendicular from origin to the line is normal .
Angle which normal makes with the positive direction of $x$ - axis.
Let $L$ be the line, jiska perpendicular distance origin $O$ se $OA=p$ hai.
The angle between the positive $x$ - axis and $OA$ be $\angle XOA=\omega$.
Abh ek perpendicular $AM$ $x$ - axis par draw kare.
$OM=p\cos \omega$, $MA=p\sin \omega$, so the coordinates of the point $A$ are ( $p\cos \omega$, $p\sin \omega$ )
$L$ is perpendicular to $OA$
The slope of the line $L$ = $-\left(\frac{1}{slopeofOA}\right)$ = $-\frac{1}{\tan \omega }$ = - $\frac{\cos \omega }{\sin \omega }$
So the equation we get,
$y-p\sin \omega$ = $-\frac{\cos \omega }{\sin \omega }(x-p\cos \omega )$ or
$x\cos \omega +y\sin \omega =p$.

Find the equation of a line which is at a distance of $5$ units from origin and the perpendicular from origin to this line makes an angle $\alpha$ from the positive direction of $x$-axis, where $\tan \alpha =\frac{4}{3}$

Here $p=5$ units and $\tan \alpha =\frac{4}{3}$
$\therefore {\mathrm{Sec}}^2\alpha =1+{\tan }^2\alpha$
$=1+\frac{16}{9}=\frac{25}{9}$
$\Rightarrow \sec \alpha =\pm \frac{5}{3}$
$\Rightarrow \cos \alpha =\pm \frac{3}{5}$
and $\sin \alpha =-\frac{\sin \alpha }{\cos \alpha }\cdot -\cos \alpha$
$=\tan \alpha \cdot \cos \alpha$
$=\frac{4}{3}\cdot (\pm \frac{3}{5})=\pm \frac{4}{5}$
$\therefore \cos \alpha =\frac{3}{5}$ and $\sin \alpha =\frac{4}{5}$
or $\cos \alpha =-\frac{3}{5}$ and $\sin \alpha =-\frac{4}{5}$
Therefore, equation of a line is
$x\cos \alpha +y\sin \alpha =p$
$\Rightarrow \frac{3x}{5}+\frac{4y}{5}=5$ or $\frac{-3x}{5}-\frac{4y}{5}=5$
$\Rightarrow 3x+4y=25$ or $3x+4y+25=0$

Prove that the locus of a moving point, which is equidistant from the lines $3x-2y=5$ and $3x+2y=5$, is a straight line.

Let the point be $(x,y)$ then
$\left|\frac{3x-2y-5}{\sqrt{9+4}}\right|=\left|\frac{3x+2y-5}{\sqrt{9+4}}\right|$
$\Rightarrow |3x-2y-5|=|3x+2y-5|$
$\Rightarrow (3x-2y-5)=\pm (3x+2y-5)$
$\Rightarrow 3x-2y-5=3x+2y-5$
or $3x-2y-5=-(3x+2y-5)$
$\Rightarrow x=\frac{5}{3}$ or $y=0$
Which are the equations of straight lines.
$\therefore$ The required locus is a straight line.

Humne earlier classes mai general equation of first degree in two variables padha hai, $Ax+By+C=0,$ Where $A,B$ and $C$ are real constant, such that A and B are not zero. Isliye $Ax+By+C=0$ equation ka graph straight line hota hai.
$\therefore$ Any equation of the form $Ax+By+C=0,$ where $A$ and $B$ are not zero simultaneously is called general linear equation or general equation of a line.
Different forms of $Ax+By+C=0$
(a) Slope-intercept form
Slope intercept form of a linear equation has the following form where the equation is solved for $y$ in terms of $x$.
If $B$ $\ne$ $0$, then $Ax+By+C=0$ can be written as
$y$ = -$\frac{A}{B}$ $x$ -$\frac{C}{B}$ or $y=mx+c$
$m$ = -$\frac{A}{B}$ and $c$ = -$\frac{C}{B}$ ( $y$ intercept is -$\frac{C}{B}$ )
If $B=0$ , then $x$ = $-\frac{C}{A}$ , jo ki ek vertical line hai aur jiska slope undefined hai and $x$ intercept is $-\frac{C}{A}$.
(b) Intercept form
If C ≠ 0, then $Ax+By+C=0$ can be written as $\frac{x}{a}+\frac{y}{b}$ = $1$
$a=$ - $\frac{C}{A}$ and $b=$ - $\frac{C}{B}$.
It is an intercept form of the equation of a line jiska $x$ intercept - $\frac{C}{A}$ hai aur $y$ intercept - $\frac{C}{B}$.
If $C=0$, then $Ax+By+C=0$ can be written as $Ax+By=0,$ it has zero intercepts on the axes.
(c) Normal form
Let $x\cos \omega +y\sin \omega =p$ be the normal form of the line represented by the equation $Ax+By+C=0$ or $Ax+By=–C.$ Thus, both the equations are same.
$\therefore$ $\frac{A}{\cos \omega }=\frac{B}{\sin \omega }$ = -$\frac{C}{P}$
$\cos \omega$ = - $\frac{Ap}{C}$ and $\sin \omega$ = - $\frac{Bp}{C}$
${\sin }^2\omega +{\cos }^2\omega$ = $1$
$p^2=\frac{C^2}{A^2+B^2}$or $p=\pm \frac{C}{\sqrt{A^2+B^2}}$
Thus, the normal form of the equation $Ax+By+C=0$ is $x\cos \omega +y\sin \omega =p$.

Find the equation of a line perpendicular to the line $\frac{x}{a}+\frac{y}{b}=1$ and passes through the mid-point of the line segment lying between the axes of the given line.

Given straight line is
$\frac{x}{a}+\frac{y}{b}=1$
This line cuts the axes at points $A(a,0)$ and $B(0,b)$.
Co-ordinates of mid point of $AB=(\frac{a+0}{2},\frac{0+b}{2})$
$=(\frac{a}{2},\frac{b}{2})$
Now, slope of given line
$m_1=-\frac{\text{Coefficient of}x}{\text{Coefficient of}y}$
$=-\frac{\frac{1}{a}}{\frac{1}{b}}$
$=-\frac{b}{a}$
Slope of perpendicular line
$m_2=-\frac{1}{m_1}$
$=-\frac{1}{\frac{b}{a}}$
$=\frac{a}{b}$
$\therefore$ Equation of line passes through $(\frac{a}{2},\frac{b}{2})$ and whose slope is $\frac{a}{b}$ is
$y-\frac{b}{2}=\frac{a}{b}(x-\frac{a}{2})$
$\Rightarrow 2by-b^2=2ax-a^2$
$\Rightarrow 2ax-2by=a^2-b^2$.

Find the distance between the parallel lines $3x+4y-7=0$ and $3x+4y+8=0$

Put $y=0$ in $3x+4y-7=0$
$3x+0-7=0$
$\Rightarrow x=\frac{7}{3}$
$\therefore$ Point $(\frac{7}{3},0)$ lies on this line
Now, the length of perpendicular from $(\frac{7}{3},0)$ to the second line $3x+4y+8=0$ is
$=\left|\frac{3\left(\frac{7}{3}\right)+0+8}{\sqrt{3^2+4^2}}\right|$
$=\left|\frac{15}{5}\right|$
$=3units$.

The distance of a point from a line is the length of the perpendicular drawn from the point to the line.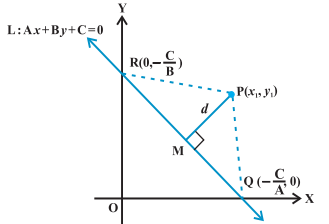

Humne $x$ and $y$ axes par ek line $L:Ax+By+C=0$ draw kari jiske points $Q$ and $R$ hai.
Coordinates of $Q$ $[-\frac{C}{A},0]$ and $R$ $[0,-\frac{C}{B}]$
Humne point $P$ se ek perpendicular $PM$ draw kra line $L$ par. Jiska distance point $P(x_1,y_1)$ se $d$ hai.
The perpendicular distance $\left(d\right)$ of a line $Ax+By+C=0$ from a point $(x_1,y_1)$ is given by
$d$ = $\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$
Distance between two parallel lines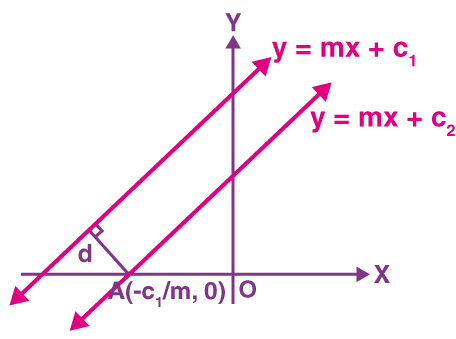

We know that slopes of two parallel lines are equal. Therefore, two parallel lines can be taken in the form.
$y$ = $mx+c_1$....(1)
$y$ = $mx+c_2$.....(2)
Line $1$, $x$ - axis ko $A$ point par intersect karti hai.
Coordinates of $A$ is $(\frac{c_1}{m},0)$
Distance between two lines is equal to the length of the perpendicular from point $A$ to line $2.$
Therefore, distance between the lines $\left(1\right)$ and $\left(2\right)$ is
$d=\frac{|c_1-c_2|}{\sqrt{1+m^2}}$
Thus, the distance d between two parallel lines $y$ = $mx+c_1$ and $y$ = $mx+c_2$ is given by $d$ = $\frac{|c_1-c_2|}{\sqrt{1+m^2}}$
If lines are given in general form, i.e., $Ax+By+C1=0$ and $Ax+By+C2=0,$ then above formula will take the form $d$ = $\frac{|C_1-C_2|}{\sqrt{A^2+B^2}}$

The equation of a line is $3x+4y-10=0$. Convert this equation into :
$\left(i\right)$ slope-intercept
$\left(ii\right)$ intercept
$\left(iii\right)$ perpendicular form

$\left(i\right)3x+4y-10=0$
$\Rightarrow 4y=-3x+10$
$\Rightarrow y=-\frac{3}{4}x+\frac{5}{2}$
Comparing with $y=mx+c$
Slope $m=-\frac{3}{4}$
$y$ intercept $c=\frac{5}{2}$
$\left(ii\right)3x+4y-10=0$
$\Rightarrow 3x+4y=10$
$\Rightarrow \frac{3x}{10}+\frac{4y}{10}=1$
$\Rightarrow \frac{x}{\frac{10}{3}}+\frac{y}{\frac{5}{2}}=1$
Comparing with $\frac{x}{a}+\frac{y}{b}=1$
Intercept on $X$-axis $=a=\frac{10}{3}$ units.
Intercept on $Y$-axis $=b=\frac{5}{2}$ units.
$\left(iii\right)3x+4y-10=0$
$\Rightarrow 3x+4y=10$
(Taking constant term positive)
Divide both sides by $\sqrt{3^2+4^2}=5$
$\frac{3}{5}x+\frac{4}{5}y=2$
Comparing with $x\cos \alpha +y\sin \alpha =p$
$\cos \alpha =\frac{3}{5}$
$\sin \alpha =\frac{4}{5}$
$p=2$ units

Convert the equation $4x+5y+7=0$ into perpendicular form and find the length of perpendicular from origin.

$4x+5y+7=0$
$\Rightarrow -4x-5y=7$
(Taking constant term positive )
Divide both side by $\sqrt{{(-4)}^2+{(-5)}^2}=\sqrt{41}$
$\frac{-4}{\sqrt{41}}x-\frac{5}{\sqrt{41}}y=\frac{7}{\sqrt{41}}$
Which is the perpendicular form of a line.
Length of perpendicular from origin to the line $=\frac{7}{\sqrt{41}}$ units

In this chapter, you have studied the following points:

1. Slope $\left(m\right)$ of a non-vertical line passing through the points $(x_1,y_1)$ and $(x_2,y_2)$ is given by m =$\frac{y_2-y_1}{x_2-x_1}$ = $\frac{y_1-y_2}{x_1-x_2}$, $x_1$ $\ne$ $x_2$


2. If a line makes an angle á with the positive direction of $x$-axis, then the slope of the line is given by $m=\tan \alpha$, α ≠ 90°.


3. Slope of horizontal line is zero and slope of vertical line is undefined.


4. An acute angle (say $\theta$) between lines $L_1$ and $L_2$ with slopes $m_1$ and $m_2$ is given by $\frac{|m_2-m_1|}{1+m_1{m}_2}$, $1+m_1{m}_2\ne 0$


5. Two lines are parallel if and only if their slopes are equal.


6. Two lines are perpendicular if and only if product of their slopes is $–1.$


7. Three points $A,B$ and $C$ are collinear, if and only if slope of $AB=$ slope of $BC.$


8. Equation of the horizontal line having distance a from the $x$-axis is either $y=a$ or $y=-a$.


9. Equation of the vertical line having distance b from the $y$-axis is either $x=b$ or $x=-b$.


10. The point $(x,y)$ lies on the line with slope m and through the fixed point $(x_0,y_0)$ if and only if its coordinates satisfy the equation $y-y_0$= $m(x-x_0)$


11. Equation of the line passing through the points $(x_1,y_1)$ and $(x_2,y_2)$ is given by $y-y_1$ = $\frac{y_2-y_1}{x_2-x_1}(x-x_1)$.


12. The point $(x,y)$ on the line with slope $m$ and $y$ intercept $c$ lies on the line if and only if $y=mx+c.$


13. If a line with slope $m$ makes $x$-intercept $d.$ Then equation of the line is $y=m(x-d)$.


14. Equation of a line making intercepts $a$ and $b$ on the $x$-and $y$-axis, respectively, is = $\frac{x}{a}+\frac{y}{b}$ = $1$


15. The equation of the line having normal distance from origin $p$ and angle between normal and the positive $x$-axis $\omega$ is given by $x\cos \omega +y\sin \omega =p$ .


16. Any equation of the form $Ax+By+C=0,$ with $A$ and $B$ are not zero, simultaneously, is called the general linear equation or general equation of a line.


17. The perpendicular distance $\left(d\right)$ of a line $Ax+By+C=0$ from a point $(x_1,y_1)$ is given by $d$ = $\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$


18. Distance between the parallel lines $Ax+By+C_1=0$ and $Ax+By+C_2=0$, is given by $d=\frac{|c_1-c_2|}{\sqrt{A^2+B^2}}$.