SETS for Class 11 MATHS
Introduction
So guys hum daily life me bahut saare objects and unke collection ki bat karte hai , for example , pack of cards , collection of stamps, collection of books and many more , in same way we have collection of different numbers in mathematics which we are going to discuss in this chapter. The theory of sets was developed by German mathematician Georg Cantor (1845-1918). He first encountered sets while working on “problems on trigonometric
series”. Today this concept is used in every branch of mathematics like in concept of relation and function, geometry, sequences, probability, etc. In this chapter we will discuss types of sets, relations of sets and even practical applications of sets.
Introduction
Today set concept is used in every branch of mathematics like in concept of relation and function, geometry, sequences, probability, etc.
Sets and their Representations
In our everyday life we have collections of objects of particular kind such as pack of card, vowels in English alphabet, rivers of India, etc and in mathematics we have collections of natural number, prime number, odd number, points, solution of equation, kind of triangles, etc. this in our mathematic we called it as set.
A set is a well-defined collection of objects.
There are two methods of representing a set :
(i) Roster or tabular form
(ii) Set-builder form.
In roster form all element are listed, the elements are being separated by commas and are enclosed within braces {}. For example, set of vowel is given by {a,e,i,o,u}. Order of element is not important but repeated elements are now allowed.
In set-builder form, all the elements of a set possess a single common property which is not possessed by any element outside the set. For example, set of vowel is given by V={x:x is a vowel in English alphabet}. We can read it as set of x such that x is vowel in English alphabet.
Sets and their Representations
A set is a well-defined collection of objects. By “well define collection” we mean that when given a set and an object, we should clearly be able to say whether a particular object is a member of set or not e.g.,
1. Collection of all good students in a class is not well define collection as there is no particular criteria for a student to be good. It can vary from person to person. So, it is not a set.
2. Collection of all student scoring marks 90 or more would be a well define collection. Therefore, it forms a set.
There are two methods of representing a set :
(i) Roster or tabular form
(ii) Set-builder form.
In roster form all element are listed, the elements are being separated by commas and are enclosed within braces {}. For example, set of vowel is given by {a,e,i,o,u}. Order of element is not important but repeated elements are not allowed.
In set-builder form, all the elements of a set possess a single common property which is not possessed by any element outside the set. For example, set of vowel is given by V={x:x is a vowel in English alphabet}. We can read it as set of x such that x is vowel in English alphabet.
The Empty Set
A set which does not contain any element is called the empty set or the null set or the void set. For example, A={x:x is even prime greater than 2}, since we do not have any prime number greater than 2 so set will be empty set.
Example 1
Write the solution set of the equation x2+x–2=0 in roster form.
So guys pehle hum iska solution find karenge , for this we are going to use middle term splitting method or you can use any method of your choice to solve this quadratic equation. So we get
x2+x–2=x2+2x−x−2=0
= x(x+2)−1(x+2)=(x+2)(x−1)=0
⇒(x+2)=0&(x−1)=0
we get , x = -2 , 1
Therefore, the solution set of the given equation can be written in roster form as {1, – 2}.
Finite and Infinite Set
A set which is empty or consists of a definite number of elements is called finite otherwise, the set is called infinite.
Let A be set of months of year then we have finite element i.e. 12 so this set is called finite set and Let B be set of natural number then we have infinite number of element in set so called infinite set.
A set consisting of single element is called a singleton set. Let C={x:x∈N and x2=9}={3} is singleton set.
The number of element of finite set A is called Cardinal Number of Finite Set ans is denoted by n(A).
Example 2
Write the set {12,23,34,45,56,67,78,89,910} in the set-builder form.
We observe that each element in the given set has the denominator one more than the numerator. Also, the numerator begins from 1 and do not exceed 9. Hence, in the set-builder form the given set can be written as {x:x=nn+1,n∈N,n≤9}
Equal Sets
Two sets A and B are said to be equal if they have exactly the same elements and we write A=B. Otherwise, the sets are said to be unequal and we write A≠B.
Let A={1,2,3,4,5} and B={3,5,2,4,1} then A and B are equal set since all elements of A lies in B and all elements of B lies in A.
Two Finite set A and B are equivalent if their cardinal number are same i.e. n(A)=n(B).
Empty Set
So guys hume pata hai empty means khaali , means jisme kuch na ho , so a set which does not contain any element is called the empty set or the null set or the void set. For example, A={x:x is even prime greater than 2}, since we do not have any even prime number greater than 2 so set will be empty set.
Subsets
A set A is said to be a subset of a set B if every element of A is also an element of B.
Subset of real numbers are set of Natural number(N), Integer(Z), Rational number(Q), Irrational number(Q), Prime number, Odd number, Even number, Whole number(W), etc.
N⊂Z⊂Q,Q⊂R,Q⊂R,N⊄Q
Let a,b∈R and a<b. Then the set of real numbers {y:a<y<b} is called an open interval and is denoted by (a,b). All the points between a and b belong to the open interval (a,b) but a,b themselves do not belong to this interval.
The interval which contains the end points also is called closed interval and is denoted by [a,b]. Thus [a,b]={x:a≤x≤b}
We may also have interval open at one side and closed at other i.e. [a,b)or(a,b].
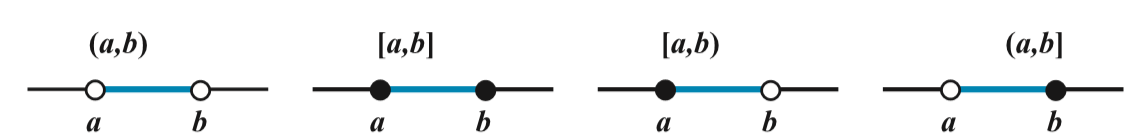
The number (b–a) is called the length of any of the intervals (a,b),[a,b],[a,b)or(a,b].
Note :→ 1. Every set is subset of itself.
2. Empty set is subset of every set.
Example 3
Which of the following sets are empty sets?
(i) A={x:x2−3=0 and x is rational },
(ii) B={x:x is an even prime number },
(iii) C={x:4<x<5,x∈N},
(iv) D={x:x2=25, and x is an odd integer }
(i) We know that there is no rational number whose square is 3. So, x2−3=0 is not satisfied by any rational number. Hence, A is an empty set.
(ii) We know that 2 is the only even prime number. Therefore, B={2}. So, B is not an empty set.
(iii) Since there is no natural number between 4 and 5. So, C is an empty set.
(iv) Since x=5,−5 satisfy x2=25 and ±5 are odd integers. Therefore, D={−5,5}. Thus, D is a non-empty set.
Power Set
The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set. For example, if A = {2, 5}, then P(A)={ φ,{ 2 }, { 5 }, { 2,5 }} .
Note:→ If number of element of A is m then number of element of P(A) is 2m or n[P(A)]=2m.
Finite and Infinite Sets
Toh bacho we all know the meaning of finite means which can be counted right and infinite means which we can not count , so a set which is empty or consists of a definite number of elements is called finite otherwise, the set is called infinite.
Let A be set of months of year then we have finite element i.e. 12 so this set is called finite set and Let B be set of natural number then we have infinite number of element in set so it is called infinite set.
A set consisting of single element is called a singleton set. Let C={x:x∈N and x2=9}={3} is singleton set.
The number of element of finite set A is called Cardinal Number of Finite Set and is denoted by n(A). e.g. A={2,3,5,7,11,13,17,19}, then n(A)=8.
Universal Set
For all cases we always have one basic set which contain each and every element, this basic set is called the “Universal Set”. The universal set is usually denoted by U. Like we have universe it is also set we will take as universe for our question which contains all set.
Example 4
State which of the following sets are finite and which are infinite:
(i) A={x:x∈Z and x2−5x+6=0}
(ii) B={x:x∈Z and x2 is even }
(iii) C={x:x∈Z and x2=36}
(iv) D={x:x∈Z and x> −10}
(i) So guys we know a quadratic equation has only two solutions , so clearly it will be a finite set , but we can also show this by finding the solution of given quadratic equation by any method that we have learnt in class 10. so we get , A={x:x∈Z and x2−5x+6=0}={2,3}
So, A is a finite set.
(ii) Guys we have learnt a property that square of a even integer is even , so set B will contain all even integer and we know they are infinite
such that ,B={x:x∈Z and x2 is even }={...,−6,−4,−2,0,2,4,6,...}
Clearly, B is an infinite set.
(iii) C={x:x∈Z and x2=36}={6,-6} ( As the square root of 36 is 6 , -6)
Clearly, C is a finite set.
(iv) D={x:x∈Z and x>−10}={-9,-8,-7,...}
Clearly, D is an infinite set.
Venn Diagrams
Relationships between sets can be represented by means of diagrams which are known as Venn diagrams. In Venn diagrams, the elements of the sets are written in their respective circles.
In below figure U={1,2,3,...,10} is the universal set of which A={2,4,6,8,10} and B={4,6} are subsets, and also B⊂A.

Equal Sets
So guys equal sets ka matlab hai aise sets jinme equal number of elements ho means unki cardinality same ho and sath he sath unka har ek element equal or same ho no matter unki position kya hai. Mathematically Two sets A and B are said to be equal if they have exactly the same elements, and we write A=B. Otherwise, the sets are said to be unequal, and we write A≠B.
Let A={1,2,3,4,5} and B={3,5,2,4,1} then A and B are equal set since all elements of A lies in B and all elements of B lies in A.
Operations on Sets
Like addition, subtraction, multiplication and division on numbers are basic operations we have union, intersection, and difference of set as basic operation on sets.
Union of sets : Let A and B be any two sets. The union of A and B is the set which consists of all the elements of A and all the elements of B, the common elements being taken only once. The symbol ‘∪’ is used to denote the union. Symbolically, we write A ∪ B and usually read as ‘A union B’. For example, A={1,2,3,4,5} and B={3,4,5,6,7}, here we have 1,2,3,4,5 in A and 3,4,5,6,7 in B and 3,4,5 common in both so, A∪B={1,2,3,4,5,6,7} taking all element of A and B but taking common element only once.
In symbols, we write.
A∪B={x:x∈Aorx∈B}
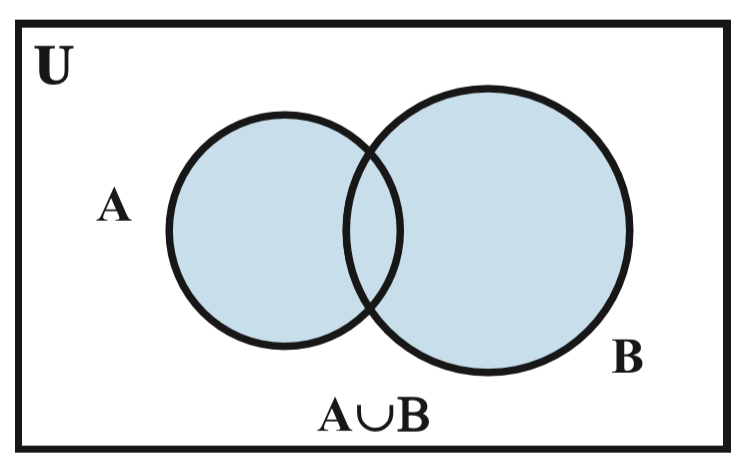
Some Properties of the Operation of Union:
(i) A∪B=B∪A (Commutative law)
(ii) (A∪B)∪C=A∪(B∪C) (Associative law)
(iii) A∪ϕ=A ( Law of identity element, ϕ is the identity of ∪)
(iv) A∪A=A (Idempotent law)
(v) U∪A=U (Law of U)
Intersection of sets: The intersection of sets A and B is the set of all elements which are common to both A and B. The symbol ∩ is used to denote the intersection. The intersection of two sets A and B is the set of all those elements which belong to both A and B. Symbolically, we write A∩B={x:x∈Aandx∈B}. For example, A={1,2,3,4,5}andB={3,4,5,6,7}, we have 3,4,5 in both set common to A∩B={3,4,5}

Some Properties of Operation of Intersection:
(i) A∩B=B∩ (Commutative law)
(ii) (A∩B)∩C=A∩(B∩C) (Associative law)
(iii) ϕ∩A=ϕ, U∩A=A ( Law of ϕ and U)
(iv) A∩A=A (Idempotent law)
(v) A∩(B∪C)=(A∩B)∪(A∩C) (Distributive law ) i.e., ∩ distributes over ∪
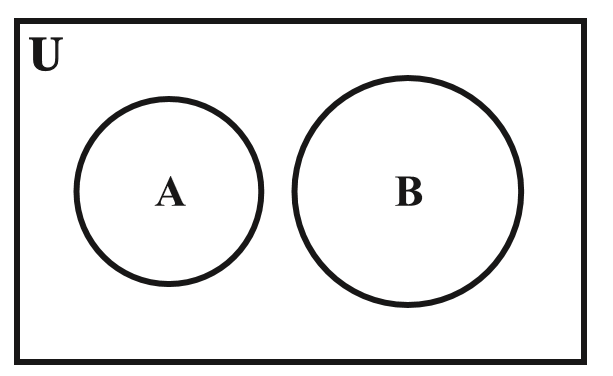
Disjoint set : If A and B are two sets such that A∩B=φ, then A and B are called disjoint sets. For example, let A={2,4,6,8} and B={1,3,5,7}. Then A and B are disjoint sets, because there are no elements which are common to A and B.
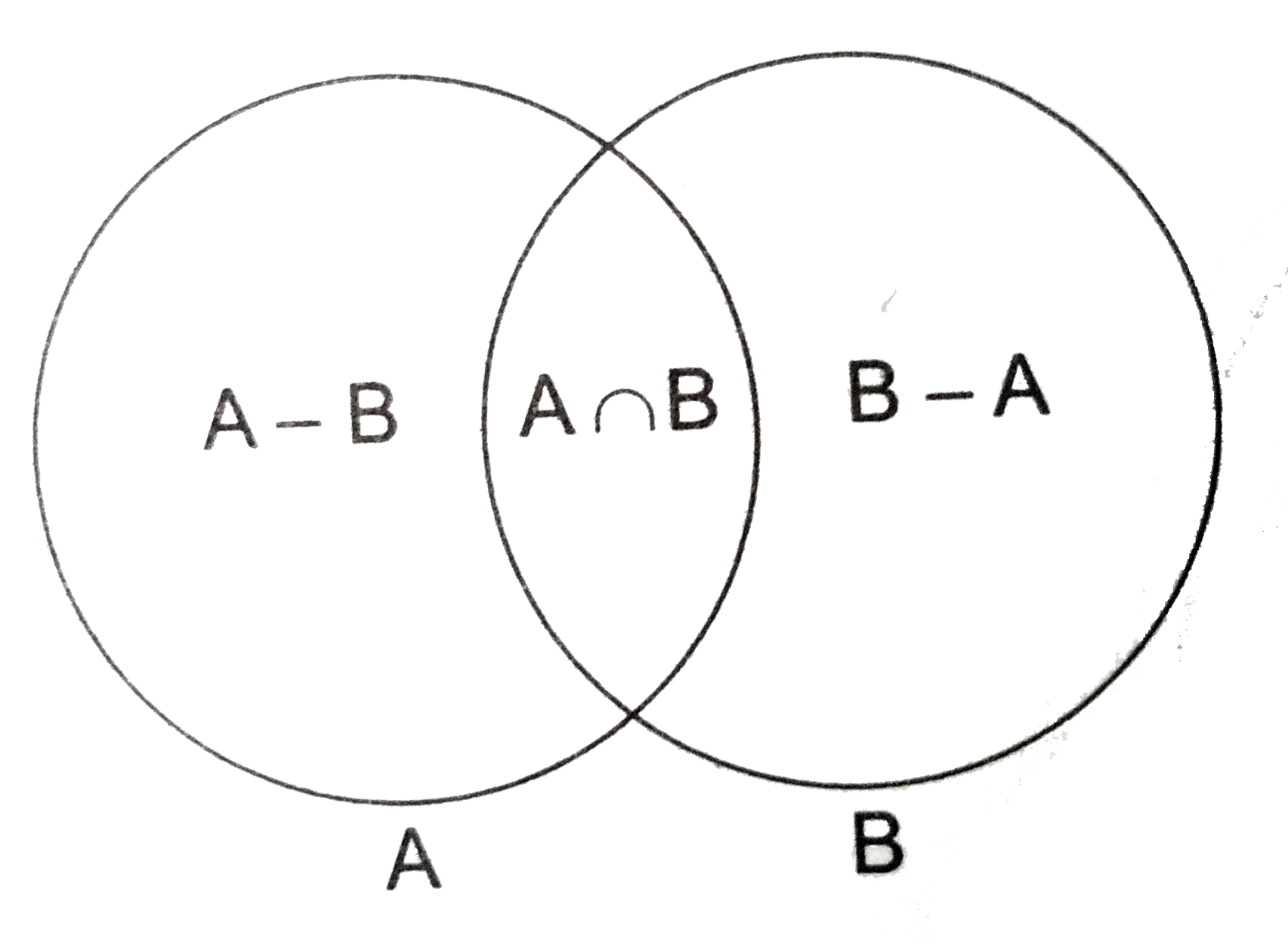
Difference of set: The difference of the sets A and B in this order is the set of elements which belong to A but not to B. Symbolically, we write A–B and read as A minus B. For example, A={1,2,3,4,5} and B={3,4,5,6,7}, here we have 1,2 element only in A so A−B={1,2} and 6,7 element only in B so B−A={6,7}.
Note :→ The sets A–B,A∩BandB–A are mutually disjoint sets, i.e., the intersection of any of these two sets is the null set. Some property are: A−B=A∩B'

Some example of venn diagram for union and intersection of three sets: 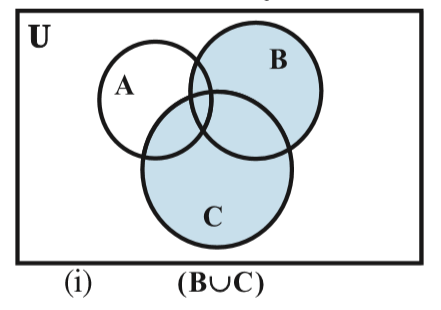
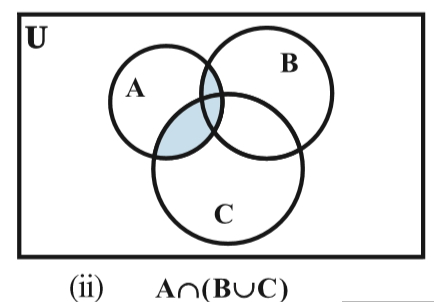
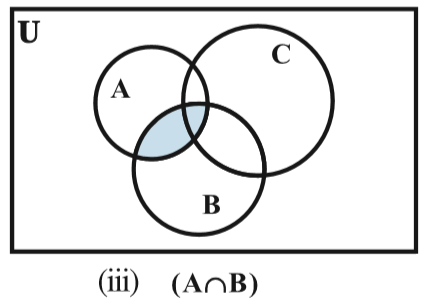
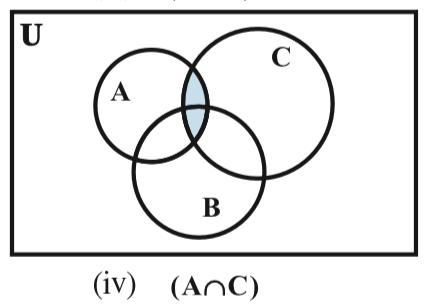
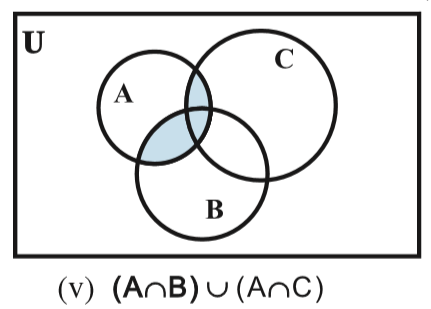
Example 5
Which of the following pairs of sets are equal? Justify your answer.
(i) A={x:x is a letter in the word LOYAL}, B={x:x is a letter of the word ALLOY}
(ii) A={x:x∈Z and x2≤8}, B={x:x∈R and x2−4x+3=0}
(i) Guys pehle hum isko roaster form me likhnge , so we have, A={L,O,Y,A,L}={L,O,Y,A} and B={A,L,L,O,Y}={L,O,Y,A}(As in sets elements can not repeat)
Now you see both sets have 4 elements and each element ( L, O, Y ,A,) of set A is same as ( A, L, O , Y)of set B
Clearly, A=B
(ii) So guys set A has all integers whose square is less than of equal to 8 , so we get
A={x:x∈Z and x2≤8}={−2,−1,0,1,2}
and in set B we will put all real numbers which are the solution of x2−4x+3=0
we get , B={x:x∈R and x2−4x+3=0}={1,3}.
We observe that 0∈A but 0∉B. So, A≠B.
Complement of a Set
Let U be the universal set and A be a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A. Symbolically, we write A′ to denote the complement of A with respect to U. Thus, A′ = {x : x ∈ U and x ∉ A }. Obviously A′ = U – A. If we see meaning A means all element which are not in set A but are present in universal set.
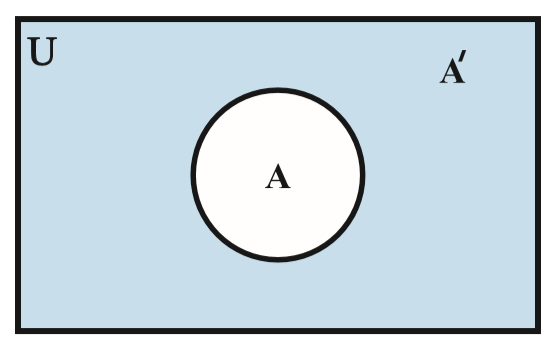
Some Properties of Complement Sets
1. Complement laws :
(i)A∪A'=U
(ii)A∩A'=ϕ
2. De Morgan's law :
(i)(A∪B)'=A'∩B'
(ii)(A∩B)'=A'∪B'
3. Law of double complementation : (A')'=A
4. Laws of empty set and universal set : ϕ'=U and U'=ϕ
This laws can be verified by using Venn diagrams.
Subsets
Guys Subset means part of a set , for example , you , your teachers , principal, peons all are part of your school , so we can say they all are subset of your school. Now let's understand it mathematically, A set A is said to be a subset of a set B if every element of A is also an element of B.
Let A={1,4,5} and B={1,2,3,4,5}, we can notice all elements of A i.e. 1,4,5 all are in B therefore, A is subset of B and represented by A⊂B. But few elements of B i.e. 2,3 are not in A therefore, B is not subset of A.
If A is subset of B and B is subset of A then we call them equal set.
Sometime subset is also represented by A⊂B if a∈A⇒a∈B which mean A will be subset of B if any element belongs to A also belongs to B.
Let A and B be two sets. If A⊂B and A≠B, then A is called a proper subset of B and B is called superset of A. For example discuss above A is proper subset and B is super set because A is subset of B and A is not equal to B.
Subsets of set of real number
Guys we know that the set of whole numbers W = { 0, 1, 2...} contains all
natural numbers , so we can say N⊂Z, Moreover it is very simple to deduce that Subset of real numbers are set of Natural number(N), Integer(Z), Rational number(Q), Irrational number(Q'), Prime number, Odd number, Even number, Whole number(W), etc.
N⊂Z⊂Q, Q⊂R, Q'⊂R.
Intervals as subsets of R
Let a,b∈R and a<b. Then the set of real numbers {y:a<y<b} is called an open interval and is denoted by (a,b). All the points between a and b belong to the open interval (a,b) but a,b themselves do not belong to this interval.
The interval which contains the end points also is called closed interval and is denoted by [a,b]. Thus, [a,b]={x:a≤x≤b}
We may also have interval open at one side and closed at other i.e. [a,b)or(a,b].
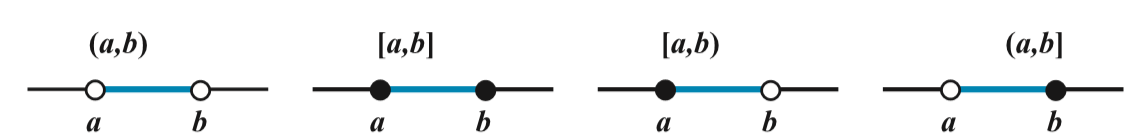
The number (b−a) is called the length of the intervals (a,b),[a,b],[a,b)or(a,b].
Note: 1. Every set is subset of itself.
2. Empty set is subset of every set.
If A and B are finite sets such that A ∩ B = φ, then
(i) n(A∪B)=n(A)+n(B)
(ii) n(A∪B)=n(A)+n(B)–n(A∩B)
(iii) n(A∪B∪C)=n(A)+n(B)+n(C)
–n(A∩B)–n(B∩C)–n(A∩C)+n(A∩B∩C)
(iv) n(A−B)=n(A)−n(A∩B)
(v) n(A△B) = n(A−B)+n(B−A)
=n(A)+n(B)−2n(A−B)
Example 6
Consider the following sets: ϕ, A={1,2}, B={1,4,8}, C={1,2,4,6,8}. Insert the correct symbol ⊂ or ⊄ between each of the following pair of sets:
(i)ϕ...B,(ii)A...B,(iii)A...C,(iv)B...C
(i) Since null set is subset of every set. Therefore, ϕ⊂B.
(ii) Clearly, 2∈A but 2∉B. So, A⊄B.
(iii) Since all elements of set A are in C and A≠C. So, A⊂C.
(iv) Clearly, all elements of set B are in set C and B≠C. So, B⊂C.
Example 7
Write the following subsets of R as intervals:
(i) {x:x∈R,−4<x≤6}
(ii) {x:x∈R,−12<x<−10}
(iii) {x:x∈R,0≤x<7}
(iv) {x:x∈R,3≤x<4}
Also, find the length of each interval .
(i) {x:x∈R,−4<x≤6}=(−4,6]. Length =6−(−4)=10
(ii) {x:x∈R,−12<x<−10}=(−12,−10). Length =−10−(−12)=2
(iii) {x:x∈R,0≤x<7}=[0,7). Length =7−0=7
(iv) {x:x∈R,3≤x≤4}=[3,4]. Length =4−3=1
Example 8
Write the following intervals in the set-builder form:
(i) (−7,0) (ii)[6,12] (iii) (6,12] (iv) [−20,3)
(i) (−7,0)={x:x∈R and −7<x<0}
(ii) [6,12]={x:x∈R and 6≤x≤12}
(iii) (6,12]={x:x∈R and 6<x≤12}
(iv) [−20,3)={x:x∈R and −20≤x<3}
Power set
So guys we have learnt about the subsets , now you are able to find all the subsets for a given set , so basically collect them all together along with ϕ (as ϕ is a subset of every set) is said to be the power set. Mathematically, The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set. For example, if A = {2,5}, then P(A)={ φ,{ 2 }, { 5 }, { 2,5 }} .
Note: If number of element of A is m then number of element of P(A) is 2m or n[P(A)]=2m.
Example 9
Write all the elements has P(A), if A={1,2,3}?
So for finding the power set of A we have write down all subsets of A , such that
ϕ , {1} , {2} , {3} , {1,2}, {2,3} , {1,3}, {1,2 , 3}
so , P(A) = { ϕ , {1} , {2} , {3} , {1,2}, {2,3} , {1,3}, {1,2 , 3}}
Universal Set
For all cases we always have one basic set which contain each and every element, this basic set is called the Universal Set. The universal set is usually denoted by U. Like we have universe it is also set we will take as universe for our question which contains all set.
Example 10
What universal set would you propose for each of the following :
(a) The set of right triangles
(b)The set of isosceles triangles
(a) So guys basically iss question me hume ek aise set ke baare me sochna hai jisme sare right angle contain ho jaaye.
So for the set of all right angles , set of triangles can be universal set as all right angles are special case of triangles.
(b)Same for the set of triangles or the set of polygons or set of triangles can work as the universal set for the set of all isosceles triangles.
Venn Diagrams
So guys we know ke diagrams ya pictures are more easy to analyse , so here we are going to draw some diagrams for sets which shows relationships between sets known as Venn diagrams. In Venn diagrams, the elements of the sets are written in their respective circles.
In below figure U={1,2,3,...,10} is the universal set of which A={2,4,6,8,10} and B={4,6} are subsets, and also B⊂A.

Example 11
For all sets A,BandC,checkA−(B−C)=(A−B)−C.
See the Venn diagrams given below.So we will first shade B- C , means we have to remove the common part between B and C from the set B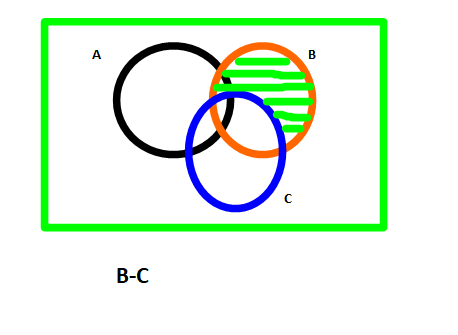
Now we will remove B-C from A that is: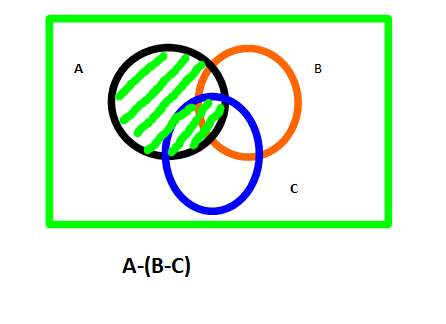
Now we will draw the right side ,(A - B) - C , as 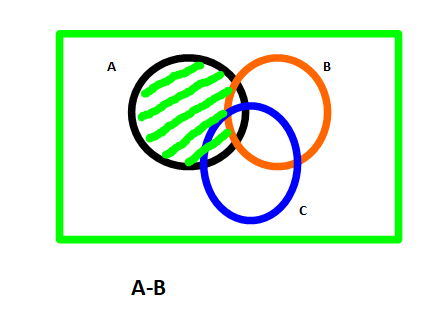
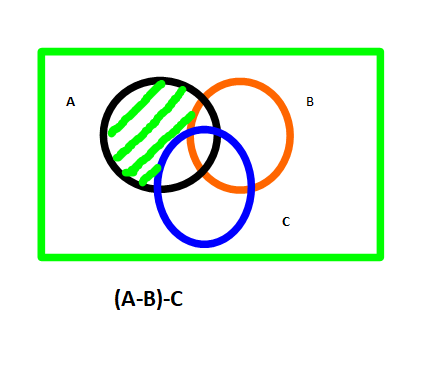
Clearly A−(B−C)≠(A−B)−C.
Hence, given statement is false.
Operations on Sets
Like addition, subtraction, multiplication and division on numbers are basic operations we have union, intersection, and difference of set as basic operation on sets.
Union of sets: This operation between set means collecting all elements of given sets , without repetition. Mathematically, Let A and B be any two sets. The union of A and B is the set which consists of all the elements of A and all the elements of B, the common elements being taken only once. The symbol ‘∪’ is used to denote the union. Symbolically, we write A∪B and usually read as ‘A union B’. For example, A={1,2,3,4,5} and B={3,4,5,6,7}, here we have 1,2,3,4,5 in A and 3,4,5,6,7 in B and 3,4,5 common in both so, A∪B={1,2,3,4,5,6,7} taking all element of A and B but taking common element only once.
In symbols, we write. A∪B={x:x∈Aorx∈B}

Some Properties of the Operation of Union:
(i) A∪B=B∪A (Commutative law)
(ii) (A∪B)∪C=A∪(B∪C) (Associative law)
(iii) A∪ϕ=A (Law of identity element, ϕ is the identity of ∪)
(iv) A∪A=A (Idempotent law)
(v) U∪A=U (Law of U)
Intersection of sets: The intersection of sets A and B is the set of all elements which are common to both A and B. The symbol ∩ is used to denote the intersection. The intersection of two sets A and B is the set of all those elements which belong to both A and B.
Symbolically, we write A∩B={x:x∈Aandx∈B}. For example, A={1,2,3,4,5}andB={3,4,5,6,7}, we have 3,4,5 in both set common to A∩B={3,4,5}

Some Properties of Operation of Intersection:
(i) A∩B=B∩ (Commutative law)
(ii) (A∩B)∩C=A∩(B∩C) (Associative law)
(iii) ϕ∩A=ϕ, U∩A=A (Law of ϕ and U)
(iv) A∩A=A (Idempotent law)
(v) A∩(B∪C)=(A∩B)∪(A∩C) (Distributive law) i.e., ∩ distributes over ∪
If A and B are two sets such that A∩B=ϕ, then A and B are called disjoint sets. For example, let A={2,4,6,8} and B={1,3,5,7}. Then A and B are disjoint sets, because there are no elements which are common to A and B.

. Difference of set: The difference of the sets A and B in this order is the set of elements which belong to A but not to B.
Symbolically, we write A–B and read as A minus B. For example, A={1,2,3,4,5} and B={3,4,5,6,7}, here we have 1,2 element only in A so A−B={1,2} and 6,7 element only in B so B−A={6,7}.
NOTE: The sets A–B,A∩BandB–A are mutually disjoint sets, i.e., the intersection of these two sets is the null set. Some properties are: A−B=A∩B'

Some example of venn diagram for union and intersection of three sets: 




Example 12
Let A={a,e,i,o,u} and B={a,i,u}. Show that A∪B=A.
As we have to find union of A and B so we will collect all elements of A nd B (remember no repetition of elements)
so , A∪B={a,e,i,o,u}
∴A∪B=A.
Note: if B⊂A, then A∪B=A.
Example 13
Let A={1,2,3,4,5,6,7,8,9,10} and B={2,3,5,7}. Find A∩B and hence show that A∩B=B.
So here we are going to choose only common elements in set A and B
so, A∩B={2,3,5,7}
∴A∩B=B.
Note: if B⊂A and that A∩B=B.
Example 14
Let A={1,2,3,4,5,6}, B={2,4,6,8}. Find A–B and B–A.
Guys A - B will contain only those elements which are in set A and not in B , means we will remove all common elements in set A and B from set A,
So, we have, A–B={1,3,5}, since the elements 1,3,5 belong to A but not to B and B–A={8}, since the element 8 belongs to B and not to A.
Note: A–B≠B–A.
Complement of Sets
Let U be the universal set and A a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A. Symbolically, we write A' to denote the complement of A with respect to U. Thus, A'={x:x∈U and x∉A}. Obviously A'=U–A. If we see meaning A' means all element which are not in set A but are present in universal set U.

Some Properties of Complement Set
1. Complement laws: (i) A∪A'=U (ii)A∩A'=ϕ
2. De Morgan's law: (i) (A∪B)'=A'∩B'(ii)(A∩B)'=A'∪B'
3. Law of double complementation : (A')'=A
4. Laws of empty set and universal set: ϕ'=U and U'=ϕ
These laws can be verified by using Venn diagrams.
Example 15
Let U be universal set of all the students of Class XI of a coeducational school and A be the set of all girls in Class XI. Find A'.
Since A is the set of all girls, A' = U- A = set of all the students of Class XI - set of all girls in Class XI
So A' is clearly the set of all boys in the class.
Practical Problems on Union and Intersection of Two Sets
So guys abi tak humne sets ke union , intersection , complement ke baare me baat ki , now we are going to deal with some practical problems which will give us an idea how this can help us in finding solution of many daily life problems . For this we will use the following formulas:
(i) Let A and B be finite sets. If A∩B=ϕ, then n (A∪B) = n ( A ) + n ( B )
(ii) If A and B are finite sets and A∩B≠ϕ, then
n(A∪B)=n(A)+n(B)–n(A∩B)
(iii) If A, B and C are finite sets, then
n(A∪B∪C)=n(A)+n(B)+n(C)–n(A∩B)–n(B∩C)–n(A∩C)+n(A∩B∩C)
Example 16
In a school there are 20 teachers who teach mathematics or physics. Of these, 12 teach mathematics and 4 teach both physics and mathematics. How many teach physics ?
Let M denote the set of teachers who teach mathematics and P denote the set of teachers who teach physics. In the statement of the problem, the word ‘or’ gives us a clue of union and the word ‘and’ gives us a clue of intersection. Therefore, we have n(M∪P)=20 , n(M)=12 and n(M∩P)=4 We wish to determine n(P). Using the result n(M∪P)=n(M)+n(P)–n(M∩P), we obtain 20=12+n(P)–4
Thus n(P)=12
Hence 12 teachers teach physics.
Example 17
In a group of 52 persons, 16 drinks tea but not coffee and 33 drink tea.
Find (i) how many drink tea and coffee both,
(ii) how many drink coffee but not tea.
Let A= set of persons who drink tea and B= set of persons who drink coffee.
Then, (A−B)= set of persons who drink tea but not coffee.
And, (B−A)= Set of persons who drink coffee but not tea.
Given n(A∪B)=52,n(A−B)=16andn(A)=33.
(i) Set of persons who drinks tea and coffee both =(A∩B).
Now, n(A−B)+n(A∩B)=n(A)
⇒n(A∩B)=n(A)−n(A−B)=(33−16)=17.
Thus, 17 persons drink tea and coffee both.
(ii) n(A∪B)=n(A)+n(B)−n(A∩B)
⇒n(B)=n(A∪B)+n(A∩B)−n(A)=(52+17−33)=36.
Now, n(B−A)+n(A∩B)=n(B).
⇒n(B−A)=n(B)−n(A∩B)=(36−17)=19.
Thus, numbers of persons who drink coffee but not tea=19.
Summary
Here are some key points of this chapter:
1.A set is a well-defined collection of objects.
2.A set which does not contain any element is called empty set.
3.A set which consists of a definite number of elements is called finite set,
otherwise, the set is called infinite set.
4.Two sets A and B are said to be equal if they have exactly the same elements.
5.A set A is said to be subset of a set B, if every element of A is also an element
of B. Intervals are subsets of R.
6.A power set of a set A is collection of all subsets of A. It is denoted by P(A).
7.The union of two sets A and B is the set of all those elements which are either
in A or in B.
8.The intersection of two sets A and B is the set of all elements which are
common. The difference of two sets A and B in this order is the set of elements
which belong to A but not to B.
9.The complement of a subset A of universal set U is the set of all elements of U
which are not the elements of A.
10.For any two sets A and B, (A ∪ B)′ = A′ ∩ B′ and ( A ∩ B )′ = A′ ∪ B′
11.If A and B are finite sets such that A ∩ B = φ, then
n (A ∪ B) = n (A) + n (B).
If A ∩ B ≠ φ, then
n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
Let's Revise
Sets: Distinct object ke well defined (means jaha koi particular rule follow kiya ja raha ho ) ko sets kehte hai.A set is always represented using capital letter and its members or elements are represented using small letters. All elements are kept in {} separated by using comma.
For eg. Set of vowels can be represented as: A = { a, e, i , o, u}
Representation of Set:
Sets ko 2 forms me represent kiya ja sakta hai
Roster or Tabular form- In the roster form , jaha sets ke saare members ko braces { } ke andar commas se seprate karke likhte hai.
Ex. N = { 1, 2, 3,, 4} is the roaster form of the set of natural number less than 5
Set-builder form- In the set-builder form, jaha set ko belong karne wale elements ki property mention karte hai.
Ex. N = {x: x is a natural number less than 5} is the set builder form of the above set.
Types of Sets :
Empty Sets: A set which does not contain any element is called an empty set or the void set or null set and it is denoted by {} or ϕ.
Singleton Set: A set consists of a single element, is called a singleton set.
Finite and infinite Set: A set which consists of a finite number of elements, is called a finite set, otherwise the set is called an infinite set.
Equal Sets: Two sets A and B are said to be equal, if every element of A is also an element of B or vice-versa, i.e. two equal sets will have exactly the same element.
Equivalent Sets: Two finite sets A and B are said to be equal if the number of elements are equal, i.e. n(A) = n(B)
Subset: Any part of set is called subset of that set.Let A = {1, 2, 3} & B = { 1, 2, 3 , 5 ,6 } be any two sets than we can clearly see that all elements of set A are in set B , so we can say set A is a subset of set B. Symbolically it is represented as A⊂B.
Total number of subset of any set having n elements : 2n
Note: ϕ is the subset of every set.
Each set is a subset of itself
Power Set:
Kisi bhi set ke saare subsets ko agar collect karke ek naya set banaoge toh us set ko Power set kahenge. Let A be any set having n elements then its power set will be represented as P(A) and it will have 2n elements in it.
Intervals as Subsets of R: Intervals ka matlab hai subset or part of the real line.
Let a and b be two given real numbers such that a<b, then
(i) an open interval denoted by (a, b) is the set of real numbers {x : a<x<b}.
(ii)
a closed interval denoted by [a, b] is the set of real numbers {x : a≤x≤b}.
(iii)intervals closed at one end and open at the others are known as semi-open or semi-closed interval and denoted by (a, b] is the set of real numbers {x : a<x≤b} or [a, b) is the set of real numbers {x : a≤x<b}.
Universal Set:
A set that contains all sets in a given context is called the universal set.
Venn-Diagrams: Aise diagrams jo sets ke relation ya connection ko represent karte hai, unhe venn diagram kehte hai. In Venn-diagrams the universal set U is represented by point within a rectangle and its subsets are represented by points in closed curves (usually circles) within the rectangle.
Operations of Sets:
Union of sets- kisi bhi set ka union nikalne ke liye we have to collab all elements of those sets without repeating them.
For eg. Let A = {a, b, c} & B = { x, y, c} , then A∪B={a,b,c,x,y}
Intersection of set-Intersection means to write down common elements of the given sets.
For eg : Let A = {a, b, c} & B = { x, y, c} , then A∩B={c}
Disjoint sets- Two sets A and Bare said to be disjoint, if they have nothing in common or A∩B=ϕ.
Difference of sets- For any sets A and B, their difference (A – B) is defined as a set of elements, which belong to A but not to B.
Complement of a set- Let U be the universal set and A is a subset of U. Then, the complement of A is the set of all elements of U which are not the element of A. Thus, A’ = U – A = {x : x∈U and x∉A}
Some Properties of Complement of Sets:
(i) A∪ A’ = ∪
(ii)
A ∩ A’ = ϕ
(iii)
∪' = ϕ
(iv)
ϕ’ = ∪
(v)
(A’)’ = A
Symmetric difference of two sets: For any set A and B, their symmetric difference is defined as the union of (A – B) & (B – A)or the elements which do not belong to both A and B. It is denoted by AΔB.
Laws of Algebra of Sets:
Idempotent Laws- For any set A, we have
(i) A∪A= A
(ii)A∩A = A
Identity Laws- For any set A, we have
(i)
A∪ϕ = A
(ii)
A∩U = A
Commutative Laws- For any two sets A and B, we have
(i)
A∪B=B∪A
(ii)
A∩B=B∩A
Associative Laws-For any three sets A, B and C, we have
(i)
A∪(B∪C)=(A∪B)∪C
(ii)
A∩(B∩C)=(A∩B)∩C
Distributive Laws- If A, B and Care three sets, then
(i) A∪(B∩C)=(A∪B)∩(A∪C)
(ii) A∩(B∪C)=(A∩B)∪(A∩C)
De-Morgan’s Laws- If A and B are two sets, then
(i)
(A∪B)’=A’∩B’
(ii)(A∩B)’=A’∪B’
Formulae to Solve Practical Problems on Union and Intersection of Two Sets:
Let A, B and C be any three finite sets, then
(i) If A∩B=ϕ, then n (A∪B) = n ( A ) + n ( B )
(ii) If A and B are finite sets and A∩B≠ϕ, then
n(A∪B)=n(A)+n(B)–n(A∩B)
(iii) If A, B and C are finite sets, then
n(A∪B∪C)=n(A)+n(B)+n(C)–n(A∩B)–n(B∩C)–n(A∩C)+n(A∩B∩C)