LIMITS AND DERIVATIVES for Class 11 MATHS
INTRODUCTION
Hello bachcho, iss chapter mai calculus ka introduction hume dekhne ko milega. Limits and derivatives se hi basically calculus ki starting hoti hai. Calculus maths mai kafi sari cheejo ke saath deal karta hai jaise ki rate of changes, for example : the speed of a falling object .

Jaise ki koi ek functiom hai y=f(x). Toh isme hum ye pta karne ki koshish karte hai ki f(x) mai change hone se y mai kya change aaya hai. Toh sabse pehle iss chapter mai hum aapko derivative ke barein mai proper idea denge (but without actually defining it). After this, hum aapko limit ki ek naive yani simple si definition batayenge aur algebra of limits ko bhi study karenge. Iske baad hum apni derivative ki definition par wapas jayenge aur kuch algebra of derivatives ko bhi study karenge. We also obtain derivatives of certain
standard functions.
Limits and derivatives bahot hi wide range wale topic hai ye sirf maths mai hi nahi balki other subjects mai bhi use hote hai jaise ki physics . We will cover the important formulas, properties and examples questions to understand the concept of limits as well as derivatives in detail.

LIMITS AND DERIVATIVES
A limit is the value that a function approaches as the input approaches some value.
The derivative is defined as the instantaneous rate of change, or slope, at a specific point of a function.
Explanation
Limits and Derivatives ye concept 11th class mai widely explain kiya gya hai ishe aap 12th and higher studies mai bhi pahoge. Issac newton ne apne rate and changes wale concept se hi calculus ko define kiya hai. Toh abh hum aage padhenge ki hum calculus ka use kese aur kaha kar sakte hai.
Intuitive Idea of Derivatives
Physical experiment ke through confirm hua hai ki jab koi body tall building ya cliff se fall hoti hai to woh 4.9t2 meters distance cover karte hai in t seconds.
Distance s in metres covered by the body as a function of time t in seconds is given by s=4.9t2.
Neeche di gayi table se hum velocity find out karna sikhenge.
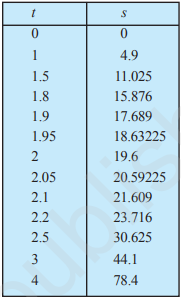
The objective is to find the veloctiy of the body at time t=2 seconds from this data. Iss problem ko solve karne ke liye hume average velocity pata honi chahiye. Average velocity hume t=t1 and t=t2 ke beech mai milegi. And time interval will get by this (t2−t1).
= Distance travelled between(t2=2)and(t1=0)Time interval(t2−t1)
= (19.6−0)m(2−0)s
= 9.8 m/s
Similarly, the average velocity between t=1 and t=2 is
(19.6−4.9)m(2−0)s
=14.7m/s
Likewise we compute the average velocity between t=t1 and t=2 for various t1.
Example 1
Evaluate limx→0{√1+x−√1−xx}.
We have,
limx→0{√1+x−√1−xx}=limx→0{(√1+x−√1−x)x.(√1+x+√1−x)(√1+x+√1−x)}
=limx→0{(1+x)−(1−x)}x(√1+x+√1−x)
=limx→02xx(√1+x+√1−x)
=limx→02(√1+x+√1−x)=1 [puttingx=0].
Example 2
Evalute limx→1x15−1x10−1
limx→1x15−1x10−1=limx→1{(x15−1x−1)÷(x10−1x−1)}
=limx→1(x15−1x−1)÷limx→1(x10−1x−1)
⇒(15×1014)÷(10×19)=1510=32.
Limits
Hum abhi kuch examples dekhenge jisse hume limit ko samjhane mai aasani hogi. Kya aapko rectangle ka area nikalna aata hai?
Yes ofcourse aata hai because aap logo ne ishe kafi baar apni pichli classes mai bhi padha hai.
Toh yaha to humne line shape ki figure (rectangle) ki baat kari hai. Abh baat karte hai circular image (circle) ki. Kya aapko iska area find out karna aata hai?
Toh answer is yes .
Aap soch rahe honge ki aapse ye basic question kyu kiye ja rahe hai?
Toh chaliye iske peeche ka reason jante hai. Bahot time pehle bahot sare mathematician ko circular shape figures ka area findout karne mai problem hoti thi. Toh unhone kafi koshish karne ke baad kuch solution nikale. Toh unke solution ko ek activity ke through samajhte hain. Toh sabse pehle hum ek circle ko 8 parts mai divide karke usko firse rearrange karte hai toh wo kuch dikhne mai neeche di gyi image ki tarah dikhega.
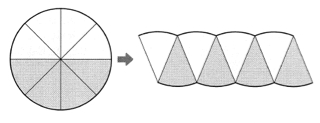
Toh abh imagine kijiye ki humne uss circle ko infinite parts mai divide kiya hai ishe hum sirf imagine kar sakte hai kyuki yeh manually possible nahi hai. Jab hum circle ko infinite parts mai divide karke aur fir ushe rearrange karenge to wo ek rectangle ki shape mai aa jayega. Aapko neeche di gyi image se zyada acha samajh aayega.
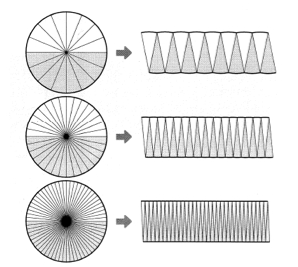
Jaisa ki humne pehle dekha hai ki lines wali figuire ka area hum easily nikaal sakte hai toh abh iss circle ne bhi line wali shape le li hai toh hamari ye problem bhi solve ho gyi. Toh jab hum imagine karke infinity wali problem ko solve kar sakte hai to hum limits ka use karke division by zero wali problem ko bhi solve kar sakte hai. Aap jante honge ki 10= Not define hota hai aur 01=0 hota hai. But hume 00=? ki value nahi pta to ishi problem ko solve karne ke liye hum limit ka use karte hain.
Limit is used when we have to find value of a function near to some value (Neighbourhood).
Neighbourhood is the key to remember the concept of limit. For example, hum ek function lete hai :-
f(x)=x+3
Jaise jaise x ki value change hogi waise waise f(x) ki value change hogi.
Jaise humne liya x=3 to f(3)=3+3=6 hoga. Lekin jab hum limit ki baat karte hai to hume ye nahi chhahiye. Jab x ki value 3 ke aaspaas ho yani neighborhood mai ho to hume uss function ki value chhahiye.
Limits two types ki hoti hai :-
(a) Left hand limit
(b) Right hand limit
limx→3x+3
Yaha par x→3 ka matlab x=3 nahi hai. Iska matlab hai ki x is approaching to 3, yani x excced ho raha hai 3 ki taraf. Jab bhi hume domain ke kisi value ke neighbourhood mai kisi function ki value chhahiye to hum number line ka use karte hai.
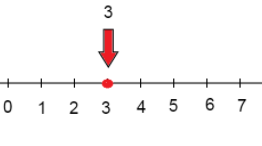
Hamare paas two limit hai to hum dono se hi value nikalenge.
Hum left hand limit ko kuch aise show karte hai L.H.L= limx→3−x+3
Agar hum left hand limit se value lete hai toh wo left side se shuru honge jaise ki 2,2.5,2.9,....
Right hand limit ko hum R.H.L=limx→3+x+3 aise show karte hai.
Agar hum right hand limit se value lete hai toh wo right side se shuru honge jaise ki 4.3.9,3.5,......
Let's understand this by an example.
Consider the function f(x)=3x. Let us try to find the limit of this function at x=2.

Jaisa ki hum pehle dekh chuke hi ki x is approaches 2 fir chhahe wo left ho ya right. The value of f(x) seem to approach 6.
limx→2−f(x)=limx→2+f(x)=limx→2f(x)=6
Aap graph mai bhi ye fact dekh sakte ho.
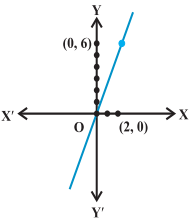
Here again we note that the value of the function at x=2 coincides with the limit at x=2.
Algebra of limits
We have observed that the limiting process respects addition, subtraction, multiplication and division as long as the limits and functions under consideration are well defined. We formalize these as a theorem without proof.
Theorem 1
Let f and g be two functions such that both limx→af(x) and limx→ag(x) exist.
(i) Limit of sum of two functions is sum of the limits of the functions, i.e.,
limx→a[f(x)+g(x)]=limx→af(x)+g(x).
(ii) Limit of difference of two functions is difference of the limits of the functions, i.e.,
limx→a[f(x)−g(x)]=limx→af(x)−g(x).
(iii) Limit of product of two functions is product of the limits of the functions, i.e.,
limx→a[f(x).g(x)]=limx→af(x).g(x).
(iv) Limit of quotient of two functions is quotient of the limits of the functions (whenever the denominator is non zero), i.e.,
limx→af(x)g(x)=limx→af(x)limx→af(x)
Theorem 2
For any positive integer n,
limx→axn−anx−a=nan−1
Proof : Dividing (xn−an) by (x−a), we see that
(xn−an)=(x−a)(xn−1+xn−2a+xn−3a2+....+xan−2+an−1)
Thus, limx→axn−anx−a=limx→a (x−a)(xn−1+xn−2a+xn−3a2+....+xan−2+an−1)
=an−1+a an−2+....+an−2(a)+an−1
=an−1+an−1+...+an−1+an−1 ( n terms)
=nan−1.
Example 3
Evaluate limx→a(xm−amxn−an).
limx→a(xm−amxn−an)=limx→a{(xm−amx−a)÷(xn−anx−a)}
=limx→a(xm−amx−a)÷limx→a(xn−a2x−a)
=(mam−1)(nan−1)
=mam−1nan−1=mnam−n.
Example 4
limx→1(2x−3)(√x−1)2x2+x−3
limx→1(2x−3)(√x−1)(2x2+x−3)=limx→1(2x−3)(√x−1)(2x+3)(x−1)
=limx→1(2x−3)(√x−1)(√x+1)(2x+3)(x−1)(√x+1)
=limx→1(2x−3)(x−1)(2x+3)(x−1)(√x+1)
=limx→1(2x−3)(2x+3)(√x+1)=(2×11−3)(2×1+3)(√1+1)=−110.
Limits of Trigonometric Functions
Hum aage janege ki kis tarah hum trigonometric functions ki limit ko findout kar sakte hai. Iske liye aapko kuch formulas dekhne honge.
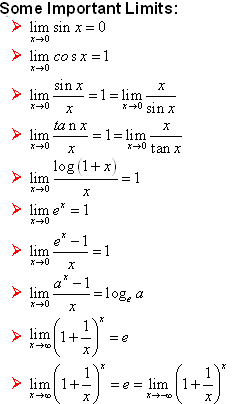
Abh hum kuch theorem dekhenge.
Theorem 3
Let f and g be two real valued functions with the same domain such that f(x)≤g(x) for all x in the domain of definition, For some a, if both limx→af(x) and limx→ag(x) exist, then limx→af(x)≤limx→ag(x).
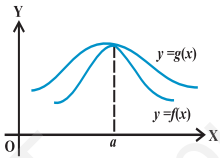
This is illustrated in given figure.
Theorem 4
Let f,g and h be real functions such that f(x)≤g(x)≤h(x) for all x in the common domain of definition. For some real number a, if limx→af(x)=l=limx→ah(x), then limx→ag(x)=l
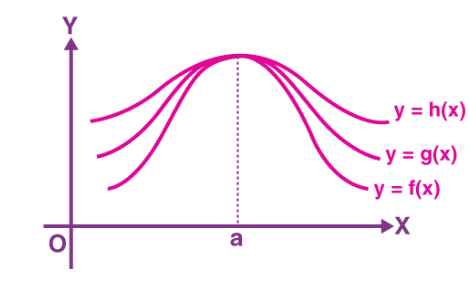
Proof : We know that sin(–x)=–sinx and cos(–x)=cosx. Hence, it is sufficient to prove the inequality for 0<x<π2.
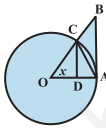
O is the centre of the unit circle such that the angle AOC is x radians and 0<x<π2.
Line segments BA and
CD are perpendiculars to OA. Further, join AC.
Then,
Area of ΔOAC< Area of sector OAC< Area of ΔOAB.
i.e., 12OA.CD<x2π<.π.(OA)2<12OA.OB.
i.e., CD<x.OA<AB.
FromΔOCD,
sinx=CDOA (Since OC=OA) and hence CD=OAsinx. Also tanx=ABOA and
hence,
AB=OA.tanx. Thus, OAsinx<OA.x<OA.tanx
Since length OA is positive, we have
sinx<x<tanx.
Since0<x<π2, sinx is positive and thus by dividing throughout by sinx, we have
1<xsinx<1cosx. Taking reciprocals throughout, we have
cosx<sinxx<1
which complete the proof.
Example 5
Example 6
Evaluate: limx→π4sinx−cosxx−π4
limx→π4sinx−cosxx−π400
limx−π4→0√2[sinx.cos(π)4−cosx.sin(π)4](x−π4)
=limx−π4→0√2.sin(x−π4)x−π4
=√2×1=√2.
Derivatives
Derivative is the rate of change of a function with respect to a variable.
Derivatives
Derivative is about how fast something is changing? Yeh topic aapko 12th class and apni higher classes mai bhi dekhne ko milega yeh topic bahot hi zyada important hai. Board exams mai iski kafi weightage hai ye calculus ka base hai isko padhne ke baad hi aap next step par pahuch sakte ho.
A derivative corresponds, in comparison to the other, to the instantaneous rate of change of a quantity. This helps to explore the moment by moment essence of a quantity. A function's derivative is expressed in the formula given below.
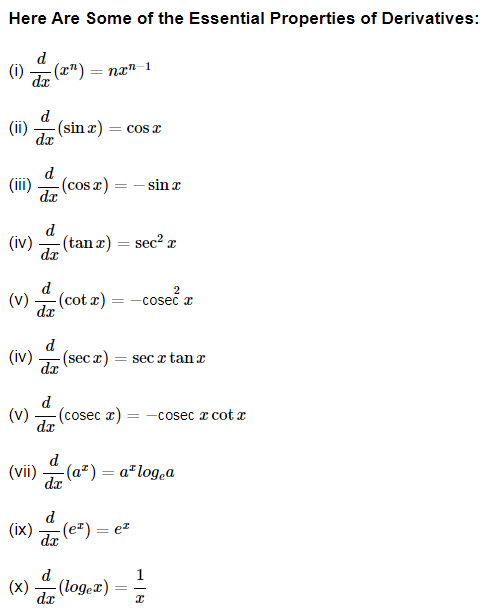
Abh hum first principle of derivative ko padhenge.
Derivative ek change hota hai. Hum ek function lete hai.
y=f(x)=x2
Jab hum x mai change karenge to y mai kya change hoga.
change in(y)change in(x) = limx→0f(x+h)−f(x)h
Uses of Derivatives

Theorem 5
Let f and g be two functions such that their derivatives are defined in a common domain.
Proof : (i) Derivative of sum of two functions is sum of the derivatives of the
functions.
ddx[f(x)+g(x)]=ddxf(x)+ddxg(x).
(ii) Derivative of difference of two functions is difference of the derivatives of
the functions.
ddx[f(x)−g(x)]=ddxf(x)−ddxg(x).
(iii) Derivative of product of two functions is given by the following product
rule.
ddx[f(x).g(x)]=ddxf(x).g(x)+f(x).ddxg(x). (iv) Derivative of quotient of two functions is given by the following quotient
rule (whenever the denominator is non–zero).
ddx(f(x)g(x))=ddxf(x).g(x)−f(x)ddxg(x)(g(x))2
Theorem 6
Derivative of f(x)=xn is nxn–1 for any positive integer n.
Proof : By definition of the derivative function, we have
f'(x)=limh→0f(x+h)−f(x)h=limh→0(x+h)n−xnh
By Binomial theorem,
hence (x+h)n−xn = h(nxn−1+......+hn−1)
df(x)dx = limh→0(x+h)n−xnh
=limh→0h(nxn−1+......+hn−1)h
=limh→0(nxn−1+......+hn−1)
=nxn−1.
Example 7
Find the derivative of cos x from first principle.
Let f(x)=cosx
⇒f(x+h)=cos(x+h)
∴f(x)=limh→0f(x+h)−f(x)h
=limh→0cos(x+h)−cosxh
=limh→0−2sin(x+h2)sin(h)22×h2
=−sinx
Example 8
Find the derivative of xn−anx−a for some constant a.
Let y=xn−anx−a
⇒dydx=ddx(xn−anx−a)
=(xa)ddx(xn−an)−(xn−an)ddx(x−d)(x−a)2
=(x−a)(nxn−1−0)−(xn−an)ddx(x−a)(x−a)2
=(x−a)(nxn−1−0)−(xn−an)(1−0)(x−a)2
=nxn−anxn−1−xn+an(x−a)2
Summary
In this chapter, we have studied the following points :-
- The expected value of the function as dictated by the points to the left of a point defines the left hand limit of the function at that point. Similarly the right hand limit.
- Limit of a function at a point is the common value of the left and right handlimits, if they coincide.
- For a function f and a real number a limx→a f(x) and f(a) may not be same ((In fact, one may be defined and not the other one).
- For functions f and g the following holds :
limx→a [f(x)±g(x)]= limx→af(x)±limx→ag(x)
limx→a [f(x).g(x)]= limx→af(x).limx→ag(x)
limx→a[f(x)g(x)]=limx→af(x)limx→ag(x) - Following are some of the standard limits :-
limx→axn−anx−a=nan−1
limx→0sinxx=1
limx→01−cosxx=0 - The derivative of a function f at a is defined by
f'(a)=limh→0f(a+h)−f(a)h - Derivative of a function f at any point x is defined by
f'x=df(x)dx=limh→0f(x+h)−f(x)h - For functions u and v the following holds:
(u±v)'=u'±v'
(uv)'=u'v+uv'
(uv)'=u'v−uv'v2 provided all are defined. - Following are some of the standard derivatives :-
ddx(xn)=nxn−1
ddx(sinx)=cosx
ddx(cosx)=−sinx