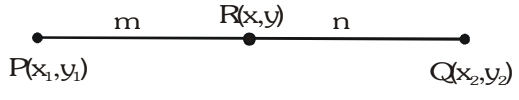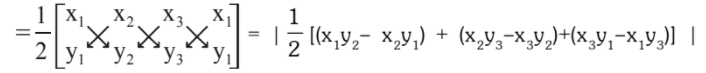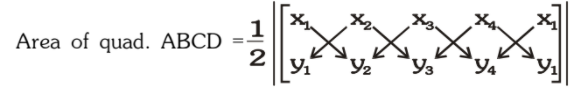INTRODUCTION TO COORDINATE GEOMETRY for Class 11 MATHS
Introduction
Hello Students, In today's class we will learn a very interesting topic which is Introduction to coordinate geometry which has a good weightage in the exam of JEE.
These notes are designed keeping in mind the basics and the recent changes in the syllabus and pattern of JEE.
You can follow Doubtnut for all the videos related to JEE 2022
Coordinate geometry is the combination of algebra and geometry. A systematic study of geometry by the use of algebra was first carried out by celebrated French philosopher and mathematician René Descartes. The resulting combination of analysis and geometry is referred as analytical geometry.
Index
Quadrants|Coordinates of a point|Polar Coordinates of a point|Distance formula and its applications|Section formula|Coordinates of some particular points|Area of Triangle
Quadrants
Let us understand some basics before we go forward.
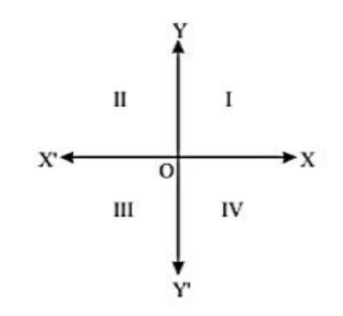
Quadrant: As the word suggests that 'Quad' means four. Quadrant is made by two mutually perpendicular lines meeting at a point O origin which are called axes. And these axes are of 2 types
- Horizontal axis X'OX is called "x-axis"
- Vertical axis Y'OY is known as "y-axis".
These two perpendicular lines divide the plane into four spaces known as Quadrants.
Their naming is done anticlockwise(as shown)- XOY=First Quadrant(Both x and y axis are positive)
- X'OY=Second Quadrant(x is negative and y is positive)
- X'OY'=Third Quadrant(Both x and y are negative)
- Y'OX=Fourth Quadrant(x is positive but y is negative)
Coordinates of a point
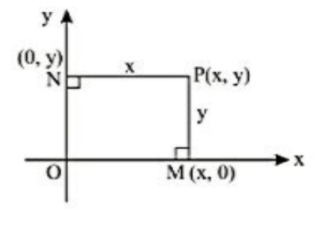
Coordinates are the combination of both xandy and for a point it is given by ordered pair (x,y) and there axes are defined by x-axis and y-axis respectively. The point of the intersection of the axes is O which is the origin of the coordinate system.
- The first entry denoted by x coordinate is known as abscissa.
- The second entry denoted by y coordinate is known as ordinate.
Note:- |x| is the perpendicular distance of the point from y-axis.
- |y| is the perpendicular distance of the point from x-axis.
- Distances along the x-axis to the right of the origin are taken as positive, distances to the left as negative.
- Distances along the y-axis above the origin are positive; distances below are negative.
- y coordinate of any point lying on the x-axis is always zero.
- x coordinate of any point lying on the y-axis is always zero.
- In Ist quadrant x>0,y>0
- IInd Quadrant x<0,y>0
- IIIrd Quadrant x<0,y<0 and
- IVth Quadrant x>0,y<0
Polar Coordinates of a point
Now we have understood the basics of coordinate system let us see see Polar coordinate system analogy with the current coordinate system.
A coordinate system in which the position of a point is determined by the length of a line segment from a fixed origin with combination of angle with the fixed line constitutes a Polar coordinate system.
Pole: The origin is called the pole and the line segment is the radius vector (r).
The angle θ between the polar axis and the radius vector is called the vectorial angle.
Note: By convention, positive values of θ are measured in an anticlockwise sense, negative values in clockwise sense. The coordinates of the point are then specified as (r,θ).
If (x,y) are cartesian co-ordinates of a point P, then :
x=rcosθ , y=rsinθ and r=√x2+y2 θ=tan−1(yx)
Distance formula and its applications
If A(x1,y1) and B(x2,y2) are two points, then AB=√(x2−x1)2+(y2−y1)2
Proof: For triangle PQR, use Pythagoras theorem
(PQ)2=(PR)2+(RQ)2
⇒(x2−x1)2+(y2−y1)2
|PQ|=√(x2−x1)2+(y2−y1)2
Note:
- Three given points A,B and C are collinear, when sum of any two distances out of AB,BC,CA is equal to the remaining third otherwise the points will be the vertices of a triangle.
- Let A,B,C & D be the four given points in a plane. Then the quadrilateral will be.
- Square if AB=BC=CD=DA AC⊥BD. Here opposite sides are parallel to each other and we can find area by taking any two sides.
- Rhombus if AB=BC=CD=DA and AC≠BD AC⊥BD. Here opposite sides are parallel. We can find area by adding the area of 2 triangles.
- Parallelogram if AB=DC,BC=AD and AC!= BD " " AC⟂̷ BD. Opposite sides are equal and parallel and area can be found out by multiplying any side with the perpendicular distance between two sides.
- Rectangle if AB=CD,BC=DA,AC=BD AC⟂̷BD. Opposite sides are parallel and area can be found out by multiplying longest and shortest sides.
Example 1
Find the distance the points, (2,−3) and (−6,3)
Let A(2,-3( and B(-6,3) be the given points. Then, AB=√(−6−2)3+(3−(−3)2)=√(−8)2+(3+3)2=√(−8)2+62=√64+36=√100=10units
Example 2
Prove that the points (0,5), (-2,-2),(5,0) and (7,7) are the vertices of a rhombus
Let the given points be A(0,5), (-2,-2),(5,0) and (7,7). Then, ABCD is a quadrilateral in which.
AB=√(−2−0)2+(−2−5)2=√(−2)2+(−7)2=√4+49=√53units
BC=√(5+2)2+(0+2)2=√(7)2+(2)2=√49+4=√53units
CD=√(7−5)2+(7−0)2=√(2)2+(7)2=√4+49=√53units
DA=√(7−0)2+(7−5)2=√72+22=√49+1=√53units
Thus, AB=BC=CD=DA=√53units
Also, AC=√(5−0)2+(0−5)2=√52+(−5)2=√50=5√2units
And BD=√(7+2)2+(7+2)2=√92+92=√81+81=√162=9√2units
∴AC≠BD.
Thus, ABCD is a quadrilateral all of whose sides are equal but its diagonals are not equal. Hence ABCD is a rhombus.
Section formula
The co-ordinates of a point dividing a line joining the points P(x1,y1) and Q(x2,y2) in the ratio m:n is given by
( a )For internal division: P−R−Q⇒ R divides line segment PQ, internally.
(x,y)≡mx2+nx1m+n,my2+ny1m+n
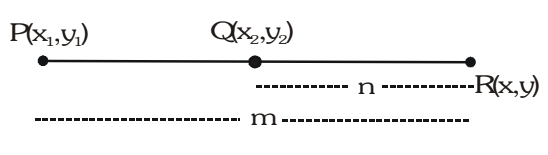
( b ) For external division: R−P−Q⇒R divides line segment PQ, externally.
(x,y)≡mx2−nx1m+n,my2−ny1m+n
PRQR<1⇒R lies on the left of P and PRQR>1⇒R lies on the right of P
Example 3
In what ratio, the line joining (−1,1)and(5,7) is divided by the line x+y=4?
Let the given line divide AB in the ratio m:1
Then, the point of divison is C=(5m−1m+1,7m+1m+1)
This point C must lie on the line x+y=4.
∴5m−1m+1+7m+1m+1=4⇔(5m−1)+(7m+1)=4(m+1)⇔8m=4⇔m=12,
So, the required ratio is 12,i.e.1:2
Example 4
Find the coordinates of the point which divides the line segment joining the points A(5,−2) and B(9,6) in the ratio 3:1
Here, (x1=5,y1=−2)and(x2=9,y2=6).Also,m=3andn=1
Let the required point be P(x,y). Then.
x=mx2+nx1(m+n)=(3×9)+(1×5)(3+1)=324=8
y=my2+ny1(m+n)=(3×6)+(1×(−2))(3+1)=(18−2)4=164=4
Hence, the required points is (8,4).
Harmonic conjugates
If two points P and Q divides the line AB internally and externally in the same ratio m:n, then P and Q are said to be harmonic conjugates of each other with respect to A and B.
i.e. APPB=AQBQ=λ (1)
Also AP,BP and AQ are in H.P. i.e.
2AB=1AP+1AQ
Proof: from (1),
APAB−AP=AQAQ−AB
AB−APAP=AQ−ABAQ
ABAP−1=1−ABAQ
2=ABAQ+ABAP
2AB=1AP+(AQ)
Examples:
( i ) Internal and external angle bisector of an angle of a triangle divide the opposite base harmonically.
BDCD=BECE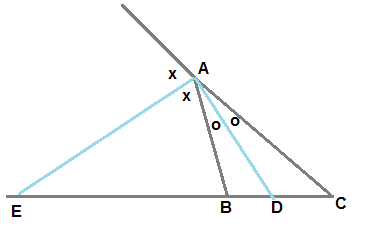
( ii ) External and internal common tangents divide the line joining the centers of the two circles externally and internally in the ratio of their radii.
OaIObI=OaEObE=rarb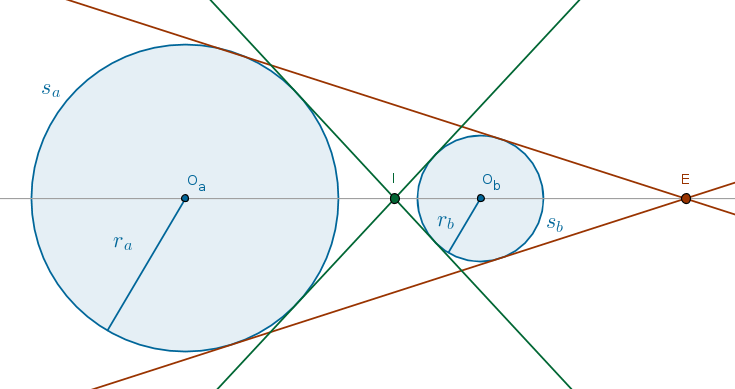
Example 5
Find the harmonic conjugates of the point R(5, 1) with respect to the points P(2, 10) and Q(6, -2)
Let R divides the line in the ratio of λ:1
R(6λ+2λ+1,−2λ+10λ+1)
6λ+2λ+1=5 −2λ+10λ+1=1
6λ+2=5λ+5 −2λ+10=λ+1
⇒λ=3 λ=3
So R'=(−18+2−2,6+10−2)
⇒R'(8,−8)
Example 6
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, −3) and (3, 4), find the vertices of the triangle.
Let x1+x22=3 y1+y22=4
⇒(x1+x2)=6 and (y1+y2)=8
Similarly (x2+x3)=2 and (y2+y3)=2
(x3+x1)=4 and (y3+y1)=−6
⇒x1−x3=4 and (x3+x1)=4
⇒x3=0 and x1=4. Also we get x2=2 by further using the other equations
⇒y1−y3=6 and (y3+y1)=−6
⇒y1=0 and y3=−6 . Also y2=8
Coordinates of some particular points
Let A(x1,y1),B(x2,y2) and C(x3,y3) are vertices of any triangle ABC, then
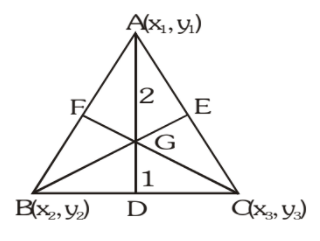
( a ) Centroid: The centroid is the point of intersection of the medians (line joining the mid point of sides and opposite vertices). Centroid divides each median in the ratio of 2:1.
Co-ordinates of centroid G(x1+x2+x33,y1+y2+y33)
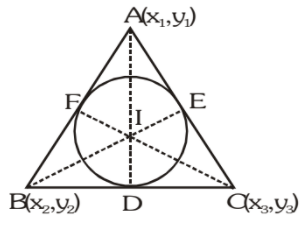
( b ) Incenter: The incenter is the point of intersection of internal bisectors of the angles of a triangle. Also it is a center of the circle touching all the sides of a triangle.
Co-ordinates of incenter I(ax1+ax2+ax3a+b+c,ay1+ay2+ay3a+b+c)
where a,b,c are the sides of triangle ABC.
Note:
- Angle bisector divides the opposite sides in the ratio of remaining sides.
e.g. BDAC=ABAC=cb - Incenter divides the angle bisectors in the ratio
(b+c):a,(c+a):b,(a+b):c
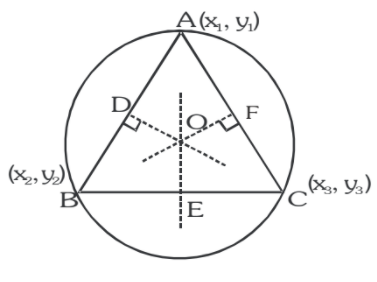
( c )Circumcenter: It is the point of intersection of perpendicular bisectors of the sides of a triangle. If O is the circumcenter of any triangle ABC, then OA2=OB2=OC2. Also it is a center of a circle touching all the vertices of a triangle.
Note:- If the triangle is right angled, then its circumcenter is the mid point of hypotenuse.
- Co-ordinates of circumcenter
(x1sin2A+x2sin2B+x3sin2Csin2A+sin2B+sin2C),(y1sin2A+y2sin2B+y3sin2Csin2A+sin2B+sin2C)
( d ) Orthocenter: It is the point of intersection of perpendiculars drawn from vertices on the opposite sides of a triangle and it can be obtained by solving the equation of any two altitudes.
Note:- If a triangle is right angled, then orthocenter is the point where right angle is formed.
- Co-ordinates of circumcenter
(x1tanA+x2tanB+x3tanCtanA+tanB+tanC),(y1tanA+y2tanB+y3tanCtanA+tanB+tanC)
Remarks:- If the triangle is equilateral, then centroid, incentre, orthocenter, circumcenter, coincide.
- Orthocenter, centroid and circumcenter are always collinear and centroid divides the line joining orthocenter and circumcenter in the ratio 2:1
- In an isosceles triangle centroid, orthocenter, incentre & circumcenter lie on the same line
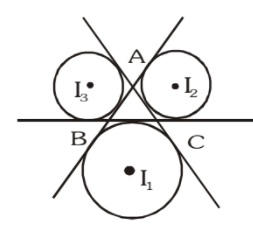
( e ) Ex-centers- The center of a circle which touches side BC and the extended portions of sides AB and AC is called the ex-center of △ABC with respect to the vertex A. It is denoted by I1and its coordinates are
I1(−ax1+bx2+cx3−a+b+c,−ay1+by2+cy3−a+b+c)
Similarly ex-centers of △ABC with respect to vertices B and C are denoted by I2 and I3 respectively , and
I2(ax1−bx2+cx3a−b+c),(ay1−by2+cy3a−b+c)
I3(ax1+bx2−cx3a+b−c,ay1+by2+cy3a+b−c
- The center of a circle which touches side BC and the extended portions of sides AB and AC is called the ex-center of △ABC with respect to the vertex A. It is denoted by I1and its coordinates are
Example 7
(0,0),(20,15),(36,15) are the vertices of triangle then the ex-centre opposite to vertex (0,0) is
In △ABC
BC=√256+0=16=a
AC=√1298+225=√1521=39=b
AB=√400+225=25=c
Excenter opposite to A(0,0)=(−ax1+bx2+cx3−a+b+c,−ay1+by2+cy3−a+b+c)
⇒(−16×0+39×20+25×36−16+39+25,−16×0+39×15+25×15−16+39+25)
⇒(168048,96048)
⇒(35,20)
Example 8
Find the coordinates of the circumcentre of the triangle whose vertices are (8,6),(8−2) and (2,−2). Also, find its circum-radius.
Let A(8,6) and B(8,−2) and C(2,−2)
P(h.k) be the circumcentre
PA=PB=PC
PA2=PB2
(h−8)2+(k−6)2=(h−8)2+(k+2)2
16k=32⇒k=2
PB2=PC2
(h−8)2+(k+2)2==(h−2)2+(k+2)2
12h=60⇒h=5
Hence coordinate of circumcentre (5,2)
Area of Triangle
Let A(x1,y1),B(x2,y2) and C(x3,y3) are vertices of a triangle, then
Area of △ABC=(12)∣∣
∣
∣∣x1y11x2y21x3y31∣∣
∣
∣∣
⇒12|[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]|
To remember the above formula, take the help of the following method
Remarks:
- If the area of triangle joining three points is zero, then the points are collinear.
- Area of Equilateral triangle : If altitude of any equilateral triangle is P, then its area= (P2√3). If a be the side of equilateral triangle, then its area =(a√34)
- Area of quadrilateral with given vertices A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)
Note: Area of a polygon can be obtained by dividing the polygon into disjoined triangles and then adding their areas.
Example 9
Find the area of the triangle whose vertices are A(4,4),B(3,−16)andC(3,−2)
Let (x1=4,y1=4),(x2=3y,y2=−16)and(x3=3,y3=−2)
Then, area of △ABC is given by
△=12.|x2(y2−y3)+x2(y3−y1)+x3(y1−y2)|
=12.|4(−16+2)+3(−2−4)+3(4+16)|
=12.|4(−56−18+60)|=12.|−14|=(12×14)=7sq. units
Hence, the area of the given triangle is 7sq. units.
Example 10
Prove that the co-ordinates of the vertices of an equilateral triangle can not all be rational.
Let A(x1y1),B(x2,y2) and C(x3,y3) be the vertices of a triangle ABC. If possible let x1,y1,x2,y2,x3,y3 be all rational.
Now area of △ABC=(12)∣∣
∣
∣∣x1y11x2y21x3y31∣∣
∣
∣∣= Rational......(i)
Since △ABC is equilateral
Area of △ABC=√34(side)2=√34(AB)2
=√34[(x1−x2)2+(y1−y2)2]=Irrational.....(ii)
From (i) and (ii)
Rational=Irrational which is contradiction
Hence x1,y1,x2,y2,x3,y3 cannot be rational
Conditions for Collinearity of 3 given points
Three given points A(x1,y1),B(x2,y2),C(x3,y3) are collinear if any one of the following conditions are satisfied.
- Area of △ABC is zero i.e.
∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣ - Slope of AB=SlopeofBC=SlopeofCA i.e.
y2−y1x2−x1=y3−y2x3−x2=y3−y1x3−x1 - Find the equation of line passing through 2 given points, if third point satisfies the given equation of the line, then three points are collinear.
Example 11
Find the value of x for which the points (x−1), (2,1)and (4,5) are collinear.
Let A(x,-1), B(2,1) and C(4,5) be the given collinear points.
Then, by collinearity of A,B,C we have: slope of AB=slope of BC
1−(−1)2−x=(5−1)(4−2)⇒22−x=2⇒2−x=1⇒x=1
Hence, x=1
Example 12
find the equations of the sides of the triangle whose vertices are (−1,8),(4,2) and (−5,−3). Also find the equation the median through (−1,−8)
Here, we make use of the equation of a line in two-point form.
Equation of AB is y−8x+1=−2−84+1
⇒5(y−8)+10(x+1)=0
⇒10x+5y−30=0
⇒2x+y−6=0
equation of BC is=y+2x−4=−3+2−5−4⇒−9(y+2)=−(x−4)
equation of AC is=y−8x+1=−3−8−5+1⇒−4(y−8)=−11(x+1)
⇒11x−4y+43=0
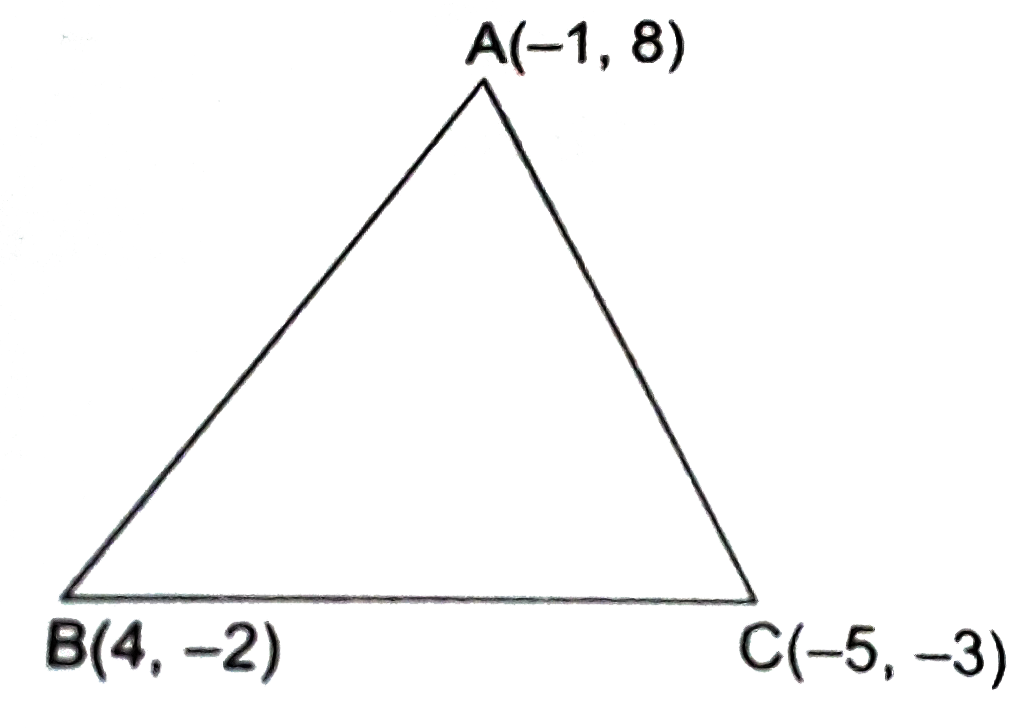
Locus
The locus of a moving point is the path traced out by that point under one or more geometrical conditions.
( a ) Equation of Locus: The equation to a locus is the relation which exists between the coordinates of any point on the path, and which holds for no other point except those lying on the path.
( b ) Procedure for finding the equation of the locus of a point :
(i) If we are finding the equation of the locus of a point P, assign coordinates (h,k) to P.
(ii) Express the given condition as equations in terms of the known quantities to facilitate calculations. We sometimes include some unknown quantities known as parameters.
(iii) Eliminate the parameters, so that the eliminant contains only (h,k) and known quantities.
(iv) Replace h by x, and k by y, in the eliminant. The resulting equation would be the equation of the locus of P.
Example 13
Let A(2,0)andB(−2,0) are two fixed vertices of ΔABC. If the vertex C moves in the first quadrant in such a way that cotA+cotB=2, then the locus of the point C is
Let say A=(−2,0) & B=(2,0)
AB is y=0
C=(x,y) . Draw CD⊥AB
⇒D=(x,0),CD=y
AD=(2+x) BD=(2−x)
CotA=2+xy CotB=2−xy
CotA+CotB=2(constant)
⇒2+xy+2−xy=K
⇒2⋅2=Ky
⇒y=2⋅2K
⇒ This is a straight line Parallel to AB at a distance of 4K
Locus of c is a straight line Parallel to AB
Example 14
The locus of the centroid of the triangle with vertices at (acosθ,asinθ), (bsinθ−bcosθ) and (1,0) is (here, θ is a parameter)
Let G(x,y) be the locus of centroid
Centroid G(x,y)⇒(x1+x2+x33,y1+y2+y33)
Let A(acosθ,bsinθ),B(bsinθ,bcosθ),c(1,0)
G(x,y)=(acosθ+bsinθ+13,asinθ−bcosθ3))
⇒3x−1=(acosθ+bsinθ)−(1)
3y=(asinθ−bcosθ)−(2)
(1)2+(2)2
(3x−1)2+(3y)2=(acosθ+bsinθ)2+(asinθ−bcosθ)2
⇒a2cos2θ+bsin2θ+2ab(sinθ)(cosθ)+a2sin2θ+b2cos2θ−2ab(sinθ)(cosθ)
(3x−1)2+(3y)2a2+b2 is the required Locus.