PARABOLA for Class 11 MATHS
Introduction
Hello Students, In today's class we will learn a very interesting topic which is Parabola which has a good weightage in the exam of JEE.
These notes are designed keeping in mind the basics and the recent changes in the syllabus and pattern of JEE.
You can follow Doubtnut for all the videos related to JEE 2022.
We have studied various forms of the equations of a line. In this Chapter, we shall study about some other curved figure made of Parabolas. The names parabola is given by Apollonius. This curve comes under the category known as conic sections Parabolic curves have a very wide range of applications in fields such as in bridges support design, designing ships and boats, focal mirror design,etc.
Index
Basic concepts and Definition|Terms related to parabola|Generalized equation of Parabola|Equation of Parabola with respect to two perpendicular lines|Chord|Position of a point with respect to parabola y2=4ax|Interaction between line and tangent|Equation of Tangent|Point of Intersection of tangents at any two points on the parabola|Equation of Normals|Three supplementary results
Basic concepts and Definition
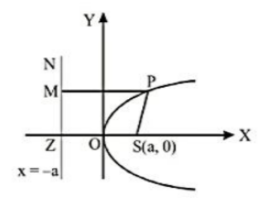
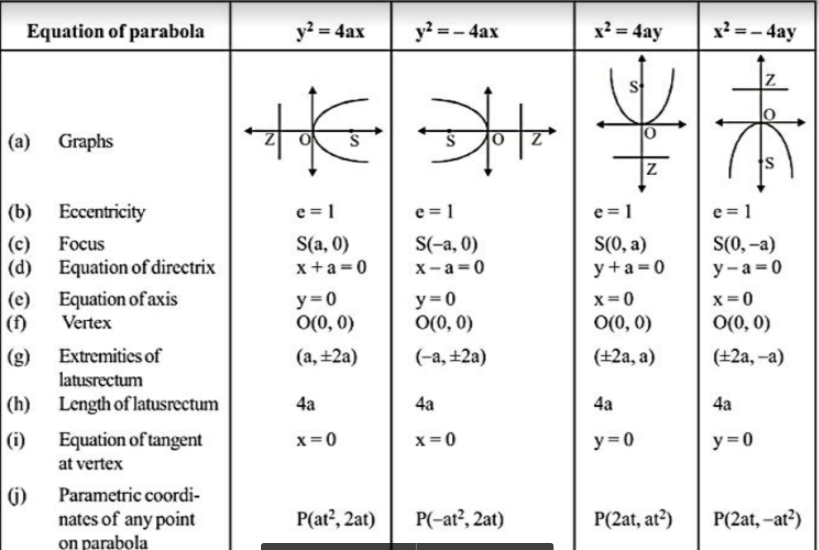
A parabola is the locus of a point which moves in a plane such that its distance from a fixed point (focus is equal to its perpendicular distance from a fixed straight line (directrix). Eccentricity of parabola is 1.
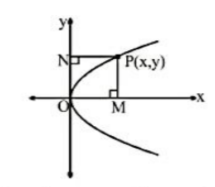
Standard Equation of a parabola : Let S be the focus and ZN is the directrix of the parabola. From S, draw SZ perpendicular to the directrix.
Let O be the middle point of ZS. Take O as the origin and OS as x-axis and OY perpendicular to OS as the y-axis.
Let ZS=2a, then ZO=OS=a. Now, S≡(a,0)and the equation of ZN is x=−a or x+a=0.
Let P(x,y) be any point on the parabola.
∴PS=PM (by definition of parabola ).
√(x−a)2+(y−0)2=|x+a|√1+0
√(x−a)2+(y)2=|(x+a)|
or (x−a)2+y2=(x+a)2
or x2−2ax+a2+y2=x2+2xa+a2
or y2=4ax
which is the required equation.
Terms related to parabola
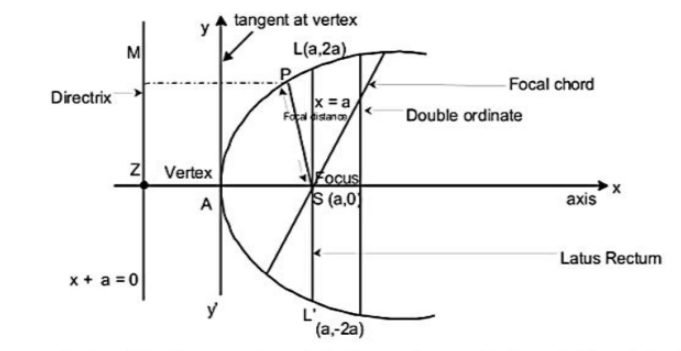
( 1 ) Axis: A straight line passes through the focus and perpendicular to the directrix is called the axis of parabola. For the parabola y2=4ax, x-axis is the axis. Since equation has even power of y therefore the parabola is symmetric about x-axis i.e. about its axis.
( 2 ) Vertex: The point of intersection of a Parabola and its axis is called the vertex of the Parabola. For the parabola y2=4ax, O(0,0) is the vertex.
( 3 ) Focal Distance : The distance of any point P(x,y) on the parabola from the focus is called the focal length (distance) of point P. The focal distance of P = the perpendicular distance of the point P from the directrix.
( 4 ) Double Ordinate : The chord which is perpendicular to the axis of Parabola or parallel to Directrix is called double ordinate of the Parabola.
( 5 ) Focal Chord : Any chord of the parabola passing through the focus is called Focal chord.
( 6 ) Latus Rectum: If a double ordinate passes through the focus of parabola then it is called as latus rectum. The extremities of the latus rectum are L(a,2a) and L’(a,—2a). Since LS=L’S=2a, therefore length of the latus rectum LL’=4a.
( 7 ) Parametric Equation of Parabola : The parametric equation of Parabola y2=4ax are x=at2,y=2at. Hence any point on this parabola is (at2, 2 at) which is also called as ‘t’ point.
Note:
- The length of the latus rectum= 2xperpendica––rdistanceoffocusomthedirectrix.<li>Ify^2 = lxthen≤n>hofthelatusrectum=l.<li>Twoparabolasaresabeequaliftheyhavesamelatusrectum.<li>Theendsofadoub≤ord∈ateofaparabolacanbetakenas(at^2, 2 at)and(at^2, — 2at).
- Parabola has no centre, but circle, ellipse, hyperbola have centre.
Some paramters related to parabola
Generalized equation of Parabola
If the equation of a parabola is either in the form x=ly2+my+n or y=lx2+mx+n then it can be reduced into generalized form. For this we change the given equation into the following forms-
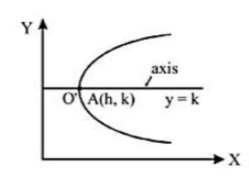
(y−k)2=4a(x−h) or (x−h)2=4a(y−k)
And then we compare from the standard equation of parabola to find all its parameters.
(A) When the equation of parabola is:
(y−k)2=4a(x−h)
Equation (i) is of the form Y2=4aX
where Y=y−k and X=x−h
( 1 ) Axis of parabola is Y=0 ,i.e. y−k=0⇒y=k
( 2 ) Coordinates of vertex of parabola are given by
X=0 and Y=0
i.e. x−h=0 and y−k=0⇒ Vertex is (h,k)
( 3 ) Tangent at the vertex to parabola (i) is given by X=0, i.e., x—h=0
Therefore, tangent at the vertex is x=h.
( 4 ) Coordinates of focus of parabola are given by
X=a and Y=0
i.e. by x−h=a and y−k=0
(a+h,k).
( 5 ) Equation of directrix of parabola is
X=−a i.e., x−h=−a
Therefore, directrix of parabola is x=h−a
( 6 ) Length of latus rectum of parabola is |4a| .
( 7 ) Coordinates of ends of latus rectum of parabola are given by
X=a & Y=±2a
i.e., by x−h=a,y—k=±2a i.e. coordinate of latus rectum is (a+h,k±2a).
( 8 ) Parametric equation is x=h+at2 and y=k+2at.
( B ) When the equation of parabola is:
(x—h)2=4a(y—k)
Equation (i) is of the form X2=4aY
where X=x−h and Y=y−k
(1) Axis of parabola is X=0, i.e., x−h=0
( 2 ) Coordinates of vertex of parabola is given by X=0 and Y=0
i.e. by x−h=0 and y−k=0
∴x=h and y=k hence vertex of parabola is (h,k)
( 3 ) Equation of tangent at the vertex to parabola is Y=0 i.e. y−k=0 or y=k
( 4 ) Coordinates of focus of parabola are given by X=0 and Y=a
i.e. by x−h=0 and y−k=a
Focus of parabola is (h,k+a)
( 5 ) Equation of directrix of parabola (i) is given by Y=−a or y−k=−a or y=k−a
( 6 ) Length of latus rectum of parabola is 4a .
( 7 ) Coordinates of ends of latus rectum of parabola are given by Y=a,X=±2a
i.e., y−k=a, X−h=±2a
Ends of latus rectum are (h±2a,k+a)
( 8 ) Parametric equation is x=h+2at and y=k+at2.
Example 1
The conic represented by the equation x2+y2−2xy+20x+10=0, is
Comparing the given equation with the equation ax2+2hxy+by2+2gx+2fy+c=0, we have
a=1,b=1,h=−1,c=10,g=10 and f=0
∴ abc+2fgh−af2−bg2−ch2=10−100=−100≠0.
and, h2−ab=(−1)2−1×1=0⇒h2=ab
Thus, we have
Δ≠0 and h2=ab
So, the given equation represents a parabola.
Example 2
The equation of a parabola having focus (3, 0) and directrix x + 3 = 0, is
Let p (x, y) be any point on the parabola. Then, √(x−3)2+(y+0)2=∣∣∣x+3√1+0∣∣∣ [Using SP= PM]
⇒ (x−3)2+y2=(x+3)2⇒y2=12x
Example 3
The length of the latusrectum of the parabola 2{(x−a)2+(y−a)2}=(x+y)2, is
We have
2{(x−a)2+(y−a)2}=(x+y)2
⇒ √(x−a)2+(y−a)2=1√2|x+y|
⇒ √(x−a)2+(y−a)2=∣∣∣x+y√2∣∣∣
Clerly, this equation represents a parabola having its focus at (a, a) and directrix x + y = 0
∴ L.R.=2 (Distance between focus and directrix)
⇒ L.R.=2∣∣∣a+a√1+1∣∣∣=2√2a
Equation of Parabola with respect to two perpendicular lines
Let P(x,y) is y point on the parabola then equation of parabola y2=4ax is considered as
(PM)2=4a(PN)
i.e. (The distance of P from its axis)^2=(latus rectum)x(The distance of P from the tangent at its vertex) where P is any point on the parabola.
Chord
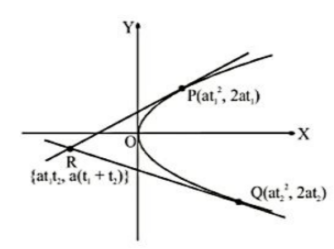
Line joining any two points on the parabola is called its chords. Let the points P(at21,2at1) and Q(at21,2at), lie on the parabola then equation of chord is
(y—2at1)=(2at2−2at1at22−at21)(x−at21)
⇒(y—2at1)=2t1+t2(x—at21)
(t1+t2)y=2x+2at1t2
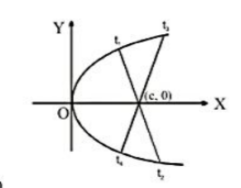
If this chord meet the x-axis at point (c,0) then from above equation
c+at1t2=0 i.e. t1⋅t2=—ca.
Note:
(i) If the chord joining t1,t2 & t3,t4 pass through a point (c,0) on the axis, then t1t2=t3t4=−ca.
( ii ) If PQ is a focal chord then t1t2=−1 or t2=−1t1
which is required relation.
Hence if one extremity of a focal chord is (at2,2at) then the other extremity will be (at2,−2at)
Position of a point with respect to parabola `y^2=4ax`
Let P(x1,y1) be a point. From P draw PM⊥AX (on the axis of parabola) meeting the parabola y2=4ax at Q(x1,y2) where Q(x1,y2) lie on the parabola therefore
Y2=4ax1 from(I)
Now, P will be outside, on or inside the parabola y2=4a.x according as ⇒(PM)2>, or <(QM)2
⇒y21>,=, or <y22
⇒y21>,= ,or <4ax1
Hence y21=4ax1>,=, or <0
Hence in short, equation of parabola region S(x,y)=y2−4ax.
( i ) If S(x1,y1)>0 then P(x1,y1) lie outside the parabola.
( ii ) If S(x1,y1)<0 then P(x1,y1) lie inside the parabola.
( iii ) If S(x1,y1)=0 then P(x1,y1) lie on the parabola.
This result holds true for circle, parabola and ellipse.
Example 4
The focal chord to y2=16x is tangent to (x−6)2+y2=2 then the possible values of the slope of this chord
The coordinates of the focus of the parabola y2=16x are (4, 0).
The equation of tangents of slope m to the circlen
(x−6)2+(y−0)2=(√2)2 are y=m(x−6)±√2√1+m2
If these tangents pass through the focus i.e. (4, 0) then
0=−2m±√2√1+m2
⇒ 4m2=2(1+m)2⇒2m2=2⇒m=±1
Example 5
If PSQ is a focal chord of the parabola y2=8x such that SP=6, then the length of SQ is
We have,
Semi-latrusrectum = HM of SP and SQ
⇒ 4=SP×SQSP×SQ⇒4=2×6×SQ6+SQ⇒SQ=3
Example 6
Let PQ be a focal chord of the parabola y2=4ax The tangents to the parabola at P and Q meet at a point lying on the line y=2x+a,a>0. Length of chord PQ is
Let (at21,2at1) and Q(at22,at2) be the end-point of a focal chord of the parabola y2=4ax. Then, t1t2=−1 and PQ=a(t2−t1)2. The tangents at P and Q intersect at a point (at1t2,a(t1+t2)) which lies on y = 2x + a.
∴ e(t1+t2)=2at1t2+a
⇒ t1+t2=−2+1+1
⇒ t1+t2=−2+1=−1 [because t1t2=−1]
∴ PQ=a(t2−t1)2
=a{(t2+ty1)2−4t1t2}=a[(−1)2−4(−1)]=5a
Interaction between line and tangent
Let the parabola be y2=4ax.....(i)
and the given line be y=mx+c...(ii)
then line may cut, touch or does not meet parabola.
The points of intersection of the line (1) and the parabola (2) will be obtained by solving the two equations simultaneously. By solving equation (i) and (ii), we get my2−4ay+4ac=0
This equation has two roots and its nature will be decided by the discriminant D=16a(a -cm)
Now, if D>0 i.e. c<(am) then line intersect the parabola at two distinct points.
If D=0 i.e. c=(am) then line touches the parabola. (It is condition of tangency)
If D<0 i.e. c>(am) , then line neither touch nor intersect the parabola.
Equation of Tangent
1. Point form
Equation of parabola is y2=4ax....(i)
Let P(x1,y1) and Q=(x,,y,) be any two points on parabola (i), then, y21=4ax1....(2)
and y22=4ax2....(3)
Subtracting (2) from (3) then, y22−y21=4a(x2—x1)
or (y2−y1x2−x1)=4ay2+y1.....(4)
Equation of PQ is y−y1=(y2−y1x2−x1)⋅(x−x1)....(5)
From (4) and (5), then y−y1=(4ay2+y1)(x−x1)
Now for tangent at P.Q→P, i.e., x2→x1 and y2→y1 then equation (6) becomes
y−y1=4a(x—x1)
or yy1−y21=2ax—2ax1
or yy1=2ax+y21−2ax1
or yy1−2ax+4ax1−2ax1 [From (2)]
or yy1=2ax+2ax1
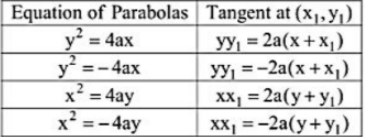
which is the required equation of tangent at (x1,y1).
The equation of tangent at (x1,y1) can also be obtained by replacing x2 by x⋅x1,y2 by yy1,x by x+x12
y by y+y12 ‘ and xy by xy1+yx12 and without changing the constant (if any) in the equation of curve.
Equation of tangent of standard Parabola
2. Slope form
The equation of tangent to the parabola y2=4ax at (x1,y1) is
yy1=2a(x+x1)....(i)
Since m is the slope of the tangent then
m=2ay1 or y1=2am
Since (x1,y1) lies on y2=4ax therefore
y21=4ax1 or (4a2m2)=4ax1⇒x1=(am2)
Substituting the values of x1 and y1 in (1), we get
y=mx+(am)
Thus, y=mx+(am) is a tangent to the parabola y2=4ax for all values of m, where m is the slope of the tangent and the co-ordinates of the point of contact is (am2,2am)
Thus y=mx+c is the tangent of y2=4ax for all values of m if only if c=am and (y—k)=m(x−h)+am is tangent to the parabola (y−k)2=4a(x−h).
Paramteric form
We have to find the equation of tangent to the parabola y2=4ax at the point (at2,2at) or ‘t’.
Since the equation of tangent of the parabola y2=4ax at (x1,y1) is
yy1=2a(x+x1).....(i)
replacing x1 by at2 and y1 by 2at, then (i) becomes
y(2at)=2a(x+at2)
ty=x+at2
Point of Intersection of tangents at any two points on the parabola
Let the given parabola be y2=4ax and two points on the parabola are
P=(at21,2at) and Q=(at22,2at)
Equation of tangents at P=(at21,2at1) and Q=(at22,2at2)
are t1y=x+at21.....(1) and t2y=x+at22......(2)
Solving these equations we get
x=at1t2, y=a(t1+t2)
Thus, the co-ordinates of the point of intersection of tangents at P(at21,2at1) and Q(at22,2at2) are R(at1t2,a(t1+t2))
Note:
( i ) The Arithmetic mean of the y-co-ordinates of P and Q(i.e. (2at1+2at22)=at1+at2 is the y - co-ordinate of the point of intersection of tangents at P and Q on the parabola.
( ii )The Geometric mean of the x-co-ordinates of P and Q (i.e. √at21×at22=at1at2 is the x co-ordinate of the point of intersection of tangents at P and on the parabola.
Example 7
Find the equation of the common tangent to the curves y2=8x and xy=-1.
The equation of tangent to y2=8x is
y=mx+2m
If it touches xy=1, then
x(mx+2m)=−1 must have equal roots
⇒ mx2+2mx+1=0 must have equal roots
⇒ 4m2−4m=0⇒m3−1=0⇒m=1.
Substituting the value of m in (i), we get
y=x+2 as the equation of the common tangent.
Example 8
The equation to the line touching both the parabolas y2=4x and x2=−32y is
The equation of any tangent to y2=4x is
y=mx+1m
If it touches the parabola x2=−32y, then equation
x2=−32(mx+1m)
i.e. x2+32mx+32m=0⇒xm3−1=0⇒m=12
Substituting the value of m in (i), we get x - 2x + 4 = 0
Example 9
If m be the slope of common tangent of y=x2−x+1 and y=x2–3x+1. Then m is equal to
Let y = mx + c be the common tangent to the two parabolas. Then, the equations.
xm+c=x2−3x+10 and mx+c=x2−x+1
must have equal roots
i.e. x2−x(3+m)+10−c=0 and x2−x(1+m)=4(1−c)
must have equal roots
∴ (3+m)2=4(10−x) and x2−x(1+m)+1−c=0
⇒ (3+m)2−(1+m)2=36⇒m=7.
Equation of Normals
1. Point form :
Since the equation of the tangent to the parabola y2=4ax at (x1,y1) is 2a(x+x1)...(1)
The slope of the tangent at (x1,y1)=2ay1
Slope of the normal at (x1,y1)=−y12a
Hence the equation of normal at (x1,y1) is
y−y1=−y12a(x−x1)
2. Slope form :The equation of normal to the parabola y2=4ax at (x1,y1) is
y−y1=−y12a(x−x1)
Since m is the slope of the normal
then m=−y12a or y1=−2am
Since (x1,y1) lies on y2=4ax therefore
y21=4ax1 or 4a2m2=4ax1
x1=am2
Substituting the values of x1 and y1 in (1) we get
y+2am=m(x−am2)....(2)
Thus, y=mx−2am−am3
is a normal to the parabola y2=4ax where m is the slope of the normal. The co-ordinates of the point of contact are (am2.−2am).
Hence y=mx+c will be normal to parabola. If and only if c=−2am−am3
Note:
3. Parametric form
Equation of normal of the parabola y2=4ax at (x1,y1) is
y−y1=−y12a(x−x1)....(1)
Replacing x1 by at2 and y1 by 2at then (I) becomes
y−2at=−t(x−at)2
or y=−tx+2at+at3
Three supplementary results
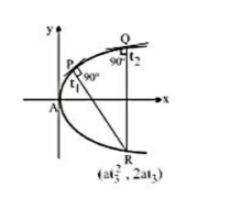
Point of intersection of normals at any two points on the parabola:Let the points P(at21,2at1) and Q(at22,2at1) lie on the parabola y2=4ax
The equations of the normals at P(at21,2at1) and Q(at22,2at2) are
y=−t1x+2at1+at31.....(i) and y=−t2x+2at2+at31.....(ii)
Hence point of intersection of above normals will be obtained by solving (i) and (ii),we get
x=2a+a(t21+t22+t1t2)
y=−at1t2(t1++t2)
If R is the point of intersection then it is
R=[2a+a(t21+t22+t1t2),−at1t2(t1+t2)]
( b ) Relation between t1 and t2 if normal at t1 meets the parabola again at t2:
Let the parabola be y2=4ax, equation of normal at P(at21,2at1) is
y=t1x+2at1+at31.....(1)
Since normal meet the parabola again at Q(at22,2at1)
∴2at2=−at1t22+2at1+at32
⇒2a(t2—t1)+at1(t22−t21)=0
a(t2−t1)[2+t1(t2+t1)]=0
a(t2−t1)≠0 ( t1 and t2 are different)
∴2+t1(t2+t1)=0
t2=−t1−2t1
If normal to the parabola y2=4ax drawn at any point (at2,2at) meet the parabola at t3 then
t3=−t−2t
⇒t2+_3+2=0....(i). It has two roots t1 & t2. Hence there are two such point P(t1) & Q(t2) on the parabola from where normals are drawn and which meet parabola at R(t3)
⇒t1+t2=−t3 & t1t2=2
Thus the line joining P(t1) & Q(t2) meet x-axis at (−2a,0)
Example 10
The normals at the ends of the latus rectum of the parabola y2=4ax are (a, 2a) and (a, -2a).
The coordinates of the end points of the latusrectum of the parabola y2=4ax are (a, 2a) and (a, -2a).
The equation of the normal at (a, 2a) is
y−2a=−2a2a(x−a)or,x+y−3a=0 ...(i)
The equation of the normal at (a, -2a) is
y+2a=−2a2a(x−a)or,x−y−3a=0 ...(ii)
Clearly, (i) and (ii) are perpendicular as the product of their slopes is -1.
Example 11
·If the normals of the parabola y2=4x drawn at the end points of its latus rectum are tangents to the circle (x−3)2(y+2)2=r2 , then the value of r2 is
The coordinates of end-points of latusrectum PQ of the parabola y2=4x are P(1, 2) and Q(1, -2). The equations of the normals P and Q are
y−2=−23(x−1)
and y+2=−−22(x−1) [Using y−y1=y12a(x−x1)]
or x+y−3=0andx−y−3=0
These are tangents to teh circle (x−3)2+(y+2)2=r2
∴ ∣∣
∣∣3−2−3√12+12∣∣
∣∣=r⇒r=√2⇒r2=2.
Example 12
The value of θ∈(−π2,π2) for which the line y=x cos θ+4 cos3 θ−14 cos θ−1 is a normal to the parabola y2=16x, is
The slope of the given line is m = cos θ.
We know that the line y = mx + c is a normal to the parabola y2=4ax, if c=−2am−am3. Therefore, the given line will be a normal to the parabola y2=16x, is
4cos3θ−14cosθ−1=−8cosθ−4cos2θ
⇒ 8cos3θ−6cosθ=1
⇒ 2(4cos3θ−3cosθ)=1
⇒ 2cos3θ=1⇒cos3θ=12⇒3θ=π3θ=π9
Example 13
The line lx+my+n=0 is a normal to the parabola y2=4ax if
The equation of the line is lx+n=0.
or,y=(−1m)x+(−nm)
This will be normal to y2=4ax, if
−nm=−2a(−1m)−a(−1m)3 {Using : c=−2am−am3}
⇒ −nm2=2alm2+al3⇒al(l2+2m2)+m2n=0