CONIC SECTIONS for Class 11 MATHS
INTRODUCTION
Hello bachcho, humne chapter 10 mai various forms of the equations of a line ke barein mai padha tha. Iss chapter mai hum kuch other curves ke barein mai padhenge jaise ki circle, ellipse, parabola, hyperbola.
Kya aap jante hai ki inn curves ko conic kyu kaha jata hai?
Agar nahi, toh koi baat nhi, inhe conic isliye bola jata hai kyuki inki formation plane ko intersect karne se hoti hai with a double napped right circular cone.
Inn curves ki bahut sare field mai kafi wide range hai, jaise ki planetary motion, design of telescope, reflectors in flashlights and automobile headlights, etc. Conic section 3D geometry ki study mai bhi bahut helpful hota hai. Aur aap iss chapter ko apni practical life se bhi relate kar paoge.
Conic Sections
A figure formed by the intersection of a plane and a circular cone. Depending on the angle of the plane with respect to the cone, a conic section may be a circle, an ellipse, a parabola, or a hyperbola.
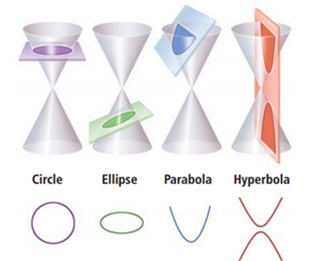
Sections of a Cone
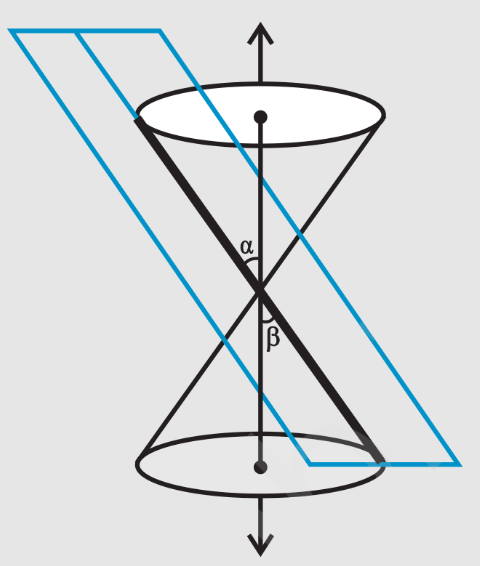
Hum ek fix vertical line l draw karte hai aur ek intersecting line m jo vertical line ko intersect karti hai ek fix point V par. Dono ke intersection se ek angle α banta hai.
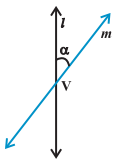
Abh suppose karo ki hum line m ko line l ke around rotate kar rahe hai par iss tarah se jisse angle α constant rahe. Line ke rotate karne se hume ek double napped right circular hollow cone milega. Uss hollow cone mai aapko uske kafi sare character ya part dekhne ko milenge.
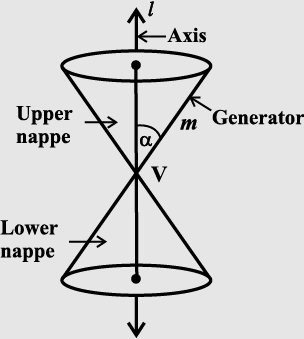
In figure, aapko V point dekhne ko milega jo ki vertex hai.
A point where two lines meet to form an angle, is called vertex
The rotating line m is called a generator of the cone. Basically wo line jo cone ko generate karti hai wo generator kehlati hai. Vertex cone ko do part mai divide karta jinhe nappes kaha jata hai. One is Upper nappe another is Lower nappe. Agar hum plane ka intersection cone ke sath karte hai toh wo section Conic section kehlata hai. Thus, conic sections are the curves obtained by intersecting a right circular cone by a plane.
Hume ek new angle β mila hai by the intersection of plane with vertical axis of cone.

Circle, ellipse, parabola and hyperbola
Hum aage following situations dekhenge ki jab plane ek cone ke nappe ko cut karta h ( other than the vertex ) to different figures and situation humare paas nikal kar aati hai.
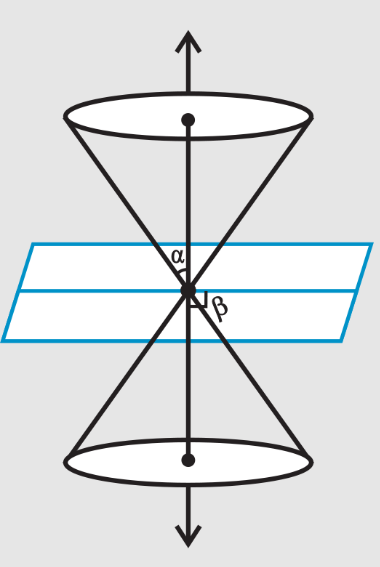
(a) When β=90∘, the section is a circle.
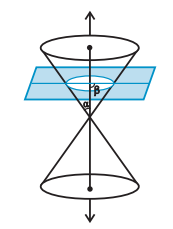
(b) When α < β < 90∘, the section is an ellipse .
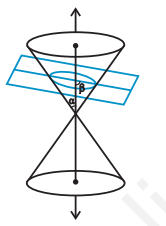
(c) When α = β, the section is parabola.
[ In (a), (b), (c) the plane cuts only one nappe of the cone].
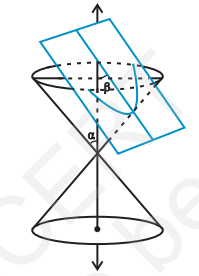
(d) When 0 ≤ β < α, the plane cuts through both the nappes and the curves of intersection is a hyperbola.
Degenerated conic sections
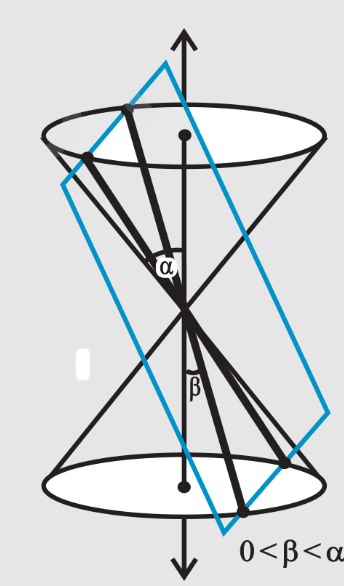
When the plane cuts at the vertex of the cone, we have the following different cases:
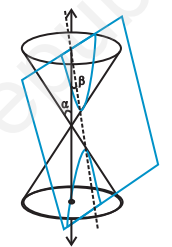
(a) When α < β ≤ 90∘, then the section is a point.
(b) When β = α yaha par plane cone ko intersecting line ke parallel aur vertex par cut kar raha hai. It is the degenerated case of a parabola.
(c) When 0 = β < α and 0 < β < α the section is a pair of intersecting straight lines. It is the degenerated case of a hyperbola.

Example 1
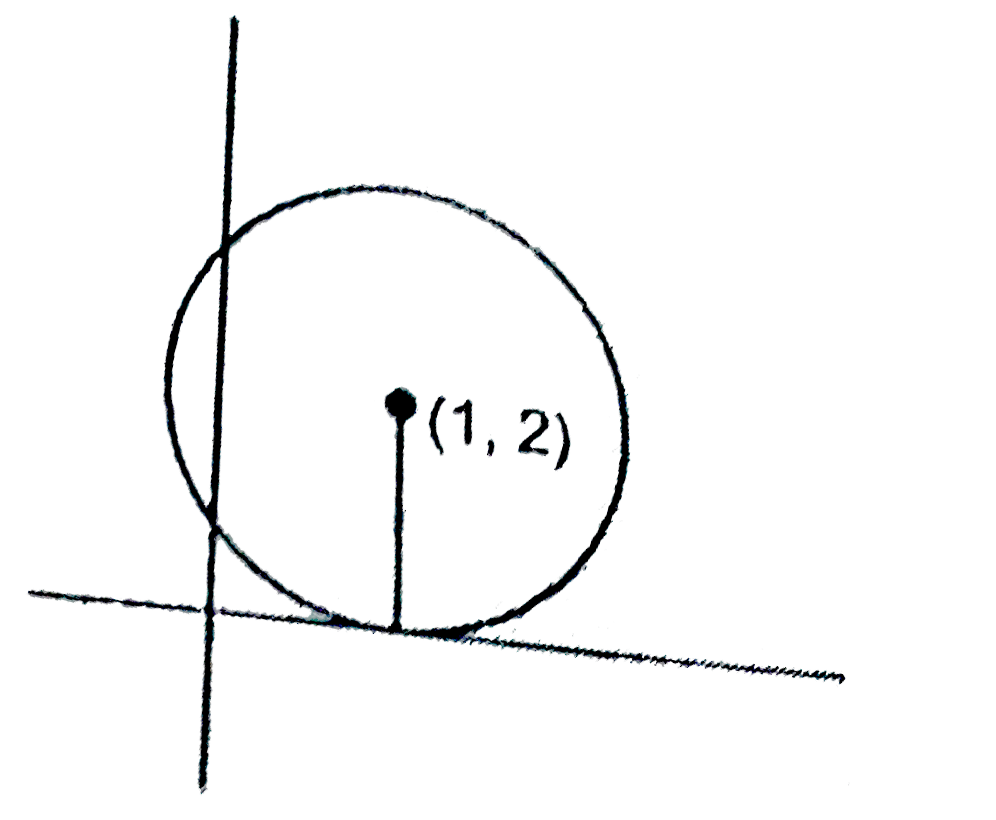
Find the equation of a circle which touches the x -axis and whose centre is (1,2)
Centre of circle (h, k) = (1, 2), circle touches the x- axis
∴ From the figure , the radius of circle a=2 units
∴ The equation of circle
(x−h)2+(y−k)2=a2
⇒(x−1)2+(y−2)2=22
⇒x2−2x+1+y2−4y+4=4
⇒x2+y2−2x−4y+1=0.
Example 2
Find the centre and radius of the circle (x−2)2+(y+5)2=49
(x−2)2+(y+5)2=49
⇒(x−2)2+(y+5)2=72
Comparing with the equation of circle
(x−h)2+(y−k)2=a2
h=2,k=−5,a=7
∴ Centre of circle :(h,k)=(2,−5)
and radius a=7.
Circle
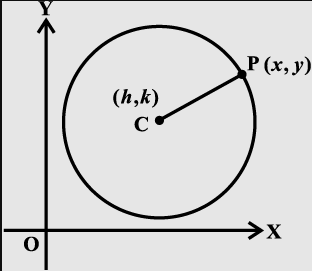
A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
Circle
The fixed point is called the centre of the circle and the distance from the centre to a point on the circle is called the radius of the circle.

Circle ki equation bahot hi simple hai, if the centre of the circle is at the origin. Given C(h,k) be the centre and r the radius of circle. Let P(x,y) be any point on the circle. Then, by the definition, |CP|=r .
By the distance formula, we have
√(x−h)2+(y−k)2=r
(x−h)2+(y−k)2=r2
Example 3
Find the equation of a circle whose centre is (2,−1) and which passes through the point (3,6).
Let C(2,−1) be the centre of the given circle and let it pass through the point P(3,6). Then, radius of the circle
=|CP|=√(3−2)2+(6+1)2=√50
∴ The required equation of the circle is
(x−2)2+(y+1)2=(√50)2
⇒x2+y2−4x+2y−45=0
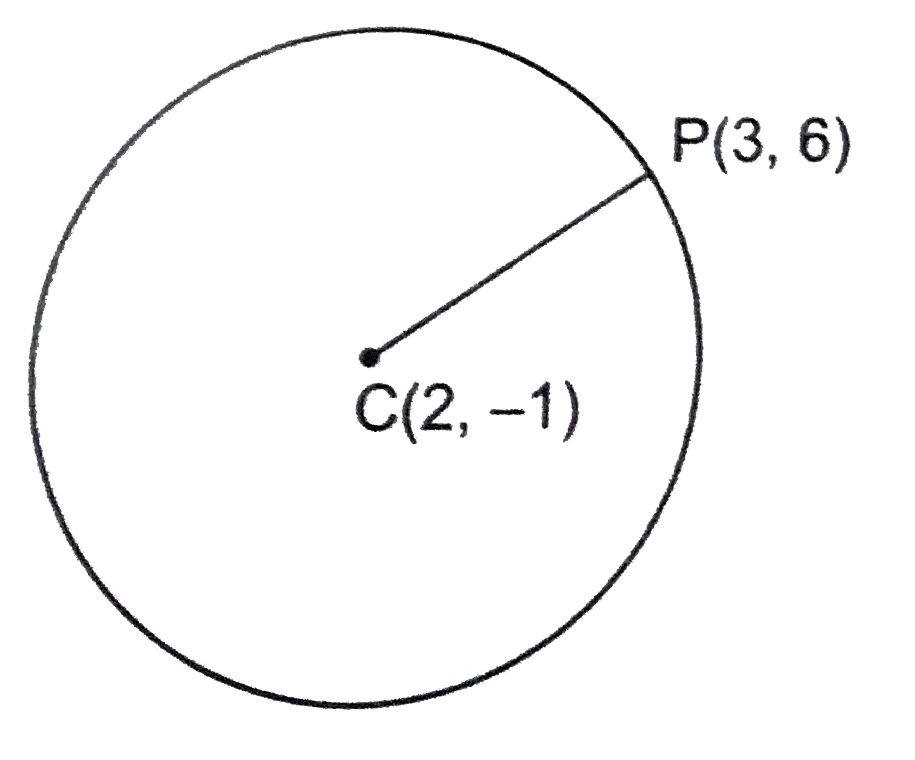
Example 4
Find the equation of a circle, the end points of one of whose diameters are A(2,−3) and B(−3,5).
We know that the equation of a circle, the end points of one of whose diameters are (x1,y1) and (x2,y2), is given by
(x−x1)(x−x2)+(y−y1)(y−y2)=0
Here, x1=2,y1=−3andx2=−3,y2=5
∴ The required equation of the circle is
(x−2)(x+3)+(y+3)(y−5)=0
⇒x2+y2+x−2y−21=0
Parabola
A symmetrical plane curve that forms when a cone intersects with a plane parallel to its side.

Parabola
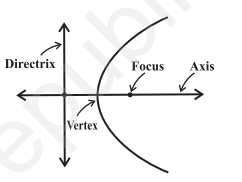
Jo ek vertical fix line hai wo directrix of the parabola hoti hai. The directrix is perpendicular to the axis of symmetry of a parabola and does not touch the parabola aur jo fix point F hai wo focus kehlata hai.
(Meaning of Para is for and bola is throwing , i.e, the shape described when you throw a ball in the air).
A line through the focus and perpendicular to the directrix is called the axis of the parabola. The point of intersection of parabola with the axis is called the vertex of the parabola.
Standard equations of parabola
Parabola ki equation simple hoti hai agar vertex origin pe hi ho and the axis of symmetry is along the x-axis or y-axis. Toh humare paas parabola ke four possible orientation nikal kar aate hai.

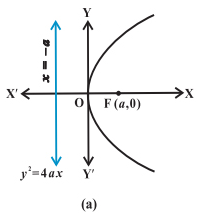

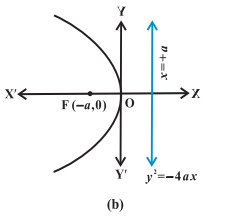

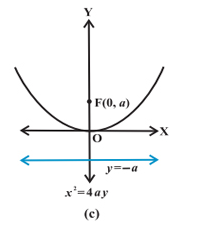

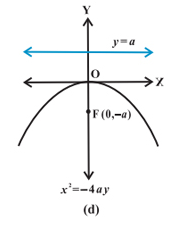
Abh hum case l yani figure (a) se parabola ki equation find out karenge.
In figure (a), focus at (a,0) a>0 and the directrix x=−a
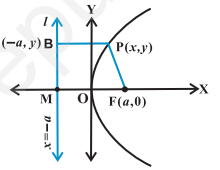
Let F be the focus and l the directrix. Abh hum ek perpendicular FM draw karenge directrix tak and bisect FM at the point O. O ko hum apna origin lenge, OX the x - axis and OY perpendicular to it as the y - axis. Directrix se focus tak ka distance hum 2a se denote karenge. Then, the coordinates of the focus are (a,0), and the equation of the directrix is x+a=0. Let P(x,y) be any point on the parabola such that
PF=PB
PB perpendicular hai l ke toh B ke coordinates (−a,y) hai.
By the distance formula, we have
PF = √(x−a)2+y2 and PB = √(x+a)2
Since PF=PB, ...........(1) we have
√(x−a)2+y2 = √(x+a)2
(x−a)2+y2 = x+a)2
x2−2ax+a2+y2=x2+2ax+a2
y2=4ax (a > 0)
Hence, any point on the parabola satisfies y2=4ax.......(2)
Conversely, let P(x,y) satisfy the equation (2)
PF = √(x−a)2+y2 = √(x−a)2+yax
√x+a2=PB........(3)
and so P (x,y) lies on the parabola.
Thus, from (2) and (3) we have proved that the equation to the parabola with vertex at the origin, focus at (a,0) and directrix x=–a is y2=4ax
Latus rectum
Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose end points lie on the parabola. Latus rectum ek line segment hai jo focus ke through pass karti hai aur parabola par lie yani parabola ko touch karti hai.
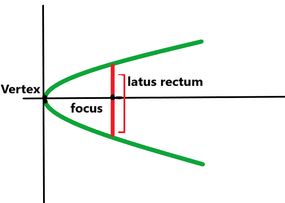
To find the Length of the latus rectum of the parabola y2=4ax
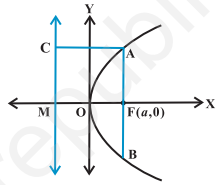
As we know, by the definition of parabola , AF = AC
AC = FM = 2a
AF=2a
AB = Length of the latus rectum = 4a
The length of the parabola's latus rectum is equal to four times the focal length.
Parabola in real life
The stretched arc of a rocket launch is parabolic.

Properties of Parabola
- The parabola is symmetric about its axis.
- The axis is perpendicular to the directrix.
- The axis passes through the vertex and the focus.
- The tangent at vertex is parallel to the directrix.
- The vertex is the midpoint of the focus and the point of intersection of directrix and axis.
- Tangents drawn to any point on the directrix are perpendicular.
Example 5
Find the equation of a parabola whose vertex is (−2,0) and focus is (0,0).
Let A (−2,0) is the vertex of the parabola and (0,0) is its focus.
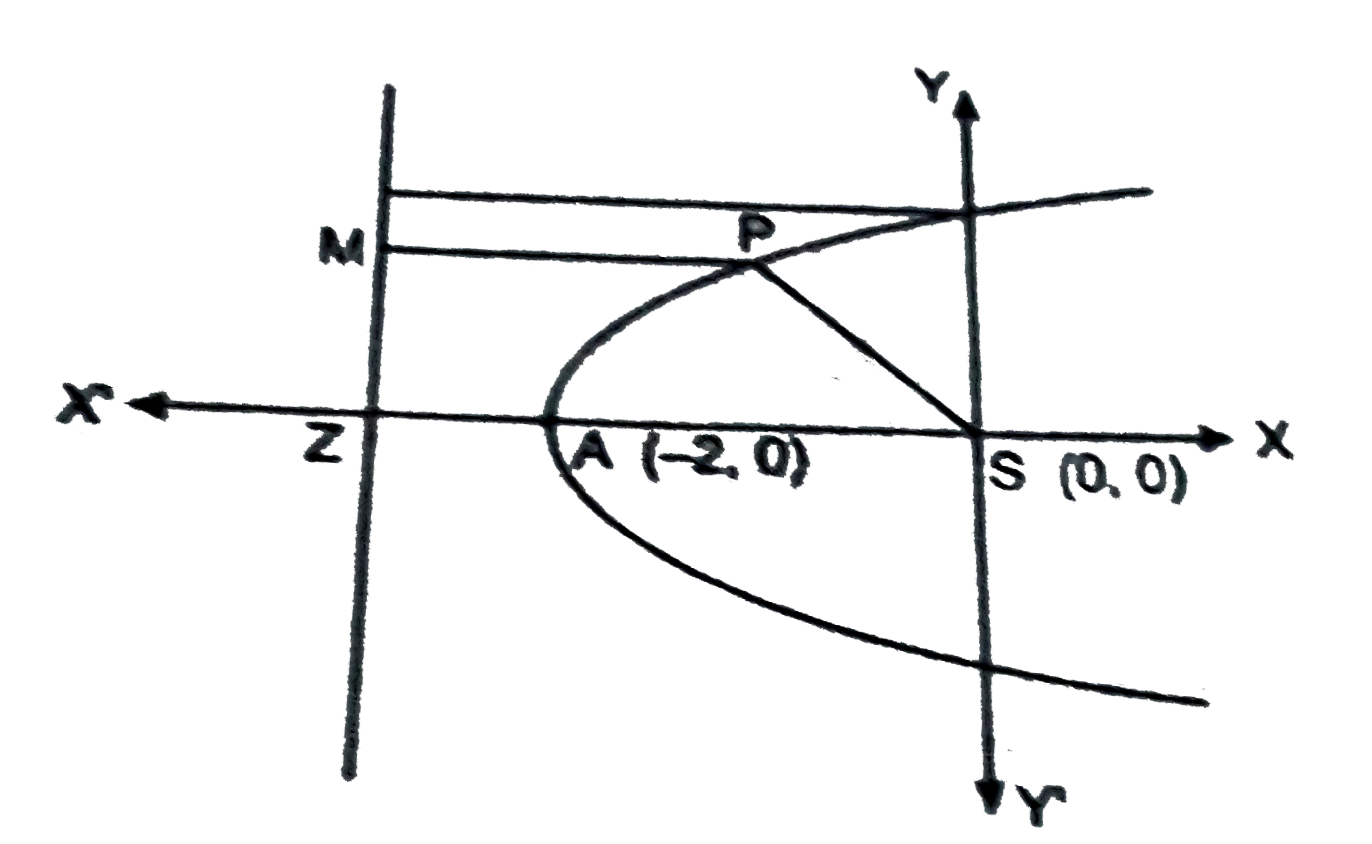
Now consider a point on x-axis such that
AZ=AS=2
∴ Co-ordinates of Z=(−4,0)
⇒ Equation of directrix ZM is x=−4.
⇒ x+4=0
Now the equation of parabola
PS=PM
Where, P(x,y) be any point on the parabola.
⇒ √(x−0)2+(y−0)2=x+4
⇒ x2+y2=(x+4)2
⇒ y2=8x+16
⇒ y2−8x−16=0
Example 6
Find the equation of a parabola whose focus is (−8,−2) and equation of directrix is y=2x−9.
Let the focus is S(−8,−2) and P (x,y) be any point on the parabola.
Now from the definition of parabola.
SP = distance of P from directrix
⇒√(x+8)2+(y+2)2=2x−y−9√22+(−1)2
⇒5(x2+16x+64+y2+4y+4)
⇒4x2+y2+81−4xy−36x+18y
⇒x2+4y2+4xy+116x+2y+259=0
Which is the required equation of parabola.
Ellipse
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.
Ellipse

The two fixed points are called the foci (plural of ‘focus’) of the ellipse. The mid point of the line segment joining the focus is called the center of the ellipse . The line segment through the focus of the ellipse is called the major axis and the line segment through the center and perpendicular to the major axis is called the minor axis . The end points of the major axis are called the vertices of the ellipse .
Hum major axis ko 2a se denote karte hai aur minor axis ko 2b and the distance between the foci by 2c. Thus, the length of the semi major axis is a and semi-minor axis is b.
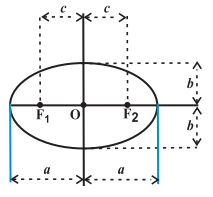
Relationship between semi-major axis, semi-minor axis and the distance of the focus from the centre of the ellipse :-
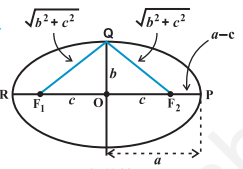
Major axis ke ek end par ek point P lete hai. Sum of the distances of the point P to the foci is
F1P + F2P = F1O + OP + F2P
(Since, F1P = F1O + OP)
= c+a+a−c
= 2a
Minor axis ke ek end par ek point Q lete hai. Sum of the distances of the point Q to the foci is
F1Q + F2Q = √b2+c2 + √b2+c2
= 2√b2+c2
Since both P and Q lies on the ellipse.
By the definition of ellipse, we have
2√b2+c2 = 2a
a=√b2+c2
a2=b2+c2
c=√a2−b2
Special cases of an ellipse
Case l : When (center) c=0 toh dono foci ellipse ke center par ek sath merge ho jati hai to a2=b2 i.e., a=b, and so the ellipse becomes circle.
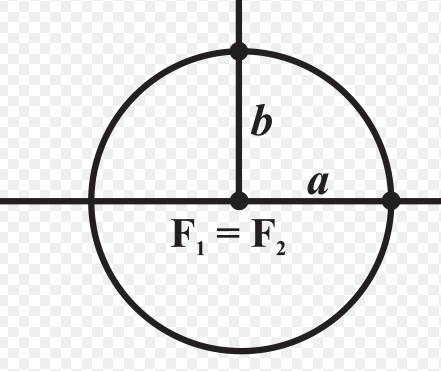
Case ll : When c=a, then b=0. The ellipse reduces to the line segment F1 F2 joining the two foci.

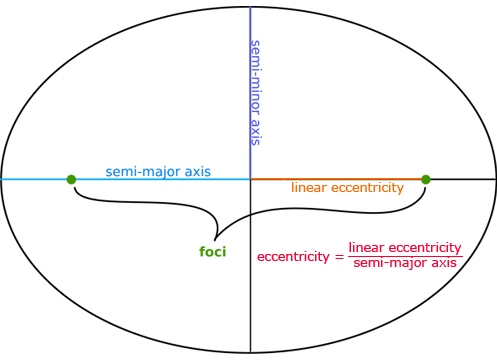
Eccentricity
Eccentricity ka basically matlab hota hai ratio , jo ki ellipse ke centre tak ke distance aur foci se ellipse ke vertices ke distance ka ratio bataye.
The eccentricity of an ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse (eccentricity is denoted by e) i.e., e=ca
Standard equations of an ellipse
The equation of an ellipse is simplest if the centre of the ellipse is at the origin and the foci are on the x - axis or y - axis . Humare paas abh do possible orientation nikal kar aate hai.
(a) When major axis is x - axis.

(b) When major axis is y - axis .
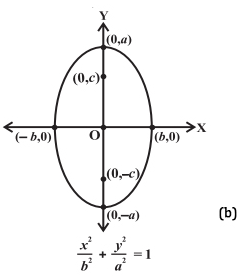
Abh hum ellipse ki equation derive karenge image (a) ki help se
Humne F1 and F2 ko as a foci liya hai aur O ko mid point of line segment of F1,F2 aur O ko as a origin bhi consider kiya hai. Jo line O se F2 ke through positive x - axis se pass hokar jati hai wo positive hoti hai aur jo line O se F1 ke through negative x - axis se pass hokar jati hai wo negative hoti hai. Let the coordinates of F1 be (−c,0) and F2 be (c,0)
Humne ellipse par ek point P (x,y) liya hai. Sum of the distances from P to the two foci be 2a So,
PF1 + PF2 = 2a........(1)
Using the distance formula, we have
√(x+c)2+y2 + √(x−c)2+y2 = 2a
√(x+c)2+y2 = 2a - √(x−c)2+y2
Squaring both sides, we get
(x+c)2+y2 = 4a2 - 4a √(x−c)2+y2 + (x−c)2 + y2
which on simplification gives
√(x−c)2+y2 = a - cax
Squaring again and simplifying, we get
x2a2 + y2a2−c2 = 1
x2a2 + y2b2 = 1 (since, c2 = a2 - b2)
Hence any point on the ellipse satisfies
x2a2 + y2b2 = 1 ....(2)
Conversely, let P (x,y) satisfy the equation (2) with 0 < c < a. Then y2 = b2 (1−x2a2)
∴ PF1 = √(x+c)2+y2
= √(x+c)2+b2(a2−x2a2)
= √(x+c)2+(a2−c2)(a2−x2a2) (since b2=a2−c2)
= √(a+cxa)2 = a+cax
Similarly, PF2 = a−cax
Hence, PF1 + PF2 = a+cax + a−cax = 2a......(3)
So, any point that satisfies x2a2+y2b2 = 1, satisfies the geometric condition and so P (x,y) lies on the ellipse.
Hence from (2) and (3), we proved that the equation of an ellipse with centre of the origin and major axis along the x - axis is
x2a2+y2b2 = 1
Latus rectum
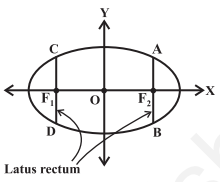
Ek ellipse ki latus rectum ek line segment hoti hai jo major axis ke perpendicular hoti hai kisi bhi foci ke through aur jiske end points ellipse par lie yani touch karte hai .
Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose end points lie on the ellipse.
To find the length of the latus rectum of the ellipse
x2a2+y2b2 = 1
Let the length of A are (c,l) ,i.e., (ae,l)
Since A lies on the ellipse x2a2+y2b2 = 1, we have
(ae)2a2 + l2b2 = 1
⇒ l2=b2(1−e2)
e2=c2a2=(a2−b2)a2=1−b2a2
∴ l2=b4a2, i.e., l=b2a
Since the ellipse is symmetric with respect to y - axis (of course, it is symmetric w.r.t. both the coordinate axes), A F2 = F2 B and so length of the latus rectum is 2b2a.
Ellipse in real life
Food items carrot, cucumber cut at an angle to its main axis results in elliptical shape and elegant look.

Properties of Ellipse
- Ellipse has two focal points, also called foci.
- The fixed distance is called a directrix.
- The total sum of each distance from the locus of an ellipse to the two focal points is constant.
- Ellipse has one major axis and one minor axis and a center.
Example 7
Find the equation of the ellipse whose major axis is 8 and minor axis is 4.
Let equation of ellipse be
x2a2+y2b2=1
Given that major axis 2a=8 and minor axis 2b=4.
⇒ a=4 and b=2
∴ Equation of ellipse
x242+y222=1
⇒ x216+y24=1.
Example 8
Find the equation of the ellipse whose centre is at origin, the distance between foci is 2 and eccentricity is 1√2.
Let the equation of the ellipse be x2a2+y2b2=1anda>b.
Here e=1√2 and the distance between foci = 2ae=2
⇒ ae=1
⇒ a(1√2)=1
⇒a=√2
⇒ a2=2
and b2=a2(1−e2)
=a2−(a2e2)
=2−1
=1
∴ Equation of ellipse
x22+y21=1
x2+2y2=2.
Hyperbola
A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.
Hyperbola
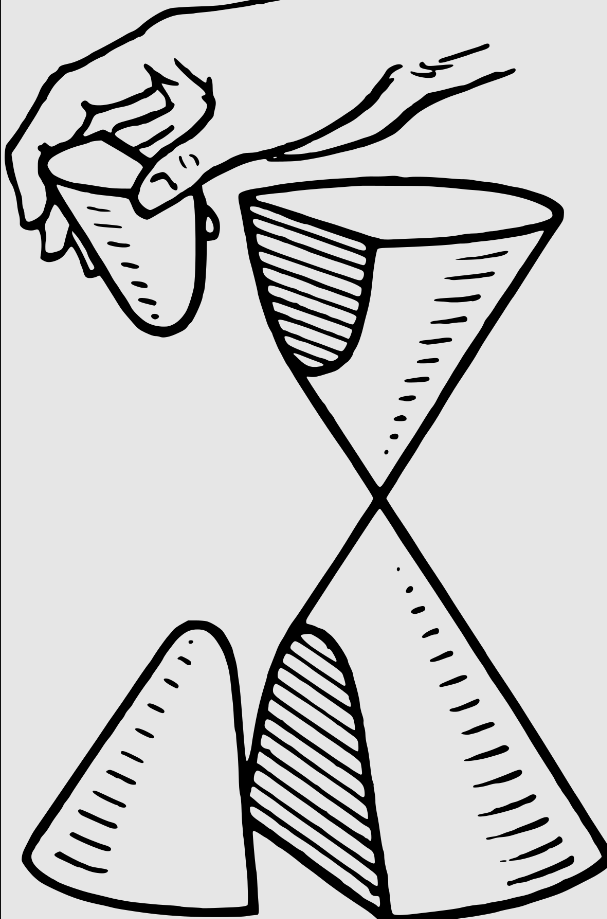
Hyperbola conic section ka ek special case hai kyuki ye hi cone ke dono nappe ko intersect karta hai.
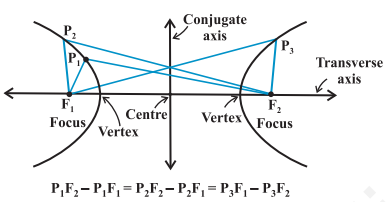
Hyperbola ki definition mai jo difference word use hua hai uska matlab hai ki farther point mai se closer point ko minus karna. Two fixed point yani F1 and F2 foci of the hyperbola kehlate hai. Jo line segment ke mid point yani foci ko join karte hai wo centre of the hyperbola kehlata hai. Jo line foci aur center se pass ho rahi hai wo transverse axis kehlati hai. Jo line center se pass aur transverse axis ke perpendicular hai wo Conjugate axis kehlati hai. Jis point par hyperbola transverse axis ko intersect kar raha h wo point vertices of the hyperbola kehlata hai.

Hum do foci ke beech ke distance ko 2c se denote karte hai aur do vertices ke beech ke distance ko 2a se denote karte hai. The length of conjugate axis is denoted by 2b and we define the quantity as b as
b=√c2−a2
Eccentricity
Just like an ellipse, the ratio e=ca is called the eccentricity of the
hyperbola. The eccentricity of a hyperbola is greater than 1.
Standard equation of Hyperbola
The equation of a hyperbola is simplest if the centre of the hyperbola is at the origin and the foci are on the x-axis or y-axis. Humare paas do possible orientation nikal kar aaye hai.
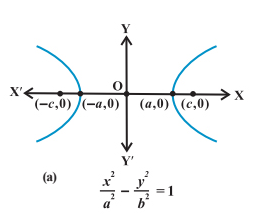
(a) When foci is on x - axis.
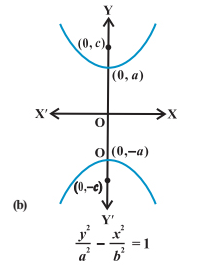
(b) When foci is on y - axis.
Abh hum image (a) se hyperbola ki equation derive karenge.
Humare paas do foci F1 and F2 hai. Let O be the origin aur jo line O and F2 se pass hokar jaye to wo positive x - axis ke through jati h . Jo line O and F1 se pass hokar jaye to wo negative x - axis ke through jati hai. Let the coordinates of F1 be (−c,0) and F2 be (c,0).
Let P(x,y) be any point on the hyperbola such that the difference of the distances from P to the farther point minus the closer point be 2a .
So given, PF1 - PF2 = 2a
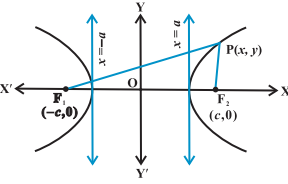
Using the distance formula, we have
√(x+c)2+y2 - √(x−c)2+y2 = 2a
√(x+c)2+y2 = 2a + √(x−c)2+y2
Squaring both sides
(x+c)2+y2 = 4a2+ 4a √(x−c)2+y2 + (x−c)2+y2
and on simplifying, we get
cxa - a = √(x−c)2+y2
On squaring again and further simplifying, we get
x2a2 - y2c2−a2 = 1
x2a2 - y2b2 = 1 (Since c2−a2=b2)
Hence any point on the hyperbola satisfies
x2a2 - y2b2 = 1
From the equation of the hyperbola we have obtained, it follows that, we
have for every point (x,y) on the hyperbola, x2a2 = 1 + y2b2 ≥ 1.
i.e, ∣∣xa∣∣ ≥ 1, i.e., x≤−a or x≥a.
Therefore no portion of the curve lies between the lines x=+a and x=−a, (i.e. no real intercept on the conjugate axis).
Similarly, we can derive the equation of the hyperbola in image (b) as y2a2−x2b2=1.
These two equations are known as the standard equations of hyperbolas.
Latus rectum
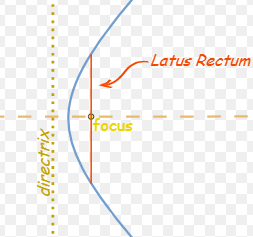
Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola. Half of the latus rectum is called the semi latus rectum.
Hyperbola in real life
A guitar is an example of hyperbola as its sides form hyperbola.

Note
A hyperbola in which a=b is called an equilateral hyperbola.
Properties of Hyperbola
- An ellipse is created by a plane intersecting a cone at the angle of its base.
- All ellipses have two foci or focal points. The sum of the distances from any point on the ellipse to the two focal points is a constant value.
- There is a center and a major and minor axis in all ellipses.
- The eccentricity value of all ellipses is less than one.
Example 9
Find the equation of hyperbola satisfying the following conditions: Foci (±4,0), the latus rectum is of length 12.
Foci (±4,0), lie on x - axis.
∴ ae=4⇒a2e2=16 . . . (1)
and latus rectum =2b2a=12
⇒ b2=6a . .(2)
⇒a2(e2−1)=6a
⇒a2e2−a2=6a
⇒ 16−a2=6a [From equation (1)]
⇒ a2+6a−16=0
⇒ (a+8)(a−2)=0
⇒ a=−8ora=2
But a cannot be negative.
∴a=2⇒a2=4
From equation (2)
b2=6×2=12
Now, equation of hyperbola
x2a2−y2b2=1
⇒x24−y212=1
⇒3x2−y2=12
Example 10
Find the equations of the hyperbola satisfying the given conditions : Foci (0,±13), the conjugate axis is of length 24.
Here, foci (0,±13) lie on y-axis
∴ be=13
⇒b2e2=169
and conjugate axis 2a=24
∴ a=12
⇒a2=144
Now,
a2=b2(e2−1)
⇒a2=b2e2−b2
⇒ 144=169−b2
⇒ b2=25
∴ Equation of hyperbola
y2b2−x2a2=1
⇒y225−x2144=1
Summary
In this chapter, we have studied the following points :-
- A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
- The equation of a circle with centre (h, k) and the radius r is (x−h)2+(y−k)2=r2
- A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point in the plane.
- The equation of the parabola with focus at (a0) a>0 and directrix x=−a is y=4ax
- Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose end points lie on the parabola.
- Parabola ke latus rectum ki length y2=4ax hai jo ki 4a hai.
- An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.
- The equation of an ellipse with foci on the x - axis is x2a2 + y2b2 = 1
- Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose end points lie on the ellipse.
- Length of the latus rectum of the ellipse x2a2 + y2b2 = 1 is 2b2a
- The eccentricity of an ellipse is the ratio between the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.
- A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.
- The equation of a hyperbola with foci on the x- axis is : x2a2 - y2b2 = 1
- Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola.
- Length of the latus rectum of the hyperbola : x2a2 - y2b2 = 1 is : 2b2a
- The eccentricity of a hyperbola is the ratio of the distances from the centre of the hyperbola to one of the foci and to one of the vertices of the hyperbola.