LINEAR INEQUALITIES for Class 11 MATHS
INTRODUCTION
So bacchon, ab tak humne one variable and two variables wale equations ko solve kr liya hai sath hi sath given statement se equation convert karna, then equations ko solve krna ye bhi hum aache se jante hai. Now, we will learn to form linear inequalities in one and two variables and solve them algebraically and graphically.
Linear Inequality
So bacchon Inequalities or kuch nhai balki aise mathematical statements hote hai jo kuch special signs ke sath likhe jate hai such as: < (less than) , > (greater than), ≤ (less than or equal) and ≥ (greater than or equal) .
Aap ek situation imagine kro, man lo aapke 5 friends hai sabhi ko aapko chocolates deni hai kyuki aapka birthday hai. Lakin aapki mother se aapko only 100 Rs hi milte hai, well in that case aapko 5 chocolates, 100 Rs ke andar hi lenei hogi. Pure 100 Rs kharch kr sakte ho aap lakin us se zayada aap kharch nahi kr sakte right !
If price of one chocolate is x then price of 5 chocolate is 5x . Therefore, we get inequality as
5x≤100.
Inequalities may be of below types :
ax+b<0
ax+b>0
ax+b≤0
ax+b≥0
ax+by<c
ax+by>c
ax+by≤c
ax+by≥c
ax2+bx+c≤0
ax2+bx+c>0.
Graphical solution of Linear Inequality in one variables
For One Variable
Let consider an inequality i.e. 5x≤100
For x=0 , L.H.S. =5×(0)=0.
Where , R.H.S=100 .
Here 0≤100, which is true.
For x=1, L.H.S. =5×(1)=5≤100 (R.H.S.), which is true.
Similarly we will check for other values,
For x=2, L.H.S. =5×(2)=10≤100 (R.H.S.), which is true.
And so on...............................................................................
..................................................................................
...................................................................................
For x=20, L.H.S. =5×(20)=100≤100 (R.H.S.), which is true.
For x=21, L.H.S. =5×(21)=105≤100 (R.H.S.), which is false.
Therefore, we can see that value of x which satisfy the inequality is {0,1,2,...,20}. Values, jo inequality ko satisy krti hai, are called solution of inequality.
Thus, hum ye keh sakte hai, any solution of an inequality in one variable is a value of the variable which makes it a true statement .
We may follow 2 rules to solve an inequality :
Rule 1 : Equal numbers may be added to (or subtracted from) both sides of an inequality without affecting the sign of inequality.
For example, if 2x−3>0 then 2x−3+3>0+3 ⇒2x>3
Rule 2 : Both sides of an inequality can be multiplied (or divided) by the same positive number. But when both sides are multiplied or divided by a negative number, then the sign of inequality is reversed.
For example, if 2x>3 then 122x>123 ⇒x>32.
if −3x>−9 then −13(−3x)<−13(−9)
[negative number is multiplied so inequality changes .]
⇒x<3
Graphically x<3 can be represented by region on line on left of 3. Yha par dyan do ki x ki jitne bhi solutions hone wale hai unme 3 included nahi hai . 
Similarly if > sign will come then region right side me hoga.
If value is not included in region, we will use hollow circle ∘.
Jaise ki aap previous example me dekh sakte hai 3 is not included.
If the value is included, we will use filled circle.
Note : In solution mark only those point which are in domain.
Example 1
Solve the inequation 3x−8<−2 and represent the solution on the number line when
(i) x∈R
(ii) x∈Z
(iii) x∈N.
Given 3x−8<−2
⇒3x<−2+8
⇒3x<6
⇒x<63
⇒x<2
(i) If x∈ R, which means solution contains all the rational and irrational numbers which is less than 2 so solution set = (−∞,2)
It can be represented on real line as follows:
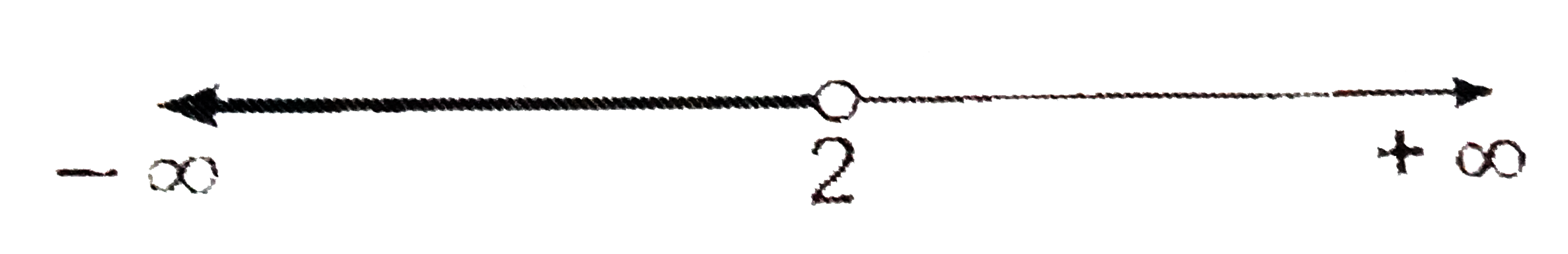
Friends yha dekho 2 solution me included nahi hai .
(ii) If x∈Z, then solution set ={...−3,−2,−1,0,1}, because here we have to take all integers jo 2 se chota ho.
It can be represented on number line as follows :
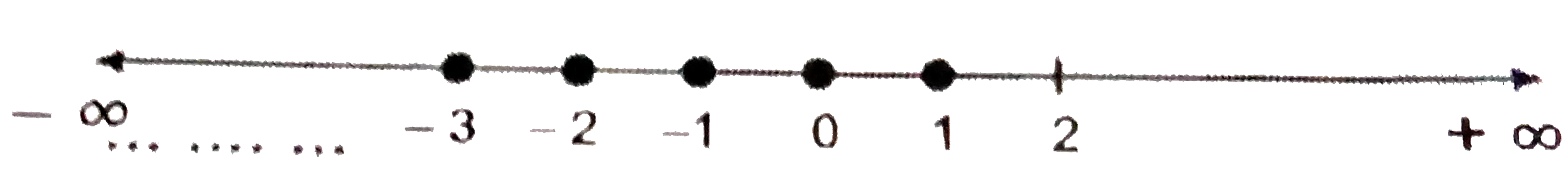
(iii) If x ∈ N, then solution set = {1}, because 1 is the only one natural number which is less than 2.
It can be represented on number line as follows :
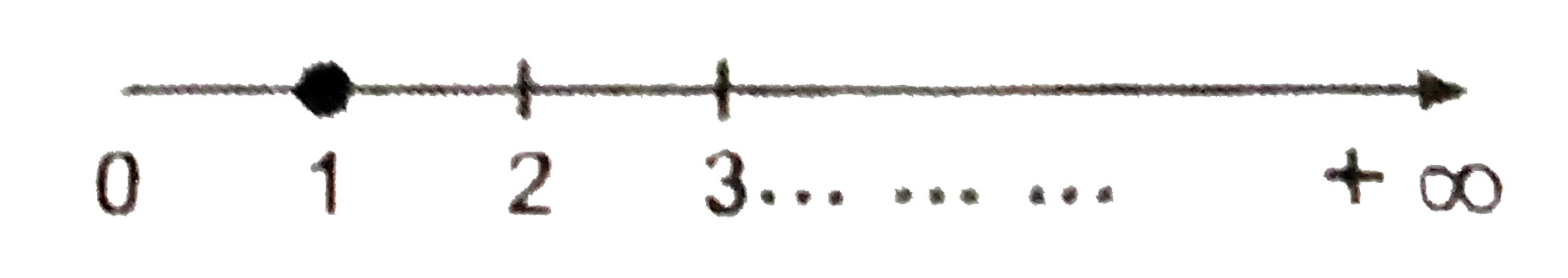
Example 2
Solve 2(2x+3)−10<6(x−2) and represent this solution on real line.
Given, 2(2x+3)−10<6(x−2)
⇒4x+6−10<6x−12
⇒4x−6x<−12−6+10
⇒−2x<−8
⇒x>4
Yha par hum ye man kr chlenge ki x ek real number hai kyuki x ko real line par show krna hai . And hum ye dekh sakte hau ki jo bhi value 4 se badi hogi that will be our solution jisme 4 ko include nahi krna hai.
∴ Solution set=(4,∞).
Solution set on number line. 
Example 3
Solve the inequation 3(x−2)5≤5(−x)3 and represent this solution on number line.
We have 3(x−2)5≤5(−x)3
Multiplying 15 on both side .
⇒15×3(x−2)5≤15×5(2−x)3
⇒9(x−2)≤25(2−x)
⇒9x−18≤50−25x
⇒34x≤68
⇒x≤2
So students , yha aapko dhyan dena hai ki our solution will be all real numbers which is less than 2, sath hi sath hume 2 ko bhi include karna hai.
∴Solution set = ( - ∞ , 2].
∴Solution set on number line
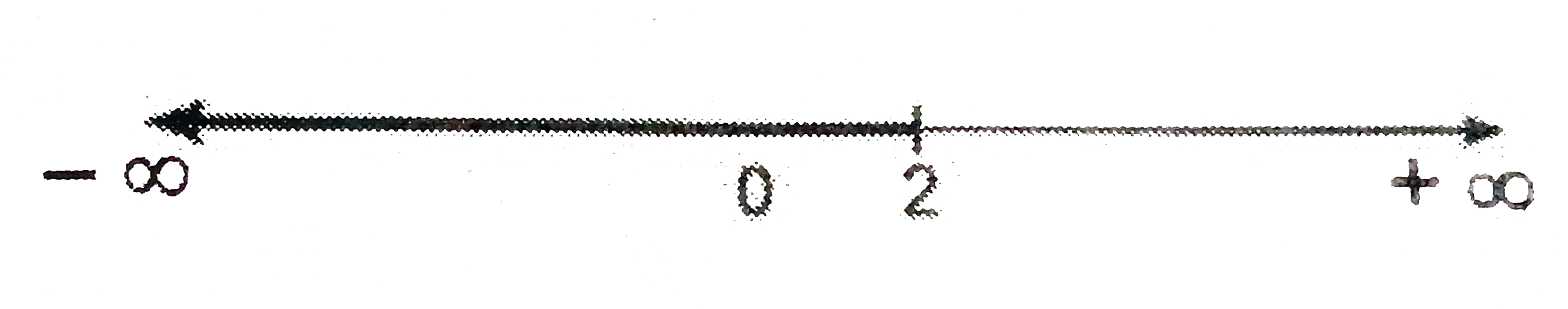
Q. So bacchon try to solve this linear iniquality x−2x+5>2.
Example 4
A student scores 65,62and70 marks is 3 subjects. Find the minimum marks scored by him in 4th subject to get an average of 64 minimum.
Let the student scores x marks in 4th subject
Then average =65+62+70+x4
But according to question minimum average should be 64.
⇒ Average is either 64 or more than 64 is also possible.
⇒65+62+70+x4≥64
⇒197+x≥256
⇒x≥59
∴ Minimum score in 4th subject =59.
Graphical solution of Linear Inequality in two Variables
In two variable let us suppose we have three possibilities :
(i) ax+by=c (ii) ax+by>c (iii) ax+by<c
To bacchon, jaisa ki hum sub jante hai, solution of linear inequality ka matlab hai aise points jo inequality ko satisfy kare.
Steps to find the region of the solution.
For linear inequality in two variable we need to first draw line by substituting inequality with = sign. After equating inequality with = sign, we get equation in form of ax+by=c.
Ab kise given equation with two variables ko graphically plot karna to hume aata hi hai. Humne previous classes me padha hai ye sab.
Let's have a quick revision. We can plot it by putting x=0 and obtain y then put y=0 and obtain x and then locate both point and join them. If it passes through origin then put some other value of y to obtain x.
Yha hum dhyan denge ki line divides the whole plane in two regions, first of all ise figure me dekho.
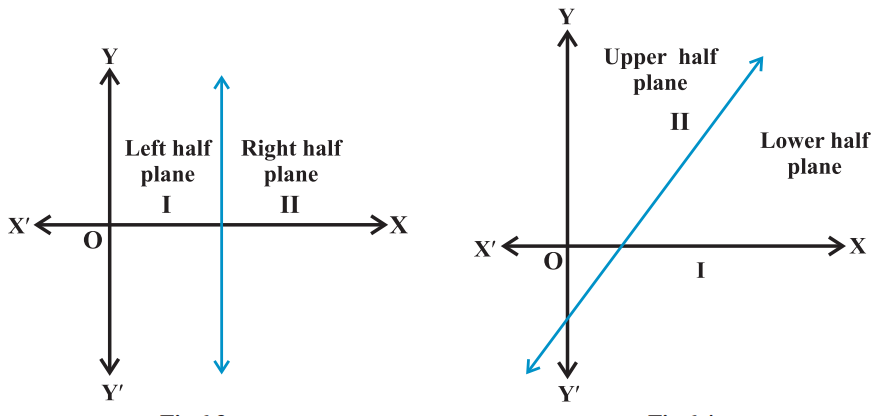
Hum two type ke cases observe kar sakte hai.
In our first case the portion which is right of line is called right half plane and portion which is on left is called left half plane.
In second case the portion which occupy upper region more is called upper half plane and portion which occupy lower region is called lower half plane.
Agar hume, ab ye pta karna hai ki humare iniquality ke liye kon sa correct region hoga, well in that case best way is, put origin (0,0) in inequality, lakin is baat ka dhyan rkhna hoga ki origin should not exist on the line .
To bacchon, yha pr jis bhi region me origin lie kre that will be our required region. Lakin agar origin khud line par lie krta hoga to yha hum koi random value lenge for example (x,y), to line ke jis bhi side par wo point lie krega that region will be our region for all the solutions.
NOTE : 1. The region containing all the solutions of an inequality is called the solution region and we will shade our solution region.
2. If an inequality is of the type ax+by≥c or ax+by≤c, points on line will be included in solution, so we will draw dark line.
3. If an inequality is of the form ax+by>c or ax+by<c, points on line will not be included in solution, so we will draw broken or dotted line.
Example 5
Solve the inequation x+y<5 by graphical method.
Given equation is x+y=5 .
At x=0 , y=5
At y=0, x=5
Yha se hume two points mil jate hai, which is required to form a line.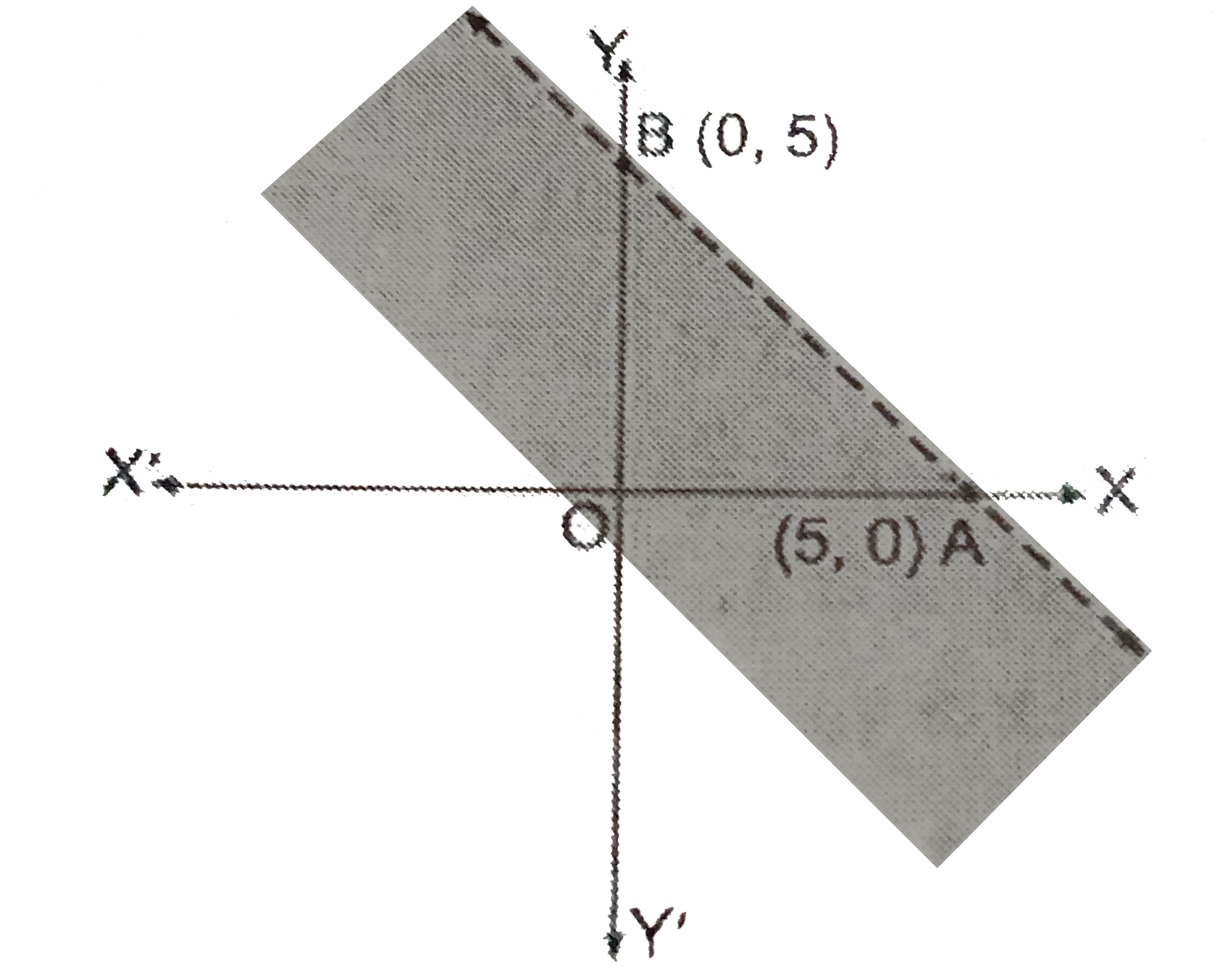
So the line passes through the points A(5,0) and B(0,5). Draw a dotted line passing through A and B.
Consider (0,0) and put in the given inequation
x+y<5
⇒0<5
Since, inequality satisfies with (0,0).
Yha hum dekh sakte hai, AB divides the XY-plane into two parts , we shade that part in which the point (0,0) lies. The shaded region is the required solution.
Example 6
Solve the inequation 2x−y≥3 by graphical method.
We have corresponding equation i.e. 2x−y=3.
At x=0, y=−3
At y=0, x=32
So students, yha we have two points to construct a line on cartesian plane.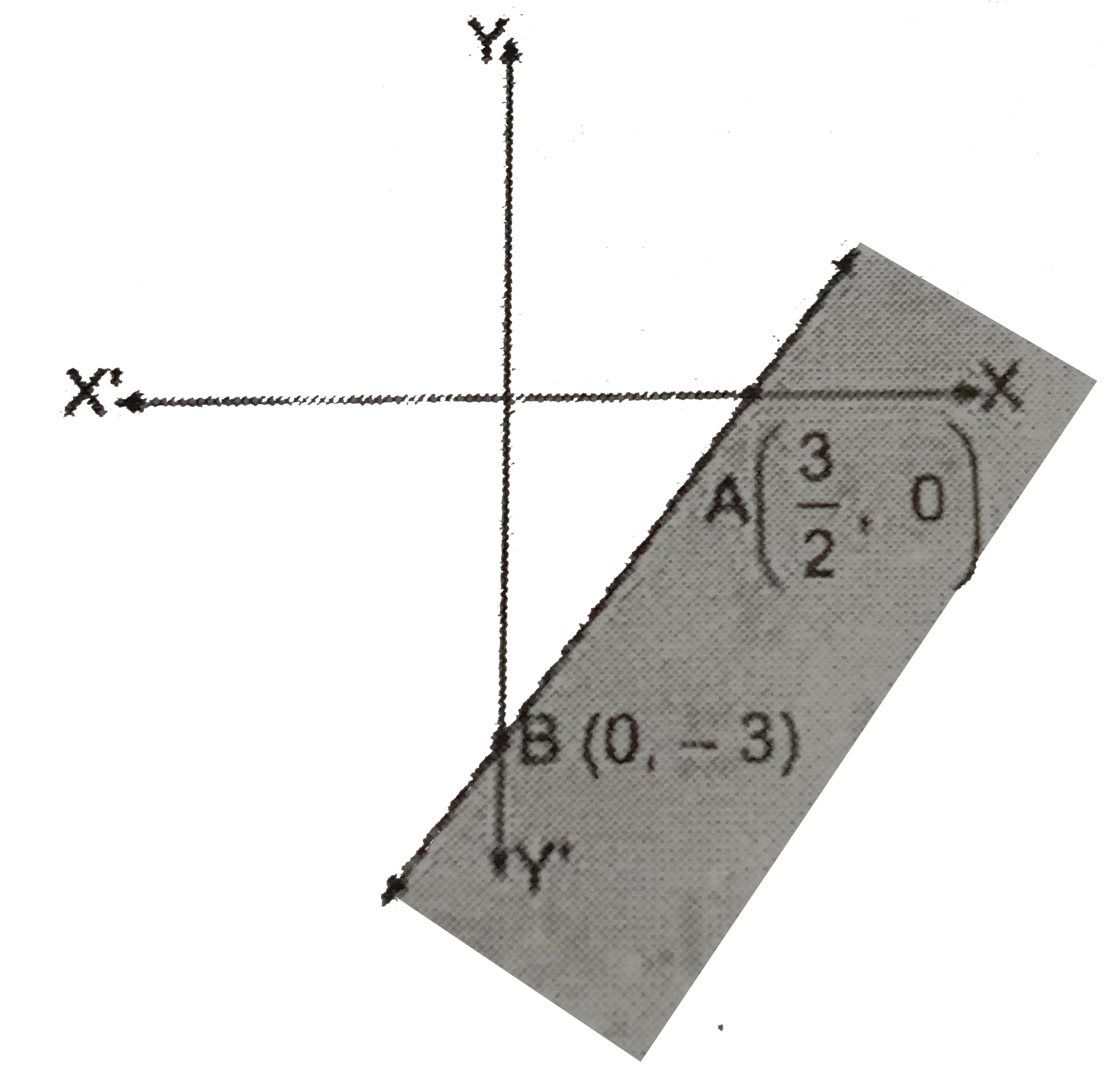
So the line 2x−y=3 passes through the points A(32,0)andB(0,−3). Draw a thick line passing through AB. Hum yha thick line isliye le rhe hai kyuki we have an inequality greater than or equal.
Now Consider a point (0,0) and put this value in the given inequation
⇒0≥3
which is false i.e. the inequation does not satisfy with (0,0). Sath hi sath, AB divides the XY−plane into two parts, we shade that region in which (0,0) does not lie. Now in the graph the shaded region is the required solution set.
Solution of System of Linear Inequalities in Two Variables
For solution of system of linear inequality in one or two variable we need to find solution region of both inequality and then find common region that will satisfy both the inequality.
If closed region is formed as solution region, then it is called bounded solution, otherwise it is called unbounded.
If no common solution is formed, then we can say that given linear inequalities does not have any solution.
Example 7
Solve the following system of inequation by graphical method:
2x+3y≤6, 3x+2y≤6, x≥0, y≥0
We have x≥0andy≥0
⇒ The solution of these inequations lies in first quadrant.
Similarly for the inequation 2x+3y≤6:
Corresponding equation is 2x+3y=6 jise further solve krne par, we notice that we are going to get a straight line which meets the X−axis and Y−axis at A(3,0) and B(0,2) respectively. Draw a thick line through AB. Put (0,0) in inequation, we get 0≤6 which is true i.e. inequation satisfies with (0,0).
Now, AB divides XY−plane into two parts, we shade that region in which the point (0,0) lies.
Similarly for the inequation 3x+2y≤6:
Corresponding equation is 3x+2y=6 jise further solve kerne par we can see that that hume ek straight line milti hai which meets the X−axis and Y−axis at C(2,0) and D(0,3) respectively. Draw a thick line through CD.
Put (0,0) in the inequation, we get 0≤6 which is true i.e. the inequality satisfies with (0,0).
CD divides XY−plane into two parts, we shade that region in which (0,0) lies.
Now the common shaded region of given four inequation is the required solution.

Summary
1. Two real numbers or two algebraic expressions related by the symbols <,>,≤or≥ form an inequality.
2. Equal numbers may be added to (or subtracted from ) both sides of an inequality.
3. Both sides of an inequality can be multiplied (or divided ) by the same positive number. But when both sides are multiplied (or divided) by a negative number , then the inequality is reversed.
4. The values of x , which make an inequality a true statement, are called solutions of the inequality.
5. To represent x<a(orx>a) on a number line, put a circle on the number a and dark line to the left (or right) of the number a.
6. To represent x≤a(orx≥a) on a number line, put a dark circle on the number a and dark the line to the left (or right) of the number x.
7. If an inequality is having ≤ or ≥ symbol, then the points on the line are also included in the solutions of the inequality and the graph of the inequality lies left (below) or right (above) of the graph of the equality represented by dark line that satisfies an arbitrary point in that part.
8. If an inequality is having < or > symbol, then the points on the line are not included in the solutions of the inequality and the graph of the inequality lies to the left (below) or right (above) of the graph of the corresponding equality represented by dotted line that satisfies an arbitrary point in that part.
9. The solution region of a system of inequalities is the region which satisfies all the given inequalities in the system simultaneously.
Let's Revise
ax+b<0
ax+b>0
ax+b≤0
ax+b≥0
ax+by<c
ax+by>c
ax+by≤c
ax+by≥c
ax2+bx+c≤0
ax2+bx+c>0
For linear inequality in two variable we need to first draw line by substituting inequality with = sign. After equating inequality with = sign we get equation in form of ax+by=c. If it passes through origin then put some other value of y to obtain x.

If closed region is formed as solution region, then it is called bounded solution, otherwise it is called unbounded.