प्रकाश-परावर्तन तथा अपवर्तन कक्षा 10 भौतिकी
भूमिका
जैसा की दिन में हम सभी चीजों को आसानी से देख सकते हैं, पर क्या रात को देखने में भी उतनी ही आसानी होती है? जी नहीं, कारण है सूर्य की उपस्थिति तथा अनुपस्थिति। किसी वस्तु के दृष्टिगोचर होने के लिए केवल सूर्य की उपस्थिति अथवा अनुपस्थिति एकमात्र कारण नहीं हैं। नीचे दिए चित्र में ध्यान दें तो स्पष्ट हैं कि दिन की स्थिति में हम वस्तु को सुगमता से देख पाते हैं, क्योंकि सूर्य का प्रकाश उपस्थित होता है, तथा रात में सूर्य का प्रकाश अनुपस्थित होता है जिस कारण से वस्तु को देखने में कठिनाई होती है।
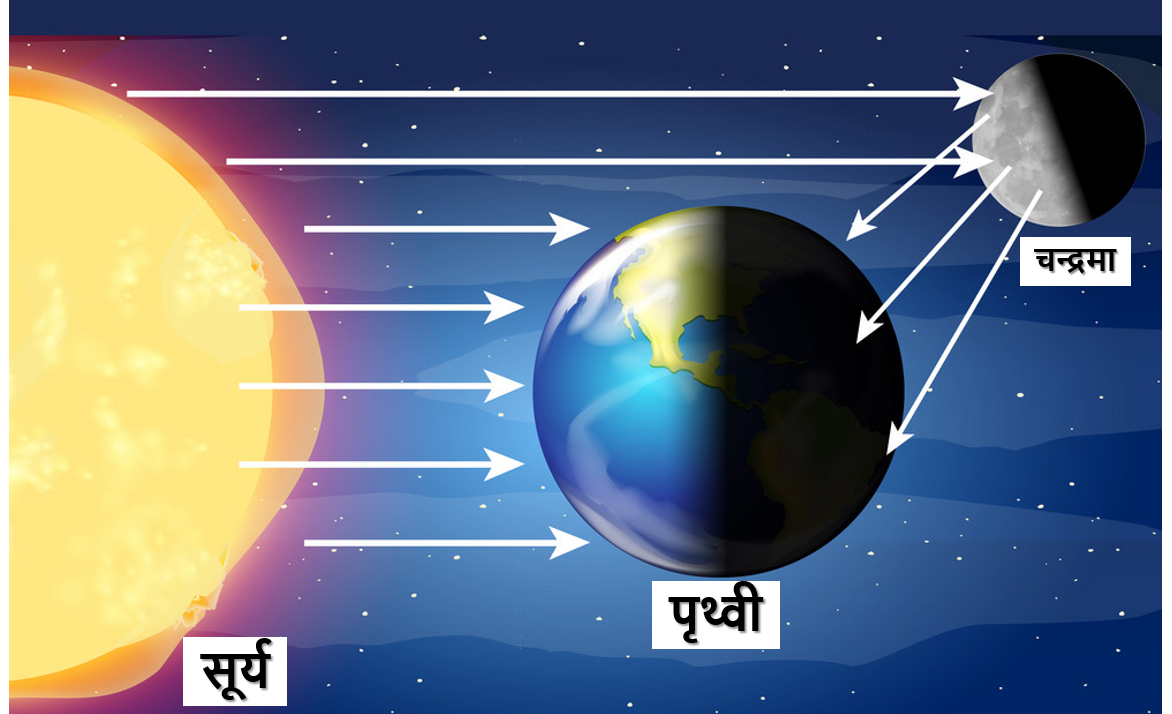
यह स्पष्ट है कि किसी वस्तु को देखने के लिए प्रकाश की उपस्थिति अनिवार्य हैं। अतः इस निष्कर्ष पर पहुंचा गया की प्रकाश एक प्रकार की ऊर्जा है, जो किसी वस्तु को देखने में सहायक है। अथवा किसी वस्तु को हम इसलिये देख सकते हैं क्योंकि प्रकाश उस वस्तु से परावर्तित होकर हमारी नेत्रों में प्रवेश कर जाती है। हमारी नेत्रों द्वारा मस्तिष्क को एक विद्युत सिग्नल भेजा जाता है, जिस से उस वस्तु के प्रतिबिंब को हम देख सकते हैं।
इस अध्याय में प्रकाश का अध्ययन हम किरणों के रूप में करेंगे। प्रकाश के गुण इस प्रकार है कि प्रकाश एक सीधी व सरल रेखा में गमन करता है। तथा प्रकाश की दोहरी प्रकृति होती है। अर्थात प्रकाश दो तरह के व्यवहार प्रदर्शित करता है। प्रकाश तरंग की भांति व्यवहार करता ही है, साथ ही साथ यह कण की भांति व्यवहार भी करता है। अतः प्रकाश गमन के लिए दो सिद्धांत अध्ययन किए जाते हैं।
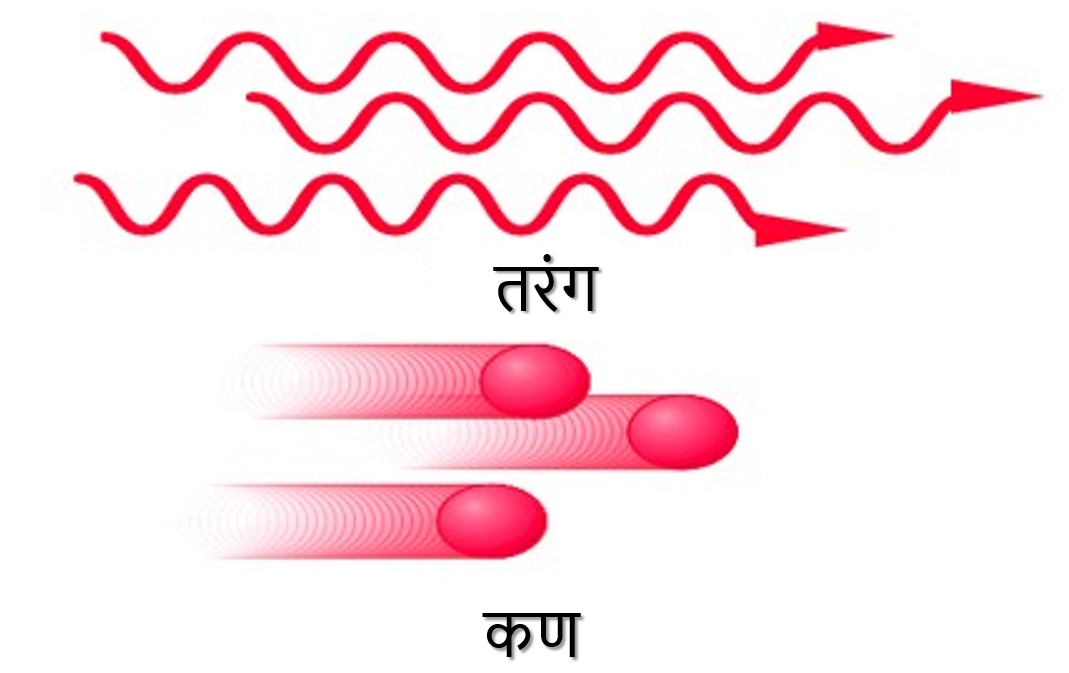
1. प्रकाश का तरंग सिद्धांत
इस सिद्धांत के अन्तर्गत प्रकाश एक विद्युत चुंबकीय तरंग है, जिसे गमन करने के लिए किसी माध्यम की आवश्यकता नहीं होती अर्थात यह वायु की अनुपस्थिति (निर्वात) में भी गति कर सकने में सक्षम है, तथा वायु की सर्वाधिक चाल निर्वात में ही होती है। जिसका अंकिक मान लगभग 3×108 मीटर प्रति सेकंड है।2. प्रकाश का कण सिद्धांत
इस सिद्धांत के अनुसार प्रकाश बहुत अधिक कणों का समुह है तथा सर्वाधिक गति से सीधी रेखा में गति करता है। जिन कणों से मिलकर प्रकाश बना है उन कणों को फोटॉन कहते हैं।परिभाषाएँ
प्रकाश ⇒ प्रकाश वह ऊर्जा है जिसके द्वारा हम वस्तुओं को देख सकते है।
प्रकाश के गुण निम्नलिखित है -
- प्रकाश सीधे रेखाओं ( सरल रेखा ) में गमन करता है।
- प्रकाश विद्युत चुंबकीय तरंग है, इसे गमन के लिए माध्यम की आवश्यकता नहीं होती।
- प्रकाश की चाल निर्वात में सर्वाधिक है : 3×108m/s
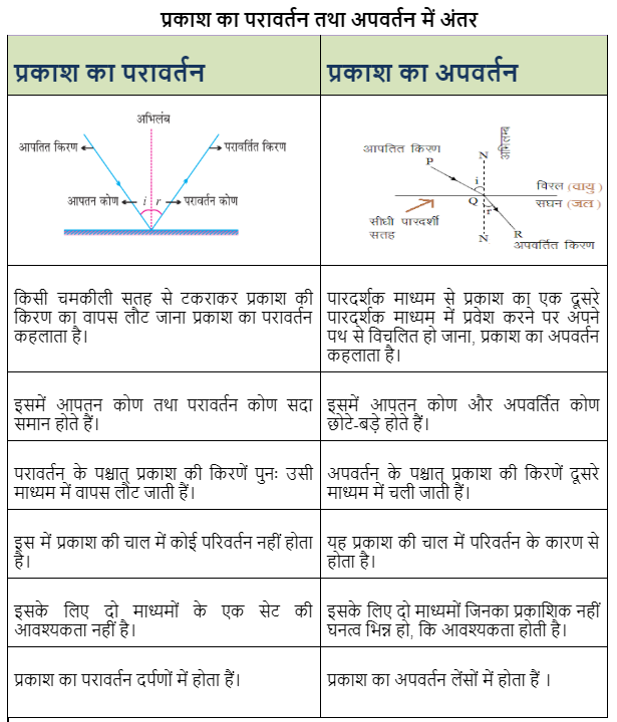
प्रकाश का परावर्तन ⇒ किसी समतल सतह पर प्रकाश की किरण का टकराकर वापस लौटने की प्रक्रिया प्रकाश का परावर्तन कहलाती है।
प्रकाश के परावर्तन के नियम निम्नलिखित है -
- आपतन कोण (आने वाली किरण के द्वारा अभिलम्ब पर बनाया गया कोण), परावर्तन कोण (परावर्तित किरण के द्वारा अभिलम्ब पर बनाया गया कोण) के बराबर होती है।
- आपतित किरण, परावर्तित किरण तथा सतह के आपतन बिन्दु पर अभिलम्ब सब एक ही तल मे होते है।
प्रतिबिंब ⇒ प्रतिबिंब का निर्माण उस बिन्दु पर होता है जहां दो या दो से अधिक प्रकाश किरण आपस में प्रतिच्छेद करें अथवा प्रतिच्छेद करती हुई प्रतीत हो।
समतल दर्पण द्वारा प्राप्त प्रतिबिंब -
- सदैव आभासी तथा सीधा प्राप्त होता है।
- प्रतिबिंब का आकार बिम्ब (वस्तु) के आकार के बराबर होता है।
- प्रतिबिंब की दूरी दर्पण से उतनी ही होगी जितनी दूरी बिम्ब की दर्पण से है।
- सदैव पार्श्व प्रतिबिंब (दाया भाग बाई ओर तथा बाय भाग दाईं ओर) प्राप्त होता है।
गोलीय दर्पण ⇒ इनका आकार अल्पगोलीय (खोखले गोले का अल्प हिस्सा) होता है, या वक्रीय होता है।
- अवतल दर्पण⇒ ऐसा गोलीय दर्पण जिसका परावर्तक पृष्ठ गोले के केंद्र की ओर वक्रित हो, अवतल दर्पण कहलाता है।
- उत्तल दर्पण⇒ उत्तल दर्पण ऐसा गोलीय दर्पण है जिसका परावर्तक पृष्ठ बाहर की ओर वक्रित होता है।
प्रकाश का अपवर्तन ⇒ जब प्रकाश एक माध्यम से दूसरे माध्यम में प्रवेश करता है तब उसकी दिशा कुछ परिवर्तित हो जाती है, यह परिघटना प्रकाश अपवर्तन कहलाती है।
प्रकाश अपवर्तन के नियम
- आपतित किरण, अपवर्तित किरण तथा दोनों माध्यम को पृथक करने वाले पृष्ठ के आपतन बिंदु पर अभिलम्ब खींचा जाए तो यह तीनों एक ही तल में होंगे।
- प्रकाश के निश्चित माध्यमों के युग्म के लिए आपतन कोण की ज्या (sine) तथा अपवर्तन कोण की ज्या (sine) का अनुपात नियत होता है। जिसे पहले माध्यम के सापेक्ष दूसरे माध्यम का अपवर्तनांक कहते हैं।
अर्थात
यदि आपतन कोण i तथा अपवर्तन कोण r हो तबsinisinr= अपवर्तनांक 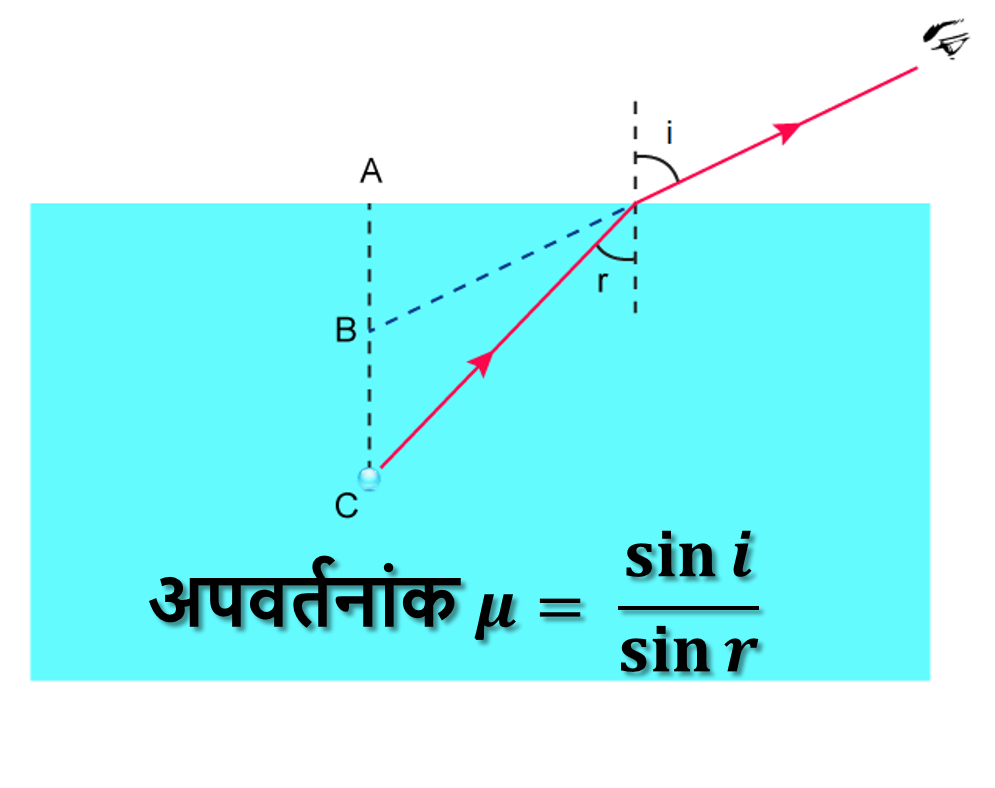
इस नियम को स्नेल का अपवर्तन का नियम भी कहते हैं।
अपवर्तनांक ⇒ किसी पदार्थ का अपवर्तनांक ज्ञात करने के लिए निर्वात में प्रकाश की चाल से विभिन्न माध्यमों में प्रकाश की चालो का अनुपात निकालते है।
यदि निर्वात में प्रकाश की चाल को c तथा किसी माध्यम में प्रकाश की चाल को v से प्रदर्शित करें तो उस माध्यम का निर्वात के सापेक्ष अपवर्तनांक
इसी तरीके से यदि वायु के सापेक्ष कांच का अपवर्तनांक निकाले तब
लेन्स ⇒ लेंस दो पृष्ठों का घिरा हुआ किसी पारदर्शी माध्यम से बना पदार्थ होता है, जिसका एक सिरा अथवा दोनों सिरा अल्प गोलीय होता हैं।
गोले में उभार अथवा गहराई के आधार पर लेंसों का दो भागों में वर्गीकरण निम्न है।
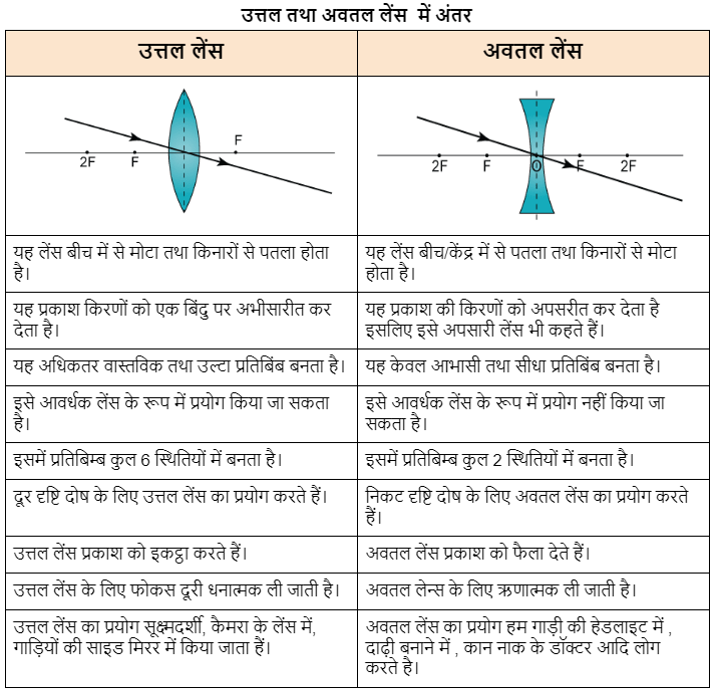
- उत्तल लेन्स ⇒ उत्तल लेंस का गोलिय भाग उभरा हुआ होता है। उत्तल लेंस में किनारों की अपेक्षा मध्य में अधिक मोटाई होती है। उत्तल लेंस प्रकाश किरणों को अभिसारित कर देता है, इसीलिए उत्तल लेंस को अभिसारी लेंस भी कहते है।
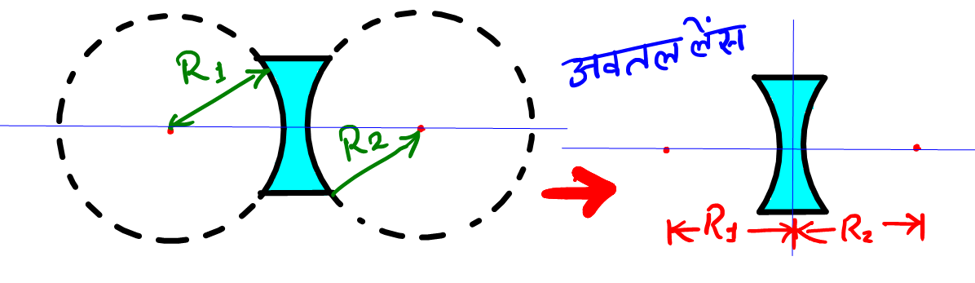
- अवतल लेंस ⇒ उत्तल लेंस के विपरीत अवतल लेंस में मध्य का भाग गहराई लिए होता है। अर्थात बीच का भाग किनारों की अपेक्षा पतला होता है। अवतल लेंस को अपसारी लेंस भी कहते हैं।
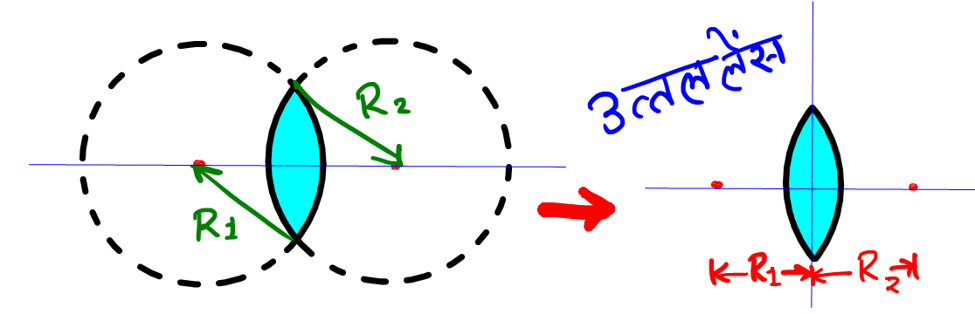
आवर्धन ⇒ लेन्स आवर्धन के अंतर्गत यह अवलोकित किया जायेगा कि वस्तु का प्रतिबिंब किस तरीके से आकार में बड़ा निर्मित होगा।
आवर्धन m = प्रतिबिंब की ऊंचाई / बिंब (वस्तु) की ऊंचाई
आवर्धन का मान 1 से कम होगा यदि प्रतिबिंब छोटा बनेगा।
लेंस की क्षमता ⇒ लेंस प्रकाश को अपरिवर्तित करके उसके मार्ग में से कुछ विचलित देती है, प्रकाश को उसके मार्ग से विचलित करना (मोड़ना) ही लेंस का कार्य है। उत्तल लेंस की क्षमता अधिक तब होगी जब लेंस प्रकाश को अधिक मोड़ पाए।
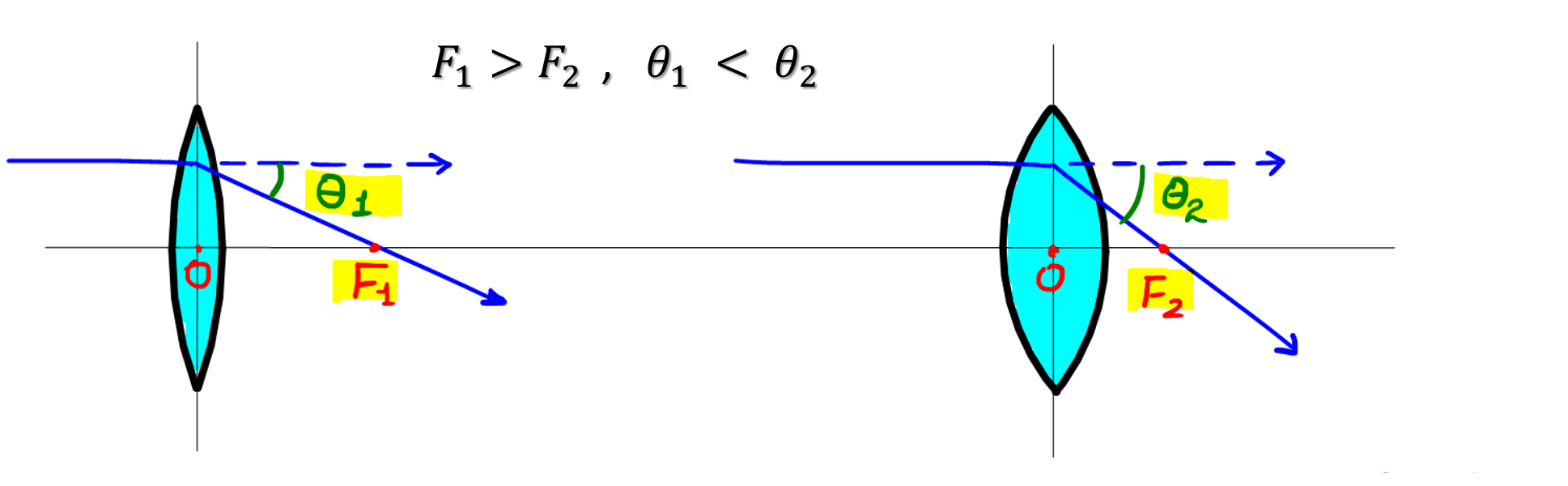
प्रकाश का परावर्तन
चिकनी सतह पर इस प्रकार की घटना को बहुत आसानी से देखा जा सकता हैं, उदाहरण के लिए रसोईघर में उपयोग होने वाले किसी थाली को देखकर प्रकाश के परावर्तन की घटना से साक्षात्कार किया जा सकता हैं।
प्रकाश का परावर्तन भौतिक विज्ञान की एक घटना है, अतः यह भी कुछ नियमों का पालन करती है जो निम्नलिखित है।
- परावर्तन कोण का मान सदैव आपतन कोण के मान के बराबर होता है। इसका अर्थ है कि सतह के ओर आने वाली प्रकाश किरण जितना कोण अभिलंब पर बनाती है उतना ही कोण सतह से परावर्तित होकर जाने वाली किरण बनाती है। यहां अभिलंब से तात्पर्य अपतन बिंदु पर उपस्थित उस लम्ब से है जो परावर्तक सतह के तल से लंबवत है।
- आपतित किरण, परावर्तित किरण तथा आपतन बिंदु पर अभिलंब एक ही तल में उपस्थित होते हैं।
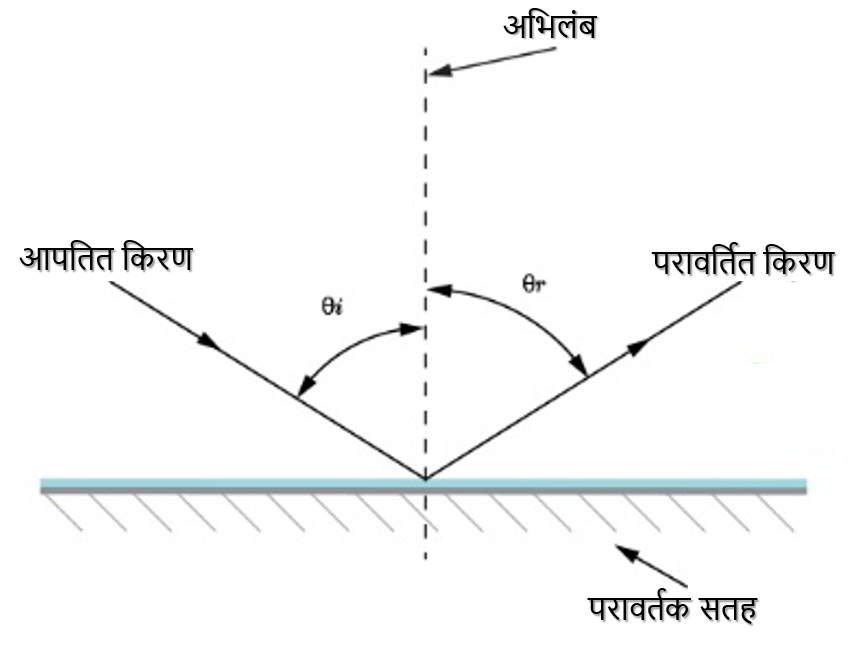
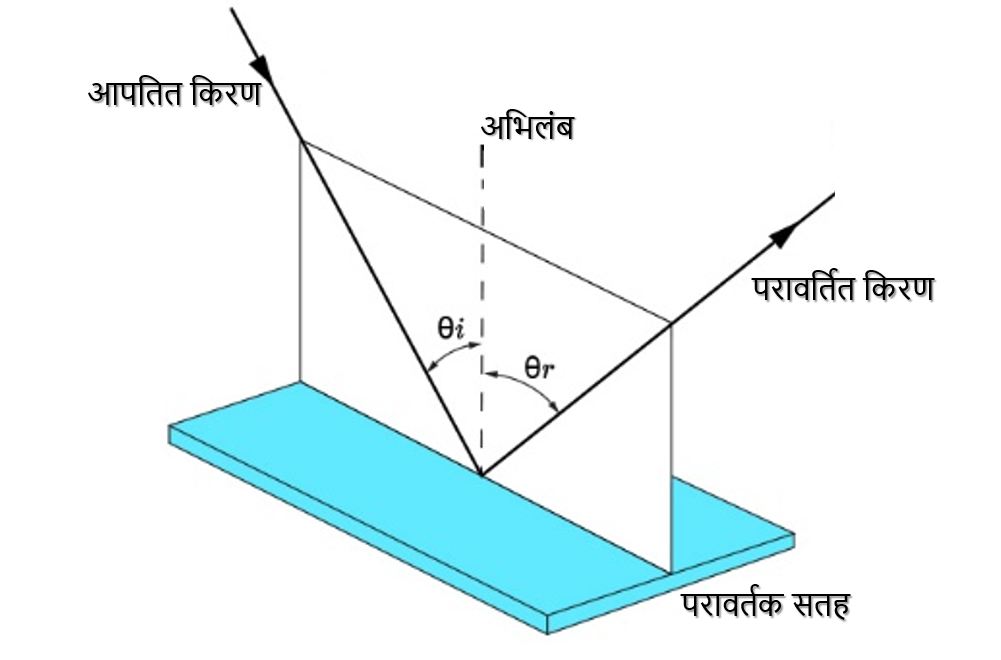
उपर्युक्त दिए गए परावर्तन के दोनो नियम सभी प्रकार के परावर्तक सतह पर लागू होते हैं, चाहे सतह समतल हो अथवा गोलीय।
अध्याय में प्रयुक्त वर्ण
गोलीय दर्पण में प्रयुक्त होने वाले कुछ वर्ण
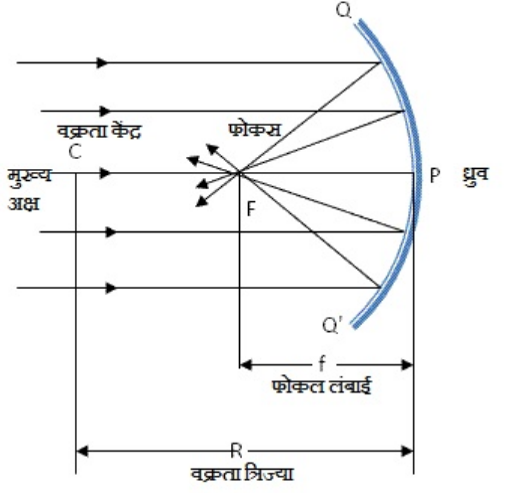
ध्रुव - गोलीय पृष्ठ के परावर्तक सतह के मध्य बिन्दु को ध्रुव (P) कहते है।
वक्रता केंद्र - जिस वक्र से उत्तल अथवा अवतल दर्पण बना है उस वक्र को यदि संपूर्ण गोले में परावर्तित कर दें तो हमें एक केंद्र बिंदु प्राप्त होता है जिसे उस दर्पण की वक्रता केंद्र (C) कहते हैं।
मुख्य अक्ष - ध्रुव तथा वक्रता त्रिज्या से होकर गुजरने वाली सरल रेखा मुख्य अक्ष कहलाती है।
वक्रता त्रिज्या - ध्रुव (P) से वक्रता केंद्र (C) की दूरी को वक्रता त्रिज्या (R) कहते हैं।
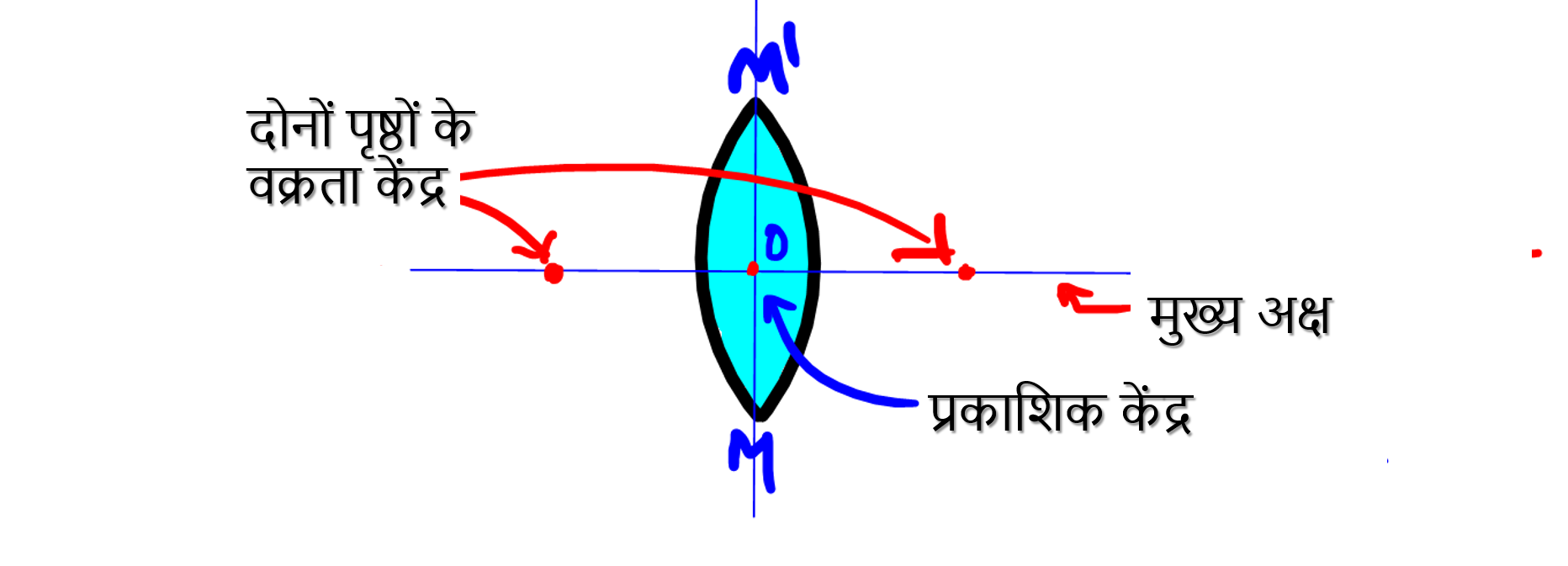
गोलीय लेंस में प्रयुक्त होने वाले कुछ वर्ण
मुख्य अक्ष - किसी लेंस का मुख्य अक्ष वह अक्ष होता है जिस अक्ष में लेंस के दोनों पृष्ठों के वक्रता केंद्र उपस्थित होते हैं।
प्रतिबिंब के प्रकार
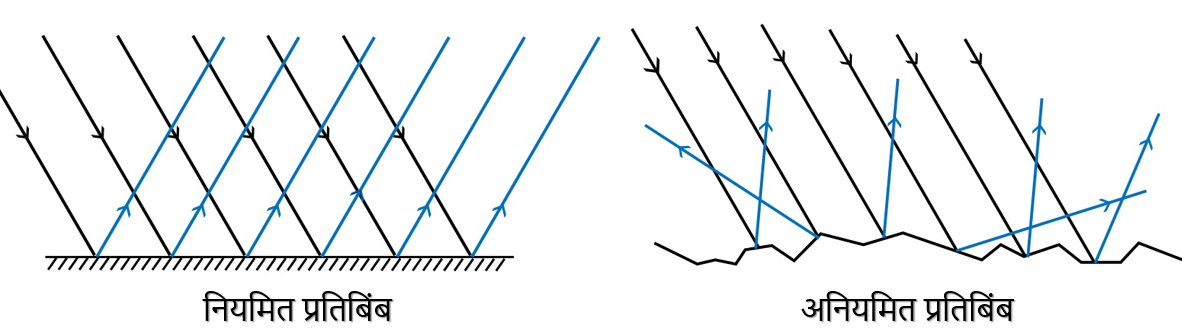
स्पष्ट प्रतिबिंब वहाँ पर बनता है जहां पर दो या दो से अधिक प्रकाश किरणें आपस में एक दूसरे को प्रतिच्छेद करें। परावर्तन के आधार पर प्रतिबिंब के दो प्रकार होते है।
- नियमित प्रतिबिंब ⇒ नियमित प्रतिबिंब के निर्माण के लिए आवश्यक है कि परावर्तक सतह चिकना हो और अच्छी तरह से पालिश किया जाए जिससे कि उस पर जो भी समांतर किरणें आपतित हो वह समांतर ही परिवर्तित हो। सबसे अच्छा उदाहरण हम समतल दर्पण के रूप में देख सकते हैं।
- अनियमित प्रतिबिंब ⇒ यदि परावर्तक सतह खुरदूरी हो तब उस स्थिति में समांतर किरणों के आपतित होने पर भी वह किरणें परावर्तित होकर समांतर नहीं रहेगी। जिस अनियमितता की वजह से प्रतिबिंब अनियमित प्राप्त होता हैं।
चिन्ह परिपाटी
गोलीय दर्पण द्वारा परावर्तन के लिए चिन्ह परिपाटी
- किसी दर्पण के लिये परिपाटी का मुल बिंदु उसी दर्पण का ध्रुव होता है तथा ध्रुव को P से दर्शाते है।
- वस्तु को हमेशा दर्पण के बायीं ओर रखा जाता है। इसका अर्थ है कि दर्पण पर वस्तु से प्रकाश बायीं ओर से आपतित होता है।
- मुख्य अक्ष के समांतर सभी दूरियाँ दर्पण के ध्रुव से मापी जाती हैं।
- मूल बिंदु के दाईं ओर मापी गई सभी दूरियां धनात्मक तथा बाईं ओर मापी गई सभी दूरियां ऋणात्मक लिया जाता है।
- मुख्य अक्ष के लंबवत तथा ऊपर की ओर (+y अक्ष के अनुदिश) मापी जाने वाली दूरियों को धनात्मक तथा नीचें की ओर (-y अक्ष के अनुदिश) मापी जाने वाली सभी दूरियों को ऋणात्मक मानेंगे।

गोलीय लेंसों के लिए चिन्ह परिपाटी
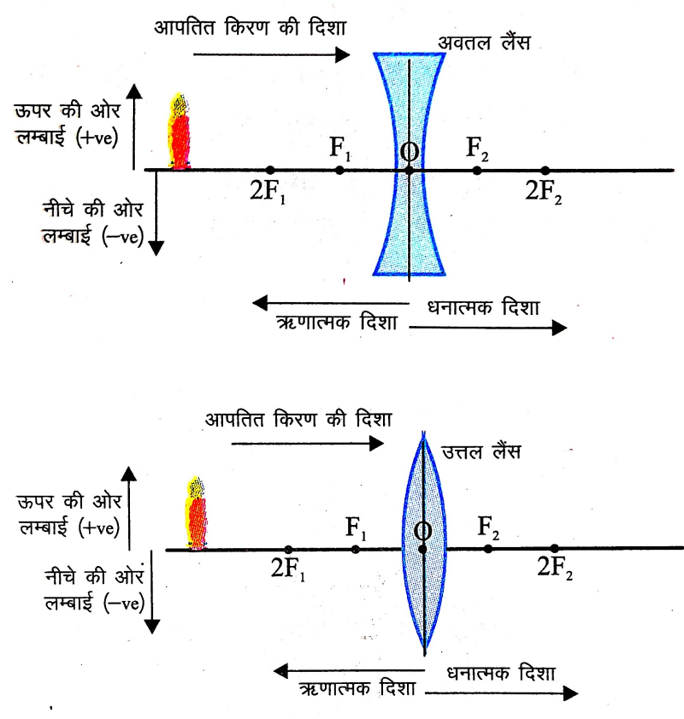
लेंसो में दाई ओर की लंबाई को धनात्मक तथा बायी ओर की लम्बाई को ऋणात्मक में लिया जाएगा तथा सारे माप प्रकाशिक केंद्र से लिया जाएगा।
दर्पण के प्रकार
आकृति के आधार पर दर्पणों को निम्न तरीके से वर्गीकृत किया गया हैं।
- समतल दर्पण
- गोलीय दर्पण
- उत्तल दर्पण
- अवतल दर्पण
समतल दर्पण
यह एक समतल पारदर्शी सतह से निर्मित होता है जिसकी एक सतह में परावर्तक पदार्थ (चाँदी के वर्क) की कलई (पॉलिश) कर दी जाती है। जिससे कि दूसरे सतह पर आने वाली प्रकाश कितने परावर्तित हो जाए। समतल दर्पण पर प्रतिबिंब सदैव सीधा प्राप्त होता है, तथा यह आभासी प्रकृति का होता है। आभासी इसलिए होता है क्योंकि यहां पर प्रकाश की दो किरणें वास्तव में प्रतिच्छेद नहीं करती अपितु हमें भ्रम होता है, अथवा आभास होता है।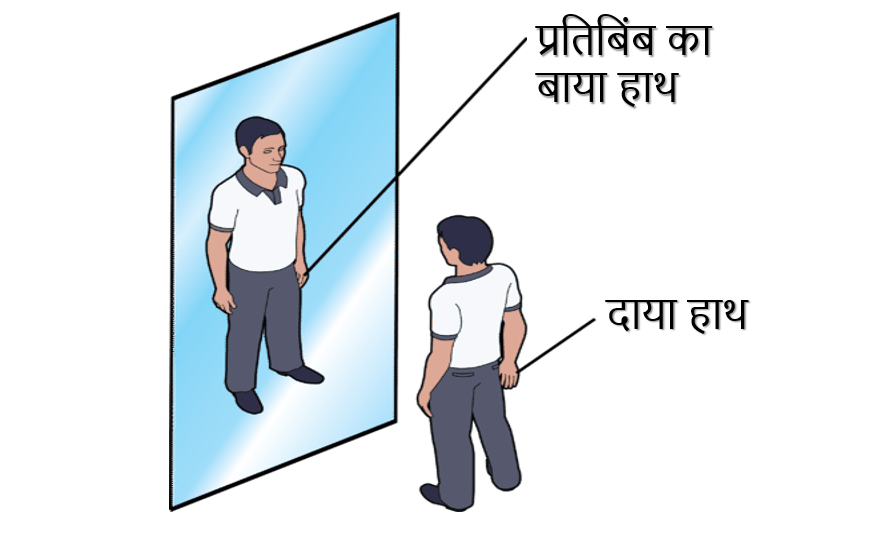
- समतल दर्पण का उपयोग हम दैनिक जीवन में स्वयं का प्रतिबिंब देखने के लिये करते है।
- समतल दर्पण से बना प्रतिबिंब सीधा होता है, तथा दर्पण से प्रतिबिंब की दूरी सदैव दर्पण से वस्तु की दूरी के बराबर होती है।
- समतल दर्पण में देखते हुए यदि हम अपना दाया हाथ उठाए तो हमें हमारे प्रतिबिंब का बाया हाथ उठा हुआ दिखेगा जिसे हम पार्श्व प्रतिबिंब कहते हैं।
- समतल दर्पण में बना प्रतिबिंब का आकार वस्तु के आकार के सामान होता है।
गोलीय दर्पण
यह समतल दर्पण से कुछ अलग प्रकार के दर्पण हैं। इनका आकार अल्पगोलीय (खोखले गोले का अल्प हिस्सा) होता है, या वक्रीय होता है।गोलीय दर्पण के दो प्रकार होते है।
- अवतल दर्पण
- उत्तल दर्पण
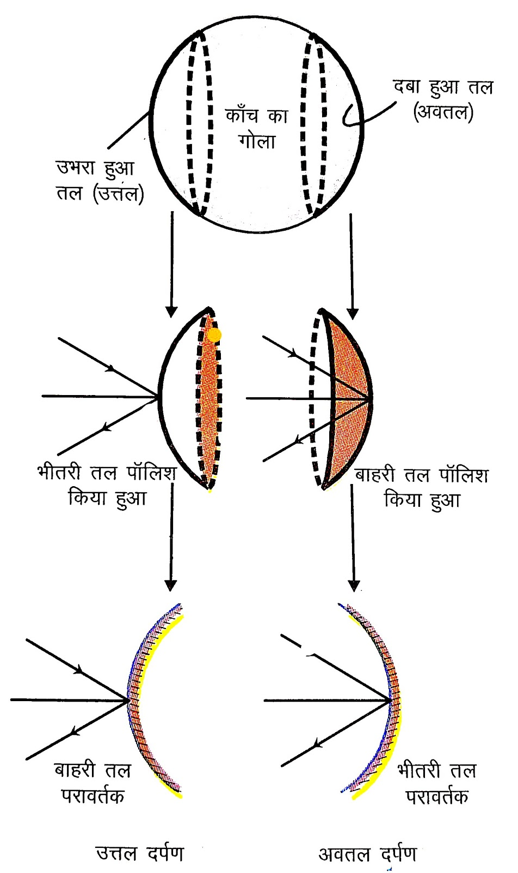
1. अवतल दर्पण
इस गोलीय दर्पण में गोले के केंद्र की ओर से बाहरी सिरे में पॉलिश कर दिया जाता है। जिससे की आंतरिक सतह परावर्तक सतह बन जाए। अवतल दर्पण का उदाहरण देखने के लिए आप रसोईघर का चम्मच का अवलोकन कर सकते हैं जिसका वह तल अवतल दर्पण की भांति व्यवहार करेगा जिस तल पर भोजन के निवाले को उठाया जाता है।2. उत्तल दर्पण
अवतल दर्पण की तरह ही समान गोलिय कांच लेकर पॉलिश यदि केंद्र से बाहर की ओर ना करते हुए अंदर की ओर कर दिया जाए तो बाहर की सतह परावर्तक सतह बन जाएगी जिसे उत्तल दर्पण कहते हैं। उसी चम्मच में पीछे की सतह जो उभरी हुई होती है उत्तल दर्पण का बहुत अच्छा उदाहरण है।
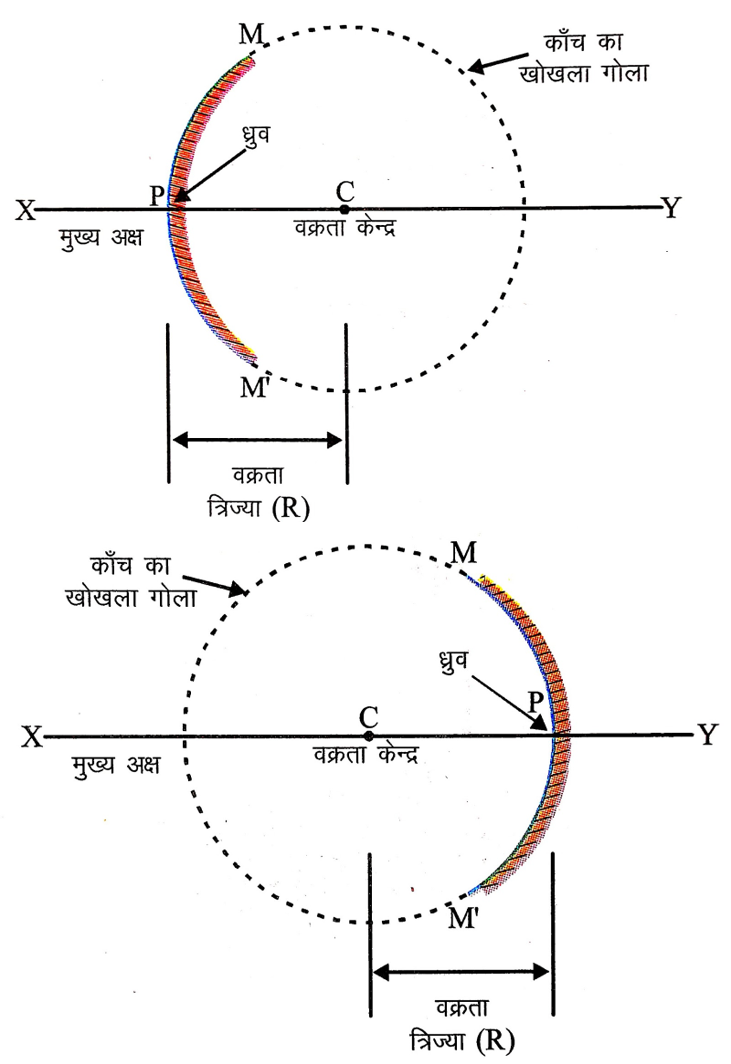
- किसी भी गोलीय पृष्ठ में परावर्तक सतह के मध्य बिंदु को ध्रुव (P) कहते हैं।
- जिस वक्र से उत्तल अथवा अवतल दर्पण बना है उस वक्र को यदि संपूर्ण गोले में परावर्तित कर दें तो हमें एक केंद्र बिंदु प्राप्त होता है जिसे उस दर्पण की वक्रता केंद्र (C) कहते हैं क्योंकि यह वक्र की त्रिज्या है।
- ध्रुव तथा वक्रता त्रिज्या से होकर गुजरने वाली सरल रेखा मुख्य अक्ष कहलाती है।
- ध्रुव (P) से वक्रता केंद्र (C) की दूरी को वक्रता त्रिज्या (R) कहते हैं।
दर्पणों के किरण आरेख
अवतल दर्पण द्वारा किरण आरेख
- दर्पण के मुख्य अक्ष के समांतर आपतित प्रकाश किरण परावर्तन के पश्चात अवतल दर्पण के मुख्य फोकस से गुजरेगी।
- अवतल दर्पण के मुख्य फोकस से गुजरने वाली किरण परावर्तन के पश्चात मुख्य अक्ष के समांतर निकलेगी।
- अवतल दर्पण के वक्रता केन्द्र से गुजरने वाली किरण परावर्तन के पश्चात उसी दिशा में वापस परावर्तित हो जाती है।
- अवतल दर्पण के बिंदु P की ओर मुख्य अक्ष से तिर्यक दिशा में आपतित किरण तिर्यक दिशा में ही परावर्तित होती है। आपतित तथा परावर्तित किरणें आपतन बिंदु पर मुख्य अक्ष से समान कोण बनाती है।
अवतल दर्पण के उपयोग
- सामान्यत: टॉर्च, सर्चलाइट तथा वाहनों की हैडलाइट में प्रकाश का शक्तिशाली समांतर किरण पुंज प्राप्त करने के लिए किया जाता है।
- दंत विशेषज्ञ अवतल दर्पणों का उपयोग मरीजों के दाँतों का बड़ा प्रतिबिंब देखने के लिए करते हैं।
- इन्हें प्राय: चेहरे का बड़ा प्रतिबिंब देखने के लिए शेविंग दर्पणों के रूप में उपयोग किया जाता है।
- सौर भट्टियों में सूर्य के प्रकाश को केंद्रित करने के लिए बड़े अवतल दर्पणों का उपयोग किया जाता है।
उत्तल दर्पण द्वारा किरण आरेख
- उत्तल दर्पण के मुख्य अक्ष के समांतर प्रकाश किरण परावर्तन के पश्चात दर्पण के मुख्य फोकस से अपसरित होती प्रतीत होगी।
- उत्तल दर्पण के मुख्य फोकस से गुजरने वाला किरण परावर्तन के पश्चात मुख्य अक्ष के समांतर निकलेगी।
- उत्तल दर्पण के वक्रता केन्द्र की ओर निर्देशित किरण परावर्तन के पश्चात उसी दिशा में वापस परावर्तित हो जाती है।
- उत्तल दर्पण के बिंदु P की ओर मुख्य अक्ष से तिर्यक दिशा में आपतित किरण तिर्यक दिशा में ही परावर्तित होती है। आपतित तथा परावर्तित किरणें आपतन बिंदु पर मुख्य अक्ष से समान कोण बनाती है।
उत्तल दर्पण के उपयोग
- उत्तल दर्पणों का उपयोग सामान्यतः वाहनों में पीछे का दृश्य देखने के लिए किया जाता है। क्योंकि ये सदैव सीधा तथा छोटा प्रतिबिंब बनाते हैं और ड्राइवर को अपने पीछे के बहुत बड़े क्षेत्र को देखने में आसानी होती हैं।
- दुकानों में इनका इस्तेमाल सिक्योरिटी दर्पण के रूप में किया जाता है।
गोलीय दर्पण से प्रतिबिंब बनने के नियम
- मुख्य अक्ष की समांतर आने वाली सभी प्रकाश किरणें केवल फोकस से होकर जाएगी अथवा जाती हुई प्रतीत होगी।
- फोकस से होकर जाने वाली अथवा फोकस की ओर आने वाली सभी प्रकाश किरणें मुख्य अक्ष के समांतर परावर्तित हो जाएगी।
- वक्रता केंद्र से गुजरने वाली अथवा वक्रता केंद्र की ओर जाने वाली प्रकाश किरण अपनी मार्ग पर वापस लौट जाएगी।
- यदि आने वाली प्रकाश किरणें गोलीय दर्पण के ध्रुव पर आकर टकराए तो वह आपतन कोण के बराबर ही परावर्तन कोण का मान लेकर परावर्तित हो जाती है।
लेंस के किरण आरेख
किसी लेंस पर यदि प्रकाश किरणें समांतर आपतित हो तो वह (उत्तल लेंस की स्थिति में) मुख्य फोकस से होकर गुजरेगी अथवा (अवतल लेंस की स्थिति में) गुजरती हुई प्रतीत होगी।

मुख्य फोकस से गुजरनें वाली किरण अपवर्तन के पश्चात लेंस के मुख्य अक्ष के समांतर हो जाएगी।
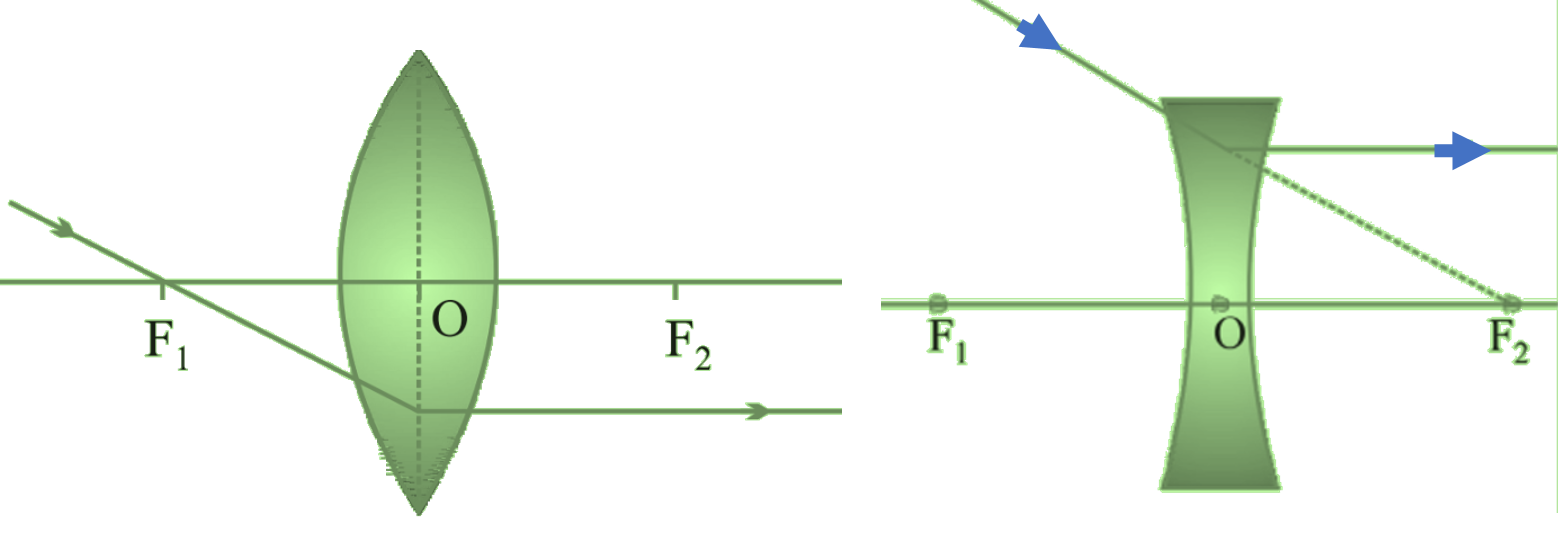
प्रकाश किरण यदि प्रकाशिक केंद्र से होकर गमन करे तो बिना विचलन के सीधी निकल जाएगी।
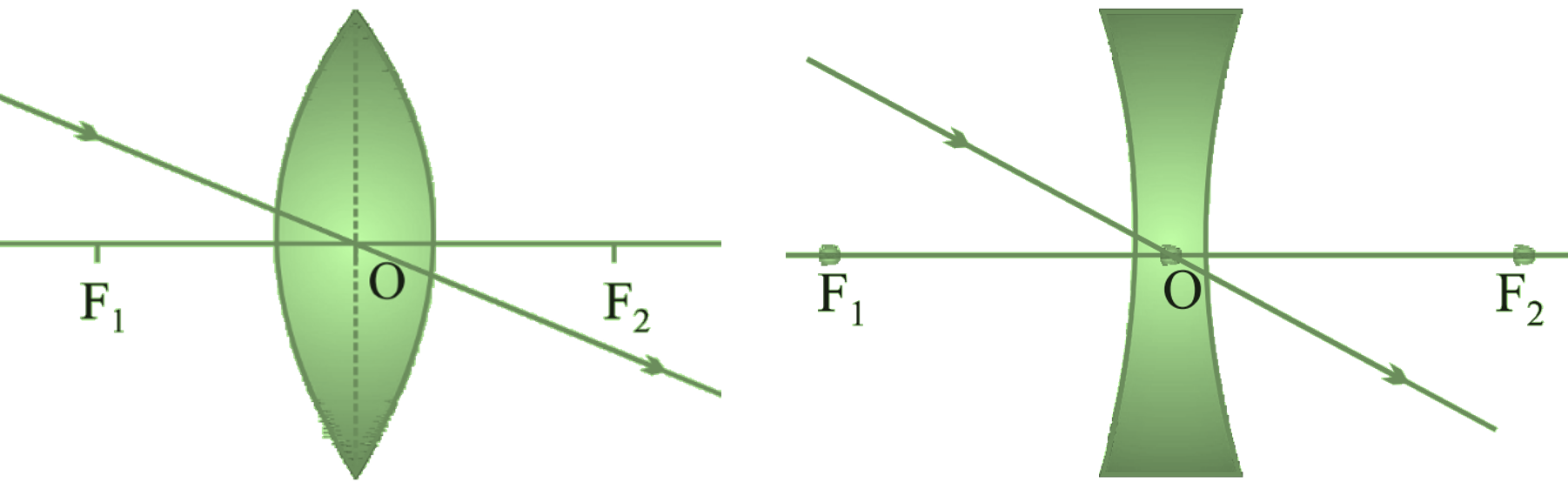
लेंसो द्वारा प्रतिबिंब बनना ⇒ उत्तल तथा अवतल दोनों लेंसो के द्वारा प्रतिबिंब बनने के नियम को किरण आरेख के सहायता से प्रदर्शित किया जा सकता हैं
नीचे दिए गए सारणी में इसका विवरण है।
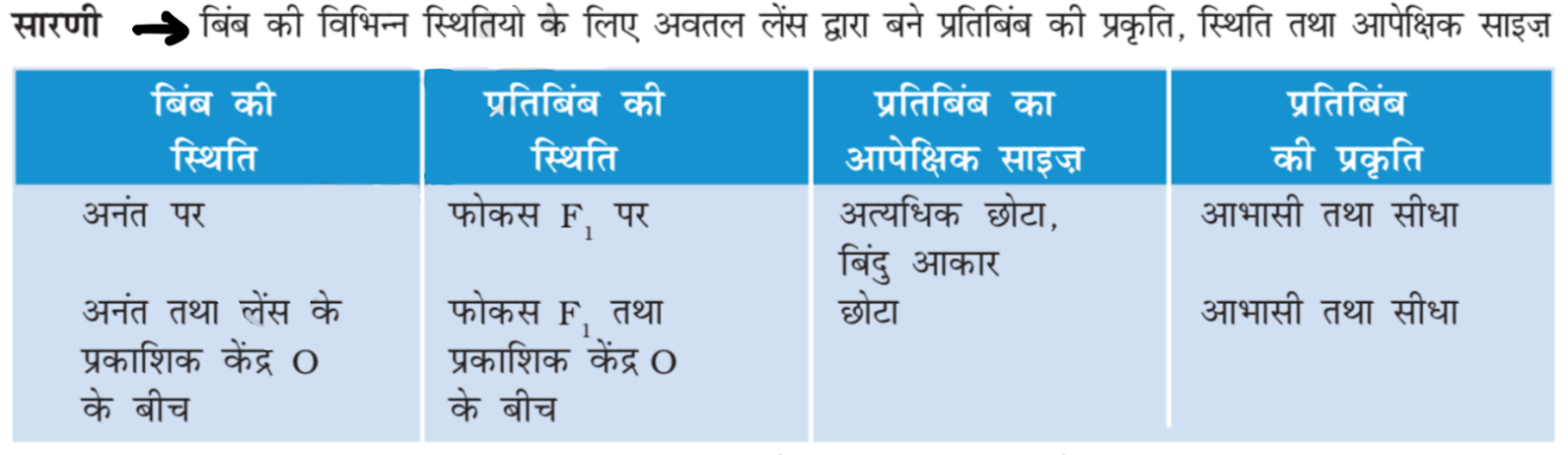
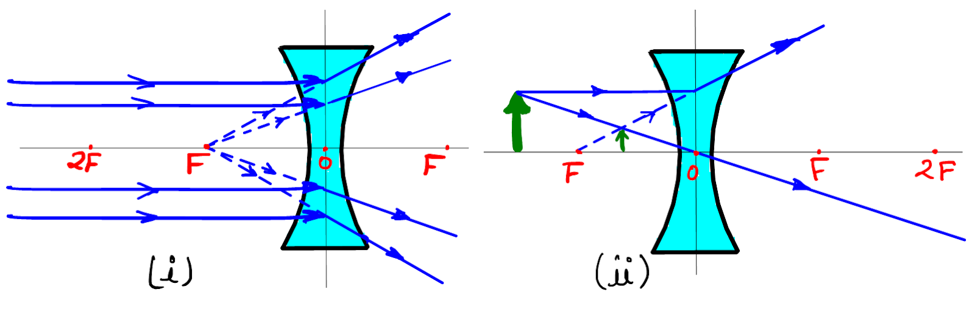

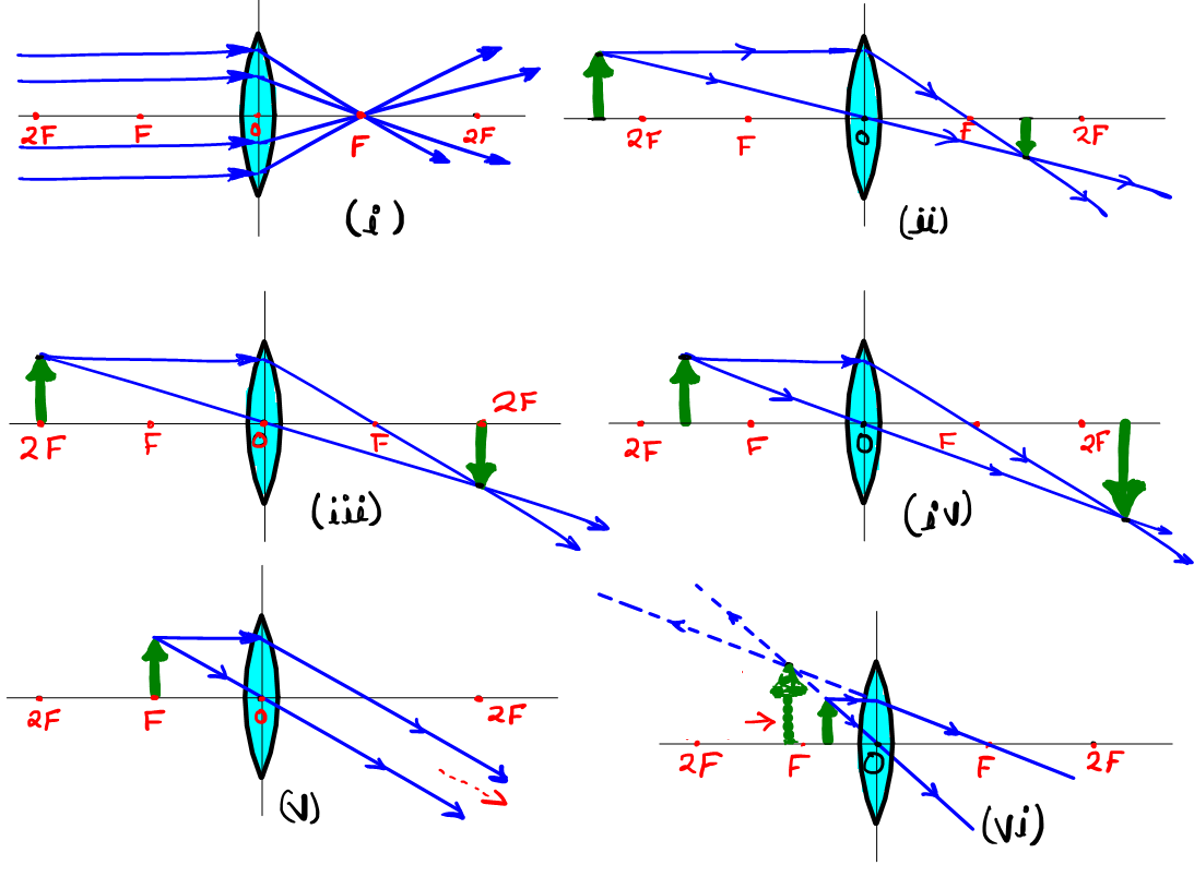
अवतल लेंस सदैव आभासी सीधा तथा छोटा प्रतिबिंब बनाता है।
अवतल दर्पण द्वारा किरण आरेख
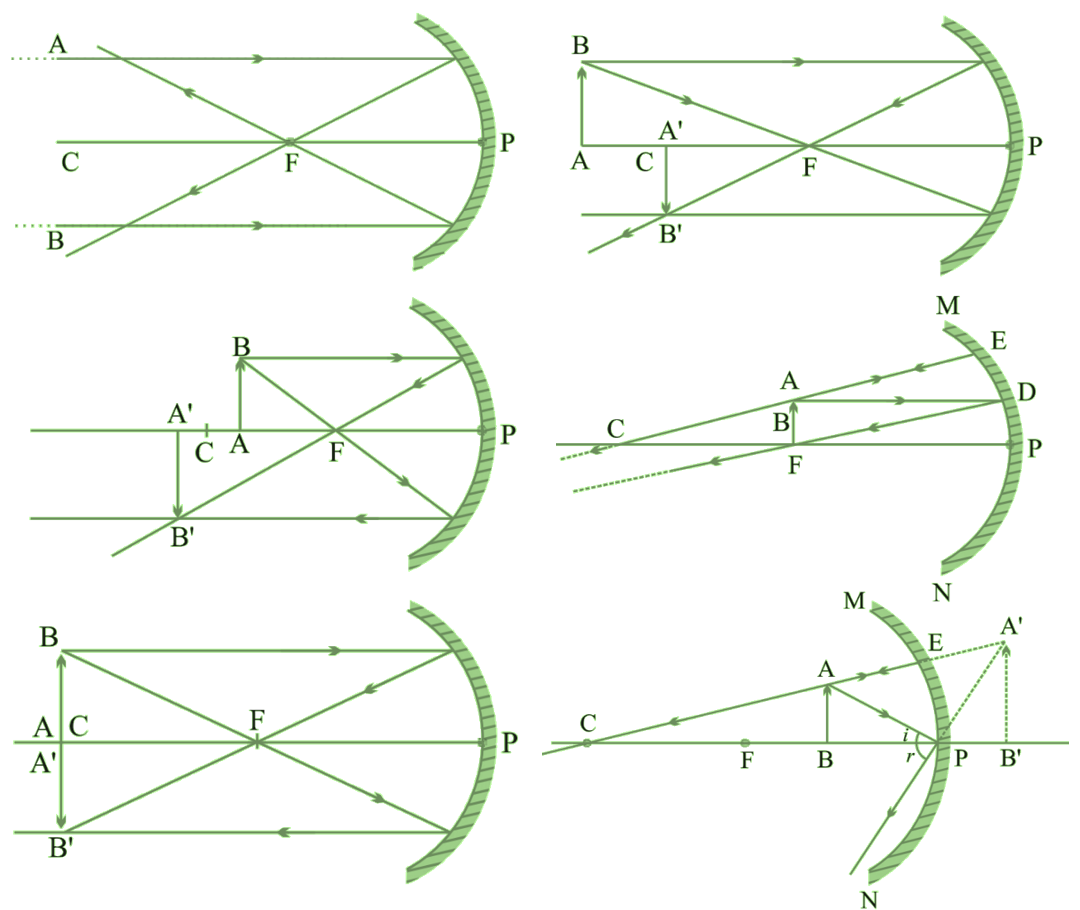
अवतल दर्पण के प्रयोग से छह प्रकार से भिन्न-भिन्न स्थितियों पर प्रतिबिंब का निर्माण संभव हैं।
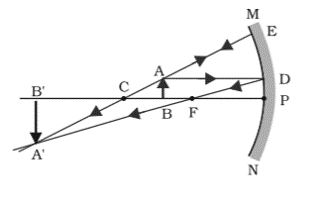
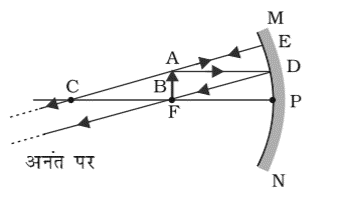
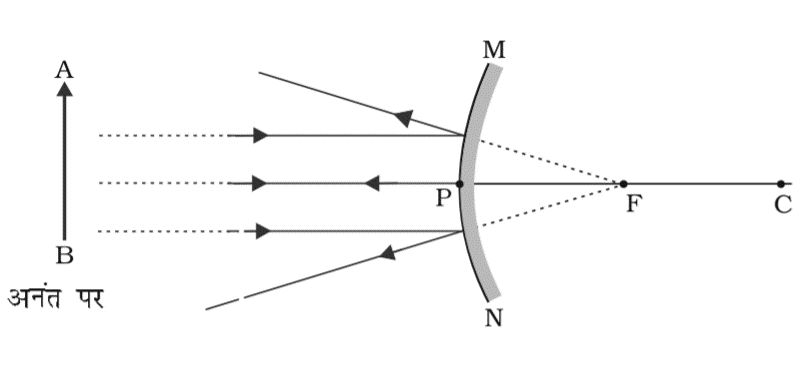
- पहली स्थिति में प्रतिबिंब निर्माण हम तब करेंगे जब वस्तु अनंत पर हो अर्थात अनंत से जो भी प्रकाश किरणें अवतल दर्पण पर आपतित होगी वह परावर्तित होकर फोकस बिंदु से ही होकर गुजरेगी। उपर्युक्त कथन में अनंत का अर्थ यह है कि प्रकाश स्त्रोत की दर्पण से दूरी तुलनात्मक रूप से अत्यधिक हो जो अनंत माना जा सके।
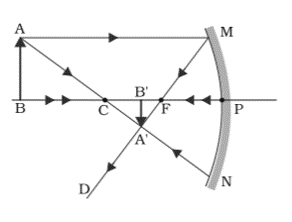
- दूसरी स्थिति में वस्तु अनंत से वक्रता केंद्र के मध्य में होगी अर्थात वस्तु की स्थिति का तुलनात्मक मापन किया जा सकता है, तब वस्तु से आपतित किरण के अनुसार प्रतिबिंब वक्रता केंद्र तथा फोकस बिंदु के मध्य में निर्मित होगा, उल्टा तथा वास्तविक बनेगा। इस स्थिति में प्रतिबिंब का आकार वस्तु के आकार से छोटा होगा।
- तीसरी स्थिति में वस्तु वक्रता केंद्र पर हो तब वहां से आपतित प्रकाश किरणें इस प्रकार परिवर्तित होगी कि प्रतिबिंब हमको वक्रता केंद्र पर ही प्राप्त होगा हालांकि यह उल्टा होगा, परंतु वास्तविक होगा। प्रतिबिंब का आकार वस्तु के आकार के समान होगा।
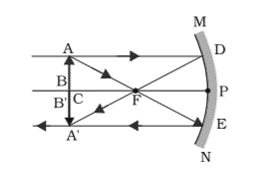
- यदि वस्तु को वक्रता केंद्र से और आगे की ओर अर्थात वक्रता केंद्र और फोकस दूरी के मध्य किसी बिंदु पर रखा जाए तब प्रतिबिंब अनंत से लेकर वक्रता केंद्र के मध्य प्राप्त होगा जो वस्तु से बड़ा तथा उल्टा होगा और यह प्रतिबिंब वास्तविक होगा।
- पांचवी स्थिति में वस्तु यदि फोकस केंद्र पर स्थित हो तो उससे निकलने वाली किरणें इस प्रकार आपतित होगी कि परावर्तित होकर वह दोनों समांतर हो जाएगी और हम जानते है की समांतर किरणें वास्तविक अथवा आभासी किसी भी अवस्था में एक दूसरे को प्रतिछेद नहीं करती। किरणें प्रतिछेद ही नहीं करेगी तो स्पष्ट हैं कि प्रतिबिंब का निर्माण भी नहीं होगा।
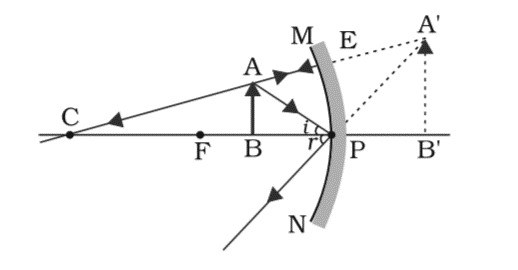
- वस्तु की अंतिम स्थिति फोकस बिंदु से लेकर ध्रुव के बीच रहेगी जहां वस्तु को हम जितने ध्रुव के निकट लाएंगे उतना वस्तु का निर्माण आकार में आवर्धित (बड़ा) होते जाएगा। जिसकी प्रकृति आभासी होगी। तथा प्रतिबिंब सीधा बनेगा।
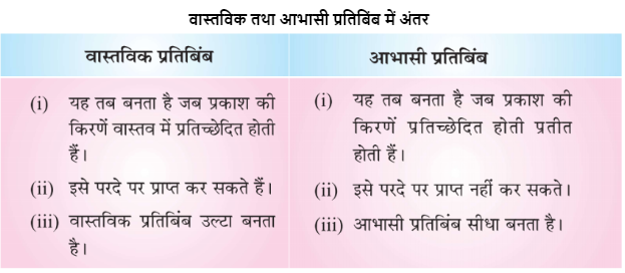
आभासी प्रकृति का प्रतिबिंब इसलिए प्राप्त हो रहा है, क्योंकि परावर्तक किरणें आपस में प्रतिछेद नहीं कर रही है, परंतु उनको पीछे की ओर बढ़ाया जाए तो हमें एक प्रतिछेद बिंदु प्राप्त होता है जहां प्रतिबिंब का निर्माण आभासी प्रकृति से होता है, इसे पर्दे पर नहीं प्राप्त किया जा सकता क्योंकि यह वास्तविकता में एक दूसरे से प्रतिछेद नहीं होती।
सूत्र
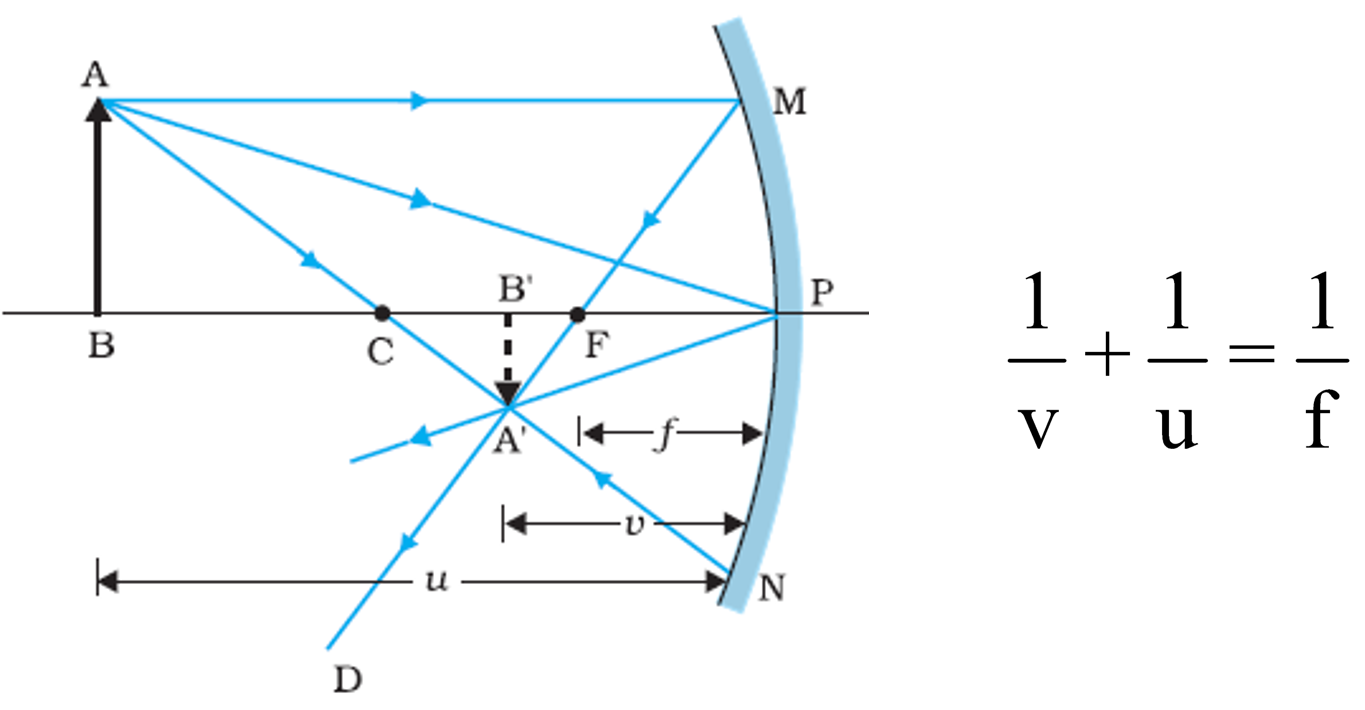
दर्पण सूत्र तथा आवर्धन ⇒ वस्तु की ध्रुव से दूरी u, प्रतिबिंब की दूरी v तथा फोकस दूरी f के बीच के संबंध को निम्न तरीके से प्रदर्शित कर सकते हैं
1v+1u=1f
आवर्धन का मान प्रतिबिम्ब की ऊंचाई तथा वस्तु की ऊंचाई का अनुपात द्वारा ज्ञात किया जा सकता हैं।
m=A'B'AB
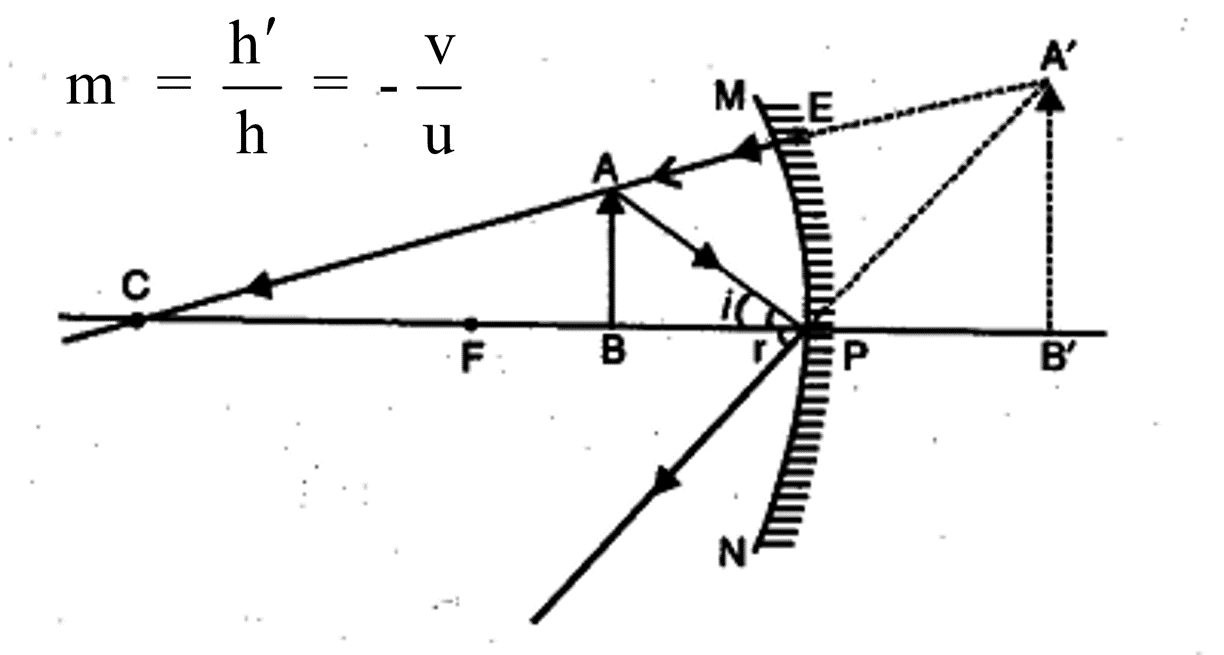
यदि m>1 तब प्रतिबिंब वस्तु से बड़ी है, और यदि m<1 तब वस्तु का प्रतिबिंब वस्तु से छोटा है।
लेंस सूत्र तथा आवर्धन
लेंस सूत्र ⇒ प्रकाशिक केंद्र से वस्तु की दूरी प्रतिबिंब की दूरी तथा फोकस दूरी में संबंध देखें तो समीकरण निम्न तरीके से प्राप्त होगा।आवर्धन ⇒ लेन्स आवर्धन के अंतर्गत यह अवलोकित किया जायेगा कि वस्तु का प्रतिबिंब किस तरीके से आकार में बड़ा निर्मित होगा।
आवर्धन m = प्रतिबिंब की ऊंचाई / बिंब (वस्तु) की ऊंचाई
आवर्धन का मान 1 से कम होगा यदि प्रतिबिंब छोटा बनेगा।
लेंस की क्षमता ⇒ लेंस प्रकाश को अपरिवर्तित करके उसके मार्ग में से कुछ विचलित देती है, प्रकाश को उसके मार्ग से विचलित करना (मोड़ना) ही लेंस का कार्य है। उत्तल लेंस की क्षमता अधिक तब होगी जब लेंस प्रकाश को अधिक मोड़ पाए।

उत्तल दर्पण द्वारा प्रतिबिंब किरण आरेख
अवतल दर्पण में छह प्रकार से प्रतिबिंब का निर्माण किया जा सकता है, परंतु उत्तल दर्पण में वस्तुओं को रखने हेतु केवल दो ही स्थितियाँ संभव हैं। अवतल दर्पण में प्रतिबिम्ब निर्माण के लिए वस्तु की छः स्थितियाँ उत्तल दर्पण में सम्भव नहीं है।
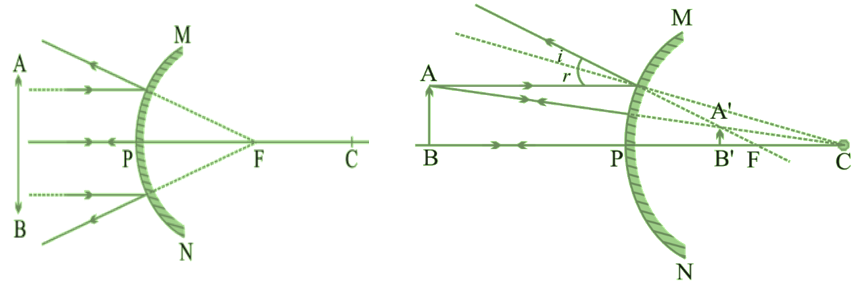
- पहली स्थिति में वस्तु अनंत पर हो तो आने वाली सभी प्रकाश किरणें समांतर आपतित होगी जो कि परावर्तित होकर इस प्रकार लौट जाएगी की फोकस बिंदु से आती हुई प्रतीत होगी। जिन्हें यदि पीछे की ओर बढ़ाया जाए तो यह सभी फोकस बिंदु पर केंद्रित होगी।
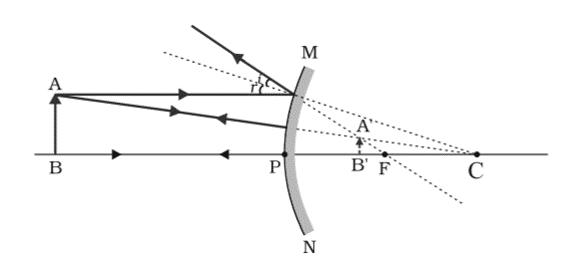
- दूसरी स्थिति मे वस्तु ध्रुव से कुछ दूरी पर हो तब प्रकाश किरण इस प्रकार परिवर्तित होगी की आपस में प्रतिछेद केवल उस स्थिति में होगा जब दोनों प्रकाश किरणों को पीछे की ओर खींचा जाए। अतः स्पष्ट है कि यहां पर प्रतिबिंब आभासी निर्मित होता है। नीचे चित्र में किरण आरेख में उल्लेख हैं की वस्तु का प्रतिबिंब सीधा बनेगा आभासी तथा आकार में छोटा बनेगा।
महत्वपूर्ण अंतर
गोलीय दर्पण द्वारा परावर्तन के लिए चिन्ह परिपाटी
- किसी दर्पण के लिये परिपाटी का मुल बिंदु उसी दर्पण का ध्रुव होता है तथा ध्रुव को P से दर्शाते है।
- वस्तु को हमेशा दर्पण के बायीं ओर रखा जाता है। इसका अर्थ है कि दर्पण पर वस्तु से प्रकाश बायीं ओर से आपतित होता है।
- मुख्य अक्ष के समांतर सभी दूरियाँ दर्पण के ध्रुव से मापी जाती हैं।
- मूल बिंदु के दाईं ओर मापी गई सभी दूरियां धनात्मक तथा बाईं ओर मापी गई सभी दूरियां ऋणात्मक लिया जाता है।
- मुख्य अक्ष के लंबवत तथा ऊपर की ओर (+y अक्ष के अनुदिश) मापी जाने वाली दूरियों को धनात्मक तथा नीचें की ओर (-y अक्ष के अनुदिश) मापी जाने वाली सभी दूरियों को ऋणात्मक मानेंगे।

दर्पण सूत्र तथा आवर्धन
यदि किसी वस्तु की स्थिति इस प्रकार व्यवस्थित की जाए कि गोलीय दर्पण के ध्रुव से u दूरी पर हो, प्रतिबिंब की स्थिति दर्पण के ध्रुव से v दूरी पर है। तथा दर्पण ध्रुव से मुख्य फोकस की दूरी जिसे फोकस दूरी भी कहते हैं, का मान f है।
तब u, v तथा f के बीच के संबंध को निम्न तरीके से प्रदर्शित कर सकते हैं
1v+1u=1f

आवर्धन का अर्थ होता है विस्तार। प्रतिबिंब का आवर्धन होगा अर्थात निर्मित प्रतिबिंब वस्तु से आकार में बड़ी दिखाई देगी। यदि प्रतिबिंब वस्तु के आकार से छोटा दिखाई देगा तो यह घटना आवर्धन का व्युत्क्रम है।
आवर्धन को m से प्रदर्शित करते हैं। आवर्धन का मान प्रतिबिम्ब की ऊंचाई तथा वस्तु की ऊंचाई का अनुपात द्वारा ज्ञात किया जा सकता हैं।
m=A'B'AB

यदि m>1 तब प्रतिबिंब वस्तु से बड़ी है, और यदि m<1 तब वस्तु का प्रतिबिंब वस्तु से छोटा है।
उदाहरण 1
किसी वाहन के पीछे देखने के आइने (rear -view mirror) के रूप में उपयोग किए जाने वाले उत्तल दर्पण की वक्रता-त्रिज्या 2.4m है। यदि एक कार इस दर्पण से 6.0 m दूर हो , तो उसके प्रतिबिंब की स्थिति, प्रकृति और आकार (size) निकालें।
दिया गया है कि दर्पण की वक्रता-त्रिज्या R=+2.4m (चूँकि दर्पण उत्तल है )
वस्तु ( कार ) की दूरी u=−6.0m ( चूँकि वस्तु दर्पण के सामने अर्थात बाई ओर है )
सूत्र f=R2 से ,
उत्तल दर्पण की फोकस-दूरी
फिर दर्पण सूत्र 1v+1u=1f से ,
1v=1+1.2m−1−6.0m
1v=11.2m+16.0m
1v=5+16.0m
1v=+66.0m=+11.0m
∴v=+1.0m
v के धनात्मक चिन्ह से स्पष्ट है, कि प्रतिबिंब दर्पण के पीछे बनता है। अतः प्रतिबिंब आभासी है।
सूत्र m=−vu से ,
आवर्धन
m के धनात्मक चिन्ह से स्पष्ट है कि प्रतिबिंब सीधा है। अतः प्रतिबिंब दर्पण के पीछे 1.0m की दूरी पर बनता है और यह प्रतिबिंब दर्पण आभासी , सीधा और कार के आकार की तुलना में 16 गुना छोटा है।
उदाहरण 2
एक गोलीय दर्पण (spherical mirror) की वक्रता-त्रिज्या 24cm है। इस दर्पण की फोकस-दूरी क्या होगी ?
दिया गया है कि गोलीय दर्पण की वक्रता-त्रिज्या R=24cm
सूत्र f=R2 से ,
अतः गोलीय दर्पण की फोकस-दूरी 12cm है।
उदाहरण 3
प्रकाश को सूर्य से पृथ्वी तक पहुंचने में 8 मिनट 20 सेकंड लगता है और सूर्य से पृथ्वी की दूरी 15 करोड़ किलोमीटर है प्रकाश की चाल ज्ञात करे ?
दिया गया है कि प्रकाश को सूर्य से पृथ्वी तक पहुंचने में लगा समय t=8 मिनट 20 सेकंड
तथा सूर्य से पृथ्वी की दूरी s=15 करोड़ किलोमीटर
s=1.5×108km
सूत्र v=st से
प्रकाश की चाल c=1.5×108km500s
c=3.0×108m/s
यह प्रकाश की चाल 3.0×108m/s है|
उदाहरण 4
2cm ऊँची एक वस्तु अवतल दर्पण से 10cm की दूरी पर रखी गई है। उसका उलटा तथा वास्तविक प्रतिबिंब अवतल दर्पण से 20cm की दूरी बन बनता है। अवतल दर्पण की फोकस-दूरी तथा आवर्धन निकाले ?
दिया गया है कि वस्तु की दूरी u=−10cm ( चूँकि वस्तु दर्पण के सामने अर्थात बाई ओर है )
प्रतिबिंब की दूरी v=−20cm ( चूँकि प्रतिबिंब वास्तविक है )
वस्तु की ऊँचाई h=+2cm ( चूँकि वस्तु प्रधान अक्ष के ऊपर की ओर है )
दर्पण सूत्र 1v+1u=1f से,
या 1f=−1−220cm=−320cm
या f=−203cm=−6.7cm (लगभग)
फिर, आवर्धन m=−vu=−(−20cm)(−10cm)=−2
अतः अवतल दर्पण की फोकस-दूरी =6.7cm तथा आवर्धन =2
प्रकाश का अपवर्तन
प्रकाश के परावर्तन में हमने सीखा कि प्रकाश किसी सतह से टकराकर किस तरह से परावर्तित हो रही थी। परंतु अपवर्तन में प्रकाश उस माध्यम में प्रवेश कर जाएगी। सिर्फ प्रवेश ही नहीं करेगी अपितु वह अपने मार्ग से कुछ विचलित भी हो जाएगी। यह दो तरीके से हट सकती है जिसका अध्ययन इस अध्याय में आगे विस्तार से किया जा सकता हैं। दैनिक जीवन में प्रकाश के अपवर्तन के बहुत से उदाहरण देखे जा सकते हैं, उनमें से कुछ उदाहरण नीचे उल्लेखित है।
- यदि पानी से भरे हुए कांच के गिलास में नींबू को डालकर अवलोकन किया जाए, तो वह अपने आकार से कुछ बड़ा व आकृति में कुछ चपटा प्रतीत होता है।
- किसी ऐसे कागज को जिस पर कुछ शब्द लिखे हुए हैं, कांच के नीचे रख कर अवलोकित करे तो सारे अक्षर कुछ उठे हुए दिखेंगे।
प्रकाश एक सीधी सरल रेखा में गति करती है, इस नियम के अनुसार ऐसे घटनाये असंभव प्रतीत होती हैं, परन्तु दैनिक जीवन में यह घटनाएँ देखे जा सकते है, जिसमे प्रकाश सीधी रेखा में ना चलकर कुछ मुड़ जा रही है। ऐसा इसलिए हो रहा है क्योंकि प्रकाश सीधे नेत्र में प्रवेश ना करके किसी माध्यम (कांच, पानी) से होकर नेत्र में प्रवेश कर रही है।
जब प्रकाश अपने माध्यम में परिवर्तन करेगी अथवा जब वह एक माध्यम से दूसरे माध्यम में प्रवेश करेगी, तथा यदि दोनों माध्यमों का प्रकाशिक घनत्व अलग-अलग हो तो प्रकाश अपने मार्ग से कुछ हट जाएगी।
किसी माध्यम का प्रकाशिक घनत्व उस पारदर्शी माध्यम के सघनता तथा विरलता पर निर्भर करता है, जिस पदार्थ का प्रकाशिक घनत्व कम होगा वह अपेक्षाकृत विरल माध्यम होगा, तथा जिसका प्रकाशिक घनत्व अधिक होगा वह अपेक्षाकृत सघन माध्यम होगा। प्रकाशिक घनत्व के आधार पर हम विभिन्न पारदर्शी पदार्थों को वर्गीकृत कर सकते हैं।
अपवर्तन के नियम
- आपतित किरण, अपवर्तित किरण तथा दोनों माध्यम को पृथक करने वाले पृष्ठ के आपतन बिंदु पर अभिलम्ब खींचा जाए तो यह तीनों एक ही तल में होंगे।
- अपवर्तन की घटना तभी संभव है जब प्रकाश किरण एक माध्यम से दूसरे माध्यम में प्रवेश करे।
- यदि प्रकाश किरण सघन माध्यम से विरल माध्यम में प्रवेश करेगी तो प्रकाश की चाल बढ़ जाएगी, जिससे वह अभिलंब से दूर हट जाएगी।
- यदि प्रकाश किरण विरल से सघन माध्यम में जाएगी, तो इस स्थिति में प्रकाश की चाल अपेक्षाकृत घट जाएगी फलस्वरूप प्रकाश अभिलंब की ओर झुकेगी।
अपवर्तनांक
प्रकाश की चाल माध्यम की सघनता तथा विरलता पर निर्भर करती है, यदि कोई प्रकाश अपने माध्यम में परिवर्तन करें तो प्रकाश की चाल मन में आमूलचूल परिवर्तन होंगे उदाहरणार्थ चाल घट जाएगी अथवा बढ़ जाएगी। प्रकाश की सर्वाधिक चाल निर्वात में होती है। अतः किसी पदार्थ का अपवर्तनांक ज्ञात करने के लिए निर्वात में प्रकाश की चाल से विभिन्न माध्यमों में प्रकाश की चालो का अनुपात निकालते है।
अपवर्तनांक को n अथवा μ से प्रदर्शित किया जाता हैं।
यदि निर्वात में प्रकाश की चाल को c तथा किसी माध्यम में प्रकाश की चाल को v से प्रदर्शित करें तो उस माध्यम का निर्वात के सापेक्ष अपवर्तनांक
μ=cv
इसी तरीके से यदि वायु के सापेक्ष कांच का अपवर्तनांक निकाले तो
gμa=vavg
स्नेल का नियम
स्नेल का अपवर्तन नियम के अनुसार प्रकाश के किसी निश्चित रंग, निश्चित माध्यमों के जोड़े के लिए यदि आपतन कोण का ज्या (sine) तथा अपवर्तन कोण का ज्या (sine) का अनुपात सदैव निश्चित रहेगा। जिसे पहले माध्यम के सापेक्ष दूसरे माध्यम का अपवर्तनांक कहते हैं।अर्थात
यदि आपतन कोण i तथा अपवर्तन कोण r हो तब
sinisinr= अपवर्तनांक

काँच की आयताकार स्लैब से अपवर्तन
काँच वायु के सापेक्ष अधिक सघन माध्यम है, इसलिए जब भी प्रकाश किरणें वायु से काँच में प्रवेश करती है तो प्रकाश की चाल काँच मे वायु के सापेक्ष अल्प रूप से कम हो जाती है, इसलिए प्रकाश किरणें अभिलंब की ओर झुक जाती है।
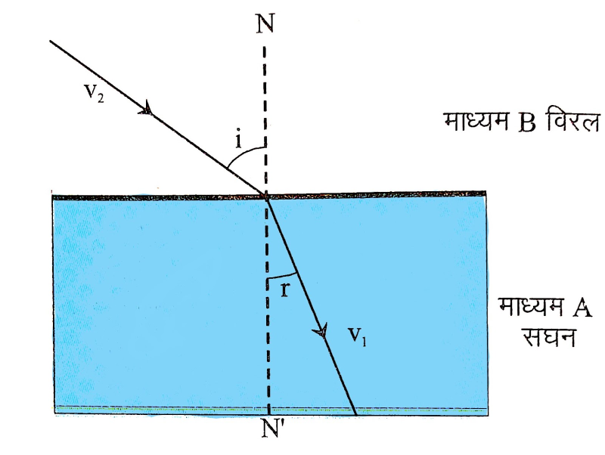
लेकिन वही प्रकाश किरणें जो काँच में गमन कर रही है अगर काँच की दूसरी सिरे से होकर काँच से बाहर वायु की ओर गमन करे तो अभिलंब से दूर हट जाती है। क्योंकि यह अपेक्षाकृत विरल माध्यम में प्रवेश कर रही है।
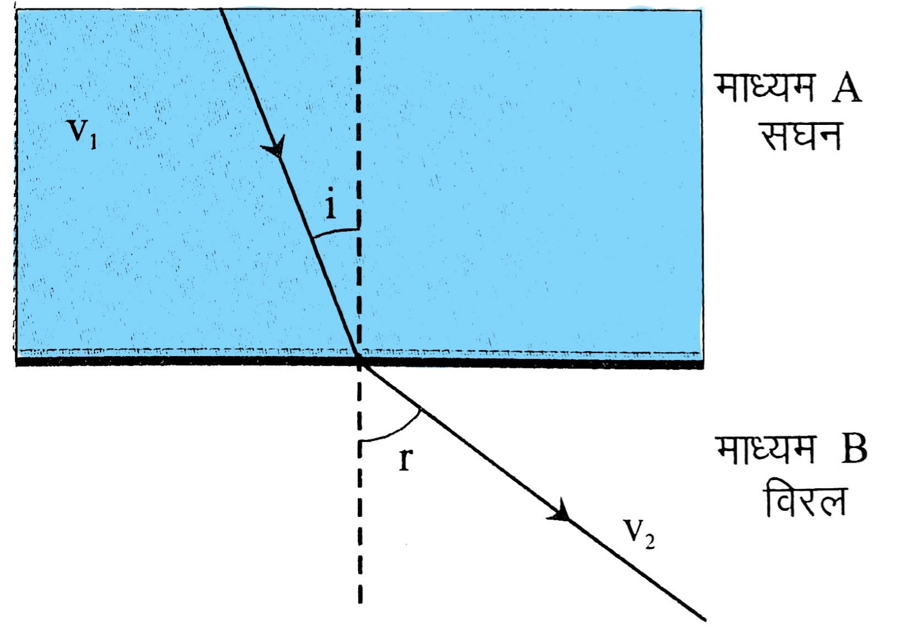
स्नेल का नियम लगाने पर
sinθ1sinθ2=gμa
तथा
sinθ3sinθ4=aμg
नीचे दिए गए सारणी में कुछ द्रव्यात्मक माध्यमों की निरपेक्ष अपवर्तनांक (निर्वात के सापेक्ष अपवर्तनांक) दिए गए हैं।
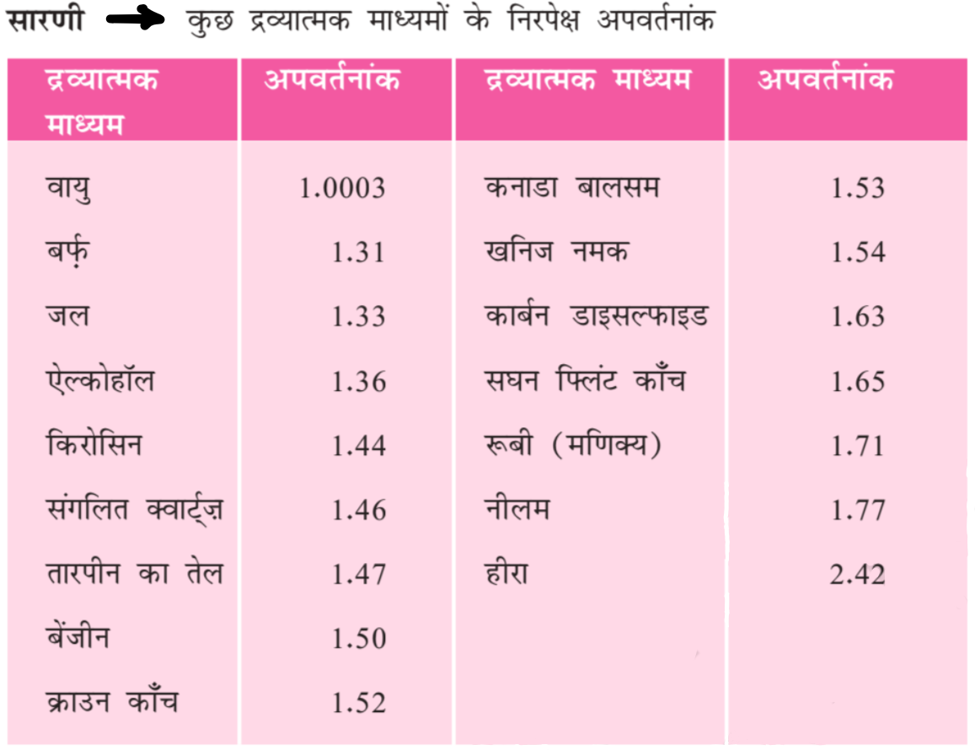
गोलीय लेंस द्वारा अपवर्तन
लेन्स
टॉर्च के सिरे पर कांच से बना एक पदार्थ होता है वह लेंस होता है, मानव नेत्र की दृष्टि दोष के उपाय हेतु उपयुक्त चश्में तथा दूरबीन में भी लेंस का उपयोग होता है।

लेंस दो पृष्ठों का घिरा हुआ किसी पारदर्शी माध्यम से बना पदार्थ होता है, जिसका एक सिरा अथवा दोनों सिरा अल्प गोलीय होता हैं।
गोले में उभार अथवा गहराई के आधार पर लेंसों का दो भागों में वर्गीकरण निम्न है।
- उत्तल लेन्स ⇒ उत्तल लेंस का गोलिय भाग उभरा हुआ होता है। उत्तल लेंस में किनारों की अपेक्षा मध्य में अधिक मोटाई होती है। उत्तल लेंस प्रकाश किरणों को अभिसारित कर देता है, इसीलिए उत्तल लेंस को अभिसारी लेंस भी कहते है।
- अवतल लेंस ⇒ उत्तल लेंस के विपरीत अवतल लेंस में मध्य का भाग गहराई लिए होता है। अर्थात बीच का भाग किनारों की अपेक्षा पतला होता है। अवतल लेंस को अपसारी लेंस भी कहते हैं।


किसी लेंस का मुख्य अक्ष वह अक्ष होता है जिस अक्ष में लेंस के दोनों पृष्ठों के वक्रता केंद्र उपस्थित होते हैं। लेंस के केंद्र बिंदु को O से प्रदर्शित कहते हैं जिन्हें प्रकाशिक केंद्र कहते हैं।

किसी लेंस पर यदि प्रकाश किरणें समांतर आपतित हो तो वह मुख्य फोकस से होकर गुजरेगी अथवा गुजरती हुई प्रतीत होगी। नीचे दिए गए चित्र में उत्तल लेंस के लिए देखा जा सकता है कि प्रकाश किरणें मुख्य अक्ष को प्रतिछेद करते हुए गुजरती है वह बिंदु उत्तल लेंस का फोकस बिंदु होगा। उसी प्रकार अवतल लेंस में की स्थिति में प्रकाश किरणे आपस में कभी प्रतिछेद नहीं करेगी। परंतु उन्ही प्रकाश किरणों को पीछे की ओर बढ़ाया जाए, तो अवतल लेंस की फोकस बिंदु पर वह प्रतिछेद करेगी।

उत्तल लेंस से किरण आरेख
- यदि कोई प्रकाश किरण मुख्य अक्ष के समांतर आपतित है तो उत्तल लेंस से अपवर्तन के पश्चात वह फोकस बिंदु से होकर गुजरेगी।
- पहली स्थिति के विपरीत यदि कोई प्रकाश किरण फोकस बिंदु से होकर उत्तल लेंस में अपवर्तित हो तो निर्गत प्रकाश किरण मुख्य अक्ष के समांतर होगी।
- यदि प्रकाश किरण लेंस के प्रकाशिक केंद्र मतलब मध्य बिंदु से होकर गुजरेगी तो अपवर्तन के पश्चात बिना विचलित हुए आगे निकल जाएगी।
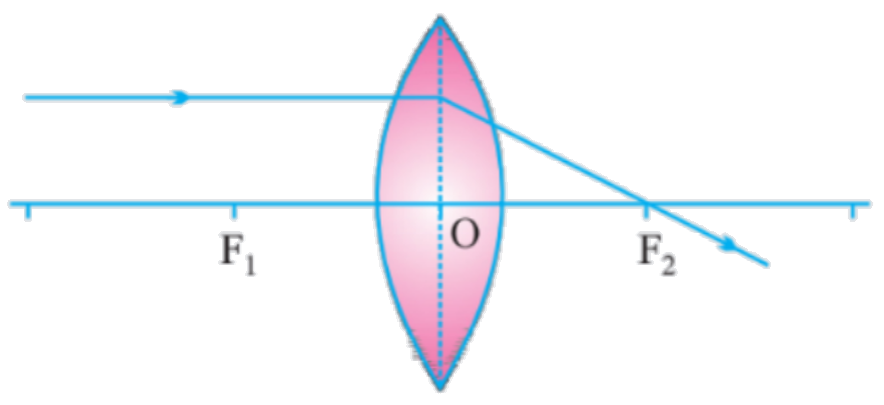
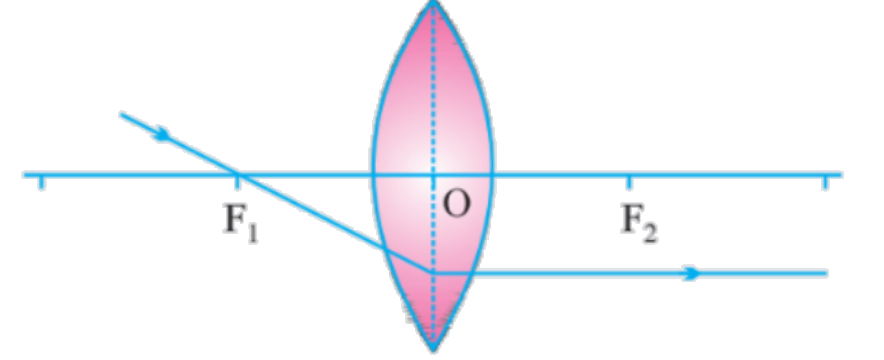
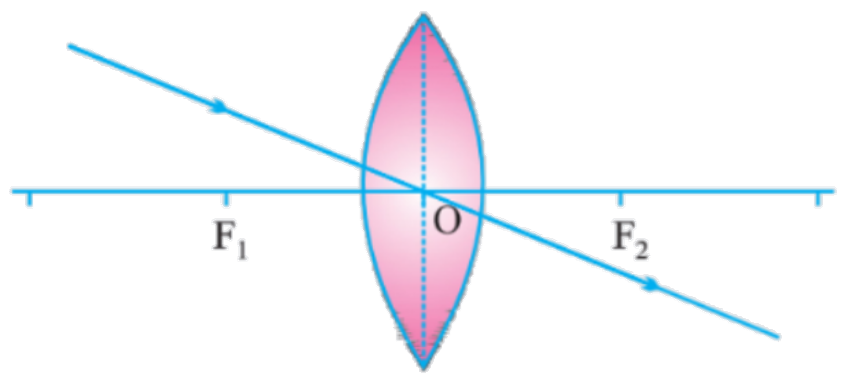
अवतल लेंस से किरण आरेख
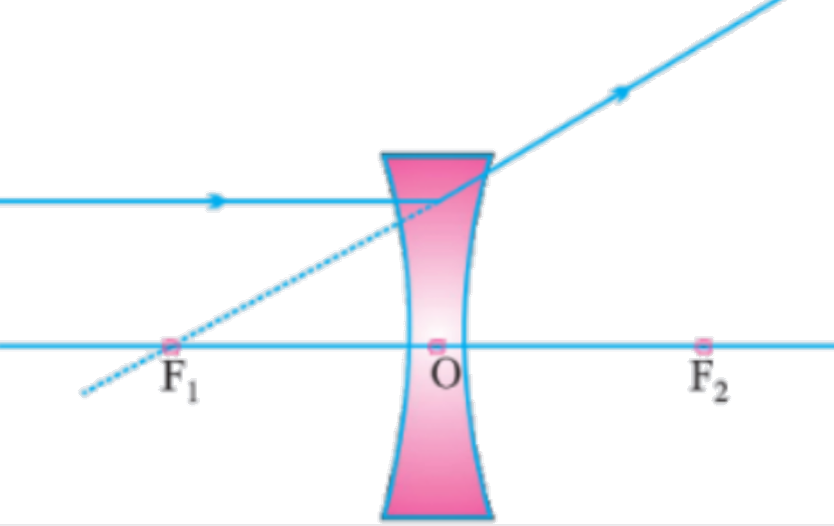
- कोई प्रकाश किरण मुख्य अक्ष के समांतर अवतल लेंस में आपतित हो, तो अपवर्तन के पश्चात इस प्रकार मुड़ेगी कि उस प्रकाश किरण को पीछे की ओर बढ़ाने पर फोकस बिंदु आती हुई प्रतीत होगी।
- पहली स्थिति के विपरीत इस स्थिति में यदि प्रकाश किरण लेन्स के दूसरे ओर के फोकस की ओर आपतित हो तब अपवर्तित होकर वह मुख्य अक्ष के समान्तर निर्गत करेगी।
- उत्तल लेंस की तरह तीसरी स्थिति अवतल लेंस की भी होगी। प्रकाश किरण यदि प्रकाशिक केंद्र से होकर गमन करे तो बिना विचलन के सीधी निकल जाएगी।


लेंसो द्वारा प्रतिबिंब बनना
उत्तल तथा अवतल दोनों लेंसो के द्वारा प्रतिबिंब बनने के नियम को किरण आरेख के सहायता से प्रदर्शित किया जा सकता हैं
नीचे दिए गए सारणी में इसका विवरण है।




अवतल लेंस सदैव आभासी सीधा तथा छोटा प्रतिबिंब बनाता है।
गोलीय लेंसों के लिए चिन्ह परिपाटी
गोलीय लेंस के लिए चिन्ह परिपाटी उसी प्रकार रहेगा, जैसा कि गोलीय दर्पण में था परंतु यहां लेंसों में सारे माप प्रकाशिक केंद्र से लिया जाएगा।
अर्थात लेंसो के लिए भी दाई ओर की लंबाई को धनात्मक तथा बायी ओर की लम्बाई को ऋणात्मक में लिया जाएगा।

लेंस सूत्र तथा आवर्धन
लेंस सूत्र ⇒ प्रकाशिक केंद्र से वस्तु की दूरी प्रतिबिंब की दूरी तथा फोकस दूरी में संबंध देखें तो समीकरण निम्न तरीके से प्राप्त होगा।
आवर्धन ⇒ लेन्स आवर्धन के अंतर्गत यह अवलोकित किया जायेगा कि वस्तु का प्रतिबिंब किस तरीके से आकार में बड़ा निर्मित होगा।
आवर्धन m = प्रतिबिंब की ऊंचाई / बिंब (वस्तु) की ऊंचाई
आवर्धन का मान 1 से कम होगा यदि प्रतिबिंब छोटा बनेगा।
लेंस की क्षमता ⇒ लेंस प्रकाश को अपरिवर्तित करके उसके मार्ग में से कुछ विचलित देती है, प्रकाश को उसके मार्ग से विचलित करना (मोड़ना) ही लेंस का कार्य है। उत्तल लेंस की क्षमता अधिक तब होगी जब लेंस प्रकाश को अधिक मोड़ पाए।

उदाहरण 5
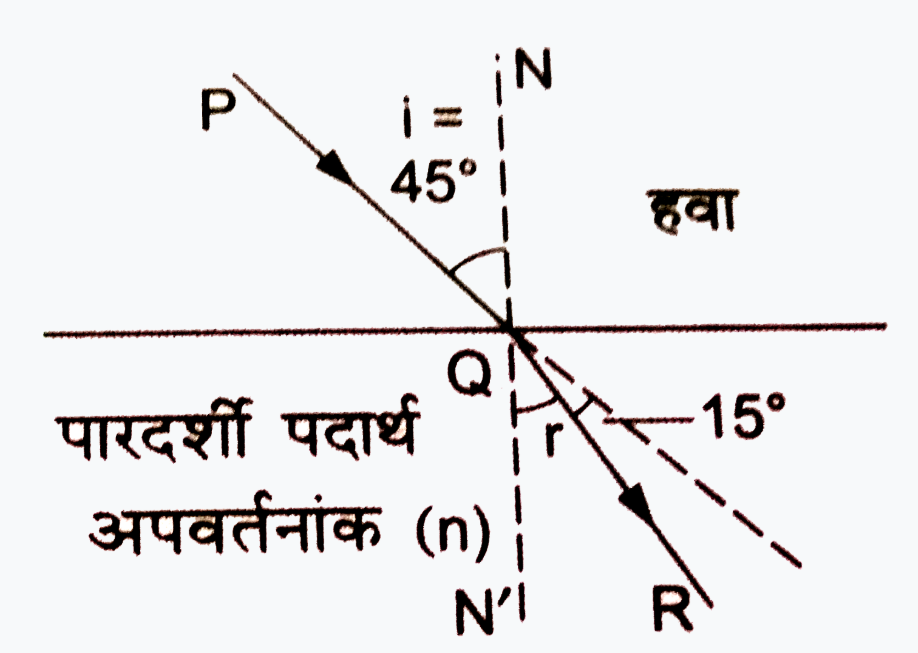
हवा में जाती हुई प्रकाश की एक किरण किसी पारदर्शी पदार्थ पर आपतित होती है यदि किरण अभिलम्ब से 45∘ का कोण बनाती है और पारदर्शी पदार्थ में प्रवेश करने पर 15∘ से मुड़ जाती हो तो पदार्थ का अपवर्तनांक निकाले ?
दिया गया है कि
आपतन का कोण i=45∘
तथा अपवर्तन का कोण r=45∘−15∘=30∘
(चूँकि, किरण 15∘ से पारदर्शी पदार्थ में मुड़ जाती है)
सूत्र n=sinisinr से
n=1√212
n=1√2×21
n=√2=1.41
अतः पारदर्शी पदार्थ का अपवर्तनांक = 1.41
उदाहरण 6
एक उत्तल लेंस किसी सुई का वास्तविक और उल्टा प्रतिबिम्ब (लेंस से) 50cm की दूरी पर बनाता है यदि प्रतिबिम्ब का आकार सुई के बराबर हो तो सुई की लेंस से दूरी क्या है ? लेंस की शक्ति भी निकालो ?
दिया गया है कि प्रतिबिम्ब की दूरी v=+50cm
(चूँकि प्रतिबिम्ब वास्तविक है)
तथा प्रतिबिम्ब का आकार, अर्थात प्रतिबिम्ब की ऊंचाई K = वस्तु का आकार, अर्थात वस्तु की ऊंचाई h
सूत्र m=h'h तथा m=vu से
∴ v=u
अतः u = -50 cm (चूँकि वस्तु लेंस के बाई ओर है)
फिर लेंस-सूत्र 1v−1u=1f से
1f=150cm+150cm
1f=1+150cm=250cm
∴ f=+25cm=+0.25m
तथा सूत्र P=1f से, लेंस की शक्ति
P=+4m−1=+4D
अतः सुई लेंस से 50 cm की दूरी पर है और लेंस की शक्ति 4 D है
विकल्पतः - हम जानते है कि उत्तल लेंस से 2f की दूरी पर रखने पर किसी वस्तु का वास्तविक उल्टा और उसके आकर के बराबर के आकार का प्रतिबिम्ब 2f की दूरी पर लेंस के दूसरी ओर बनता है अतः उपर्युक्त प्रश्न में
2f=50cm, ∴ f=+25cm
और P=100f(cm)=10025D=4D
उदाहरण 7
एक उत्तल लेंस वस्तु (बिंब) का वास्तविक और उल्टा प्रतिबिम्ब लेंस से 40cm पर बनाता है। यदि प्रतिबिम्ब का आकार वस्तु (बिंब) के आकार के बराबर हो, तो वस्तु (बिंब) लेंस से कितनी दूरी पर है और लेंस की क्षमता क्या है?
चूँकि वस्तु (बिंब) और प्रतिबिम्ब के आकार बराबर है, इसलिए वस्तु (बिंब) लेंस की दुगनी फोकस-दूरी पर रखा है,
अर्थात u=2f फिर u=40m
इसलिए 2f=40cm या f=20cm
तथा क्षमता P=(10020) डाइऑप्टर = 5 D
उदाहरण 8
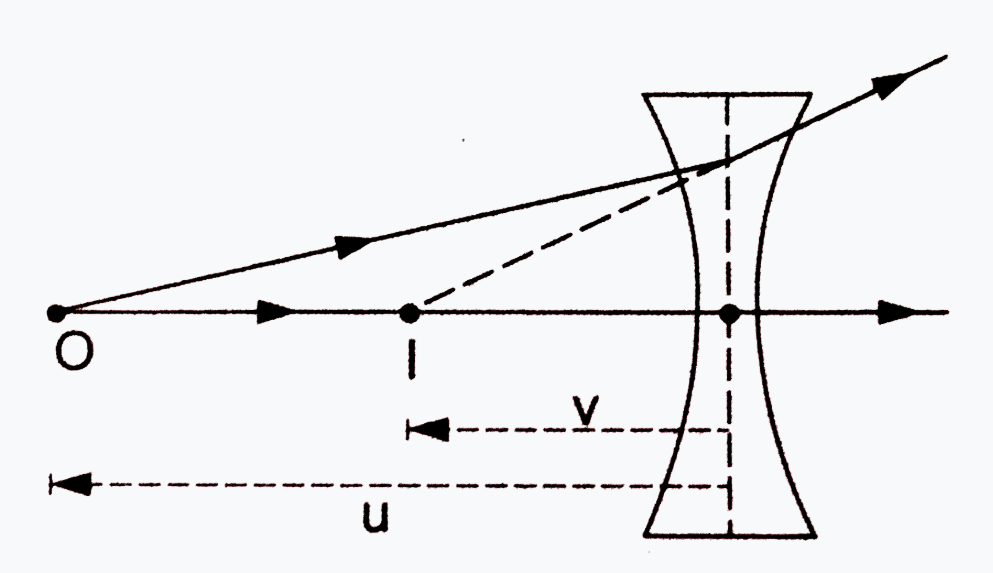
एक अवतल लेंस से 30cm की दूरी पर रखी एक वस्तु का प्रतिबिम्ब लेंस से 20cm की दूरी पर बनता है लेंस की फोकस-दूरी निकाले ?
दिया गया है कि वस्तु की दूरी x=−30cm
(चूँकि वस्तु लेंस के बाई ओर है)
तथा प्रतिबिंब की दूरी v=−20cm
(चूँकि अवतल लेंस में प्रतिबिंबआभासी और वस्तु की ओर ही अर्थात बाई और बनता है)
लेंस-सूत्र 1v−1u=1f से,
1f=−120cm+130cm
1f=−3+260cm
1f=−160cm
∴f=−601cm
f=−60cm
(ऋणात्मक चिह्न इंगित करता है कि लेंस अवतल है)
अतः, अवतल लेंस की फोकस-दूरी =60cm है।
कुछ महत्वपूर्ण अंतर


