SURFACE AREA AND VOLUMES for Class 10 MATHS
Introduction
To bachcho aapne class IX mein area of square, circle, triangle aur volume of cube, cuboid, sphere, cone, cylinder find karna seekha tha lekin ab hum padhenge how to find the surface area and volume of combination of solids, conversion of one solid to other and frustum of cone.
Let's Learn
Bachcho agar aapne dhyan se dekha ho ki truck ke piche laga container, laboratory mei test tube ya phir rocket, ye sare objects different different solids ke combination se bane hai jaise oil container is a combination of cylinder and two hemi-spheres, test tube is a combination of a cylinder and a hemi-sphere and rocket is a made up of a cone and cylinder. Ab hum es type ke sare objects ka surface area and volume find karne wale hai jo humari day to day life se connected hai, Isn't sound interesting ! But before doing this we need to take recap of important formulas and basic idea about surface area and volumes.
Important Definition
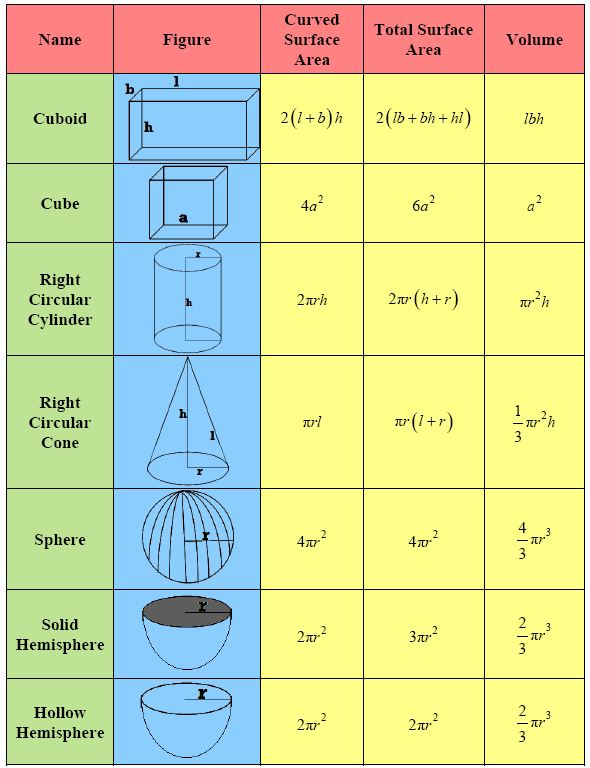
1. The surface area of a solid object is a measure of the total area that the surface of the object occupies.
2. The amount of 3-dimensional space something takes up is called volume.
3. The curved surface area is defined as the area of only curved surface, leaving the circular top and base.
4. Total surface area is the area of the curved surface as well as the bases.
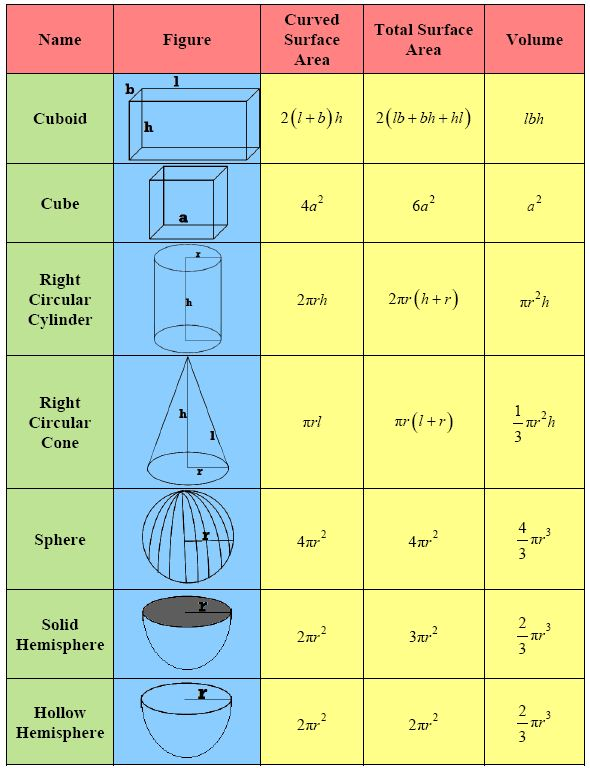
Important Formulas
Surface Area of a Combination of Solids
Bachcho jab bhi hume koi badi problem solve karne ko di jati hai to hum usse small parts me break kar lete hai. For example : Agar hume ek toy jiska top cone ki shape me hai aur base ek hemisphere se bana hai ka total surface find karna hai to iske liye hum curved surface area of cone aur curved surface area of hemisphere ko add kar denge. To combination of solids mein hum isi type ki problems se deal karnge. Let's understand it better by an example.
Example 1
Two cubes each of volume 64 cm3are joined end to end. Find the surface area of the resulting cuboid.
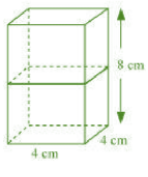
Bachcho you can see in figure that how two cubes are joined end to end such that their total volume is 64cm3.
We know that Volume of cube = (side)3
given volume is 64cm3
So volume = 64cm3=(side)3
43=(side)3
we get side = 4cm
Surface area of resulting cuboid =2(lb+bh+hl)
So you can see length is equal to 4cm, width is 4cm, and height is 8cm, put all values in above formula
Surface area of resulting cuboid = 2(4×4+4×8+8×4)
Surface area of resulting cuboid =160cm2
Hence, surface area of resulting cuboid is 160cm2.
Example 2
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius .The total height of the toy is 15.5 cm. Find the total surface area of the toy
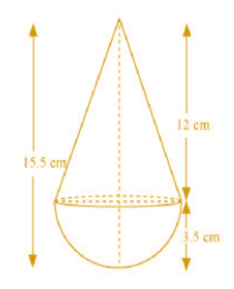
So students ye toy ek cone aur ek hemisphere se milke bana hai, to iska total surface area nikalne ke liye hume CSA of cone and CSA of hemisphere ko add karna padega. Iske liye hume cone ki slant height find karni hogi
Radius of cone =3.5cm
Height of cone =15.5−3.5=12cm
Radius of hemisphere =3.5cm
Slant height of cone (l)=√r2+h2=√(3.5)2+(12)2=√12.25+144=√156.25=12.5
The total surface area of the toy = CSA of cone + CSA of hemisphere
= πrl+2πr2
= 227×3.5×12.5+2×227×3.52
=214.5cm2
Hence, the total surface area of the toy is 214.5cm2.
Example 3
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
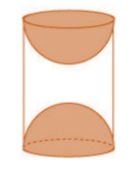
Students es wooden article ka total surface area find karne ke lie hume CSA of cylinder and CSA of two hemisphere ko add karna padega.
Radius of hemispherical part = radius of cylindrical part (r)=3.5cm
Height of cylindrical part (h)=10cm
The total surface area of the article = CSA of cylinder + 2(CSA of hemisphere)
=2πrh+2×2πr2
=2π×3.5×10+2×2π×3.5×3.5
=70π+49π=119π=119×227=374cm2
Hence, the total surface area of the article is 374cm2.
Volume of a Combination of Solids
So students you all know now volume is the total space occupied by any solid. Previous class me hum cuboid, cube, cylinder, sphere, cone jaise bahut sare 3-D solids ka volume find karna seekh chuke hai but ab hum find karne wale hai volume of combination of solids. For example : Agar hume ek capsule jo ki ek cylinder and 2 hemisphere se milkr bana hai ka volume find karna hai, to iske liye hum volume of cylinder and dono hemisphere ke volume ko add karenge (Refer to given figure).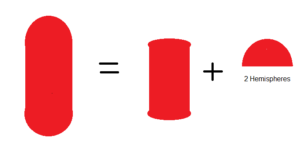
So this is the same process as we did in class 9 along with combining the volume of two solids together.
Example 4
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
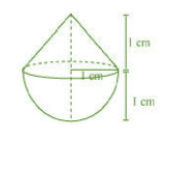
Students you can see ye given solid ek cone and ek hemisphere se milke bana hai, to poore solid ka volume find karne ke liye hum in dono ke volume ko add karne wale hai.
Height of conical part (h)= radius of conical part (r)=1cm
Radius of conical part (r)= radius of hemispherical part (r)=1cm
Volume of solid = Volume of conical part + Volume of hemispherical part
= 13πr2h+23πr3
Now put all required values here
= 13π×12×1+23π×13
On solving we get, volume of given solid =πcm3.
Example 5
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
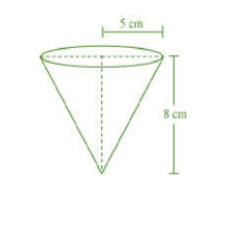
Bachcho jaisa ki hum pta hai ki es vessel me agar hum ek lead shot daalnge to uss lead shot ke volume ke equal hi water bhar flow out ho jayega, so if need n lead shot for this process to volume of water that flows out of vessel will be equal to volume of n lead shot.
Height of vessel (h)=8cm
Radius of vessel (r1)=5cm
Radius of lead shot (r2)=0.5cm
Maan lo n lead shot humne es vessel me drop kiye
Therefore, Volume of water flows out = n×Volume of 1 lead shot
⇒14×Volume of conical vessel = n× Volume of 1 lead shot
⇒14×13π(r1)2h=n×43π(r2)3
⇒(r1)2h=n×16(r2)3
⇒52×8=n×16×(0.5)3
⇒n=25×816×(0.5)3=100
Hence, the number of lead shots dropped in the vessel is 100.
Conversion of Solid from One Shape to Another
Conversion of one solid to another solid means changing the shape of solid like changing a cone into cylinder, a sphere in a cube or cuboid, changing a cone into a sphere or hemisphere. For example : I have a glass full of water and glass is in shape of cylinder and I remoulade the glass in shape of a sphere, so you can see only the shape is changed whereas the volume is still same. So such types of problems comes under this section, lets get a better understanding by example.
Example 6
A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
Let r be the radius of sphere jo ki hume find karni hai and R be the radius of given conical model
R=6cm.
Height of conical model (h)=24cm
So According to question, Volume of cone = Volume of sphere
13πR2h=43πr3(π is cancelled on both sides)
13×6×6×24=43×r3
This gives, r3=3×3×24
r3=3×3×3×2×2×2
r=6cm
Therefore, the radius of the sphere is 6cm.
Example 7
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Soln.
Yaha hum dekh sakte hai ki ek cylindrical container me fill ice cream ko ice cream cone me fill kiya jata hai.
Maan lo uss pure container ko khali karne ke liye hume n ice cream ki need hogi, it means
Volume of cylindrical container = n×Volume of 1 ice cream cone
Since we know ice cream cone is a combination of a cone and a hemisphere
Radius of cylinder (r)=6cm
Height of cylinder (h)=15cm
Radius of cone = Radius of hemisphere (R)=3cm
Height of cone (H)=12cm
Therefore, volume of cylinder = n×(volume of cone + volume of hemisphere)
⇒πr2h=n(13πR2H+23πR3)(π is cancelled on both sides)
⇒62×15=n(13×9×12+23×33)
36×15=n(36+18)
⇒n=36×1554
⇒n=10
Hence, the number of cones filled with ice cream is 10.
Example 8
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
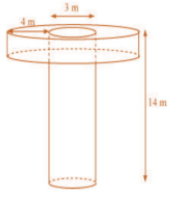
So you can see embankment is in the shape of hollow cylinder with internal radius (r)=32m and outer radius (R)=32+4m=112m
Depth of well (h)=14m
Width of embankment =4m
Let the height of embankment =H
Now according to question, the earth dug out from the well = Volume of embankment
⇒πr2h=π(R2−r2)H
⇒π(32)2×14=π((112)2−(32)2)×H(cancel π on both side)
On solving this we get, H=98=1.125m
Hence, the height of embankment is 1.125m.
Summary
In this chapter, you have studied the following points:
- To determine the surface area of an object formed by combining any two of the basic solids, namely, cuboid, cone, cylinder, sphere and hemisphere.
- To find the volume of objects formed by combining any two of a cuboid, cone, cylinder, sphere and hemisphere.
- Given a right circular cone, which is sliced through by a plane parallel to its base, when the smaller conical portion is removed, the resulting solid is called a Frustum of a Right Circular Cone.
- The formulae involving the frustum of a cone are:
(i) Volume of a frustum of a cone =13πh(r21+r22+r1r2).
(ii) Curved surface area of a frustum of a cone =πl(r1+r2) where l=√h2+(r1−r2)2
(iii) Total surface area of frustum of a cone =πl(r1+r2)+π(r21+r22) where h= vertical height of the frustum, l= slant height of the frustum
r1 and r2 are radii of the two bases (ends) of the frustum.
Let's Revise
- Sabse pahle aap yah samjh lo ki Total Surface Area ka mtlb sum of all the areas of solid hota hai jabki Curved Surface Area ka mtlb area of the curved surface of solid excluding circular top and bottom hota hai aur Volume of Solid ka mtlb total space occupied by the body hota hai.
- Chalo ab hum kuch formulaes recall kartey hai.

- Surface area of combined solids :
- Volume of Combined Solid :

Hume es chapter mein kuch aise hi solids ka volume find karna hoga jo do ya do se jyada prefect solids se milakr bana hoga.
Note : Jab hum ek solid ko deform ya melt karkey koi dusra solid banatey hai tab volume change nhi hota hai.
- Frustum of Cone :
(i) Volume of the frustum of the cone =(13)πh((r1)2+(r2)2+r1r2).
(ii) the curved surface area of the frustum of the cone =π(r1+r2)l
where l=√h2−(r1−r2)2
(iii) Total surface area of the frustum of the cone =πl(r1+r2)+π(r1)2+π(r2)2,
where l=√h2−(r1−r2)2.