SOME APPLICATIONS OF TRIGONOMETRY for Class 10 MATHS
INTRODUCTION TO TRIGONOMETRY
To bachho chapter 8 mei aapne padha tha ki hum trigonometry kyu padh rahe hai tab humne dekha tha ki trigonometry ka basic application kya hai observer aur object ke beech ka distance aur object ki height so, basically trigonometry ka main application Height aur Distance hai. Jisko hum es chapter mei dekhenge ki trigonometry ka use kya hai yani hum day-to-day life situation mein trigonometry applications ko kese apply kar sakte hai.
Heights and Distances
To dekho height and distance ke concept ko to humne trigonometry mein padha hai ab hum ek situation consider karte hai. Let's say aap apni balcony se ek building ki aur dekh rhe hai to yha aap ek observer hai aur jis building ki taraf aap dekh rhe hai wo object ho gya ab yha observer ki eye se object ke top tak ek imaginary line form hoti hai es line ko Line of sight bolte hai aur jo sidhi line ja rahi hai ushe hum Horizontal kahenge aur third side hmari kya hogi, object ki height. To basically yha ek triangle form ho gya. Let's say observer ek minar ki aur dekh rha hai to minar ke top se observer aur horizontal ke beech ek angle form hua jaisa ki hum figure mei dekh sakte hai eshe hum angle of elevation kehte hai. 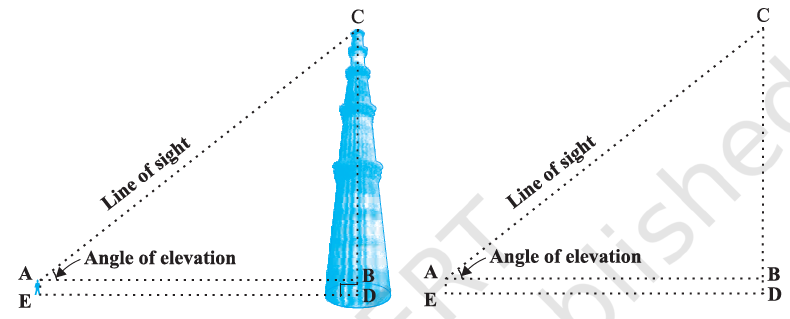
Thus, the line of sight is the line drawn from the eye of an observer to the point in the object viewed by the observer. To humne dekha basically Line of sight aur Horizontal ke beech jo angle form hota hai humne ushe study karna hai. To yha par two cases bante hai
Case I. Maan lo aap surface par khde hai aur ek kite ko observe kar rahe hai to kite yha ek object ho gyi aur aap observer to aap upar ki aur dekh rahe hai to line of sight aur horizontal ke beech jo angle form hoga ushe hum angle of elevation kahenge naam se hi samjh ata hai elevation yani up, higher level basically vo case jismei apko apni neck raise karna padh rha hai or you have to look head up to see the object.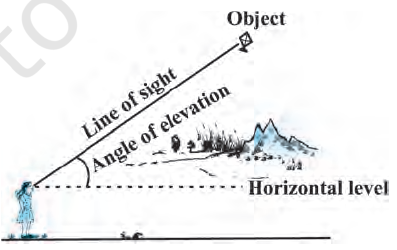
Case II. Ab hum ek situation consider karte hai maan lo aap apni balcony mei khde hai aur neeche ek ball hai to vo ball apka object ho gyi ab aapke aur ball ke beech ek imaginary line form hui i.e. line of sight aur agar aap sidha dekhenge i.e. horizontal level ke beech jo angle form hoga ushe of angle of depression khte hai. 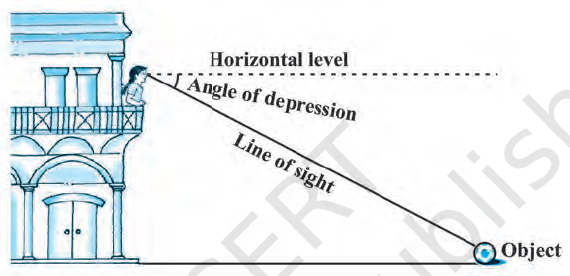
Basically aap jab horizontal level se neeche ki aur dekhte hai to angle of depression form hota hai aur agar upar ki aur dekhte hai to angle of elevation.
Key Concept
Angle Of Elevation: The angle of elevation is relevant for objects above horizontal level.
It is the angle formed by the line of sight with the horizontal level.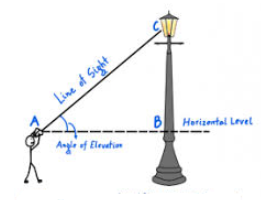
Angle Of Depression: The angle of depression is relevant for objects below horizontal level.
It is the angle formed by the line of sight with the horizontal level.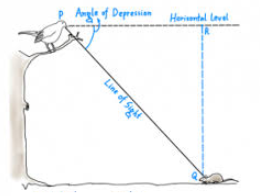
Let's Learn
Now, you may identify the line of sight, and the angle so formed. But can you identify angle of elevation or angle of depression ?
To chalo ab hum phirse qutub minar ki situation ko consider karte hai 
ab agar aapko es minar ki height CD nikalni hai without actually measuring it, to aap konsi information use karenge? You will need to know the following :
(i) The distance DE at which the student is standing from the foot of the minar.
(ii) The angle of elevation, ∠BAC, of the top of the minar.
(iii) The height AE of the student.
Chalo hum maan lete hai ki hume ye teeno condition pta hai. Still, kya hum height nikal sakte hai minar ki?
In figure CD=CB+BD. Yha BD aur AE equal hai jo ki student ki height hai.
BC nikalne ke liye hum trigonometry ratios use karenge of ∠BAC or ∠A
Ab dekho △ABC mei, hume ∠A find out karna hai to side BC uske opposite hai in relation. To hum konsi trigonometry identity use kar sakte hai? Jiske paas ye two values ho jo hmare pass hai perpendicular or base to hmari search narrow down hoti hai tanA or cotA pe
Therefore, tanA=BCAB or cotA=ABBC jo ki solve karne pe humme kya degi BC ki value. Or by adding AE to BC, to aapko kya mil jayega height of the minar.
To chalo ab kuch problems solve karte hai by applying the concept we have just discussed.
Example 1
A ladder 15m long just reaches the top of a vertical wall. If the ladder makes an angle of 60∘ with the wall, find the height of the wall.
Dekhiye student, applications of trigonometry ke questions mein most important thing hai uska figure, agar aapne figure shi se bna liya then aapko koi bhi problem nhi hogi question ko solve krne mein. So sbse phle hum given information ke according figure bnaenge. Let OX be the horizontal ground D and let OA be the ladder learning against the wall AB. Then
OA=15 m, ∠OAB=60∘ and ∠OBA=90∘.
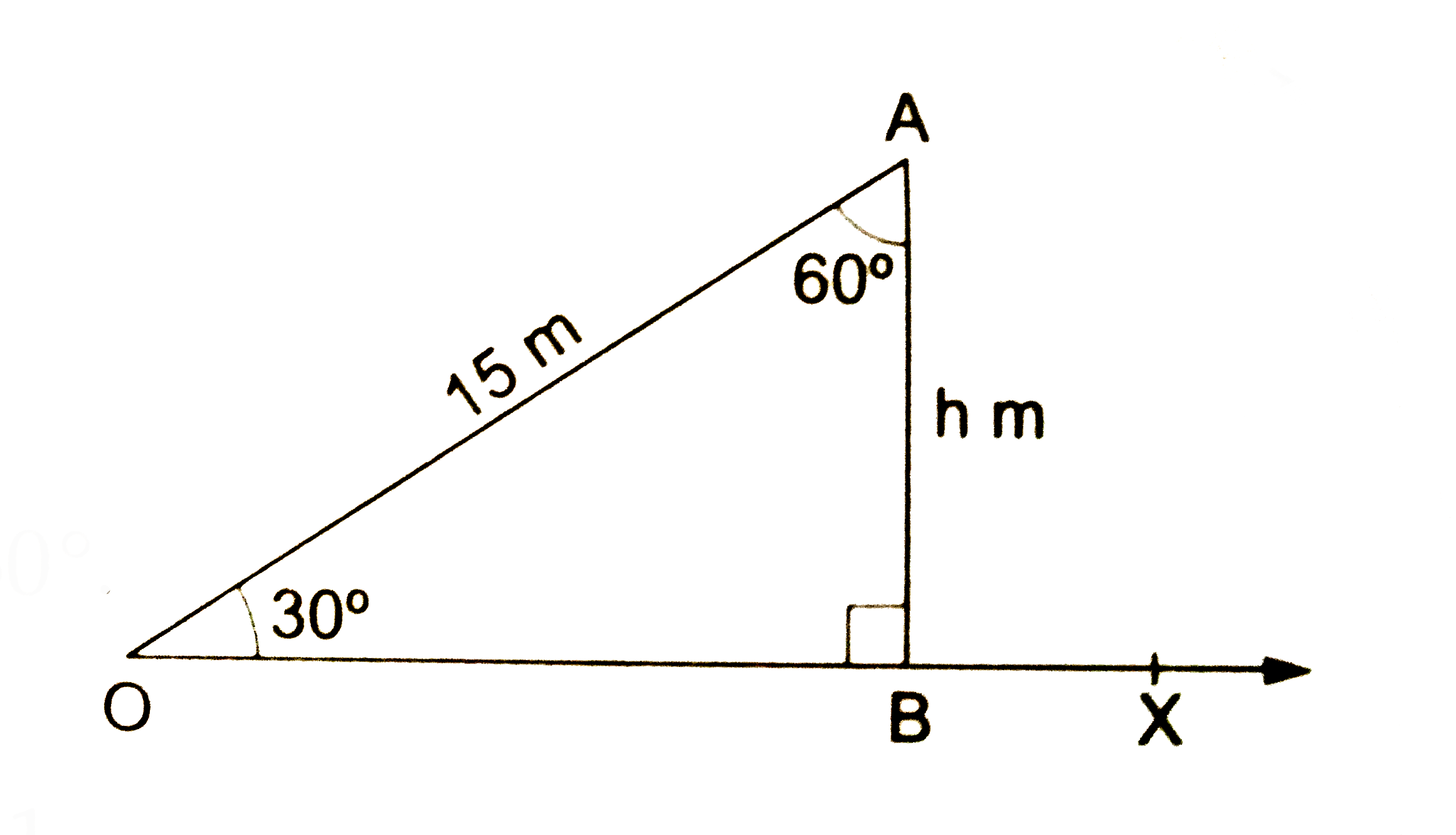
Let AB=h metres.
Now ∠AOB=(90∘−60∘)=30∘
From right ΔOBA, we have
ABOA=sin30∘=12⇒h15=12
⇒h=15×12=7.5
Hence the height of the wall is 7.5 metres.
Example 2
The angle of elevation of the top of a vertical tower from a point on the ground is 60∘. From another point 10 m vertically above the first, its angle of elevation is 30∘. Find the height of the tower.
So, students es question mei hume height of tower nikalna hai to jaisa ki meine apko ex. 1 mei btaya sabse important kya hai fig. to sabse pehle hum fig. bnayenge yha question mei hume clearly diya gya ki observer ground se tower ke top ki aur dekh rha hai yani ki upar ki aur to ye kya hua angle of elevation aur ye hume given bhi hai i.e. 60∘ to ab hum maan lete hai ki tower ki height h metre hai ab 10m ki height se observer tower ki aur dekh rha hai jha se angle hai 30∘ to abhi observer 10m ki height pe hai yani tower ki height bhi 10m to hai. Aur humne tower ki height kya mani thi h meter to yani usse upar kitni hui (h−10)m. 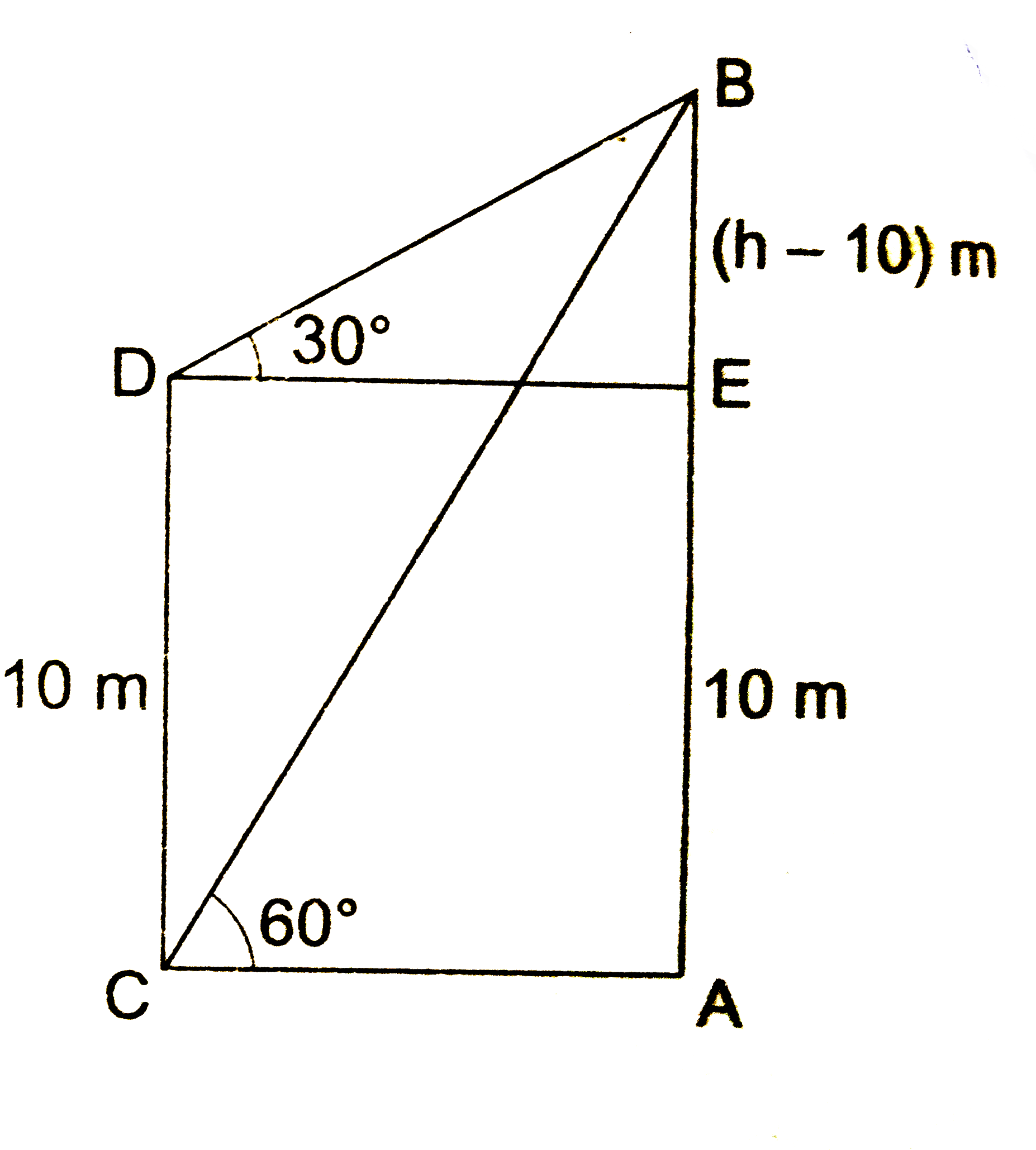
Let the height of the tower be h metres.
From right ΔCAB, we have
CAAB=cot60∘⇒CAh=1√3.
⇒CA=h√3 ...(i)
From right ΔBED, we have
DEBE=cot30∘⇒DE(h−10)=√3
⇒DE=√3(h−10) ...(ii)
But, CA=DE.
∴h√3=√3(h−10)→3h−30=h
⇒2h=30⇒h=15m.
Example 3
A 1.5m-tall boy is standing at some distance from a 30m-tall building. The angle of elevation from his eyes to the top of the building increases from 30∘ to 60∘ as he walks towards the building. Find the distance he walked towards the building.
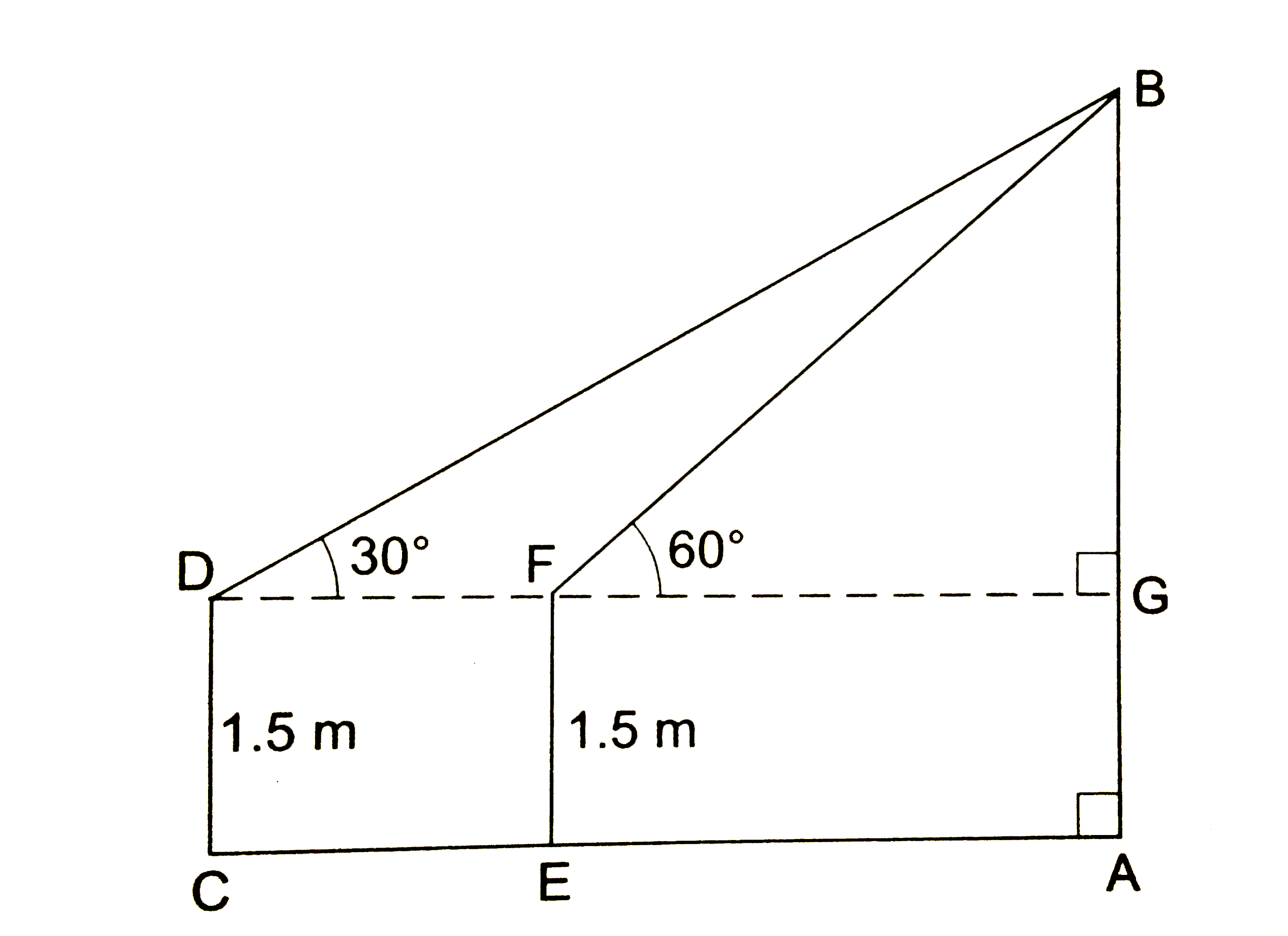
Let AB be the building and let CD and EF be the two positions of the boy. Draw DFG ∣∣ CEA. Then,
CD=EF=1.5 m , ∠GDB=30∘ and ∠GFB=60∘.
AB=30m,GB=30m−1.5m=28.5 m
From right ΔDGB , we have
DGGB=cot30∘⇒DG28.5m=√3⇒DG=57√32m
From right ΔFGB, we have
FGGB=cot60∘⇒FG28.5m=1√3⇒FG=572√3m. ∴DF=DG−FG=(57√32−572√3)m=(171−572√3)m
=1142√3m=57√3m=57√3×√3√3m=19√3m.
Hence, the required distance is 19√3 m.
Example 4
The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30∘ and the angle of depression of its shadow in water of lake is 60∘. Find the height of the cloud from the of water.
Let AB be the surface of the lake and let P be a point vertically above A such that AP=60 m.
Let C be the position of the cloud and let D be its reflection in the lake.
Draw, PQ⊥CD. Then
∠QPC=30∘,∠QPD=60∘,
BQ=AP=60 m
Let CQ=x m. Then,
BD=BC=(x+60)m.
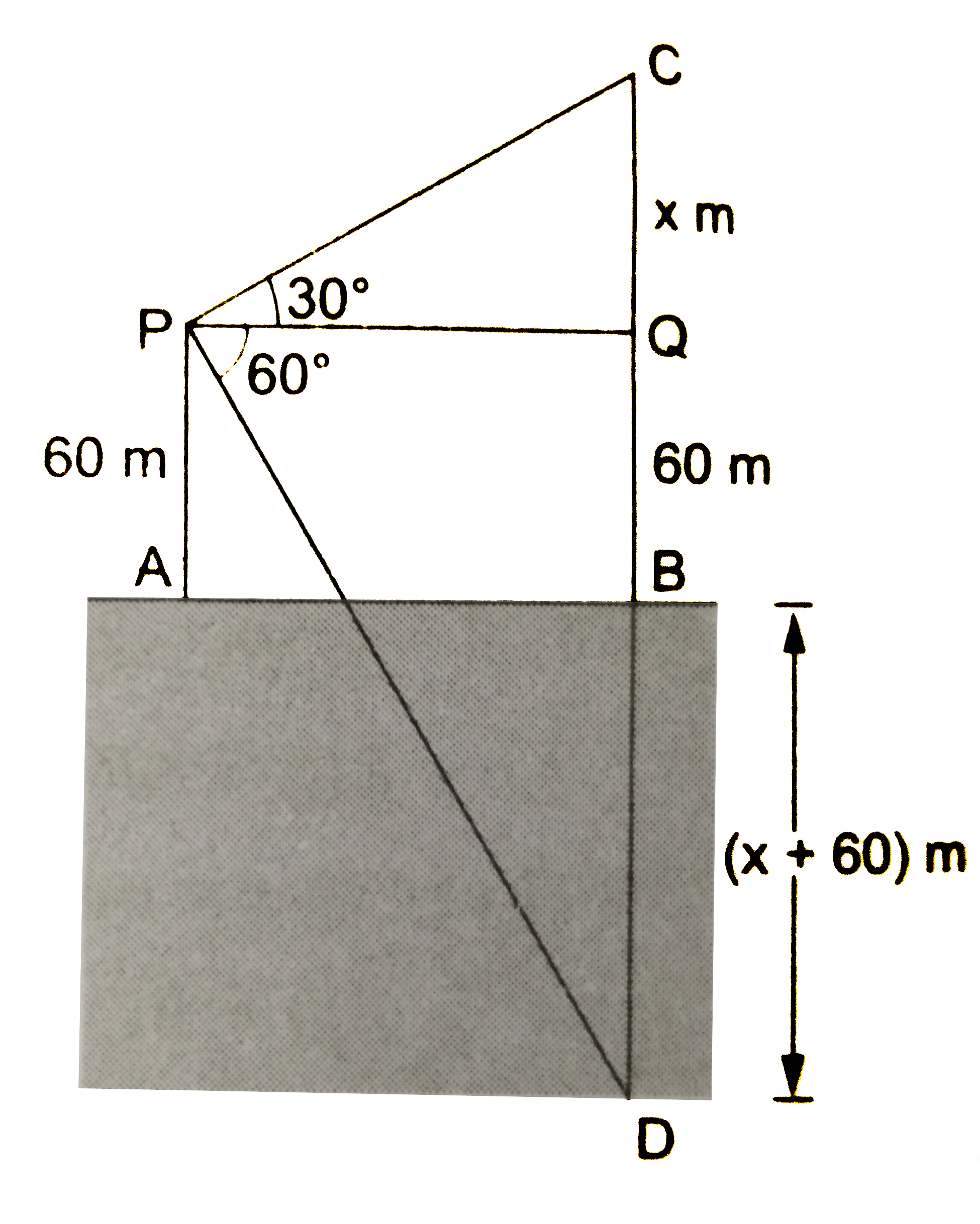
From right ΔPQC, we have
PQCQ=cot30∘=√3
⇒PQxm=√3⇒PQ=x√3m. ...(i)
From right ΔPQD, we have
PQQD=cot60∘=1√3.
⇒PQ(x+60+60)m=1√3⇒PQ=(x+120)√3m ...(ii)
Equating the values of PQ from (i) and (ii), we get
x√3=(x+120)√3
⇒3x=x+120⇒2x=120⇒x=60.
∴ Height of the cloud from the surface of the lake is 120m.
Example 5
Two pillars of equal heights stand on either side of a road which is 100m wide. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60∘ and 30∘. Find the height of each pillar and position of the road. [Take √3=1.732.]

Let AB and CD be two pillars, each of height h metres and AC be the road that AC=100 m.
Let O be the point of observation on AC.
Also, ∠AOB=60∘ and ∠COD=30∘,
AB⊥AC and CD⊥AC.
From right ΔOAB, we have
ABOA=tan60∘=√3
⇒hx=√3⇒h=√3x ...(i).
From right ΔOCD, we have
CDOC=tan30∘=1√3.
⇒h(100−x)=1√3⇒h=(100−x)√3 ...(ii)
Equating the values of h from (i) and (ii) , we get
√3x=(100−x)√3⇒3x=(100−x)⇒4x=100⇒x=25.
Putting x=25 m in (i), we get
h=(25×√3)=(25×1.732)=43.3.
Hence, the height of each pillar is 43.3 m and the point of observation is 25 m away from the first pillar.
Example 6
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30∘, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60∘. Find the time taken by the car to reach the foot of the tower from this point.
Let CD is highway and AB is tower.
C is the initial position of the car and D is the position after 6 seconds.
In △ADB,
ABDB = tan60∘
⇒ ABDB = √3
⇒ DB=AB√3
In △ABC,
ABBC=tan30∘
⇒ ABBD+DC = 1√3
⇒ AB√3 = BD+DC
⇒ AB=AB√3+DC [Putting the value of BD]
⇒ AB√3−AB√3 = DC
⇒ DC = 3AB−AB√3 = 2AB√3
The time taken to travelled CD (= 2AB√3) distance = 6 sec
Therefore, the speed of the car = distancetime = 2AB√36 = AB3√3 m/s
The time taken to travelled BD (=AB√3) distance = DistanceSpeed = AB√3AB3√3 = 3 sec
Hence, car will take 3 seconds to reach the foot of the car.
Note → Most important thing is to draw a figure first.
Summary
In this chapter, you have studied the following points :-
1. (i) The line of sight is the line drawn from the eye of an observer to the point in the object viewed by the observer.
(ii) The angle of elevation of an object viewed, is the angle formed by the line of sight with the horizontal when it is above the horizontal level, i.e., the case when we raise our head to look at the object.
(iii) The angle of depression of an object viewed, is the angle formed by the line of sight with the horizontal when it is below the horizontal level, i.e., the case when we lower our head to look at the object.
2. The height or length of an object or the distance between two distant objects can be determined with the help of trigonometric ratios.
Let's Revise
To bachcho ab hum Some Applications of Trigonometry chapter ka revision karne wale hai.
Iss chapter mein hum trigonometry ka use karkey height and distance ke question ko solve kartey hai.
Jab ek observer point O se kisi object A ko dekhta hai tab OA line of sight kahlata hai.
Suppose karo ki point O se tum apne eye level se upar kisi object A ko dekh rhey ho, tab line of sight jo angle banati hai horizontal line ke saath jo point O se pass kar rhi hai, ussey angle of elevation of A as we seen from O kahtey hai.
Suppose karo ki tum point O se apne eye level se niche kisi object B ko dekh rhey ho, tab line of sight jo angle banati hai horizontal line ke saath jo point O se paas kar rhi hai, ussey angle of depression of B for A kahtey hai.
- Iss chapter mein hum kuch iss tarh ki problems ko solve kartey hai
(i) Measuring the heights of towers or big mountains
(ii) Determining the distance of the shore from the sea
(iii) Finding the distance between two celestial bodies
(iv) Ladder problems, etc.