REAL NUMBERS for Class 10 MATHS
INTRODUCTION
Bachcho es chapter mein hum padhenge real numbers ke baare mein vse to hum numbers ke baare mei pichli classes se padhte aa rhe hai lekin ab hum real numbers ke baare mein aur detail mein padhenge. Ismei hum 2 important properties cover karenge The Euclid’s division algorithm and The Fundamental Theorem of Arithmetic. Euclid’s division algorithm mein hum discuss karenge 2 positive integers ki divisibility ke baare mein. Let's say 'a' ek positive integer hai aur agar 'a' ko hum divide karte hai dusre positive integer 'b' se toh humare pass ek remainder ayega r jo ki 'b' se chota hoga. Iski aur bhi bahut sari properties hoti hai divisibility se related jaise ki HCF of two positive integers. To chalo ab hum es chapter ko detail mein padhte hai.
INTRODUCTION
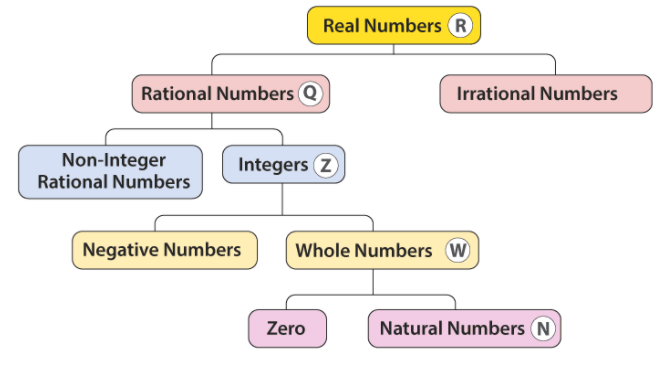
Number System
Natural Numbers : (N)={1,2,3....∞}
Whole Numbers : (W) = {0,1,2,3....∞}
Integers : (I) = {–∞,........–3,–2,–1,0,1,2,3....∞}
Positive Integers : (I+)={1,2,3...∞}
Negative Integers = (I–)={–∞,....–3,–2,–1}
Non-negative Integers = {0,1,2,3........}
Non-positive Integers = {–∞,....–3,–2,–1,0}
Even Integers = {....–6,–4,–2,0,2,4,6...}
Odd Integers = {–5,–3,–1,1,3,5......}
Note:
(i) Zero is neither positive nor negative.
(ii) Zero is even number.
(iii) Positive means >0.
(iv) Non-negative means ≥0.
Let's Learn
Toh sabse pehle es chapter mein hum padhenge numbers ke baare mei
Toh bachcho, numbers kya hote hai ?
Numbers mein sabse pehle hmare pass aate hai natural numbers wo numbers jo ki nature se derive hote hai unhe hum natural numbers khte hai.
1. N = Natural Numbers
Basically jitne bhi counting numbers hote hai N=1,2,3....
2. W = Whole Numbers
Ab dusre ate hai hmare pass whole numbers agar hum natural number mein 0 add karde to wo whole numbers khlate hai
W=0,1,2,3...
→ Abh humne natural numbers aur whole numbers dono ki baat kr li. Lekin agar mai aapse puchu ki 0 se pehle kya aata hai to aap kya kahenge −1, is it so aur us se pehle −2,−3.... Ye sabhi negative numbers khlate hai.
3. Integers
To ab negative numbers aur whole numbers dono ko ek saath hum integers khte hai. Integers kise khte hai yeh to humne pdh liya abh hum padhenge integers kishe nhi khte. Wo numbers jo fractional ya decimal form mein hote hai unhe hum integers nhi khte.
Note : → Negative Integers are {−1,−2,−3,−4,−5,...}
Positive Integers or non negative numbers are {1,2,3,4,5,...}
0 is neither positive nor negative
We can put that all together like this:
Integers = {...,−4,−3,−2,−1,0,1,2,3,4,...}
4. Even Numbers
Even numbers wo numbers hote hai jo multiples of 2 hote hai mtlb jinhey 2 se divide kiya ja sakta hai. Inhe hum 2n ki form mei likh sakte hai jaha n humara koi bhi natural number ho sakta hai
If n=1, then number becomes 2 which is even
If n=2, number becomes 4 which is even and so on.
5. Odd Numbers
Aise numbers jo 2 ke multiples nhi hotey ya jinhey 2 se divide karne par remainder 1 aye unhey odd number kaha jata hai. Inhey hum 2n+1 ki form mein likh sakte hai jaha n koi bhi natural number ho sakta hai.
1,3,5,7,... all are odd numbers.
6. Prime Numbers
Wo natural no's jo ki 1 se bade hote hai aur keval 1 se aur khudse divisible hote hai unhe hum prime numbers khte hai. Prime numbers ke do factor hote hai 1 aur woh number khud for ex.- 2,3,5,7 & 11 etc.
* 1 prime number nhi hota kuki iska keval ek hi factor hai
7. Coprime Numbers
Ase do numbers jinka koi common factor na ho other than 1 coprime khlate hai
for ex. 18 and 35 factors of 18 are 1,2,3,6,9 aur 35 ke factors hai 1,5,7 to inme keval 1 hi ek common factor hai iska matlab 18 aur 35 co-prime hai.
8. Composite Numbers
Wo natural numbers jo 1 se divisible , khudse aur baki dusre number se bhi divisible ho unhe hum composite numbers khte hai for ex.- 4,6,8,9,10 etc.
NOTE : * 1 is neither prime nor a composite number abh hume numbers ke baare mein toh jankari ho gyi to abh hum apna level thoda sa badhayenge toh abh hum padhenge rational numbers ke baare mein.
9. Rational Numbers
Wo numbers jo ki pq (where p and q are integers), ki form mei represent kiye jate hai, where q≠0, rational numbers khlate hai.
10. Irrational numbers
Aise numbers jinhe pq, (where p and q are integers and q≠0), ki form mein nhi likha jaa sakta unhey irrational numbers kaha jata hai. In fact we can say that the numbers which are not rational numbers are called irrational numbers.
For example : π, √3, √5 irrational numbers khlate hai.
Fraction : `(p)/(q)`
(a) Proper Fraction = 35:Nr<Dr
(b) Improper Fraction =53:Nr>Dr
(c) Mixed Fraction = 2+35
(d) Compound Fraction = 2356
(e) Complex Fraction = 2⋅13
(f) Continued Fraction = 2+22+2+....
This is usually written in the more compact form 2+12+12+....
1. Euclid’s Division lemma
To bachcho ab hum sikhne vale hai Euclid’s Division lemma ke baare mein lekin ye sikhne se phle hum thoda sa basic revise karte hai. Aap sabne division algorithm to sekha hi hoga jisme agar apko 39 ko 5 se divide karna ho to yha 39 hmara Dividend aur 5 Divisor kahlata hai aur 39 ko 5 se divide karne per hume remainder kya milega 4 which is less than 5. 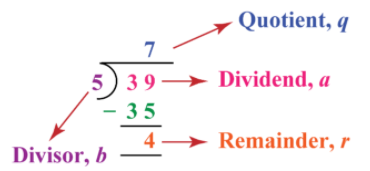
So, let Dividend be a, Divisor be b, Quotient q and Remainder r. As we know that
Dividend = Divisor × Quotient + Remainder
i.e., a=bq+r
To bachcho yhi to hmari Euclid’s Division lemma theorem hai where 0≤r<b.
Rational Numbers (Q):
All the numbers that can be represented in the form pq, where p and q are integers and q≠0, are called rational numbers. Integers, Fractions, terminating decimal numbers, non-terminating but repeating decimal numbers are all rational numbers.
Q={pq:p,q∈I and q=!0}
Note:
(i) Integers are rational numbers, but converse need not be true.
(ii) A rational number always exists between two distinct rational numbers; hence infinite rational numbers exist between two rational numbers.
2. What is Euclid's Division Algorithm?
Bachho Algorithm kya hoti hai ? Algorithm basically kisi work ko krne ki steps ki ek series hoti hai. For example : hum chai bnate hai to uske liye sbse phle hum thoda water lete hai, fir use gas per rkhkr boil krte hai, then we add leaves of tea, ginger, sugar etc. and fir boil krte hai and then milk add krte hai aur es tarh se humari chai ban jati hai. Basically ye chai bnane ke step hai that means ye chai bnane ki algorithm hai. Same esi type se hum Euclid division lemma ka use karke kisi specific problem ko solve krne ki steps bnate hai jise hum Euclid's Division Algorithm khte h. Aur wo specific problem hai two numbers ka HCF nikalna. So Euclid's Division Algorithm mein hum Euclid's Division Lemma ki equation ko baar baar apply karke 2 number ka highest common factor (HCF) nikalte hai. To chlo ab hum ek example se samjhte hai.
Euclid's Division Algorithm Example - Finding HCF
Agar hmare pass 2 number hai 320 aur 132 hme iska HCF nikalne hai toh isphe hum Euclid's Division Lemma lgayenge
320=132(2)+56
Ab humne kya dekha jho HCF hai (call it x) wo 320 aur 132 dono ka common factor hai toh ishe 56 yani ki remainder ka bhi factor hona chahiye to abh hum division lemma apply karenge 132 aur 56 pe.
132=56(2)+20
Ab esi tarh se HCF x jho hai common factor hai 132 aur 56 ka toh ishe 20 ka bhi factor hona chaiye to agle step mein hum division lemma apply karenge 56 aur 20 pe,
56=20(2)+16
Ab jaise ki hmne pehle dekha x jho hai dono ka common factor hai 56 aur 20 ka to yeh 16 ka bhi hoga, to agle step mein hum division lemma apply karenge 20 aur 16 pe,
20=16(1)+4
Ab x jo hai dono ka common factor hai 20 aur 16 ka to abh yeh 4 ka bhi hoga ab last step mei humare pass hai,
16=4(4)+0
Ab humare pass koi remainder nhi bacha to ab hum kah sakte hai second last remainder 4 jo hai wo 320 aur 132 ka HCF hai.
HCF(320,132)=4
To 4 humara original pair ka common factor hai.
Irrational Numbers (Qc):
There are real numbers which cannot be expressed in pq form. Non-Terminating non repeating decimal numbers are irrational number
e.g. .e≈2.71 is called Napier's constant and π≈3.14
Note :
(i) Sum of a rational number and an irrational number is an irrational number e.g. 2+√3
(ii) If a∈Q and b∈Q, then ab= rational number, only if a=0.
(iii) Sum, difference, product and quotient of two irrational numbers need not be an irrational number or we can say, result may be a rational number also.
Theorem 1.1
Euclid’s Division Lemma: Given positive integers a and b, there exist unique integers q and r satisfying a=bq+r,0≤r<b.
Euclid’s division algorithm is a technique to compute the Highest Common Factor
(HCF) of two given positive integers. Recall that the HCF of two positive integers a
and b is the largest positive integer d that divides both a and b.
To obtain the HCF of two positive integers, say c and d, with c>d, follow the steps below :
Step 1 : Apply Euclid’s division lemma, to c and d. So, we find whole numbers, q and r such that c=dq+r, 0≥r>d.
Step 2 : If r=0, d is the HCF of c and d. If r≠0, apply the division lemma to d and r.
Step 3 : Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.
This algorithm works because HCF(c,d)=HCF(d,r) where the symbol HCF(c,d) denotes the HCF of c and d, etc.
Real Numbers (R):
All rational and irrational numbers are called real numbers
Example 1
Using Euclid's algorithm,find the HCF of 4052 and 12576.
a=12576, b=4052
Euclid's Division Algorithm use karte hue kya aya hmare pass
a=bq+r
12576=4052×3+420
to remainder kya hai hmara 420 jo ki 0 ke equal nhi hai to hum dubara se euclid's division theorem lgayenge 4052=420×9+272
jbh tak hmara pass remainder 0 ke equal nhi aa jata tbh tk hum euclid's division algorithm lgayenge 420=272×1+148
again remainder is not equal to 0 toh dubara se lgayenge
272=148×1+124
again remainder = 124 which is ≠0
124=24×5+4
again remainder =4
24=4×6+0
toh HCF kya hua 4052 and 12576 ka 4
HCF(4052,12576)=4.
NATURE OF THE DECIMAL EXPANSION OF RATIONAL NUMBERS
→ Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form , pq, where p and q are coprime, and the prime factorisation of q is of the form 2n5m, where n, m are non-negative integers.
Example,
(i) 13125=1353=13×2323×53=104103=0.104
(ii) 14588625=22×7×52154=26×7×52124×54=233408104=23.3408
These examples show us how we can convert a rational number of the form pq, to an equivalent rational number of the form , ab, where b is a power of 10. Therefore, the decimal expansion of such a rational number terminates.
→ Let x=pq be a rational number, such that the prime factorisation of q is of the form 2n5m, where n, m are non-negative integers. Then x has a decimal expansion which terminates.
Now we will discuss rational numbers whose decimal expansions are non-terminating and recurring(repeating). Consider 17 , divisor is 7 and we get remainders 3, 2, 6, 4, 5, 1, 3, 2, 6, 4, 5, 1, . . . Hence, 0 will not show up as a remainder. But remainders will start repeating after a certain stage. So, we will have a block of digits, 142857, repeating in the quotient of 17 . Since 17 is rational number not covered in any theorem so our next theorem is based on this.
→ Let x=pq , where p and q are coprimes, be a rational number, such that the prime factorisation of q is not of the form 2n5m, where n, m are non-negative integers. Then, x has a decimal expansion which is non-terminating repeating (recurring) .
Hence we can finally conclude that the decimal expansion of every rational number is either terminating or non-terminating repeating (recurring).
Example 2
Show that n2−n is divisible by 2 for every +ve integer n.
Maan lo koi positive integer hai 2q or2q+1 ki form kisi integer q ke liye to hum dono case dekhenge
Case I : jbh n=2q hoga
n2−n = 4q2−2q = 2q(2q−1)=2m [ here m=q(2q−1) ]
that means n2−n is divisible by 2.
Case II : jbh n=2q+1 hoga
n2−n=(2q+1)2−(2q+1)
=4q2+1+4q−2q−1
=4q2+2q
= 2q(2q+1)
=2m' [ here m'=q(2q+1) ]
So, n2−n jo hai 2 se bhi divisible hai
Hence, n2−n jo hai 2 se divisible hoga sabhi +ve integer m aur m' ke liye.
Euclid’s Division lemma or Euclid's Division Algorithm
Given positive integers a and b, there exist unique integers q and r satisfying a=bq+r,0≤r<b.
Euclid’s division algorithm is a technique to compute the Highest Common Factor
(HCF) of two given positive integers. Recall that the HCF of two positive integers a
and b is the largest positive integer d that divides both a and b.
To obtain the HCF of two positive integers, say c and d, with c>d, follow the steps below :
Step 1 : Apply Euclid’s division lemma, to c and d. So, we find whole numbers, q and r such that c=dq+r, 0≥r>d
Step 2 : If r=0, d is the HCF of c and d. If r≠0, apply the division lemma to d and r.
Step 3 : Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.
This algorithm works because HCF(c,d)=HCF(d,r) where the symbol HCF(c,d) denotes the HCF of c and d, etc.
APPLICATION OF EUCLID'S DIVISION LEMMA FOR FINDING H.C.F. OF POSITIVE INTEGERS
Example: Find HCF of 56 and 72.
Steps:
Apply lemma to 56 and 72.
Take bigger number and locate ‘b’ and ‘r’. 72=56×1+16
Since 16≠0, consider 56 as the new dividend and 16 as the new divisor. 56=16×3+8
Again, 8≠0, consider 16 as new dividend and 8 as new divisor. 16=8×2+0.
Although Euclid’s Division lemma is stated for only positive integers, it can be extended for all integers except zero, i.e., b≠0.
3. Fundamental Theorem of Arithmetic
To bachcho ab hum padhenge Fundamental Theorem of Arithmetic ke baare mein. To sabse pehle hum iski definition dekhte hai : -
" Every composite number can be uniquely expressed as a product of primes, except for order in which these prime factors occur. "
So this statement means chahey koi bhi composite number ku na ho ushe hum prime numbers ke product ki form mein express kar saktey hai aur sabse important baat ye hai ki jin prime numbers se hum unhe express kar rahe hai wo unique hoga ignoring the order of numbers. For example apne apni pichli classes mein prime factorisation to padha hi hoga yeh bhi bilkul waisa hi hai kaisey chaliye dekhte hai. Maan lo humme 262 ke factors nikalne hai. So, by Prime Factorisation :
262=2×131×1
To ismei hum dekh sakte hai ki 2 aur 131 kya hai prime numbers hum eshe ase bhi likh saktey hai.
262=1×131×2 = 1×2×131
jsa ki humne upar mention kiya tha " ignoring the order " esse hmara matlab tha ki order matter nhi karta agar hum dono ka product dekhe to humme 262 hi milega that is same. And the second thing is dusre koi bhi prime numbers ko multiply karke hum 262 nhi laa saktey isliye statement mein unique word use kiya jata hai.
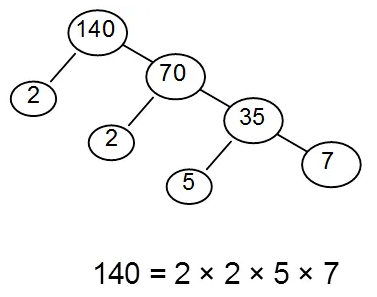
Let we take few more examples of prime factorizations :
10=2×5
19=19
35=5×7
140=2×2×5×7
Constructing a factor tree
Steps
Repeat the process till all the primes are obtained ∴ Prime factorization of 48=24×3
Theorem 1.2
Every composite number can be expressed ( factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.
You have already learnt how to find the HCF and LCM of two positive integers using the Fundamental Theorem of Arithmetic in earlier classes, without realising it!
This method is also called the prime factorisation method.
The Fundamental Theorem of Arithmetic says that every composite number can be factorised as a product of primes. For example, 2=2,4=2×2,253=11×23, and so on. In general, given a composite number x, we factorise it as x=p1p2...pn, where p1,p2,.....,pn are primes and written in ascending order, i.e., p1≤p2≤...≤pn . Let us take some large number, say, 32760, and factorise it as shown :
So we have factorised 32760 as 2×2×2×3×3×5×7×13 as a product of primes, i.e., 32760=23×32×5×7×13 as a product of powers of primes.
THE FUNDAMENTAL THEOREM OF ARITHMETIC
Every composite number can be expressed as a product of primes, and this expression is unique, apart from the order in which they appear.
Applications:
1.To locate HCF and LCM of two or more positive integers.
2.To prove irrationality of numbers.
3.To determine the nature of the decimal expansion of rational numbers.
Example 3
Find the HCF and LCM of 26 and 91 and verify that L.C.M X H.C.F = product of two numbers.
To sabse pahale hum 26 aur 91 ke prime factors nikalenge so,
26=2×13
91=7×13
so 26 aur 91 ka HCF kya hua 13
HCF(26,91)=13
aur LCM kya hua 26 aur 91 ka
LCM(26,91)=13×2×7=26×7=182
LCM×HCF=13×182= 2366
so dono no ka product kya hua that is = 26×91 = 2366
to iska matlab LCM×HCF = Product of two numbers.
Example 4
Find the HCF and LCM of 108,120 and 252 using prime factorisation method.
By prime factorisation, we get
108=(22×33)
120=(23×3×5)
252=(22×32×7)
HCF (108,120,252)= product of common terms with lowest power
(22×3)=(4×3)=12
LCM (108,120,252)= product of prime factors with highest power
=(23×33×5×7)=7560
HCF=12andLCM=7560.

4. Irrational Numbers
Bachcho irrational no's kya hota hai irrational no's wo numbers hote hai jo ki decimal form mei non-terminating and non-repeating decimals ki form mei express kiye jate hai unhe hum irrational number bolte hai.
* Har ek non-terminating and non-repeating decimal irrational khlate hai.
Types of irrational no.
Type 1. Let's say 0.1010010001... yeh ek non-terminating and non-repeating decimal hai islie ye ek irrational no. hai. Non terminating ye islie hai kyonki iska end term nhi pta aur ye non repeating islie kyonki ye ek certain pattern ke baad repeated nhi hai.
For ex. 0.12112111211112...,is irrational
0.232232223..., is irrational
Type 2. agar 'm' ek positive integer hai jo ki ek perfect square nhi hai then √m is irrational jse ki √3,√6,√7 etc., yeh sabhi no's irrational hai.
Type 3.agar 'm' ek positive integer hai jo ki ek perfect cube nhi hai then 3√m irrational hoga. For ex : 3√2,3√3,3√4,3√5...etc yeh sabhi irrational hai.
Type 4. pi jo hai irrational hai, jabki 227 rational hai.
Theorem 1.3
Let p be a prime number. If p divides a2, then p divides a, where a is a positive integer.
Proof : Let the prime factorisation of a be as follows :
a=p1p2 ...pn, where p1,p2, ..., pn are primes, not necessarily distinct.
Therefore, a2=(p1p2...pn)(p1p2...pn)=p21p22...p2n.
Now, we are given that p divides a2. Therefore, from the Fundamental Theorem of Arithmetic, it follows that p is one of the prime factors of a2. However, using the uniqueness part of the Fundamental Theorem of Arithmetic, we realise that the only prime factors of a2 are p1p2...pn. So p is one of p1,p2,...pn.
Now, since a=p1p2...pn,p divides a.
We are now ready to give a proof that √2 is irrational.
The proof is based on a technique called ‘proof by contradiction’.
Theorem 1.4
√2 is irrational.
Proof : Let us assume, to the contrary, that √2 is rational.
So, we can find integers r and s(≠0) such that √2=rs.
Suppose r and s have a common factor other than 1. Then, we divide by the common factor to get √2=ab, where a and b are coprime.
So, b√2=a.
Squaring on both sides and rearranging, we get 2b2=a2. Therefore, 2 divides a2.
Now, by above Theorem, it follows that 2 divides a.
So, we can write a=2c for some integer c.
Substituting for a, we get 2b2=4c2, that is, b2=2c2.
This means that 2 divides b2 , and so 2 divides b (again using above Theorem with p=2).
Therefore, a and b have at least 2 as a common factor.
But this contradicts the fact that a and b have no common factors other than 1.
This contradiction has arisen because of our incorrect assumption that √2 is rational.
So, we conclude that √2 is irrational.
Example 5
Show that 3√2 is irrational.
To hum maan lete hai ki 3√2 ek rational number hai.
eshe hum contradictory method se solve karenge
agar 3√2 rational hai to eshe hum ab ki form mei likh sakte hai and where b≠0 denominator 0 ke equal nhi hona chahiye and a aur b hmare integers hai asa jruri nhi hai ki a aur b coprime ho toh inko coprime bnane ke liye hum common factors ko cancel out karenge to hmare pass bachega 3√2=ab
So by, Rearranging, we get √2=a3b.
Since 3, a and b are integers, a3b is rational, and so √2 is rational.
But this contradicts the fact that √2 is irrational.
So, we conclude that 3√2 is irrational.
Example 6
Prove that (3+5√2) is irrational.
Let us assume, to the contrary , that (3+5√2) is rational.
Then , there exist co-primes a and b (b≠0) such that
3+5√2=ab
⇒5√2=ab−3=a−3bb
⇒√2=a−3b5b , which is rational because a,b are integers.
Thus, √2 is also rational.
But, this contradicts the fact that √2 is irrational. So, our asumption is incorrect.
Hence, (3+5√2) is irrational.
Theorem 1.5
Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form , pq, where p and q are coprime, and the prime factorisation of q is of the form 2n5m, where n, m are non-negative integers.
Example,
(i) 13125=1353=13×2323×53=104103=0.104
(ii) 14588625=22×7×52154=26×7×52124×54=233408104=23.3408
These examples show us how we can convert a rational number of the form pq, to an equivalent rational number of the form , ab, where b is a power of 10. Therefore, the decimal expansion of such a rational number terminates.
Theorem 1.6
Let x=pq be a rational number, such that the prime factorisation of q is of the form 2n5m, where n, m are non-negative integers. Then x has a decimal expansion which terminates..
Now we will discuss rational numbers whose decimal expansions are non-terminating and recurring(repeating). Consider 17 , divisor is 7 and we get remainders 3, 2, 6, 4, 5, 1, 3, 2, 6, 4, 5, 1, . . . Hence, 0 will not show up as a remainder. But remainders will start repeating after a certain stage. So, we will have a block of digits, 142857, repeating in the quotient of 17 . Since 17 is rational number not covered in any theorem so our next theorem is based on this.
Theorem 1.7
Let x=pq , where p and q are coprimes, be a rational number, such that the prime factorisation of q is not of the form 2n5m, where n, m are non-negative integers. Then, x has a decimal expansion which is non-terminating repeating (recurring) .
Hence we can finally conclude that the decimal expansion of every rational number is either terminating or non-terminating repeating (recurring).
5. Decimal Expansion of Rational Numbers
To bachcho ab hum padhne vale hai decimal expansions of Rational number. As you know that rational number do tarh ke hotey hai Terminating aur Non Terminating Repeating. Upar mention theorem ki help se bina long division method ko use kiye hum bata saktey hai wo Terminating hai ya Non Terminating aap soch rahe honge kaise ? To chaliye dekhte hai
⇒ Theorem mein clearly likha hai ki agar denominator (q) ke prime factors nikalne par wo 2n×5m ki form mein ata hai to wo terminating hoga otherwise non - terminating. [where n and m are non-negative integers]
Examples se samajhte hai
1. 320
yha denominator kya hai 20 that means q=20
q=20=2×2×5×1=22×51×1
=22×51
yha hum dekh saktey hai ki jab humne 20 ke prime factors nikale to wo 2n×5m ki form mein aye where n=2,m=1 isliye 320 ek terminating rational number hai.
2. 345
Here q=45=32×51×1=32×51
yha hum dekh saktey hai ki q ko factorise karne ke baad 32×51 aya hai jo ki 2n×5m ki form mein nahi hai isliye ye Non Terminating Repeating rational number hai.
3. 3125
Here q=125=53×1
Hum dekh saktey hai ki 125 ko factorise karne ke baad 53×1 aya hai jise hum 20×53×1 bhi likh saktey hai kyon ki kisi bhi real number ki power agar 0 ho to uski value 1 hoti hai aur hum dekh saktey hai ki ab 125=20×53, 2n×5m ki form mein hai isliye ye ek terminating rational number hai.
Example 7
Without actually calculating, state whether the following rational numbers have a terminating or non-terminating repeating decimal expansion.
(i) 27343
(ii) 191600
(i)27343 = 2773
to 'q' kiske equal hai 73 ke jo ki 2m×5n ke equal nhi hai
so iska matlab yeh ek non-terminating decimal hai
(ii)191600 = 1926×52
jse ki jo abh hmara denominator hai woh kis form mei hai 2m×5n since q= 26×52 to ye ek terminating decimal representation hai .
Example 8
What can you say about the prime factorisation of the denominators of the following rationals :
(i) 34.12345 (ii) 34.¯¯¯¯¯¯¯¯5678
(i) Since 34.12345 has terminating decimal expansion. So, its denominator is of the form 2m×5n, where m,n are non-negative integers.
(ii) Since 34.¯¯¯¯¯¯¯¯5678 has non-terminating repeating decimal expansion. So, its denominator has factors other than 2 or 5.
Summary
* Algorithm to locate HCF and LCM of two or more positive integers :
Step I. HCF aur LCM nikalne ke liye do positive integers ko factorize kare aur unhe unke prime factors ki power ki form mei increasing order mei likhe.
Step II. HCF nikalne ke liye sabse pahale common prime factors nikale aur phir least power ko multiply kare to get HCF.
Step III. LCM nikalne ke liye greatest power vale factors ko dhondhe aur unhe multiply kar de to get the LCM.
* Irrational numbers wo no's jo non repeating aur non terminating decimal form mei hote hai irrational no's khlate hai.
* To determine the nature of the decimal expansion of rational numbers :
Let x=pq ek rational number hai agar q ke factor 2m×5n ke equal hai, jha m aur n non negative integers hai to x ek terminating decimal expansion hai
Let x=pq ek rational number hai agr q ke factor 2m×5n ke equal nhi hai toh x ek non-terminating but repeating decimal expansion hai.
Let's Revise
- Lemma : - Ek proven statement jo ki use ki jati hai dusri statement ko prove karne ke liye.
- Euclid Division Lemma
For any 2 given positive integer a and b there exist two unique whole numbers q and r such that
a=bq+r,0≤r<b
where, a and b are positive integer
q and r are unique integer . - HCF(a,b)×LCM(a,b) = product of a and b
- HCF divides LCM completely .
- For a rational number in form pq
(i) if q=2m×5n where 0≤m,n then pq is a terminating decimal .
(ii) if q≠2m×5n then pq is a non - terminating repeating.