POLYNOMIALS for Class 10 MATHS

To bachcho es chapter mein hum padhenge polynomials ke baare mein vse toh polynomials ke baare mein humne class IX mein bhi pdha hai. Kya hota hai polynomials ? Asi expressions jo ki
$p\left(x\right)=a_0+a_{1}x+a_2{x}^2+...a_n{x}^n$ , where $a_n\ne 0$
ki form mein ho. $x$ ki highest power ko hum degree of polynomials khte hai, aur $a_0$, $a_{1}x$, $a_2{x}^2$ expression ki terms hai. $x$ ke product mein jo constant hota hai usse hum coefficient khte hai, yha $a_0$, $a_1$, $a_2$,...,$a_n$ variable $x$ ke coefficient hai aur real numbers hai. $x$ ki har ek power non negative integer hogi. Ab hum dekhte hai

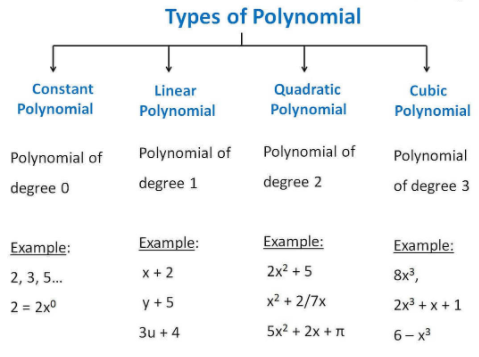
Types of polynomials.

Is the equation $x^0$ a polynomial?

• Linear Polynomial : Wo polynomial jinki degree $1$ hoti hai linear polynomial khlate hai.
  Ek linear polynomial $p\left(x\right)=ax+b$ ki form mei hote hai , where $a\ne 0$
  $\therefore$ $ax+b$ is a Linear Equation of Degree $1$
  For ex. $(3x-5)$, $(\sqrt{2}x+3)$, $(x-\frac{5}{8})$etc.,... are all linear polynomial.


• Quadratic Polynomial : Wo polynomial jinki degree $2$ hoti hai Quadratic Polynomial khlate hai.
  Ek Quadratic polynomial $p\left(x\right)=a{x}^2+bx+c$ ki form mei hote hai, where $a\ne 0$
  $\therefore$ $a{x}^2+bx+c$ is a Quadratic Equation of Degree $2$.
  For ex. $(3x^2+5x-8)$, $(y^2-3y+\sqrt{3})$, etc., are all quadratic polynomials.


• Cubic Polynomial : Wo polynomial jinki degree $3$ hoti hai Cubic Polynomial khlate hai.
  Ek cubic polynomial $p\left(x\right)=a{x}^3+b{x}^2+cx+d$ ki form mei hote hai, where $a\ne 0$
  $\therefore$ $a{x}^3+b{x}^2+cx+d$ is a Cubic Equation of Degree 3
  For ex. $(2x^3-3x^2+8x+1)$, $(z^3+2z^2-\sqrt{3}z+3)$, etc., are all Cubic Polynomials.

NOTE : The degree of a polynomial is the highest degree of its monomials (individual terms) with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer.
$\therefore$ Degree of zero polynomial is not-defined.

STANDARD DEFINITION OF POLYNOMIALS
An expression of the form $p\left(x\right)=a_0+a_{1}x+a_2{x}^2+............a_n{x}^n$, where $a_n\ne 0$ , is called a polynomial in x of degree n.
Here $a_0$, $a_1$, $a_2$...................,$a_n$ are real numbers and each power of $x$ is a non-negative integer.

Ek real number $\alpha$ zero of polynomial tabhi khlata hai agar polynomial $p\left(x\right)$ ka value $x=\alpha$ ke liye $0$ ho.
Value of a polynomial at a point or (Value at a given point) is the value obtained by the polynomial at that point.
Example : Let $p\left(x\right)=x^2-2x-3$. Find (i) $p\left(3\right)$ and (ii) $p(-1)$
What do you conclude ?
$\left(i\right)$ Hmare pass hai $p\left(x\right)=x^2-2x-3$ then ab humne kya krna hai esh polynomial pe $p\left(3\right)$ ki value nikalni hai aur iske liye hum simply equation mei $x=3$ put kartey hai.
We have $p\left(x\right)=x^2-2x-3$
$p\left(3\right)$ = $(3^2-2\times 3-3)$
$=(9-6-3)$
$=0$
$\left(ii\right)$ $p(-1)=\{{(-1)}^2-2\times (-1)-3\}$
=$(1+2-3)$
= $0$
Humney yah dekha ki equation mein jab humney $x$ ko $3$ aur $-1$ se repalce kiya tab humey result $0$ mila, isliye ab hum kah saktey hai ki $3$ aur $-1$ zeros of polynomial hai $p\left(x\right)$ ke.

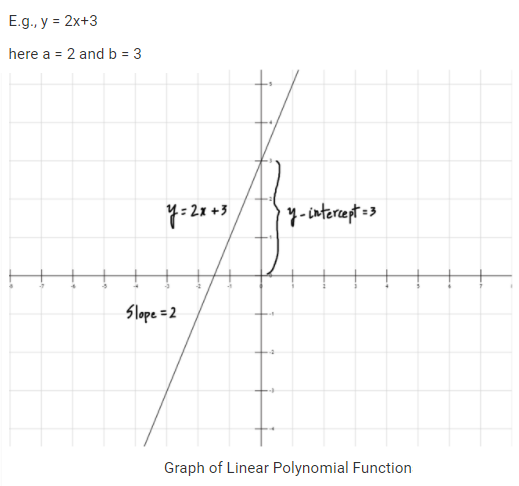
Ek linear polynomial ko line graph se represent kiya jata hai.

• Standard form : $P\left(x\right)=ax+b$, where $a$ and $b$ are constants. It forms a straight line.
  
  Quadratic polynomial can be represent by a parabola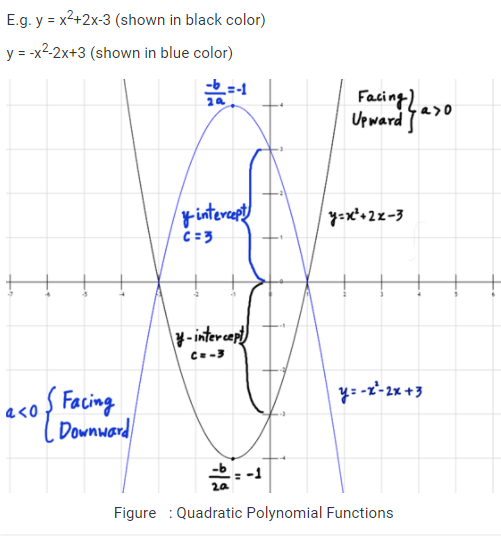
  
  Cubic polynomial by a cubic curve,, etc.
  Jis points pe yeh graph x-axis ko intercept kartey hai, uss point pe polynomial function zero ke equal hota hai, it represents the zeroes or roots of the polynomial.

• Jo Linear Polynomial ka graph hai vo x-axis ko maximum ek point pe cut karega , a linear polynomial has at most one zero.


• Jo Quadratic Polynomial ka graph hai voh x-axis ko maximum do point pe cut karega, therefore, a quadratic polynomial can have a maximum of two zeroes. Iss case mei, graph ka shape parabola hoga.
  Kisi bhi Quadratic Polynomial of $a{x}^2+bx+c$, $a\ne 0$, ke graph ka shape ( either open upwards or open downwards ) $x^2$ ke coefficient ke sign par depend krta hai.
  Agar $a>0$, to parabola upar ki aur open hoga.
  Agar $a<0$, to parabola neeche ki aur open hoga.


• Jo Cubic Polynomial hai voh x-axis ko cut karega maximum teen point pe. A Cubic Polynomial has maximum of three zeroes.

In general, koi bhi $n^{th}$-degree polynomial x-axis ko cut karega at maximum of $n$ points.
Therefore, an $n^{th}$-degree polynomial has a maximum of n zeroes.

Polynomials can easily be represented graphically.
E.g. Agar hume plot krna hai polynomial $p\left(x\right)=x-2$ to hum iska zero of polynomial nikalenge.
Zero of polynomial $p\left(x\right)$ x-coordinate hai uss point ka jis point pe p(x) ka graph intersect karega x-axis ko.
to hum $x-2$ ko $0$ se equate karenge to polynomial $p\left(x\right)$ intersect karega x-axis ko at $x=2$ pe, thus zero of polynomial is 2.
Linear Polynomial $ax+b$, where $a\ne 0$, ka exactly ek hi zero hota hai.
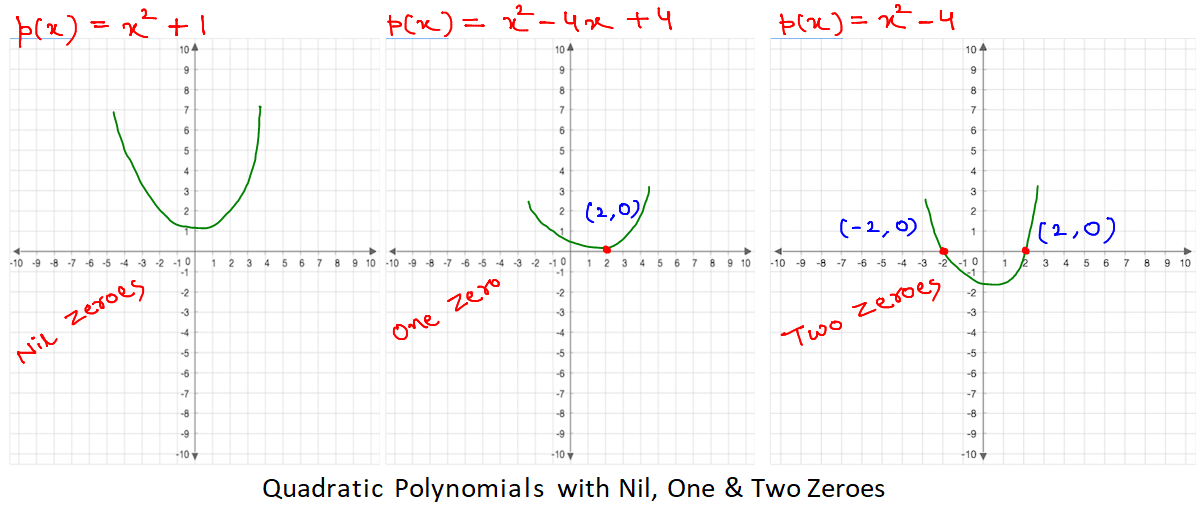
E.g. Maan lo ek quadratic polynomial hai $p\left(x\right)=x^2+1$ to hum ess equation ko $0$ se equate karke iske zeroes nikalenge to hmare pass aya $x=\sqrt{-}1$ to yeh ek imagnary number hai yani iske koi zeroes nhi hai to iska graph x-axis ko intersect nhi karega.
E.g. Maan lo ek Quadratic polynomial hai $p\left(x\right)=x^2-4x+4$ to isse jab hum $0$ se equate karenge to hmare pass $x$ ka value aya $2$ to iska ek hi zero hai $2$ to ess polynomial ka graph x-axis ko keval ek baar touch karega at $x=2$.
E.g. Agr hmare pass ek Quadratic polynomial hai $p\left(x\right)=x^2-4$ to esse jab hum $0$ se equate karenge to hmare pass do zeroes aye $x=+2,-2$ to ess polynomial ka graph intersect karega x-axis ko 2 places pe, $x=2$ aur $x=-2$ pe.
Graph of above examples is below.

$\Rightarrow$ If $\alpha$ and $\beta$ zeroes of quadratic polynomial, $p\left(x\right)=a{x}^2+bx+c$, where $a\ne 0$
Toh $(x-\alpha )$ aur $(x-\beta )$ factors honge $p\left(x\right)$ ke
$(a{x}^2+bx+c)$ = $k(x-\alpha )(x-\beta )$, jha $k$ ek constant hai
= $k\{x^2-(\alpha +\beta )x+\alpha \beta \}$
= $k{x}^2-k(\alpha +\beta )x+k\left(\alpha \beta \right)$
abh hum $x$ ki same power ke coefficients ko compare karenge
$k=a$, $-k(\alpha +\beta )$ = b, and $k\left(\alpha \beta \right)=c$
$-a(\alpha +\beta )$ = b and $a\left(\alpha \beta \right)$ = c
to iska matlab $k$ is equal to $a$ $(k=a)$.
$(\alpha +\beta )$ = $\frac{-b}{a}$ and $\alpha \beta$ = $\frac{c}{a}$
$\therefore$ Sum of zeroes = -$\frac{\text{coefficient of}x}{\text{coefficient of}{x}^2}$
Product of zeroes =$\frac{\text{constant term}}{\text{coefficient of}{x}^2}$

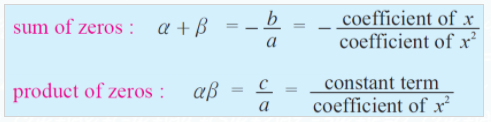
$\Rightarrow$ If $\alpha$, $\beta$, $\gamma$ are the zeroes of the cubic polynomial (cubic polynomial ke maximum $3$ zeroes hotey hai), $p\left(x\right)=a{x}^3+b{x}^2+cx+d$, where $a\ne 0$, then
$\left(i\right)$ The sum of zeroes of the cubic polynomial = $\alpha +\beta +\gamma$ $=\frac{-b}{a}=$ $\frac{-\text{coefficient of}{x}^2}{\text{coefficient of}{x}^3}$
$\left(ii\right)$ Sum of the product of zeroes taken two at a time $=\alpha \beta +\beta \gamma +\gamma \alpha =\frac{c}{a}=$ $\frac{\text{coefficient of}x}{\text{coefficient of}{x}^3}$
$\left(iii\right)$ Product of zeroes = $\alpha \beta \gamma$ = $\frac{-d}{a}$ = $\frac{-\text{constant term}}{\text{coefficient of}{x}^3}$

Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and the coefficients: $x^2+7x+12$.

Hume diya gya hai polynomial $p\left(x\right)=x^2+7x+12$
Sabse pahale hum es equation ke zeroes nikalenge
$x^2+7x+12=0$
$(x+3)(x+4)=0$
to $x$ kya aa gya hmare pass
$x=-3,-4$
Hum isko verify bhi kar sakte hai by checking sum of roots and product of roots. So let's verify it,
Sum of roots $=\frac{-b}{a}=\frac{-7}{1}=-7=-3-4$
Product of roots $=\frac{c}{a}=\frac{12}{1}=12=(-4)(-3)$
Hence Proved.

Find the zeroes of the polynomial $2x^2+5x-12$ and verify the relationship between its zeroes and coefficients.

Let the given polynomial be denoted by $f\left(x\right)$. Then,
$f\left(x\right)=2x^2+5x-12$
$=2x^2+8x-3x-12$
$=2x(x+4)-3(x+4)$
$=(x+4)(2x-3)$.
$\therefore F\left(x\right)=0\Rightarrow (x+4)(2x-3)=0$
$\Rightarrow x+4=0\text{or}2x-3=0$
$\Rightarrow x=-4\text{or}x=\frac{3}{2}.$
So, the zeroes of $f\left(x\right)$ are $-4\text{and}\frac{3}{2}.$
Sum of the zeroes = $(-4+\frac{3}{2})=\frac{-5}{2}=-\frac{\text{coefficient of}x}{\text{coefficient of}{x}^2}$
Product of the zeroes = $(-4)\times \frac{3}{2}=\frac{-12}{2}=\frac{\text{constant term}}{\text{coefficient of}{x}^2}$

Find a quadratic polynomial, the sum and product of whose zeroes are $-5\text{and}6$ respectively.

Let $\alpha \text{and}\beta$ be the zeroes of the required polynomial $f\left(x\right)$.
Then , $(\alpha +\beta )=-5\text{and}\alpha \beta =6.$
$\therefore F\left(x\right)=x^2-(\alpha +\beta )x+\alpha \beta$
$=x^2-(-5)x+6$
$=x^2+5x+6.$
Hence, the required polynomial is $f\left(x\right)=x^2+5x+6.$

To bachcho humney class $IX$ mein quadratic polynomial ko linear polynomial se divide karna shekha tha lekin ab hum cubic polynomial ke liye division algorithm sekhne wale hai.
"If $p\left(x\right)$ and $g\left(x\right)$ are any two polynomials with $g\left(x\right)$ ≠ $0$, then we can find polynomials $q\left(x\right)$ and $r\left(x\right)$ such that
$p\left(x\right)=g\left(x\right)\times q\left(x\right)+r\left(x\right)$,
where $r\left(x\right)=0$ or degree of $r\left(x\right)$ < degree of $g\left(x\right)$".
This result is known as the Division Algorithm for polynomials.
Isse hum ek example se samjhtey hai.
Exmaple : Divide $3x^3+x^2+2x+5$ by $1+2x+x^2$.
Solution: To bachcho sabse phle hum kya karenge, Dividend aur Divisor ko standard form mein likhenge that means in decreasing order.
So, Dividend = $3x^3+x^2+2x+5$ and Divisor = $x^2+2x+1$.
Step 1: To obtain the first term of the quotient, divide the highest degree term of the dividend (i.e., $3x^3$) by the highest degree term of the divisor (i.e., $x^2$). This is $3x$. Then carry out the division process. What remains is $5x^2–x+5$
Step 2 : Now, to obtain the second term of the quotient, divide the highest degree term of the new dividend (i.e., $–5x^2$) by the highest degree term of the divisor (i.e., $x^2$). This gives $–5$. Again carry out the division process with $–5x^2–x+5$.
Step 3: What remains is $9x+10$. Now, the degree of $9x+10$ is less than the degree of the divisor $x^2+2x+1$. So, we cannot continue the division any further.
So, the quotient is $3x–5$ and the remainder is $9x+10$. Also,
$(x^2+2x+1)\times (3x–5)+(9x+10)=3x^3+6x^2+3x–5x^2–10x–5+9x+10$
$=3x^3+x^2+2x+5$.
Hume es example ka jo result mila hai useey hum dekh saktey hai ki,
Dividend = Divisor × Quotient + Remainder.
So, this is similar to Euclid Division Lemma which you have studied in Chapter 1.

If the polynomial $(x^4+2x^3+8x^2+12x+18)$ is divided by another polynomial $(x^2+5)$, the remainder comes out to be $(px+q)$. Find the values of $p$ and $q$.

Let $f\left(x\right)=(x^4+2x^3+8x^2+12x+18)\text{and}g\left(x\right)=(x^2+5).$
On dividing $f\left(x\right)\text{by}g\left(x\right),$ we get

Now, $px+q=2x+3\Rightarrow p=2\text{and}q=3.$

What real number should be subtracted from the polynomial $(3x^3+10x^2-14x+9)$ so that $(3x-2)$ divides it exactly?

On dividing $(3x^3+10x^2-14x+9)$ by (3x-2), we get

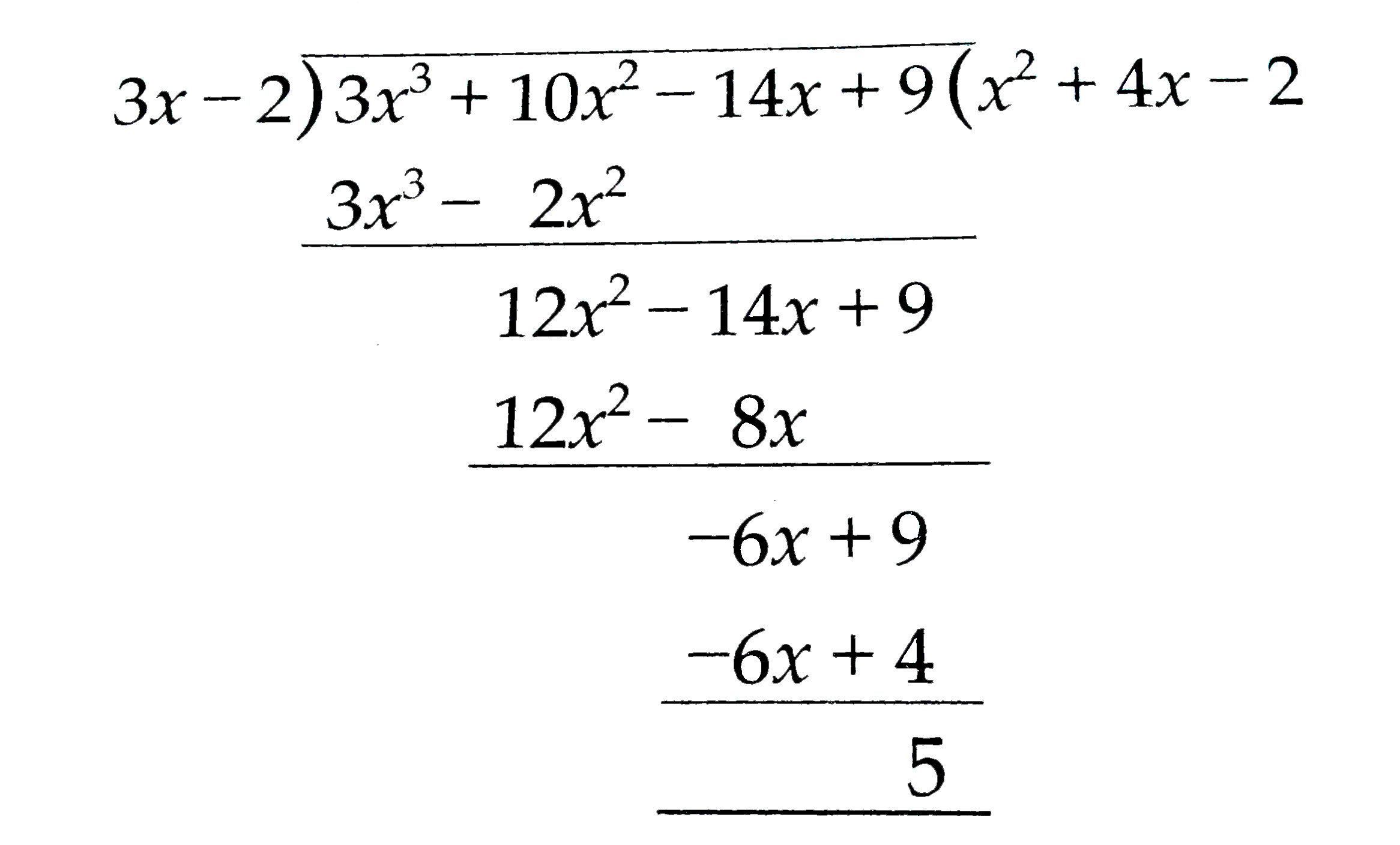
Required number to be subtracted = 5.

I. If $\alpha$ and $\beta$ are the zeroes of $p\left(x\right)=a{x}^2+bx+c$ , where $a\ne 0$ then
(i) $\alpha$ + $\beta$ = $\frac{-b}{a}$
(ii) $\alpha \beta$ = $\frac{c}{a}$
II. A quadratic polynomial whose zeroes are $\alpha$ and $\beta$ is given by
$p\left(x\right)=\{x^2-(\alpha +\beta )x+\alpha \beta \}$
III. If $\alpha ,\beta ,\gamma$ are the zeroes of, $p\left(x\right)=a{x}^3+b{x}^2+cx+d$, then
$\left(i\right)$ $\alpha +\beta +\gamma =\frac{-b}{a}$
$\left(ii\right)$ $\alpha \beta +\beta \gamma +\gamma \alpha =\frac{c}{a}$
$\left(iii\right)$ $\alpha \beta \gamma =\frac{-d}{a}$

• Polynomial is an algebraic expression if the power of variable is non-negative integer.


• Form: $p\left(x\right)=a^0{x}^0+a^1{x}^1+a^2{x}^2+...a^n{x}^n$, where $a^n$ ≠ $0$


• Types of Polynomials Based on its Terms :
  ⇒ Monomials : Agar term ek hai to expression monomial khlati hai. For ex. $2x^3$, $6$, etc.
  ⇒ Binomials : Agar terms do hai to expression binomial khlati hai. For ex. $6x^2+5x$, $5y^3+3y$, etc.
  ⇒ Trinomials : Agar terms teen hai to expression trinomial khlati hai. For ex. $5x^2-3x+8$, $6y^2+3y+7$, etc.


• Degree of a polynomial : Kisi polynomial ke individual terms ki highest power ko degree kahtey hai.
  For Example : Degree of $p\left(x\right)=x^3+3x$, is $3$.


• Types of Polynomials Based on its Degree :
  $\Rightarrow$ Constant Polynomials : Jin Polynomial ki degree $0$ hoti hai.
  For example: $2$, $-3$, etc.
  $\Rightarrow$ Linear Polynomial : Jin Polynomials ki degree $1$ hoti hai.
  Yeh linear polynomial $p\left(x\right)=ax+b$ , where $a\ne 0$ ki form mein hote hai.
  For example: $x+5$, $5x+10$, etc.
  $\Rightarrow$ Quadratic Polynomial : Jin polynomials ki degree 2 hoti hai.
  Yeh quadratic polynomial $a{x}^2+b$ ,where $a\ne 0$ ki form mein hotey hai.
  For example : $5x^2+5x+8$, $4x^2+6x+7$, etc.
  $\Rightarrow$ Cubic Polynomials : Jin polynomials ki degree $3$ hoti hai.
  Yeh cubic polynomial $p\left(x\right)=a{x}^3+b{x}^2+cx+d$, where $a\ne 0$ ki form mein hotey hai.
  For example : $5x^3+5x^2+4$, $4t^3+7$, etc.


• Zeroes of Polynomial : Ek real number $\alpha$ zero of polynomial tabhi khlata hai jab polynomial ka value $x=\alpha$ ke liye $0$ ho.
  Aur jo value es equation ko satisfy karta hai vo equation ka root khlata hai.


• Graphical Properties :
  ⇒ Linear polynomial : Ek Linear polynomial ka graph straight line hota hai aur wo $x$ axis ko ek point pe cut karta hai so bachcho iska mtlb hai ki linear polynomial ka maximum ek root hota hai.
  ⇒ Quadratic polynomial : Ek Quadratic polynomial ka graph parabola se represent hota hai aur aksar $x$ axis ko do point pe cut karta hai that means a quadratic polynomial has maximum two roots.
  ⇒ Cubic Polynomial : Ek Cubic Polynomial ka graph cubic curve se represent hota hai aur aksar ye $x$ axis ko $3$ point pe cut karta hai matlab cubic polynomial ke maximum $3$ roots hotey hai.


• Relation between zeroes and coefficients of a quadratic polynomial :
  $\Rightarrow$ If $\alpha$ and $\beta$ are zeroes of the polynomial, $p\left(x\right)=a{x}^2+bx+c$, where $a\ne 0$ then
  $\left(i\right)$ The sum of zeroes of quadratic polynomial = $\alpha +\beta =-\frac{b}{a}$
  $\left(ii\right)$ The product of zeroes of quadratic polynomial = $\alpha \beta =\frac{c}{a}$ (product of zeroes).
  $\Rightarrow$ If $\alpha$, $\beta$, $\gamma$ are the zeroes of the cubic polynomial (cubic polynomial ke maximum $3$ zeroes hotey hai), $p\left(x\right)=a{x}^3+b{x}^2+cx+d$, where $a\ne 0$, then
  $\left(i\right)$ The sum of zeroes of the cubic polynomial = $\alpha +\beta +\gamma$ $=\frac{-b}{a}=$ $\frac{-\text{coefficient of}{x}^2}{\text{coefficient of}{x}^3}$
  $\left(ii\right)$ Sum of the product of zeroes taken two at a time $=\alpha \beta +\beta \gamma +\gamma \alpha =\frac{c}{a}=$ ("coefficient of "x)/("coefficient of "x^3)
  $\left(iii\right)$ Product of zeroes = $\alpha \beta \gamma$ = $\frac{-d}{a}$ = $\frac{-\text{constant term}}{\text{coefficient of}{x}^3}$
.

• Division Algorithm: If $p\left(x\right)$ and $g\left(x\right)$ are any two polynomials with $g\left(x\right)\ne 0$, then we can find polynomials $q\left(x\right)$ and $r\left(x\right)$ ($q\left(x\right)$ = polynomial obtained as quotient, $r\left(x\right)$ = polynomial obtained as remainder) such that
  $p\left(x\right)=g\left(x\right)\times q\left(x\right)+r\left(x\right),$
  where $r\left(x\right)=0$ or degree of $r\left(x\right)$ < degree of $g\left(x\right)$.


• Some Algebraic Identities:
  $\left(1\right)$ ${(X+Y)}^2=X^2+Y^2+2XY$
  $\left(2\right)$ ${(X-Y)}^2=X^2+Y^2-2XY$
  $\left(3\right)$ $X^2-Y^2=(X+Y)(X-Y)$
  $\left(4\right)$ ${(X+Y+Z)}^2=X^2+Y^2+Z^2+2XY+2YZ+2XZ$
  $\left(5\right)$ ${(X+Y)}^3=X^3+Y^3+3XY(X+Y)$
  $\left(6\right)$ ${(X-Y)}^3=X^3-Y^3-3XY(X-Y)$