Complete Solutions to CASE BASED/SOURCE- BASED INTEGRATED QUESTIONS of chapter RAY OPTICS AND OPTICAL INSTRUMENTS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | RAY OPTICS AND OPTICAL INSTRUMENTS |
| U-LIKE SERIES | CASE BASED/SOURCE- BASED INTEGRATED QUESTIONS |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
When an object is placed normally on the principal axis of a spherial mirror at a distance 'a' from its pole, its image is formed at a distance 'v' from the pole of mirror such that `(1)/(v)+(1)/(u)=(1)/(f)`, where f = focal length of given mirror.
The relation is called mirror formula and is true for all types of mirrors under all conditions. However, values of u, v and f must be put with proper signs are per the sign convention followed. If 'h' be the height of the linear object and h' the height of image, then ratio `(h')/(h)` is called linear magnification or lateral magnification and its value m is given as :
`m=(h')/(h)=-(v)/(u)`
(a) A planer object of length 3 cm and breadth 2 cm is held normal to the principal axis of a concave mirror of focal length 20 cm at a distance of 30 cm from its pole. Where is its image formed?
View SolutionWhen an object is placed normally on the principal axis of a spherial mirror at a distance 'a' from its pole, its image is formed at a distance 'v' from the pole of mirror such that `(1)/(v)+(1)/(u)=(1)/(f)`, where f = focal length of given mirror.
The relation is called mirror formula and is true for all types of mirrors under all conditions. However, values of u, v and f must be put with proper signs are per the sign convention followed. If 'h' be the height of the linear object and h' the height of image, then ratio `(h')/(h)` is called linear magnification or lateral magnification and its value m is given as :
`m=(h')/(h)=-(v)/(u)`
What is the surface area of image of linear object formed by the given concave mirror?
View SolutionWhen an object is placed normally on the principal axis of a spherial mirror at a distance 'a' from its pole, its image is formed at a distance 'v' from the pole of mirror such that `(1)/(v)+(1)/(u)=(1)/(f)`, where f = focal length of given mirror.
The relation is called mirror formula and is true for all types of mirrors under all conditions. However, values of u, v and f must be put with proper signs are per the sign convention followed. If 'h' be the height of the linear object and h' the height of image, then ratio `(h')/(h)` is called linear magnification or lateral magnification and its value m is given as :
`m=(h')/(h)=-(v)/(u)`
A small match box lies along the principal axis of a concave mirror and one end of match box is at centre of curvature of the mirror. Draw a ray diagram to show its image. Is its magnetification uniform?
View SolutionWhen an object is placed normally on the principal axis of a spherial mirror at a distance 'a' from its pole, its image is formed at a distance 'v' from the pole of mirror such that `(1)/(v)+(1)/(u)=(1)/(f)`, where f = focal length of given mirror.
The relation is called mirror formula and is true for all types of mirrors under all conditions. However, values of u, v and f must be put with proper signs are per the sign convention followed. If 'h' be the height of the linear object and h' the height of image, then ratio `(h')/(h)` is called linear magnification or lateral magnification and its value m is given as :
`m=(h')/(h)=-(v)/(u)`
(d) Define longitudinal magnification.
View SolutionWhen an object is placed normally on the principal axis of a spherial mirror at a distance 'a' from its pole, its image is formed at a distance 'v' from the pole of mirror such that `(1)/(v)+(1)/(u)=(1)/(f)`, where f = focal length of given mirror.
The relation is called mirror formula and is true for all types of mirrors under all conditions. However, values of u, v and f must be put with proper signs are per the sign convention followed. If 'h' be the height of the linear object and h' the height of image, then ratio `(h')/(h)` is called linear magnification or lateral magnification and its value m is given as :
`m=(h')/(h)=-(v)/(u)`
(e) Find an expression for longitudinal magnification of a small object placed linearly along the axis of a spherical mirror.
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
`P=(1)/(f)=(n-1)((1)/(R_(1))-(1)/(R_(2)))`
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and `R_(1) and R_(2)` are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, `R_(1) and R_(2)` with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., `|R_(1)|=|R_(2)|=R" (say)"`
Let the given biconvex lens be divided in two equal parts, as shown in Fig. (a), along a section YY' which is perpendicular to the principal axis of lens. What is the power of each part?

View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
`P=(1)/(f)=(n-1)((1)/(R_(1))-(1)/(R_(2)))`
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and `R_(1) and R_(2)` are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, `R_(1) and R_(2)` with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., `|R_(1)|=|R_(2)|=R" (say)"`
How is your answer modified if the given biconvex lens is divided into two parts along a section XX' along its principal axis ?
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
`P=(1)/(f)=(n-1)((1)/(R_(1))-(1)/(R_(2)))`
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and `R_(1) and R_(2)` are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, `R_(1) and R_(2)` with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., `|R_(1)|=|R_(2)|=R" (say)"`
If twoplanoconvex lenses fromed as a result of (a) are joined together as shown in Fig. (b), what is the net power of the combination ?
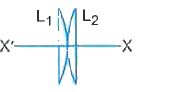
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
`P=(1)/(f)=(n-1)((1)/(R_(1))-(1)/(R_(2)))`
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and `R_(1) and R_(2)` are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, `R_(1) and R_(2)` with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., `|R_(1)|=|R_(2)|=R" (say)"`
If two lens parts obtained in (b) are joined together as shown in Fig. (c), (i) what is the net power of the combination?
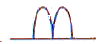
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
`P=(1)/(f)=(n-1)((1)/(R_(1))-(1)/(R_(2)))`
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and `R_(1) and R_(2)` are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, `R_(1) and R_(2)` with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., `|R_(1)|=|R_(2)|=R" (say)"`
How is result of part (d) modified if two parts are placed together as shown in Fig. (c)(ii)?
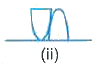
View SolutionAnswer question (a) - (e) on the basis of data given in the following table and your understanding of the relation studied concepts :
In a school laboratory following lenses are available :

All these lenes are converging lenses.
Which two lenses would you select to design a compound microscope and why?
View SolutionAnswer question (a) - (e) on the basis of data given in the following table and your understanding of the relation studied concepts :
In a school laboratory following lenses are available :

All these lenes are converging lenses.
Which two lenses would you choose to prepare an astronomical telescope? Give reason for your choice.
View SolutionAnswer question (a) - (e) on the basis of data given in the following table and your understanding of the relation studied concepts :
In a school laboratory following lenses are available :

All these lenes are converging lenses.
Draw the ray diagram for image formation of a far off object in normal arrangement of astronomical telescope.
View SolutionAnswer question (a) - (e) on the basis of data given in the following table and your understanding of the relation studied concepts :
In a school laboratory following lenses are available :

All these lenes are converging lenses.
(d) What should be teh distance between objective and eye piece of your telescope and what is the expected value of its magnifying power?
View SolutionAnswer question (a) - (e) on the basis of data given in the following table and your understanding of the relation studied concepts :
In a school laboratory following lenses are available :

All these lenes are converging lenses.
Why do we prefer an objective lens of large aperature in a telescope?
View SolutionA ring angled isosceles prism KLM of refractive index `n_(1)` is placed inside a rectangular block PQRS of refractive index `n_(2)` as shown in the adjoining Fig. The rectangular box is surrounded by a medium of refractive index `n_(3)`. A ray of light AB enters the rectangular block normally. Depending upon the relationships between `n_(1), n_(2) and n_(3)`. it takes one of the four possible paths.
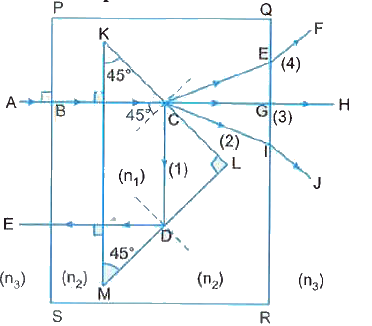
Under what condition the ray follows the path no. 1 (i.e., path ABCI)?
View SolutionA ring angled isosceles prism KLM of refractive index `n_(1)` is placed inside a rectangular block PQRS of refractive index `n_(2)` as shown in the adjoining Fig. The rectangular box is surrounded by a medium of refractive index `n_(3)`. A ray of light AB enters the rectangular block normally. Depending upon the relationships between `n_(1), n_(2) and n_(3)`. it takes one of the four possible paths.
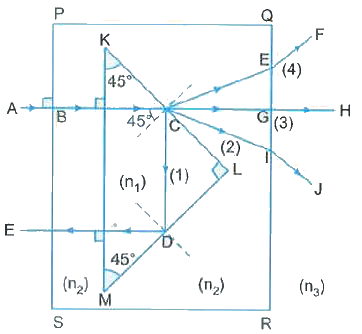
Under what condition the ray follows the path no. 2 (i.e., path ABCIJ)?
View SolutionA ring angled isosceles prism KLM of refractive index `n_(1)` is placed inside a rectangular block PQRS of refractive index `n_(2)` as shown in the adjoining Fig. The rectangular box is surrounded by a medium of refractive index `n_(3)`. A ray of light AB enters the rectangular block normally. Depending upon the relationships between `n_(1), n_(2) and n_(3)`. it takes one of the four possible paths.
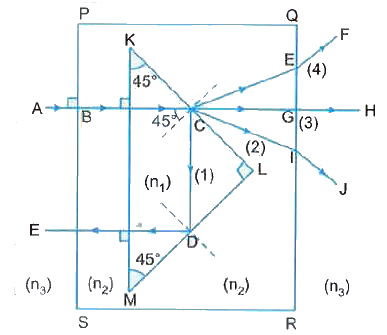
State the condition for light ray to travel along path no. 3 (i.e., path ABCGH).
View SolutionA ring angled isosceles prism KLM of refractive index `n_(1)` is placed inside a rectangular block PQRS of refractive index `n_(2)` as shown in the adjoining Fig. The rectangular box is surrounded by a medium of refractive index `n_(3)`. A ray of light AB enters the rectangular block normally. Depending upon the relationships between `n_(1), n_(2) and n_(3)`. it takes one of the four possible paths.
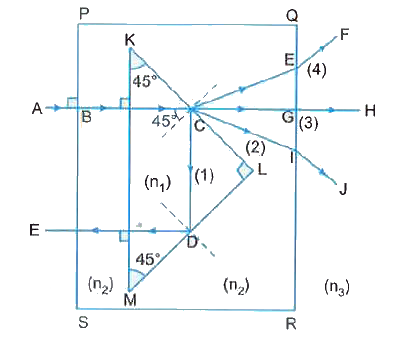
What is the condition for light ray to proceed along the path no. 4 (i.e., path ABCEF)?
View Solution
CASE BASED/SOURCE- BASED INTEGRATED QUESTIONS questions and complete solutions for chapter RAY OPTICS AND OPTICAL INSTRUMENTS of U-LIKE PHYSICS (HINGLISH) of Class 12
All Exercises from U-LIKE SERIES Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS
- ASSERTION-REASON TYPE QUESTIONS
- CASE BASED/SOURCE- BASED INTEGRATED QUESTIONS
- FILL IN THE BLANKS
- LONG ANSWER QUESTIONS-I
- LONG ANSWER QUESTIONS-II
- MULTIPLE CHOICE QUESTIONS
- N.C.E.R.T. TEXTBOOK EXERCISES
- SELF ASSESSMENT TEST (SECTION A)(FILL IN THE BLANKS)
- SELF ASSESSMENT TEST (SECTION A)(MULTIPLE CHOICE QUESTIONS)
- SELF ASSESSMENT TEST (SECTION B)
- SHORT ANSWER QUESTIONS
- TRUE OR FALSE
- VERY SHORT ANSWER QUESTIONS