Complete Solutions to LONG ANSWER QUESTIONS-I of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| U-LIKE SERIES | LONG ANSWER QUESTIONS-I |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Write using Biot-Savart law, the expression for the magnetic field `vecB` due to an element `vecdl` carrying current I at a distance `vecr` from it in vector form. Hence, derive the expression for the magnetic field due to a current loop of radius R at a point P distant x from its centre along the aixs of the loop.
View SolutionState Biot- Savart law. Use to obtain the magnetic field at a point due to a long, staright current carrying wire.
View SolutionA long solenoid of length 'l' having carries a current I. Deduce the expression for the magnetic field in the interior of the solenoid.
View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic field along the aixs of a current carrying solenoid of length l and having N number of turns.
View SolutionWhat does a toroid consist of ? Show that for an ideal toroid of closely wound turns, the magnetic field (i) inside the toroid is constant, and (ii) in the open space inside and exterior to the toroid is zero.
View SolutionAn iron ring of relative permeability `mu_r`, has windings of insulated copper wire of n turns per unit length. When the current in the windings is I, find the expression for the magneitc field in the ring.
View SolutionA long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View SolutionConsider the motion of a charged particle of mass m and charge q moving with velocity `vecv` in a magnitude field `vecB`. If `vecv` is perpendicular to `vecB`, show that it describe a circular path having angular frequency `omega = (qB)/(m)`
View SolutionDeduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
View SolutionA uniform magnetic field `vecB` is set up along the positive x-axis. A particle of charge q and mass m moving with a velocity `vecv` enters the field at the origin in X - Y plane such that it has velocity components both along and perpendicular to the magnetic field `vecB`. Trace, giving reasons, the trajectory followed by the particle. Find out the expression for the distance moved by the particle along the magnetic field in one rotation.
View Solution(a) Write the expression for the force `vecF` acting on a particle of mass m and charge q moving with velocity `vecv` in a magnetic field `vecB`. Under what conditions will it move in (i) a circular path and (ii) a helical path?
(b) Show that the kinetic enery of the particle moving in magnetic field remains constant.
View Solution(i) Obtian the expression for the cyclotron frequency.
(ii) A deuteron and a proton are accelerated by the cyclotron. Can both be accelerated with the same oscillator frequency ? Give reason to justify your answer.
View SolutionDerive an expression for the force acting on a current carrying conductor placed in a uniform magnetic field. Name the rule which gives the direction of the force. Write the condition for which this force will have (i) maximum (ii) minimum value.
View SolutionWrite the expression for the force `vecF` acting on a charged particle of charge q moving with a velocity `vecv` in the presence of both electric field `vecE` and magnetic field `vecB` . Obtain the condition under which the particle moves underflected through the fields.
View SolutionTwo long straight parallel current conductors are kept at a distance d from each other in air. The direction of current in both the conductors is the same. Find the magnitude and direction of the force between them. Hence, define one ampere.
View SolutionA rectangle loop of size `l xx b` carrying a steady current I is placed in a uniform magnetic field `vecB`. Prove that the torque `vec(tau)` acting on the loop is given by `vec(tau) = vecm xx vecB`, where `vecm` is the magnetic moment of the loop.
View SolutionTwo small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.
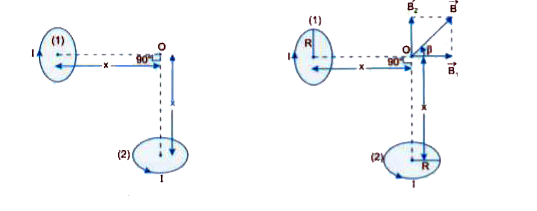
View SolutionA circular coil of 200 turns and radius 10 cm is placed in a uniform magnetic field of 0.5 T, normal to the plane of the coil. If the current in the coil is 3.0 A, calculate the :
(i) Total troque on the coil, (ii) total force on the coil, (iii) average force on each electron on each electron in the coil, due to the magnetic field.
Assume, the area of cross-section of the wire to be `10^(-5) m^(2)` and the free electron density as `10^(29) m^(-3)`.
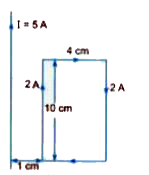
View SolutionA rectangular loop of wire of size 4 cm `xx` 10 cm carries a steady current of 2A. A straight long wire carrying 5A current is kept near the loop (fig). If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
View SolutionA wire AB is carrying current of 12 A and is lying on the table. Another wire CD carrying 5 A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB . [Take the value of `g = 10 ms^(-2)]`
View SolutionA circular coil, having 100 turns of wire of radius (nearly) 20 cm each, lies in the X-Y plane with its centre at the origin of coordinates. Find the magnetic field at the point `(0, 0, 20sqrt(3)cm)`, when the coil carries a current of `(2/pi)` A.
View SolutionState the underlying principle of working of a moving coil galvonometer. Write two reasons why a galvometer cannot be used as such to measure current in a given circuit. Name any two factors on which the current sensitivity of a galvonometer depends.
View SolutionA moving coil galvonometer of resistance `R_G` gives a full scale deflection for current `I_g`. Use the suitable circuit diagram convert it into an ammeter of range 0 to `I (I > I_g)`. Deduce the expression for the shunt required for this conversion. Hence, write the expression for the resistance of the ammeter thus obtained.
View SolutionA moving coil galvonometer of resistance `R_G` gives a full scale deflection when a current `I_g` flows through its coil. It can be converted into an ammeter of range 0 to `I(I > I_g)` when a shunt of resistance S is connected across its coil. If this galvanometer is converted into an ammeter of range 0 to 2I, find the expression for the shunt required in terms of `S and and R_G`.
View SolutionBriefly explain how you will convert a moving coil galvonometer into a voltmeter of given range.
View Solution(a) State the principle of working of a galvonometer.
(b) A galvonometer of resistance G is converted into a voltmeter to measure upto V volts by connecting a resistance `R_1` in series with the coil. If a resistance `R_2` is connected in series with it, then it can measure upto V/2 volts. Find the resistance, in terms of `R_1 and R_2`, required to be connected to convert it into a voltmeter that can read upto 2 V. Also find the resistance G of the galvanometer in terms of `R_1 and R_2` .
View Solution(a) Define the current sensitivity of a galvonometer .
(b) The coil area of a galvonometer is `16 xx 10^(-4) m^(2)`. It consists of 200 turns of wire and is in a magnetic field of 0.2 T. The restoring torque constant of the suspended fibre is `10^(-6) N m` per degree . Assuming the magnetic field to be radial, calculate the maximum current that can be measured by the galvanometer if the scale can acomodate `30^@` deflection.
View SolutionA solenoid, of length 1.0 m, has a radius of 1 cm and has a total of 1000 turns wound on it. It carries a current of 5 A. Calculate the magnitude of the axial magnetic field inside the solenoid. If an electron were to move with a speed of `10^(4) m s^(-1)` along the axis of this current carrying solenoid, what would be the force experienced by electron ?
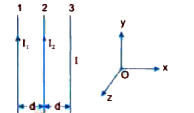
View SolutionThree long straight parallel wires are kept as shown in the fig. The wire (3) carries a current I.
(i) The direction of flow of current I in wire (3) is such that the net force on wire (1) due to the other two wires, becomes zero.
What will be the direction of current I in the two cases ?
Also obtain the relation between the magnitude of currents `I_1, I_2 and I_3`.
View SolutionAn electron moves around the nucleus in a hydrogen atom of radius `0.51 Å` , with a velocity of `2 xx 10^(5) m s^(-1)` . Calculate the following :
(i) the equivalent current due to orbital motion of electron,
(ii) the megnetic field produced at the centre of the nucleus,
(iii) the magnetic associated with the electron.
View SolutionA galvanometer with a coil of resistance 120 ohm shows full scale full scale deflection for a current of 2.5 mA. How will you convert the galvonometer into an ammeter of range 0 to 7.5 A ? Determine the net resistance of the ammeter. When an ammeter is put in a circuit, does it read slightly less or more than the actual current in the original circuit ? Justify your answer.
View SolutionDerive an expression for the magnetic moment `vec(mu)` of an electron revolving around the nucleus in terms of its angular momentum `vecl`. What is the direction of the magnetic moment of the electron with respect to its angular momentum?
View SolutionAn electron of mass `m_e`, revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence, prove that the magnetic moment associated with it is expressed as `vec(mu) = - e/(2 m_e) vecL`, where `vecL` is the orbital angular momentum of the electron. Give the significance of negative sign.
View Solution
LONG ANSWER QUESTIONS-I questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of U-LIKE PHYSICS (HINGLISH) of Class 12
All Exercises from U-LIKE SERIES Class 12 PHYSICS MOVING CHARGES AND MAGNETISM
- ADDITIONAL EXERCISES
- ASSERTION-REASON TYPE QUESTIONS
- CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
- FILL IN THE BLANKS
- LONG ANSWER QUESTIONS-I
- LONG ANSWER QUESTIONS-II
- MULTIPLE CHOICE QUESTIONS
- N.C.E.R.T. TEXTBOOK EXERCISES
- SELF ASSESSMENT TEST (SECTION A) (FILL IN THE BLANKS)
- SELF ASSESSMENT TEST (SECTION A) (MULTIPLE CHOICE QUESTIONS)
- SELF ASSESSMENT TEST (SECTION B)
- SELF ASSESSMENT TEST (SECTION C)
- SELF ASSESSMENT TEST (SECTION D)
- SHORT ANSWER QUESTIONS
- TRUE OR FALSE
- VERY SHORT ANSWER QUESTIONS