Complete Solutions to CHECKPOINT of chapter RIGID BODY DYNAMICS - I of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS - I |
| RESNICK AND HALLIDAY | CHECKPOINT |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
A disk can rotate about its central axis like a merry-go-round. Which of the following pairs of values for its initial and final angular positions, respectively, give a negative angular displacement: (a) -3 rad, +5 rad, (b) -3 rad, -7 rad, ( c) 7 rad, -3 rad?
View SolutionIn four situations, a rotating body has angular position `theta(t)` given by (a) `theta=3t-4`, (b) `theta=-5t^(3)+4t^(2)+6`, ( c) `theta=2//t^(2)-4//t`, and (d) `theta=5t^(2)-3`. To which situations do the angular equations of Table 10-1 apply?
View SolutionA cockroach rides the rim of a rotating merry-go-round. If the angular speed of this system (merry-go-round + cockroach) is constant, does the cockroach have (a) radial acceleration and (b) tangential acceleration? If `omega` is decreasing, does the cockroach have ( c) radial acceleration and (d) tangential acceleration?
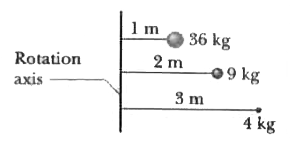
View SolutionThe figure shows three small spheres that rotate about a vertical axis. The perpendicular distance between the axis and the center of each sphere is given. Rank the three spheres according to their rotational inertia about that axis, greatest first.
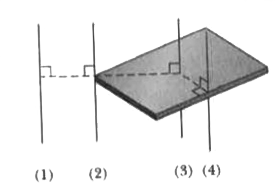
View SolutionThe figure shows a book-like object (one side is longer than the other) and four choices of rotation axes, all perpendicular to the face of the object. Rank the choices according to the rotational inertia of the object about the axis, greatest first.
View SolutionFind the moment of inertia of a half uniform ring (mass m, radius r) about its center.
View SolutionFind moment of inertia of a uniform solid sphere (mass m, radius r) about a tangent.
View SolutionFind moment of inertia of a uniform rectangular plate (mass m) about axis AB lying in its plane and passing through center as shown in the figure.

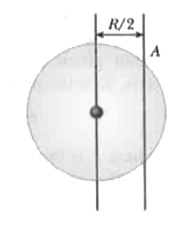
View SolutionFind moment of inertia of a uniform ring (mass m, radius r) about chord AA' at distance R/2 from center.
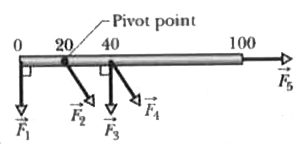
View SolutionThe figure shows an overhead view of a meter stick that can pivot about the dot at the position marked 20 (for 20 cm). All five forces on the stick are horizontal and have the same magnitude. Rank the forces according to the magnitude of the torque they produce, greatest first.
View SolutionThe position vector `vecr` of a particle points along the positive direction of a z axis. If the torque on the particle is (a) zero, (b) in the negative direction of x, and ( c) in the negative direction of y, in what direction is the force causing the torque?
View SolutionFind torque due to gravity at any time t about point of projection. If a body of mass m is projected at an angle `theta` with speed `v_(0)` at t = 0.
View SolutionThe figure shows an overhead view of a meter stick that can pivot about the point indicated, which is to the left of the stick's midpoint. Two horizontal forces, `vecF_(1)andvecF_(2)`, are applied to the stick. Only `vecF_(1)` is shown. Force `vecF_(2)` is perpendicular to the stick and is applied at the right end. If the stick is not to turn, (a) what should be the direction of `vecF_(2)`, and (b) should `F_(2)` be greater than, less than, or equal to `F_(1)`?
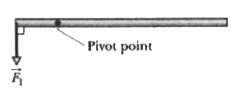
View SolutionIn part a of the figure, particles 1 and 2 move around point O in circles with radii 2 m and 4 m. In part b, particles 3 and 4 travel along straight lines at perpendicular distances of 4 m and 2 m from point O. Particle 5 moves directly away from O. All five particles have the same mass and the same constant speed. (a) Rank the particles according to the magnitudes of their angular momentum about point O, greatest first. (b) Which particles have neagtive angular momentum about point O?

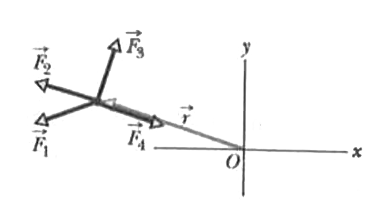
View SolutionThe figure shows the position vector `vecr` of a particle at a certain instant, and four choices for the direction of a force that is to accelerate the particle. All four choices lie in the xy plane. (a) Rank the choices according to the magnitude of the time rate of change (dl/dt) they produce in the angular momentum of the particle about point O, greatest first. (b) Which choice results in a negative rate of change about O?
View SolutionA uniform disk, a thin hoop (ring), and a uniform sphere, all with the same mass and same outer radius, are each free to rotate about a fixed axis through its center. Assume the hoop is connected to the rotation axis by light spokes. With the objects starting from rest, identical forces are simultaneously applied to the rims, as shown. Rank the objects according to their angular momentum after a given time t, least to greatest.

View SolutionA rhinoceros beetle rides the rim of a small disk that rotates like a merry-go-round. If the beetle crawls toward the center of the disk, do the following (each relative to the central axis) increase, decrease, or remain the same for the beetle-disk system: (a) rotational inertia, (b) angular momentum, and ( c) angular speed?
View SolutionA rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed `v_(0)` hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.

View Solution
CHECKPOINT questions and complete solutions for chapter RIGID BODY DYNAMICS - I of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12