Complete Solutions to EXAMPLE of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| NEW JOYTHI PUBLICATION | EXAMPLE |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
A company manufactures two proudcts. A and B on which the profits erarned per unit areRs. 30 and Rs. 40 respectively. Each product is procced on two machines `M_(1) and M_(2)`. One unit of product A requires on hour of processing time on `M_(1) and 2` hours on `M_(2)` While one unit of product B requires one hour each on `M_(1) and M_(2)`. Machines `M_(1) and M_(2)` are availabe atmost 10 hours and 12 hours respectivrely during working day. The company wants to know how many units of proudcts A and B should be produced to maximise the profit.
to formulate a linearprogramming problem
(i) Write the objective function.
(ii) Write all contraints.
View SolutionCondier the following problem. A manufacture produced tables and chairs. It takes 3 hours of work on machine A mind 1 hour of work on machine B to produce one table and 2 hours of work on machine A and 3 hours on machine B to produce 1 chair . He erars a profit fo Rs. 50 per table and Rs 40 per chair. Hoperates the machines a and B for atmost 12 hours hours respectively. how many tables and chairs should be produce each day to maximise his profit ?
(i) Write the objective function.
(ii) Write the constrains.
View SolutionA firm produced 2 different products A and B. Each product has to undergo three operations before takes the shape. The profit per unit and time required per unit of each product in each operation is tabulated below.
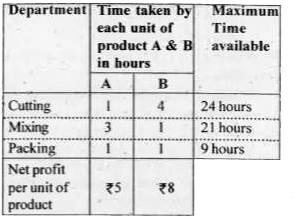
To formulate a linear programming problems write
(i) the non-negativity constraints
(ii) Cutting constraints .
(iii) Mixing constraints
(iv) Packing constraints
(v) Objective function
View SolutionA tyre manufactureing company produces tyres of cars and buses. Three machines A, B, C are to be used for the production of these typres. Machines A and C are available for operation atmost 11 hours, whereas B must be operated for atleast 6 hours a day. the time required for construction of one typre the three machines given in the following table.

Comapy sells all the tyres and gets a profit of Rs. 100 Rs 150 on a tyre of a car and bus respectively. The company wants to know how many numbers of each item to be produced to maximise the profit.
To formulate a linear programmining problem,
(i) Write the objective function.
(ii) Write all constraints.
View SolutionConsider the linear inequalities
`2x+3yle6, 2x+y le 4, x ge0, y ge0`
(i) Mark the feasible region.
(ii) Maximise the function `Z=4x+5y` subject to the given constraints.
View Solution(i) Draw the graph of `5x+4y=40,x=4,y=5`
(ii) Solve the following LPP graphically maximise `Z=3x+5y`
Subject to the conditions `5x+4y le 40, x le 4, y le 5, x,y ge0`
View SolutionConsider the linear programming problem Maximize `Z=4x+y`
Subject to the constraints.
`x+y le 50`
`3x+y le 90`
`x gt 0, y gt 0`
(i) Draw its feasible region.
(ii) Find the corner points of the feasbile region.
(iii) Find the corner at whcih Z attains its maximum.
View SolutionSolve the following linear programming problem graphically.
Minimize `Z=200 x+500 y`
subject to the constraints:
`x+2y ge10`
`3x+4y le 24`
`x ge0, y, ge0`
View SolutionMinimise and maximise `Z=3x+9y` subject to the constraints.
`x+3y le 60`
`x+y ge 10`
`x le y`
`x ge 0, y ge 0`
View SolutionConsider the linear programming problem.
Maximize `Z=x+y`
Subject to `2x+y-3ge0`
`x-2y+1 le 0`
`yle 3`
`x le 0, y le 0`
(i) Draw its fesible region.
(ii) Find the corner points of the feasible region.
(iii) Find the corner at which Z attains its maximum.
View SolutionSolve the following linear programming problem graphically :
Minimize `Z=x+2y`
subject to `2x+y ge 3, x+2y ge 6,x,y ge 0`.
View SolutionMinimise `Z=3x+2y`
Subject to the constraints
`x+yge8`
`3x+5y le 15`
`x ge0, y ge0`
View SolutionManu has Rs. 36,000 for purchaes of rice and wheat. A bag of rice and a bag of wheat cost Rs 180 and Rs 120 respectively. He has a storage capacity for 250 bages only. He ears a profit of Rs 11 and Rs. 9 per bag of rice and wheat respectively.
(i) formulate an LPP to maximise the profit
(ii) Solve the LPP.
View SolutionA furniture dealer sells only tables and chairs. He has Rs. 12,000 to invest and a space to store 90 pieces. A tables costs him Rs. 400 and a chair Rs 100. He can sell a table at a profit of Rs. 75 and a chair at a profit of Rs. 25. Assume that he can sell the items. The dealer wants to get maximum profit.
(i) By defining suitabale variables, write the objective function.
(ii) Write the constraints.
(iii) Maximise the objective function graphically.
View SolutionA company produes two types of cricket ball A and B. the production time of one ball of type B is double the type A (Time in units) . The company has a time to produce a maximum 2000 balls per day. The supply of raw material is sufficient for the production of 1500 balls (both A and B) per day. the company wants to make maximum profit by making profit fo Rs 3 from a ball of tye A and Rs. 5 from a ball of type b. Then
(i) By defining suitable variables, write the objective function.
(ii) Write the constraints.
(iii) How many balls should be produced in each type per day in order to get maximum profit ?
View SolutionA manufacturing company makes tow models A and B of product. Each piece of model A reqwuires 9 labour hours for fabricating and 1 hour labour for finishing . Each piece of model Brequires 12 labour hours for fabricating and 3 labour hours for fininshing. for fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of Rs. 8,000 on each piece of modle A and Rs 12,000 on each piece of model B. How many pieces of model A and B should be manufactured per week to realise a maximum profit ? What is the maximum profit per week ?
View SolutionA bakery owner makes two types of cakes A and B. three machines are needed for this pupose. The time in (minutes) required for each type of cake in each machine is given below.
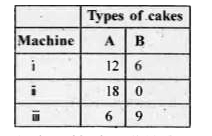
Each machines is available for atmost 6 hours per day. Assume that all cakes will be sold out every day. The bakery owner wants to make maximum pforit per day by making Rs. 7.5 from type A and Rs. 5 from type B.
a Write the objective function by defining suitable variables.
b Write the constraints.
c Find the maximum profit graphically.
View SolutionThere are two factories located at place P and the other the place Q. From these locations, a certain commodity is to be delivered to eachof the three depots situated A, B and C. the weekly requirement of the de-pots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is gien below.
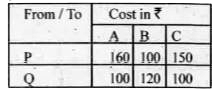
How many units should be transported from each factory to each depot in order that the transportation cost in minimum ? What whill be the minimum transportation cost ?
View SolutionThe graph of a linear programming problem is given below. The shaded region is the feasible region. The objective function is Max `Z=px+qy`
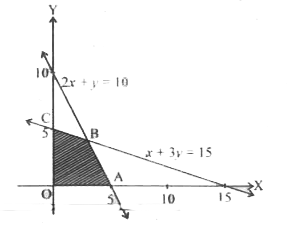
(i) What are the coordinates of the corners of the feasible region.
(ii) Write the constraints.
(iii) If the Z occurs at A and B, what is the relation between p and q.
(iv) If q=1 write the objective, function.
(v) Find the Max Z.
View Solution
EXAMPLE questions and complete solutions for chapter LINEAR PROGRAMMING of NEW JYOTHI MATHS (TAMIL ENGLISH) of Class 12