Complete Solutions to Examples of chapter VECTOR ALGEBRA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | VECTOR ALGEBRA |
| NEW JOYTHI PUBLICATION | Examples |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
Represent graphically a displacement of 40 km, `30^(@)` west of south.
View SolutionClassify the following measures as scalars and vectors.
(i) 5seconds (ii) `1000cm^(3)` (iii) 10 Newton
(iv)` 30 (km)/("hr") `(v)`10 g//cm^(2)` (vi) 20 m/s towards North
View SolutionIn the figure, which of the vectors are
(i) Collinear vectors
(ii) Equal vectors
(iii) Cointial vectors
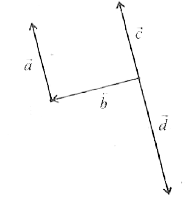
View SolutionFind the values of x, y and z so that the vectors `vec a = x hat i + 2 hat j + z hat k` and `vec b = 2hati + y hat j + hat k` are equal.
View SolutionLet `vec a = hat i + 2 hat j` and `vec b = 2 hat i + hat j`. Is `|veca| = |vec b|`.Are the vectors `vec a` and `vec b` equal ?
View SolutionFind the sum of the vectors
`vec a = hat i - 2 hat j + hat k , vec b = -2 hat i + 4 hat j + 5 hat k` and `vec c = hat i - 6 hat j - 7 hat k`
View SolutionFind a unit vector in the direction of the vector `vec a = 2 hat i + 2 hat j + hat k`.
View SolutionFind a vector in the direction of `veca = hat i - 2 hat j` that has a magnitude 7 units.
View SolutionFind a vector in the direction of `vec r = 3 hat i - 4 hat j` that has a magnitude 9.
View SolutionFind the value of x for which `x(hat i + hat j + hat k)` is a unit vector.
View SolutionFind a unit vector in the direction of the sum of vectors `vec a = 2 hat i + 2 hat j - 5 hat k` and `vec b = 2 hat i + hat j + 3 hat k`.
View SolutionConsider the vectors `vec a = 2 hat i + 2 hat j - 5 hat k` and `vec b= -hat i + 7 hat k`
(a).Find `vec a + vec b`.
(b) Find a unit vector in the direction of `vec a + vec b`.
View SolutionLet `veca = hat i + hat j + hat k, vec b = 2 hat i + 3 hat j`
`vec c = 3 hat i + 5 hat j - 2 hat k`, `vec d = - hat j + hat k`
(i) Find `vec b - vec a`.
(ii) Find the unit vector along `vec b - vec a`.
(iii) Prove that `vec b - vec a` and `vec d - vec c` are parallel vectors.
View SolutionShow that the vectors `2 hat i + 3 hat j + 4 hat k` and `4 hat i + 6 hat j + 8 hat k` are collinear.
View SolutionWrite the direction ratios of the vector `vec a = hat i - hat j + 2 hat k` and hence calculate the direction cosines.
View SolutionFor any three vectors `veca, vec b, vec c` prove that `(vec a + vec b)+ vec c = vec a + (vec b + vec c)`
View SolutionFind the vector joining the points P(2, 3, 0) and Q(-1, -2, -4) directed from P to Q
View SolutionLet A(1, 2, 4) and B(2, -1, 3) be two points.
(i) Find `vec (AB`)
(ii) Find a unit vector along `vec(AB)`
View SolutionShow the points A(3^i-2^j+^k) ,B(^i-3^j+5^k ) and C(2^i+^j-4^k) are the vectors of a right angled triangle.
View SolutionFind the direction cosines of the vector joining the points A(1, 2,3) and B(-1, -2, 1) directed from A to B.
View SolutionShow that the points with the position vectors `2 hat i + 6 hat j + 3 hat k, hat i + 2 hat j + 7 hat k` and `3 hat i + 10 hat j - hat k` are collinear.
View SolutionFind the position vector of a point R which divides the line joining two points P and Q whose position vectors are `hat i + 2 hat j - hat k` and `- hat i + hat j + hat k` respectively, in the ratio 2 : 1
(i) internally (ii) externally
View SolutionABCD is a rectangle with A as the origin. `vec b` and `vec d` are the position vectors of B and D respectively.
(i) What is the position vector of C?
(ii) If P, Q, R and S are midpoints of sides of AB, BC, CD and DA respectively, find the position vector of P, Q, R,S,
View SolutionIf `vec a, vec b, vec c, vec d` respectively are the position vectors representing the vertices A, B, C, D of a parallelogram then write `vec d` in terms of `vec a, vec b` and `vec c`
View SolutionFind the position vector of the centroid of a triangle when the position vectors of the vertices are given.
View SolutionUsing vectors prove that the diagonals of a parallelogram bisect each other.
View SolutionFind the angle between the vectors
`vec a = 3 hat i + 4 hat j + hat k`
`vec b = 2 hat i + 3 hat j - hat k` .
View SolutionFind angle `theta` between the vectors `vec a = hat i + hat j - hat k` and `vec b = hat i - hat j + hat k`.
View SolutionFind the angle between the vecctors `vec a` and `vec b` with magnitudes 1 and 2 respectively and when `vec a. vec b = sqrt(3)`
View SolutionIf ` -> a=5 hat i- hat j-3 hat k` and ` -> b= hat i+3 hat j-5 hat k` then show that the vectors ` -> a+ -> b` and ` -> a- -> b` are perpendicular.
View SolutionIf `vec a = 3 hat i - hat j - 5 hatk, vec b = hat i - 5 hat j + 3 hat k`, show that `vec a + vec b` and `vec a - vec b` are perpendicular.
(b) Given the position vectors of three points `A(hat i - hat j + 2 hat k)` B`(4 hat i + 5 hat j + 8 hat k)` C`(3 hat i + 3 hat j + 6 hat k)`
(i) Find `vec(AB)` and `vec(AC)`
(ii) Prove that A, B, C are collinear points.
View SolutionIf ` hat i+ hat j+ hat k ,2 hat i+5 hat j ,3 hat i+2 hat j-3 hat k` and ` hat i-6 hat j- hat k` are the position vectors of points A, B, C and D respectively, then find the angle between ` -> A B` and ` -> C D` . Deduce that ` -> A B` and ` -> C D`
View SolutionShow that the points `A(-2 hat i + 3 hat j + 5 hat k)` , B(`hat i + 2 hat j + 3 hat k`) and C(`7 hat i - hat k`) are collinear.
View SolutionABCD is a parallelogram with A as the origin. vec b` and `vec d` are the position vectors of B and D respectively.
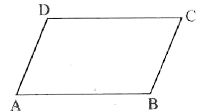
a.What is the position vector of C?
(b) What is the angle between `vec(AB)` and `vec (AD)`?
(c) Find `vec(AC)`
(d) If `|vec(AC)| = |vec (BD)|`, show that ABCD is rectangle.
View Solution(i) If `vec a, vec b` and `vec a + vec b` are unit vectors, then prove that the angle between `vec a` and `vec b` is `(2pi)/(3)`
(ii) If `(2 hat i + hat j - 3 hat k`) and `(m hat i + 3 hat j - hat k)` are perpendicular to each other , then find m.
View SolutionFind `lambda` for which `vec a = lambda hat i - hat j + 5 hat k` and `vec b = 3 hat i + 4 hat j - hat k` are orthogonal.
View SolutionLet `vec a, vec b` and `vec c` be the three vectors such that `|veca| = 3 , |vec b| = 4, |vec c| = 5`, and each one of them being perpendicular to the sum of the other two . Find `|vec a + vec b + vec c|`.
View SolutionThree vectors `veca, vec b and vec c` satisfy the condition `vec a + vec b + vec c = 0`.Evaluate the quantity. `mu = vec a.vec b + vec b.vec c+ veca.vec c` if `|vec a| = 1, |vec b| = 4, |vec c| = 2`
View SolutionFind `|vec a - vec b|`, if two vectors `vec a` and `vec b` are such that `|vec a | = 2, |vec b| = 3` and `vec a.vec b = 4`.
View SolutionIf `vec a` is any vector, show that `vec a = (vec a. hat i ) hat i + (vec a. hat j) hat j + (vec a. hat k) hat k`.
View SolutionIf `theta` is the angle between the unit vectors `vec a` and `vec b`, then prove that `sin (theta)/(2) = 1/2|vec a - vec b|`
View SolutionFor any two vectors `veca` and `vec b` show that `|vec a. vec b| le |vec a||vec b|`.
View SolutionFor any vectors `vec a vec b`, show that `|vec a + vec b| le |vec a| + |vec b|`.
View SolutionIf `vec alpha = 3 hat i - hat j` and ` vec beta = 2 hat i + hat j - 3 hat k`, then express, `vec beta` in the form `vec beta = vec beta_(1) + vec beta_(2)`, where `vec beta_(1)` is parallel to `vec alpha` and` vec beta_(2)` is perpendicular to `vec alpha`.
View SolutionFind the projection of the vector `vec alpha = 2 hat i + 3 hat j + 2 hat k` on the vector `vec b = hat i + 2 hat j + hat k`.
View SolutionFind the projection of `hat i + hat j + hat k` in the direction of `hat i + hat j`.
View SolutionLet `vec a = lambda hat i + hat j + 4 hat k` and `vec b = 2 hat i + 6 hat j + 3 hat k`. If the projection of `vec a` and `vec b` is 4 units, find `lambda`.
View SolutionFind the projection vector of `vec b = hat i + 2 hat j + hat k` along the vector `vec a = 2 hat i + hat j + 2 hat k`.
View SolutionFind `|vec a xx vec b|` if `vec a = 2 hat i - hat j + 3 hat k` and `vec b = 3 hat i - 5 hat j + 2 hat k`.
View SolutionIf` veca = hat i - hat j + hat k, vec b = 2 hat i + hat j + 3 hat k`, then
(i) Find `vec a + vec b , vec a - vec b` and `vec a. vec b`.
(ii) Find `(vec a + vec b) xx (vec a - vec b)`.
(iii) Find a unit vector perpendicular to both `vec a + vec b` and `vec a - vec b`.
View SolutionThe position vectors of the vertices of `DeltaABC` are `3 hat i - 4 hat j - 4 hat k`, `2 hat i - hat j + hat k` and `hat i - 3 hat j - 5 hat k` respectively.
(i) Find `vec (AB),` `vec(BC)` and `vec(CA)`.
(ii) Prove that `DeltaABC` is a right angled triangle.
(iii) Find the unit vector perpendicular to both ` vec (AB)` and `vec(BC)`.
View SolutionGiven `vec a = 4 hat i - hat j + 3 hat k` and `vec b = -2 hat i + hat j - 2 hat k`.
(i) Find a unit vector perpendicular to both `vec a` and `vec b`.
(ii) Find a vector of magnitude 9 which is perpendicular to both `vec a` and `vec b`.
View SolutionThe value of `hat i ( hat j xx hat k) + hat j ( hat i xx hat k ) + hat k (hat i xx hat j)` is
View SolutionIf `theta` is the angle between any two vectors `vec a` and `vec b` , then `|vec a. vec b| = | vec a xx vec b|`, when `theta` is equal to
View SolutionGiven `| vec a|=10 ,| vec b|=2n d vec adot vec b=12 ,fin d| vec axx vec b|dot`
View SolutionIf `| vec a|=2,|b|=5` and `| vec ax vec b|=8,` find ` vec adot vec bdot`
View SolutionProve that
`vec a xx (vec b + vec c) + vec b xx(vec a + vec c)+ vec c xx(vec a + vec b) = vec 0`
View SolutionProve that if the vectors `vec a, vec b, vec c` satisfy `vec a+ vec b + vec c = vec 0`, then `vec bxx vec c = vec c xx vec a = vec a xx vec b`
View SolutionFor any two vectors `vec a` and `vec b` , prove that `| vec a xx vec b|^(2) = |vec a|^(2)|vec b|^(2) - (vec a . vecb)^(2) = [[veca.veca veca .vecb], [veca.vecb vec b.vecb]]`
View SolutionLet `vec a = hat i + 4 hat j + 2 hat k, vec b = 3 hati - 2 hat j + 7 hat k` and `vec c = 2 hat i - hat j + 4 hat k`.Find a vector `vec d` which is perpendicular to both `vec a` and `vec b` and `vec c.vec d` = 15.
View SolutionConsider the points A(1, 2, 3), B(4, 0, 4) and C(-2, 4, 2).
(a). Find `vec(AB)` and `vec(BC)`
(b) Show that the points A, B, C are collinear.
View SolutionConsider the triangle ABC with vertices A(1, 1, 1) B(1, 2, 3) and C(2, 3, 1).
(a) Find`vec(AB)` and `vec(AC)`
Find `vec (AB) xx vec (AC)`
(c) Hence find the area of the triangle ABC.
View SolutionLet A(2,3, 4) B(4, 3, 2), C(5, 2,-1) be three points
(i) Find AB and BC.
(ii) Find the area of `DeltaABC`
View SolutionFor any three vectors `vec a, vec b , vec c` , show that `vec a xx (vec b + vec c) + vec b xx (vec c + vec a) + vec c xx (vec a + vec b) = 0`
View SolutionGiven A(1,1,1) , B(1, 2, 3) and C(2, 3, 1) are the vertices of `DeltaABC`. Find the area of `DeltaABC`.
View SolutionConsider the triangle ABC with vertices A(1,2,3) , B(-1, 0, 4) and C(0, 1, 2)
(a) Find `vec (AB)` and `vec (AC)`
Find `angle A`.
(c) Find the area of triangle ABC.
View SolutionFind the area of a parallelogram whose adjacent sides are given by the vectors ` -> a=3 hat i+ hat j+4 hat k`and ` -> b= hat i- hat j+ hat k`.
View SolutionFind the area of the parallelogram determined by the vectors `vec a = hat i + hat j + 3 hat k`, `vec b = 3 hat i - 4 hat j + 5 hat k`.
View SolutionConsider the vectors
`vec a = hat i - 7 hat j + 7 hat k, 3 hat i - 2 hat j + 2 hat k`
(a) Find `vec a.vecb`
(b) Find the angle between `vec a` and `vec b`.
View SolutionThe adjacent sides of a parallelogram are `vec a = 3 hat i + lambda hat j + 4 hat k` and `vec b = hat i - lambda hat j + hat k`
(i) Find `vec a xx vec b`
(ii) If the area of the paralleogram is `sqrt 42` square units, find the value of `lambda`.
View SolutionFind the area of a parallelogram for which the vectors `2 hat i + hat j` and `3 hat i + hat j + 4 hatk` are adjacent sides.
View SolutionFind `[vec a, vec b, vec c]` if `vec a = hat i - 2 hat j + 3 hat k`, `vec b = 2 hat i - 3 hat j + hat k` and `vec c = 3 hat i + hat j - 2 hat k`.
View SolutionFind `vec a.(vec b xx vec c)`, if `vec a = 2 hat i + hat j + 3 hat k, vec b = - hat i + 2 hat j + hat k` and `vec c = 3 hat i + hat j + 2 hat k`.
View SolutionShow that the vectors ` vec a = hat i - 2 hat j + 3 hat k, vec b = -2 hat i + 3 hat j - 4 hat k` and `vec c = hat i - 3 hat j + 5 hat k` are coplanar.
View SolutionShow that the vectors `vec a = hat i - 2 hat j + 3 hat k`, `vec b = -2 hat i +3hat j - 4 hat k` and `vec c = hat i - 3 hat j + 5 hat k` are coplanar.
View SolutionConsider the vectors `vec a = hat i + 3 hat j + hat k` ,`vec b = 2 hat i - hat j - hat k` and `vec c = lambda hat i + 7 hat j + 3 hat k`
(i) Find `[ vec a, vec b, vec c]`
(ii) Find the value of `lambda`, if the vectors `vec a, vec b` and `vec c` are coplanar.
View SolutionFind `lambda` if the vectors `hat i - hat j + hat k`, `3 hat i + hat j + 2 hat k` and `hat i + lambda hat j - 3 hat k` are coplanar.
View SolutionConsider the 4 points A, B, C and D with position vectors `4 hat i + 8 hat j + 12 hat k, 2 hat i + 4 hat j + 6 hat k`, `3 hat i + 5 hat j + 4 hat k` and `5 hat i + 8 hat j ++ 5 hat k`.
(i) Find `vec(AB), vec(AC), vec (AD)`
(ii) Show that the 4 points are coplanar.
View SolutionConsider the 4 points A(3, 2, 1) B(4, x, 5) C(4, 2, -2) and D(6, 5, -1)
(i) Find `vec(AB) , vec (AC)` and `vec(AD)`.
(ii) If the points A, B, C and D are coplanar, find the value of x.
View SolutionLet `vec a = hat i + hat j + hat k , vec b = hat i ` and `vec c = c_(1)hat i + c_(2)hat j + c_(3)hat k`. If `c_(1) = 1` and `c_(2) = 2` , find `c_(3)` which makes `vec a, vec b` and `vec c` coplanar.
View SolutionLet `vec a = hat i + hat j + hat k , vec b = hat i ` and `vec c = c_(1)hat i + c_(2)hat j +c_(3)hat k`. Then if `c_(2) = -1` and `c_(3) = 1`, show that no value of `c_(1)` can make `vec a, vec b` and `vec c` coplanar.
View Solution(i)Show that `[ vec a + vec b, vec b + vec c, vec c + vec a] = 2 [vec a vec b vec c]`.
(ii)If `vec a, vec b, vec c` are coplanar, prove that `vec a + vec b, vec b + vec c, vec c + vec a` are also coplanar.
View SolutionShow that the vectors `vec a, vec b` and `vec c` are coplanar if `vec a + vec b, vec b + vec c, vec c+ vec a` are coplanar.
View SolutionFind the volume of a parallelopiped with coterminous edges represented by the vectors `3 hat i + 4 hat j , 2 hat i + 3 hat j + 4 hat k` and `5 hat k`.
View SolutionProve that `[ vec a, vec b, vec c + vec d]` = `[ vec a, vec b, vec c] + [ vec a, vec b , vec d]`.
View SolutionShow that four points with position vectors `6 hat i - 7 hat j, 16 hat i - 19 hat j - 4 hat k`, `3 hat i - 6 hat k` and `2 hat i + 5 hat j + 10 hat k` are not coplanar.
View Solution
Examples questions and complete solutions for chapter VECTOR ALGEBRA of NEW JYOTHI MATHS (TAMIL ENGLISH) of Class 12
All Exercises from NEW JOYTHI PUBLICATION Class 12 MATHS VECTOR ALGEBRA
- ADDITIONAL QUESTIONS FOR PRACTICE 10.1
- ADDITIONAL QUESTIONS FOR PRACTICE 10.2
- ADDITIONAL QUESTIONS FOR PRACTICE 10.3
- ADDITIONAL QUESTIONS FOR PRACTICE 10.4
- ADDITIONAL QUESTIONS FOR PRACTICE 10.5
- CONTINUOUS EVALUATION
- Examples
- OBJECTIVE TYPE QUESTIONS
- SOLUTION TO EXERCISE MISCELLANEOUS EXERCISE
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.1
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.1 (Answer the following as true or false )
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.2
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.3
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.4
- UNIT TEST